On a two-strain epidemic model involving delay equations

1.   Introduction

The notion of indistinguishability operator was introduced by Trillas in 1982 (^[47]). The essential goal for which such operators were introduced was to fuzzify the crisp notion of equivalence relation. Let us recall that, given a t-norm $T$, an indistinguishability operator for $T$ on a (non-empty) set $X$ is a fuzzy binary relation $I:X\times X\rightarrow [0, 1]$ that fulfills for all $x, y, z\in X$ the following conditions:

Of course, we assume that the reader is familiar with the basics of t-norms (see ^[25] for a full treatment of the t-norms theory).

according to ^[25] we say that it is a $T$-equality:

Notice that indistinguishability operators are also known as $T$-fuzzy equivalences in the literature (see, for instance, ^[25]).

It must be pointed out that, given $x, y\in X$, the value $I(x, y)$ can be comprehended as the degree of indistinguishability (or similarity) between $x$ and $y$. Transitivity is crucial in order to interpret indistinguishability operators as a fuzzy version of crisp equivalence relations. Indeed, $T$-transitivity states (note that each t-norm $T$ induces a different fuzzy equivalence relation), through the degree of indistinguishability from $x$ to $y$ and from $y$ to $z$, a lower bound of the degree of indistinguishability from $x$ to $z$, which allows to avoid the celebrated Poincaré paradox (see ^[39] for a deeper discussion). This fact has made these operators very useful in a large number of problems that arise naturally in decision-making, artificial intelligence, and computer science (see, for instance, ^{[1,11,20,21,22,26,34,36,37,39,49,50]}).

Among the different issues studied for these operators, the aggregation problem has been thoroughly explored. In 2002, Pradera, Trillas, and Castiñeira first tackled such a problem (^[38]). Let us recall that, given a t-norm $T$ and $n\in \mathbb{N}$, a function $F: [0, 1]^n \to [0, 1]$ is called an indistinguishability operator aggregation function for $T$ provided that the function $\widetilde{I}: X \times X \to [0, 1]$, defined for all $x, y\in X$ by

is an indistinguishability operator on a non-empty set $X$ for $T$, when $\{I_i\}^n_{i = 1}$ is a collection of indistinguishability operators on $X$ for $T$. A broad description of this kind of functions was conducted in (^[38]). However, in the above reference, only sufficient conditions were given to ensure that a function is an indistinguishability operator aggregation function.

In 2016, Mayor and Recasens were able to yield a characterization of indistinguishability operator aggregation functions in ^[32]. The aforementioned characterization involves the notion of $T$-triangular triplet. Following ^[32], given a $T$-norm, a triplet $(a, b, c)$, with $a, b, c\in [0, 1]^n$, is said to be an $n$-dimensional $T$-triangular triplet provided that

for all $i = 1, \ldots, n$.

In view of the above notion, the aforesaid characterization is provided by Theorem 1.1 below. In order to introduce such a result, let us recall that a function $F:[0, 1]^n \rightarrow [0, 1]$ transforms $n$-dimensional T-triangular triplets into $1$-dimensional T-triangular triplets provided that $(F(a), F(b), F(c))$ is a $1$-dimensional $T$-triangular triplet whenever $(a, b, c)\in [0, 1]^{n}$ is a $n$-dimensional $T$-triangular triplet.

Theorem 1. Let $T$ be a t-norm and $n\in \mathbb{N}$. Then, the following claims are equivalent to each other:

(1) The function $F:[0, 1]^n \rightarrow [0, 1]$ is an indistinguishability operator aggregation function for $T$.

(2) The function $F:[0, 1]^n \rightarrow [0, 1]$ fulfills the following:

(2.1) $F$ transforms $n$-dimensional T-triangular triplets into $1$-dimensional T-triangular triplets.

(2.2) $F(1_{n}) = 1$, where $1_n\in [0, \, 1]^n$ with $(1_n)_i = 1$ for all $i = 1, \ldots, n$.

In ^[24] (see also ^[38,39]), Jacas and Recasens solved the aggregation problem in a more general context. Specifically, the aggregation problem of indistinguishability operators with respect to a collection of t-norms was posed and solved. Notice that, given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{i = 1}$ and a non-empty set $X$, the collection $\{(I_i, T_i)\}^{n}_{i = 1}$ is a family of indistinguishability operators for $\mathcal{T}$ on $X$ provided that, for each $i\in \{1, \ldots, n\}$, $I_i$ is an indistinguishability operator for $T_i$ on $X$. Thus, given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{i = 1}$, a function $F:[0, 1]^n \rightarrow [0, 1]$ is said to be a $\mathcal{T}$-indistinguishability operator aggregation function for $T$ provided that, for every family $\{(I_i, T_i)\}^{n}_{i = 1}$ of indistinguishability operators for $\mathcal{T}$ on a non-empty set $X$, the fuzzy binary relation $\widetilde{I}:X \times X \to [0, 1]$, defined for all $x, y\in X$, by

is an indistinguishability operator for $T$ on $X$. When $T_i = T$ for all $i = 1, \ldots, n$, the above concept recovers as a particular case the concept of indistinguishability operator aggregation function for $T$.

The description yielded in ^[24,38,39] about $\mathcal{T}$-indistinguishability operator aggregation functions is not based on triangle triplets and, thus, differs from the description yielded in Theorem 1.1. Motivated by this fact, Calvo, Fuster-Parra, and Valero extended Theorem 1.1, providing a characterization of $\mathcal{T}$-indistinguishability operator aggregation functions in terms of triangle triplets and related notions in ^[40] (see Theorems 34 and 36 in the aforesaid reference).

In a few applied problems, the notion of indistinguishability operator can be too narrow. In these cases, the degree of similarity or indistinguishability needs to be measured with respect to a parameter. In order to formalize this concept, Miñana and Valero introduced the notion of modular indistinguishability operator in ^[33]. Specifically, given a non-empty set $X$ and a t-norm $T$, a modular indistinguishability operator for $T$ on $X$ is a fuzzy set $E:X\times X\times]0, +\infty[\rightarrow [0, 1]$ satisfying, for all $x, y, z\in X$ and for all $t, s\in]0, +\infty[$, the conditions below:

(MI1) $E(x, x, t) = 1$,

(MI2) $E(x, y, t) = E(y, x, t)$,

(MI3) $T(E(x, y, t), E(y, z, s))\leq E(x, z, t+s)$.

Notice that the value $E(x, y, t)$ yielded by a modular indistinguishability operator can be understood as a measurement of similarity between $x$ and $y$ relative to the parameter $t$. Thus, the greater $E(x, y, t)$, the more similar are $x$ and $y$ relative to $t$.

An instance of this kind of similarities is known as fuzzy metrics in the sense of Kramosil and Michalek (see ^[13,27]). The fact that fuzzy metrics measure with respect to a parameter has been crucial in showing their utility. A recent handbook compiling the latest advances in the study of fuzzy metrics and applications can be found in ^[17]. Chapter 7 is dedicated to expose the latest developments based on the use of such metrics in image processing and in measuring perceptual color differences. However, notice that, in contrast to the concept of modular indistinguishability operator, the axiomatics of fuzzy metrics imposes that the t-norm must be continuous and, in addition, that the function $E_{x, y}:]0, +\infty[\rightarrow [0, 1]$, defined by $E_{x, y}(t) = E(x, y, t)$, must be left-continuous. Again, these impositions can limit their applicability. Recent applications of modular indistinguishability operators to swarm intelligence can be found in ^{[1,19,20,21,22,48]}.

The next example provides an instance of modular indistinguishability operator, which is not a fuzzy metric (see ^[33] for more details).

Example 1. Let $d$ be a metric on a non-empty set $X$. Define the fuzzy set $E^{d}$ on $X\times X\times]0, +\infty[$ by:

It is not hard to check that $E_{d}$ is a modular indistinguishability operator for the product t-norm $T_P$ on $X$ but the function $E^{d}_{x, y}$ is not left-continuous.

The duality relationship between indistinguishability operators and metrics has been explored in detail in the literature. Particularly, techniques to induce indistinguishability operators from metrics, and vice-versa, via additive generators and pseudo-inverses have been studied in ^{[7,8,14,15,18,35,38,39,49]} (see also the references therein). Inspired by these studies, in ^[33], Miñana and Valero investigated the aforesaid duality relationship between modular indistinguishability operators and modular metrics in the sense of ^[5,6]. Hence, those techniques for inducing metrics from indistinguishability operators and vice-versa have been extended to the modular case, and unknown techniques for inducing fuzzy metrics and modular metrics from each other have also been obtained.

In many real-world scenarios, specifically in fields like computer science and artificial intelligence, metrics are not always the best tool for adequately capturing dissimilarity relationships among objects. This limitation has been addressed by Matthews in ^{[28,29,30,31]}, where the metric notion was extended to the notion of relaxed metric. Such new metrics weaken the strict requirement that the distance between distinct points must be positive and even that self-distances must be zero. This new metric notion has found practical applications in several fields like bioinformatics, asymptotic complexity of algorithms, logic programing, parallel computing, and program verification (see ^{[3,23,28,29,30,31,42,43,44,45,46]}).

On account of ^[3,30], a relaxed metric on a non-empty set $X$ is a mapping $d: X \times X \rightarrow \mathbb{R}^{+}$ that fulfills the following properties for all $x, y, z \in X$:

(RM1) $d(x, y) = d(y, x)$,

(RM2) $d(x, y)\leq d(x, z)+d(z, y)$.

The example below yields a sample of relaxed metric that is not a metric.

Example 2. Let $\Sigma^{\infty}$ be the set of all finite and infinite sequences over an alphabet $\Sigma$. Denote by $l(v)$ the length of $v$ with $v\in\Sigma^{\infty}$. Hence, $l(v)\in \mathbb{N}\cup \{\infty\}$ for all $v\in\Sigma^{\infty}$. Set $\Sigma_{F} = \{v\in\Sigma^{\infty}: l(v)\in \mathbb{N}\}$ and $\Sigma_{\infty} = \{v\in\Sigma^{\infty}: l(v) = \infty\}$. Thus, we have that $\Sigma^{\infty} = \Sigma_{F}\cup \Sigma_{\infty}$. Define the function $d_{\Sigma}:\Sigma^{\infty }\times \Sigma^{\infty }\rightarrow [0, 1]$ by $d_{\Sigma}(v, w) = 2^{-l(v, w)}$ for all $v, w\in \Sigma^{\infty}$, where $l(x, y)$ stands for the longest common prefix of $x$ and $y$ [it is clear that $l(x, y) = 0$ when $x$ and $y$ have not any common prefix] and, in addition, we assume that $2^{-\infty} = 0$. It is a simple matter to verify that $d_{\Sigma}$ is a relaxed metric on $\Sigma^{\infty}$. Observe that $d_{\Sigma}(v, v) = 2^{-l(v)}$, which is different from $0$ when $v\in\Sigma_{F}$ and that $d_{\Sigma}(v, w) = 0$ if and only if $u = w\in \Sigma^{\infty}$.

Recently, Bukatin, Kopperman, and Matthews suggested that the logic counterpart of the notion of relaxed metric is a generalized notion of indistinguishability operator (see ^[3,9]). Such a notion of indistinguishability is known as relaxed indistinguishability operator (local indistinguishability operator in ^[2,4]). Recall that, a relaxed indistinguishability operator $E$ for a t-norm $T$ on a non-empty set $X$ is a fuzzy set $E: X\times X \rightarrow [0, 1]$ that fulfills (O2) and (O3). Besides, a relaxed indistinguishability operator fulfills the small-self indistinguishability property (or it is a SSI-relaxed indistinguishability operator) if it satisfies for all $x, y\in X$ the following:

(O4) $E(x, y) \leq E(x, x)$.

Notice that SSI-relaxed indistinguishability operators are called weakly reflexive fuzzy binary relations in ^[34].

The example below shows a relaxed indistinguishability operator that does not hold the SSI property.

Example 3. Set $X = \{1, 2, 3\}$. Define the fuzzy set $E_{X}:X\times X\rightarrow [0, 1]$ by

A straightforward computation yields that $E_{X}$ is a relaxed indistinguishability operator for $T_{P}$ on $X$. In addition, $E_{X}$ does not fulfill the SSI condition because $E_{X}(1, 3) = \frac{1}{2}$ and $E_{X}(1, 1) = \frac{1}{4}$.

The following example provides an instance of SSI-relaxed indistinguishability operator.

Example 4. Consider the set $\Sigma_{F}$ introduced in Example 2. Define the fuzzy set $E_{\Sigma}:\Sigma^{\infty}\times \Sigma^{\infty}\rightarrow [0, 1]$ for all $v, w\in \Sigma^{\infty}$ by $E_{\Sigma}(v, w) = 1-2^{-l(v, w)}$. It is not hard to see that $E_{\Sigma}$ is a SSI-relaxed indistinguishability operator for the t-norm $T_{\min}$ on $\Sigma^{\infty}$.

It is worth mentioning that the relaxed indistinguishability operator given in Example 4 is not an indistinguishability operator, since it does not fulfill condition (O1).

separate points provided that $E(x, y) = E(x, x) = E(y, y) \Rightarrow x = y$ for all $x, y\in X$.

In ^[12], Fuster-Parra, Martín, Miñana, and Valero extended the duality relationship between metrics and indistinguishability operators to the relaxed approach. Concretely, they developed specific techniques for generating from each other relaxed metrics and (SSI-)relaxed indistinguishability operators via the use of additive generators and their associated pseudo-inverses. More recently, in ^[2,4], Calvo and Recasens obtained representation results for relaxed indistinguishability operators, extending those known for classical indistinguishability operators. In ^[40], both the notion of family of indistinguishability operators for a collection of t-norms $\mathcal{T}$ and $\mathcal{T}$-indistinguishability operator aggregation function were proposed in the relaxed context and, in addition, characterizations of such functions were obtained extending Theorem 1.1. Specifically, and according to ^[40], given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{i = 1}$ and a non-empty set $X$, the collection $\{(I_i, T_i)\}^{n}_{I = 1}$ is a family of (SSI-)relaxed indistinguishability operators for $\mathcal{T}$ on $X$ provided that, for each $i\in \{1, \ldots, n\}$, $I_i$ is a (SSI-)relaxed indistinguishability operator for $T_i$ on $X$. Moreover, given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{i = 1}$, a function $F:[0, 1]^n \rightarrow [0, 1]$ is said to be a $\mathcal{T}$-(SSI-)relaxed indistinguishability operator aggregation function for $T$ provided that, for every family $\{(I_i, T_i)\}^{n}_{i = 1}$ of (SSI-)relaxed indistinguishability operators for $\mathcal{T}$ on a non-empty set $X$, the fuzzy set $\widetilde{I}:X \times X \to [0, 1]$, defined for all $x, y\in X$, by

is a (SSI-)relaxed indistinguishability operator for $T$ on $X$. When $T_i = T$ for all $i = 1, \ldots, n$, a $\mathcal{T}$-(SSI-)relaxed indistinguishability operator aggregation function is said to be a $T$-(SSI-)relaxed indistinguishability operator aggregation function.

With the intention of introducing the aforesaid characterizations, we need to recall the following notions. According to ^[40], given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{I = 1}$, a triplet $(a, b, c)\in [0, 1]^n$ is said to be a $n$-dimensional $\mathcal{T}$-triangular triplet provided that $T_i(a_i, b_i)\leq c_i$, $T_i(a_i, c_i)\leq b_i$ and $T_i(b_i, c_i)\leq a_i$ for all $i = 1, \ldots, n$. Moreover, a function $F:[0, 1]^{n}\rightarrow [0, 1]$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet when $(F(a), F(b), F(c)$ is a $T$-triangular triplet if $(a, b, c)$ is a $n$-dimensional $\mathcal{T}$-triangular triplet.

In view of the above notions, the announced characterizations can be stated as follows (see Theorems 30 and 32 in ^[40]).

Theorem 2. Let $n\in \mathbb{N}$. If $\mathcal{T} = \{T_{i}\}_{i = 1}^{n}$ is a collection of t-norms, $T$ is a t-norm and $F:[0, 1]^{n}\rightarrow [0, 1]$ is a function, then the claims below are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-relaxed indistinguishability operator aggregation function for $T$.

(2) $F$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet.

Theorem 3. Let $n\in \mathbb{N}$. If $\mathcal{T} = \{T_{i}\}_{i = 1}^{n}$ is a collection of t-norms, $T$ is a t-norm and $F:[0, 1]^{n}\rightarrow [0, 1]$ is a function, then the claims below are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-SSI-relaxed indistinguishability operator aggregation function for $T$.

(2) The function $F:[0, 1]^n \rightarrow [0, 1]$ fulfills the following:

(2.1) $F$ is monotonic ($F(a)\leq F(b)$ when $a_i \leq b_i$ for all $i = 1, \ldots, n$)..

(2.2) $F$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet.

Observe that every $\mathcal{T}$-SSI-relaxed indistinguishability operator aggregation function is always a $\mathcal{T}$-relaxed indistinguishability operator aggregation function. However, the opposite is generally not true, as the example below shows.

Example 5. Consider the function $F:[0, 1]^2 \to [0, 1]$ defined by

It is not hard to check that $F$ transforms $2$-dimensional $T_D$-triangular triplets into a $T_D$-triangular triplet. Hence, by Theorem 1.2, it is a $T_D$-relaxed indistinguishability operator aggregation. However, it is not monotonic. So, by Theorem 1.3, it is not a $T_D$-SSI-relaxed indistinguishability operator aggregation.

Although some steps have been taken into the study of relaxed indistinguishability operators, many theoretical aspects of this kind of generalized indistinguishability operators remain to be explored at this stage. In particular, the notion of modular indistinguishability operators has not been extended to the relaxed framework.

Inspired, on the one hand, by the utility of measuring with respect to a parameter and, on the other hand, by the importance of the aggregation problem in real-world problems, in this paper we introduce the notion of modular (SSI)-relaxed indistinguishability operator and focus our efforts on the study of the associated aggregation problem. Thus, we introduce the notion of modular (SSI)-relaxed indistinguishability operator aggregation function for a family of t-norms $\mathcal{T}$ extending the counterparts formulated for classical non-modular relaxed indistinguishability operators in ^[40]. Moreover, we provide characterizations of such functions in the spirit of Theorems 2 and 3.

Unlike the non-modular case, the class of those functions fusing modular $\mathcal{T}$-relaxed indistinguishability operators is shown to match the class of $\mathcal{T}$-transitive fuzzy relation aggregation functions (a concept that will be introduced in Section 2). In the case of modular $\mathcal{T}$-SSI-relaxed indistinguishability operators, we get that the class of functions that are able to aggregate them is exactly the class formed by the $\mathcal{T}$-SSI-relaxed indistinguishability operator aggregation functions. Moreover, we get a surprising equivalence of the aforementioned class with the class of those functions merging a special type of modular $\mathcal{T}$-SSI-relaxed indistinguishability operator that we have called monotonic. Furthermore, the differences between the modular and the non-modular aggregation problem are specified and illustrated by means of suitable examples. Finally, conclusions and future work are exposed.

The remainder of the paper is organized as follows. Section 2 is dedicated to exploring the modular $\mathcal{T}$-relaxed indistinguishability operators and the related aggregation problem. Section 3 is devoted to the study of modular $\mathcal{T}$-SSI-relaxed indistinguishability operators and the linked aggregation problem. Finally, Section 4 outlines the conclusions drawn and the future work.

2.   Modular relaxed indistinguishability operators: the aggregation problem

In ^[40], the problem of merging a family of transitive fuzzy relations was addressed. In particular, given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{i = 1}$ and a non-empty set $X$, the collection $\{(I_i, T_i)\}^{n}_{I = 1}$ is a family of transitive fuzzy relations for $\mathcal{T}$ ($\mathcal{T}$-transitive for short) on $X$ when, for each $i\in \{1, \ldots, n\}$, $I_i$ is a fuzzy set on $X\times X$ that is $T_i$-transitive, i.e., it satisfies (O3).

In the same reference, the notion of $\mathcal{T}$-transitive fuzzy relation aggregation function was introduced. Concretely, given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{i = 1}$, a function $F:[0, 1]^n \rightarrow [0, 1]$ is said to be a $\mathcal{T}$-transitive fuzzy relation aggregation function for a t-norm $T$ provided that, for every family $\{(I_i, T_i)\}^{n}_{i = 1}$ of $\mathcal{T}$-transitive fuzzy relation on a non-empty set $X$, the fuzzy set $\widetilde{I}:X \times X \to [0, 1]$, defined for all $x, y\in X$, by

is $T$-transitive. Of course, when $T_i = T$ for all $i = 1, \ldots, n$, a $\mathcal{T}$-transitive fuzzy relation aggregation function is called a $T$-transitive fuzzy relation aggregation function.

The solution to the aggregation problem for transitive fuzzy relations was given by the following result, which characterizes $\mathcal{T}$-transitive fuzzy relation aggregation functions (see Theorem 17 in ^[40]).

Theorem 4. Let $n\in \mathbb{N}$. If $\mathcal{T} = \{T_{i}\}_{i = 1}^{n}$ is a collection of t-norms, $T$ is a t-norm and $F:[0, 1]^{n}\rightarrow [0, 1]$ is a function, then the claims below are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-transitive fuzzy relation aggregation function for $T$.

(2) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$.

Taking into account the preceding information, we face the aggregation problem of modular relaxed indistinguishability operators in the following. For this purpose, we first introduce a few pertinent notions.

Definition 1. Let $X$ be a non-empty set. A modular relaxed indistinguishability operator for a t-norm $T$ on $X$ is a fuzzy set $E:X\times X\times]0, +\infty[\rightarrow [0, 1]$ satisfying, for all $x, y, z\in X$ and for all $t, s\in]0, +\infty[$ the conditions (MI2) and (MI3).

The next example gives an instance of modular relaxed indistinguishability operators.

Example 6. Consider the fuzzy set $E:[0, \infty[\times [0, \infty[\times]0, +\infty[\rightarrow [0, 1]$ defined by $E(x, y, t) = e^{-\frac{\max\{x, y\}}{t}}$ for all $x, y\in [0, \infty]$ and for all $t\in]0, +\infty[$. Then, it is easily seen that $E$ is a modular relaxed indistinguishability operator for the product t-norm $T_P$ on $[0, \infty[$. Observe that $E(x, x)\neq 1$ for all $x\in]0, +\infty[$ and, thus, that $E$ is not a modular indistinguishability operator because it does not fulfills (MI1).

In the following, we set out the previous notion when we count on a collection of t-norms extending the non-modular counterpart introduced in ^[40].

Definition 2. Let $X$ be a non-empty set and let $\mathcal{T} = \{T_i\}^{n}_{i = 1}$ be a collection of t-norms. The collection $\{(E_i, T_i)\}^{n}_{I = 1}$ is a family of modular relaxed indistinguishability operators for $\mathcal{T}$ on $X$ provided that, for each $i\in \{1, \ldots, n\}$, $E_i$ is a modular relaxed indistinguishability operator for $T_i$ on $X$.

The last element necessary to be able to pose the aggregation problem is that of aggregation function.

Definition 3. Let $\mathcal T = \{T_i\}$ be a collection of t-norms and let $T$ be a t-norm. A function $F:[0, 1]^n \rightarrow [0, 1]$ is said to be a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$ if for every family $\{(E_i, T_i)\}^{n}_{i = 1}$ of $\mathcal{T}$-modular relaxed indistinguishability operators on a non-empty set $X$, the fuzzy set $\widetilde{E}:X \times X \times\, ]0, +\infty[\to [0, \, 1]$, defined for all $x, y\in X$ and for all $t\in]0, +\infty[$, by

is a modular relaxed indistinguishability operator for $T$ on $X$.

If $T_i = T$ for all $i = 1, \ldots, n$, then $F$ will be said to be a $T$-modular relaxed indistinguishability operator aggregation function.

From here on out, we describe $\mathcal{T}$-modular relaxed indistinguishability operator aggregation functions in the spirit of Theorems 2 and 3.

Theorem 5. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then the following statements are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$.

(2) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$.

(3) $F$ is a $\mathcal{T}$-transitive fuzzy relation aggregation function for $T$.

Proof. (2) ⇒ (1) Let $\{(I_i, T_i)\}_{i = 1}^n$ be a family of modular relaxed indistinguishability operators for $\mathcal{T}$ on a non-empty set $X$. Clearly, the fuzzy set $\widetilde{E}$ satisfies (MI2). Aiming to show that $\widetilde{E}$ is a relaxed indistinguishability operator for $T$ on $X$, it remains to prove that $\widetilde{E}$ is $T$-transitive. It is obvious that $T_i(E_i(x, y, t), E_i(y, z, s))\leq E_i(x, z, t+s)$ for all $x, y, z\in X$ and for all $t, s\in]0, +\infty[$. Hence, we deduce that $T(\widetilde E(x, y, t)), \widetilde E(y, z, s))\leq \widetilde E (x, z, t+s)$ for $x, y, z\in X$ and for all $t, s\in]0, +\infty[$. So $\widetilde{E}$ is a relaxed indistinguishability operator for $T$ on $X$.

(1) ⇒ (2) Assume that $(a, b, c)\in [0, 1]^n$ with $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$. Consider the set $X = \{x, y, z\}$ where $x, y, z$ are different from each other. Define, for all $i = 1, \ldots, n$, the family of fuzzy sets $\{E_i\}^{n}_{i = 1}$ on $X\times X\times]0, +\infty[$ as follows: $E_i(x, x, t) = E_i(y, y, t) = E_i(z, z, t) = 1$ for all $t\in]0, +\infty[$ and, in addition,

Next, we show that each $E_i$ is a relaxed indistinguishability operator for $T_i$ on $X$. It is enough to prove that each $E_i$ fulfills $T_i$-transitivity, i.e., (MI3). Two cases can be distinguished.

Case 1. $t + s \leq 1$. Then $t, s \leq 1$. Hence, we have that $E_i(u, v, t+s) = E_i(u, v, t) = E_i(u, v, s)$ for all $u, v\in X$. So we obtain

and

for all $u, v\in X$.

Moreover,

for all $u, v, w\in X$ with all different from each other.

Case 2. $t+s > 1$. We consider three possibles subcases.

Case 2.1. $t, s \leq 1$. Then, we have that

and

for all $u, v\in X$. Moreover,

for all $u, v, w\in X$ all different from each other.

Case 2.2. $t\leq 1$ and $s > 1$ (the reasoning is analogous if $s\leq 1$ and $t > 1)$. Then, we obtain that

and

for all $u, v\in X$. Besides,

for all $u, v, w\in X$ all different from each other.

Case 2.3. $t, s > 1$. Then, $E_i(u, v, t+s) = E_i(u, v, t) = E_i(u, v, s)$ for all $u, v\in X$. So we obtain

and

for all $u, v\in X$.

Moreover,

for all $u, v, w\in X$ all different from each other.

Therefore, we have shown that each $E_i$ is a relaxed indistinguishability operator for $T_i$ on $X$ and, hence, that the collection $\{(E_i, T_i)\}^{n}_{i = 1}$ is a family of modular relaxed indistinguishability operators for $\mathcal{T}$ on $X$. Since $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$, we obtain that $\widetilde{E}$ is a modular relaxed indistinguishability operator for $T$ on $X$. Hence, we deduce that

The equivalence (2) ⇒ (3) is warranted by Theorem 4. □

From the former result, we immediately derive the next one when $T_i = T$ for all $i\in \{1, \ldots, n\}$ in the collection $\mathcal{T } = \{T_i\}_{i = 1}^n$.

Corollary 6. Let $n \in \mathbb N$ and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then the following statements are equivalent to each other:

(1) $F$ is a $T$-modular relaxed indistinguishability operator aggregation function.

(2) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T(a_i, b_i)\leq c_i$ for all $i=1, \ldots, n$.

(3) $F$ is a $T$-transitive fuzzy relation aggregation function.

On account of ^[40], given a collection of t-norms $\mathcal{T} = \{T_i\}^{n}_{I = 1}$, a function $F: [0, \, 1]^n \to [0, \, 1]$ dominates a t-norm $T$ with respect to $\mathcal{T} = \{T_i\}_{i = 1}^n$ provided that

for all $a, b \in [0, \, 1]^n$. In the case in which $T_i = T$ for all $i = 1, \ldots, n$, the former notion recovers the classical one in which $F$ dominates the t-norm $T$ (see, for instance, ^[10]).

Bearing in mind the exposed concepts, the next result, which relates all of them, can be found as Proposition 15 in ^[40].

Proposition 7. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F: [0, 1]^n \to [0, 1]$ is a function, then among the claims below (1) ⇒ (2) ⇒ (3) ⇒ (4) ⇒ (5)

(1) $F$ is monotonic and dominates the t-norm $T$ with respect to $\mathcal{T}$.

(2) $F$ is a $\mathcal{T}$-transitive fuzzy relation aggregation function for $T$.

(3) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$.

(4) $F$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet.

(5) $F$ dominates the t-norm $T$ with respect to $\mathcal T$.

Form Theorem 5 and Proposition 7, we get a bit more information about $\mathcal{T}$-modular relaxed indistinguishability operator aggregation functions.

Theorem 8. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F: [0, 1]^n \to [0, 1]$ is a function, then among the claims below (1) $\boldsymbol \Rightarrow$ (2) $\boldsymbol \Rightarrow$ (3) $\boldsymbol \Rightarrow$ (4) $\boldsymbol \Rightarrow$ (5) $\boldsymbol \Rightarrow$ (6).

(1) $F$ is monotonic and dominates the t-norm $T$ with respect to $\mathcal{T}$.

(2) $F$ is a $\mathcal{T}$-transitive fuzzy relation aggregation function for $T$.

(3) $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$.

(4) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$.

(5) $F$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet.

(6) $F$ dominates the t-norm $T$ with respect to $\mathcal T$.

It is worth mentioning that in Proposition 1 of ^[41], it was proved that under the hypothesis of monotony, (6) $\boldsymbol \Rightarrow$ (3). In consequence, it seems natural to wonder whether every $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function is always monotonic and, thus, if the reciprocal of such an implication is always true. However, the following example answers the posed question negatively.

Example 7. Consider the function $F:[0, 1]^2 \to [0, 1]$ defined by

It is routine to verify that $F$ is a $\mathcal T$-modular relaxed indistinguishability operator aggregation function for $T_D$, where $\mathcal T = \{T_1, T_2\}$ is any collection of t-norms. Clearly, $F$ is not monotonic.

Hereinafter, we reveal the role that monotonic functions play in the aggregation of $\mathcal T$-modular relaxed indistinguishability operators. With this in mimd, we need to introduce a special type of modular relaxed indistinguishability operator that we call monotonic.

Definition 4. Let $X$ be a non-empty set. A modular relaxed indistinguishability operator for a t-norm $T$ on $X$, $E:X\times X\times]0, +\infty[\rightarrow [0, 1]$ is called monotonic provided that the function $E_{x, y}:]0, +\infty[\rightarrow [0, 1]$ is monotonic.

The subsequent example yields an instance of monotonic modular relaxed indistinguishability operator.

Example 8. Consider the fuzzy set $E:[0, 1[\times [0, 1[\times]0, +\infty[\rightarrow [0, 1]$ defined by $E(x, y, t) = \max\{x, t, \frac{t}{t+1}\}$. Then, it is an easy task to confirm that $E$ is a modular relaxed indistinguishability operator for $T_D$ on $[0, 1[$. Moreover, it is clear that the function $E_{x, y}:]0, +\infty[\rightarrow [0, 1]$ is monotonic.

Example 6 shows a sample of non-monotonic modular relaxed indistinguishability operator. The example below gives another one.

Example 9. Consider a non-empty set $X$. Define the fuzzy set $E:X\times X\times]0, +\infty[\rightarrow [0, 1]$ by

A straightforward computation gives that $E$ is a modular relaxed indistinguishability operator for the product t-norm $T_p$ on $X$. Nevertheless, fixed $x, y \in X$, the function $E_{xy}:]0, +\infty[\rightarrow [0, 1]$ is not monotonic because $E_{xy}\left(\frac{1}{2}\right) = \frac{1}{4} < \frac{1}{2} = E_{xy} \left(\frac{1}{4} \right)$.

The definition of family of modular monotonic relaxed indistinguishability operators for a collection of t-norms $\mathcal{T}$ and the notion of $\mathcal{T}$-modular monotonic relaxed indistinguishability operator aggregation function for $T$ can be adapted in the obvious way from Definitions 2 and 3, respectively.

When the aggregation is made by means of monotonic functions, we have the surprising characterization given in Theorem 2.7. As a means to state such a result, we need an auxiliary result.

Proposition 9. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F:[0, \, 1]^n \to [0, \, 1]$ is a monotonic function, then the following claims are equivalent to each other:

(1) $F$ dominates the t-norm $T$ with respect to $\mathcal T$.

(2) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$.

(3) $F$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet.

Proof. (1) $\boldsymbol \Rightarrow$ (2). Let $(a, b, c)$, with $a, b, c \in [0, \, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$. The monotony of $F$ gives that

Moreover, $F$ dominates the t-norm $T$ with respect to $\mathcal T$ by assumption, then we obtain that

as claimed.

(2) $\boldsymbol \Rightarrow$ (3). It is evident.

(3) $\boldsymbol \Rightarrow$ (1). Let $a, b \in [0, \, 1]^n$. Then, each $(a_i, b_i, T_i(a_i, b_i))$ is a $T_i$-triangular triplet. By assumption $\left(F(a), \, F(b), \, F(T_1(a_1, b_1), \, \ldots, \, T_n(a_n, b_n)) \right)$ is a $T$-triangular triplet. Hence, we conclude that $F$ dominates the t-norm $T$ with respect to $\mathcal{T}$. □

Theorem 10. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then the following statements are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-modular monotonic relaxed indistinguishability operator aggregation function for $T$.

(2) $F$ is monotonic and $F$ transforms $n$-dimensional $\mathcal T$-triangular triplets into a $T$-triangular triplet.

(3) $F$ is monotonic and $F$ dominates the t-norm $T$ with respect to $\mathcal T$.

Proof. (1) $\boldsymbol \Rightarrow$ (2). First of all, we show that $F$ is monotonic. Let $a, b\in [0, 1]^n$ such that $a\leq b$. Consider a set $X = \{x, y\}$ with $x\neq y$. Define the collection of fuzzy sets $\{E_i\}^{n}_{i = 1}$ on $X\times X\times]0, +\infty[$ by $E_i(x, y, t) = E_i(y, x, t) = a_{i}$ and $E_i(x, x, t) = E_i(y, y, t) = b_{i}$ for all $i = 1, \ldots, n$ and for all $t\in]0, +\infty[$. Then, $\{E_i\}^{n}_{i = 1}$ is a family of monotonic modular relaxed indistinguishability operators for $\mathcal{T}$ on $X$. Then, $\widetilde{E}$ is a monotonic modular relaxed indistinguishability operator for $T$ on $X$. Thus we have that $F(a) = F(E_1, \ldots, E_n)(x, y, 1) = \widetilde{E}_{x, y}(1)\leq \widetilde{E}_{x, y}(2) = F(E_1, \ldots, E_n)(x, x, 1) = F(b)$. Therefore, we get that $F$ is monotonic.

Suppose that $(a, b, c)\in [0, 1]^{n}$ is a $n$-dimensional $\mathcal{T}$-triangular triplet. Fix $X = \{x, y, z\}$ with $x, y, z$ different from each other. Consider the collection of fuzzy sets $\{E_i\}^{n}_{i = 1}$ on $X$ given by $a_i = E_i(x, y, t) = E_i(y, x, t), b_i = E_i(y, z, t) = E_i(z, y, t), c_i = E_i(x, z, t) = E_i(z, x, t)$ and $E_i(x, x, t) = E_i(y, y, t) = E_i(z, z, t) = 1$ for all $i = 1, \ldots, n$ and for all $t\in]0, +\infty[$. Then $\{E_i\}^{n}_{i = 1}$ is a family of monotonic modular relaxed indistinguishability operators for $\mathcal{T}$ on $X$. Hence, we deduce that $\widetilde{E}$ is a monotonic modular relaxed indistinguishability operator for $T$ on $X$. It follows that it is $T$-transitive. Therefore, $(F(a), F(b), F(c))$ is a $1$-dimensional $T$-triangular triplet.

(2) $\boldsymbol \Rightarrow$ (3). It is derived from Proposition 9.

(3) $\boldsymbol \Rightarrow$ (1). Theorem 8 guarantees that $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$. Assume that $\{(E_i, T_i)\}_{i = 1}^n$ is a family of modular $\mathcal T$-monotonic relaxed indistinguishability operators on a non-empty set $X$. Then, $\widetilde{E}$ is a monotonic modular relaxed indistinguishability operator for $\mathcal{T}$ on $X$. Next, we show that $\widetilde{E}_{x, y}$ is a monotonic function for all $x, y\in X$. Indeed, fixed $x, y\in X$ and consider $t, s\in]0, +\infty[$ such that $t\leq s$. Then, we have that $\widetilde{E}_{x, y}(t) = F(E_1(x, y, t), \ldots, E_n(x, y, t))\leq F(E_1(x, y, s), \ldots, E_n(x, y, s)) = \widetilde{E}_{x, y}(s)$. In conclusion, $F$ is a $\mathcal{T}$-modular monotonic relaxed indistinguishability operator aggregation function for $T$.

□

The correspondence between $\mathcal{T}$-modular monotonic relaxed indistinguishability operator aggregation functions and $\mathcal{T}$-modular relaxed indistinguishability operator aggregation functions is given in the below result, which is deduced immediately from Theorems 8, and 10.

Theorem 11. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms, and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then among the following claims (1) $\boldsymbol \Rightarrow$ (2):

(1) $F$ is a $\mathcal{T}$-modular monotonic relaxed indistinguishability operator aggregation function for $T$.

(2) $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$.

Example 7 proves that the implication (2) $\boldsymbol \Rightarrow$ (1) in the statement of the above theorem is not verified in general.

The connection among the $\mathcal{T}$-modular relaxed indistinguishability operator aggregation functions and $\mathcal{T}$- relaxed indistinguishability operator aggregation functions is provided in the following result, which is derived from Theorems 5, 8 and 2.

Theorem 12. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then among the following claims (1) $\boldsymbol \Rightarrow$ (2):

(1) $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$.

(2) $F$ is a $\mathcal{T}$-relaxed indistinguishability operator aggregation function for $T$.

Example 5 shows that the implication (2) $\boldsymbol \Rightarrow$ (1) in the statement of the above theorem is not verified in general. Concretely, it provides an instance of a $T_D$-relaxed indistinguishability operator aggregation function, which is not a $T_D$-modular relaxed indistinguishability operator aggregation function.

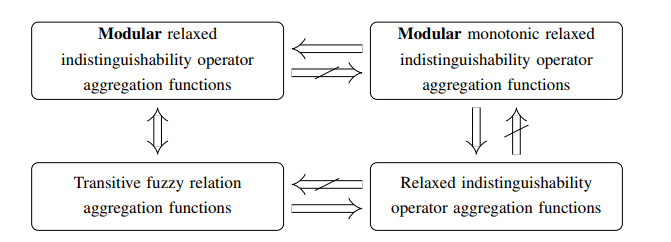
Figure 1 summarizes the relationships found up to this point.

3.   Modular SSI-relaxed indistinguishability operators: the aggregation problem

As exposed in Section 1, the notion of family of SSI-relaxed indistinguishability operators for a collection of t-norms $\mathcal{T}$ was introduced in the literature, and a characterization of $\mathcal{T}$-SSI-relaxed indistinguishability operator aggregation functions was obtained in ^[40] (see Theorem 3). In this section, we introduce such notions in the modular framework and provide a description of the appropriate aggregation functions extending in some sense the aforementioned theorem. With such an objective in mind, we introduce a few pertinent concepts.

Definition 5. Let $X$ be a non-empty set. A modular SSI-relaxed indistinguishability operator for a t-norm $T$ on $X$ is a modular relaxed indistinguishability operator $E:X\times X\times]0, +\infty[\rightarrow [0, 1]$ satisfying the condition $E(x, y, t)\leq E(x, x, t)$ for all $x, y, z\in X$ and for all $t\in]0, +\infty[$.

From the previous notion, we retrieve the notion of SSI-relaxed indistinguishability operator given in Section 1.

Example 6 gives an instance of modular SSI-relaxed indistinguishability operator.

Definition 6. Let $X$ be a non-empty set and let $\mathcal{T} = \{T_i\}^{n}_{i = 1}$ be a collection of t-norms. The collection $\{(E_i, T_i)\}^{n}_{i = 1}$ is a family of modular SSI-relaxed indistinguishability operators for $\mathcal{T}$ on $X$ provided that, for each $i\in \{1, \ldots, n\}$, $E_i$ is a modular SSI-relaxed indistinguishability operator for $T_i$ on $X$.

Next, we adapt the notion of aggregation function.

Definition 7. Let $\mathcal T = \{T_i\}$ be a collection of t-norms and let $T$ be a t-norm. A function $F:[0, 1]^n \rightarrow [0, 1]$ is said to be a $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation function for $T$, if for every family $\{(E_i, T_i)\}^{n}_{i = 1}$ of $\mathcal{T}$-modular SSI-relaxed indistinguishability operators on a non-empty set $X$, the fuzzy set $\widetilde{E}:X \times X \times\, ]0, +\infty[\to [0, \, 1]$, defined for all $x, y\in X$ and for all $t\in]0, 1[$ by

is a modular SSI-relaxed indistinguishability operator for $T$ on $X$.

If $T_i = T$ for all $i = 1, \ldots, n$, then $F$ will be said to be a $T$-modular SSI-relaxed indistinguishability operator aggregation function.

Similar to the non-SSI case, there are modular SSI-relaxed indistinguishability operators that are not monotonic, as the next example shows.

Example 10. Consider a non-empty set $X$. Define the fuzzy set $E:X\times X\times]0, +\infty[\rightarrow [0, 1]$ by

It is immediate that $E$ is a modular SSI-relaxed indistinguishability operator for the drastic t-norm $T_D$ on $X$. Next, fix $x \in X$. Then, the function $E_{xx}:]0, +\infty[\rightarrow [0, 1]$ is not monotonic due to the fact that $E_{xx}\left(\frac{1}{4}\right) = \frac{1}{2} > \frac{1}{4} = E_{xx} \left(1 \right)$.

The posterior result yields a full description of $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation functions.

Theorem 13. Let $n \in \mathbb N$, let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then the following claims are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation function for $T$.

(2) $F$ is monotonic and $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$

(3) $F$ is monotonic and $F$ transforms $n$-dimensional $\mathcal T$-triangular triplet into a $T$-triangular triplet.

(4) $F$ is monotonic and $F$ dominates the t-norm $T$ with respect to $\mathcal T$.

(5) $F$ is a $\mathcal{T}$-SSI-relaxed indistinguishability operator aggregation function for $T$.

(6) $F$ is a $\mathcal{T}$-modular monotonic relaxed indistinguishability operator aggregation function for $T$.

(7) $F$ is a $\mathcal{T}$-modular monotonic SSI-relaxed indistinguishability operator aggregation function for $T$.

Proof. (1) $\boldsymbol \Rightarrow$ (2). The arguments to those applied to the proof of (1) $\boldsymbol \Rightarrow$ (2) in Theorem 5 remain valid to show that $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_i(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$.

Next, assume that $a, b\in [0, 1]^n$ with $a\leq b$. Consider the modular relaxed indistinguishability operator constructed in the proof of (1) $\boldsymbol \Rightarrow$ (2) in Theorem 10, i.e., the collection of fuzzy sets $\{E_i\}^{n}_{i = 1}$ on $X\times X\times]0, +\infty[$ defined by $E_i(x, y, t) = E_i(y, x, t) = a_{i}$ and $E_i(x, x, t) = E_i(y, y, t) = b_{i}$ for all $i = 1, \ldots, n$ and for all $t\in]0, +\infty[$, where $X = \{x, y\}$ with $x\neq y$.. It is clear that $\{(E_i, T_i)\}^{n}_{i = 1}$ is a family of modular SSI-relaxed indistinguishability operators for $\mathcal{T}$ on $X$. Then, $\widetilde{E}$ is a modular SSI-relaxed indistinguishability operators for $T$ on $X$. Thus, $F(a) = \widetilde{E}(x, y, t)\leq \widetilde{E}(x, x, t) = F(b)$.

(2) $\boldsymbol \Rightarrow$ (1). Let $\{(E_i, T_i)\}_{i = 1}^n$ be a family of modular SSI-relaxed indistinguishability operators for $\mathcal{T} = \{T_i\}_{i = 1}^n$ on $X$. It is obvious that the fuzzy set $\widetilde{E}$ satisfies (MI2). By Theorem 5, we deduce that $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T$ and, thus, $\widetilde{E}$ is a modular relaxed indistinguishability operator aggregation function for $T$ on $X$. It remains to prove that $\widetilde{E}$ is a modular SSI-relaxed indistinguishability operator for $T$ on $X$. On the one hand, we have that $E_i(x, y, t)\leq E_i(x, x, t)$ for all $x, y\in X$, for all $t\in]0, +\infty[$ and for all $i = 1, \ldots, n$ and, on the other hand, $F$ is monotonic. Then

for all $x, y\in X$ and for all $t\in]0, +\infty[$. Accordingly, we have shown that $\widetilde{E}$ is a modular SSI-relaxed indistinguishability operator for $T$ on $X$, as claimed.

The equivalences (2) $\boldsymbol \Leftrightarrow$ (3)$\boldsymbol \Leftrightarrow$ (4)$\boldsymbol \Leftrightarrow$ (5)$\boldsymbol \Leftrightarrow$ (6) are assured by Proposition 9 and Theorems 10 and 3.

(6) $\boldsymbol \Rightarrow$ (7). Consider a family $\{(E_i, T_i)\}^{n}_{i = 1}$ of $\mathcal{T}$-modular monotonic SSI-relaxed indistinguishability operator on a non-empty set $X$. Then, $\widetilde{E}$ is a modular monotonic relaxed indistinguishability operator for $T$ on $X$. It remains to prove that it is a modular monotonic SSI-relaxed indistinguishability operator. Theorem 10 gives that $F$ is monotonic. Since $E_i(x, y, t)\leq E_i(x, x, t)$ for all $x, y\in X$, for all $t\in]0, +\infty[$ and for all $i = 1, \ldots, n$ we get that

for all $x, y\in X$ and for all $t\in]0, +\infty[$. So $\widetilde{E}$ is a modular monotonic SSI-relaxed indistinguishability operator for $T$ on $X$.

(7) $\boldsymbol \Rightarrow$ (3). Let $a, b\in [0, 1]^n$ such that $a\leq b$. Consider, again, the set $X = \{x, y\}$ with $x\neq y$ and the collection of fuzzy sets $\{E_i\}^{n}_{i = 1}$ on $X\times X\times]0, +\infty[$ by $E_i(x, y, t) = E_i(y, x, t) = a_{i}$ and $E_i(x, x, t) = E_i(y, y, t) = b_{i}$ for all $i = 1, \ldots, n$ and for all $t\in]0, +\infty[$. Then, $\{E_i\}^{n}_{i = 1}$ is a family of monotonic modular SSI-relaxed indistinguishability operators for $\mathcal{T}$ on $X$. Then, $\widetilde{E}$ is a monotonic modular SSI-relaxed indistinguishability operator for $\mathcal{T}$ on $X$. Thus, we have that $F(a) = F(E_1, \ldots, E_n)(x, y, 1) = \widetilde{E}_{x, y}(1)\leq \widetilde{E}_{x, y}(2) = F(E_1, \ldots, E_n)(x, x, 1) = F(b)$. Therefore, we get that $F$ is monotonic.

Suppose that $(a, b, c)\in [0, 1]^{n}$ is a $n$-dimensional $\mathcal{T}$-triangular triplet. Fix $X = \{x, y, z\}$ with $x, y, z$ different from each other. Consider the collection of fuzzy sets $\{E_i\}^{n}_{i = 1}$ on $X$ constructed in (1) $\boldsymbol \Rightarrow$ (2) of the proof of Theorem 10, that is, the collection $\{E_i\}^{n}_{i = 1}$ given by $a_i = E_i(x, y, t) = E_i(y, x, t), b_i = E_i(y, z, t) = E_i(z, y, t), c_i = E_i(x, z, t) = E_i(z, x, t)$ and $E_i(x, x, t) = E_i(y, y, t) = E_i(z, z, t) = 1$ for all $i = 1, \ldots, n$ and for all $t\in]0, +\infty[$. Then, $\{E_i\}^{n}_{i = 1}$ is a family of monotonic modular SSI-relaxed indistinguishability operators for $\mathcal{T}$ on $X$. Hence, we deduce that $\widetilde{E}$ is a monotonic modular relaxed indistinguishability operators for $T$ on $X$. It follows that it is $T$-transitive. Therefore, $(F(a), F(b), F(c))$ is a $1$-dimensional $T$-triangular triplet.

□

In the particular case in which $T_i = T$ for all $i\in \{1, \ldots, n\}$ in the collection $\mathcal T = \{T_i\}_{i = 1}^n$, we deduce from the above theorem the next corollary.

Corollary 14. Let $n \in \mathbb N$ and let $T$ be a t-norm. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then the following claims are equivalent to each other:

(1) $F$ is a $T$-modular SSI-relaxed indistinguishability operator aggregation function.

(2) $F$ is monotonic and $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$

(3) $F$ is monotonic and $F$ transforms $n$-dimensional $T$-triangular triplet into a $T$-triangular triplet.

(4) $F$ is monotonic and $F$ dominates the t-norm $T$.

(5) $F$ is a $T$-SSI-relaxed indistinguishability operator aggregation function.

(6) $F$ is a $T$-modular monotonic relaxed indistinguishability operator aggregation function.

(7) $F$ is a $T$-modular monotonic SSI-relaxed indistinguishability operator aggregation function.

Figure 2 summarizes the aforementioned results.

It seems natural to question what is the interconnection between the $\mathcal{T}$-modular relaxed indistinguishability operator aggregation functions and $\mathcal{T}$-modular relaxed SSI-indistinguishability operator aggregation functions. Theorems 5 and 13 ensure that every $\mathcal{T}$-modular relaxed SSI-indistinguishability operator aggregation function is always a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function. Example 7 shows that the opposite is not generally fulfilled. Nonetheless, the situation is very different when the minimum t-norm $T_{\min}$ is involved. In this direction, we have the interesting equivalence provided by Theorem 16.

In ^[40], the next equivalence was proved as Theorem 40.

Theorem 15. Let $n\in \mathbb{N}$ and let $\mathcal{T} = \{T_{i}\}_{i = 1}^{n}$ be a collection of t-norms. If $F:[0, 1]^{n}\rightarrow [0, 1]$ is a function, then the next assertions are equivalent:

(1) $F$ is monotonic and $F$ dominates the t-norm $T_{\min}$ with respect to $\mathcal{T}$.

(2) $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_{\min}(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$

(3) $F$ transforms $n$-dimensional $\mathcal{T}$-triangular triplets into $1$-dimensional $T_{\min}$-triangular triplets.

In the light of the former theorem, we get the announced equivalence below.

Theorem 16. Let $n \in \mathbb N$ and let $\mathcal T = \{T_i\}_{i = 1}^n$ be a collection of t-norms. If $F: [0, \, 1]^n \to [0, \, 1]$ is a function, then the following claims are equivalent to each other:

(1) $F$ is a $\mathcal{T}$-modular relaxed indistinguishability operator aggregation function for $T_{\min}$.

(2) $F$ is a $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation function for $T_{\min}$.

Proof. (1) $\boldsymbol \Rightarrow$ (2). By Theorem 5, we have that $T(F(a), F(b))\leq F(c)$ whenever $a, b, c\in [0, 1]^n$ such that $T_{\min}(a_i, b_i)\leq c_i$ for all $i = 1, \ldots, n$. By Theorem 15, we deduce that $F$ is monotonic and $F$ dominates the t-norm $T_{\min}$ with respect to $\mathcal{T}$. Theorem 13 gives that $F$ is a $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation function for $T_{\min}$.

(2) $\boldsymbol \Rightarrow$ (1). By Theorems 5 and 13. □

4.   Conclusions and future work

The notion of modular indistinguishability operator was introduced in the literature with the aim of extending the concept of similarity but measuring with respec to a parameter. Such operators have shown to be useful in several applications, but many theoretical aspects remain to be studied.

In this paper, we have extended to the modular approach the notion of (SSI)-relaxed indistinguishability operator when a collection of t-norms $\mathcal{T}$ is involved. Since the aggregation problem for the non-modular version of such indistinguishability operators have been posed and solved in the literature recently (Theorems 2 and 3), we have addressed the aggregation problem for the modular ones.

Hence we have introduced for the first time the notion of modular (SSI)-relaxed indistinguishability operator aggregation function with respect to a collection of t-norms $\mathcal{T}$, that is, those functions that allow to merge this new type of indistinguishability operators. We have obtained characterizations of such functions. In particular, Theorem 5 states that $\mathcal{T}$-modular relaxed indistinguishability operator aggregation functions are exactly the $\mathcal{T}$-transitive fuzzy relation aggregation functions introduced in ^[40] and, thus, that these functions transform a very special kind of $n$-dimensional $\mathcal{T}$-triangular triplet into $1$-dimensional $T$-triangle triplets (where $T$ is a t-norm). Moreover, Theorem 13 provides a characterization of $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation functions, showing that such functions must be monotonic, and transforms ordinary $n$-dimensional $\mathcal{T}$-triangular triplets into $1$-dimensional $T$-triangular triplets. Therefore, the class of $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation functions coincides with the class formed by their non-modular counterparts. Furthermore, it has been proved that $\mathcal{T}$-modular SSI-relaxed indistinguishability operator aggregation functions are able to merge a special type of modular relaxed indistinguishability operators that we have called monotonic. We have shown, in addition, that every $\mathcal{T}$-relaxed SSI-indistinguishability operator aggregation function is always a $\mathcal{T}$-relaxed indistinguishability operator aggregation function but that the opposite is not true. However, we have discovered that both types of functions are the same when the minimum t-norm is involved.

In the literature, one can find a special type of (SSI)-relaxed indistinguishability operators, which are said to be separate points. The aggregation problem associated with this type of indistinguishability operators was explored in ^[16]. As a future work, we plan to introduce the modular counterpart of these indistinguishability operators, to describe the functions that are capable to merge them and, finally, to explore the existing interconnection between the modular (SSI)-relaxed indistinguishability operator aggregation problem and the corresponding problem in which the operators separate points.

Author contributions

Maria del Mar Bibiloni-Femenias: Investigation, Writing–original draft; Oscar Valero: Conceptualization, Investigation, Writing–review & editing, Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is part of project PID2022-139248NB-I00 funded by MICIU/AEI/10.13039/501100011033 and ERDF/EU.

The authors wish to express their gratitude to Dr. Juan José Miñana for many stimulating conversations which have helped us to improve the content of this paper.

Conflict of interest

Prof. O. Valero is an editorial board member for AIMS Mathematics and was not involved in the editorial review and the decision to publish this article. The authors declare no conflict of interest in this paper.