Multi-modal feature selection with self-expression topological manifold for end-stage renal disease associated with mild cognitive impairment

1.   Introduction

As an important green and clean building material, RMC is extensively applied in modern civil engineering, which can effectively reduce the pollution of dust and noise on construction sites. In terms of technological processes, RMC has the characteristics of plant production, centralized mixing, mechanized transportation and three-dimensional pumping, which can help enhance construction quality and efficiency. In terms of social benefits, it has the advantages of resource conservation, green production and carbon emission reduction, which can help promote construction sustainable development.

In the construction of large-scale plane foundations in urban public buildings, such as the China National Stadium, Winter Olympic venues, Daxing International Airport and etc., a huge amount of RMC needs to be continuously delivered to the construction site with a strict time window. Meanwhile, RMC plants are usually scattered and located far from the city center. The production and transportation capacity of single RMC plant cannot meet the project requirements. Thus, the problem of collaborative supply of multiple RMC plants has become increasingly prominent.

As a special building material, RMC has the following characteristics: 1) production: make-to-order, no inventory; 2) transportation: loaded into the RMC truck immediately after mixing completed, almost no waiting time; unique shipping destination, no mixed loading; and 3) pouring: pumped as continuously as possible and completed before the initial setting, the idle time of the equipment has an upper limit. Due to the time-sensitivity of RMC, continuous operation of production, transportation and pouring should be required. Otherwise, it may cause quality defects such as cold joints, or even construction accidents.

With the increased number of projects under construction at present, there comes the situation that in the meantime the RMC plant processes orders from different projects, and one construction site is supplied by multi-plants. To give full play to the excellent performance of the RMC structure, ensure the quality of construction products and improve work efficiency, it is necessary to integrate the production resources available and reasonably arrange the collaborative production and transportation to meet the requirements of construction sites. This has become an important topic for RMC plants and construction enterprises in recent years which also received extensive attention from international scholars ^[1]. For the RMC vehicle scheduling problem, many studies have been conducted to improve transportation efficiency which provide the scientific basis ^{[1, 2, 3, 4, 5, 6]}. However, most of the existing studies are from the view of single RMC plant operation. The integration of different RMC plants to achieve collaboratively supply has not been thoroughly studied yet.

Production and transportation collaborative scheduling of RMC is a kind of multi-stage joint decision problem which focuses on the operational level of supply chain. As early as 1996, Thomas and Griffin ^[7] pointed out the importance of coordinated production and transportation scheduling in supply chain management. Related research has gradually increased over the past decade. Chen et al. ^[8], Wang et al. ^[9] and Moons et al. ^[10] reviewed that research progress. Given the complex nature of the problem, heuristic methods and genetic algorithms can provide efficient computational insights. Different from other algorithms, GA search from one population of solutions to another, rather than from individual to individual. Random chromosome mutations also help to solve the problem more broadly. Genetic algorithms were widely used to solve the distribution problem of supplying multiple construction sites ^{[11, 12]}. However, the limitation of GA is that certain problems are hard to present in the form of chromosomal coding ^[13]. For addressing this issue, a double-layer coding is designed in the paper according to the corresponding relationships between the RMC factory and the construction site which performs roulette selection and different evolutionary operations respectively. The method decreases the decoding complexity and improving the diversity of feasible solutions.

This paper focuses on the coordinated supply of multiple RMC plants, and a collaborative scheduling model for RMC production and transportation (CS-RMCPT) is established. For solving procedure, an improved double chromosome synchronous evolution genetic algorithm is designed and programmed to find the optimization scheme with the minimum interrupted pouring time and the shortest total path. Furthermore, data experiments are performed on two scenarios, conventional basic engineering and large-scale basic engineering, then compared with experience values. The results show that the scheduling scheme of the model and algorithm is better than the empirical output under both scenarios. It proves that the synergistic scheduling optimization method can satisfy the interruption pouring time and the initial condensation time and ensure the timely supply of RMC on the construction site.

The remainder of this paper is organized as follows. Section 2 summarizes the existing RMC supply chain research, including order scheduling, RMC production, and transportation scheduling. In Section 3, a model for coordinated supply of multi-RMC plants considering the interruption of pouring time and fuel consumption is established. In Section 4, an improved genetic algorithm with double chromosome synchronous evolution is designed. Two kinds of project cases are introduced in Section 5 to verify the proposed model and algorithm through data experiments. Finally, Section 6 gives the general conclusions and future research.

2.   Literature review

To improve the supply efficiency of RMC, a lot of work has been done which focuses on transportation scheduling and optimization to meet the practical needs of plant operation.

2.1.   Single RMC plant supply

From the perspective of single plant operation, research results have been accumulated so far to study the production and transportation scheduling of RMC, especially the latter.

The researchers used Fast messy genetic algorithms and Cyclone simulation technology to meet the requirements of continuous pouring and then optimized the waiting time of vehicles at the same time. Yan et al. ^{[2, 3]} integrated the production of RMC and vehicle scheduling to establish a model and used spatio-temporal network technology to evolve the problem into a mixed-integer network flow problem with boundary conditions. On this basis, the emergency of failure at the production point was considered. Durbin and Hoffman ^[14] established a spatio-temporal network model for the problem and solved the problem using a network flow optimization method with tabu search and cost minimization. Lin et al. ^[15] established the vehicle scheduling model based on the job shop scheduling problem. Maghrebi et al. ^[1] proposed a time-series genetic algorithm for the distribution of large-scale RMC vehicles and proved its robustness through a large number of data experiments. Gaikwad and Thakare ^[16] developed a genetic algorithm user interface model in Matlab which was used to get an uninterrupted scheduling plan for RMC and to reduce the waiting time. Yan et al. ^[17] built a mixed-integer network flow model based on the problem of scheduling plan adjustment caused by temporary agitator failure during transportation and used numerical programming to solve it. Nuntana and Wuthichai ^[18] used the bee colony algorithm to optimize the scheduling problem of RMC trucks from a single mixing station to multiple construction sites. The goal was to minimize the total waiting time of RMC trucks. Cai ^[19] designed a multi-objective genetic algorithm to solve the scheduling problem of RMC vehicles while optimizing the idle waiting time on the construction site and the waiting time of RMC trucks at the construction site. The shortcoming is that the delivery time and unloading time of the RMC trucks are estimated based on past delivery experience, which is not accurate enough. Wu ^[20] established a vehicle scheduling model to minimize transportation costs and balance the workload of drivers and solved it through an ant colony algorithm to obtain a task dispatching solution. Gao ^[21] considered the constraints of multiple vehicles, capacity, total operating time, and customer demand time window, and designed a two-stage heuristic algorithm to solve the dynamic delivery problem of RMC. The disadvantage is that the multi-parking problem and the driver's rest time window are not considered in the dynamic environment. Xu ^[4] established a vehicle scheduling model to maximize the profit of the mixing station, used a genetic algorithm to solve the model, and obtained the vehicle scheduling plan that minimizes the downtime waiting time and the RMC truck waiting time for unloading. Liang ^[22] established a concrete vehicle scheduling optimization strategy, solved the specific cases with genetic algorithms, and verified the effectiveness of the model and algorithm.

2.2.   Coordinated supply of multiple RMC plants

In comparison to the above research from the view of single RMC plant, there are fewer studies in terms of the coordinated supply of multiple RMC plants. Matsatsinis ^[23] studied the distribution of RMC for multiple construction sites under time window constraints. Yang et al. ^[6] established a multi-objective optimal delivery model with time window constraints and demand delay attributes, improved the encoding method of genetic algorithm according to the characteristics of the model, and optimized the waiting time of multi-plants and multi-site RMC transportation. Liu et al. ^[24] studied the collaborative supply mode of multiple mixing plants. Naso et al. ^[25] combined the construction heuristic algorithm and genetic algorithm to model and solve the distribution problem. Schmid et al. ^[26] used mixed-integer linear programming and variable neighborhood search methods to generate and optimize feasible solutions. Liu et al. ^[27] proposed a spatio-temporal network model that integrates production and vehicle scheduling for the situation of multiple RMC plants and designed a heuristic algorithm embedded with 8 sets of joint priority rules to solve the problem. Wu ^[28] built a model of distribution vehicle scheduling in RMC plants centered on distribution stations. The simulated anneal-particle swarm optimization algorithm was used to solve the vehicle scheduling model, and the optimal cost and cost variation range were obtained, which solved the vehicle scheduling problem centered on the distribution station. Considering limited traveling, casting time, number of trucks, allowable weight for transfer and distance from multiple RMC plants to different construction sites, Srichandum and Pothiya proposed an improved ant colony optimization algorithm to generate RMC vehicle scheduling plans with multiple plants and sites to minimize transportation costs ^[29]. Yang et al. ^[30] established a mathematical model aimed at the collaborative distribution of transport vehicles waiting for pouring at multiple construction sites and used an improved double-layer operator coding genetic algorithm to solve the model, which effectively reduced the waiting time of transport vehicles and construction sites.

Most of the above-mentioned research studies are focused on the vehicle distribution scheduling in the transportation link which has little consideration on the production processes in the factory and pouring processes on construction site.

2.3.   Order scheduling

The practical production operation of the precast industry is make-to-order (MTO) ^[31]. In the existing research results, order scheduling mainly focuses on the process industry, solving the problem of order assignment, acceptance or rejection and plant selection, which can be employed to explore new perspectives on the collaborative scheduling of RMC production and transportation.

In 1995, Dawood ^[31] first mentioned the uniqueness of the RMC industry and used the theory of workshop scheduling method to automatically generate production scheduling plans. At the strategic level, Mahdokht et al. ^[32] established a multi-layer decision support system to support the order acceptance/rejection decision under the mixed mode of make-to-stock production and make-to-order production. Weiszer et al. ^[33] developed a discrete-event simulation model with input parameters as a decision tool to select an appropriate vehicle scheduling strategy for the RMC delivery process to reduce vehicle waiting time and station idle time. At the operational level, Kianfar et al. ^[34] designed four order dispatch rules for the production environment with dynamic order arrival to minimize the order rejection cost and delay time. Abdollahpour and Rezaian ^[35] designed a cloud-based simulated annealing algorithm and artificial immune algorithm for a waiting-free hybrid flow shop environment with capable machines. In terms of concrete supply management, Liu et al. ^[24] established a supply-demand balance table and solved the optimal distribution plan for collaborative supply. Zhang et al. ^[36] proposed a rescheduling strategy and a hybrid heuristic algorithm to realize the re-arrangement of ready-mix trucks in response to dynamic customer needs. Maghrebi et al. ^[1] designed a two-stage sequential heuristic algorithm to solve the problem of plant resource allocation and vehicle scheduling. Guo et al. ^[37] proposed a more realistic objective function in the vehicle scheduling algorithm, using an improved particle swarm optimization algorithm to provide a solution to the dynamic changes of temporarily increasing or canceling orders, and increasing or decreasing the number of available pump trucks. Chen et al. ^[38] proposed a two-step coordination approach that uses a 4D model to monitor demand fluctuations and then a Covariance Matrix Adaptation Evolution Strategy (CMA-ES) heuristic evolutionary algorithm was used to modify the original order when demand fluctuations occur. The construction site priority rules, the RMC production plant priority rules, and the allocation rules were introduced into the scheduling model.

With few numbers of published studies on multi-plant collaborative supply from the perspective of global optimization, to meet the practical requirements for the time continuity of pouring operation, it is necessary to establish relevant optimization model and solution algorithm considering the transportation capacity of different RMC plants and the pumping requirement of the construction site and to conduct useful theoretical exploration and engineering and application.

3.   Problem description and mathematical model

3.1.   Parameters

The symbols used in this paper are defined as below:

$I$ number of ready-mixed concrete plants

$J$ number of construction sites

$R_{i}$ ready-mixed concrete plant i, $i=1, 2, \cdots, I$

$C_{j}$ construction sites j, $j=1, 2, \cdots, J$

$D_{j}$ order demand for ready-mixed concrete on $C_{j}$

$G$ carrying capacity of ready mixed concrete trucks

${d_{jk}}$ sub orders in units of single-vehicle decomposed by $D_{j}$, $k=1, \cdots, \left[\frac{D_{j}}{G}\right]$

$S T_{d jk}^{v}$ vehicle starting time of ${d_{jk}}$

$W T_{d_{j k}}^{v}$ vehicle waiting time of ${d_{jk}}$

$E T_{d_{jk}}^{v}$ vehicle arriving time of ${d_{jk}}$ at the construction site

$S T_{d_{ j k}}^{p}$ pumping start time of ${d_{jk}}$

$W T_{d_{j k}}^{p}$ pumping interruption time of ${d_{jk}}$

$E T_{d_{jk}}^{p}$ end time of pumping ${d_{jk}}$

$B T d_{j k}$ vehicle return time to the plant of ${d_{jk}}$

$V_{i}$ number of vehicles owned by $R_{i}$

$V_{i}^{u}$ number of available vehicles for $R_{i}$

$L T$ loading time of ready-mixed concrete truck

$U T$ unloading time of ready-mixed concrete truck

$C T$ cleaning and preparation time of ready-mixed concrete truck

$T S_{ij}$ transportation time from $R_{i}$ to $C_{j}$

${ IST }$ initial setting time of ready-mixed concrete

$IT$ maximum allowable interruption time of ready-mixed concrete pouring

$P T_{j}$ demand-supply time of ready-mixed concrete based on $C_{j}$

$S$ total mileage per day of the ready-mixed concrete truck

$f_{e}$ fuel consumption per kilometer of the ready-mixed concrete truck

$p_e$ fuel price

$p_{z}$ penalty coefficient for early arrival of the ready-mixed concrete truck

$p_{w}$ penalty coefficient for late arrival of the ready-mixed concrete truck

3.2.   Problem description

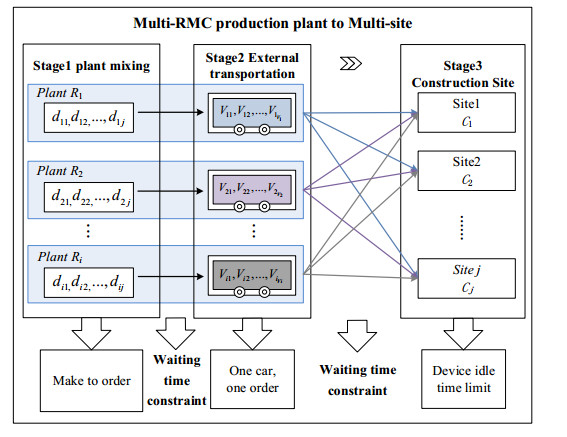
The problem considered in the paper can be described as follows: There are J planned projects which are located at the site $C_{1}, C_{2}, \cdots, C_{j}$ with the demand for RMC $D_{1}, D_{2}, \cdots D_{j}$ and the start time $P T_{1}, P T_{2}, \cdots, P T_{j}$, $j=1, 2, \cdots, J$. There are I RMC plants in the supply area, namely $R_{1}, R_{2, }, \cdots, R_{j}$, $i=1, 2, \cdots, I$, which has $V_{i}$ RMC trucks and the delivery time from $R_{i}$ to $C_{j}$ is $T S_{ij}$. By reasonably allocate the order demand of each construction site to meet the constraints of initial setting time, pumping interval, and transportation capacity, the optimization schedule is to be achieved to minimize the total cost which include the fuel consumption cost, the penalty cost of interruption pumping and vehicle waiting time. The production, transportation, and pouring process of the RMC are illustrated in Figure 1 and the problem assumptions is shown as follows:

● The RMC trucks have the same capacity;

● The transportation time is constant;

● Pumping is the only on-site unloading method;

● The RMC plant has sufficient production capacity;

● The RMC truck must be cleaned after pumping, and the cleaning time is constant;

● The concrete is the same type for one construction site.

3.3.   Critical time calculation

Step 1: Decoding the chromosomes that have been synchronously evolved through the genetic algorithm to obtain the delivery sequence from each RMC plant to each construction site, and number each RMC truck $k$ set from the plant $i$ to the construction site $j$.

Step 2: Calculating the ideal departure time of each vehicle, that is, for vehicles sent to the same construction site, the next vehicle just arrived when the pouring of the previous vehicle was completed.

$S T_{d_{j 1}}^{v}$ represents the ideal departure time of the first vehicle on the construction site, $P T_{j}$ represents the earliest pouring time required by the construction site $j$, and $T S_{i j}$ represents the transportation time from the plant $i$ to the construction site $j$.

Step 3: Correcting the departure time. The ideal departure time of step 2 is the optimal departure time under the assumption that there are sufficient RMC trucks in the plant. However, in actual situations, there may be no available vehicles in the plant at the ideal departure time. At this time, correct the actual departure time. That is, the actual departure time is the earliest return time of the vehicle plus vehicle cleaning time and mixed loading time.

$S T_{d_{j k}}^{v}$ represents the actual departure time of the $k$ vehicle on the construction site $j$, and $\min B T_{d_{ik}}$ represents the earliest return time of the $k$ vehicle from the site $j$.

Step 4: Calculating the time when the vehicle arrives at the construction site, the time when pumping starts, the time when pumping ends, and the time when the vehicle is returned to the plant.

According to the actual departure time $S T_{d j k}^v$, the time when the vehicle arrives at the construction site $E T_{d j k}^v$, the time when pouring starts $E T_{djk}^{v}$, the time when pouring ends $E T_{djk}^{p}$, and the time when the vehicle is returned to the plant $B T_{djk}$ can be calculated.

3.4.   Mathematical formulation

The mathematical model of the above order distribution problem is constructed as follows:

S.t.

$f_{e} P_{e} S$ represents the cost of fuel consumption of all the RMC trucks participating in the delivery of a single day, $p_{z} \max W T_{d_{jk}}^{v}$ represents the opportunity cost of waiting for vehicles in the RMC plant, and $p_{w} \max W T_{d_{j k}}^{p}$ represents the opportunity cost of waiting on the construction site.

Equation (10) represents the maximum allowable interrupted pouring time constraint, where $\forall C_{j}$ the interrupted pouring time is less than or equal to the maximum allowable interrupted pouring time $I T$; Equation (11) represents the initial setting time constraint, and $\forall d_{j k}$ the time from the start of loading to the end of pumping is less than or equal to the initial setting of the ready-mixed concrete $S T$. Setting time; Equation (12) represents the constraints of available vehicles in the plant, and the number of available vehicles in each plant at the moment is less than or equal to the number of vehicles in the RMC plant.

4.   Genetic algorithm for CS-RMCPT

As a mature optimization algorithm, genetic algorithm (GA) simulates the natural evolution process over a period of time. It uses variable string encoding (chromosome encoding), randomly generates a set of feasible solutions (initial population), calculates and ranks the fitness value of each chromosome, retains the optimal solution, and uses these to generate new possibilities Solution (genetic operator). The genetic algorithm iteratively applies genetic operators (such as crossover and mutation) to change the current population to a new population. By repeatedly evaluating the new generation of chromosomes, or the genetic algorithm reaches a given number of cycles, an acceptable solution will be found.

The key to GA lies in the coding of chromosomes, the design of genetic operators, and the iterative evolution mechanism to determine which chromosomes are selected in each generation of the population to enter the next generation. In addition, GA defines a fitness function to evaluate the quality of chromosomes. The double chromosome synchronous evolutionary GA proposed in this paper is based on the research results of Wang et al. ^[39]. Figure 2 describes the GA solution framework and then details each step.

4.1.   Chromosome encoding and decoding

The encoding methods of chromosomes include binary encoding, random key method, real number encoding, etc. In many-to-many problems, binary encoding and random key methods are prone to produce illegal offspring in cross mutation. Therefore, this paper adopts a real-numbered dual-chromosome encoding method, where the X chromosome represents the RMC plant and the Y chromosome represents the construction site. Examples will be given below.

Supposing there are 3 RMC plants, numbered 1, 2, and 3. There are 4 construction sites, numbered 1, 2, 3, and 4. The volume of the RMC truck is 6 cubic meters, and the RMC demand at the 4 construction sites is 20, 30, 24, and 30 cubic meters respectively. Due to the characteristics of one truck and one cargo of the RMC truck, the number of vehicles required for construction sites 1, 2, 3, and 4 can be calculated as 4, 5, 4, and 5 respectively. A total of 18 vehicles are required for transportation. Therefore, in this example, the length of the chromosome is 18. As shown in Figure 3, the number of 1–4 in the X chromosome is random, that is, special cases of all 1 or all 2, 3, and 4 may occur; the Y chromosome represents the construction site, and the number of different numbers is equal to the number of vehicles required each construction site.

4.2.   Evaluation function

The model selects the fuel consumption cost of all trucks on the day and the total vehicle waiting time/pouring interruption time penalty as the evaluation criteria. Different from Eq (7), to unify the two target magnitudes and highlight the importance of the interruption pouring time, multiplied the latter by a coefficient $\omega$, namely

In each iteration of the genetic algorithm, a chromosome with a smaller function value (a better fitness value) is selected as the parent of the next generation.

For example, the fuel consumption per kilometer in the evaluation function is set as 0.31 L/km, the fuel price is 5.22 yuan/L, the daily transportation distance is 30 km, there is 1 RMC plant, 1 cite and 1 order, the early arrival time is 5 minutes, the penalty coefficient for early arrival of the RMC truck is 10 yuan/min, the late arrival time is 6 minutes, the penalty coefficient for late arrival of the RMC truck is 12 yuan/min. ω is 0.7. The calculation Equation is 0.31 × 5.22 × 30 + 0.7 × (10 × 5 + 12 × 6) = 133.9 yuan.

4.3.   Evolution strategy

In the algorithm of the article, chromosome X and chromosome Y are relatively independent, which respectively represent the RMC order plant selection decision and the RMC order site selection decision, and any chromosome X and chromosome Y can be combined into a feasible order scheduling plan. The basic idea of the algorithm proposed in this paper is shown in Figure 2. First, the initial population ${ popX }$ composed of chromosome X and the initial population ${ popY }$ composed of chromosome Y are randomly generated, and the fitness value is calculated. Subsequently, according to the roulette method, the chromosomes with higher fitness values are selected. For the selected chromosomes, the genetic operators of X and Y are respectively used to evolve populations ${ popX }$ and ${ popY }$ to generate a new generation of populations $[{ off } f X, { off } Y]$. Then evaluating whether the termination condition is met, if it is satisfied, decode and end $[{ off } f X, { off } Y]$; if it is not satisfied, continue iterating until the stopping criterion is reached.

4.4.   Genetic operators

The individual X represents the PC plant number, and the number of different numbers is not limited. Therefore, the traditional GA crossover and mutation operators are used to evolve the individual X, named as $X_{\_} {Crossover }$ and $X_{-M u t a t i o n}$.

Individual Y represents the construction site number, and the number of different numbers is fixed. Traditional crossover and mutation operators are prone to produce illegal offspring. To solve this problem, Li and Tong ^[40] proposed a parthenogenetic algorithm (PGA). PGA is an improved algorithm of GA ^[41]. It uses genetic recombination operators instead of crossover operators. Each offspring individual corresponds to only one parent. The offspring can be generated by changing the position of the gene in the parent instead of the gene value. Ensure the legitimacy of genetic individuals. As shown in Figure 4, this paper adopts the evolution group of transposition operator, shift operator, and inversion operator, which are equivalent to exchange neighborhood, insertion neighborhood, and reverse order neighborhood, respectively. The algorithm uses these three operators to evolve ${ popY }$, named $Y_{-} {Exchange() }$, $Y_{{_Shift() }}$ and $Y_{-} {Inverse() }$ respectively. To maintain the diversity of the population, the positions of the genes to be exchanged by the three operators are randomly generated.

4.5.   Time complexity analysis of algorithms

In this algorithm, assuming the size of the population is n. It adopts double chromosome synchronous evolution, with the X and Y chromosomes evolving independently. Construction sites and factories need to be one-to-one correspondence to calculate the cost of fuel consumption and the opportunity cost of waiting time during decoding. Therefore, the time complexity for calculating the fitness function of X and Y chromosomes is O(n²) and the computational complexity of calculating the optimal target value is O(n). In chromosome evolution, X chromosome adopts crossover and mutation, and their time complexity are both O(n). Y chromosome adopts transposition, translocation and inversion, and their time complexity all are O(n). The time complexity of this algorithm is shown as follows:

5.   Case study

5.1.   Parameter settings

To evaluate the performance of the developed genetic algorithm and test the application performance of the model in conventional foundation engineering and large-scale foundation engineering, some RMC companies and some construction sites in Beijing, China were selected, and some workday records were selected. Computational experiments were carried out on two practical cases collected. Three RMC plants $R_1$, $R_{2}$, $R_{3}$ in a certain area supply concrete to four construction sites $C_1$, $C_2$, $C_3$, $C_ 4$ in the area. The three plants use the same type of RMC truck, with a full load capacity of 6 $m^{3}$. The cleaning preparation time of the RMC truck is 8 minutes, and the charging time is 2 minutes, that is, the preliminary preparation time is 10 minutes. The average speed of the RMC truck is 60 km/h, and the RMC truck pumps the single-car RMC for 10 minutes. Each RMC plant has one RMC truck. The initial setting time of RMC is 100 min, and the maximum allowable interruption time is 45 min. The price of No. 0 diesel oil is 5.22 yuan/L, the fuel consumption of the RMC truck is 0.31 L/km, the penalty coefficient $p z$ of the given RMC truck is 0.5, and the penalty coefficient for the late arrival of the RMC truck $p w$ is 0.5.

Case 1: Scenario 1 is a conventional foundation project. The RMC order data and RMC plant data required for this project are shown in Tables 1 and 2, respectively.

Case 2: Scenario 2 is a large-scale foundation project. The RMC required in a single day is relatively large. The required concrete order data and the RMC plant data are shown in Tables 3 and 4, respectively.

5.2.   Results and discussion

The algorithm and data experiment were implemented with Matlab R2017b software on computer with an Intel Core i5-4210U, 1.7 GHz, and 8 GB random access memory. The algorithm parameters are set by reference to the existing research results and combined with experimental tests. The initial population size ${ popsize }$ is set to 300, and the maximum evolution generation number $max G e n$ is set to 1200.

When the X chromosome evolving, refer to parameter settings in the genetic algorithm of chromosome scheduling rule based on processing time (GA_DR_P) proposed by Joo and Kim ^[43], and the crossover and mutation probabilities are 0.8 and 0.2, respectively, which are predetermined by extensive preliminary experimentations. For the mutation operator probability of the Y chromosome, since inserting and switching neighborhoods are widely used in scheduling algorithms and they are very effective neighborhood structures, the optimization effect of these two neighborhoods is similar. In this paper, referring to parameter settings in the coevolutionary genetic algorithm ^[43], the shift and transposition probability are set to equal and relatively high values, both of which are 0.4, the inversion probability based on the inverse neighborhood is set to a relatively low value of 0.2.

According to the data given by the actual engineering case, the two cases are defined as small-scale case and large-scale case. In the algorithm, the chromosome length of small-scale case is 26, and the chromosome length of large-scale case is 61. The output results of the program running five times in case 1 are shown in Figures 5–7, and the data corresponding to the five running results are shown in Table 5. The total cost in Figure 7 converges at about 500 iterations. However, there is early convergence and falling into local optimum before 200 generations, so a larger maximum number of iterations is selected. or small cases, the vehicle wait time can be optimized to 0, where the total cost is minimized when the vehicle path is minimal. The output results of scene two after five runs are shown in Figures 8–10. The relevant data is shown in Table 6. In Figure 10, the convergence speed of large-scale case is much faster than that of small-scale case, and there is also a stage of falling into local optimum. For vehicle waiting time, it cannot be optimized to 0 in large-scale case. It shows that the larger the scale of the project, the more difficult it is to achieve on-time delivery. In addition, the minimum path of the vehicle and the waiting time of the vehicle are difficult to achieve the minimum at the same time, so each target is often not optimal in multi-objective optimization.

In the empirical scheduling scheme, the nearest RMC plant in the area is selected as the supplier for each site and supplied only by that plant. For the order D_j, $\operatorname{cost}_{j}=d_{j k} \cdot 2 v \cdot \min T S_{ij}+p_{2} \max W T_{djk}^{v}+p_{w} \max W T_{djk}^{p}$. At this time, if the order quantity is small, the single plant can basically meet the RMC demand of the site, and there is seldom stoppage for materials. However, when the site order volume is large, it is very likely to be due to the lack of transportation capacity of a single plant, resulting in site shutdown for materials, the construction progress and quality of the adverse impact, reflecting the defects of a single supply mode.

According to the result, the cost of the case 1 empirical scheduling scheme was 2076.5 yuan reduced to 1689.4, and for case 2 was 9097.3 yuan reduced to 6841.8. The algorithm proposed in this paper saved 18.6 and 24.8% of the cost and meet the maximum initial setting time and maximum interrupted pouring time constraints. For projects with less RMC demand, the advance/delay cost of transportation vehicles can be reduced to 0 by applying a reasonable production and transportation scheduling scheme, and the transportation fuel consumption and cost can be minimized to meet the construction plan of the project. In this way, the incremental cost of the project in the production and transportation stages is minimized. However, for projects with a large demand for RMC, it is difficult to meet the advance/delay cost of 0. Therefore, due to the high demand of large-scale projects and the pressure of factory supply, the requirements for optimal scheduling schemes are more stringent. Although the just-in-time delivery cannot be fully realized, the incremental cost of the production and transportation phase can also be minimized to meet the construction needs.

6.   Conclusions and future research

The collaborative scheduling of RMC production and transportation is very important for the engineering project progress, cost and quality of the project, especially in the construction of large public buildings. Considering the collaborative supply of multiple RMC plants according to the requirements from multiple construction sites, a multi-objective optimization model achieving the minimum interruption of pouring time and the total fuel consumption, is proposed. A double chromosome synchronous evolutionary genetic algorithm is designed and implemented. By comparing with the empirical value, it is proved that the cooperative scheduling optimization method proposed in this paper can greatly reduce the total cost of production and transportation. The algorithm not only meets the construction site interruption time of pouring and concrete initial setting time, but also reduces the oil consumption to the greatest extent, and ensures the just-in-time supply and environment friendly.

The collaborative scheduling optimization method of RMC production and transportation based on the genetic algorithm proposed in this paper can be directly applied to practical RMC plant and construction site, which can ensure the orderly operation of RMC supply by optimizing the allocation of RMC plant resources, improving production and transportation efficiency, and reducing costs.

In the follow-up study, the new energy RMC truck should also be considered as a transport vehicle in the model, in order to make the RMC scheduling process more environmentally friendly, save energy, and promote sustainable development. And the corresponding algorithm will be designed to further improve the practicability.

Acknowledgments

The authors acknowledge the construction workers and mentors who have carefully offered their insights on the construction organization management.

Conflict of interest

The authors declare there is no conflict of interest.