Multi-stage hybrid evolutionary algorithm for multiobjective distributed fuzzy flow-shop scheduling problem

1.   Introduction

In the context of economic globalization, the emergence of global cooperation models and the advancement of science and technology have led to changes in the traditional manufacturing environment. The manufacture of large-scale products is no longer being carried out by local factories alone, but by a variety of different enterprises around the world. These multiple factories with supply and demand relationships form a distributed manufacturing system, and as collaborative manufacturing among companies becomes more common, distributed manufacturing has become a common production mode ^[1].

The distributed flow-shop scheduling problem (DFSP) is a variant of the flow-shop scheduling problem (FSP). In the case of the DFSP, the jobs to be processed should be allocated to the appropriate shop first. Second, a reasonable sequence of jobs should be carried out in the shops. The objective is to solve the optimal job sequence under certain constraints, so as to achieve efficient resource allocation and utilization ^[2]. The DFSP considers the realistic constraints of multiple factories. Compared with a single factory, the DFSP is more in line with the current distributed manufacturing environment, and it is a hot topic in the field of production and manufacturing.

In real-life production scheduling, unexpected situations such as sudden machine breakdowns and power interruptions may occur. These uncertainties can affect the accuracy of scheduling and eventually cause time parameters such as production scheduling to become a fuzzy value. So the originally deterministic parameters are unable to accurately describe the actual production scheduling problem. Therefore, it is important to take uncertainty into account in shop scheduling problems. The fuzzy flow-shop scheduling problem (FFSP) combines fuzzy theory with the FSP. Compared with the traditional production scheduling problem, the FFSP is more consistent with the actual production situation and has more practical research significance.

However, with the gradual expansion of production scale and the increasing complexity of the production environment, more and more objectives need to be optimized, and the shop scheduling problem has become a complex multiobjective optimization problem. The multiobjective distributed fuzzy flow-shop scheduling problem (MoDFFSP) considers both the distributed manufacturing environment and the uncertain fuzzy production time under the conditions of multiobjective optimization. Therefore, the research on this problem has important practical significance.

Today, there are more and more methods for dealing with scheduling optimization problems. Traditional mathematical methods, such as enumeration and the branch and bound method, are suitable for small and simple problems due to their high computational complexity. Therefore, heuristics and meta-heuristics (such as the genetic algorithm (GA), simulated annealing, tabu search, particle swarm optimization, differential evolution (DE), etc.) are used to solve complex combinatorial optimization problems ^[3]. Compared with traditional methods, meta-heuristics affords great improvements in solution time and solution quality, and it can be used to deal with shop scheduling problems.

GAs constitute a typical type of evolutionary algorithm and a heuristic intelligent algorithm proposed earlier. The algorithm has good robustness and an adaptive random search mechanism, making it suitable for solving various combinatorial optimization problems in reality. At the same time, it does not require continuous or differentiable optimization objects, and it is suitable for combinatorial optimization problems in non-convex spaces. GAs have been widely used to solve production scheduling problems. However, the disadvantage is that when dealing with more complex optimization problems, the GA will have insufficient convergence and local search capabilities to obtain high-quality and diverse solutions.

DE represents an algorithm that updates individuals based on the differences between individuals. It also has good robustness, a simple structure, easy implementation and strong global convergence ability. DE does not need to use the characteristic information of the problem, and it is suitable for solving some optimization problems in complex environments that cannot be solved by using conventional mathematical programming methods. It can effectively deal with the DFFSP. However, the disadvantage of DE is that it readily falls into the local optimum value of the objective function, especially when the dimension of the problem increases; the effect of DE is not satisfactory.

Each classical algorithm has its unique advantages; inevitably there are some disadvantages, and no single algorithm can solve all problems ^[4]. At present, a variety of different evolutionary algorithms are complementary and being combined to form a new hybrid evolutionary algorithm, which combines the advantages of different algorithms and complements the defects of a single algorithm, thereby enhancing the performance of the algorithm and better handling the multiobjective scheduling optimization problem ^[5].

In reality, the most complex problems are composed of many constraints and multiple conflicting objectives. When dealing with such problems, these objectives need to be considered at the same time, and as good as possible to achieve the best effect under certain conditions. However, although most of the existing algorithms consider convergence and distribution performance simultaneously in the optimization process, in the actual algorithm execution process, the individual evolutional direction in the solution space is different in different periods of the population during the evolution process. There are few adjustment strategies for different stages, which cannot accurately regulate different stages. Therefore, it is necessary to propose a multi-stage hybrid evolutionary algorithm with sequence difference-based differential evolution (MSHEA-SDDE).

The main contributions of this study can be summarized as follows:

1) The hybrid sampling strategy is used as the global search strategy, and the sequence difference-based differential evolution (SDDE) is used as the local search strategy. The combination of these two strategies balances the convergence and distribution performance of the algorithm at different stages.

2) The enhanced SDDE strategy is introduced to guide the evolution of poor individuals to better individuals, taking into account the different evolutional directions of the individuals in the solution space at different stages in the evolutionary process.

3) The algorithm is divided into three stages according to different periods of iteration, and different SDDE strategies are used in different stages. In the first stage, the hybrid sampling strategy makes the population rapidly converge toward the Pareto front (PF) in multiple directions. In the second stage, SDDE_1 is designed to accelerate the convergence and distribution speed of the algorithm. In the last stage, SDDE_2 is employed to guide individuals to search the local area of the PF, thereby further improving the convergence and distribution performance.

4) The triangular fuzzy number (TFN) represents the fuzzy processing time of the job, a method of bivector representation of job and factory is designed for the DFFSP for encoding and decoding and genetic operators are also designed.

The proposed MSHEA-SDDE is compared with a non-dominated sorting genetic algorithm (NSGA-II) ^[6], an improved-strength Pareto evolutionary algorithm (SPEA2) ^[7], a multiobjective evolutionary algorithm based on decomposition (MOEA/D) ^[8], a fast multiobjective hybrid evolutionary algorithm (MOHEA) ^[9] and a hybrid multiobjective evolutionary algorithm with differential evolution (HMOEA-DE) ^[10]. The results show that MSHEA-SDDE not only has excellent convergence performance, but can also guarantee that the obtained solutions have good distribution performance and diversity.

The remaining sections of this paper are organized as follows. Section 2 reviews the relevant research work on the MoDFFSP in recent years. Section 3 presents the mathematical model of the MoDFFSP. A detailed description of the proposed MSHEA-SDDE and the main strategies are shown in Section 4. Experimental results and analysis are given in Section 5. Section 6 provides a summary of the full paper as a conclusion, along with the future work.

2.   Related work

In recent years, due to various uncertainties in real-world manufacturing systems, fuzzy theory has been widely used in fuzzy scheduling to describe uncertainty and a great deal of research has been done on the FSP; however, to the best of our knowledge, research on the DFFSP is still in its infancy, although it has received considerable attention from both academics and practitioners. Next, a review of closely related work is carried out.

As the real production environment becomes more complex and uncertain, there are increasing studies on the FFSP using fuzzy theory. In order to deal with a special structured n-job of three machine flow-shop scheduling with piecewise quadratic fuzzy processing times. Khalifa et al. developed a fuzzy approach with the help of a heuristic algorithm to minimize the rental cost of machines given the specified rental cost ^[11].

A trapezoidal membership function is used to represent the processing times, and an exact algorithm is proposed to achieve that minimization of the total waiting time of jobs ^[12]. Vinoba and Selvamalar presented triangular, trapezoidal and octagonal fuzzy numbers to solve the FFSP, and a branch and bound algorithm was adopted, which is modified to a fuzzy scenario with the objective of minimizing the makespan ^[13]. Li et al. considered the assembly DFFSP; an imperialist competitive algorithm with empire cooperation was developed to minimize the fuzzy makespan ^[14]. The above are all about the single-objective FFSP. In reality, multiple objectives need to be considered simultaneously, but the literature on solving the MoDFFSP is very limited. However, it is very common as a variant of the DFSP. Moreover, compared with the non-distributed environment, the research on distributed shop scheduling problems has great application value in the field of production.

Xi and Lei applied the integration of reinforcement learning and meta-heuristics to solve the two-stage distributed hybrid flow-shop scheduling problem (DHFSP) with fuzzy processing time ^[15]. They constructed a novel Q-learning-based teaching-learning based optimization to minimize the makespan. Li et al. proposed an improved brainstorming optimization algorithm for the type-two fuzzy distributed hybrid flow-shop problem (FDHFSP) with bivariate volume representations ^[16]. Cai and Lei studied the energy-efficient DHFSP under fuzzy processing time and proposed a collaborative restructuring frog-hopping algorithm with the objective of simultaneously optimizing the fuzzy maximum completion time, total consistency indicator and fuzzy total energy consumption ^[17]. Wang and Li studied the FDHFSP and proposed a shuffled frog-leaping algorithm with the collaboration of multiple search strategies to optimize multiple objectives simultaneously ^[18]. Cai et al. designed a collaborative variable search to optimize the total agreement index and fuzzy makespan simultaneously; seven neighborhood structures and two global search operators were used in two cooperated variable search parts to generate high quality solutions ^[19].

For the distributed permutation flow-shop scheduling problem (DPFSP), Ying et al. investigated the no-idle DPFSP with the objective of minimizing the makespan, they also presented an iterated reference greedy algorithm for effectively solving this problem ^[20]. Baysal et al. proposed an artificial bee colony (ABC) algorithm for the multiobjective distributed fuzzy permutation flow-shop scheduling problem (DFPFSP) ^[21]. Lin et al. proposed a backtracking search hyper-heuristic algorithm to solve the assembly DPFSP, and the backtracking search algorithm was employed as the high-level strategy to manipulate the low-level heuristics to operate in the solution space ^[22]. Baysal et al. developed an ABC algorithm to solve the multiobjective DFPFSP, where the process times and due dates of the jobs are considered as triangular and trapezoidal fuzzy numbers for the DFPFSP ^[23]. Wang et al. presented a fuzzy logic-based hybrid estimation of distribution algorithm (FL-HEDA) to address the DPFSP under the condition of machine breakdown with the makespan criterion ^[24]. The FL-HEDA hybridizes the probabilistic model of estimation of distribution algorithm with crossover and mutation operators of a GA to produce new offspring.

Recent years, more variants of the DFSP have been proposed in the literature by combining some constraints or multiobjectivity. In consideration of the uncertainty of manufacturing systems, Shao et al. investigated a distributed fuzzy blocking flow-shop scheduling problem in which there are multiple homogeneous factories and each one is set as a flow-shop with no intermediate buffers between any consecutive machines ^[25]. Aiming at the energy-aware distributed flow-shop with flexible assembly scheduling problem, a cooperative memetic algorithm with feedback was proposed by Wang and Wang to minimize the total tardiness and energy consumption ^[26]. Lu et al. studied an energy-efficient DPFSP with heterogeneous factories with makespan and total energy consumption as the objectives, including a hybrid multiobjective optimization algorithm, which integrates the iterated greedy; an efficient local search is designed to solve it ^[27].

As an important energy-efficient scheduling problem, the energy-efficient DFSP plays an essential part in green manufacturing. In recent years, it has attracted much attention. The energy consumption and carbon-efficient characteristics were considered by Zhao et al. ^[28,29]. They presented a hyper-heuristic algorithm with Q-learning to address the energy efficiency of the distributed blocking flow-shop scheduling problem (DBFSP). Moreover, a Pareto-based discrete Jaya algorithm was proposed to solve the carbon-efficient DBFSP with the criteria of total tardiness and total carbon emission. Pan et al. aimed to solve the distributed energy-efficient parallel machine scheduling problem by integrating factory assignment and machine assignment into an extended machine assignment to handle the coupled relations of subproblems ^[30]. Zhao et al. investigated an energy-efficient distributed no-wait flow-shop scheduling problem with sequence-dependent setup time for the minimization of makespan and total energy consumption and a cooperative meta-heuristic algorithm based on Q-learning was proposed to address it ^[31].

Different from the single-objective problem, multi-objective scheduling problems have high complexity. From the above literature, it can be seen that more and more scholars are using hybrid intelligent algorithms to deal with multiobjective optimization in different fields. Due to the shortcomings of a single algorithm, hybrid intelligent algorithms can combine the advantages of different algorithms to complement the defects of a single algorithm. Therefore it can better deal with more complex multiobjective optimization problems. Lu et al. investigated a DHFSP, a Pareto-based multi-objective hybrid iterated greedy algorithm was designed by integrating the merits of genetic operators and iterated greedy heuristics ^[32]. Considering the distributed manufacturing problem in an uncertain environment, Zheng et al. proposed a co-evolutionary algorithm with a specific problem strategy for the multiobjective fuzzy distributed hybrid assembly line scheduling problem with the objectives of optimizing fuzzy total tardiness and robustness through the use of a reasonable combination of estimation distribution algorithm and iterative greedy search ^[33]. Zhang et al. proposed a multiobjective particle swarm optimization with directional search (MoPSO-DS) to solve the DFPFSP ^[34]. MoPSO-DS divides the particle swarm into three subgroups, and three subgroups are biased in different regions of the PF. Then, particles are updated in the direction of the partiality.

Although the research on the above scheme uses a hybrid algorithm to improve the convergence and distribution performance of the algorithm, in the actual algorithm execution process, the evolutional direction of the individual in the solution space is different at different stages of the population evolutionary process. There are few adjustment strategies, and it is impossible to accurately control different stages. Moreover, the evolutionary algorithm has been proved to be one of the algorithms that can effectively solve multiobjective optimization problems. However, the performance research and applications of multiobjective evolutionary algorithms in uncertain environments are less. Therefore, this work combines a GA with a DE algorithm and a MSHEA-SDDE is proposed to study the MoDFFSP.

3.   Problem formulation

3.1.   Operations on fuzzy number

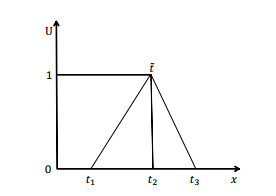
Among the fuzzy numbers, the TFN is a method of converting uncertain fuzzy linguistic variables into definite values. In the production scheduling problem, researchers mostly use the TFN to represent the fuzzy processing time of the job. That is, $\tilde{t} = (t_{1}, t_{2}, t_{3})$, where $t_{1}$, $t_{2}$ and $t_{3}$ represent the optimal ideal processing time of the job, the processing time without accident and the processing time in the worst case respectively. The fuzzy processing time represented by the TFN is shown in Figure 1.

The function definition formula of the TFN is as follows:

In order to deal with the fuzzy processing time, arithmetic operations of fuzzy numbers are used, including addition, subtraction, maximum and ranking operations. In the study, the fuzzy maximum and ranking operations are used to determine the starting time and sequence of each job in the process, and the fuzzy addition and subtraction operations are used to determine the completion time of the jobs in the process.

For two TFNs $A = (a_{1}, a_{2}, a_{3})$ and $B = (b_{1}, b_{2}, b_{3})$, the addition, subtraction, ranking and maximum operations are shown as follows ^[35].

1) Addition and subtraction operations

$A + B = (a_{1} + b_{1}, a_{2} + b_{2}, a_{3} + b_{3})$

$A - B = (a_{1} - b_{1}, a_{2} - b_{2}, a_{3} - b_{3})$

2) Ranking operation

The following criterions are adopted to rank two TFNs ^[36].

$\text{ Step 1: }$ Compare $F_{1}(A) = (a_{1}, 2a_{2}, a_{3}) / 4$ ^[37]; if $F_{1}(A) > F_{1}(B)$, then $A > B$.

$\text{ Step 2: }$ If the $F_{1}$ value of $A$ and $B$ are the same, compare $F_{2}(A) = a_{2}$; if $F_{2}(A) > F_{2}(B)$, then $A > B$.

$\text{ Step 3: }$ If the $F_{1}$ and $F_{2}$ values of $A$ and $B$ are the same, compare $F_{3}(A) = a_{3} - a_{1}$; if $F_{3}(A) > F_{3}(B)$, then $A > B$.

3) Maximum operation

If $A > B$, then $A \vee B = A$; otherwise $A \vee B = B$ ^[38].

3.2.   Problem description

In the MoDFFSP, the objective is to select a suitable factory for the job and find a reasonable order of the job in each factory, which minimizes the fuzzy maximum completion time of the jobs in all factories and the fuzzy maximum total flow time of all jobs in all factories simultaneously. In this problem, each job can be assigned to any factory, and once the distribution of jobs between factories is determined, no jobs can be transferred to another factory. The notations of the MoDFFSP are defined as follows:

Indices

$i$: index of job, ($i = 1, 2, \ldots, n$);

$j$: index of machine, ($j = 1, 2, \ldots, m$);

$k$: index of factory, ($k = 1, 2, \ldots, f$).

Parameters

$n$: the total number of jobs;

$m$: the total number of machines in each factory;

$f$: the total number of factories;

$o_{k}$: the total number of jobs allocated to the $k$th factory;

$\pi^k$: the job sequences in factory $k$, $\pi^k = \{ \pi^k_1, \pi^k_2, \ldots, \pi^k_{i}, \dots, \pi^k_{o_k} \}$;

$\tilde{t}^{\text{P}}_{i, j, k}$: fuzzy processing time of job $i$ on machine $j$ in factory $k$.

Decision Variables

$\tilde{t}^{\text{C}}_{i, j, k}$: fuzzy completion time of job $i$ on machine $j$ in factory $k$;

Mathematical Model

Two objective functions are used to evaluate the solution, where one is the minimization of the fuzzy maximum completion time of the jobs in all factories, which can be calculated by using Eq (3.2), and the other is the minimization of the fuzzy maximum total flow time of all jobs in all factories, which can be calculated by using Eq (3.3). Equation (3.4) expresses the initial value of calculating the fuzzy time. The first step of each job is executed on machine 1, so the fuzzy completion time of the jobs on the first machine within each factory can be calculated by using Eq (3.5). Since job 1 is the first job to be operated, it is the first to be processed on each machine, so the fuzzy completion time of job 1 on each machine can be calculated by using Eq (3.6). Equation (3.7) is used to calculate the fuzzy completion time for each of the remaining jobs for each process. Figure 2 shows the Gantt chart of the DFFSP, taking two factories and four jobs and two machines as an example. The sequence of jobs is ($j_1, j_2, j_3, j_4$), and the corresponding factories are ($f_1, f_2, f_2, f_1$). After the sequence of jobs is determined, the processing time arrangement mechanism of the jobs on the machine is different from the traditional precision time processing arrangement due to the use of the improved discrete sorting coding method.

Job 1: Machine 1: (1, 2, 3), Machine 2: (2, 3, 6)

Job 2: Machine 1: (1, 2, 4), Machine 2: (2, 5, 8)

Job 3: Machine 1: (2, 7, 8), Machine 2: (5, 8, 9)

Job 4: Machine 1: (2, 5, 6), Machine 2: (4, 7, 9)

Through the calculation of the above formula, the values of the two objectives of the DFFSP can be obtained. The fuzzy completion time of the jobs of factory 1 is (7, 14, 18), and that of factory 2 is (8, 17, 21); the longest fuzzy completion time of the jobs among all factories is used as the final fuzzy completion time, so the fuzzy completion time of the jobs of the DFFSP is (8, 17, 21). In addition, the fuzzy total flow time of the DFFSP is determined by the fuzzy completion time of all jobs in the factory. The total fuzzy flow time for factory 1 is (10, 19, 27), and that for factory 2 is (11, 24, 33); the fuzzy total flow time is the longest and final total flow time in all factories, so the total fuzzy flow time for the DFFSP is (11, 24, 33).

4.   Proposed method

4.1.   Overview of the MSHEA-SDDE

The proposed MSHEA-SDDE consists mainly of a hybrid evolutionary algorithm (HEA) with a hybrid sampling strategy and an SDDE local search strategy. The hybrid sampling strategy is divided into an edge region sampling strategy based on the vector-evaluated GA (VEGA) ^[39] and a central region sampling strategy based on the Pareto-dominating and dominated relationship-based fitness function (PDDR-FF) ^[40]. Among them, the edge region sampling strategy can select the individuals near to the edge region of the PF so as to better hold the individuals with good performance on the single objective. The central region sampling strategy uses the PDDR-FF to evaluate the dominance of individuals in the population, and thus selects individuals with a larger dominance area near to the central region of the PF. The combination of the two sampling strategies can help the MSHEA-SDDE to search for solutions in multiple regions of the PF, as well as improve the convergence and distribution performance of the algorithm. The multi-stage SDDE local search strategy is to guide individuals to search local areas directionally by comparing sequence differences between individuals according to different periods of algorithm iteration so as to improve the local search ability of the MSHEA-SDDE.

During the execution of the MSHEA-SDDE, the evolutional directions of individuals in the solution space in different periods of the evolution of the population are different. In the early stages of the evolutionary process, the evolutional direction of individuals is mainly toward the true PF that is, when the optimization objective of the MSHEA-SDDE is to improve the convergence performance. In the middle and late stages of the evolutionary process, the individuals evolve toward further convergence to the true PF, while also exploring local regions of the PF. The idea of many hybrid algorithms is to enhance local search capabilities, but it is often easy to overlook the trade-off between convergence performance and distribution performance in the first and middle stages of the MSHEA-SDDE. Therefore, the proposed MSHEA-SDDE focuses on applying SDDE strategies with different evolutional directions to the MSHEA-SDDE in stages. At the same time, through different design strategies in the three stages, the convergence and distribution performance in the evolution of the MSHEA-SDDE are correspondingly improved, thereby improving the overall performance of the MSHEA-SDDE. The framework of MSHEA-SDDE is shown in Figure 3.

4.2.   Encoding and decoding

In this paper, the fuzzy processing time due to the job is represented by the TFN. Therefore, an improved discrete sorting encoding method is adopted in the experiment. The number of genes on the chromosome represents the sequence number of the job to be processed, while the real number representing the precise processing time on the gene is adjusted to a TFN represented by an array. Besides, in order to cope with the DFFSP in the multi-factory situation, we adopt a bivector to represent each individual in the problem space. Therefore, the encoding process consists of two parts, where the first vector represents the sequence of the jobs, and each gene in this vector is the job number and does not repeat; the sequence of the job in the solution can be obtained through the gene sequence on this vector ^[41]. The second part of the vector represents the factory sequence, and each gene in this vector corresponds to the factory number but can be repeated.

Figure 4 shows an example of the encoding for an individual with a chromosome divided into two parts: job sequence and the factory sequence. The first $\{5\}$ on the job sequence $\{5, 4, 3, 2, 8, 6, 7, 1\}$ represents job 5, while the second $\{4\}$ represents job 4. In the factory sequence $\{1, 2, 3, 3, 2, 1, 1, 2\}$, the first $\{1\}$ represents the factory number corresponding to job 1, the second $\{2\}$ represents the factory number corresponding to job 2 and so on. Each job corresponds to a factory number, each job will be assigned to the corresponding factory for processing and each factory has an assigned sequence of jobs. This encoding method can intuitively express each job and its corresponding factory.

In the decoding process, the jobs are distributed to different factories for processing according to their factory sequence numbers. In decoding, both parts of the chromosome are traversed from left to right. First, the corresponding job of factory 1 is selected and put together as the internal distribution of the job of factory 1, and without changing the front and rear positions of the jobs, the preserved job order is the operation order of the internal job of factory 1. Then, operate factory 2 according to the steps of factory 1, pick out the parts of factory 2 and put them together without changing the order, complete the distribution of the parts of factory 2 and the sorting of the internal parts of factory 2, and so on. This encoding and decoding method can solve the problem of allocating jobs to factories, as well as the sorting problem of the job inside of the factory in the DFFSP. Figure 5 shows an example of decoding with eight jobs and three factories.

4.3.   Genetic operators

For the selection operator, a binary tournament selection is used as the selection operator. In the edge selection strategy, binary tournament selection is also used to generate sub-populations. Two individuals are randomly selected in the population and the function value of one of the optimization objectives in Eqs (4.2) and (4.3) is compared; then, the individual with better performance on the objective is selected and placed in the corresponding sub-population. In the central selection strategy, individuals are ranked according to their fitness values and the best performers are selected as the elite population. Using the binary tournament selection as the selection operator allows individuals with high fitness values to be retained under the condition of ensuring the diversity of solutions.

For the crossover operator, since this work adopts the encoding method of bivectors, different crossover operations are carried out for the two parts of a chromosome. First, for the job vector, the order crossover (OX) method is used. While ensuring the sufficient diversity of individuals in the population, the OX method also pays attention to the partially connected gene segments in the chromosome; thus, the gene sequences of some excellent chromosomes can be better retained in the offspring individuals. As for the factory vector, the effect of sequential crossover is not obvious because the factory sequence number can be repeated, so the single-point crossover is adopted in this part. The single point crossing method randomly generates an integer in the job sequence, and the random number is the mark position of the single point crossing. Figure 6 shows an example of a process that uses the crossover operator for two parent individuals.

As shown in Figure 6, in the job vector part, the parent chromosome 1 is $\{1, 4, 3, 2, 8, 6, 7, 5\}$, and the parent chromosome 2 is $\{8, 2, 6, 5, 7, 3, 4, 1\}$; there are two mark points in the chromosome. Mark points 1 and 2 on parent chromosome 1 with the gene fragments $\{3, 2, 8, 6\}$, which are retained in the same order and position on the offspring chromosome, and are not selected in parent chromosome 2 to avoid illegal chromosome solution. Then, in parent chromosome 2, unselected genes are put into the offspring chromosome in sequence after the gene locus of mark point 2. After the last gene of the parent chromosome is put into the offspring, the selection continues from the first gene of the parent chromosome until all alleles are selected.

In the factory vector part, the factory vector of the parent chromosome 1 is $\{1, 2, 3, 1, 2, 3, 1, 2\}$ and the factory vector of the parent chromosome 2 is $\{3, 2, 1, 3, 2, 1, 3, 2\}$. Because of the single-point crossover method, only one marked position is set in the factory vector part. For example, the marked position in Figure 6 is 2. Then combine the genes on the 0 and 1 loci in the parent 1 factory vector with the genes from 2 to the maximum length of the chromosome in the parent 2 factory vector to generate the factory vector of the offspring chromosome $\{1, 2, 1, 3, 2, 1, 3, 2\}$.

In terms of mutation operators, two different mutation operators are also used. For the job vector, the exchange mutation method is adopted; the specific operation is to randomly select two gene positions on the vector and then exchange the gene information within the two positions. As for the factory vector, because the factory sequence number can be repeated, the effect of exchange variation is not obvious, so the single-point mutation method is adopted for this part. In this method, a gene locus is randomly selected in the factory sequence and the factory sequence number expressed on this gene locus is randomly changed to other factory sequence numbers. Figure 7 shows an example of a process that uses the mutation operator on an individual.

As shown in Figure 7, in the part of job vector, the parent chromosome is $\{1, 4, 3, 2, 8, 6, 7, 5\}$, and the two gene locus 2 and 5 are randomly selected. The exchanged genes are $\{3\}$ and $\{6\}$, and the offspring chromosome after exchange is $\{1, 4, 6, 2, 8, 3, 7, 5\}$. In the factory vector, the factory vector of the parent chromosome is $\{1, 2, 3, 1, 2, 3, 1, 2\}$; the single point mutation is to randomly selects a gene locus; for example, the factory number on gene locus 2 is 3, and the gene on this locus is randomly changed to another factory number 1. Thus, the generated offspring chromosome factory vector is $\{1, 2, 1, 1, 2, 3, 1, 2\}$.

4.4.   Mixed selection strategy

In the proposed MSHEA-SDDE, the HEA uses a hybrid selection strategy as the global search strategy, which combines the edge selection strategy based on the VEGA and the center selection strategy based on the PDDR-FF. Among them, the edge selection strategy can select the individuals whose edge regions close to the PF are biased toward the two objectives so as to better save the individuals with better performance on the single objective. The center selection strategy uses the PDDR-FF to evaluate the dominant area of individuals in the solution space so as to select individuals with a large dominant area near to the center region of the PF. The following formula is used to calculate the PDDR-FF value of individual $X_{i}$.

where $q(X_{i})$ is the number of individuals dominating individual $X_{i}$, $p(X_{i})$ is the number of individuals dominated by individual $X_{i}$ and $popSize$ is the population size. It can be seen from the formula that when the $eval$ value of an individual is smaller, it indicates that this individual has a large dominated area, the individual performs better and the $eval$ value of non-dominated individuals is less than 1. Therefore, after obtaining the $eval$ value of individuals and ranking it; the individuals with a small $eval$ value are selected from small to large, which can filter out non-dominated individuals and individuals with a large dominated area.

The hybrid selection strategy formed by the combination of the two selection strategies can help the MSHEA-SDDE to search for solutions in multiple regions of the PF, as well as to improve the convergence and distribution performance of the MSHEA-SDDE. Figure 8 illustrates the main mechanism of the hybrid selection strategy.

4.5.   Multi-stage SDDE strategy

To further improve the quality of the solution, a multi-stage SDDE strategy is investigated in this paper. SDDE is a local search strategy based on sequence differences between individuals in the population. The strategy searches the population generated by the hybrid strategy in the iterative process of the MSHEA-SDDE, which is used to strengthen the search ability of individuals in their surrounding areas so as to further improve the quality of the solution set. The multi-stage SDDE includes SDDE_1 and SDDE_2. According to the different stages of the MSHEA-SDDE evolutionary process, the SDDE strategy is combined with the HEA to improve the convergence and distribution performance.

When the hybrid strategy in the HEA is used to evolve the population, the population can quickly converge to the PF in the early iteration of the MSHEA-SDDE. In the middle iteration of the MSHEA-SDDE, the population obtained by the hybrid strategy converges to the PF in the solution space. At this time, the SDDE_1 local search strategy can guide the population to further converge to the true PF. In the later iteration of the MSHEA-SDDE, the population has converged to near the true PF; at this time, the evolutional direction of the individual in the SDDE strategy is adjusted, and SDDE_1 is adjusted to SDDE_2 so that the MSHEA-SDDE guides the individual to explore the optimal solution in the single objective direction. Thus, the diversity of final solutions is improved and the distribution performance of the MSHEA-SDDE is improved. The algorithm process of the MSHEA-SDDE is shown in Figure 9.

The main process of SDDE_1 is divided into the following three steps.

$\text{ Step 1: }$ Three individuals $S_{1}, S_{2}, S_{3}$ are randomly selected from the population according to the PDDR-FF value, so that $eval$ $(S_{1})$ $<$ $eval$ $(S_{2})$ $<$ $eval$ $(S_{3})$.

$\text{ Step 2: }$ An exchange sequence method is used to obtain the sequence differences between the better performing individuals $S_{1}$ and $S_{2}$.

$\text{ Step 3: }$ Obtain the sequence difference between $S_{1}$ and $S_{2}$ according to a certain scale ratio, and then act on the poorly performing individual $S_{3}$.

Figure 10 shows the main mechanism of SDDE_1, and Eq (4.2) is used to represent the main process of SDDE_1.

where $(S_{1}-S_{2})$ represents the sequence difference between individuals $S_{1}$ and $S_{2}$, $F$ denotes the scale ratio of individual sequence difference and $S$ represents the new individual obtained by the SDDE strategy for individual $S_{3}$. The main process of the SDDE_1 strategy is to randomly select three different individuals in the population, use an exchange sequence to detect the difference between the two individuals with better performance and take a certain proportion of the difference to act on the individual with worse performance. The SDDE_1 strategy can guide the population to converge better to the PF and improve the convergence performance of the MSHEA-SDDE.

In the later iteration stage of the MSHEA-SDDE, the population has converged to the PF by using the hybrid sampling strategy and SDDE_1 local search strategy, and the individuals in the population are distributed in multiple regions of the PF. However, using the SDDE_1 strategy makes the individuals in the population evolve in the direction of a small PDDR-FF value, which may lead to an insufficient solution search for the edge and local areas of the PF. For this situation, we propose the SDDE_2 strategy, which adjusts the selection and evolutional direction of individuals in SDDE_1, in order to improve the search ability of the MSHEA-SDDE for the PF edge and local region. The operation process of SDDE_2 is as follows.

$\text{ Step 1: }$ According to the PDDR-FF value, three individuals $S'_{1}$, $S'_{2}$, $S'_{3}$ with a PDDR-FF value less than 1 are randomly selected from the population so that $eval$ $(S'_{1})$ $<$ $eval$ $(S'_{2})$ $<$ $eval$ $(S'_{3})$ $<$ $1$.

$\text{ Step 2: }$ The exchange sequence method is used to obtain the sequence difference between the better performing individuals $S'_{1}$ and $S'_{2}$.

$\text{ Step 3: }$ Obtain the sequence difference between $S'_{1}$ and $S'_{2}$ according to a certain scale ratio, and then act on the individual $S'_{3}$ with a large PDDR-FF value.

Figure 11 shows the main mechanism of SDDE_2, and Eq (4.3) is used to represent the main process of SDDE_2.

where $(S'_{1} -S'_{2})$ still represents the sequence difference between individuals $S'_{1}$ and $S'_{2}$, $F$ represents the scale ratio of individual sequence difference, and $S'$ represents the new individual obtained by individual $S'_{3}$ through the SDDE strategy. However, the difference between the SDDE_2 strategy and SDDE_1 strategy is that the PDDR-FF values of the three individuals selected in the first step of the SDDE_2 strategy are all less than 1. These three individuals are non-dominated solutions located on the PF. It also guides individuals with small PDDR-FF values to evolve in the direction of large PDDR-FF values. This adjustment method can make the selected individuals search the edge and local areas of the PF without reducing the convergence performance of the MSHEA-SDDE, allowing the MSHEA-SDDE to find the optimal solution in the two single objective directions in the non-dominated solution and improve the distribution of the final solution. The SDDE_2 strategy should be used in the late iteration of the MSHEA-SDDE. Using this strategy too early will lead to the elite individuals having smaller PDDR-FF values near the central region of the population during the iteration process, which may make the MSHEA-SDDE fall into the local optimal value. In the later stage of the MSHEA-SDDE, the SDDE_1 strategy is adjusted to the SDDE_2 strategy, which can improve the distribution performance while ensuring the convergence performance of the MSHEA-SDDE.

5.   Experimental results

In this section, in order to verify the performance of the proposed MSHEA-SDDE, the experiments compare the proposed algorithm with NSGA-II ^[6], SPEA2 ^[7], MOEA/D ^[8], MOHEA ^[9] and HMOEA-DE ^[10]. In these comparison algorithms, for the algorithm with an elite population, the non-dominated solution in the elite population is taken as the final solution of the algorithm, and for the algorithm without an elite population, the non-dominated solution in the last generation solution set is taken as the final solution of the algorithm. The maximum number of iterations for all algorithms is set to 600, the population size is 100 and each algorithm is run 30 times on each problem to take the average for comparison. In order to evaluate the performance of the algorithm, we selected six multiobjective algorithm evaluation indicators such as generational distance (GD), inverted generational distance (IGD), hypervolume (HV), spacing (SP), spread (Spread) and coverage ($C$) to evaluate and compare the performance of the algorithm. If the significance result is "-", it means that the comparison algorithm is significantly weaker than the main algorithm; if the result is "*", it indicates that the difference is not significant; if the result is "+", it means that the comparison algorithm is better than the main algorithm. All experiments were run on the same machine in the same experimental environment; the machine was configured with an Intel Core i7-9750H CPU, 16 GB memory and a Windows 10 operating system. The experiment was implemented in JAVA language. The experimental results are presented in a table, where the bold font indicates the best performing value in that part.

In terms of data sets of the DFFSP, this experiment uses an improved data set based on the Taillard benchmark data set. Since standard time is adopted in the standard data set and the characteristics of fuzzy processing time are not considered, the improved method is to randomly adjust the standard time to a fuzzy time within a small range to meet the fuzzy processing time of the job requirement ^[42]. The specific adjustment operation refers to the idea in the literature ^[43]; according to the Eq (5.1), the standard time in the FSP data set is extended to the fuzzy time.

In the above formula, ${t}_{ij}$ is the standard time in the data set of the FSP and $\tilde{t}_{ij}$ is the expanded fuzzy time used in this paper. Based on the fuzzy data set, we added additional factory parameters to form the DFFSP. Twelve different scales of data were used for testing, namely, five machines, 10 machines and 20 machines, corresponding to 20 jobs, 50 jobs, 100 jobs, 200 jobs and 500 jobs. Using data of different scales can verify the optimization effect of the algorithm, ranging from simple to complex processing situations.

5.1.   Parameter settings

Different combinations of the crossover rate $Cr$ and mutation rate $Mr$ in MSHEA_SDDE and scale ratio $F$ in SDDE were tested. Due to excessive experimental data, only the most valuable interval is shown here, and the ranges are as follows: $Cr \in \{0.6, 0.7, 0.8, 0.9\}$, $Mr \in \{0.1, 0.2, 0.3\}$, $F \in \{0.5, 0.6, 0.7, 0.8\}$. The performance of MSHEA_SDDE on the problem of three factories, 20 jobs and five machines was selected for the comparison test. The test results are shown in Table 1.

From the experimental results in Table 1, it can be seen that the algorithm performs better when the crossover rate is 0.8 and the scale ratio $F$ is 0.8. When the mutation rate is 0.2, the combination achieves two first, and when the mutation rate is 0.3, the combination achieves two first and one second. Therefore, the parameter combinations of crossover rate $Cr$ = 0.8, mutation rate $Mr$ = 0.3 and SDDE scale ratio $F$ = 0.8 were used in the subsequent experiments.

The algorithm parameter settings are shown in Table 2. All algorithms set the same population size and use the same maximum number of iterations, and the crossover rate and mutation rate are set to a fixed value. Among them, compared with MSHEA-SDDE, HMOEA-DE does not consider using the DE strategy at different times at different stages.

5.2.   Effectiveness of strategies

Two key strategies SDDE_1 and SDDE_2 in MSHEA-SDDE were introduced in the previous section. It is worth mentioning that in the early stage of the evolutional process, although there are individuals with various fitness values in the population, most of the individuals with poor performance may be caused by too few iterations. Therefore, the SDDE_1 strategy adopted from the beginning of the iteration may affect the diversity of individuals in the population and reduce the distribution performance. Similarly, if the SDDE_2 strategy is applied in the early or middle iteration of the MSHEA-SDDE, the elite individuals with good PDDR-FF values in the central region of the population may evolve toward the local region solution earlier. As a result, the excellent individuals in the central region are destroyed, which affects the convergence performance of the entire algorithm.

According to the results in the parameter settings section, in order to prove these ideas and verify the appropriate use timing of SDDE_1 and SDDE_2 in the MSHEA-SDDE, this part of the experiment involved 12 groups in the MSHEA-SDDE with different timing combinations of the two strategies in 12 fuzzy distributed flow factories of different scales. The test on the scheduling problem used the five indicators of GD, IGD, HV, SP and Spread to verify the convergence and distribution performance of the MSHEA-SDDE. Due to the large amount of experimental data and it being difficult to fully display, we recorded the statistics of the top three rankings of different combinations on 12 problems in the table, and each indicator had 36 results on 12 problems. As well as the statistics of the number of times that different combinations ranked first on 12 problems, each indicator had 12 results on 12 problems. The specific statistical results are shown in Tables 3 and 4.

As shown in Tables 3 and 4, the usage timings of SDDE_1 and SDDE_2 are separated by "/", where "x$\%$E/y$\%$E" means that SDDE_1 was used when MSHEA-SDDE ran to x$\%$, and the MSHEA-SDDE used SDDE_2 when running to y$\%$. For example, "15$\%$E/66$\%$E" means that SDDE_1 was added after the MSHEA-SDDE algorithm iterated to 15$\%$, and SDDE_1 was adjusted to SDDE_2 after the MSHEA-SDDE algorithm iterated to 66$\%$. From the statistical results in Table 3, the combination result of "15$\%$E/90$\%$E" ranks the top three times the most for the five indicators, and the performance of the three indicators GD, IGD and HV is more obvious. In Table 4, the combination of "15$\%$E/90$\%$E" shows less obvious advantages, but still outperformed other combinations in terms of GD, IGD, HV and SP, which is basically consistent with our previous study idea. Therefore, adding the SDDE_2 strategy at an appropriate time in the late iteration of the MSHEA-SDDE can not only ensure the convergence performance of the MSHEA-SDDE, but it can also improve the distribution performance. In the subsequent experiments, the timing of "15$\%$E/90$\%$E" was used in MSHEA-SDDE for comparative experiments.

Other components of the proposed strategy are the exchange sequence strategy and the hybrid sampling strategy, whose effectiveness has been verified in papers ^[5,44] and will no longer be verified here.

5.3.   Results and discussion

This section analyzes algorithm performance through various indexes. Tables 5 to 10 show the comparative test results of all algorithms on the six evaluation indicators. The significance analysis results obtained by the Wilcoxon rank sum test are shown in the H.T. column of the tables.

Table 5 shows the results of the GD indicator, which reflects the convergence performance of the algorithm. From the experimental results, MSHEA-SDDE performed best on 10 test questions and second on two test questions. In the Wilcoxon rank sum test results, except for HMOEA-DE, MSHEA-SDDE had a significant difference with all other comparative algorithms. It can be proved that MSHEA-SDDE has better convergence performance, and that it is also better than other comparison algorithms.

The IGD indicator can not only be used to evaluate the convergence performance of the solution, but it can also be used to judge the difference between the distribution of the solution and the distribution of the solution on the PF. The smaller the value of IGD, the better the convergence performance and distribution performance of the algorithm. From the IGD indicator results shown in Table 6 and the Wilcoxon rank sum test results, MSHEA-SDDE also performed best again on 10 questions, and performed second best on two questions. The experimental results prove that MSHEA-SDDE not only has good convergence performance, but it also has good distribution performance.

Table 7 shows the results for the HV indicator. The HV indicator can be used to evaluate the quality of the algorithm according to the size of the solution space. The larger the indicator value, the larger the dominance area of the solution obtained by the algorithm. From the experimental results, MSHEA-SDDE performed best on 10 questions. It can be seen that MSHEA-SDDE had better convergence and distribution performance than the other comparison algorithms.

In terms of the SP and Spread indicators in Tables 8 and 9, MSHEA-SDDE performed well on the Spread indicator and had the best performance on eight questoins, but had average performance on the SP indicator. It is because the DFFSP is based on the actual problem with a variety of constraints and the number of final solutions obtained by the algorithm is small. As a result, the continuity performance of the individuals in the final solution set is not very prominent, which makes the performance of the SP indicator unsatisfactory and affects the SP indicator. The Spread indicator performed better, which indicates that the final solution set obtained by the algorithm is more widely distributed. In general, MSHEA-SDDE has better distribution performance than the other comparison algorithms.

In addition, the Wilcoxon rank sum test results of MSHEA-SDDE and MOHEA-DE were mostly insignificant. From the experimental results of the C indicator in Table 10, MSHEA-SDDE outperformed HMOEA-DE on nine questions, and almost outperformed other comparative algorithms on all problems. It indicates that the solutions obtained by MSHEA-SDDE are better than HMOEA-DE, and that the MSHEA-SDDE has the best convergence performance.

From the experimental results of the C indicator, it can be further seen that the solution obtained by MSHEA-SDDE is closer to the real PF. Therefore, the model of the MoDFFSP proposed in this paper is effective, and the proposed MSHEA-SDDE has better convergence and distribution performance than other comparative algorithms.

6.   Conclusions

In this paper, MSHEA-SDDE has been proposed to solve the MoDFFSP. This algorithm consists of a global search strategy based on a hybrid selection strategy and a local search strategy based on multi-stage sequence difference DE. In the hybrid sampling strategy, the population is divided into multiple sub-populations according to different objectives so that the population evolves to multiple regions of the PF. The multi-stage sequence difference DE strategy considers the different requirements for convergence and distribution performance of the MSHEA-SDDE in different iteration periods and uses the corresponding sequence difference strategy in different periods to further improve the convergence and distribution performance of MSHEA-SDDE. In the first iteration stage of the the MSHEA-SDDE, the global search strategy of hybrid selection is used to make the population converge to the PF quickly. In the second stage of the MSHEA-SDDE iteration, a local search strategy based on sequence difference is used to improve the convergence performance by improving the performance of individuals with poor fitness values in the population. In the third iteration stage of the MSHEA-SDDE, the evolutional direction of the sequence differential strategy is adjusted to guide the population to search multiple areas of the PF, which is used to improve the distribution performance. An encoding and decoding approach with genetic operators relevant to the problem is included. The experimental results show that MSHEA-SDDE has better convergence and distributional performance than other multiobjective optimization algorithms.

The proposed MSHEA-SDDE can produce good scheduling solutions, but it also has the shortcoming that the CPU running time is not the shortest. The main reason is the computational time overhead of differential evolution search, but the experimental analysis shows that it can significantly improve the convergence and distribution performance of the MSHEA-SDDE. Therefore, how to reduce the computation time of the MSHEA-SDDE needs to be further investigated. With the development of industrialization, there will be a variety of variations of shop scheduling. These scheduling problems are more complex and require intelligent algorithms for optimization. In the future work, it is appropriate to consider some strategies such as the ABC algorithm, ant colony algorithm, simulated annealing, tabu search and other optimization algorithms, which can be improved and used as a local search strategy to improve intelligent algorithms, or the use of techniques such as neural networks and deep learning, which may also produce good results.

Acknowledgments

This research work was supported by the National Natural Science Foundation of China (U1904167), Innovative Funds Plan of Henan University of Technology (2020ZKCJ02), Innovative Research Team (in Science and Technology) in University of Henan Province (21IRTSTHN018), Zhengzhou Science and Technology Collaborative Innovation Project (21ZZXTCX19) and the Grant-in-Aid for Scientific Research (C) of the Japan Society of Promotion of Science (19K12148).

Conflict of interest

The authors declare that there is no conflict of interest.