1.
Introduction
After the Industrial Revolution, the process of industrialization and urbanization in the world for more than 200 years has created abundant material wealth for human beings and brought great social development. However, in this process, human beings have excessively consumed natural resources, the combustion of coal, oil and other energy sources and the emission of greenhouse gases such as CO2 have brought serious environmental pollution, destroyed the balance of the ecosystem, and caused global climate change to heat up, threatening the safety of human existence [1]. Climate change has become a major challenge facing human society today [2]. In this context, 195 parties signed the Paris Agreement at the United Nations Framework Convention on Climate Change (UNFCCC) in 2015. The purpose of the Paris Agreement is to deal with climate change, prevent global temperatures from rising by 2 degrees Celsius from pre-industrial levels this century, and control the increase within 1.5 degrees Celsius [3]. Previous studies have shown that compared with current policies, the implementation of the Paris Agreement will help reduce global greenhouse gases (GHGs) to a certain extent, but it is not enough to achieve the 2 degrees' Celsius target [4]. More recently, in 2021, the COP26 was held in Glasgow, UK. During the meeting, negotiators sought to resolve outstanding issues in the 2015 Paris Agreement, and at the same time, worked to prevent global temperatures from rising by more than 1.5 degrees Celsius before industrialization in this century. This means that the world pays more attention to the changes in the climate environment. The European Union, the United States, and the International Council for Sustainable Standards have all released climate change-related guidelines in 2022, requiring companies to disclose climate change-related information [5,6]. China has also proposed a dual-carbon strategy of carbon peaking by 2030 and carbon neutrality by 2060, and has issued a series of programs and policies for this purpose. The promotion of climate change guidelines and the dual-carbon strategy will have a very important impact on the transformation and development of my country's industries, especially some industries with high emissions and high energy consumption. Related research reports pointed out that the root cause of climate warming is greenhouse gases, and carbon dioxide is an important part of greenhouse gases. Therefore, reducing carbon emissions is the only way to deal with climate change, save resources and energy, and protect the ecological environment.
At the 5th Plenary Session of the 18th CPC Central Committee, President Xi Jinping put forward the "five major development concepts": innovation, coordination, green, openness and sharing, and especially took the green development as a significant concept of China's overall development. Generally speaking, carbon emissions are considered a threat to the environmental quality; in addition, it is considered a threat to its productivity in the manufacturing sector [7]. In a related paper by Umar et al. [8], it was claimed that natural resources are not conducive to China's environmental sustainability because it was found that higher natural resource rents would have a positive impact on carbon emission levels. Ahmed et al. [9] also carefully studied the impact of natural resource rents on China's ecological footprint, asserting that higher natural resource rents would inhibit environmental quality by increasing this footprint. According to Wang et al. [10], the energy sector is one of the largest contributors to greenhouse gas (GHG) emissions. Lin et al. [11] believe that renewable energy is an important factor for China to achieve a low-carbon economic development path. The research results of Tsai and Jhong [12] show that government policy-makers can effectively reduce carbon emissions through total amount control (TQC) to solve the problem of environmental degradation. As the green development strategy has become people's mutual recognition, governments and corporations come to realize that environmental pollution not only wastes natural resources, but also brings enormous economic costs. The research of Xu et al. [13] shows that due to the increasing concern about environmental issues worldwide and the huge pressure on China to reduce emissions, promoting enterprises to go green and sustainable through the carbon market has become an important channel. Achieving low-carbon and green development and solving these environmental problems are the current economic strategic objectives of China. Many companies have also incorporated the development goals of energy conservation and emission reduction into their long-term development strategies. However, the existing cost accounting system in China does not have cost accounting for carbon emission indicators. Therefore, most Chinese companies do not include carbon emission costs in their production costs. As a result, Chinese companies do not have sufficient incentives to reduce carbon emissions.
Therefore, the continuous growth in carbon emissions has also raised the attention of the management practice circle gradually. Cost accounting of carbon emission has recently become topical [14,15,16]. Lohmann [14] for example, labeled cost accounting of carbon emission as a 'carbon black box' due to the intangibility of carbon emissions and unclear cost objects. In 2007, Janek Ratnatunga [17] proposed a systematic description of carbon emission accounting, and he believed that carbon emission accounting and carbon solid accounting should be collectively referred to as carbon accounting, and carbon emission accounting is an important part of the carbon accounting system. On this basis, Lin [15] further proposed that carbon emission accounting can be divided into: carbon emission trading accounting, carbon emission cost accounting and carbon tax accounting. It was beneficial to improve the calculation system for environmental cost accounting by researching, classifying and managing costs incurred in emissions of carbon dioxide and other greenhouse gases. Carbon emissions accounting is an accounting information system that reflects the carbon emitted in all aspects of an enterprise's production process. Based on a review of global conclusions, O'Mahony [18] details recent developments in carbon taxes. Park et al. [19] analyzed the impact of energy-saving technologies on residential carbon dioxide emissions by comparing Korea and China. The study by Wang et al. [20] examines the impact of economic globalization on environmental degradation (CO2 emissions) in G7 countries between 1996 and 2017. Xu et al. [21], according to the tracking and investigating of the Carbon Disclosure Project (CDP), believed that some companies had already taken actions, and they had begun to disclose information related to carbon emission costs on the occurrence of climate warming. In Hossein et al. [22] article, they proposed a carbon accounting method for appropriately distributing carbon load among countries, which helped to accurately account for the fairness of emission responsibilities. Unfortunately, because the disclosed carbon information lacked uniformity and comparability, there was no way to express its usefulness to decision-makers and stakeholders. The findings of Hatice and Gökhan [23] suggest that there is a mutually important relationship between environmental accounting and performance, however, the study found that companies' environmental accounting practices are at a low level. Therefore, the author shown, at the end of the article, the opinion that the government or relevant agencies should formulate uniform and feasible disclosure rules on carbon emission information to strengthen the practical value of those disclosed information.
Although Chinese scholars started late, they still put forward theories more in line with China's national conditions on the basis of studies in other countries. Carbon activities can be calculated and controlled through two levels of material flow and value flow in the carbon emission process, so as to calculate and manage carbon emission costs [24]. Huang et al. [25] studied the production cycle list of specific iron and steel enterprises in China, and got the conclusion that their carbon emission mainly comes from domestically produced products and the amount of emissions are affected by the manufacturing process, manufacturing technology and the degree of product processing. Han and Wang [26] also combined the case analysis and application of carbon cost accounting for iron and steel companies, which incorporate the life cycle method and the operating cost method to establish a new carbon cost accounting system and deepened the accounting unit to the operating level. By measuring and disclosing the capacity of carbon credit assets related to carbon emissions and carbon storage activities, relevant research had been conducted [27]. Zhang et al. [28] mentioned that China has launched a carbon emissions trading market and established a national carbon emissions trading system, all requiring accurate carbon audits to reflect corporate carbon emissions. Experts and scholars define and analyze the concept of carbon cost based on multiple dimensions and multiple backgrounds. The definition and types of carbon cost corresponding to different research angles also show differences. Some scholars are concerned about the early prevention cost, however, it ignores the carbon costs incurred during production, processing, storage, and transportation; some scholars emphasize the internal and external differences in carbon costs, ignoring the differences before and after the company's production and processing. There are major limitations, which may not be conducive to the development of carbon emission reduction activities.
In summary, some scholars in the world use integrated design methods and technologies to evaluate the results and cost-effectiveness of implementing low-carbon management, and their evaluation technologies and methods have begun to take shape. However, the development of low-carbon management evaluation in China is relatively weak. This situation is inconsistent with the continuous development trend of China's low-carbon management theory and practice. Through the collation of international literature, it can be found that China's research on cost accounting of carbon emission is later than other countries, and the breadth and depth of the research are slightly inferior. Chinese scholars have not yet reached a unified conclusion on the concept of carbon cost. In addition, due to a lack of environmental attention in the past, there has been little study on the cost accounting of the carbon emission method applied to companies, so the calculated knowledge of the company's carbon cost is vague. The current cost accounting of the carbon emission model cannot create a solid foundation for company managers to choose from. A suitable and appropriate mechanism for confirming, measuring, and disclosing carbon costs has not been built. There is still a large gap between the cost accounting of carbon emissions generated by enterprises in the production process and the practices of developed countries. The need for developing a thorough cost accounting of carbon emission model has become critical.
The purpose of this paper is to confirm and account for all internal and external costs of carbon emissions generated in the entire production process of the company, so as to build a comprehensive internal and external carbon cost accounting system for the company, effectively control the cost of corporate carbon emissions, and promote the green development of the company.
Consequently, the current paper seeks to make the following contributions to the existing literature. First, in terms of carbon cost measurement, the paper quantifies carbon cost based on the production processes of energy companies using specific measuring methodologies. Second, in terms of the cost accounting of carbon emissions, this paper splits the carbon emission cost for energy companies into internal and external costs of carbon emissions. Third, the value of material flow in each production process and the carbon emissions at each stage is calculated using the established formula model. The product life cycle, internalization of external costs, and other relevant factors are all included in the research process of this paper. We believe that cost accounting of carbon emissions would lead companies to adapt to the demands of the low-carbon era and achieve sustainable growth.
The remainder of the paper is structured as follows. Section two describes the concept of carbon emission costs, the classification of carbon emission costs, and the measurement method of carbon emission costs. Section three considers the determination of the cost accounting of carbon emission (i.e., internal and external accounting of carbon emission activities). Section four entails developing a model of the cost accounting of carbon emission and a cost model from internal and external perspectives. The final section summarizes the paper.
2.
Theoretical framework
2.1. Definition of carbon emission costs
To a large extent, the green economy and low-carbon economy we are advocating need to reduce the companies' carbon dioxide emissions and enhance resource utilization ratio. Ge [29] believes that in the current background, the construction and practice of cost accounting of carbon emission are still difficult. Kou [30] put forward a series of suggestions on how Chinese companies can implement strategic cost management under the conditions of a low-carbon economy. The companies' carbon emission costs calculated effectively will be beneficial to help them reduce emissions reasonably. The calculation of carbon emission costs not only contains various aspects, but also requires synthetically considering environmental impacts. There are many factors incurring costs and the value of resources invested is also one-to-one correspondence in traditional cost accounting. Yet, there are many uncertainties in the measurement of carbon emission costs, and the external costs of carbon emissions activities require more relevant data and methods to account for.
Many scholars have analyzed and researched the costs of carbon emissions at the current stage, and they pointed out that the costs arise from the part of exceeded prescribed carbon emissions, including the costs of controlling carbon emissions and other losses. As the costs caused by carbon emissions during the production cycle of an enterprise, the essential attribute of carbon emissions costs is a kind of expenses. It can be further considered that carbon emission costs are generated by the loss of resources due to carbon emissions and the outflow of various economic benefits that can be measured in money to control carbon emissions.
There is no uniform conclusion on the definition of carbon emission costs in academia. Several recognized definitions are shown below. Firstly, in terms of the life cycle of companies' products, it is considered that carbon emission costs are the relevant costs and compensations incurred in the use, conversion and disposal of raw materials and energy during the production process. In addition, it is the total expenses paid for the purpose of prevention, treatment and maintenance of carbon emissions, including the loss of excessive emissions of greenhouse gases such as carbon dioxide. The third one is the outflow of all kinds of economic benefits that can be converted into monetary units for measurement to prevent, maintain and control greenhouse gas emissions during a corporate's life cycle. In conclusion, the carbon emission costs are defined as above from different perspectives, representing diverse nature, characteristics and defined scopes of carbon emission costs.
2.2. Classification of carbon emission costs
Yang et al. [31] systematically described the carbon emission cost model, including the classification of carbon costs. Carbon emission costs can be classified into two parts. Positive costs represent the expenses incurred by the effective use of substances and energy throughout the manufacturing cycle of products. These, meanwhile, show the cost of converting input materials into qualified products during the production process. Negative products mainly contain the greenhouse gases and different wastes emitted by the company in manufacturing process, which bring negative impacts on the external environment of companies. According to the research of Zhang and Li [32], carbon emission costs can be divided into the following five types: raw material carbon emission costs; artificially formed carbon emission costs; manufacturing costs related to carbon emission costs; waste disposal carbon emission costs; recycling the carbon emission costs in the process.
Apart from that, carbon emission costs can also be categorized by the purposes of the enterprise's cost, and the composition is illustrated in Table 1.
Carbon emission costs, at last, can be split into internal carbon emission costs and external carbon emission costs, according to carbon cost features and spatial scope. Among them, internal costs, generated within an enterprise, refer to expenses measured by currency that are borne and paid by the enterprise that discharges greenhouse gases in terms of energy, materials, systems and the like during the production and operation. The external costs chiefly refer to the part of costs that cannot be afforded by the enterprise, which are caused by environmental impacts in regard to the external emissions of carbon dioxide and other harmful substances incurred in operating and producing. Although external costs cannot be confirmed and measured, the climate quality is indeed affected due to corporate carbon emission activities, which can be converted into internally accountable costs through special methods.
2.3. Measurement methods of carbon emission costs
2.3.1. Material Flow Cost Accounting (MFCA)
Based on the law of conservation of mass, MFCA tracks the changes in the amount of input, conversion and consumption of raw materials and energy in the production process of the enterprise, so as to calculate its amount and value. Cao and Zhang [33] use the principles of material flow cost accounting to systematically explain the development process and analysis system of resource value flow accounting.
During the movement of materials, the best way for companies to reduce environmental damage is to control pollution by reducing carbon emissions, that is, to control resource consumption by improving the effective utilization rate and recycling rate of materials.
It can motivate managers to take corresponding improvements for specific processes and links by calculating the flow, emission and consumption of materials in the production process from both the quantity and value. Thus, this process can improve the quality of materials used, increase the utilization of materials and energy, reduce the resources consumed in production, control carbon emissions and drop its threat to the environment.
2.3.2. Life Cycle Assessment (LCA)
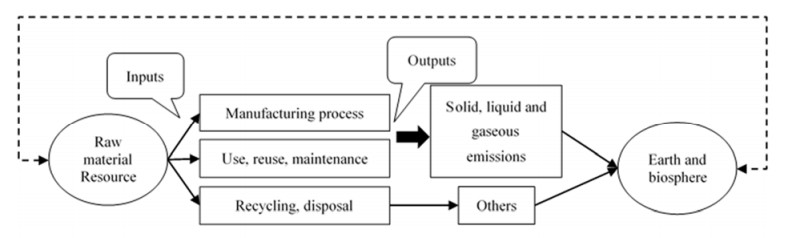
As a method of evaluating the environmental loads or impacts arising from products, LCA has attracted international attention in recent years. The entire life cycle of a product is the whole stage from product design, raw material extraction through manufacturing, recycling and final processing. The potential environmental impacts, during the production process, in relation to inputs and outputs are assessed by interpreting inventory records and analyzing the environmental impacts based on the key components determined in LCA. It specifically is depicted in Figure 1.
As it is an environmental impact assessment system, LCA generally consists of four components: goal definition and scope, inventory analysis, impact assessment, and interpretation. LCA not only considers the internal carbon costs of an enterprise, but also the external carbon emission costs of the enterprise, which can reflect both the internal operating efficiency and the external environmental efficiency of the enterprise. This method calculates and confirms the carbon emission costs generated during the overall life cycle of the product, thus, it can ensure the completeness of the costs during the production cycle.
At present, relatively mature, stable and usable databases have been formed abroad, especially in countries with earlier use of environmental costs such as Japan and Europe. The effect of its use is clearly reflected in the process of various environmental management performance evaluations. The principle methods for evaluations include Maximum-Abatement Cost method (MAC), Environmental Policy Priorities Index for Japan (JEPIX) and Life-cycle Impact Assessment Method based on Endpoint modelling (LIME).
LIME, a method of LCA, is usually used to evaluate the impact of products on the environment, and it focuses on how much a company needs to spend to reduce the impact on environment caused by substances. However, since there is no a set of related applicable calculation standards or systems in China, the LIME values refer to Japanese standards. In the comprehensive coefficient table about environmental damage released by Japan in 2005, over 1000 environmentally-affecting substances in 11 areas were classified in detail, such as global warming, ozone layer holes and air pollution. These emissions and wastes were unified into standard units. These standard units were roughly divided into three categories: weight-kg, gas-m3, and electricity-kwh. The corresponding discount rate could be selected from the discount rate table to determine the LIME coefficient value, and the final impact of each substance on the environment could be calculated approximately by the multiplication of the LIME value by the standard unit. Ifeyinwa and Sun [34] concluded that equipment costs and carbon emission costs are the main components of manufacturing costs. The life cycle cost of green manufacturing products is lower than that of similar products manufactured in traditional manufacturing.
3.
Research design
Most of the accounting and research on carbon emission costs generally focused on the carbon emission costs related to raw materials, energy and electricity in the past, while the carbon emission costs related to direct materials, such as product design, packaging and product transportation were comparatively neglected. In that case, the calculation of carbon emission costs should traverse the entire production life cycle of the product, including product design, manufacture, sales, transportation and disposal within the company. Xiao et al. [35] also constructed the three-dimensional information model and theoretical system framework of "material flow-value flow-organization" of environmental management accounting based on material flow cost accounting and life cycle theory.
3.1. Internal cost accounting for carbon emission activities
When calculating the carbon emission activities within the enterprise, based on the traditional cost gradual carry-over fractional step method and combined with the material flow-value flow method, the internal cost of the enterprise is transferred in each process or node and divided according to the flow content of the main elements in each production process, mainly the cost of raw materials and energy, the labor cost of intermediate inputs, etc.
The calculation of environmental pollution and damage value discharged by carbon (waste) needs to utilize the relevant technologies and methods related to environmental disciplines, such as LCA. Then, the added value of energy circulation, mainly based on the accounting principles of total industrial output value and industrial added value, is figured up on the basis of summarizing profits and taxes.
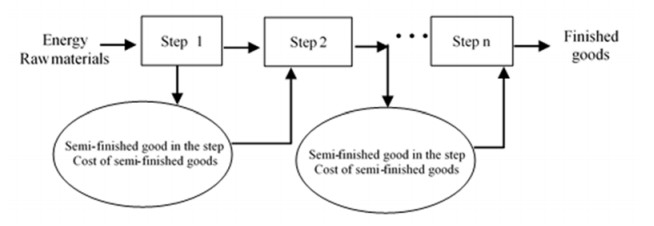
3.1.1. Traditional cost carry-over model
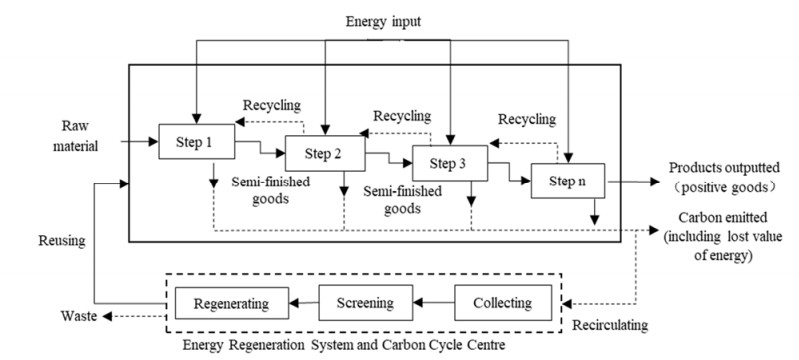
The gradual carry-over fractional step method requires to account cost spent at each part of the production steps of the product, and the finished product cost is achieved in the last step. The detailed procedures are shown in Figure 2. The final cost of the product in the gradual carry-over method = the production cost in step 1 + the production cost in step 2 +...+ the production cost in step n. The energy and materials, in the gradual carry-over method, are regarded as one input from the beginning of production, and only the expenditure is transferred in each process.
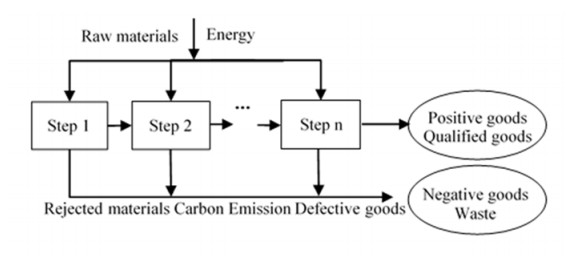
Although the raw material and energy flow analysis method is similar to the gradual carry-over method, the raw materials and energy are input in each process, and the carbon emissions generated in each process, then, would be calculated. During the manufacturing process, enterprises use various production equipment and pour raw materials and energy into each step that generates not only positive products like semi-manufactured products and finished products, but also negative products like contaminants and waste. The value of positive and negative products in each step varies with the different processes and the specific changes are provided in Figure 3.
3.1.2. Carbon cost accounting model
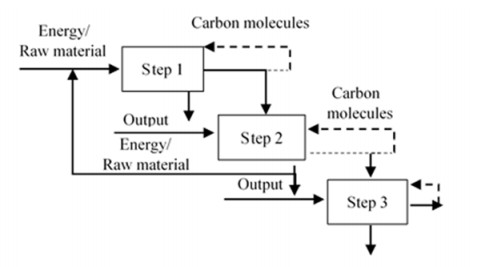
The corporate carbon flow cost accounting model is a mutual reference and integration of the above two methods. It is similar to the material inflow route of the enterprise with the process as the material center, while the outflow route is more complicated, including the transfer of qualified products to downstream firms and the waste discharged out of the industrial chain. In flow manufacturing companies, substances are usually analyzed with a certain element as a model (such as carbon element), pursuing continuous changes in material flow routes. Also shown in Figure 4 is the corporate carbon flow cost accounting model that comprises the input flow of the material flow and energy (carbon flow) carried from the upstream chain and the output flow of finished products, by-products and waste discharged from the system.
In order to calculate the volume of the carbon flow of the enterprise, this paper also takes reference of the material flow analysis method and Figure 5 illustrates how the process runs. Material flow analysis is a traditional method that aims to investigate the material transformation process in industrial activities. Through the quantitative analysis and evaluation of its utilization status, it is possible to effectively figure out points in the metabolic process that can boost material utilization efficiency or recovery rate.
Carbon cost can be incurred in each production process of enterprises, so that, carbon cost would be measured through multiple accounting methods and field measurements. By means of the extension of the cost accounting model, a bidirectional accounting model is established that can connect the internal cost and external cost of carbon emission activities, and comprehensive analysis and evaluation are validly adopted. Thus, more relevant data and information support can be provided for the in-depth development of the circular economy of enterprises and effective cost information support and guidance would be offered for the scientific decision-making and management of enterprise managers.
The resources inputted in the internal production process of the enterprise, as shown in Figure 6, mostly include the use of equipment, raw materials, labor, energy, etc., which eventually form positive products like semi-finished products and finished products and negative products including waste products through various processes. Apart from that, many wastes are discharged outside the company and those make a negative impact on the external environment of the company. The carbon emission costs are constantly circulating of the production process, and are automatically categorized into raw materials, energy and labor costs by the flow in the process. In the meantime, some indirect costs associated with the production process, such as equipment depreciation and related production costs, can also be allocated according to the same standard, thereby forming the positive and negative values of the products. The waste generated in carbon emission activities is, without doubt, a negative value.
As a consequence, it is possible to have a clearer understanding about the transfer process of carbon cost by tracking and reflecting the valuable information in the production process of the enterprise, such as resource input and consumption, output and waste, etc. A wide range of carbon emission cost data can be revealed on the premise of reduction of resource consumption and carbon emissions, so as to be valuable reference for making decisions by management. What's more, as the carrier of the physical consumption of resources and the transformation of value forms, enterprise not just, through the whole-process value analysis of the "vertical flow" of resources owned, clarifies the changes in the value form of resources in the production process, but also conduces to analyze and evaluate the circulation, recycle, utilization efficiency and environmental efficiency of the internal resources, and then provide a theoretical basis for the enterprise carbon performance evaluation.
3.2. External cost accounting for carbon emission activities
The carbon dioxide emitted outside of the company will increase the social cost resulted from the company's environmental damage as well as reducing the related social welfare. The external carbon emission cost is distinguished from the internal cost and it is characterized by its intangibility, the uncertainty of the data, and the unpredictability and unmeasurable value of potential influencing factors. Although it is difficult to quantify the monetary value of related carbon costs such as carbon dioxide emissions, the amount can be determined by studying its physical and chemical properties and combining them with the relevant descriptions of calculation standards performed by relevant agencies.
What is most easily neglected is that carbon emissions still have certain negative externalities. The negative externalities are mainly manifested at the macro level, for example, pollution to the environment; global warming, rising in sea level, and more extreme climates due to excessive carbon dioxide emissions; harm to human health, wildlife generated by smog, dust and toxic gases, and so on. In addition, the government and society will carry out environmental governance after the environment is polluted, which raises the government budget and social governance costs. It also means that, with the growth in carbon emissions at the present time, the environmental quality that future generations can enjoy will be getting worse, and the cost to govern environment is getting higher.
The cost of corporate carbon emission waste is reflected in both quantity and value. Based on the life cycle assessment method, it can reflect the negative impact on the external environment and cost losses that arise from corporate production activities, then form an integrated cost accounting model. For production-oriented enterprises, the negative value brought from environmental pollution and losses in corporate activities is measured. Because it can not only describe the social costs that the company is responsible to bear, but present the social responsibilities that enterprises should fulfill for achieving low-carbon economy, conserving energy and reducing emission that are vigorously advocated.
There is not a set of calculation systems and standards suitable for calculating the external costs of carbon emission activities of enterprises in China. After comprehensively considering many methods such as the life cycle assessment method, combined with its advantages and disadvantages and the characteristics of domestic enterprises, the life cycle environmental impact assessment method (LIME) based on the endpoint model is selected for analyze in the paper. In the above method, the environmental impact assessment is carried out on the emissions that are unfriendly to the environment. While, there is a wide scope in emissions and more than 1000 types are currently introduced. Since the amount discharged can be quantified in currency, it is specifically suitable for enterprises, especially manufacturing companies, to calculate external carbon costs.
The cost accounting of carbon emission model can quantify the changes in carbon costs in each process by tracking the changes in finished and semi-finished products in each process, thereby encouraging companies to save energy and cut emissions in product design, raw material input, manufacturing and other processes. What is more, when internal carbon cost accounting is combined with external, data support for companies can be provided to specify emission reduction rectification plans. Through the expanded accounting model and cost calculation, those can be measured that are the internal and external costs of the entire product life cycle during the company's material flow and value flow. So that, the measure can offer more relevant data and information support to deepen the circular economy and effective cost information support and guidance for enterprises' managers in daily management and decision-making, and then achieve a balance between enterprises' development and environmental protection.
4.
Results and discussion
The carbon cost is divided into two parts: the internal carbon emission costs and the external environmental damage carbon emission costs [36]. Through above analysis, the carbon cost is divided into internal carbon cost and external carbon cost that are calculated by using MFCA and LIME respectively. Based on the two-dimensional method to account for internal and external costs of carbon emissions, comprehensive analysis and detailed evaluation are carried out to identify the emission mitigation potentiality of each production process.
Therefore, the formula can be constructed as follows:
where IC is the internal carbon emission costs, and WEIV is the external carbon emission costs.
4.1. Internal carbon cost model
The internal cost mainly contains the specific data list of the input materials, energy and waste discharged in each process. These data about expenses are collected and classified according to the amount of resource consumption and the inflow and output of each element. Thus, there are seven major types: raw material cost, energy cost, labor cost, factory cost, positive product cost, negative product cost and governance cost.
The negative cost of the product refers to the negative impact of the excessive consumption of environmental resources during the extensive production process of the enterprise. It consists of three parts. Initially, there are the carbon emission costs. China signed The Paris Agreement on April 22, 2016, so that the carbon emission costs are considered as a key expenditure item to calculate environmental costs. Secondly, there are the pollution cost and governance expense, that is, relevant environmental expenses incurred in the production process, such as, pollution discharge fees, environmental insurance premiums, and heavy environmental damage fines due to excessive emissions that damage the environment. Thirdly, there are various taxes related to environment, such as resource taxes and environmental taxes.
Environmental governance costs and restoration expenses refer to the costs paid by the company after it causes pollution or damage to the environment, which is afforded to reduce environmental pollution, like pollution treatment costs, environmentally friendly equipment purchase and maintenance costs, environmental protection training costs, etc. In addition, those also contain the costs and expenses incurred by enterprises in some countries when they implement economic measures, such as environmental taxes and the levy of pollution fees and fines on enterprises that exceed standard, to protect the environment.
In the above formula, MCn is the raw material input cost of the nth process or node; ECn is the energy cost of the nth process; LCn is the labor cost of the nth process; FCn is the factory cost of the nth process; PCn is the qualified product and positive product cost of the nth process; NCn is the waste product and negative product cost of the nth process; Qpn is the carbon content of the nth process; GC is the governance cost in the environment.
4.2. External carbon cost model
Among them, WEInj is the discharge amount of j types of wastes that have impacts on the environment in the nth process or node; UEIVnj is the unit environmental impact value of j types of wastes in the nth process or node. According to the LIME method, the waste and carbon emissions are multiplied by the LIME coefficient to obtain the external carbon emission costs. Since LIME is a method proposed by Japanese scholars, the standard currency of its quantitative unit is the Japanese Yen, which is distinguished from the RMB. In order to make a comparison and analysis between the carbon emission cost more accurately, carbon accounting should also be considered to perform, and the LIME coefficient should be converted into RMB through the year-end exchange rate before calculation.
The whole procedure mainly has the following five steps: 1) Collecting the amount of carbon dioxide emissions generated by each production process or node, including producing emissions, processing capacity, resource utilization, etc.; 2) Establishing a standardized system to measure carbon emissions; 3) Identifying the unified standard unit of emissions and waste, and selecting the corresponding discount rate from the discount rate table to determine the LIME coefficient. It should be noted that because the currency unit of the LIME database is the Yen, it is necessary to convert it into RMB according to the exchange rate when the carbon external cost is obtained; 4) Multiplying the carbon dioxide emissions collected in the first step by the external damage cost per unit of carbon emissions, so as to get the total external damage carbon emission costs for each process or node of the company's production; 5) Compiling a summary table of external damage costs of carbon emissions. The carbon emission activities in each process can be obtained after calculating based on the data in the LIME database. Moreover, the costs can be connected to forming a material circulation route map that can match its carbon flow route.
By constructing a total cost model of carbon emissions, the cost and value of related materials and energy in each link can be determined and quantified, and changes in various manufacturing processes of different finished products and semi-finished products of the enterprise can be tracked. Besides, the internal carbon emission costs are combined with the external cost to provide the enterprise with data support and determine the priority of emission reduction rectification. And then, managers would be suggested to save energy and reduce emissions as much as possible in the process of product development, selection of raw materials and transportation, so as to minimize the total carbon emission costs. Through the scientific measurement analysis of the internal and external costs of carbon emissions, the related cost information about material consumption and waste can be clearly shown, and an optimized path and decision-making support also can be offered for conserving energy and abating emissions. Therefore, there will be a win-win situation in economy and environment to be occurred.
5.
Summary and conclusions
Based on the status quo of the enterprise and the traditional cost accounting system, this paper uses material flow cost accounting, product life cycle assessment and other methods to conduct systematic research to determine and quantify the internal and external costs of carbon emissions generated by energy companies. Build a carbon cost accounting system for Chinese energy companies, scientifically measure carbon costs, and better reflect material consumption and waste cost information of Chinses energy companies. The total carbon emission cost model provides companies with a cost accounting of carbon emission method and proposes reasonable emission reduction measures based on relevant data and information, in order to improve the overall cost management ability of the enterprise and the decision-making ability of the company's top management.
With the establishment of China's carbon emissions trading market, it is the premise of the establishment of carbon trading market that enterprises need to conduct accounting and measurement of carbon dioxide. A good cost accounting of carbon emission is conducive to the analysis and control of carbon costs for enterprises, and limited risk avoidance is an important prerequisite for maintaining the competitiveness of enterprises and achieving sustainable development. For the government, the allocation of carbon allowances can be carried out according to the carbon emissions of enterprises. It also provides good conditions for carbon performance evaluation and avoids "greenwashing" behaviors of enterprises.
Two directions are suggested for future research in this paper. Firstly, academics should continue to refine the accounting model of carbon emissions costs. Due to the huge differences in carbon emissions between different industries, there is no generic model yet. Different features between industries need to be considered to maximize the goal to reduce low-carbon emissions when constructing the cost accounting model to make the model more practical. Secondly, governments of all countries should optimize accounting standards and related technical standards for carbon emissions, such as introducing related policies or formulating a unified standard. International organizations and governments are also expected to unify accounting standards in the foreseeable future. Companies have a reference to follow and improve through continuous practice to calculate the carbon emission activities. The carbon emission cost information on corporate activities is thus fairly presented.
Acknowledgments
This work was supported by the Natural Science Foundation of Hunan Province under Grant number 2022JJ31021.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: