Threshold dynamics of a viral infection model with defectively infected cells

1.   Introduction

Infectious diseases caused by viral infections such as influenza, AIDs, heptitis B/C, and the current COVID-19 pandemic have always been being a big threat to both public health and economy. Though the underlying infection mechanisms in hosts are very complex, mathematical modeling has been an effective tool to understand the infection and to provide guidelines on control. One of the simplest viral infection models,

was proposed and investigated by Nowak et al. ^[1,2,3]. Here $x(t)$, $y(t)$, and $v(t)$ are the densities of uninfected target cells, infected target cells, and free viruses at time $t$, respectively. We refer the readers to the citations for the biological meanings of the positive parameters. Model (1.1) has been modified by many researchers to better understand the interaction mechanism between viruses and host cells in more detail and to evaluate the efficiency of associated therapies. For example, we refer to some on latent infection ^[4], on eclipse stage ^[5], on immune response ^[6,7,8], on cellular reservoirs ^[9,10,11], on treatment ^[9], on the effects of delay ^[10,12], on co-infection ^[6,13], on the effect of drug abuse on HIV dynamics ^[14].

It was pointed out in ^[15,16] that, for some infectious diseases induced by viruses, the infected cells could contain defective viruses, that is, these infected cells produce defective proviruses that will not produce any offspring viruses. To model this phenomenon, Nowak and May ^[17] divided the infected cells into three classes, longer lived latently infected cells ($y_1$), actively infected cells ($y_2$) that produce large quantities of free viruses in a short time, and defectively infected cells ($y_3$) that contain mutated virus genomes and cannot produce new virions. They proposed the following viral infection model,

where the parameter $p_i$ ($i = 1$, $2$, $3$) denotes the probability that upon infection a cell will become an infected cell of type $y_i$, $\sum_{i = 1}^3p_i = 1$, $\delta_i$ ($i = 1$, $2$, $3$) is the death rate of the associated infected cells, $\gamma$ is the transfer rate of latently infected cells to actively infected ones, $k_1$ and $k_2$ are the numbers of free viruses produced by a latently infected cell and an actively infected cell, respectively. Model (1.2) can also be used to describe low steady state viral loads ^[18].

Model (1.2) includes some previously studied viral infection models. For example, Korobeinikov ^[19] investigated the global stability of the case where $p_2 = p_3 = k_1 = 0$, that is, after being infected, susceptible cells must undergo a latent stage before producing viruses and there is no defectively infected cells. The case where, after being infected, susceptible cells become either latent or active, and only actively infected cells can produce viruses, that is, $p_3 = k_1 = 0$ and $p_1 = 1-\alpha$, $p_2 = \alpha$ with $\alpha\in (0, 1)$, was studied in ^[20,21]. When $p_3 = \gamma = 0$ and $p_1 = 1-\alpha$, $p_2 = \alpha$ with $\alpha\in (0, 1)$, the corresponding model is the same as that with treatment in ^[21], where $y_1$ and $y_2$ are the populations of infected cells under different drug effects. However, to the best of our knowledge, the dynamical behavior of model (1.2) with $p_1p_2p_3\gamma\ne 0$ is not completely understood.

With respect to the analysis of viral dynamic models, the stability of equilibria plays a very important role in understanding the mechanism of virus infection and outcome of treatment. To name a few, ^[19] dealt with some basic virus dynamics models, ^[9,20] considered models with eclipse stages of infected cells, ^[21,22] investigated models with nonlinear incidences, ^[23,24] modeled Zika virus, and ^[25,26] included the immune response. One of the most powerful approaches to determine the global stability of equilibria of differential equations is Lyapunov's direct method. The key to applying this method is to construct an appropriate Lyapunov function. It requires both that the constructed function be positively definite and that its derivative along solutions of the system be negative definite or negative semi-definite. These two requirements are interrelated. In practice, it is often difficult to fulfill the second requirement or it is complicated to verify it for a positive definite function. By now, lots of techniques and methods have been developed for studying the stability of dynamic models in some applied disciplines. We refer to some for the basic framework ^[27]. In ^[28] we found a new type of function to construct Lyapunov functions while in ^[29] we provided a new way to do so with commonly used Volterra-type functions and quadratic functions. Moreover, to verify the negative (semi-)definiteness of the derivative of a class of Lyapunov functions along solutions of the system, a graph-theoretic approach and an algebraic approach were developed by Guo et al. ^[30] and Li et al. ^[31], respectively. Recently, for stability of disease models with immigration of infected hosts, McCluskey ^[32] gave a general result on finding algebraic conditions under which the Lyapunov function for a model without immigration of infected hosts extends to be a valid Lyapunov function for the corresponding system with immigration of infected hosts. In spite of the rich literature, the global stability of equilibria of many dynamical models still can not be proved theoretically.

The purpose of this paper is to provide a new approach to discuss the global stability of equilibria of system (1.2). Our approach has three features. Firstly, there is a correlation between the two Lyapunov functions used to prove global stability of the infection-free equilibrium and the infection equilibrium. Secondly, the specific form of Lyupunov functions used is universal. Lastly, compared with existing approaches, ours here to verify the negative definiteness or negative semi-definiteness of the derivatives of the Lyapunov functions along solutions is relatively simple. We would mention that viral dynamical models share many features with the classical compartmental models of infectious diseases (see, for example, ^[33] on SIR and SIRS models with nonlinear incidences, ^[34] for stage-structured epidemic models, ^[35,36] for models with asymptomatic and symptomatic infectious individuals, and ^[37] for some cholera models) and even models of vector-borne diseases (to name a few, see ^[38,39,40] for vector-borne disease models with two transmission routes for the host population, ^[41] for a model on vector-borne relapsing diseases, ^[42] for a vector-borne disease model with human and vectors immigration, and references therein). We expect that the approach here can be applied to study the global stability of equilibria of such models.

Note that $y_3$ is decoupled from the other equations in model (1.2). As a result, we only need to focus on

where $c_1 = \delta_{1}+\gamma$, $c_2 = \delta_{2}$, and $0 < p_1+p_2\le 1$. It is easy to see that every solution of (1.3) with a nonnegative initial condition exists globally and is also nonnegative. The rest of the paper is organized as follows. In the next section, we derive the expression of the basic reproduction number of viruses with the approach of the next generation matrix and determine the equilibria of (1.3). Section 3 is the main part of this paper, which is devoted to establishing a threshold dynamics for (1.3). The paper ends with a brief conclusion and discussion.

2.   The basic reproduction number and equilibria

We first obtain the expression of the basic reproduction number (of viral particles) of model (1.3) by employing the method of the next generation matrix developed by van den Driessche and Watmough ^[43]. For this purpose, we denote $z = (y_1, y_2, v, x)^T$. Then model (1.3) can be rewritten as

where

Obviously, model (1.3) always has the infection-free equilibrium $P_0 = (x_0, 0, 0, 0)$, where $x_0 = \frac {{\lambda}}{{\mu}}$. Accordingly, system (2.1) has an equilibrium $\bar P_0(0, 0, 0, x_0)$ corresponding to $P_0$.

The Jacobian matrices of $\mathcal {F}(z)$ and $\mathcal {V}(z)$ at the infection-free equilibrium $\bar P_0$ are

respectively, where

Then the basic reproduction number, $R_0$, of model (1.3) is the spectral radius of the next generation matrix $FV^{-1}$, that is,

The three terms in $R_0$ correspond to the three ways that viral particles are produced. In a wholly population of uninfected target cells of size $x_0$, suppose a viral particle is introduced. During its lifespan, $\frac{1}{c}$, it will infect $\frac{\beta x_0}{c}$ uninfected target cells. Among them $p_1\frac{\beta x_0}{c}$ will be latently infected and $p_2\frac{\beta x_0}{c}$ will be actively infected. For the latently infected cells, during their lifespan $\frac{1}{c_1}$, $\frac {p_1\beta x_0k_1}{cc_1}$ viral particles will be produced and $\frac{\gamma p_1\beta x_0}{cc_1}$ actively infected cells will be produced. Then during the lifespan $\frac{1}{c_2}$, the total $\frac{p_2\beta x_0}{c}+\frac{\gamma p_1\beta x_0}{cc_1}$ actively infected cells will produce $\frac{k_2}{c_2}(\frac{p_2\beta x_0}{c}+\frac{\gamma p_1\beta x_0}{cc_1})$ viral particles. Therefore, a total of $R_0$ viral particles will be produced. This biologically explains $R_0$ as the average number of secondary viral particles produced by introducing a typical viral particle into a population of uninfected cells.

Next we find the equilibria of (1.3). An equilibrium satisfies

It follows from (2.3a) that

Substituting it into (2.3b) gives

Now substituting (2.4) and (2.5) into (2.3c), we get

Finally, substituting (2.4)–(2.6) into (2.3d) yields

Thus, for (2.3), we have

Obviously, $v = 0$ produces the infection-free equilibrium $P_{0}$. For $v^*$ to give a biologically relevant equilibrium, we require $v^* > 0$ or equivalently $R_0 > 1$. In summary we have obtained the following result on equilibria of (1.3).

Theorem 1. Model $(1.3)$ always has the infection-free equilibrium $P_{0}$. Furthermore, when $R_0 > 1$, there is also a unique infection equilibrium $P^{*}(x^{*}, {y_{1}}^{*}, {y_{2}}^{*}, v^{*})$, where$v^* = \frac{\mu}{\beta}(R_0-1)$ and

3.   A threshold dynamics

In this section, by applying the approach of Lyapunov's direct method, we establish a threshold dynamics determined by $R_0$ for (1.3).

We first show the boundedness of solutions of (1.3). Let $q\in (0, \min\{\frac{c_1-\gamma}{k_1}, \frac{c_2}{k_2}\})$. A straightforward calculation yields

where $\rho = \min \{\mu, c_1-\gamma-qk_1, c_2-qk_2, c\}$. It follows that

and hence

Moreover, similarly, it follows from $\frac{dx}{dt}\le \lambda-\mu x$ that

The above discussion implies that solutions of (1.3) are bounded. Moreover, it is easy to see that the set

is positively invariant and attracting for system (1.3).

The following result on the existence of solutions to a set of inequalities will be used to construct appropriate Lyapunov functions.

Lemma 2. For the parameters $\gamma$, $c$, $\beta$, and $p_i$, $k_i$, $c_i$ ($i = 1$, $2$) of $(1.3)$, if

then the following system of inequalities on $m$, $n$, and $q$,

must have positive solutions.

Proof. It follows from the first two inequalities of (3.2) that

Hence it is necessary that

and

This, combined with the last two inequalities of (3.2), gives the following system of inequalities on $n$ and $q$,

It is easy to see that the system of linear equations on $n$ and $q$,

has a unique solution

Note that $q^* < \frac{c_1}{p_1k_1}$ and the condition (3.1) is equivalent to $\frac{\beta \rho}{c}\le q^*$. Then the solution set of (3.6) is given by

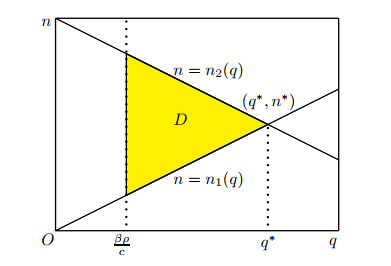
where $n_1(q) = \frac {qk_2}{c_2}$ and $n_2(q) = \frac {c_1-qp_1k_1}{p_1{\gamma} +p_2c_1}$ are derived from system (3.7) corresponding to the first two inequalities of (3.6) (see Fig. 1).

Clearly, for $(n, q)\in D$, we have $n < \frac{1}{p_2}$ and $\frac{n\gamma +qk_1}{c_1} < \frac{1-np_2}{p_1}$. Thus, for $(n, q)\in D$, we can choose $m$ according to (3.3). Then such $(m, n, q)$ is a positive solution of (3.2).

Notice that $\frac{cc_2c_1}{\beta[p_1k_1c_2+k_2(p_1\gamma +p_2c_1)]} = \frac{x_0}{R_0}$ according to the expression of $R_0$ defined by (2.2). Then the condition (3.1) can be rewritten as $0 < \rho\le \frac{x_0}{R_0}$.

The next two results follow from the proof of Lemma 2 and will be useful in applying Lyapunov's direct method.

Corollary 3. Suppose $\rho < \frac{x_0}{R_0}$, i.e., $\frac{\beta \rho}{c} < q^*$. Then there are positive numbers $m$, $n$, and $q$ satisfying the following system of inequalities,

Corollary 4. Suppose $\rho = \frac{x_0}{R_0}$, i.e., $\frac{\beta \rho}{c} = q^*$. Then $(3.2)$ only has the unique solution,

in other words, only the equalities hold.

Denote

Let $(x(t), y_1(t), y_2(t), v(t))$ be a solution of (1.3) with $(x_0, y_{10}, y_{20}, v_0)\in \Omega$. Then $x(t) > 0$ for $t > 0$. If further $(x_0, y_{10}, y_{20}, v_0)\in \Omega_0$, then the solution is positive for $t > 0$. Thus $\Omega_0$ is a positively invariant set of (1.3).

Now we are ready to prove the main result of this paper, a threshold dynamics of (1.3) determined by the basic reproduction number $R_0$.

Theorem 5. If $R_0\le 1$, then the infection-free equilibrium $P_0$ of $(1.3)$ is globally asymptotically stable in $\Omega$, while if $R_0 > 1$, then the infection equilibrium $P^*$ is globally asymptotically stable in $\Omega_0$.

Proof. As mentioned earlier, the approach is Lyapunov's direct method. To construct appropriate Lyapunov functions, we need the Volterra-type function $g:(0, \infty)\ni u\mapsto u-1-\ln u$. Note that $g$ is nonnegative and attains its global minimum $0$ only at $u = 1$.

We first consider the infection-free equilibrium $P_0$ with a Lyapunov function of the form,

where $m$, $n$, and $q$ are positive numbers to be determined. Note that $L_1$ can be regarded as well-defined by the discussion just a few lines above. Clearly, $L_1$ is positive definite about $P_0$, that is, the function $L_1$ is zero only at $P_0$ and positive at other points. The derivative of $L_1$ along solutions of system (1.3) is given by

For $L_1'\le 0$ on $\Omega$, it is sufficient that

With the definition of $q^*$ in (3.8) and $x_0 = \frac{\lambda}{\mu}$, we see that $R_0$ can be expressed as $R_0 = \frac{\beta x_0}{cq^*}$. Then $R_0\le 1$ is equivalent to $x_0\le \frac{cq^*}{\beta}$. Thus (3.12) is the same as (3.2) with $\rho = x_0$. We distinguish two cases to finish this part.

Case 1: $R_0 < 1$. Then $x_0 < \frac{cq^*}{\beta}$. By Corollary 3, we can choose positive $m$, $n$, and $q$ satisfying (3.9) with $\rho = x_0$. As a result, $L_1'$ is negative definite about $P_0$, namely, the function $L_1'$ is zero only at $P_0$ and negative at other points. It follows from Lyapunov Theorem ^[44] that $P_0$ is globally asymptotically stable in $\Omega$ if $R_0 < 1$.

Case 2: $R_0 = 1$. Then $x_0 = \frac{cq^*}{\beta}$ and Corollary 4 tells us that the positive numbers $m$, $n$, and $q$ determined by (3.10) with $\rho = x_0$ are the unique solution of the inequalities (3.12). Consequently, $L_1' = -\frac{\mu(x-x_0)^2}{x}\le 0$ and

Let $(x(t), y_1(t), y_2(t), v(t))$ be a solution of (1.3) in $M_1$. Then $x(t) = x_0$. It follows that $0 = \frac{dx(t)}{dt} = \lambda-\mu x(t)-\beta x(t)v(t) = -\beta x_0v(t)$, which gives $v(t)\equiv 0$. Thus $0 = \frac{dv(t)}{dt} = k_1y_1(t)+k_2y_2(t)-cv(t) = k_1y_1(t)+k_2y_2(t)$ produces $y_1(t) = y_2(t) = 0$ as $y_1(t)\ge 0$ and $y_2(t)\ge 0$. This shows that the largest invariant set of (1.3) in $M_1$ is the singleton $\{P_0\}$. Therefore, by LaSalle Invariance Principle ^[27], $P_0$ is globally asymptotically stable in $\Omega$ if $R_0 = 1$.

To sum up, $P_0$ is globally asymptotically stable in $\Omega$ if $R_0\le 1$.

Next, we consider the stability of the infection equilibrium $P^*$ in $\Omega_0$ with the Lyapunov function candidate,

where $m$, $n$, and $q$ are positive numbers to be determined. Again we can assume that $L_2$ is well-defined on $\Omega_0$. $L_2$ is positive definite about $P^*$ and the derivative of $L_2$ along solutions of system (1.3) is

where

Since $L_2' = 0$ for $\frac{x}{x^*} = \frac {y_1}{y_1^*} = \frac{y_2}{y_2} = \frac{v}{v^*} = 1$, we have $C = -F(x^*, y_1^*, y_2^*, v^*)$.

We define a function $F^*(x, y_1, y_2, v)$ related to $F(x, y_1, y_2, v)$ by

A straightforward calculation shows

According to system (2.3) satisfied by the infection equilibrium $P^*(x^*, y_1^*, y_2^*, v^*)$, we have $F^*(x, y_1, y_2, v) = 0$. Therefore,

Recall that $g(u)\ge 0$ for $u > 0$ and $g(u) = 0$ if and only if $u = 1$. To make $L_2'\le 0$, it suffices that the positive numbers $m$, $n$, and $q$ satisfy the following system of inequalities,

Again, (3.16) is the same as (3.2) with $\rho = x^*$. According to Corollary 4, the system of inequalities (3.16) has a unique positive solution,

and in fact all the equalities of (3.16) hold. Then with these $m$, $n$, and $q$, $L_2'$ becomes

It follows that $L_2'\le 0$ and

Let $(x(t), y_1(t), y_2(t), v(t))$ be a solution of (1.3) in $M_2$. Then $x(t) = x^*$ and $\frac{y_1(t)}{y_1^*} = \frac{y_2(t)}{y_2^*} = \frac{v}{v^*} = \theta(t)$ for a positive function $\theta$. It follows from $0 = \frac {dx(t)}{dt} = \lambda -\mu x(t)-\beta x(t)v(t) = \lambda -\mu x^*-\beta x^*v(t) = \beta x^*(1-\theta(t))$ that $\theta(t)\equiv 1$, which implies that the largest invariant set of system (1.3) in $M_2$ is the singleton $\{P^*\}$. Therefore, LaSalle Invariant Principle^[27] tells us that $P^*$ is globally asymptotically stable in $\Omega_0$.

4.   Conclusion and discussion

In this paper, for a viral infection model with defectively infected cells, we obtained a threshold dynamics, which is completely determined by the basic reproduction number of virus $R_0$. That is, the virus dies out when $R_0\le 1$ while the virus persists and the viral load approaches a positive number when $R_0 > 1$. In practice, for diseases described by this model, any measure makes $R_0$ below unity is quite effective. The explicit expression of $R_0$ provides guidelines on how to increase or decrease parameter values by appropriate control strategies. Even if we cannot make $R_0\le 1$, the global stability of the infection equilibrium tells us that we can still change the values of parameters to make the viral load below the tolerance level.

The obtained result is established by Lyapunov's direct method. The Lyapunov function for the infection-free equilibrium is a linear combination of the Volterra-type function (for the uninfected target cells) and linear functions (for the other three variables) but the one for the infection equilibrium is a linear combination of only Volterra-type functions. Surprisingly, the coefficients satisfy the same set of inequalities to make the derivatives along solutions negative (semi-)definite. This shows that there is a correlation between the two Lyapunov functions with given forms. It solves the problem of constructing Lyapunov functions used to prove the global stability of infection equilibrium to certain extent, since it is often difficult to find a suitable Lyapunov function for the positive equilibrium, but easy for the boundary equilibrium.

Furthermore, for the given form of Lyapunov function, we used the method of undetermined coefficients to determine them. By this method, all the suitable coefficients of the given form can be found. Therefore, it has the advantage of universality, which has been shown in ^[31,45]. But, with respect to proving the negative definiteness or negative semi-definiteness of the derivative of the Lyapunov function along solutions of the model, the approach used here is different from those in ^[31,45].

According to the algebraic approach proposed in ^[31,45], even if the coefficients of the Lyapunov function ($L_2$) are given, in order to show the negative or negative semi-negative definiteness of its derivative ($L_2'$), the derivative ($L_2'$) must be expressed in the following form

where the expressions of $b_i$'s ($i = 1$, 2, 3, $4$) also need to be determined. For low dimensional differential systems, the approach of rearranging the terms in the derivative is feasible, but it is not so easy for systems with higher dimensions. Thus the approach of proving the global stability of the infection equilibrium here is concise. It can also indicate that this approach is relatively simple for proving the global stability of the endemic equilibria of high dimensional epidemic models in ^[37,46].

Acknowledgments

This work is supported partially by the National Natural Science Foundation of PR China (Nos. 11971281, 12071268, 12071418).

Conflict of interest

The authors declare there is no conflict of interest.