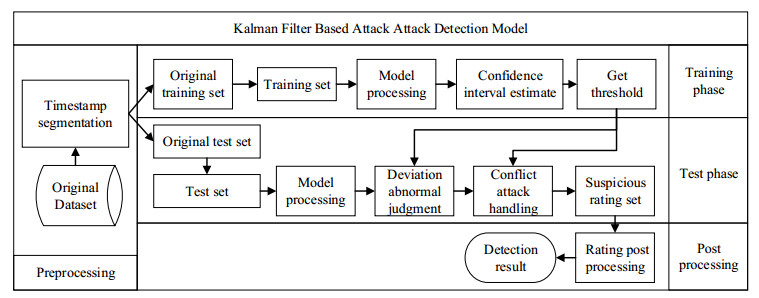
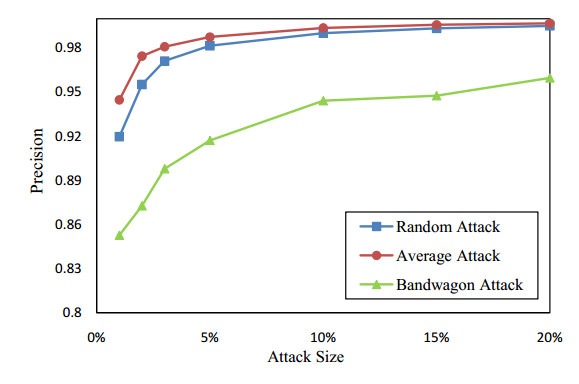
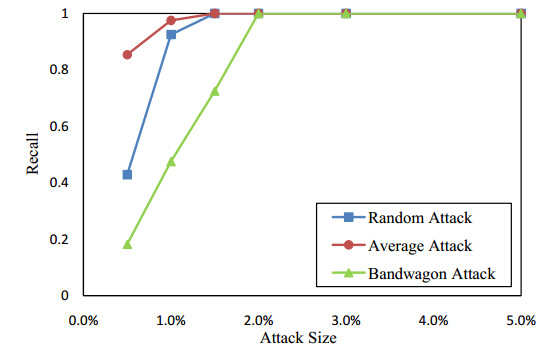
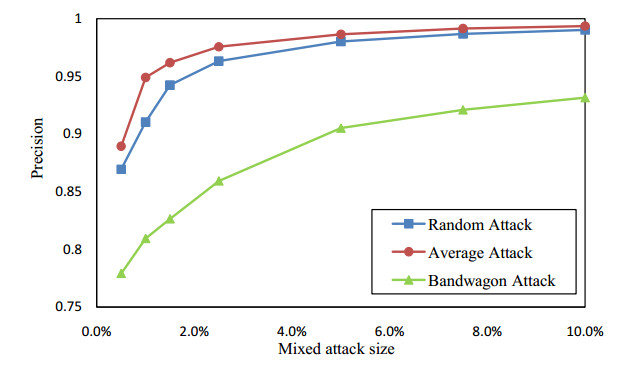
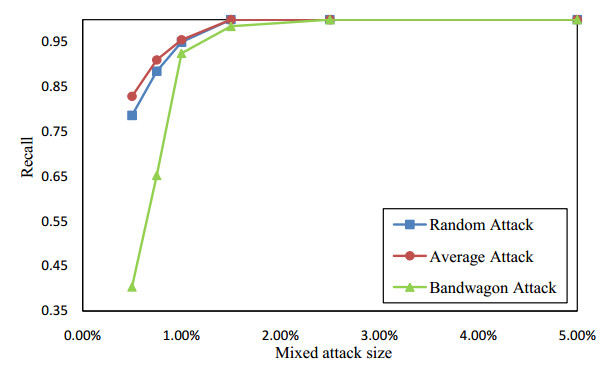
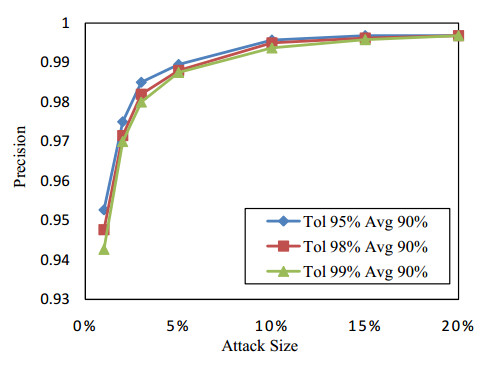
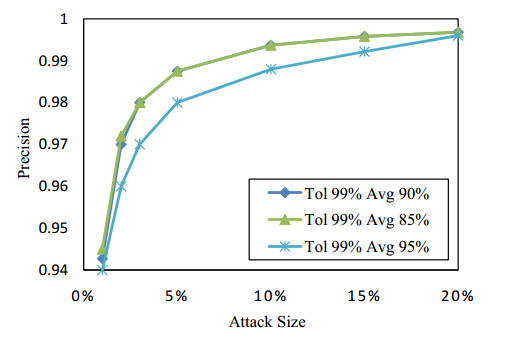
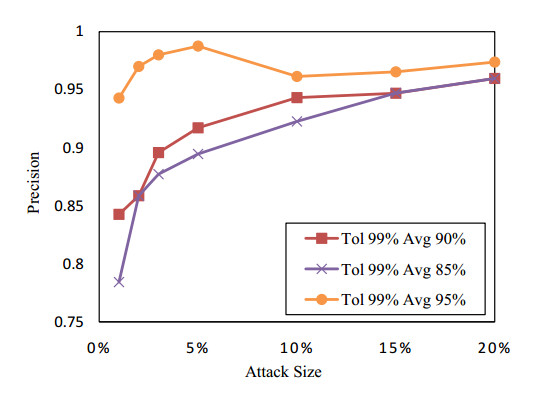
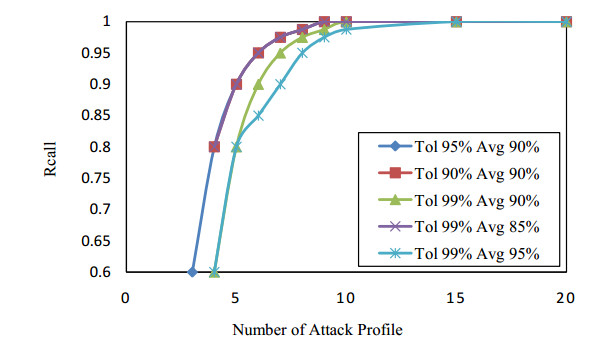
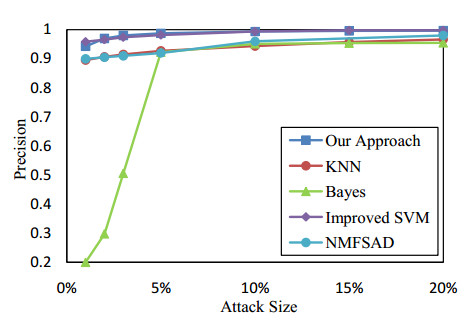
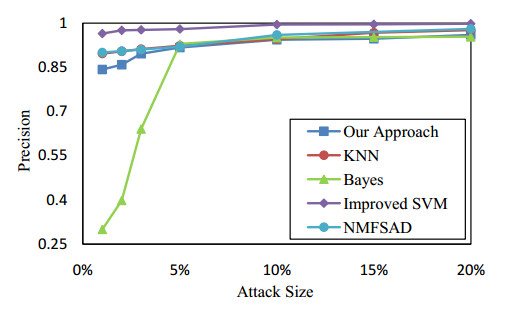
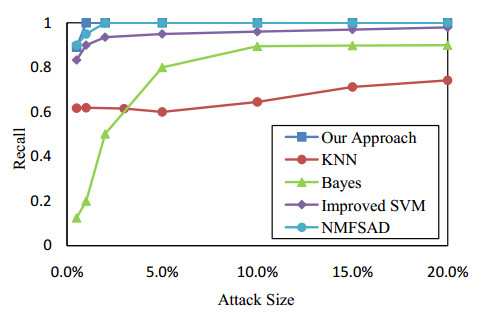
Collaborative filtering has been widely used in recommendation systems to recommend items that users might like. However, collaborative filtering based recommendation systems are vulnerable to shilling attacks. Malicious users tend to increase or decrease the recommended frequency of target items by injecting fake profiles. In this paper, we propose a Kalman filter-based attack detection model, which statistically analyzes the difference between the actual rating and the predicted rating calculated by this model to find the potential abnormal time period. The Kalman Filter filters out suspicious ratings based on the abnormal time period and identifies suspicious users based on the source of these ratings. The experimental results show that our method performs much better detection performance for the shilling attack than the traditional methods.
1.
Introduction
We consider the following nonlinear parabolic system with damping and diffusion:
with the following initial and boundary conditions:
Here σ,α,β and ν are constants with α>0, β>0, T>0, and QT=(0,1)×(0,T). The function ξ(t) is measurable in (0,T). System (1.1) was originally proposed by Hsieh in [1] as a substitution for the Rayleigh–Benard equation for the purpose of studying chaos, and we refer the reader to [1,2,3] for the physical background. It is worthy to point out that with a truncation similar to the mode truncation from the Rayleigh–Benard equations used by Lorenz in [4], system (1.1) also leads to the Lorenz system. In spite of it being a much simpler system, it is still as rich as the Lorenz system, and some different routes to chaos, including the break of the time-periodic solution and the break of the switching solution, have been discovered via numerical simulations [5].
Neglecting the damping and diffusion terms, system (1.1) is simplified as
It has two characteristic values: λ1=ψ+√ψ2−σν and λ2=ψ−√ψ2−σν. Obviously, the system is elliptic if ψ2−σν<0, and it is hyperbolic if ψ2−σν>0. In particular, it is always strictly hyperbolic if σν<0.
The mathematical theory of system (1.1) has been extensively investigated in a great number of papers; see [6,7,8,9,10,11,12,13,14,15,16] and the references therein. However, there is currently no global result with large initial data because it is very difficult to treat the nonlinear term of system (1.1) in analysis. Motivated by this fact, we will first study the well-posedness of global large solutions of the problem given by (1.1) and (1.2) for the case in which σν<0, and then we will discuss the limit problem as α→0+, as well as the problem on the estimation of the boundary layer thickness. For the case in which σν>0, we leave the investigation in the future.
The problem of a vanishing viscosity limit is an interesting and challenging problem in many settings, such as in the boundary layer theory (cf.[17]). Indeed, the presence of a boundary layer that accompanies the vanishing viscosity has been fundamental in fluid dynamics since the seminal work by Prandtl in 1904. In this direction, there have been extensive studies with a large number of references that we will not mention here. As important work on the mathematical basis for the laminar boundary layer theory, which is related to the problem considered in this paper, Frid and Shelukhin [18] studied the boundary layer effect of the compressible or incompressible Navier–Stokes equations with cylindrical symmetry and constant coefficients as the shear viscosity μ goes to zero; they proved the existence of a boundary layer of thickness O(μq) with any q∈(0,1/2). It should be pointed out that, for the incompressible case, the equations are reduced to
where μ is the shear viscosity coefficient and v and w represent the angular velocity and axial velocity, respectively. Recently, this result was investigated in more general settings; see for instance, [19,20,21] and the references therein. In the present paper, we will prove a similar result to that obtained in [18]. Note that every equation in (1.3) is linear. However, equation (1.1)2, with a nonconservative term 2ψθx, is nonlinear. It is the term that leads to new difficulties in analysis, causing all previous results on system (1.1) to be limited to small-sized initial data.
The boundary layer problem also arises in the theory of hyperbolic systems when parabolic equations with low viscosity are applied as perturbations (see [22,23,24,25,26,27,28]).
Formally, setting α=0, we obtain the following system:
with the following initial and boundary conditions:
Before stating our main result, we first list some notations.
Notations: For 1≤p,s≤∞, k∈N, and Ω=(0,1), we denote by Lp=Lp(Ω) the usual Lebesgue space on Ω with the norm ‖⋅‖Lp, and Hk=Wk,2(Ω) and H10=W1,20(Ω) as the usual Sobolev spaces on Ω with the norms ‖⋅‖Hk and ‖⋅‖H1, respectively. Ck(Ω) is the space consisting of all continuous derivatives up to order k on Ω, C(¯QT) is the set of all continuous functions on ¯QT, where QT=(0,1)×(0,T) with T>0, and Lp(0,T;B) is the space of all measurable functions from (0,T) to B with the norm ‖⋅‖Lp(0,T;B), where B=Ls or Hk. We also use the notations ‖(f1,f2,⋯)‖2B=‖f‖2B+‖g‖2B+⋯ for functions f1,f2,⋯ belonging to the function space B equipped with a norm ‖⋅‖B, and for L2(QT)=L2(0,T;L2).
The first result of this paper can be stated as follows.
Theorem 1.1. Let α,β,σ and ν be constants with α>0,β∈(0,1) and σν<0. Assume that (ψ0,θ0)∈H1([0,1]) and ξ∈C1([0,T]), and that they are compatible with the boundary conditions. Then, the following holds:
(i) For any given α>0, there exists a unique global solution (ψ,θ) for the problem given by (1.1) and (1.2) in the following sense:
Moreover, for some constant C>0 independent of α∈(0,α0] with α0>0,
where the function ω(x):[0,1]→[0,1] is defined by
(ii) There exists a unique global solution (¯ψ,¯θ) for the problem given by (1.4) and (1.5) in the following sense:
and
for any functions ζ,φ∈C1(¯QT) with φ(1,t)=φ(0,t) for all t∈[0,T] such that, as α→0+,
where M(QT) is the set of the Radon measures on QT, and
(iii) For some constant C>0 independent of α∈(0,1),
Remark 1.1. The L2 convergence rate for ψ is optimal whenever a boundary layer occurs as α→0+. The reason why this is optimal will be shown by an example in Section 3.3.
We next study the boundary layer effect of the problem given by (1.1) and (1.2). Before stating the main result, we first recall the concept of BL–thickness, defined as in [18].
Definition 1.2. A nonnegative function δ(α) is called the BL–thickness for the problem given by (1.1) and (1.2) with a vanishing α if δ(α)↓0 as α↓0, and if
where (\psi, \theta) and (\overline\psi, \overline\theta) are the solutions for the problems given by (1.1), (1.2) and (1.4), (1.5), respectively.
The second result of this paper is stated as follows.
Theorem 1.3. Under the conditions of Theorem 1.1, any function \delta(\alpha) satisfying the condition that \delta(\alpha) \downarrow0 and \sqrt{\alpha}/\delta(\alpha) \rightarrow 0 as \alpha \downarrow 0 is a BL–thickness whenever (\overline\psi(1, t), \overline\psi(0, t))\not\equiv(\xi(t), \xi(t)) in (0, T) .
Remark 1.2. Here, the function \theta satisfies the spatially periodic boundary condition that has been considered in some papers, e.g., [3,29,30]. One can see from the analysis that Theorems 1.1 and 1.3 are still valid when the boundary condition of \theta is the homogeneous Neumann boundary condition or homogeneous Dirichlet boundary condition.
The proofs of the above theorems are based on the uniform estimates given by (1.6). First, based on a key observation of the structure of system (1.1), we find two identities (see Lemma 2.1). In this step, an idea is to transform (1.1) _2 into an equation with a conservative term (see (2.4)). And then, from the two identities, we deduce some basic energy-type estimates (see Lemma 2.2). The condition \sigma\nu < 0 plays an important role here. With the uniform estimates in hand, we derive the required uniform bound of (\alpha^{1/4}\|\psi_x\|_{L^\infty(0, t; L^2)}+\alpha^{3/4}\|\psi_{xx}\|_{L^2(Q_T)}) for the study of the boundary layer effect via standard analysis (see [18,19]). See Lemma 2.3 with proof. The uniform bound of \|(\psi, \theta)\|_{L^\infty(Q_T)} is derived by a more delicate analysis (see Lemma 2.4). Finally, the boundary estimate \|\omega^{1/2}\psi_x\|_{L^\infty(0, T; L^2)}\leq C is established (see Lemma 2.6), through which we complete the proof for the estimation of the boundary layer thickness.
Before ending the section, let us introduce some of the previous works on system (1.1). It should be noted that most of those works focus on the case when \sigma\nu > 0 . In this direction, Tang and Zhao [6] considered the Cauchy problem for the following system:
with the following initial condition: (\psi, \theta)(x, 0) = (\psi_0, \theta_0)(x)\rightarrow (0, 0)\; \; \hbox{as}\; \; x \rightarrow \pm\infty, where 0 < \alpha < 1 and 0 < \nu < 4\alpha(1-\alpha) . They established the global existence, nonlinear stability and optimal decay rate of solutions with small-sized initial data. Their result was extended in [7,8] to the case of the initial data with different end states, i.e.,
where \psi_{\pm}, \theta_{\pm} are constant states with (\psi_+-\psi_-, \theta_+-\theta_-)\not\equiv(0, 0) . For the initial-boundary value problem on quadrants, Duan et al. [9] obtained the global existence and the L^p decay rates of solutions for the problem given by (1.13) and (1.14) with small-sized initial data. For the Dirichlet boundary value problem, Ruan and Zhu [10] proved the global existence of system (1.1) with small-sized initial data and justified the limit as \beta\rightarrow 0^+ under the following condition: \nu = \mu\beta for some constant \mu > 0 . In addition, they established the existence of a boundary layer of thickness O(\beta^{\delta}) with any 0 < \delta < 1/2 . Following [10], some similar results on the Dirichlet–Neumann boundary value problem were obtained in [11]. For the case when \sigma\nu < 0 , however, there are few results on system (1.1). Chen and Zhu [12] studied the problem given by (1.13) and (1.14) with 0 < \alpha < 1 ; they proved global existence with small-sized initial data and justified the limit as \alpha \rightarrow 0^+ . In their argument, the condition \sigma\nu < 0 plays a key role. Ruan and Yin [13] discussed two cases of system (1.1): \alpha = \beta and \alpha\not\equiv\beta , and they obtained some further results that include the C^\infty convergence rate as \beta\rightarrow 0^+ .
We also mention that one can obtain a slightly modified system by replacing the nonlinear term 2\psi\theta_x in (1.1) with (\psi\theta)_x . Jian and Chen [31] first obtained the global existence results for the Cauchy problem. Hsiao and Jian [29] proved the unique solvability of global smooth solutions for the spatially periodic Cauchy problem by applying the Leary–Schauder fixed-point theorem. Wang [32] discussed long time asymptotic behavior of solutions for the Cauchy problem. Some other results on this system is available in [33,34,35] and the references therein.
The rest of the paper is organized as follows. In Section 2, we will derive the uniform a priori estimates given by (1.6). The proofs of Theorem 1.1 and Theorem 1.3 will be given in Section 3 and Section 4, respectively.
2.
A priori estimates
In the section, we will derive the uniform a priori estimates by (1.6), and we suppose that the solution (\psi, \theta) is smooth enough on \overline Q_T . From now on, we denote by C a positive generic constant that is independent of \alpha \in (0, \alpha_0] for \alpha_0 > 0 .
First of all, we observe that (\tilde\psi, \tilde{\theta}): = (2\psi, 2\theta/\nu) solves the following system:
with the following initial and boundary conditions:
From the system, we obtain the following crucial identities for our analysis.
Lemma 2.1. (\tilde\psi, \tilde{\theta}) satisfies the following for all t \in [0, T] :
and
Proof. Multiplying (2.1) _1 and (2.1) _2 by \tilde{\psi} and \sigma\nu , respectively, adding the equations and then integrating by parts over (0, 1) with respect to x , we obtain (2.2) immediately.
We now multiply (2.1) _2 by e^{\tilde{\theta}} to obtain
Integrating it over (0, 1) with respect to x , we get (2.3) and complete the proof. □
Lemma 2.2. Let the assumptions of Theorem 1.1 hold. Then, we have the following for any t\in[0, T] :
and
Proof. Integrating (2.2) and (2.3) over (0, t) , respectively, we obtain
and
From the inequalities e^x\geq 1+x and xe^x\geq -1 for all x\in\mathbb{R} , and given \beta\in (0, 1) , we derive from (2.8) that
so that
We now treat the second term on the right-hand side of (2.7). Integrating (2.1) _1 over (0, 1) with respect to x , multiplying it by \xi(t) and then integrating over (0, t) , we obtain
Combining (2.9) and (2.10) with (2.7), and noticing that \sigma\nu < 0 , we obtain (2.5) by using the Gronwall inequality.
Combining (2.5) and (2.10) with (2.7) yields
Let \varphi = \iint_{Q_t} \tilde\theta dxd\tau . Then, (2.11) is equivalent to
which implies that |\varphi|\leq C. This, together with (2.11), gives (2.6) and completes the proof.
□
Lemma 2.3. Let the assumptions of Theorem 1.1 hold. Then, for any t\in[0, T] ,
and
Proof. Multiplying (1.1) _2 by \theta , integrating over (0, 1) , and using (2.5) and Young's inequality, we have
From the embedding theorem, W^{1, 1}\hookrightarrow L^\infty , and Young's inequality, we have
Plugging it into (2.14), taking \varepsilon sufficiently small and using the Gronwall inequality, we obtain
Rewrite (1.1) _1 as
Taking the square on the two sides, integrating over (0, 1) and using (2.5), we obtain
From the embedding theorem, W^{1, 1}\hookrightarrow L^\infty , and the Hölder inequality, we have
hence, by Young's inequality,
Plugging it into (2.17), taking \varepsilon sufficiently small and using (2.16), we obtain the following by applying the Gronwall inequality:
This completes the proof of the lemma.
□
For \eta > 0 , let
Obviously, h_\eta\in C(\mathbb{R}), I_\eta \in C^1(\mathbb{R}) and
With the help of (2.18), we obtain the following estimates, which are crucial for the study of the boundary layer effect.
Lemma 2.4. Let the assumptions of Theorem 1.1 hold. Then, for any t\in[0, T] ,
In particular, \|(\psi, \theta)\|_{L^\infty(Q_T)}\leq C.
Proof. Let W = \psi_x . Differentiating (1.1) _1 with respect to x , we obtain
Multiplying it by h_\eta(W) and integrating over Q_t , we get
By applying |h_\eta(s)|\leq 1 , we have
By using h_\eta'(s)\geq 0 for s\in\mathbb{R} , we have
We now estimate I_3 . Since \theta(1, t) = \theta(0, t) , it follows from the mean value theorem that, for any t\in [0, T] , there exists some x_t\in(0, 1) such that \theta_x(x_t, t) = 0 ; hence,
It follows from (1.1) _1 that
Consequently, thanks to |h_\eta(s)|\leq 1 ,
Plugging (2.21)–(2.23) into (2.20), and letting \eta \rightarrow 0^+ , we deduce the following by noticing that \lim_{\eta\rightarrow 0^+}I_\eta(s) = |s| :
Plugging (1.1) _2 into the final term of the right-hand side on (2.24), and by using (2.5) and (2.16), we obtain the following by using the Gronwall inequality:
By using the embedding theorem, (2.5) and (2.25), we have
where {\bf P}(t) = \iint_{Q_t} \theta_t^2 dxd\tau.
Multiplying (1.1) _2 by \theta_t and integrating over Q_t , we have
By applying (2.5), (2.12), (2.16), (2.26) and Young's inequality, we deduce the following:
and
Substituting (2.28) and (2.29) into (2.27), and noticing that \iint_{Q_T} \theta_x^2 dxdt\leq C , we obtain the following by using the Gronwall inequality:
This, together with (2.25), gives
And, the proof of the lemma is completed.
□
Lemma 2.5. Let the assumptions of Theorem 1.1 hold. Then, for any t\in[0, T] ,
Proof. Multiplying (1.1) _2 by \theta_{xx} , integrating over (0, 1) and using Lemmas 2.2–2.4, we have
where we use the estimate with \varepsilon sufficiently small based on a proof similar to (2.15):
It follows from (2.31) that
Similarly, multiplying (1.1) _1 by \alpha\psi_{xx} , and integrating over (0, 1) , we have
Then, by integrating over (0, t) and using (2.32) and the Hölder inequality, we obtain
where
To estimate {\bf A}(t) , we first integrate (1.1) _2 over (x, 1) for x\in [0, 1] , and then we integrate the resulting equation over (0, 1) to obtain
By applying Lemmas 2.3 and 2.4, we obtain
Similarly, we have
Therefore,
From the embedding theorem, W^{1, 1}\hookrightarrow L^\infty , and the Hölder inequality, we have
therefore, by the Hölder inequality and Young's inequality, we obtain the following for any \varepsilon\in(0, 1) :
Combining (2.37) and (2.38) with (2.34), and taking \varepsilon sufficiently small, we obtain (2.30) by using the Gronwall inequality. The proof of the lemma is completed. □
As a consequence of Lemma 2.5 and (2.32), we have that \alpha^{1/2}\iint_{Q_T} \theta_{xx}^2dxdt \leq C.
Lemma 2.6. Let the assumptions of Theorem 1.1 hold. Then, for any t\in[0, T] ,
where \omega is the same as that in (1.7).
Proof. Multiplying (1.1) _1 by \psi_{xx}\omega(x) and integrating over Q_t , we have
where
By applying Lemmas 2.3 and 2.4, we have
and, by substituting (1.1) _2 into I_2 , we get
To estimate I_3 , we first multiply (1.1) _2 by \theta_x\omega'(x) , and then we integrate over Q_t to obtain
where
Note that |E|\leq C by Lemmas 2.3 and 2.4. Then, given \sigma\nu < 0 , we have
Combining (2.35) and (2.36) with (2.42), we obtain
Substituting (2.40), (2.41) and (2.43) into (2.39), we complete the proof of the lemma by applying the Gronwall inequality.
In summary, all uniform a priori estimates given by (1.6) have been obtained. □
3.
Proof of Theorem 1.1
3.1. Existence and uniqueness
For any fixed \alpha > 0 , the global existence of strong solutions for the problem given by (1.1) and (1.2) can be shown by a routine argument (see [29,36]). First, by a smooth approximation of the initial data satisfying the conditions of Theorem 1.1, we obtain a sequence of global smooth approximate solutions by combining the a priori estimates given by (1.6) with the Leray–Schauder fixed-point theorem (see [36, Theorem 3.1]). See [29] for details. And then, a global strong solution satisfying (1.6) is constructed by means of a standard compactness argument.
The uniqueness of solutions can be proved as follows. Let (\psi_2, \theta_2) and (\psi_1, \theta_1) be two strong solutions, and denote (\Psi, \Theta) = (\psi_2-\psi_1, \theta_2-\theta_1). Then, (\Psi, \Theta) satisfies
with the following initial and boundary conditions:
Multiplying (3.1) _1 and (3.1) _2 by \Psi and \Theta , respectively, integrating them over [0, 1] and using Young's inequality, we obtain
and
where we use \|\psi_{2}\|_{L^\infty(Q_T)}+\|\theta_{1x}\|_{L^\infty(0, T; L^2)}\leq C and
First, by adding (3.2) and (3.3), and then using the Gronwall inequality, we obtain that \int_0^1\big(\Psi^2+\Theta^2\big)dx = 0\; \; \hbox{on}\; \; [0, T] so that (\Psi, \Theta) = 0 on \overline Q_T . This completes the proof of Theorem 1.1(ⅰ).
3.2. Vanishing diffusion limit
The aim of this part is to prove (1.10) and (1.11). Given the uniform estimates given by (1.6) and Aubin–Lions lemma (see [37]), there exists a sequence \{\alpha_n\}_{n = 1}^\infty , tending to zero, and a pair of functions (\overline\psi, \overline\theta) satisfying (1.8) such that, as \alpha_n\rightarrow 0^+ , the unique global solution of the problem given by (1.1) and (1.2) with \alpha = \alpha_n , still denoted by (\psi, \theta) , converges to (\overline\psi, \overline\theta) in the following sense:
where \mathcal{M}(Q_T) is the set of Radon measures on Q_T . From (3.4), one can directly check that (\overline\psi, \overline\theta) is a global solution for the problem given by (1.4) and (1.5) in the sense of (1.8) and (1.9).
We now return to the proof of the uniqueness. Let (\overline\psi_2, \overline\theta_2) and (\overline\psi_1, \overline\theta_1) be two solutions, and denote (M, N) = (\overline\psi_2-\overline\psi_1, \overline\theta_2-\overline\theta_1) . It follows from (1.9) that
and
By using Young's inequality, we immediately obtain
where we use \psi_2 \in L^\infty(Q_T), \theta_{1x}\in L^\infty(0, T; L^2) , and the estimate with \varepsilon sufficiently small:
Then, the Gronwall inequality gives (M, N) = (0, 0) a.e. in Q_T . Hence, the uniqueness follows.
Thanks to the uniqueness, the convergence results of (3.4) hold for \alpha\rightarrow 0^+ .
Finally, by using Lemma 2.3, we immediately obtain
So, \alpha\psi_x^2\rightarrow 0 strongly in L^2(Q_T) as \alpha\rightarrow 0^+ . Thus, the proof of Theorem 1.1(ⅱ) is completed.
In addition, the following local convergence results follows from (1.6) and (3.4):
for any \epsilon\in (0, 1/4) . Consequently, the equations comprising (1.1) hold a.e in Q_T .
3.3. Convergence rate
This purpose of this part is to prove (1.12). Let (\psi_i, \theta_i) be the solution of the problem given by (1.1) and (1.2) with \alpha = \alpha_i \in (0, 1) for i = 1, 2 . Denote U = \psi_2-\psi_1 and V = \theta_2-\theta_1 . Then it satisfies
Multiplying (3.7) _1 and (3.7) _2 by U and V , respectively, integrating them over Q_t and using Lemmas 2.3–2.5, we have
and
where we use \|\psi_2\|_{L^\infty(Q_T)}+\|\theta_{1x}\|_{L^\infty(0, T; L^2)}\leq C and the estimate with \varepsilon sufficiently small:
Then, the Gronwall inequality gives
We now fix \alpha = \alpha_2 , and then we let \alpha_1\rightarrow 0^+ to obtain the desired result by using (1.10) and (1.11).
In summary, we have completed the proof of Theorem 1.1.
We next show the optimality of the L^2 convergence rate O(\alpha^{1/4}) for \psi , as stated in Remark 1.1. For this purpose, we consider the following example:
It is easy to check that (\overline\psi, \overline\theta) = (0, e^{(\beta-1)t}) is the unique solution of the problem given by (1.4) and (1.5). According to Theorem 1.3 of Section 4, a boundary layer exists as \alpha\rightarrow 0^+ . To achieve our aim, it suffices to prove the following:
Suppose, on the contrary, that there exists a subsequence \{\alpha_n\} satisfying \alpha_n\rightarrow 0^+ such that the solution of the problem given by (1.1) and (1.2) with \alpha = \alpha_n , still denoted by (\psi, \theta) , satisfies
where o(1) indicates a quantity that uniformly approaches to zero as \alpha_n\rightarrow 0^+ . Then, by using the embedding theorem, we obtain
Hence, we get that \|\psi\|_{L^\infty(0, T; L^\infty)}\rightarrow 0\; \; \hbox{as}\; \; \alpha_n\rightarrow 0^+ by using (3.9) and \alpha_n^{1/2}\|\psi_x\|_{L^2}^2 \leq C . On the other hand, it is obvious that \|\theta-\overline\theta\|_{L^\infty(0, T; L^\infty)}\rightarrow 0\; \; \hbox{as}\; \; \alpha_n\rightarrow 0^+ by using (1.11). This shows that a boundary layer does not occur as \alpha_n\rightarrow 0^+ , and this leads to a contradiction. Thus, (3.8) follows. This proof is complete.
4.
Proof of Theorem 1.3
Thanks to \sup_{0 < t < T}\int_0^1(\psi_x^2+\overline\psi_x^2) \omega(x)dx\leq C , we have
By the embedding theorem, and from Theorem 1.1(ⅲ), we obtain the following for any \delta \in (0, 1/4) :
Hence, for any function \delta(\alpha) satisfying that \delta(\alpha)\downarrow 0 and \sqrt{\alpha}/\delta(\alpha)\rightarrow 0 as \alpha\downarrow 0 , it holds that
On the other hand, it follows from (1.11) that \|\theta-\overline\theta\|_{L^\infty(0, T; L^\infty)}\rightarrow 0\; \; \hbox{as}\; \; \alpha \rightarrow 0^+ . Consequently, for any function \delta(\alpha) satisfying that \delta(\alpha)\downarrow 0 and \sqrt{\alpha}/\delta(\alpha)\rightarrow 0 as \alpha\downarrow 0 , we have
Finally, we observe that
whenever (\overline\psi(1, t), \overline\psi(0, t)) \not\equiv(\xi(t), \xi(t)) on [0, T] . This ends the proof of Theorem 1.3.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
We would like to express deep thanks to the referees for their important comments. The research was supported in part by the National Natural Science Foundation of China (grants 12071058, 11971496) and the research project of the Liaoning Education Department (grant 2020jy002).
Conflict of interest
The authors declare that there is no conflict of interest.












 DownLoad:
DownLoad: