A metapopulation model for sylvatic T. cruzi transmission with vector migration

1.   Introduction

Human immunodeficiency virus (HIV) and HIV treatment have always received extensive attention by many researchers. In 1996, Dr. He invented the famous 'cocktail' therapy, namely highly active antiretroviral therapy (HAART), from which AIDS has changed from an 'incurable disease' to a controllable 'chronic disease' ^[1]. Since then, more attention has been paid to antiviral drug therapies which aim to boost virus-specific immune response by resisting or destroying viral infections ^[2,3,4,5,6]. Hence, HAART can effectively control viral replication in patients for a long time, and patients can even live to their life expectancy. However HAART has some limitations, for instance, HIV is not completely eradicated, and the virus remains hidden in some immune cells, returning once the patient has stopped taking the antiviral; life-long HAART is thus required ^[7], which brings many inconveniences and various side effects. Therefore, numerous HIV scientists are devoted to seeking novel cures for AIDS including immunotherapy ^{[7,8,9,10,11]} of AIDS.

At present, the immunotherapy of AIDS has the following aspects: Anti-HIV strategy based on antibody, such as broadly neutralizing antibodies (bNabs) ^[8], immune checkpoint blockers (ICBs) ^[12] and antibody-mediated cell strategies to eliminate HIV infection ^[7]; Strategy of therapeutic vaccine based on HIV-1; Other immunotherapies, such as the $ \alpha4\beta7 $ blocker (vedolizumab) ^[13], can significantly reduce the exposure of target cells to HIV by blocking the surface of $ CD4^{+} $ T lymphocytes $ \alpha4\beta7 $ molecules to restrict the return of $ CD4^{+} $ cells to the intestinal mucosa; Immunotherapy combined with antiviral therapy and so on. The strategy of HIV-1 therapeutic vaccine is based on a class of HIV-infected people known as "elite controllers" ^[14]. Studies have found that very few infected people can "peacefully coexist" with the virus for a long time. Their immune system can naturally control the replication of the virus and avoid the damage of the virus to the immune system. "Therapeutic vaccine" aims to reactivate the immune system of the infected person through the vaccine, so that the infected person can spontaneously produce specific $ CD8^{+} $ T lymphocyte for HIV-1. After interruption of antiviral treatment, it can still inhibit the virus and achieve functional cure.

It was argued that sustained virus-specific immunity for HIV infection may be established via early therapy and structured therapy interruptions ^[15,16]. Later, using a mathematical framework, Komarova et al. ^[17] show that a single phase of antiviral therapy is also possible to achieve this goal. Essentially, it is shown by ^[17] that a immune-free equilibrium (no sustained immunity) and an immune control equilibrium (with sustained immunity) are both stable. This bistability allows a solution from the basin of the attraction of the immune-free equilibrium to be lifted to that of the immune control equilibrium via a single phase of therapy, resulting in sustained immunity when the treatment is stopped.

However, HIV is rapidly reproduced and quickly becomes resistant to any single drug ^{[18,19,20,21]}. A multi-institutional team of researchers, led by the Wistar Institute, has announced the results of a clinical trial that showed the immune system can engage in fighting HIV infection if given the right boost. In their studies, HIV-infected volunteers suspended their daily antiretroviral therapy to receive weekly doses of interferon-$ \alpha, $ an antiviral chemical produced by the human immune system. Dramatically, 45 percent of these patients sustained the HIV control under the lower level. These researches provide the first clinical evidence for reducing the persistent amount of HIV in patients and increasing the ability to control HIV without continued antiretroviral therapy ^[22]. Hence, boosting specific immune responses by therapeutic vaccine or immune regulation with interferon is possible and promising.

One traditional model with antiviral drug therapy, sketched the connection among uninfected cells, infected cells and virus, was proposed by Nowak et al. ^[23], which has been extensively and deeply probed ^[24,27]. Another classical model depicted the relation between virus and immune cells was used to snatch the boosting immunity by single or multiple phases of therapy ^[17,28,29]. But how to tangle and capture reasonably the interaction among uninfected cells, virus and immune cells is challenging. Furthermore, if combining antiviral drug with immune regulation therapy, what is the dynamic outcome of three populations? In order to sustain viral suppression and immunological motivation, which parameters and why can be adjusted to regulate therapy schemes? If we acquire these parameters, further how to optimize these parameters to boost immune responses to sustain viral suppression at the minimum cost after stopping treatment? These are significative and challenging pursuits.

The outline is instructed as follows: In Section 2, a mathematical model is formulated. In Section 3, the well-posedness and the existence of equilibrium are explored. The stability of system (2.5) as well as Hopf bifurcation are discussed in Section 4. In Section 5, the sensitivity of the periodic solution with sustained immunity is investigated. In Section 6, combination treatment is discussed in detail. Finally, some conclusions are drawn in Section 7.

2.   Model formulation

To answer the above issues, after principally consulting ^[17,23,29] and other literatures, we list several main models and then formulate our model.

$ \bullet $ Uninfected cells, infected cells, virus model and immune response model

Viral reproduction always involves host cells and uses the cellular machinery for the synthesis of their genome and other components. Nowak et al. ^[30] describe the relationship between the populations of uninfected cells, $ x, $ infected cells that produce virus, $ y, $ and free virus particles, $ v, $ the abundance of virus-specific CTLs $ z $, and design a simple but natural mathematical model based on ordinary differential equations ^[23,24,30]:

Uninfected cells are produced at a constant rate $ s $ and die at the rate $ dx. $ Free virus infects uninfected cells to produce infected cells at rate $ \beta xv. $ Infected cells die at rate $ \mu y. $ New virus is produced from infected cells at rate $ ky $ and dies at rate $ \omega v. $ The average life-times of infected cells are thus given by $ 1/\mu. $ Hence, the average number of virus particles produced over the lifetime of a single infected cell (the burst size) is given by $ k/\mu. $ The rate of CTL proliferation in response to antigen is given by $ cyz $. In the absence of stimulation, CTLs decay at rate $ bz $. Infected cells are killed by CTLs at rate $ pyz $.

By the quasi steady-state assumption for the turnover of free virus is much faster than that of infected cells ^[25,26], we know that $ y = (\omega/k)v $ at steady-state from the 3th equation of the above model, that is, the amount of free virus is simply proportional to the number of infected cells. Hence the 2nd and 4th equations of the above model are equivalent to $ v' = k\beta xv/\omega-\mu v-pvz $ and $ z' = \omega cvz/k-bz $, respectively. For convenience, let $ k/\omega = \vartheta. $ Then the above four-dimensional model is reduced to a three-dimensional one:

$ \bullet $ Virus and immune response model

Note that the immune response after viral infection is universal and necessary to eliminate or control the disease. Antibodies, cytokines, natural killer cells, and T cells are essential components of a normal immune response to a virus. Indeed, in most viral infections, cytotoxic T lymphocytes (CTLs) play a critical role in antiviral defense by attacking virus-infected cells. It is believed that they are the main host immune factor that limit the development of viral replication in vivo and thus determine virus load ^[30,31,32]. Therefore, the population dynamics of viral infection with CTL response has been paid much attention in the last few decades. Komarova et al. ^[17] established a mathematical model to explore the relation between the virus population $ v $ and a population of immune cells $ z $:

The virus population is assumed to grow logistically: $ r $ is the viral replication rate at low viral loads, and assume that this rate decreases linearly with increased viral load to reach zero at a viral load $ k. $ The virus population decays at a rate $ a. $ Overall, this gives a logistic growth with a net growth rate $ r-a $ and a carrying capacity of $ k(r-a)/r. $ Moreover, virus is killed by the CTL response at a rate $ pvz $, corresponding to lytic effector mechanisms of CTL response. Immune cells at time $ t $ due to virus activation, expand at a rate $ {cvz}/{1+\eta v} $ ^[33,34], which depends on the viral load and the number of immune cells at time $ t, $ and implies that when the virus load is low, the level of immune response is simply proportional to both the virus population, $ v, $ and the immune response, $ z, $ but that the immune response saturates when the virus load is sufficiently high. Immune cells die at rate $ b $ and are inhibited by the virus population at rate $ mvz $ ^[28].

In addition, it has been recognized that the immune response is not instantaneous and the process involves a sequence of events such as antigenic activation, selection, and proliferation of the immune cells. It is believed that they are the main host immune factor that limit the development of viral replication in vivo and thus determine virus load ^[35,36]. Therefore, the time lag between these events should be taken into consideration in modeling and the relationship between virus population and a population of immune cells can be simply described as:

The virus population grows at a rate described by the function $ M(v). $ Immune expansion is determined by the virus load and the number of immune cells $ z $ at time $ t-\tau $ and $ \tau $ is the time lag for the production of new immune cells mediated by the infection, which is described by the function $ h(v(t-\tau), z(t-\tau)). $ Functions $ g_{1}(v, z) $ and $ g_{2}(v, z) $ represent the interaction between immune cells and virus and further $ h, \; g_{1} $ and $ g_{2} $ can be written as Holling functional response.

$ \bullet $ Uninfected cells, virus and immune response model with combined treatment

For the sake of deep studying the dynamic behavior of immune response in human body, tangling (2.1) with (2.3), one formulates a model consisted of three variables including uninfected target cells $ x $, virus $ v $, and CTL response $ z $. Specifically, insetting a phased immunotherapy into a continuous antiviral treatment (such as reverse transcriptase inhibitors (RTIs)) ^{[24,27,28,37]}, the following model with hybrid treatment comes into being:

where

Now before the detailed indagation, several symbols are given. Suppose that the patient remains on the antiviral treatment during the whole course of patient observed $ [0, T] $. While $ t_{1}\in(0, T) $ and $ t_{2}\in(0, T) $ with $ t_1 < t_2 $ are the initial and terminal time of immunotherapy respectively. Then $ [0, t_1] $ and $ [t_2, T] $ are called the single antiviral treatment session (ATTS), while $ [t_1, t_2] $ is referred to as the combined treatment session (CTS). $ 0\leq\varepsilon_0, \; \varepsilon^*\leq 1 $ describe the effectiveness of antiretroviral drugs ^[38] during ATTS and CTS; $ \bar{b}^*\geq 0 $ represents the efficacy of immunotherapy, which could boost specific immune responses by therapeutic vaccine or immune regulation with interferon. The biological meaning of parameters is presented in Table 1.

The initial conditions for system (2.4) are

where $ R_{+}^{3} = {{(x, v, z)\in R^{3}: x\geq 0, v\geq 0, z\geq 0}} $. Therefore, all the standard results on existence, uniqueness and continuous dependence on initial condition of solutions are evidently satisfied.

Due to the inability of single antiviral therapy to eradicate HIV infection for many patients, in this paper we devote to the therapeutic effect of the intermittent immunotherapy based on a continuous antiviral treatment. So we firstly aim at the dynamic behaviors of following model which is the case in model (2.4) under $ \Psi\equiv\varepsilon $ and $ \Theta(t)\equiv0 $:

3.   Equilibria and reproduction thresholds

For the nonnegativeness and boundedness of solutions, we state the following lemma.

Lemma 3.1. There exists a positively invariant box $ \Omega = [(x, v, z) \in R_{+}^{3} : 0 \leq x \leq \dfrac{M}{\vartheta}, 0 \leq v \leq M, 0 \leq z \leq \dfrac{c}{p}M] $ in $ R_{+}^{3} $ such that all solutions of (2.5) with nonnegative initial conditions approach $ \Omega $ as $ t \rightarrow \infty, $ where $ M = \dfrac{s\vartheta}{\mu}+\kappa $, $ \mu = min\{a, b, d\} $ and $ \kappa $ is a positive constant.

Proof. Solving $ v(t) $ in the second equation of (2.5) yields

Next we show that $ x(t) $ is nonnegative for $ t > 0 $. Assume to the contrary that $ x(t)\geq 0 $ for $ t \in [0, \hat{t}) $ and $ x(\hat{t}) = 0 $ with $ x'(\hat{t}) < 0 $ for some $ \hat{t} > 0 $. Then it follows from the first equation of system (2.5) that $ x'(\hat{t}) = s > 0 $. This is a contradiction. Thus $ x(t) \geq 0 $ for all $ t \geq 0. $ Similarly, we can obtain that $ z(t) $ is nonnegative for $ t > 0 $.

Adding up the three equations of (2.5), one gets

where $ \mu = min\{a, b, d\}. $ By the comparison theorem, we obtain that $ \lim_{t\rightarrow\infty}(\vartheta x(t)+v(t)+\dfrac{p}{c}z(t+\tau)) \leq \dfrac{s\vartheta}{\mu}. $ That is, for a positive constant $ \kappa, \; \vartheta x(t)+v(t)+\dfrac{p}{c}z(t) \leq \dfrac{s\vartheta}{\mu}+\kappa\dot{ = } M $ holds for $ \tau = 0 $ and $ t $ large enough. Then we get a positively invariant box $ \Omega = \{(x, v, z) \in R_{+}^{3} : 0 \leq x \leq \dfrac{M}{\vartheta}, 0 \leq v \leq M, 0 \leq z \leq \dfrac{c}{p}M \} $ in $ R_{+}^{3} $ by the non-negativity of $ x(t), v(t) $ and $ z(t) $, such that all solutions with nonnegative initial conditions approach as $ t \rightarrow \infty. $

Next, we consider the existence of equilibrium by the right side of system (2.5).

$ \bullet $ Virus-free equilibrium

Clearly, system (2.5) admits a virus-free equilibrium $ E_{0} = (x_{0}, 0, 0), $ corresponding to the maximal level of healthy $ CD4^{+} T $ cells and the extinction of free virus, where $ x_{0} = {s}/{d}. $

$ \bullet $ Virus-boom and immune-free equilibrium

When $ z = 0, $ we solve the first two equation of the right side of (2.5) obtains a virus-boom and immune-free equilibrium $ E_{1}(x_{1}, v_{1}, 0), $ corresponding to partial $ CD4^{+} T $ cells are infected but no CTL response, where

This implies that the level of the virus depends on related parameters of uninfected cells and the virus. In addition, we know that if $ {(1-\varepsilon)\vartheta\beta s}/{(ad)} > 1 $, then system (2.5) has a virus-boom and immune-free equilibrium and the virus load in direct proportion to the population of uninfected cells at $ E_{1}. $ At this time, there is a linear relationship between the virus and the uninfected cells because of the disappearance of immune response.

$ \bullet $ Virus-suppression and immune-boost equilibrium

In the case of $ z\neq 0 $, corresponding to CTL response, assume that the $ E_{i}^{*}(x_i^{*}, v_i^{*}, z_i^{*})\; (i = 1, 2) $ is a virus-suppression and immune-boost equilibrium with $ x_i^{*} > 0, v_i^{*} > 0, z_i^{*} > 0. $ Solving the the first two equation of the right side of (2.5) yields

Obviously, $ x_i^{*} > 0\; \mbox{for}\; v_i^{*} > 0\; \mbox{and}\; z_i^{*} > 0, $ that is $ s(1-\varepsilon)\vartheta\beta-a((1-\varepsilon)\beta v_i^{*}+d) > 0, $ which is equivalent to $ v_i^{*} < {s(1-\varepsilon)\vartheta\beta-ad}/{(a(1-\varepsilon)\beta} = v_1. $ This shows that the sustained immunity exists if and only if the virus load is less than the number of virus at $ E_{1}. $

It follows from the third equation of (2.5) that $ E_i^{*} $ exists if and only if $ v_i^{*} $ is a positive root of the quadratic polynomial

provided that $ v_i^{*} < v_{1}. $ Furthermore, suppose that

$ (H_{1}): \quad c > (\sqrt{m}+\sqrt{b\eta})^{2} $

holds, then $ g(v) $ has two positive zeros:

According to the formula of $ v_{1}^{*} $ and $ v_{2}^{*} $, we know that the level of the virus depends on related parameters of immune factors, that is $ c, m, b, \eta, $ where $ c $ is proliferation rate of immune cells, which could boost immune response however the existence of $ m, b, \eta $ could suppress the immune response. Hence if $ c > m+b\eta $, i.e., positive feedback is greater than negative feedback, then there exists immune response and positive equilibrium. Otherwise, if $ c < m+b\eta $, then no CTL response and there is no positive equilibrium.

$ \bullet $ Remark on different virus loads

From the above calculations, we know that the virus load $ v_1 $ is administrated by the proliferation, decay of uninfected cells as well as the infectivity of virus when the immune response is free; whereas the load virus $ v^*_{1, 2} $ is dominated by immune response and is independent of it's increment and decrement when CTL effector is activated. Intuitively, this opinion is ridiculous. I think the argument maybe is caused by neglecting the proliferation of virus.

$ \bullet $ Reproduction thresholds

Let

where $ (1-\varepsilon)\vartheta\beta $ represents infection rate of $ CD4^{+} $ T cells under antiretroviral treatment, $ {s}/{d} $ is the population of uninfected cells without infection and $ {1}/{a} $ is the average life-times of free virus ^[24]. Thus, the ratio $ R_0 $ describes the average number of newly infected cells generated from one infected cell at the beginning of the infectious process, which is called the basic reproduction number. Further, from the existence of both virus-suppression and immune-boost equilibrium $ E_1 $ and virus-boom and immune-free equilibrium $ E_i^* $, we know that the $ R_0 $ is a fundamental measure, which determines whether a virus spreads within the host or becomes extinct. If $ R_0 > 1 $, the virus can establish an infection. In this case, the immune response expands and the system converges to the equilibriums $ E_1 $ or $ E_i^* $.

Furthermore we define two threshold values as

Lemma 3.2. Assume that $ (H_{1}) $ is satisfied, that is, positive feedback is greater than negative feedback.

$ (a) $ If

holds, corresponds to the average number of newly infected cells produced by an infected cell is no more than 1, then the infection-free equilibrium $ E_{0}(x_{0}, 0, 0) $ is the only biologically meaningful equilibrium.

$ (b) $ If

holds, corresponds to the average number of newly infected cells produced by an infected cell is greater than 1 but no more than the threshold $ R_{1} $, then there are two equilibria: $ E_{0} $ and immune-free equilibrium $ E_{1}(x_{1}, v_{1}, 0). $

$ (c) $ If

holds, corresponds to the average number of newly infected cells produced by an infected cell is greater than 1 but no more than the threshold $ R_{2} $ $ (R_{2} > R_{1}), $ then there are three equilibria: $ E_{0}, \; E_{1} $ and additional equilibrium $ E_{1}^{*}(x_{1}^{*}, v_{1}^{*}, z_{1}^{*}) $.

$ (d) $ If

holds, corresponds to the average number of newly infected cells produced by an infected cell large enough and larger than $ R_{2}, $ then there are four equilibria: $ E_{0}, \; E_{1}, \; E_{1}^{*} $ and $ E_{2}^{*}(x_{2}^{*}, v_{2}^{*}, z_{2}^{*}). $

$ \bullet $ Relation of virus loads with parameters under immune-emerging

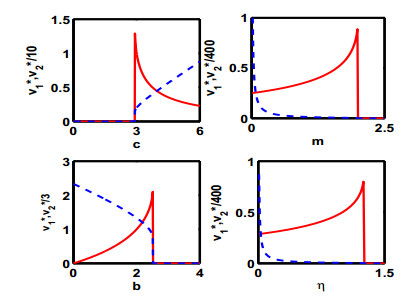
In immune-emerging case, equilibria $ E_{1} $ and $ E^*_{1} $ are stable. In view of the fact the immune-emerging virus load $ v^*_1 $ is less than immune-free virus load $ v_1 $, we know that $ E^*_{1} $ is more medically desirable. In addition, from Figure 1, immune-emerging virus load $ v^*_1 $ is amplified as $ b, m $ and $ \eta $ increases, while it is descended as $ c $ increases. So it is feasible that treating the AIDS by arousing immunity. Particularly, the virus load $ v^*_1 $ sharply changes near the threshold values, which will contribute to devise therapeutic schedules.

4.   Dynamics of system (2.5)

In this section, we consider system (2.5) and study its dynamics.

4.1.   Global stability of infection-free equilibrium

Theorem 4.1. If $ R_{0} \leq 1, $ then $ E_{0} $ is globally asymptotically stable in $ \Omega; $ while if $ R_{0} > 1, $ then $ E_{0} $ is unstable.

Proof. Linearizing (2.5) about $ E_{0} $, we obtain the characteristic equation

and results that if $ R_{0} < 1, $ then $ E_{0} $ is locally asymptotically stable and if $ R_{0} > 1, $ then $ E_{0} $ is a saddle point, hence unstable.

Defined a Lyapunov functional $ L(x_{t}, v_{t}, z_{t}) = v_{t}(0), $ where $ x_{t}(\theta) = x(t + \theta), v_{t}(\theta) = v(t + \theta), z_{t}(\theta) = z(t + \theta) $ for $ \theta\in [-\tau, 0]. $ Calculating the time derivative of $ L $ along the solutions of system (2.5), we have

Obviously, $ L'\mid(2.5) \leq0 $ for all $ x(t), v(t), z(t)\geq 0 $ provided that $ R_{0} \leq1. $ $ L' = 0 $ only if $ v = 0. $ It can be verified that the maximal compact invariant set in $ {L'\mid(2.5) = 0} $ is the singleton $ E_{0} $. Thus it follows from the Lyapunov-LaSalle Invariance Principle ^[39] that $ E_{0} $ is globally asymptotically stable in $ \Omega. $

4.2.   Stability of immune-free equilibrium

The characteristic equation associated with the linearization of system (2.5) at $ E_{1} $ is

where

Note that $ E_{1} $ exists if and only if $ R_{0} > 1, $ therefore, the two eigenvalues $ \lambda_{1} $ and $ \lambda_{2} $ of the characteristic equation at $ E_{1} $ satisfy $ \lambda_{1}+\lambda_{2} = -a_{1} < 0, \; \; \lambda_{1}\lambda_{2} = a_{2} > 0. $ As a consequence, both $ \lambda_{1} $ and $ \lambda_{2} $ must have negative real parts. Therefore $ E_{1} $ is asymptotically stable if all zeros of $ g_{2}(\lambda) $ have negative real parts, where

By analyzing the distribution of zeros of $ g_{2}(\lambda), $ we have the following result.

Theorem 4.2. Consider system (2.5) under the assumption $ (H_{1}). $ If either (3.3) or (3.5) holds, then $ E_{1} $ is locally asymptotically stable, and if (3.4) holds, then $ E_{1} $ is unstable.

Proof. It is easy to prove that $ E_{1} $ is stable when $ \tau = 0 $. Next we consider the distribution of the zeros of $ g_{2}(\lambda) $ when $ \tau > 0. $ Assumption $ (ii) $ of ^[40] holds, which ensures that no zero will come in from infinity. That is, $ Re(\lambda) < +\infty $ for any zero of $ g_{2}(\lambda). $ This, together with the fact that all zeros of $ g_{2}(\lambda) $ depend continuously on $ \tau $ ^[41], implies that, as $ \tau $ increases, the zeros of $ g_{2}(\lambda) $ can cross the imaginary axis only through a pair or pairs of nonzero purely imaginary zeros. Suppose that $ i\omega\; (\omega > 0) $ is a zero of $ g_{2}(\lambda). $ Substituting $ i\omega\; (\omega > 0) $ into the equation $ g_{2}(\lambda) = 0 $ and separating the real and imaginary parts, we obtain

The above yields

Note that $ \dfrac{cv_{1}}{1+\eta v_{1}}-mv_{1}-b = -\dfrac{g(v_{1})}{1+\eta v_{1}}. $ If (3.3) or (3.5) holds, then $ g(v_{1}) > 0, $ and thus the righthand side of (4.2) is negative. Therefore Eq (4.2) has no positive roots and hence $ g_{2}(\lambda) $ has no purely imaginary zeros for all $ \tau > 0. $ That is, in this case, $ E_{1} $ is asymptotically stable for all $ \tau > 0. $ If (3.4) holds, then $ g(v_{1}) < 0 $ and Eq (4.2) has one positive root, which we denote by $ \bar{\omega}. $ This shows that $ g_{2}(\lambda) $ admits a pair of purely imaginary roots $ \pm i\bar{\omega} $ for $ \tau = \bar{\tau}_{j} $ with

Now we check the transversality condition. Substituting $ \lambda(\tau) $ into the characteristic equation $ g_{2}(\lambda) = 0 $ and differentiating the resulting equation with respect to $ \tau $, we obtain

It follows from (4.1) and (4.3) that

This implies that $ \left[ \dfrac{d(Re\lambda(\tau))}{d\tau} \right]_{\tau = \bar{\tau}_{j}, \lambda = \bar{\omega i}} > 0. $ Therefore, there exists a pair of complex conjugate eigenvalues crossing to the right at $ \tau = \bar{\tau}_{j} $ and remaining to the right of the imaginary axis when $ \tau > \bar{\tau}_{j}. $ Thus the characteristic equation (4.1) always has roots with positive real parts for all $ \tau \geq0 $ and $ E_{1} $ is unstable provided (3.4) holds.

4.3.   Stability of positive equilibrium and Hopf bifurcation

The characteristic equation associated with the linearization of system (2.5) at $ E_{i}^{*} $ $ (i = 1, 2) $ is

with

When $ \tau = 0, $ it is easy to prove that $ E_{1}^{*} $ is asymptotically stable, i.e., all roots of the characteristic equation (4.4) for $ i = 1 $ have negative real parts. As $ \tau $ increases, a stability switch at $ E_{1}^{*} $ can occur only when there are some characteristic roots crossing the imaginary axis to the right. Thus we consider the possibility of having a pair of purely imaginary roots $ \lambda = \pm i\omega\; (\omega > 0) $ for Eq (4.4) when $ \tau > 0 $. Substituting $ \lambda = \pm i\omega\; (\omega > 0) $ into Eq (4.4) and separating the real and imaginary parts, one obtains

Squaring and adding both equations of (4.5), we get

Let $ m = \omega^{2}, $ it follows

where

Now let's seek for the conditions that (4.7) has at least one positive root.

Lemma 4.1. Consider (4.7), we can obtain

$ (i) $ If $ A_{3} < 0, $ then (4.7) must have at least one positive root.

$ (ii) $ If $ A_{3} \geq0 $ and $ \Delta \leq0 $ then (4.7) has no positive roots.

$ (iii) $ If $ A_{3} \geq0 $ and $ \Delta > 0, $ then (4.7) must have positive roots if and only if $ m_{2} > 0 $ and $ h(m_{2})\leq0. $

Proof. For $ A_{3} < 0, $ we know that $ {\lim_{m \to +\infty}h(m)} = +\infty $ and $ h(0) = A_{3} < 0, $ thus $ h(m) $ must have at least one positive root. In the case of $ A_{3} \geq0, $ we get

Let $ \Delta = 4A_{1}^{2}-12A_{2}, $ $ h(m) = 0 $ does not have a positive real root for $ \Delta \leq0 $ and if $ \Delta > 0, $ then two roots of (4.7) are $ m_{1} = \dfrac{-2A_{1}-\sqrt{\Delta}}{6}, $ $ m_{2} = \dfrac{-2A_{1}+\sqrt{\Delta}}{6}. $

Furthermore, $ h''(m) = 6m+2A_{1}. $ It is easily seen that $ h''(m_{1}) < 0 $ and $ h''(m_{2}) > 0 $, which implies that $ m_{1} $ is a local maximum of $ h(m) $ and $ m_{2} $ is a local minimum of $ h(m). $ It is obvious that $ h(m) $ is increasing for $ (-\infty, m_{1}] $ or $ (m_{2}, +\infty), $ and $ h(m) $ is decreasing if $ m\in(m_{1}, m_{2}]. $ Assume to the contrary that $ m_{2} \leq0, $ then $ h(m_{2}) \leq h(0) = A_{3} $ and $ h(m) > h(0) $ for any $ m > 0, $ thus $ h(m) $ has no roots for all $ m\in(0, +\infty). $ This is a contradiction. On the other hand, if $ m_{2} > 0 $ and $ h(m_{2}) = 0, $ then $ m_{2} $ is a root of $ h(m) $ when $ A_{3} \geq0 $ and $ \Delta > 0. $ And if $ h(m_{2}) < 0, $ we know that $ \lim_{m\rightarrow\infty}h(m) = +\infty, $ which implies that there exists $ m_{3} > m_{2} $ such that $ h(m_{3}) > 0. $ therefore $ h(m) $ must have at least one positive root provided that $ m\in(m_{2}, m_{3}). $

Consequently we have the following result. Assume that (4.7) has positive roots. Without any loss of generality, we may assume there exists three roots and three roots of (4.6) are $ m_{1}^{*}, \; m_{2}^{*}, \; m_{3}^{*}, $ we have

Solving Eqs (4.5) for $ \tau $ yields

where $ k = 1, 2, 3, \; j = 0, 1, 2, 3, \ldots. $

Let

Lemma 4.2. Assume that $ h'(\omega_{0}^{2}) \neq0, $ then (4.4) admits a pair of purely imaginary roots $ \pm i\omega_{0} $ for $ \tau = \tau_{0} $ and $ \dfrac{d(Re(\lambda(\tau)))}{d\tau}\mid_{\tau = \tau_{0}, \lambda = \omega_{0} i}\neq 0. $

Proof. Let

Thus, (4.4) is equivalent to

This shows that $ F(\lambda) = -G(\lambda)e^{-\lambda\tau}. $ Substituting $ \pm i\omega $ into Eq (4.10), we obtain

Squaring and subtracting both equations of above two yields

In fact, (4.11) is equivalent to (4.6), we get

Next differentiating the resulting equation with respect to $ \omega $

Consider that $ \lambda = i\omega_{0} $ is not a single root of (4.10), we have

A direct calculation gives $ F'(i\omega_{0})+G'(i\omega_{0})e^{-i\omega_{0}\tau_{0}}-\tau_{0}G(i\omega_{0})e^{-i\omega_{0}\tau_{0}} = 0. $ Substituting $ \lambda = i\omega_{0} $ into (4.10), we obtain

The above yields

therefore

It follows from (4.12) and (4.13) that

We may assume that $ h'(\omega_{0}^{2}) \neq0, $ which implies that $ Im\tau_{0} \neq0. $ This is a contradiction. Next we check the transversality condition for $ h'(\omega_{0}^{2}) \neq0. $ Differentiating Eq (4.10) with respect to $ \tau, $ one obtains

By (4.10), we have

It follows from (4.12) that

This shows that if $ h'(\omega_{0}^{2}) \neq0, $ the transversality condition for Hopf bifurcation is satisfied.

With the help of Lemmas 4.1 and 4.2, we have the following results.

Theorem 4.3. If (3.4) and $ (H_{1}) $ are satisfied, by the definition of $ \tau_{0} $ and $ \omega_{0}, $ we have

$ (i) $ If $ A_{3} \geq0 $ and $ \Delta \leq0, $ then $ E_{1}^{*} $ is locally asymptotically stable for any $ \tau \geq0. $

$ (ii) $ If $ A_{3} < 0 $ or $ A_{3} \geq0, $ $ \Delta > 0 $ and $ h(m_{2}) \leq0 $ with $ m_{2} > 0, $ then $ E_{1}^{*} $ is locally asymptotically stable for $ \tau \in[0, \tau_{0}]. $

$ (iii) $ If the conditions of $ (ii) $ are satisfied and $ h'(\omega_{0}^{2}) \neq0, $ then thus $ E_{1}^{*} $ is unstable for $ \tau > \tau_{0}, $ and system (2.5) undergoes Hopf bifurcations at $ E_{1}^{*} $ along a sequence of $ \tau $ values $ \tau_{0}^{j}, j = 0, 1, \ldots $

Our next result shows that $ E_{2}^{*} $ is unstable whenever it exists.

Theorem 4.4. Assume that $ (H_{1}) $ is satisfied. If (3.5) holds, then $ E_{2}^{*} $ is unstable for all $ \tau \geq0. $

Proof. By (4.4), we have

Note that $ G_{2}(0) < 0 $ and $ G_{2}(\infty) > 0 $ for any $ \tau \geq 0, $ thus as long as $ E_{2}^{*} $ exists, the associated characteristic equation must have at least one positive real root and hence $ E_{2}^{*} $ is always unstable for $ \tau \geq 0. $

4.4.   Stability of Periodic Solutions

In the previous section, we obtained conditions for Hopf bifurcation to occur when $ \tau = \tau_{0}. $ In this section, formulae for determining the direction of Hopf bifurcation and stability of bifurcating periodic solutions of system (2.5) at $ \tau_{0} $ shall be presented by employing the normal form method and center manifold theorem introduced by Hassard et al. ^[42]. Throughout this section, we always assume that the system (2.5) undergoes Hopf bifurcation at the positive equilibrium $ E_{1}^{*} $ for $ \tau = \tau_{0} $, and then $ \pm i\omega_{0} $ denotes the corresponding purely imaginary roots of the characteristic equation at the positive equilibrium $ E_{1}^{*}. $

For convenience, let $ t = s\tau, $ $ x(s\tau) = x_{1}(s), $ $ y(s\tau) = y_{1}(s), $ $ z(s\tau) = z_{1}(s), $ and $ \tau = \tau_{0}+\mu, $ $ \mu\in R. $ Still denote $ s = t, $ then the system (2.5) can be written as an FDE in $ C = C([-1, 0], R^{3}) $ as

where $ u(t) = (x_{1}(t), x_{2}(t), x_{3}(t)) $ and $ u_{t}(\theta) = u(t+\theta) = (x_{1}(t+\theta), x_{2}(t+\theta), x_{3}(t+\theta))\in C, $ and $ L_{\mu} :C\rightarrow R^{3}, F: R \times C \rightarrow R^{3} $ are given by

and $ F(\mu, \phi) = (\tau_{0}+\mu)(F_{1}, F_{2}, F_{3})^{T}, $ where $ \phi(\theta) = (\phi_{1}(\theta), \phi_{2}(\theta), \phi_{3}(\theta))^{T}\in C. $ It follows from (2.5) that

and

where

Here $ L_{\mu} $ is a one parameter family of bounded linear operator in $ C[-1, 0] \rightarrow R^{3}. $ By the Riesz representation theorem, there exists a matrix whose components are bounded variation functions $ \eta(\theta, \mu)\; \mbox{in}\; [-1, 0] \rightarrow R^{3}, $ such that

In fact, we choose

where $ \delta $ is the Dirac delta function, then (4.15) is satisfied. For $ \phi(\theta) \in C[-1, 0] \rightarrow R^{3}, $ define

In order to study the Hopf bifurcation problem, we transform system (4.14) into the operator equation of the form

The adjoint operator

where $ \eta^{T} $ is the transpose of the matrix $ \eta. $

The domains of $ A\; \mbox{and}\; A^{*} $ are in $ C[-1, 0] $ and $ C[0, 1] $ respectively, for $ \phi\in C[-1, 0] $ and $ \psi\in C[0, 1]. $ In order to normalize the eigenvectors of operator $ A $ and adjoint operator $ A^{*}, $ we need to introduce the following bilinear form

here $ \eta(\theta) = \eta(\theta, 0). $

By the last section of the discussion, we know that $ \pm i\omega_{0}\tau_{0} $ are the eigenvalues of $ A, $ thus they are also eigenvalues of $ A^{*}. $ We have the following results.

Lemma 4.3. Assume that $ q(\theta) = (1, q_{1}, q_{2})^{T}e^{-i\omega_{0}\tau_{0}\theta} $ and $ q^{*}(s) = D(1, q_{1}^{*}, q_{2}^{*})^{T}e^{i\omega_{0}\tau_{0}s} $ be the eigenvectors of A respects to $ i\omega_{0}\tau_{0}, $ and adjoint operator $ A^{*} $ respects to $ -i\omega_{0}\tau_{0}, $ respectively, then $ \langle q^{*}(s), q(\theta)\rangle = 1, $ $ \langle q^{*}(s), \bar{q}(\theta)\rangle = 0, $

where

Proof. Let $ q(\theta) $ is the eigenvector of $ A, $ which is respect to $ i\omega_{0}\tau_{0}, $ we have $ A(\theta)q(\theta) = i\omega_{0}\tau_{0}q(\theta). $ Then

The above yields

Let $ q^{*}(\theta) = D(1, q_{1}^{*}, q_{2}^{*})^{T}e^{i\omega_{0}\tau_{0}\theta} $ is the eigenvector of $ A^{*}, $ which is respect to $ -i\omega_{0}\tau_{0}. $ Similarly, we also have

Furthermore,

Next we consider $ \langle q^{*}, q\rangle, $

Obviously, if

then $ \langle q^{*}, q\rangle = 1. $ On the other hand,

therefore, $ \langle q^{*}, q\rangle = 0, $ and the proof is complete.

Next, we study the stability of bifurcating periodic solutions. We first construct the coordinates to describe a centre manifold $ C_{0} $ near $ \mu = 0 $, which is a local invariant. Assume that $ u_{t} $ is the solution of (4.14) for $ \mu = 0, $ we define

On the center manifold $ C_{0}, $ we have $ w(t, \theta) = w(p(t), \bar{p}(t), \theta), $ where

and $ p $ and $ \bar{p} $ are local coordinates of centre manifold $ C_{0} $ in the direction of $ q^{*} $ and $ \bar{q}^{*} $ respectively.

The existence of centre manifold $ C_{0} $ enables us to reduce (4.16) to an ordinary differential equation in a single complex variable on $ C_{0}. $ For the solution $ u_{t}\in C_{0} $ of (4.16), since $ \mu = 0, $

and we rewrite this equation as

where

It follows from (4.17) and (4.18) that we can obtain the following form

The above yields

In the following we focus on the computation of $ W_{20}(\theta) $ and $ W_{11}(\theta), $ (4.16) and (4.19) imply that

Comparing the coefficients of equations (4.20) and (4.21), we get

For $ \theta \in[-1, 0], $ according to (4.19) and (4.20), we get

Comparing the coefficients of Eqs (4.21) and (4.23), we obtain

Next, substituting (4.24) in (4.22) yields

According to $ q(\theta) = (1, q_{1}, q_{2})^{T}e^{i\omega_{0}\tau_{0}\theta}, $ thus we derive

where $ E_{1} = (E_{11}, E_{1, 2}, E_{1, 3})^{T}, \; \; E_{2} = (E_{21}, E_{22}, E_{23})^{T}. $ Then we have

where $ \eta(\theta) = \eta(\theta, 0). $ Furthermore, $ H_{20}(0) = -g_{20}q(0)-\bar{g}_{02}\bar{q}(0)+2\tau_{0}(E_{11}, E_{12}, E_{13})^{T}. $

By (4.24), we obtain$ (2i\omega_{0}\tau_{0}- \int_{-1}^{0}d\eta(\theta)e^{2i\omega_{0}\tau_{0}\theta})E_{1} = 2\tau_{0}(k_{1}, k_{2}, k_{3})^{T}, $ which is rewritten as

And a direct calculation yields

where

and

Similarly, we have

where

and

Now from $ w_{20}(\theta) $ and $ w_{11}(\theta) $, we can calculate the following values:

These formulas give a description of the Hopf bifurcating periodic solutions of (2.5) at $ \tau = \tau_{0} $ on the center manifold. From the discussion above, we have the following theorem.

Theorem 5. For the periodic solution of (2.5), the following results hold.

$ (i) $ The periodic solution is supercritical (subcritical) if $ U > 0\; (U < 0); $

$ (ii) $ The bifurcating periodic solutions are orbitally asymptotically stable (unstable) with asymptotical phase if $ M < 0\; (M > 0); $

$ (iii) $ The period of the bifurcating periodic solutions increase (decrease) if $ T_{2} > 0\; (T_{2} < 0). $

4.5.   Simulations of bistability

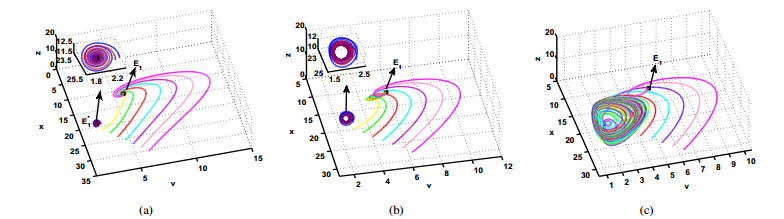
It is shown in Theorems 4.3 and 4.5 that system (2.5) admits one or multiple periodic solutions. These periodic solutions can be either stable or unstable. For the parameters given from Table 1, if (3.5) and $ (H_{1}) $ are satisfied and thus system (2.5) admits four equilibria: $ E_{0} = (70, 0, 0), $ $ E_{1} \approx(11.11, 5.89, 0), $ $ E_{1}^{*} = (25, 2, 12.5), $ $ E_{2}^{*} \approx (18.92, 3, 7.03), $ where $ E_{1} $ is asymptotically stable provided (3.5) holds for $ \tau\geq 0 $. By some computation one gets the bifurcation value $ \omega_{0} = 0.1946 $ and $ \tau_{0} = 1.1241. $ From Theorems 4.3, we know that the transversal condition is satisfied, thus the positive equilibrium $ E_{1}^{*} $ is asymptotically stable for $ \tau < \tau_{0} $ and unstable for $ \tau > \tau_{0}, $ and when $ \tau = \tau_{0}, $ (2.5) undergoes Hopf bifurcation at the positive equilibrium $ E_{1}^{*}. $ By the algorithms derived in Section 4.4, we can obtain $ C_{1}(0) = -0.0956-0.4901i $ and $ M = -0.1912 < 0, $ implying the bifurcating periodic solutions are orbitally asymptotically stable. Further $ U = 18.3944 > 0 $ and $ T_{2} = 22.9542 > 0 $ show that the Hopf bifurcation is supercritical. In the light of the above aspects, two conclusions are achieved:

● If $ \tau \in[0, \tau_{0}], $ system (2.5) emerges a bistability called type Ⅰ which holds two stable equilibria $ E_{1} $ and $ E_{1}^{*} $ (see Figure 2(a));

● If $ \tau \in (\tau_{0}, +\infty) $ system (2.5) appears a bistability defined by type Ⅱ which possesses a stable equilibrium $ E_{1} $ and a stable periodic solution (see Figure 2(b) and (c)).

Then we ran numerical simulations to illustrate the above results as follows.

By comparing Figure 2(b) with (c), we can find that the domain of attraction of periodic solution can be expanded by boosting proliferation rate $ c $ of immune cells given the same parameter value and initial value. Thus it can be seen that the immune parameter $ c $ affects the period or amplitude of the periodic solution, but the influence of other parameters on it is unknown. In order to find out the influence of other parameters on the period and amplitude of the periodic solution, and to solve the problem of which parameters can adjust the treatment scheme, we will fist analyze the sensitivity of period and amplitude of the periodic solution to parameters.

5.   Sensitivity of periodic solution

In this section, we use a sensitivity analysis method proposed in ^[46,47], and focus on sensitivities of amplitude and of the period when our delay model (2.5) admits a periodic solution. First, compute all of sensitivity equations with respect to all parameters in system (2.5), taking particularly $ \varepsilon $ and $ b $ as examples in following:

and

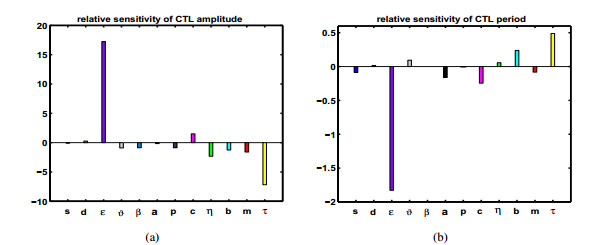
Solving the sensitivity equations, and according to the circumscription of sensitivities of the limit cycle in ^[46], we obtain the relative sensitivities of the amplitude and of the period shown in Figure 3. The effective impact of $ \tau $ on both amplitude and period of the CTL immune response reveals that it is transparent that the positive equilibrium $ E_{1}^{*} $ switches from stable to unstable and a stable limit cycle occurs with the increase of the time lag. In addition, the amplitude and period of CTL response also depend on antiviral therapy parameter $ \varepsilon, $ immune parameters $ c, m, b $ and $ \eta, $ which indicates that effective combination of antiviral therapy and immunotherapy is needed for successful treatment.

6.   Optimal combined treatment strategy

The above sensitivity analyses illuminate that parameters $ \varepsilon, $ $ c, m, b $, $ \eta $ and $ \tau $ are impressible for the periodic solution regulating the sustained immunity. But we only schedule both $ \varepsilon $ and $ b $ relating to the therapy rather than the other parameters being intrinsic for individual organisms. Taking a patient performed a continuous antiretroviral therapy of 1000 days but with an unsuccessful outcome as a example, we firstly simulate a combined treatment by introduce a phased immunotherapy into the continuous antiviral treatment and then adjust the therapeutic session as well as the insetting time to quest the preferable therapeutic regimen by model (2.4).

6.1.   Combined treatment

In the following, we invariably take $ T = 1000 $ days. Now we take initial states of (2.4) as follows: $ x(0) $ = 25 cells/$ \mu l $, $ v(0) $ = 5 virus/$ \mu l $, $ z(0) $ = 10 cells/$ \mu l $, and $ \tau = 2.6, $ other parameter values are given in Table 1. Then for system (2.4), the immune-free equilibrium $ E_1 $ is stable while virus-suppression and immune-boost equilibrium $ E_1^* $ is unstable (see Figure 4(a) and (d)). That is, immune is free and the virus settles down at an equilibrium level. These symptoms expose that single antiretroviral treatment can not defeat the virus even if the dosage is high. So we inset a phased immunotherapy into a continuous antiviral treatment and formulate a hybrid model (2.4). Thus, we try to regulate CTL response by changing the value of $ \bar{b} $. Referencing the works ^[17,28] and incorporating two types of bistability in the above, as well as the oscillatory viral loads and immune cells of the clinical data during therapies ^[29], we aim at proposing a immunotherapy tactics to achieve the sustained immunity in the form of periodic oscillation.

Now we evaluate the efficacy of these treatments by simulations. For the sick individual dominated by parameters in Table 1.

After a continual immunotherapy with $ \bar{b} = 0.05 $ from $ t_1 = 100$th day to $ t_2 = 250$th day, and then interrupting therapy with $ \bar{b} = 0 $ formulates the sustained immunity with a low viral load (see Figure 4(b) and (e)). From mathematics angle, we alter the solution of (2.4) from the basin of the attraction of the immune-free equilibrium to the immune control balance through the immunotherapy when the treatment is ceased. We perform another therapeutic regimen by increasing the immunotherapy dose of patient to $ \bar{b} = 0.07 $ during the same course of treatment and then stoping immunotherapy. Figure 4(c) and (f) manifest that even if the immunity of patient is enhanced and the virus load is depressed during therapeutic session, unfortunately they soon return to premarital levels after suspending immunotherapy. The unappealing outcomes arise due to the improper dosage of immunotherapy. Therefore we will seek the optimal combined treatment scheme in the next subsection.

6.2.   Optimal Combined treatment

In this subsection we firstly promote the above treatment scheme by optimizing the cost function meanwhile building the consistent immunity on HIV. Furthermore, we adjust the therapeutic session and the start time of immunotherapy treatment to quest the preferable therapeutic regimen.

In order to acquire the optimal therapeutic regimens, define cost function as follows:

where $ p_{1}, $ $ p_{2} $ describe the prices of antiviral therapy and immunotherapy, respectively, $ p_{3} $ is the weight factor and $ \varepsilon_0 $ is an idiomatic dosage, while

where $ D $ is the therapy parameters admissible domain of $ \varepsilon\times\bar{b} $. $ J_0 $ denotes the accumulated viruses (AV) during the observation course of patient. The first and third integrals represent respectively the AV of the patient prior to combined treatment and after stopping immunotherapy, while the second one trace the AV during combined treatment.

● Our aim is to find $ (\varepsilon^*, \bar{b}^*)\in D $ to minimize the objective functional $ J $ and meanwhile make the solution of system (2.4) with $ (\varepsilon^*, \bar{b}^*) $ at $ t_2 $ to alight on the attractive basin of the periodic solution of system (2.4) with $ \varepsilon = \varepsilon_0, $ $ \bar{b} = 0 $.

Just as we mentioned in the above, our optimal problem differs the traditional one so that Pontryagin Maximum Principle is invalid. So we contribute an efficient algorithm aiming at mounting a defense to HIV infection at the lowest cost by selecting the appropriate antiviral parameter $ \varepsilon $ and immunotherapy parameter $ \bar{b} $ during CTS.

● Algorithm:

● Step 1. Give parameters domain $ \varepsilon\times \bar{b}\in D $ and a fixed interval $ [0, T] $ as well as $ t_1\in(0, T) $ and $ t_2\in(0, T) $ with $ t_1 < t_2 $, respectively;

● Step 2. Latticing domain $ D $ by step length $ h $ to yield $ n $ sets of data $ (\varepsilon_i, \bar{b}_i) $ for $ i = 1, 2, \cdots, n $;

● Step 3. Solve (2.4) with $ \varepsilon = \varepsilon_0 $ and $ \bar{b} = 0 $ in $ t\in[0, t_1] $. Then substitute $ (\varepsilon_i, \bar{b}_i) $ into system (2.4) and furthermore solve it in $ t\in(t_1, t_2] $ and seek all of $ (\varepsilon_i^j, \bar{b}_i^j) $ which make $ (x(t_2), v(t_2), z(t_2)) $ alight on the attractive basin of the periodic solution of system (2.4) with $ \varepsilon = \varepsilon_0 $ and $ \bar{b} = 0 $;

● Step 4. Substitute all of $ (\varepsilon_i^j, \bar{b}_i^j) $ into the cost function and find the $ (\varepsilon_i^*, \bar{b}_i^*) $ which minimizes the cost function.

In the above algorithm, the positive parameter pairs $ (\varepsilon_i, \bar{b}_i) $, $ (\varepsilon_i^j, \bar{b}_i^j) $ and $ (\varepsilon_i^*, \bar{b}_i^*) $ are called the combined treatment strategy, the successful combined treatment strategy and the optimal combined treatment strategy, respectively.

For convenience, we always take $ \varepsilon_0 = 0.8 $, $ \varepsilon\times \bar{b}\in D = [0.7, 0.9]\times[0, 0.2] $ and $ h = 0.01 $ together with $ p_{1} = 2, $ $ p_{2} = 2.5, $ $ p_{3} = 1.5 $ in the following simulations. Then latticing domain $ D $ obtains 441 sets of data, namely, 441 kinds of combinations of treatment strategies. The other parameters of system (2.4) are the same as Table 1.

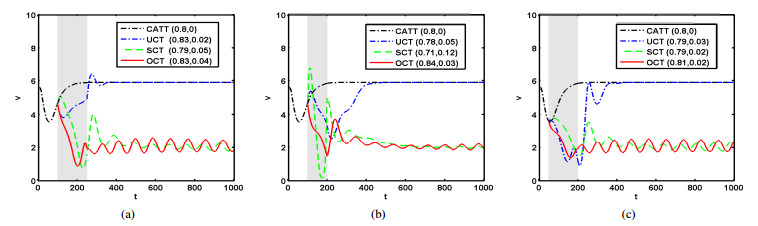
Scheme 1. Taking $ t_1 = 100 $ day and $ t_2 = 250 $ day implies that the combined treatment session is 150 days. Our goal is to find a set of parameters $ (\varepsilon^*, \bar{b}^*)\in D $ that authorizes the patient to establish sustained immunity after 150 days of combination treatment at the lowest cost. For this reason, we seek parameters to ensure that at the end of combination treatment the solution of the system $ (x(250), v(250), z(250)) $ is in the attractive basin of the periodic solution of the system (2.4) without immunotherapy, resulting in a periodic solution with sustained immunity. Along with the idea of Algorithm, we found the 7 sets of successful treatment parameters from the 441 sets of data, listed in the Table 2. After replacing 7 sets data into the objective function $ J $, the optimal therapeutic regimen $ (\varepsilon^{*}, \bar{b}^{*}) = (0.83, 0.04) $ making $ min\; J = 5083 $ can be acquired.

Next we shorten CTS from 150 days to 100 days and still keep the start time of immunotherapy treatment at 100th day. Now we will simulate another optimal therapeutic regimen as follows.

Scheme 2. Taking $ t_1 = 100 $ day and $ t_2 = 200 $ day implies that the combined treatment session is 100 days. According to the above algorithm, we seek out 6 sets of successful data listed in Table 3 and further catch the optimal therapeutic regimen $ (\varepsilon^{*}, \bar{b}^{*}) = (0.84, 0.03) $ authorizes the patient to establish sustained immunity after 100 days of combination treatment at the lowest cost $ min\; J = 5327 $.

Finally, we adjust the start time of treatment and keep the CTS 150 days to quest the optimal therapeutic regimen.

Scheme 3. Taking $ t_1 = 50 $ and $ t_2 = 200 $ day implies that the combined treatment advances 50 days than Scheme 1. By the above algorithm, 8 sets of successful data listed in Table 4 are explored out and further we obtain the optimal therapeutic regimen $ (\varepsilon^{*}, \bar{b}^{*}) = (0.81, 0.02) $ authorizes the patient to establish sustained immunity after 150 days of combination treatment at the lowest cost $ min\; J = 4949 $.

From Figure 5, it is indicated that the levels of virus rapidly increase and then fall sharply during the combined treatment session. After stoping immunotherapy, levels of virus slightly climb and quickly perform a periodic oscillation implying that the patient has established sustained immunity. By comparison, early mediating immunotherapy in Scheme 3 suppresses the load of virus lower than Scheme 1 during combined treatment (see Figure 5(a) and (c)). Moreover, shortening CTS does not reduce but magnify the cost function $ J $. On the whole, Scheme 3 is the best one. So designing a combined treatment schedule synthesizes the antiviral parameter $ \varepsilon $, immunotherapy parameter $ \bar{b} $, combined treatment session, as well as initial and terminal time of immunotherapy.

7.   Conclusion and discussion

Despite many new approaches to treat HIV virus, including HAART, immunotherapy, structured treatment interruption ^[15,16] and so on, the enthusiasm, due to the inability of therapy to eradicate HIV infection, has been aroused to formulate rational therapeutic strategies to establish sustained immunity to suppress viruses after stopping therapy. Studies have shown that AIDS patients can improve their ability to control HIV through therapeutic vaccines or interferon immunomodulation after suspension of antiretroviral therapy ^[23]. In this paper, we establish an uninfected cells, virus and immune response model with continuous antiretroviral therapy meanwhile also taking into account the time lag needed for the expansion of immune cells.

Firstly, we have investigated the dynamic behavior of the model (2.5). By defining a basic regeneration number $ R_{0}, $ which describes the average number of newly infected cells generated from one infected cell, we found that the basic regeneration number $ R_{0} $ and the time lag $ \tau $ both play crucial roles in determining the CTL response dynamics. As $ R_{0} $ increases, the dynamics shift through four possible outcomes: (i) If $ R_{0} < 1, $ then number of infected cells is so small that the virus does not spread, the system converges to the infection-free equilibrium $ E_{0} $ which is globally stable (Theorem 4.1); (ii)As $ R_{0} $ increases, i.e., the number of infected cells is gradually increasing, then the virus is able to infect the host without a sustained CTL response, the system converges to the immune-free equilibrium $ E_{1}, $ which is always locally stable (Theorem 4.2); (iii) If $ R_{0} $ exceeds the first threshold, $ R_{1} $, then the CTL response controls the virus; the system either converges to the positive equilibrium $ E_{1}^{*}, $ or the system admits at least one periodic solution, which depends on the time lag $ \tau $ (Theorem 4.3); (iv) If $ R_{0} $ sufficiently large and $ R_{0} > R_{2}, $ then the number of infected cells is large enough to cause the virus to multiply, so either the system is stimulated by the virus to produce sustained immunity, or the immune function is lost due to too much virus, which depends on the load of virus. This is a bistability, namely, the system converges to either immune-free equilibrium $ E_{1} $ or positive equilibrium $ E_{1}^{*} $ (with the increase of time delay, it converges to a stable periodic solution), depending on different initial conditions.

Secondly, the sensitivity analysis method proposed in ^[46] were applied to acquire the sensitivities of the amplitude and the period with respect to all of parameters when model (2.5) admits a periodic solution. Results indicate that parameters $ \varepsilon, $ $ c, p, b $, $ \eta $ and $ \tau $ are impressible for the periodic solution symbolizing the sustained immunity. But we only schedule both $ \varepsilon $ and $ b $ relating to the therapy rather than the other parameters being intrinsic for individual organisms. This offers primordial motivations to propose an optimal treatment tactics by combining the continuous antiretroviral therapy with a phase of immunotherapy (which efficiency denoted by $ \bar{b} $) to achieve the sustained immunity.

Furthermore, taking a patient performed a continuous antiretroviral therapy of 1000 days but with an unsuccessful outcome (see Figure 4(a) and (d)) as a example, we simulate a combined treatment by introduce immunotherapy of 150 days and then adjust the therapeutic session as well as the start time of immunotherapy treatment to quest the preferable therapeutic regimen. Incorporating two types of bistability on system (2.4), and the oscillatory viral loads and immune cells of the clinical data during therapies ^[29], we mathematically alter the solution of (2.4) from the basin of the attraction of the immune-free equilibrium to the immune control balance when the treatment is ceased, meanwhile minimize the cost function through the a period of immunotherapy. Because our optimal problem differs the traditional one, we contribute an efficient algorithm, by meshing a special domain on the antiretroviral and immunotherapy parameters $ \varepsilon $ and $ \bar{b} $, to find successful combined treatment schemes and further seek the optimal one. By comparison, simulations exhibit that early mediating immunotherapy in Scheme 3 suppresses the load of virus lower than Scheme 1 during combined treatment (see Figure 5(a) and (c)), but shortening CTS in Scheme 2 does not reduce but magnify the cost function $ J $.

Finally, it's also worth pointing out, even if our findings can provide some insights into the design of effective and rational therapeutic strategies to boost sustained immunity to quell viruses, the accuracy of therapeutic strategies depends on the step $ h $ of meshing in Algorithm. In addition, the general algorithm to seek the therapeutic session as well as the start and stop time of immunotherapy is significant and pendent.

Acknowledgments

The work was supported by the National Natural Science Foundation of China (11971023, 11871371).

Conflict of interest

The authors declare that there is no conflict of interest.