Theoretical models for chronotherapy: Periodic perturbations in funnel chaos type

1.   Introduction

In the last few decades, more and more scholars have studied fractional-order neural networks (FONNs) due to their powerful functions ^[1,2]. FONNs have been accurately applied to image processing, biological systems and so on ^[3,4,5,6] because of their powerful computing power and information storage capabilities. In the past, scholars have studied many types of neural network (NN) models. For example, bidirectional associative memory neural networks (BAMNNs) ^[7], recurrent NNs ^[8], Hopfield NNs ^[9], Cohen-Grossberg NNs ^[10], and fuzzy neural networks (FNNs) ^[11]. With the development of fuzzy mathematics, Yang et al. proposed fuzzy logic (fuzzy OR and fuzzy AND) into cellular NNs and established FNNs. Moreover, when dealing with some practical problems, it is inevitable to encounter approximation, uncertainty, and fuzziness. Fuzzy logic is considered to be a promising tool to deal with these phenomena. Therefore, the dynamical behaviors of FNNs have attracted extensive research and obtained abundant achievements ^{[12,13,14,15]}.

The CVNNs are extended from real-valued NNs (RVNNs). In CVNNs, the relevant variables in CVNNs belong to the complex field. In addition, CVNNs can also address issues that can not be addressed by RVNNs, such as machine learning ^[16] and filtering ^[17]. In recent years, the dynamic behavior of complex valued neural networks has been a hot topic of research for scholars. In ^[16], Nitta derived some results of an analysis on the decision boundaries of CVNNs. In ^[17], the author studied an extension of the RBFN for complex-valued signals. In ^[18], Li et al. obtained some synchronization results of CVNNs with time delay. Overall, CVNNs outperform real-valued neural networks in terms of performance, as they can directly process two-dimensional data.

Time delays are inescapable in neural systems due to the limited propagation velocity between different neurons. Time delay has been extensively studied by previous researchers, such as general time delay ^[19], leakage delays ^[20], proportional delays ^[21], discrete delays ^[22], time-varying delays ^[23], and distributed delays ^[24]. In addition, the size and length of axonal connections between neurons in NNs can cause time delays, so scholars have introduced distributed delays in NNs. For example, Si et al. ^[25] considered a fractional NN with distributed and discrete time delays. It not only embodies the heredity and memory characteristics of neural networks but also reflects the unevenness of delay in the process of information transmission due to the addition of distributed time delays. Therefore, more and more scholars have added distributed delays to the NNs and have made some new discoveries ^[26,27]. On the other hand, due to the presence of external perturbations in the model, the actual values of the parameters in the NNs cannot be acquired, which may lead to parameter uncertainties. Parameter uncertainty has also affected the performance of NNs. Consequently, scholars are also closely studying the NNs model of parameter uncertainty ^[28,29].

The synchronization control of dynamical systems has always been the main aspect of dynamical behavior analysis, and the synchronization of NNs has become a research hotspot. In recent years, scholars have studied some important synchronization behaviors, such as complete synchronization (CS) ^[30], global asymptotic synchronization ^[31], quasi synchronization ^[32], finite time synchronization ^[33], projective synchronization (PS) ^[34], and Mittag-Leffler synchronization (MLS) ^[35]. In various synchronizations, PS is one of the most interesting, being characterized by the fact that the drive-response systems can reach synchronization according to a scaling factor. Meanwhile, the CS can be regarded as a PS with a scale factor of 1. Although PS has its advantages, MLS also has its unique features. Unlike CS, MLS can achieve synchronization at a faster speed. As a result, some scholars have combined the projective synchronization and ML synchronization to study MLPS ^[36,37]. However, there are few papers on MLPS of FOFNNs. Based on the above discussion, the innovative points of this article are as follows:

$\bullet$ According to the FNNs model, parameter uncertainty and distributed delays are added, and the influence of time-varying delay, distributed delay, and uncertainty on the global MLPS of FOFCVNNs is further considered in this paper.

$\bullet$ The algebraic criterion for MLPS was obtained by applying the complex valued direct method. Direct methods and algebraic inequalities greatly reduce computational complexity.

$\bullet$ The design of nonlinear hybrid controllers and adaptive hybrid controllers greatly reduces control costs.

Notations: In this article, $C$ refers to the set of complex numbers, where $O = O^{R}+iO^{I}\in C$ and $O^{R}, O^{I}\in R$, $i$ represents imaginary units, $C^{n}$ can describe a set of n-dimensional complex vectors, $\overline{O_{\psi}}$ refers to the conjugate of $O_{\psi}$. $|O_{\psi}| = \sqrt{O_{\psi}\overline{O_{\psi}}}$ indicating the module of $O_{\psi}$. For $O = (O_{1}, O_{2}, \ldots, O_{n})^{T}\in{C}^{n}, ||O|| = (\sum\limits_{\psi = 1}^{n}|O_{\psi}|^{2})^{\frac{1}{2}}$ denotes the norm of $O$.

2.   Preliminaries

In this section, we provide the definitions, lemmas, assumptions, and model details required for this article.

Definition 2.1. ^[38] The Caputo fractional derivative with $0 < \Upsilon < 1$ of function $O(t)$ is defined as

Definition 2.2. ^[38] The one-parameter ML function is described as

Lemma 2.1. ^[39] Make $Q_{\psi}, O_{\psi}\in C(w, \psi = 1, 2, \ldots, n, )$, then the fuzzy operators in the system satisfy

Lemma 2.2. ^[40] If the function $\vartheta(t)\in C$ is differentiable, then it has

Lemma 2.3. ^[41] Let $\widehat{\xi}_{1}, \widehat{\xi}_{2}\in C$, then the following condition:

holds for any positive constant $\chi > 0$.

Lemma 2.4. ^[42] If the function $\varsigma(t)$ is nondecreasing and differentiable on $[t_{0}, \infty]$, the following inequality holds:

where constant $\jmath$ is arbitrary.

Lemma 2.5. ^[43] Suppose that function $\hbar(t)$ is continuous and satisfies

where $0 < \alpha < 1$, $\gamma\in R$, the below inequality can be obtained:

Next, a FOFCVNNS model with distributed and time-varying delays with uncertain coefficients is considered as the driving system:

where $0 < \alpha < 1$; $O(t) = ((O_{1}(t), ..., O_{n}(t))^{\top}$; $O_{w}(t), w = 1, 2, ..., n$ is the state vector; $a_{w}\in R$ denotes the self-feedback coefficient; $m_{w\psi}\in C$ stands for a feedback template element; $\bigtriangleup m_{w\psi}\in C$ refers to uncertain parameters; $\mu_{w\psi}\in C$ and $\upsilon_{w\psi}\in C$ are the elements of fuzzy feedback MIN and MAX templates; $\bigvee$ and $\bigwedge$ indicate that the fuzzy OR and fuzzy AND operations; $\tau(t)$ indicates delay; $I_{w}(t)$ denotes external input; and $f_{\psi}(\cdot)$ is the neuron activation function.

Correspondingly, we define the response system as follows:

where $U_w(t) \in {C}$ stands for controller. In the following formula, ${}_{{t_0}}^CD_t^\alpha$ is abbreviated as $D^{\alpha}$.

Defining the error as $k_{w}(t) = Q_{w}(t)-SO_{w}(t)$, where $S$ is the projective coefficient. Therefore, we have

where ${f_{\psi}\widetilde{k_{\psi}(t)}} = f_{\psi}(Q_{\psi}(t))-f_{\psi}(SO_{\psi}(t))$.

Assumption 2.1. $\forall O, Q\in C$ and $\forall L_{\varpi} > 0$, $f_{\varpi}(\cdot)$ satisfy

Assumption 2.2. The nonnegative functions $b_{w\psi}(t)$ and $c_{w\psi}(t)$ are continuous, and satisfy

Assumption 2.3. The parameter perturbations $\triangle m_{w\psi}(t)$ bounded, then it has

where $M_{w\psi}$ is all positive constants.

Assumption 2.4. Based on the assumption for fuzzy OR and AND operations, the following inequalities hold:

where $\delta_{\psi}$ and $\eta_{\psi}$ are positive numbers.

Definition 2.3. The constant vector $O^{*} = (O_{1}^{*}, \ldots, O_{n}^{*})^{T}\in{C}^{n}$ and satisfy

whereupon, $O^{*}$ is called the equilibrium point of (2.1).

Definition 2.4. System (2.1) achieves ML stability if and only if $O^{*} = (O_{1}^{*}, \ldots, O_{n}^{*})^{T}\in\mathbb{C}^{n}$ is the equilibrium point, and satisfies the following condition:

where $0 < \alpha < 1, \; \rho, \ \eta > 0, \; \Xi(0) = 0$.

Definition 2.5. If FOFCVNNS (2.1) and (2.2) meet the following equation:

so we can say it has achieved projective synchronization, where $S\in R$ is projective coefficient.

3.   Main results

In this part, we mainly investigate three theorems. According to the Banach contraction mapping principle, we can deduce the result of Theorem 3.1. Next, we construct a linear hybrid controller and an adaptive hybrid controller, and establish two MLPS criteria.

Theorem 3.1. $\mathbb{B}$ is a Banach space. Let $||O||_{1} = \sum\limits_{\psi = 1}^{n}|{O_{\psi}}|$. Under Assumptions 2.1–2.4, if the following equality holds:

then FOFCVNNS (2.1) has a unique equilibrium point with $O^{*} = (O_{1}^{*}, \ldots, O_{n}^{*})^{T}\in\mathbb{C}^{n}$.

Proof. Let $O = (\widetilde{O_{1}}, \widetilde{O_{2}}, \ldots, \widetilde{O_{n}})^{\top} = (a_{1}O_{1}, a_{2}O_{2}, \ldots, a_{n}O_{n})^{\top}\in R^{n}$, and construct a mapping $\varphi:\mathbb{B}\rightarrow {\mathbb{B}}$, $\varphi (x) = (\varphi_{1}(O), \varphi_{2}(O), \ldots, \varphi_{n}(O))^\top$ and

For two different points $\alpha = (\alpha_{1}, \ldots, \alpha_{n})^\top, \beta = (\beta_{1}, \ldots, \beta_{n})^\top$, it has

According to Assumption 2.1, we get

Next, we have

From Assumption 2.3, then it has

Finally, we obtain

where $\varphi$ is obviously a contraction mapping. From Eq (3.2), there must exist a unique fixed point $\widetilde{O^{*}}\in C^{n}$, such that $\varphi(\widetilde{O^{*}}) = \widetilde{O^{*}}$.

Let $O_{\psi}^* = \frac{\widetilde{O_{\psi}^*}}{a_{\psi}}$, we have

Consequently, Theorem 3.1 holds.

Under the error system (2.3), we design a suitable hybrid controller

By substituting (3.10)–(3.12) into (2.3), it yields

Theorem 3.2. Based on the controller (3.10) and Assumptions 2.1–2.4, systems (2.1) and (2.2) can achieve MLPS if the following formula holds:

Proof. Picking the Lyapunov function as

By application about derivative $v_{1}(t)$, we derive

Following Lemma 2.2, it has

Substituting Eq (3.13) to (3.17), we can get

Combining Lemma 2.3, one gets

Based on (3.19), we derive

According to Assumptions 2.1 and 2.3, Lemma 2.3, we can get

Based on Lemma 2.3, one has

Combining Assumption 2.4 and Lemma 2.1, one obtains

Substituting (3.23) into (3.22), it has

Thus,

Substituting (3.20)–(3.25) into (3.18), we get

Applying the fractional Razumikhin theorem, the inequality (3.26) is as follows:

Apparently, from Lemma 2.5, it has

and

Moreover,

From Definition 2.4, system (2.1) is Mittag-Leffler stable. From Definition 2.5 and $\lim_{t\rightarrow \infty}||k(t)|| = 0$, the derive-response systems (2.1) and (2.2) can reach MLPS. Therefore, Theorem 3.2 holds.

Unlike controller (3.11), we redesign an adaptive hybrid controller as follows:

Taking (3.12) and (3.32) into (3.31), then

Theorem 3.3. Assume that Assumptions 2.1–2.4 hold and under the controller (3.31), if the positive constants $\Upsilon_{1}$, $\Upsilon_{2}$, $\Omega_{1}$, and $\Omega_{2}$ such that

we can get systems (2.1) and (2.2) to achieve MLPS.

Proof. Taking into account the Lyapunov function

By utilizing Lemmas 2.2 and 2.4, then it has

Substituting (3.32) into (3.36), one has

Substituting (3.33) into $R_{1}$ yields

According to the inequality (3.20), it has

Substituting (3.39) and (3.21)–(3.25) into (3.38), we have

Substituting (3.37) and (3.40) into (3.36), we finally get

By applying fractional-order Razumikhin theorem, the following formula holds:

Let $\Xi = \min\Big(\Upsilon_{1}-\Upsilon_{2}\Omega_{2}, 2p\Big)$, then

According to Lemma 2.5, one has

From Eq (3.35), we can deduce

and

Therefore, it has

and

Obviously, from Definition 2.4, system (2.1) is Mittag-Leffler stable. From Definition 2.5 and $\lim_{t\rightarrow \infty}||k(t)|| = 0$, systems (2.1) and (2.2) can reach MLPS.

Remark 3.1. Unlike adaptive controllers ^[12], linear feedback control ^[16], and hybrid controller ^[34], this article constructs two different types of controllers: nonlinear hybrid controller and adaptive hybrid controller. The hybrid controller has high flexibility, strong scalability, strong anti-interference ability, and good real-time performance. At the same time, hybrid adaptive controllers not only have the good performance of hybrid controllers but also the advantages of adaptive controllers. Adaptive controllers reduce control costs, greatly shorten synchronization time, and can achieve stable tracking accuracy. Different from the research on MLPS in literature ^[33,34,35], this paper adopts a complex valued fuzzy neural network model, while fully considering the impact of delay and uncertainty on actual situations. At the same time, it is worth mentioning that in terms of methods, we use complex-value direct method, appropriate inequality techniques, and hybrid control techniques, which greatly reduce the complexity of calculations.

4.   Examples

In this section, we use the MATLAB toolbox to simulate theorem results.

Example 4.1. Study the following two-dimensional complex-valued FOFCVNNS:

where $\ O_{w}(t) = O_{w}^{R}(t)+iO_{w}^{I}(t)\in C, \ O_{w}^{R}(t), O_{w}^{I}(t)\in R, \ \tau_1(t) = \tau_2(t) = |\text{tan(t)}| \, \ I_1(t) = I_2(t) = 0, \ f_{p}(O_{p}(t)) = \text{tanh}(O_{p}^{R}(t))+i\text{tanh}(O_{p}^{I}(t)).$

The response system is

where ${Q_w}(t) = Q_w^R(t) + iQ_w^I(t) \in {C}$. The initial values of $(4.1)$ and $(4.2)$ are

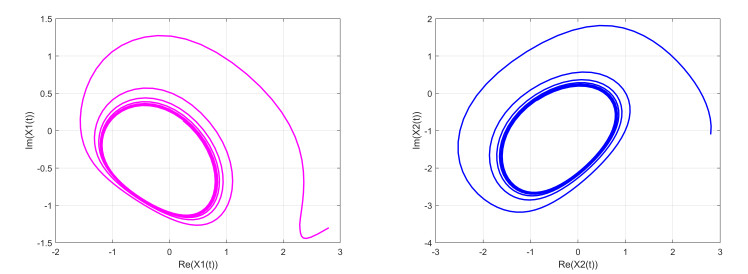
The phase portraits of system $(4.1)$ are shown in Figure 1. The nonlinear hybrid controller is designed as (3.10), and picking $\alpha = 0.95,$ $S = 0.55,$ $\delta_{1} = \delta_{2} = 1.1$, $\eta_{1} = \eta_{2} = 1.3$, $L_{1} = L_{2} = 0.11$, $\lambda = 0.5$. By calculation, we get $\varpi_{1} = 4.47 > 0$, $\varpi_{2} = 0.71$. Taking $\Omega_{1} = 1.5,$ then $\varpi_{1}-\varpi_{2}\Omega_{1} > 0$. This also confirms that the images drawn using the MATLAB toolbox conform to the theoretical results of Theorem $3.2$. Figures 2 and 3 show the state trajectory of $k_{w}(t)$ and $||k_{w}(t)||$ without the controller (3.10). Figures 4 and 5 show state trajectories and error norms with the controller (3.10), respectively.

Example 4.2. Taking $\alpha = 0.95$, $S = 0.97,$ $k_{1} = k_{2} = 5.1,$ $\varsigma_{1} = \varsigma_{2} = 0.2,$ $\varsigma_{1}^{*} = 5,$ $\varsigma_{2}^{*} = 8,$ $\delta_{1} = \delta_{2} = 1.1,$ $\eta_{1} = \eta_{2} = 1.5,$ $L_{1} = L_{2} = 0.1.$ The remaining parameters follow the ones mentioned earlier. According to calculation, $\Upsilon_{1} = 12.49,$ $\Upsilon_{2} = 7.36$. Let $\Omega_{2} = 1.1$, then we have $\Omega_{1}-\Upsilon_{2}\Omega_{2} > 0$. Figure 6 depicts the state trajectory diagram of $k_{w}(t)$ with adaptive controller (3.31). Figure 7 describes the error norm $||k_{w}(t)||$ with controller (3.31). According to Figure 8, it is easy to see that the control parameters $\varsigma_{w}(t)$ are constant.

Example 4.3. Consider the following data:

Let the initial value be

Picking $\alpha = 0.88,$ $S = 0.9,$ $\delta_{1} = \delta_{2} = 1.2$, $\eta_{1} = \eta_{2} = 1.5$, $L_{1} = L_{2} = 0.1$, $\lambda = 0.5$, $\Omega_{1} = 2$. After calculation, $\varpi_{1} = 6.62 > 0$, $\varpi_{2} = 2.28$, and $\varpi_{1}-\varpi_{2}\Omega_{1} > 0$. Similar to Example 4.1, Figures 9 and 10 show the state trajectory of $k_{w}(t)$ and $||k_{w}(t)||$ without the controller (3.10). Figures 11 and 12 show state trajectories and error norms with the controller (3.10), respectively.

Example 4.4. Taking $\alpha = 0.88$, $S = 0.9,$ $k_{1} = k_{2} = 2.2,$ $\varsigma_{1} = \varsigma_{2} = 0.2,$ $\varsigma_{1}^{*} = 4,$ $\varsigma_{2}^{*} = 9,$ $\delta_{1} = \delta_{2} = 1.1,$ $\eta_{1} = \eta_{2} = 1.5,$ $L_{1} = L_{2} = 0.1,$ $\Omega_{2} = 2$. The other parameters are the same as Example 4.3, where $\Upsilon_{1} = 22.29,$ $\Upsilon_{2} = 10.67$, and $\Omega_{1}-\Upsilon_{2}\Omega_{2} > 0$. Thus, the conditions of Theorem $3.3$ are satisfied. Figure 13 depicts the state trajectory diagram of $k_{w}(t)$ with adaptive controller (3.31). Figure 14 describes the error norm $||k_{w}(t)||$ with controller (3.31). Control parameters $\varsigma_{w}(t)$ are described in Figure 15.

5.   Conclusions

In this paper, we studied MLPS issues of delayed FOFCVNNs. First, according to the principle of contraction and projection, a sufficient criterion for the existence and uniqueness of the equilibrium point of FOFCVNNs is obtained. Second, based on the basic theory of fractional calculus, inequality analysis techniques, Lyapunov function method, and fractional Razunikhin theorem, the MLPS criterion of FOFCVNNs is derived. Finally, we run four simulation experiments to verify the theoretical results. At present, we have fully considered the delay and parameter uncertainty of neural networks and used continuous control methods in the synchronization process. However, regarding fractional calculus, there is a remarkable difference between continuous-time systems and discrete-time systems ^[14]. Therefore, in future work, we can consider converting the continuous time system proposed in this paper into discrete time system and further research discrete-time MLPS. Alternatively, we can consider studying finite-time MLPS based on the MLPS presented in this paper.

Authors contributions

Yang Xu: Writing–original draft; Zhouping Yin: Supervision, Writing–review; Yuanzhi Wang: Software; Qi Liu: Writing–review; Anwarud Din: Methodology. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflicts of interest.