Output statistics, equivocation, and state masking

1.   Introduction

The problem of approximating a certain output distribution over a noisy channel appears in many works in Information Theory ^{[1,2,3,4,5,6,7,8,9]}. Here we consider a variant of this problem where the approximation error—measured in normalized relative entropy—is not required to approach zero as the number of channel uses increases. Instead, we study the trade-off between the approximation error and the rate of the codebook.

Consider a discrete memoryless channel (DMC) with finite input and output alphabets $\mathcal{X}$ and $\mathcal{Y}$, respectively, and channel law

Let $\hat{Q}_Y$ be a probability mass function (PMF) on $\mathcal{Y}$ such that

We wish to approximate its $n$-fold product $\hat{Q}_Y^{\times n}$. A length-$n$ rate-$R$ codebook is given by

When a codeword is chosen equiprobably from $\mathcal{C}$ and sent over $n$ uses of the channel, the output distribution is

The approximation error that we consider is

Assume that there exists an input PMF $Q_X$ such that $\hat{Q}_Y = Q_X W$, by which notation we mean

Wyner's Soft-Covering Lemma ^[1] asserts that there exists a sequence of codebooks like (3) such that (5) tends to zero as $n\to\infty$ provided

Later, Cuff ^[5,6] showed that, under (7), the unnormalized relative entropy $D\big(P_{Y^n}\big\|\hat{Q}_Y^{\times n}\big)$ can also be made to approach zero, as can the total variation distance between $P_{Y^n}$ and $\hat{Q}_Y^{\times n}$. Furthermore, the probability that a randomly generated codebook (according to $Q_X$) produces an output distribution that is not close to $\hat{Q}_Y^n$ in total variation distance is doubly-exponentially small in $n$.

Now consider the case where again $\hat{Q}_Y = Q_X W$, but where $R$ approaches $I(Q_X, W)$ from below. Furthermore, assume that $Q_X$ and $\hat{Q}_Y$ are capacity-achieving input and output distributions, respectively, so $I(Q_X, W)$ equals the capacity of the channel. Then there exists a sequence of codes such that (5) approaches zero [2, Theorem 15], [3, Theorem 2]. In fact, any sequence of "good codes"—those whose rates approach capacity and whose average error probabilities approach zero as $n\to\infty$—must be such that (5) tends to zero as $n\to\infty$. This result has been generalized to codes with nonvanishing error probability ^[8,9].

In all results that we recalled above, the minimum of (5) approaches zero as $n\to\infty$. Here we are interested in cases where $R$ is not large enough for (5) to approach zero. Specifically, either $R$ is smaller than and possibly bounded away from $I(Q_X, W)$ for any $Q_X$ such that $\hat{Q}_Y = Q_X W$, or there exists no input distribution that can induce $\hat{Q}_Y$ via $W$. In Section 2, we study the tradeoff between the rate $R$ and the approximation error (5) in such cases.

The Soft-Covering Lemma and its stronger versions are useful in many problems in information-theoretic security. For example, the original version of the lemma can be used to derive the secrecy capacity of the wiretap channel, although Wyner did not observe this connection in his original work ^[10].

Here we demonstrate two applications of the rate-error tradeoff that we derive. The first is an alternative proof of the achievability of the rate-equivocation region of the wiretap channel; see Section 3. The second application is in state masking ^[11,12]. Specifically, we derive capacity subject to state masking when the decoder has channel-state information (CSI); see Section 4.

2.   Output statistics

2.1.   An identity

The following simple identity will be used repeatedly in our proofs.

Lemma 1. Let $P_{X^n Y^n}$ be a joint distribution on $\mathcal{X}^n\times \mathcal{Y}^n$ such that $P_{Y^n|X^n} = W^{\times n}$, and let $\bar{P}_{XY}$ be its average distribution on $\mathcal{X}\times \mathcal{Y}$. Further, let $\hat{Q}_Y$ be a distribution on $\mathcal{Y}$. The following holds:

Proof. We will use the following well-known identity (which is easily verified by expanding its both sides): For $Q_Y = Q_X W$,

Replacing $Q_X$, $W$, and $\hat{Q}_Y$ in the above respectively by $P_{X^n}$, $W^{\times n}$, and $\hat{Q}_Y^{\times n}$, we obtain

where the last step follows by applying (9) again, this time with $Q_X$ replaced by $\bar{P}_X$. □

2.2.   Direct result

Theorem 2. (Direct result). Given some DMC (1) and $\hat{Q}_Y$ satisfying (2), fix a PMF $Q_X$ on $\mathcal{X}$ and let $Q_Y = Q_X W$. For any $R < I(Q_X, W)$, $\epsilon > 0$, and $\zeta > 0$, let $\mathsf{C}$ be a random codebook whose entries are independent and identically distributed (IID) according to $Q_X$. Then, as $n\to\infty$, the probability that $\mathsf{C}$ satisfies both of the following tends to one:

(C1) The average probability of a decoding error (by an optimal decoder) is at most $\epsilon$;

(C2) Let $P_{Y^n}$ be given by (4), then (5) is upper- and lower-bounded as

Proof. Let $P_{X^n}^\mathsf{C}$ be the uniform distribution over the codewords of $\mathsf{C}$, and let $\bar{P}_X^\mathsf{C}$ denote its average PMF on $\mathcal{X}$, i.e.,

By standard arguments (see, e.g., ^[13]) we can deduce that, for sufficiently large $n$, with high probability, the average decoding error probability of $\mathsf{C}$ is less than $\epsilon$, i.e., it satisfies (C1). Furthermore, by the Law of Large Numbers, as $n\to\infty$, $\bar{P}_X^\mathsf{C}(x)$—which is random because $\mathsf{C}$ is random—converges to $Q_X(x)$ with probability one for all $x\in \mathrm{supp} (Q_X)$. Therefore, for any $\alpha > 0$, for sufficiently large $n$, we have, with high probability,

where $\delta_{ \text{TV}}(\cdot, \cdot)$ denotes the total variation distance:

By the union bound, we deduce that, with high probability, $\mathsf{C}$ satisfies both (C1) and (15). We fix $\mathsf{C} = \mathcal{C}$ for any $\mathcal{C}$ satisfying (C1) and (15) and show that it must also satisfy (C2) (for an appropriately chosen $\alpha$), which will then conclude the proof. From now on, we drop the superscript $\mathsf{C}$: $P_{X^n Y^n}$ denotes the joint input-output distribution on $\mathcal{X}^n\times \mathcal{Y}^n$ resulting from sending a uniformly chosen codeword from $\mathcal{C}$, and $\bar{P}_{XY}$ denotes its average PMF on $\mathcal{X}\times \mathcal{Y}$. We can upper- and lower-bound $I(X^n; Y^n)$ as

where the lower bound (first inequality) follows by Fano's Inequality ^[13], and the upper bound (second inequality) because there are only $2^{nR}$ codewords, so $H(X^n)\le nR$. Using (17) together with Lemma 1, we have

and also

Denote

which is finite due to (2). Then

We combine (19) and (22) to obtain that, for sufficiently large $n$,

Similarly, by (20) and (22),

Combining (24) and (25) and choosing $\alpha < \zeta/d$ (strictly) proves (13). □

2.3.   Converse results

We first present a lower bound on (5) for any codebook.

Theorem 3 (Converse: General lower bound). For all $n$, any code $\mathcal{C}$ satisfies the following: Let $P_{Y^n}$ be given by (4). Then

where $Q_Y = Q_X W$.

Proof. We have the following standard upper bound on $I(X^n; Y^n)$ that follows by the chain rule, the channel being memoryless, and concavity of mutual information in the input distribution:

where $\bar{P}_X$ is the average PMF on $\mathcal{X}$ induced by the codebook. Also recall the upper bound (second inequality) in (17). Combining these two bounds with Lemma 1 immediately yields

which continues to hold when its right-hand side (RHS) is minimized over $\bar{P}_X$. □

Maximizing (5) over all codebooks is trivial: one should choose all codewords to be identical and to consist only of the input symbol $x^*$ that maximizes $D\big(W(\cdot|x^*) \big\| \hat{Q}_Y\big)$. The problem becomes meaningful when we require the codebook to have a small decoding error probability, in which case we have the following upper bound.

Theorem 4 (Converse: Upper bound for decodable codes). Any code $\mathcal{C}$ with decoding error probability less than or equal to $\epsilon$ must satisfy: There exists some $Q_X$ such that, for $Q_Y = Q_X W$,

Proof. Choose $Q_X = \bar{P}_X$, the average input PMF induced by the codebook, then (29) follows by Fano's Inequality together with (27), and (30) follows by Fano's Inequality together with Lemma 1. □

2.4.   Asymptotic expressions

The above results yield the following asymptotics on (5). First, combining Theorems 2 and 3, we have

where the minimum on the left-hand side is over all length-$n$ rate-$R$ codebooks. If we only allow codes with vanishing decoding error probabilities—which, with some abuse of notation, we denote as $\mathcal{C}_ \text{cor}$—then, by Theorems 2 and 4,

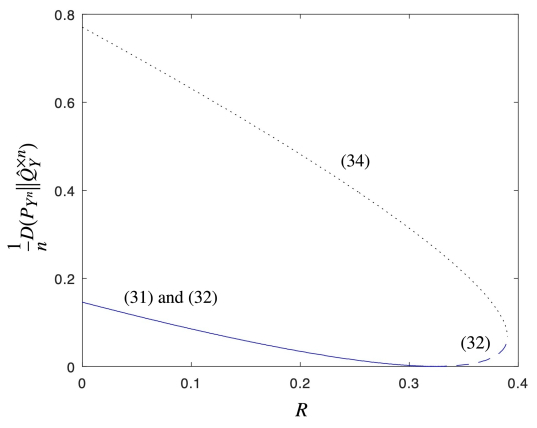
Note that (31) and (32) coincide when

Beyond this threshold, (31) remains zero, whereas (32) increases with $R$.

Finally, again for codes with vanishing decoding error probabilities, Theorems 2 and 4 together imply

Note that (32) is meaningful only when $R$ is below the capacity of the channel; else correct decoding would not be possible, and the minimization on both sides would be over empty sets; similarly for (34).

Due to the identity (9), the minimization on the RHS of (31) (when restricted to $Q_X$ such that $I(Q_X, W)\ge R$) and (32) is linear, and so is the maximization on the RHS of (34). Therefore they are achieved on the boundary, as we demonstrate in the following example.

Example 5. Let $W$ be a binary symmetric channel with crossover probability $p\in(0, 0.5)$, and let $\hat{Q}_Y$ be Bernoulli$(q)$ with $q\in(p, 0.5)$, so $D\big(W(\cdot|0) \big\| \hat{Q}_Y\big) < D\big(W(\cdot|1) \big\| \hat{Q}_Y\big)$. It then follows that the minimum on the RHS of of (32) is achieved by using $0$ as frequently as possible, i.e., it is achieved by $Q_X^*$ being Bernoulli$(a^*)$ such that $I(Q_X^*, W) = R$ and $a^* < 0.5$. Similarly, the maximum on the RHS of (34) is achieved by Bernoulli$(1-a^*)$. We plot (31), (32), and (34) for this example in Figure 1.

2.5.   Relation to soft covering

Our results above recover the Soft-Covering Lemma ^[1] as well as its converse, and the proofs are considerably simpler than the ones that are usually seen in the literature. We prove both direct and converse results with the approximation error measured by the normalized relative entropy (5). As shown in ^[5], (5) tending to zero is a weaker requirement than $\delta_{ \text{TV}}(P_{Y^n}, \hat{Q}_Y^{\times n})$ tending to zero, so the direct result that we recover (which is the same as Wyner's original version ^[1]) is weaker than those in ^[5,6], but the converse we prove is stronger than a converse stated in terms of $\delta_{ \text{TV}}(P_{Y^n}, \hat{Q}_Y^{\times n})$.

The converse to the Soft-Covering Lemma asserts that, in order for (5) to approach zero as $n\to\infty$, $R$ must satisfy

This follows immediately from Theorem 3: For the RHS of (26) to approach zero, both summands inside the minimization must tend to zero. This means $Q_Y = Q_X W$ must tend to $\hat{Q}_Y$, and $R$ must approach or exceed $I(Q_X, W)$.

For the direct Soft-Covering Lemma, we apply Theorem 2, choose $Q_X$ to be such that $Q_Y = \hat{Q}_Y$, and let $R$ approach $I(Q_X, W)$ from below. Then the second inequality in (13) implies that the normalized relative entropy (5) can be made arbitrarily close to zero.^*

^*Note that our proof of the direct Soft-Covering Lemma builds upon the classic proof that, with high probability, the random codebook $\mathsf{C}$ admits a small decoding error probability. The latter is standard, albeit nontrivial.

3.   Equivocation in the wiretap channel

Consider a wiretap channel characterized by input alphabet $\mathcal{X}$, two output alphabets $\mathcal{Y}$ and $\mathcal{Z}$, and channel law $W(y, z|x)$, $(x, y, z)\in \mathcal{X}\times \mathcal{Y} \times \mathcal{Z}$. A length-$n$ rate-$R$ code consists of a stochastic encoder that maps a message $m\in\{1, \ldots, 2^{nR}\}$, possibly together with some local randomness, to $x^n$, and a decoder that maps $y^n$ to $\hat{m}\in\{1, \ldots, 2^{nR}\}$; an error occurs whenever $\hat{m}\neq m$. A rate-equivocation pair $(R, \Delta_ \text{eq})$ is said to be achievable if there exists a sequence of length-$n$ rate-$R$ codes (indexed by $n$) whose error probability tends to zero as $n\to\infty$, and

The following result is well known ^[10,14]; we provide a simple proof via Theorem 2.^†

^†The optimal rate-equivocation region also involves an auxiliary random variable $U$ satisfying the Markov relation $U \mathrel{\multimap}- X \mathrel{\multimap}- (Y, Z)$. The direct part of that result can be obtained immediately from Theorem 6 by viewing $U$, instead of $X$, as the channel input. We therefore focus on proving the achievability result that does not involve $U$.

Theorem 6. For any input distribution $P_X$ such that $I(X; Y) > I(X; Z)$, any rate-equivocation pair $(R, \Delta_ \mathit{\text{eq}})$ satisfying the following is achievable:

Proof. Fix some $R' > 0$. Generate a codebook

IID according to $P_X$. The encoder draws $L$ uniformly at random over $\{1, \ldots, 2^{nR'}\}$. It then maps $(m, \ell)$, with $m$ being the message, to the codeword $x^n(m, \ell)$, which it subsequently sends to the channel.

Following standard procedures ^[13], one can show that the probability that the randomly generated codebook has small average error probability (even for decoding both $m$ and $\ell$) will tend to one as $n\to\infty$ provided

We next study equivocation. Let $\mathsf{C}$ denote the entire (randomly generated) codebook, let $\mathsf{C}(m)$ denote $\{X^n(m, 1), \ldots, X^n(m, 2^{nR'})\}$, the random sub-codebook for message $M = m$, and let $P_{Z^n|\mathsf{C}(m)}$ denote the distribution at the eavesdropper given $M = m$ and with a uniformly chosen $L$. Then

By Theorem 2, for any $\alpha > 0$, for all sufficiently large $n$,

Let $B(m)$ be the indicator function

then $\{B(m)\}$ are IID Bernoulli$(p)$ for some $p\le \alpha$. Denote

then

Now define

then, by the definition of $B$,

Consequently,

Thus, there must be a code $\mathsf{C} = \mathcal{C}$ such that the decoding error probability is small and

where $\beta\triangleq \alpha+2\alpha d'$ can be made arbitrarily close to zero. This means we can achieve equivocation

Combining (40) and (53) together with

and eliminating $R'$, we obtain the desired result. □

4.   State masking with CSI at decoder

State masking was first studied in ^[11] in a setting where the encoder has noncausal CSI while the decoder does not. Here we are mainly interested in the setting where the encoder does not have CSI but the decoder does.

4.1.   Problem setup and results

Consider a state-dependent DMC with input alphabet $\mathcal{X}$, output alphabet $\mathcal{Y}$, state alphabet $\mathcal{S}$, and channel law

The state sequence is IID according to $P_S$. In a length-$n$ rate-$R$ code, the encoder is a possibly stochastic mapping

and the decoder is a mapping from the output $y^n$ and the state sequence $s^n$ to its guess of the message:

As usual, we say a decoding error occurs if $\hat{m}\neq m$, and we consider the average error probability, where the average is over a uniformly drawn message and the randomness of the state sequence. We impose the following state-masking constraint: For some given constant $K > 0$, the joint distribution induced by a uniformly drawn message, the encoder, the random state sequence, and the channel law must satisfy, for all $n$,

The supremum over all rates that are achievable—in the sense that the average error probability can be made arbitrarily small as $n\to\infty$ while (58) is satisfied—is called the capacity in this setting.

Theorem 7. The capacity of the state-dependent DMC with CSI at the decoder under the constraint (58) is given by

over joint distributions of the form $P_X(x)P_S(s)W(y|x, s)$ subject to

To approach this capacity, it is sufficient to use deterministic encoders.

Proof. See Section 4.2. □

The above result may look rather natural by itself, but perhaps less so once compared to previous results on state masking without decoder CSI. When the encoder has noncausal CSI and the decoder has no CSI, the single-letter state-masking capacity formula in ^[11] involves a constraint on $I(S; U, Y)$ rather than just $I(S; Y)$ as in (60), where $U$ is the auxiliary random variable in Gel'fand-Pinsker coding ^[15].

For a more direct comparison with Theorem 7, let us consider the setting in which neither encoder nor decoder has CSI, so the encoder is the same as above, while (57) is replaced by

Define capacity similarly as above. When $K\downarrow 0$, the problem becomes so-called state obfuscation, and the capacity is given by [12, Theorem 3], of which the next theorem can be considered a generalization. Its proof does not use the results from Section 2; we include this result for comparison and its proof for completeness.

Theorem 8. The capacity of the state-dependent DMC without CSI under the constraint (58) is given by

over joint distributions $P_{U}(u)P_{X|U}(x|u) P_S(s) W(y|x, s)$—where $U$ is an auxiliary random variable taking values in some finite set $\mathcal{U}$—subject to the condition

Proof. See Section 4.3. □

Note that not only is (62) different from (59), but so is (63) from (60). The difference becomes even more apparent when we only allow deterministic encoders:

Remark 9. In the no-CSI setting, if the encoder is restricted to being a deterministic mapping, then capacity becomes

over joint distributions $P_X(x) P_S(s) W(y|x, s)$ subject to the condition

The proof is similar to that of Theorem 8 and is omitted.

4.2.   Proof of Theorem 7

We start with the converse part of the theorem, which is rather straightforward. Take any (possibly random) code satisfying (58). Let $\bar{P}_{XYS}$ denote the average distribution on $\mathcal{X}\times \mathcal{Y}\times \mathcal{S}$ induced by a uniformly drawn codeword, the random states, and the channel. We start from (58) to derive the following bound:

where the last step follows because every $S_i$ has the same distribution, and because $I(S; Y)$, for fixed $P_S$, is convex in $P_{Y|S}$. On the other hand, since the decoder knows $S$, we can view the pair $(Y, S)$ as the output of the channel. Using standard arguments invoking Fano's Inequality, we can show

for some $\epsilon > 0$ that approaches zero as $n\to\infty$ and as the error probability is required to vanish. The converse part of the theorem follows from (71) and (72).

We next prove the direct part with the help of Theorem 2. Let $P_X$ be an input distribution such that $P_{XYS}(x, y, s) \triangleq P_X(x) P_S(s) W(y|x, s)$ satisfies

for some $K' < K$. All single-letter mutual informations in the following are computed according to $P_{XYS}$.

Once again, because the decoder knows $S$, the effective output of the channel is the pair $(Y, S)$. We can apply Theorem 2 with the choice

to obtain that, for any

there exists a deterministic length-$n$ rate-$R$ code with small error probability that induces a distribution $P_{Y^n S^n}$ satisfying, for some small $\epsilon'$,

We can now bound $I(S^n; Y^n)$ as

where the last step follows from (78). Since $K' < K$, and since $R$ can be chosen to be arbitrarily close to $I(X; Y, S)$, we conclude that $I(S^n; Y^n)$ is smaller than $nK$ for sufficiently large $n$. The proof is concluded by noting that the construction works for all $K' < K$.

4.3.   Proof of Theorem 8

We start with the converse part. Take a code that has a small error probability and that satisfies (58). Let $P_{X^n Y^n S^n}$ be the joint distribution induced by sending a uniformly drawn codeword through the channel. Define

Let $T$ be uniformly distributed over $\{1, \ldots, n\}$ and independent of everything else. With a slight abuse of notation, define $U \triangleq (U_T, T)$, $Y\triangleq Y_T$, and $S\triangleq S_T$. We first upper-bound $I(M, Y^n; S^n)$ as

for some $\epsilon$ that approaches zero when the error probability approaches zero and $n\to\infty$. The last step follows by (58) and Fano's Inequality. We then lower-bound $I(M, Y^n; S^n)$ as

where (87) follows because $S^n$ is IID; and (91) because $T$ is independent of $S_T$. Combining (85) and (91), we have

On the other hand, using a standard argument invoking Fano's Inequality, we can show

Combining (92) and (95) proves the converse part of the theorem.

We next prove the direct part of the theorem. Fix any finite set $\mathcal{U}$ and joint distribution $P_{UX}$ on $\mathcal{U}\times \mathcal{X}$. Generate a codebook by picking the codewords $\{u^n(1), \ldots, u^n(2^{nR})\}$ IID according to $P_U$. To send message $m$, the sender first passes $u_1(m), \ldots, u_n(m)$ independently through $P_{X|U}$, and then sends the resulting $x$-sequence to the channel. Thus, effectively, we have a channel whose input alphabet is $\mathcal{U}$ instead of $\mathcal{X}$.

It follows from standard arguments that, with high probability, the randomly generated code has small average decoding error probability provided $R < I(U; Y)$. We shall show that, again with high probability, the code will also satisfy the constraint (58). Then it will follow from the union bound that there exist codes that satisfy both. To check (58), first write

For the first term on the RHS of (98), we have

Since the codebook is generated IID according to $P_U$, by the Law of Large Numbers, the RHS divided by $n$ tends to $H(Y|U)$ with probability one. Therefore, for every $\epsilon > 0$, for sufficiently large $n$, with high probability,

with the understanding that $H(Y|U)$ is computed according to the chosen joint distribution. For the second term on the RHS of (98), we have

because the state-dependent channel $P_{Y|US}$ is memoryless. Again by the Law of Large Numbers, for sufficiently large $n$, with high probability,

Summarizing (98), (100), and (102), with high probability

So (58) is indeed satisfied with high probability if $I(S; U, Y) < K$ and $\epsilon$ is sufficiently small. This completes the proof.

Use of AI tools declaration

The author declares that no Artificial Intelligence (AI) tools were utilized in creating this article.

Acknowledgments

The author thanks Stefan Moser, Sergio Verdú, and Shun Watanabe for inspiring discussions and email exchanges. He also thanks Guest Editor Igal Sason and the anonymous reviewers for their helpful comments.

Conflict of interest

The author declares no conflicts of interest.