Analytical methods in fractional biological population modeling: Unveiling solitary wave solutions

Azzh Saad Alshehry; Safyan Mukhtar; Ali M. Mahnashi; Azzh Saad Alshehry; Safyan Mukhtar; Ali M. Mahnashi

doi:10.3934/math.2024773

AIMS Mathematics

2024, Volume 9, Issue 6: 15966-15987. doi: 10.3934/math.2024773

Previous Article Next Article

Research article Special Issues

Analytical methods in fractional biological population modeling: Unveiling solitary wave solutions

1.
Department of Mathematical Sciences, Faculty of Sciences, Princess Nourah Bint Abdulrahman University, P.O.Box 84428, Riyadh 11671, Saudi Arabia
2.
Department of Basic Sciences, Preparatory Year, King Faisal University, Al-Ahsa 31982, Saudi Arabia
3.
Department of Mathematics and Statistics, College of Science, King Faisal University, Al-Ahsa 31982, Saudi Arabia
4.
Department of Mathematics, Faculty of Science, Jazan University, P.O. Box 2097, Jazan 45142, Kingdom of Saudi Arabia

We examine a biological population model of fractional order (FBPM) in this paper using the Riccati-Bernoulli sub-ODE approach. Many scenarios in computational biology make use of this fundamental fractional model. Of particular note is that our study's FBPM uses fractional derivatives to track changes in the density populations. The study is concerned with the construction of new solitary wave solutions for the FBPM, a system of two nonlinear fractional ordinary differential equations. In this investigation, we use the conformable derivative as the fractional derivative. The Backlund transformation is the foundation of the solution process. We create a variety of families of soliton wave solutions and explain different physical behaviours that are inherent in the problems we explore. In particular, we apply the suggested methods to investigate rational, periodic, and hyperbolic solutions. The solutions found in various classes provide insightful information about the underlying physical mechanisms. To sum up, our current methods are superior instruments for analyzing different families of solutions in fractional-order issues.

Keywords:

Citation: Azzh Saad Alshehry, Safyan Mukhtar, Ali M. Mahnashi. Analytical methods in fractional biological population modeling: Unveiling solitary wave solutions[J]. AIMS Mathematics, 2024, 9(6): 15966-15987. doi: 10.3934/math.2024773

Related Papers:

[1]	M. Ali Akbar, Norhashidah Hj. Mohd. Ali, M. Tarikul Islam . Multiple closed form solutions to some fractional order nonlinear evolution equations in physics and plasma physics. AIMS Mathematics, 2019, 4(3): 397-411. doi: 10.3934/math.2019.3.397
[2]	Saima Noor, Azzh Saad Alshehry, Asfandyar Khan, Imran Khan . Innovative approach for developing solitary wave solutions for the fractional modified partial differential equations. AIMS Mathematics, 2023, 8(11): 27775-27819. doi: 10.3934/math.20231422
[3]	Khalid Khan, Amir Ali, Muhammad Irfan, Zareen A. Khan . Solitary wave solutions in time-fractional Korteweg-de Vries equations with power law kernel. AIMS Mathematics, 2023, 8(1): 792-814. doi: 10.3934/math.2023039
[4]	Khalid K. Ali, Mohamed S. Mohamed, M. Maneea . Optimal homotopy analysis method for (2+1) time-fractional nonlinear biological population model using ${{J}}$ -transform. AIMS Mathematics, 2024, 9(11): 32757-32781. doi: 10.3934/math.20241567
[5]	Baojian Hong, Jinghan Wang, Chen Li . Analytical solutions to a class of fractional coupled nonlinear Schrödinger equations via Laplace-HPM technique. AIMS Mathematics, 2023, 8(7): 15670-15688. doi: 10.3934/math.2023800
[6]	Zhao Li, Shan Zhao . Bifurcation, chaotic behavior and solitary wave solutions for the Akbota equation. AIMS Mathematics, 2024, 9(8): 22590-22601. doi: 10.3934/math.20241100
[7]	Obaid Algahtani, Sayed Saifullah, Amir Ali . Semi-analytical and numerical study of fractal fractional nonlinear system under Caputo fractional derivative. AIMS Mathematics, 2022, 7(9): 16760-16774. doi: 10.3934/math.2022920
[8]	Ikram Ullah, Muhammad Bilal, Javed Iqbal, Hasan Bulut, Funda Turk . Single wave solutions of the fractional Landau-Ginzburg-Higgs equation in space-time with accuracy via the beta derivative and mEDAM approach. AIMS Mathematics, 2025, 10(1): 672-693. doi: 10.3934/math.2025030
[9]	Mustafa Inc, Hadi Rezazadeh, Javad Vahidi, Mostafa Eslami, Mehmet Ali Akinlar, Muhammad Nasir Ali, Yu-Ming Chu . New solitary wave solutions for the conformable Klein-Gordon equation with quantic nonlinearity. AIMS Mathematics, 2020, 5(6): 6972-6984. doi: 10.3934/math.2020447
[10]	Faeza Lafta Hasan, Mohamed A. Abdoon, Rania Saadeh, Ahmad Qazza, Dalal Khalid Almutairi . Exploring analytical results for (2+1) dimensional breaking soliton equation and stochastic fractional Broer-Kaup system. AIMS Mathematics, 2024, 9(5): 11622-11643. doi: 10.3934/math.2024570

Abstract

1. Introduction

Fractional calculus (FC) has been a key tool in many scientific fields in recent years, and it has been used to formulate many novel and state of the art models. Fractional derivative operators are important because they can improve the accuracy of models even when important real parameters are not precisely known. Fractional differential operators of many kinds, including Caputo-Fabrizio, Caputo, Riemann-Liouville, and Atangana-Baleanu, are covered in the scientific literature ^[1,2,3]. The latter operators have proven to be effective in a variety of real-world models, especially in the field of biology. As an example, Ghanbari and Cattani ^[4] have successfully used the Atangana-Baleanu derivative to simulate two Lotka-Volterra models with mutualistic predation. An ideal control plan for a novel variable order fractional tumor model under immune suppression was put forth by Sweilam et al. ^[5]. Using fractional differential mathematical models that included memory effects, Danane et al. ^[6] investigated the dynamics of the hepatitis B virus infection. A new fractional model of the human liver was presented by Baleanu et al. ^[7] using the Caputo-Fabrizio fractional derivative, which is based on the exponential kernel. A novel model of fractional SIRS-SI malaria transmission was introduced by Kumar et al. ^[8]. Using the Atangana-Baleanu operator, Singh et al. ^[9] examined the dynamic behaviour of a fractional fish farming model. Readers with an interest in practical models utilising fractional derivatives are referred to references ^{[10,11,12,13]} for additional investigation. It is crucial to remember that understanding interactions in these kinds of models depends on how they are solved. This means that there are two main ways to solve mathematical models, analytically or numerically to robustly apply approximate results. Analytical approaches assert themselves as powerful mathematical tools when numerical methods fail. The application of fractional derivatives to scientific investigations has been conducted both analytically and numerically in numerous studies ^{[14,15,16,17,18,19]}. The purpose of these studies were to explore fractional derivative properties and applications in many different contexts using mathematical expressions and computational simulations ^{[20,21,22,23,24]}.

The investigation of analytical solutions for fractional partial differential equations (FPDEs) poses a significant difficulty, leading to the emergence of many mathematical approaches aimed at tackling this complex issue ^[25,26,27]. Researchers are particularly drawn to analytical solutions due to their ability to offer a comprehensive understanding of the fundamental physical processes, and to reveal the exact behavior of the modeled system, surpassing the capabilities of numerical methods ^[28,29,30]. Hence, the pursuit of analytical solutions within the domain of fractional partial differential equations (FPDEs) is regarded as a pivotal and dynamic field of study ^[31]. Within the realm of scientific literature, a multitude of mathematical techniques have been utilized to effectively address the analytical resolution of fractional partial differential equations (FPDEs). This exemplifies the wide range of methodologies employed by researchers in this field. Several techniques ^{[32,33,34,35,36,37,38,39,40]} have been notably included among the methods being considered. Every method has distinct advantages, expanding the range of techniques that may be used to solve fractional partial differential equations (FPDEs) and enhancing our understanding of these intricate mathematical models ^{[41,42,43,44,45]}.

Furthermore, a specific group of fractional partial differential equations (PDEs) presents difficulties when attempting to solve them using traditional approaches. The proposed approach ^[46,47,48], known for its ability to do complex algebraic calculations, is utilized for the derivation of solitary wave solutions, peaked wave solutions, and precise wave solutions. By employing a traveling wave transformation and the Riccati-Bernoulli equation, the specific partial differential equations (PDEs) undergo a smooth conversion into a set of algebraic equations. This method simultaneously functions as a powerful mathematical tool for solving certain issues in mathematical biology, demonstrating strong and effective performance. Further, the employed methodology produces finite solutions, resulting in reliable and efficient outcomes for the equation under investigation. Significantly, the notable characteristic of this phenomenon resides in the incorporation of an unbounded assortment of solutions for the partial differential equations. The Backlund transformation is also utilized to reveal a limitless sequence of solutions. Moreover, the present study aims to employ this methodology in order to elucidate the fractional biological population model. The results obtained make a substantial contribution to the understanding of practical physical difficulties and complex scenarios, demonstrating the wide range of scientific fields in which the suggested methodology may be effectively used.

Biological population models are essential in many areas of life and greatly advance our knowledge of the dynamics of the environment, public health, and ecology. These models are essential to ecology because they help anticipate and control species interactions, population increase, and the effects of changing environmental conditions on ecosystems. They also act as essential instruments in conservation biology, assisting researchers in determining a species' susceptibility and creating successful conservation plans. Biological population models play a key role in public health research by helping to understand how infectious diseases spread, assess programs, and forecast the start of epidemics. Numerous scientific studies have been conducted by scholars from different fields to investigate a range of epidemic models with the goal of clarifying the complexities of disease transmission dynamics and offering crucial information for the creation of successful public health interventions ^{[49,50,51,52]}. In this study, we aim at solving the fractional biological population model with the help of the presented methodology based on the Backlund transformation and based on the previous work in fractional modeling. Traditional methods are often inadequate at capturing the nuanced dynamics of biological populations due to the intricacies of ecological modeling. The purpose of this study is to build upon the foundation laid by previous research and provide new insight into the complex interplay of factors influencing population dynamics. Moreover, this paper aims to investigate a wide range of soliton wave solutions, which could reveal hitherto undiscovered phenomena and improve our comprehension of ecological systems and capacity to tackle urgent environmental problems. The mathematical model of the general biological model can be represented as ^[53]:

$\begin{equation} \left\{ \begin{aligned} & D_t^\alpha(F) = D_x^\beta(D_x^\beta(F)) + D_y^\gamma(D_y^\gamma(F)) + \chi(F), & \quad & x, y \in \Omega, \quad t \geq 0. \\ & F = F(x, y, t), & \quad & 0 < \alpha, \beta, \gamma \leq 1. \end{aligned} \right. \end{equation}$

(1.1)

Consider the following: In mathematical biology, population density is presented as the variable ( $F$ ), and the population contribution from births and deaths is presented as the variable ( $\chi$ ). For a region ( $\Omega$ ), ( $F$ ) and ( $\chi$ ) are both time ( $t$ ) and position ( $x, y$ ) dependent functions that describe the distribution dynamics of the diffusion of a biological species over ( $\Omega$ ). For a specific time ( $t$ ) and position ( $x, y$ ), the $F (x, y, t)$ function measures the number of people in a unit volume. In each given subregion, the integral of $F (x, y, t)$ offers a thorough representation of the entire population at any given ( $t$ ). Conversely, the function $\chi(F)$ explicates the average rate of individual introduction per unit volume at ( $x, y$ ) as a result of births and deaths. Three relevant cases are presented, illustrating the intricate relationship between population dynamics and the underlying processes of birth and death, and emulating the constitutive equations for $\chi(F)$ for $\alpha\rightarrow1$ .

$\begin{align} (i) & \quad \chi(F) = k, \quad \text{where } k \text{ is an arbitrary constant. This leads to the Malthusian Law.} \\ (ii) & \quad \chi(F) = F(k_1 - k_2 F), \quad \text{where } k_1 \text{ and } k_2 \text{ are positive constants. This leads to the Verhulst Law.} \\ (iii) & \quad \chi(F) = -kF^\delta, \quad \text{where } k \geq 0 \text{ and } 0 < \delta < 1. \text{ This leads to porous media.} \end{align}$

In the current investigation, we consider several forms of Eq (1.1), defining the particular forms as follows:

$\begin{equation} D_t^\alpha(F) = D_x^\beta(D_x^\beta(F)) + D_y^\gamma(D_y^\gamma(F)) + K \left(F^2 - \delta \right). \end{equation}$

(1.2)

$\begin{equation} D_t^\alpha(F) = D_x^\beta(D_x^\beta(F)) + D_y^\gamma(D_y^\gamma(F)) + F \left(1 - \delta F \right). \end{equation}$

(1.3)

The operator that represents the derivatives of order $\alpha$ adheres to the definition provided in reference ^[54].

$\begin{equation} \begin{split} D_\varphi^\beta{\rho(\varphi)} = \lim\limits_{t \to 0} \frac{\rho(t(\varphi)^{1-\beta}-\rho{(\varphi)})}{t}, 0 < \beta\leq1. \end{split} \end{equation}$

(1.4)

This investigation leverages the subsequent properties of this derivative:

$\begin{equation} \left\{ \begin{aligned} &D_\varphi^\beta \varphi^j = j \varphi^{j-\beta}.\\ &D_\varphi^\beta\left(j_1 \eta(\varphi) \pm j_2 t(\varphi)\right) = j_1 D_\varphi^\beta(\eta(\varphi)) \pm j_2 D_\varphi^\beta(t(\varphi)).\\ &D_\varphi^\beta \chi\left[\xi^\tau(\varphi)\right] = \chi_{\xi}^{\varphi}(\xi(\varphi)) D_\varphi^\beta \xi(\varphi). \end{aligned} \right. \end{equation}$

(1.5)

2. Methodology

Suppose the following fractional partial differential equation were to arise:

$\begin{equation} P_1\left(f, D^\alpha_t (f), D^\beta_{\zeta_1} (f), D^{\gamma}_{\zeta_2} (f), fD^{\beta}_{\zeta_1} (f), \ldots \right) = 0, 0 < \alpha, \beta, \gamma\leq 1. \end{equation}$

(2.1)

The above polynomial consists of both the fractional order derivatives and the nonlinear terms. The primary steps of this method will be discussed intensively, and we will consider the more sophisticated wave transformation as a possible means to observe the feasible solutions for Eq (1.1).

$\begin{equation} \begin{aligned} & F(x, y, t) = e^{i\psi} f(\psi). \end{aligned} \end{equation}$

(2.2)

where,

$\begin{equation} \begin{aligned} &\psi(x, y, t) = p \left ({\frac {{t}^{\alpha}}{\alpha}}\right )+ q \left ( {\frac {{x}^{\beta}}{\beta}} \right )+ r\left ( {\frac {{y}^{\gamma}}{\gamma}}\right ), \quad p, q, r \in R. \end{aligned} \end{equation}$

(2.3)

Whereas $\psi$ represents the phase function. These functions are related to the complex variables $x$ and $y$ , as well as the temporal variable $t$ , hence demonstrating their reliance on the precise coordinates and time. Equation (2.1) is subject to a modification resulting in the emergence of a nonlinear ordinary differential equation (NODE), assuming the modified mathematical expression.

$\begin{equation} P_2\left(f, \frac {df}{d\psi} , \frac {d^2f}{d\psi^2}, f\frac {df}{d\psi}, \ldots \right) = 0. \end{equation}$

(2.4)

Consider the formal solution for Eq (2.4)

$\begin{equation} {f}(\psi) = \sum\limits_{i = -n}^{n} b_i{\vartheta(\psi)}^i. \end{equation}$

(2.5)

The $b_i$ constants must be found under the constraint that $b_n \neq 0$ , $b_{-n} \neq 0$ at the same time. Meanwhile, the Backlund transformation that follows produces the function.

$\begin{equation} \vartheta(\psi) = \frac{-\tau Y + X \phi(\psi)}{X + Y \phi(\psi)}. \end{equation}$

(2.6)

Let ( $\tau$ ), ( $X$ ), and ( $Y$ ) be constants, with the condition that $Y\neq0$ . Additionally, let $\phi(\psi)$ be a function that may be defined as:

$\begin{equation} \frac{d{\phi}}{d\psi} = \tau +{\phi(\psi)^2}. \end{equation}$

(2.7)

The solutions of Eq (2.7) are widely recognized ^[55] to be as follows:

$\begin{align} (i) &\quad\text{If}\quad \tau < 0, \quad\text{then}\quad \phi(\psi) = -\sqrt{-\tau}\tanh(\sqrt{-\tau}\psi), \quad \text{or}\quad \phi(\psi) = -\sqrt{-\tau}coth(\sqrt{-\tau}\psi). \end{align}$

(2.8)

$\begin{align} (ii) &\quad\text{If}\quad \tau > 0, \quad\text{then}\quad \phi(\psi) = \sqrt{\tau}\tan(\sqrt{\tau}\psi), \quad\text{or}\quad \phi(\psi) = -\sqrt{\tau}cot(\sqrt{\tau}\psi). \end{align}$

(2.9)

$\begin{align} (iii) &\quad\text{If}\quad \tau = 0, \quad\text{then}\quad \phi(\psi) = \frac{-1}{\psi}. \end{align}$

(2.10)

It should be noted that, out of the theoretical framework for Eq (2.4), it is possible to describe the positive integer $(N)$ by utilizing the homogeneous balancing principles. These principles equate the nonlinear variables of Eq (2.5) in terms of the highest order derivatives. Indeed, for some degree $D[{f}(\psi)] = N$ , the degrees of the associated expressions are

$\begin{equation} D\left[\frac{d^p f}{d\psi^p}\right] = N + p, \quad D\left[f^J \frac{d^p f}{d\psi^p}\right]^s = NJ + s(p + N). \end{equation}$

(2.11)

In other words, combining Eq (2.5) and Eq (2.7) into Eq (2.4) and then redistributing the terms with respect to the power of ${f(\psi)}$ and setting them equal to zero, algebraic equations are created that may then be solved. When Maple is used, this system is algorithmically solved to yield numerical values for the parameters. As a result, this method allows one to solve accurately Eq (2.1) using the solutions, which have the characteristics of solitons.

3. Evaluation of problems

Here, we utilize the process outlined in Section 2 to determine exact single wave solutions for the fractional biological population model (1). We examine two particular scenarios within the biological population model, simplifying each by using the wave transformation described in Eq (2.2) to make the associated equations easier to understand.

3.1. Problem 1

Examine the first case of the biological population model provided by Eq (1.2). Here, we present the model following the transformation, which yields a nonlinear ordinary differential equation (NODE) from the initial fractional partial differential equation (FPDE).

$\begin{equation} \begin{aligned} p F' - \left ( q^2 + r^2 \right ) F'' - K \left ( F^2 - \delta \right) = 0. \end{aligned} \end{equation}$

(3.1)

In the study we incorporate the replacement given in Eq (2.5) into Eq (3.1) as well as Eqs (2.7) and (2.4). Carefully collecting coefficients associated with $\phi^{i}(\psi)$ , an algebraic system of equations is built and then set equal to zero. With the aid of the computational tool Maple, we are able to solve the system of algebraic equations given above and obtain the following results:

Case 1

$\begin{equation} \begin{split} &b_{{0}} = 1/2\, \sqrt {-{\tau}^{-1}}b_{{-1}}, b_{{1}} = 0, b_{{-1}} = b_{{-1}}, b_ {{-2}} = 1/2\, \tau\sqrt {-{\tau}^{-1}}b_{{-1}}, b_{{2}} = 0, p = 10\, \left( {q}^{2} +{r}^{2} \right) {\frac {1}{\sqrt {-{\tau}^{-1}}}}, q = q, \\ &r = r, \delta = -{ \frac {{b_{{-1}}}^{2}}{\tau}}, K = -12\, \tau \left( {q}^{2}+{r}^{2} \right) { \frac {1}{\sqrt {-{\tau}^{-1}}}}{b_{{-1}}}^{-1}. \end{split} \end{equation}$

(3.2)

Case 2

$\begin{equation} \begin{split} &b_{{0}} = 2\, b_{{2}}\tau, b_{{1}} = 4\, \sqrt {-\tau}b_{{2}}, b_{{-1}} = -4\, \sqrt { }b_{{2}}\tau, b_{{-2}} = b_{{2}}{\tau}^{2}, b_{{2}} = b_{{2}}, p = -20\, \sqrt {-\tau} \left( {q}^{2}+{r}^{2} \right) , q = q, \\ &r = r, \delta = 64\, {b_{{2}}}^{2}{\tau}^{ 2}, K = -6\, {\frac {{q}^{2}+{r}^{2}}{b_{{2}}}}. \end{split} \end{equation}$

(3.3)

Assuming Case 1, we get the following families of solutions for,

$\begin{equation} \begin{aligned} \psi = {\frac {q{x}^{\beta}}{\beta}}+{\frac {r{y}^{\gamma}}{\gamma}}+10\, \left( {r}^{2}+{q}^{2} \right) {t}^{\alpha}{\frac {1}{\sqrt {-{\tau}^{-1 }}}}{\alpha}^{-1}.\\ \end{aligned} \end{equation}$

(3.4)

Family 1: When $\tau < 0$ , Eq (1.2) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} F_1(x, y, t) = &e^{i\psi} \left[ \frac{1}{2}\tau\sqrt{-\tau^{-1}}b_{-1} \left( X-Y\sqrt{-\tau}\tanh \left( \sqrt{-\tau}\psi \right) \right)^{2} \right.\left( -{\tau}Y-X\sqrt{-\tau}\tanh \left( \sqrt{-\tau}\psi \right) \right)^{-2} \\ &+ \frac{b_{-1} \left( X-Y\sqrt{-\tau}\tanh \left( \sqrt{-\tau}\psi \right) \right)}{-{\tau}Y-X\sqrt{-\tau}\tanh \left( \sqrt{-\tau}\psi \right)}+ \left. \frac{1}{2}\sqrt{-\tau^{-1}}b_{-1} \right]. \end{split} \end{equation}$

(3.5)

$\begin{equation} \begin{split} F_2(x, y, t) = &e^{i\psi} \left[ \frac{1}{2}\tau\sqrt{-\tau^{-1}}b_{-1} \left( X-Y\sqrt{-\tau}\coth \left( \sqrt{-\tau}\psi \right) \right)^{2} \right.\left( -{\tau}Y-X\sqrt{-\tau}\coth \left( \sqrt{-\tau}\psi \right) \right)^{-2} \\ &+ \frac{b_{-1} \left( X-Y\sqrt{-\tau}\coth \left( \sqrt{-\tau}\psi \right) \right)}{-{\tau}Y-X\sqrt{-\tau}\coth \left( \sqrt{-{\tau}}\psi \right)}+ \left. \frac{1}{2}\sqrt{-{\tau}^{-1}}b_{-1} \right]. \end{split} \end{equation}$

(3.6)

Family 2: When ${\tau} > 0$ , Eq (1.2) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} F_3(x, y, t) = & e^{i\psi} \left[ \frac{1}{2}{\tau}\sqrt{-{\tau}^{-1}}b_{-1} \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^{2} \right. \left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^{-2} \\ &+ \frac{b_{-1} \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)}{-{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right)}+ \left. \frac{1}{2}\sqrt{-{\tau}^{-1}}b_{-1} \right]. \end{split} \end{equation}$

(3.7)

$\begin{equation} \begin{split} F_4(x, y, t) = & e^{i\psi} \left[ \frac{1}{2}{\tau}\sqrt{-{\tau}^{-1}}b_{-1} \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^{2} \right.\left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^{-2} \\ &+ \frac{b_{-1} \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right)}+ \left. \frac{1}{2}\sqrt{-{\tau}^{-1}}b_{-1} \right]. \end{split} \end{equation}$

(3.8)

Family 3: When ${\tau} = 0$ , Eq (1.2) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} &F_5(x, y, t) = e^{i\psi}\left[1/2\, {\tau}\sqrt {-{{\tau}}^{-1}}b_{{-1}} \left( X-{\frac {Y}{\psi}} \right) ^{2 } \left( -{\tau}Y-{\frac {X}{\psi}} \right) ^{-2}+b_{{-1}} \left( X-{\frac {Y}{\psi}} \right) \left( -{\tau}Y-{\frac {X}{\psi}} \right) ^{-1}+1/2\, \sqrt {-{{\tau}}^{-1}}b_{{-1}}\right]. \end{split} \end{equation}$

(3.9)

Assuming Case 2, we get the following families of solutions for,

$\begin{equation} \begin{aligned} \psi = {\frac {q{x}^{\beta}}{\beta}}+{\frac {r{y}^{\gamma}}{\gamma}}-20\, { \frac {\sqrt {-{\tau}} \left( {r}^{2}+{q}^{2} \right) {t}^{\alpha}}{\alpha}}.\\ \end{aligned} \end{equation}$

(3.10)

Family 1: When ${\tau} < 0$ , Eq (1.2) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} F_6(x, y, t) = & e^{i\psi}\left[ \frac{b_2{\tau}^2 \left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right.- 4 \frac{\sqrt{-{\tau}}b_2{\tau} \left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right)} \\ & + 2b_2{\tau} + 4 \frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)}{X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right)}+ \left. \frac{b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.11)

$\begin{equation} \begin{split} F_7(x, y, t) = & e^{i\psi}\left[ \frac{b_2{\tau}^2 \left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right.- 4 \frac{\sqrt{-{\tau}}b_2{\tau} \left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right)} \\ & + 2b_2{\tau} + 4 \frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)}{X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right)}+ \left. \frac{b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.12)

Family 2: When ${\tau} > 0$ , Eq (1.2) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} F_8(x, y, t) = & e^{i\psi}\left[ \frac{b_2{\tau}^2 \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2} \right.- 4\frac{\sqrt{-{\tau}}b_2{\tau} \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)}{-{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right)} + 2b_2{\tau} \\ & + \frac{4\sqrt{-{\tau}}b_2 \left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)}{X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right)}.+ \left. \frac{b_2 \left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.13)

$\begin{equation} \begin{split} F_9(x, y, t) = & e^{i\psi}\left[ \frac{b_2{\tau}^2 \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2} \right.- 4\frac{\sqrt{-{\tau}}b_2{\tau} \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right)}+ 2b_2{\tau} \\ & + \left. 4\frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)}{X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right)} \right.+ \left. \frac{b_2 \left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.14)

Family 3: When ${\tau} = 0$ , Eq (1.2) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} F_{10}(x, y, t) = & e^{i\psi} \left[ b_2{\tau}^2 \left( X-{\frac {Y}{\psi}} \right)^2 \left( -{\tau}Y-{\frac {X}{\psi}} \right)^{-2} \right.- 4\sqrt{-{\tau}}b_2{\tau} \left( X-{\frac {Y}{\psi}} \right) \left( -{\tau}Y-{\frac {X}{\psi}} \right)^{-1} + 2b_2{\tau} \\ & + \left. 4\sqrt{-{\tau}}b_2 \left( -{\tau}Y-{\frac {X}{\psi}} \right) \left( X-{\frac {Y}{\psi}} \right)^{-1} \right.+ \left. b_2 \left( -{\tau}Y-{\frac {X}{\psi}} \right)^2 \left( X-{\frac {Y}{\psi}} \right)^{-2} \right]. \end{split} \end{equation}$

(3.15)

3.2. Problem 2

Examine the second case of the biological population model provided by Eq (1.3). Here, we present the model following the transformation, which yields a nonlinear ordinary differential equation (NODE) from the initial fractional partial differential equation (FPDE).

$\begin{equation} \begin{aligned} p F' - \left ( q^2 + r^2 \right ) F'' - F \left ( 1 - \delta F \right) = 0. \end{aligned} \end{equation}$

(3.16)

In the study we incorporate the replacement given in Eq (2.5) into Eq (3.16) as well as Eqs (2.7) and (2.4). Carefully collecting coefficients associated with $\phi^{i}(\psi)$ , an algebraic system of equations is built and then set equal to zero. With the aid of the computational tool Maple, we are able to solve the system of algebraic equations given above and obtain the following results:

Case 1

$\begin{equation} \begin{split} &b_{{0}} = -{\frac {b_{{-2}}}{{\tau}}}, b_{{1}} = 0, b_{{-1}} = 2\, \sqrt {-{{\tau}}^{-1} }b_{{-2}}, b_{{-2}} = b_{{-2}}, b_{{2}} = 0, p = -{\frac {5}{12}}\, \sqrt {-{{\tau}}^ {-1}}, \\ &q = 1/12\, \sqrt {-{\frac {6+144\, {r}^{2}{\tau}}{{\tau}}}}, r = r, \delta = -1/4\, { \frac {{\tau}}{b_{{-2}}}}, K = K. \end{split} \end{equation}$

(3.17)

Case 2

$\begin{equation} \begin{split} &b_{{0}} = 10\, b_{{2}}{\tau}, b_{{1}} = 4\, \sqrt {-{\tau}}b_{{2}}, b_{{-1}} = -4\, \sqrt {-{\tau}}b_{{2}}{\tau}, b_{{-2}} = b_{{2}}{{\tau}}^{2}, b_{{2}} = b_{{2}}, p = -{\frac {5}{24} }\, {\frac {\sqrt {-{\tau}}}{{\tau}}}, \\ &q = 1/24\, \sqrt {-{\frac {-6+576\, {r}^{2}{\tau}}{{\tau} }}}, r = r, \delta = 1/16\, {\frac {1}{b_{{2}}{\tau}}}, K = K. \end{split} \end{equation}$

(3.18)

Assuming Case 1, we get the following families of solutions for,

$\begin{equation} \begin{aligned} &\psi = 1/12\, \sqrt {-{\frac {6+144\, {r}^{2}{\tau}}{{\tau}}}}{x}^{\beta}{\beta}^{-1}+{ \frac {r{y}^{\gamma}}{\gamma}}-{\frac {5}{12}}\, \sqrt {-{{\tau}}^{-1}}{t}^{ \alpha}{\alpha}^{-1}. \end{aligned} \end{equation}$

(3.19)

Family 1: When ${\tau} < 0$ , Eq (1.3) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} G_1(x, y, t) = & e^{i\psi} \left[ \frac{b_{-2} \left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\Psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right.+ 2\sqrt{-{\tau}^{-1}}b_{-2} \left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)\\ &\left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^{-1} - \left. \frac{b_{-2}}{{\tau}} \right]. \end{split} \end{equation}$

(3.20)

$\begin{equation} \begin{split} G_2(x, y, t) = & e^{i\psi} \left[ \frac{b_{-2} \left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\Psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right.+ 2\sqrt{-{\tau}^{-1}}b_{-2} \left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)\\ &\left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^{-1} - \left. \frac{b_{-2}}{{\tau}} \right]. \end{split} \end{equation}$

(3.21)

Family 2: When ${\tau} > 0$ , Eq (1.3) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} G_3(x, y, t) = & e^{i\psi} \left[ \frac{b_{-2} \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2} \right. + 2\sqrt{-{\tau}^{-1}}b_{-2} \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)\\ &\left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^{-1} - \left. \frac{b_{-2}}{{\tau}} \right]. \end{split} \end{equation}$

(3.22)

$\begin{equation} \begin{split} G_4(x, y, t) = & e^{i\psi} \left[ \frac{b_{-2} \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2} \right. + 2\sqrt{-{\tau}^{-1}}b_{-2} \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right) \\ &\left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^{-1}- \left. \frac{b_{-2}}{{\tau}} \right]. \end{split} \end{equation}$

(3.23)

Family 3: When ${\tau} = 0$ , Eq (1.3) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} &G_5(x, y, t) = e^{i\psi} \left[b_{{-2}} \left( X-{\frac {Y}{\psi}} \right) ^{2} \left( -{\tau}Y-{\frac {X} {\psi}} \right) ^{-2}+2\, \sqrt {-{{\tau}}^{-1}}b_{{-2}} \left( X-{\frac {Y} {\psi}} \right) \left( -{\tau}Y-{\frac {X}{\psi}} \right) ^{-1}-{\frac {b_ {{-2}}}{{\tau}}}\right]. \end{split} \end{equation}$

(3.24)

Assuming Case 2, we get the following families of solutions for,

$\begin{equation} \begin{aligned} &\psi = -{\frac {1}{96}}\, {\frac { \left( -1+96\, {r}^{2}{\tau} \right) {x}^{\beta}} {{\tau}\beta}}+{\frac {r{y}^{\gamma}}{\gamma}}-{\frac {5}{24}}\, {\frac { \sqrt {-{\tau}}{t}^{\alpha}}{{\tau}\alpha}}. \end{aligned} \end{equation}$

(3.25)

Family 4: When ${\tau} < 0$ , Eq (1.3) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} G_6(x, y, t) = & e^{i\psi} \left[ \frac{b_2{\tau}^2 \left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right. - 4\frac{\sqrt{-{\tau}}b_2{\tau} \left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right)} \\ & + 10b_2{\tau} + 4\frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)}{X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right)} + \left. \frac{b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( X-Y\sqrt{-{\tau}}\tanh \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.26)

$\begin{equation} \begin{split} G_7(x, y, t) = & e^{i\psi} \left[ \frac{b_2{\tau}^2 \left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right. - 4\frac{\sqrt{-{\tau}}b_2{\tau} \left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right)} \\ & + 10b_2{\tau} + 4\frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)}{X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right)} + \left. \frac{b_2 \left( -{\tau}Y-X\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2}{\left( X-Y\sqrt{-{\tau}}\coth \left( \sqrt{-{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.27)

Family 5: When ${\tau} > 0$ , Eq (1.3) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} G_8(x, y, t) = & e^{i\psi} \left[ \frac{b_2{\tau}^2 \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2} \right.- 4\frac{\sqrt{-{\tau}}b_2{\tau} \left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)}{-{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right)} \\ & + 10b_2{\tau} + 4\frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)}{X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right)}+ \left. \frac{b_2 \left( -{\tau}Y+X\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( X+Y\sqrt{{\tau}}\tan \left( \sqrt{{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.28)

$\begin{equation} \begin{split} G_9(x, y, t) = & e^{i\psi} \left[ \frac{b_2{\tau}^2 \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2} \right. - 4\frac{\sqrt{-{\tau}}b_2{\tau} \left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)}{-{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right)} \\ & + 10b_2{\tau} + 4\frac{\sqrt{-{\tau}}b_2 \left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)}{X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right)} + \left. \frac{b_2 \left( -{\tau}Y-X\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2}{\left( X-Y\sqrt{{\tau}}\cot \left( \sqrt{{\tau}}\psi \right) \right)^2} \right]. \end{split} \end{equation}$

(3.29)

Family 6: When ${\tau} = 0$ , Eq (1.3) brings about the resulting single-wave solutions:

$\begin{equation} \begin{split} G_{10}(x, y, t) = & e^{i\psi} \Bigg[ b_2{{\tau}}^2 \left( X-{\frac{Y}{\psi}} \right)^2 \left( -{\tau}Y-{\frac{X}{\psi}} \right)^{-2} - 4\sqrt{-{\tau}}b_2{\tau} \left( X-{\frac{Y}{\psi}} \right) \left( -{\tau}Y-{\frac{X}{\psi}} \right)^{-1} \\ & + 10b_2{\tau} + 4\sqrt{-{\tau}}b_2 \left( -{\tau}Y-{\frac{X}{\psi}} \right) \left( X-{\frac{Y}{\psi}} \right)^{-1} + b_2 \left( -{\tau}Y-{\frac{X}{\psi}} \right)^2 \left( X-{\frac{Y}{\psi}} \right)^{-2} \Bigg]. \end{split} \end{equation}$

(3.30)

4. Results and discussion

When it comes to biological population models, the Riccati-Bernoulli sub-ODE approach is a potent analytical technique that is especially useful in the field of advanced biological sciences. The efficiency of the approach resides in its capacity to provide a multitude of periodic and single traveling wave solutions, each with unique properties. Interestingly, this is accomplished without the need of discretization and linearization steps, which are frequently used in problem-solving techniques. Consequently, the results provided by this method are accurate solutions for various biological population models in modern biological science. Specifically, this method contributes to knowing the dynamics of the constituents of biological populations through revealing the complicated rules that regulate biological events. This method is context-aware for the subtleties of biological systems and is further complimented by its ability to produce multiple solutions with different parameters.

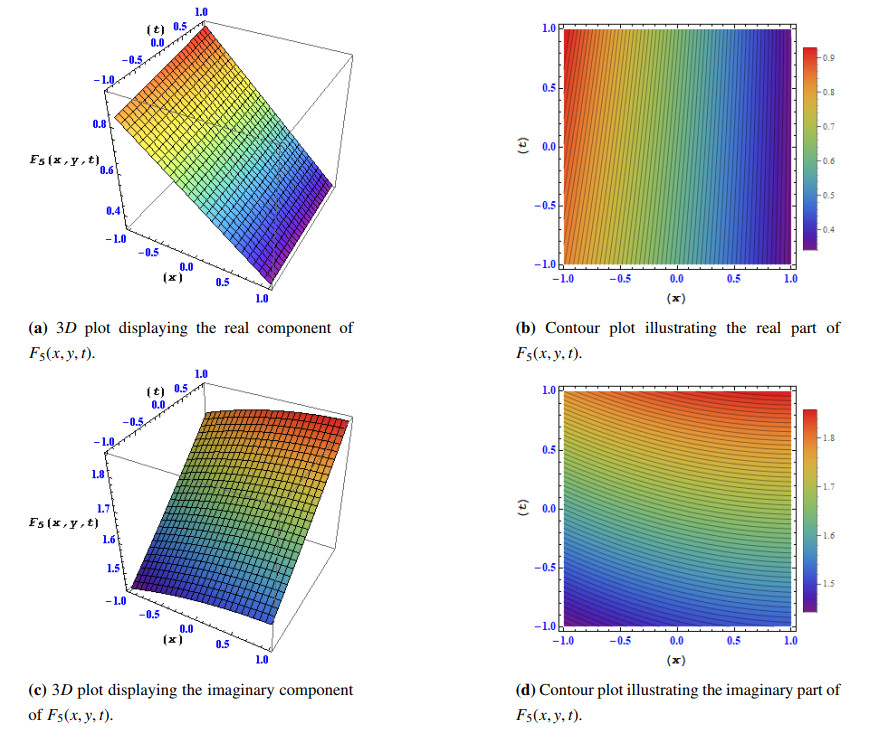
Additionally, the preferred families of analytical solutions produced by the method provide appropriate references for solving biological modeling analytically. From an analytical perspective, it enables accurate prediction of analytical results and also supports stability investigations, which helps make computer models of biological populations accurate. Soliton generation due to the solitons, ability to travel with minimum energy loss is another feature of the method. When describing wave motion in biological population models, soliton dynamics follows the same rules. Solitons represent population dynamics and phenomena that can spread a lot and maintain their shape even after interacting with other population waves in a unique biological population model. This fact that phenomena resulting in solitons emerge as a consequence of this unique emphasis on linear and nonlinear effects grants us a fresh perspective on how populations act in higher biological science. An effective and computationally practical way for addressing complex algebraic computations is the Riccati-Bernoulli sub-ODE method. It is commonly known that creating a general analytical technique that can be used for any type of nonlinear partial differential equation (NLPDE) is extremely difficult, and the Riccati-Bernoulli sub-ODE method is no different. This approach, like other analytical techniques, aims to get exact solutions for Eq 1.1. It is crucial to remember that efforts to improve the effectiveness of the Backlund and sub-ODE transformations are still underway. Subsequent efforts will concentrate on developing these approaches to unleash even more potent potential, which will enable the identification of precise solutions for a wider range of NLPDEs. For the problems considered, the proposed approach produces three different families of solitary wave solutions. The solitary wave solutions that fall into these categories are rational when ( $\tau = 0$ ), hyperbolic when ( $\tau > 0$ ), and periodic when ( $\tau < 0$ ). Figures 1–6 show the wave behaviors of these solutions graphically, giving a thorough knowledge of their dynamic properties.

Figure 1. Within these visualizations, differing degrees of granularity are displayed for the complex factors of

$F_{5}(x, y, t)$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. Within these visualizations, differing degrees of granularity are displayed for the complex factors of

$F_{8}(x, y, t)$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. Within these visualizations, differing degrees of granularity are displayed for the complex factors of

$F_{10}(x, y, t)$ . in this plots.

DownLoad: Full-Size Img PowerPoint

Figure 4. Within these visualizations, differing degrees of granularity are displayed for the complex factors of

$G_{1}(x, y, t)$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. Within these visualizations, differing degrees of granularity are displayed for the complex factors of

$G_{5}(x, y, t)$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. Within these visualizations, differing degrees of granularity are displayed for the complex factors of

$G_{9}(x, y, t)$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In this current work, Riccati-Bernoulli sub-ODE techniques are systematically applied to fractional-order biological population models. The graphical illustrations of the acquired solutions validate the effectiveness of the suggested strategies. The analysis indicates a change in the geometric features of the issues under various circumstances. Notably, the new approaches provide a more insightful and efficient comprehension of the dynamics inherent in the researched physical phenomena when compared to alternative analytical methods. The investigation includes three important traveling wave solutions: solutions for rational, hyperbolic, and trigonometric functions. These answers add to a thorough comprehension of the various behaviors displayed by various physical events. In addition, the current method's adaptability is investigated in order to obtain new families of solutions for the given problem. The improved method makes it easier to design solutions that are closely matched with the physical challenges that arise in applied research by adding a free parameter to the solution.

Authors contributions

All authors equally contributed this manuscript and approved the final version.

Use of AI tools declaration

The authors declare they have not used AI tools in the creation of this article.

Acknowledgments

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R183), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (GrantA134).

Data availability

The data related to this study is available from the corresponding author upon reasonable request.

Funding

Conflict of interest

The authors declare no conflicts of interest.

References

[1]	A. Atangana, D. Baleanu, New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model, 2016. https://doi.org/10.48550/arXiv.1602.03408
[2]	M. Caputo, M. Fabrizio, A new definition of fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 1 (2015), 73–85. http://doi.org/10.12785/pfda/010201 doi: 10.12785/pfda/010201
[3]	A. Akgul, A novel method for a fractional derivative with non-local and non-singular kernel, Chaos Soliton. Fract., 114 (2018), 478–482. https://doi.org/10.1016/j.chaos.2018.07.032 doi: 10.1016/j.chaos.2018.07.032
[4]	B. Ghanbari, C. Cattani, On fractional predator and prey models with mutualistic predation including non-local and nonsingular kernels, Chaos Soliton. Fract., 136 (2020), 109823. https://doi.org/10.1016/j.chaos.2020.109823 doi: 10.1016/j.chaos.2020.109823
[5]	N. H. Sweilam, AL-MekhlafiSM, A. S. Alshomrani, D. Baleanu, Comparative study for optimal control nonlinear variable-order fractional tumor model, Chaos Soliton. Fract., 136 (2020), 109810.
[6]	J. Danane, K. Allali, Z. Hammouch, Mathematical analysis of a fractional differential model of HBV infection with antibody immune response, Chaos Soliton. Fract., 136 (2020), 109787.
[7]	D. Baleanu, A. Jajarmi, H. Mohammadi, S. Rezapour, A new study on the math ematical modelling of human liver with Caputo-Fabrizio fractional derivative, Chaos Soliton. Fract., 134 (2020), 109705.
[8]	D. Kumar, J. Singh, M. Al Qurashi, D. Baleanu, A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying, Adv. Differ. Equ., 2019 (2019), 278.
[9]	J. Singh, D. Kumar, D. Baleanu, A new analysis of fractional fish farm model associated with Mittag-Leffler-type kernel, Int. J. Biomath., 13 (2020), 2050010.
[10]	X. J. Yang, M. Abdel-Aty, C. Cattani, A new general fractional-order derivative with Rabotnov fractional-exponential kernel applied to model the anomalous heat transfer, Therm. Sci., 23 (2019), 1677–1681.
[11]	S. Kumar, R. Kumar, C. Cattani, B. Samet, Chaotic behaviour of fractional predator-prey dynamical system, Chaos Soliton. Fract., 135 (2020), 109811.
[12]	M. H. Heydari, Z. Avazzadeh, C. Cattani, Taylors series expansion method for non-linear variable-order fractional 2d optimal control problems, Alex. Eng. J., 59 (2020), 4737–4743.
[13]	D. Baleanu, H. Mohammadi, S. Rezapour, Analysis of the model of HIV-1 infection of CD4+CD 4 + t-cell with a new approach of fractional derivative, Adv. Differ. Equ., 2020 (2020), 71.
[14]	V. P. Dubey, J. Singh, A. M. Alshehri, S. Dubey, D. Kumar, Forecasting the behavior of fractional order Bloch equations appearing in NMR flow via a hybrid computational technique, Chaos, Soliton. Fract., 164 (2022), 112691.
[15]	V. P. Dubey, J. Singh, A. M. Alshehri, S. Dubey, D. Kumar, Numerical investigation of fractional model of phytoplankton-toxic phytoplankton-zooplankton system with convergence analysis, Int. J. Biomath., 15 (2022), 2250006.
[16]	V. P. Dubey, J. Singh, S. Dubey, D. Kumar, Some integral transform results for Hilfer-Prabhakar fractional derivative and analysis of free-electron laser equation, Iran. J. Sci., 47 (2023), 1333–1342.
[17]	V. P. Dubey, J. Singh, A. M. Alshehri, S. Dubey, D. Kumar, Analysis and Fractal Dynamics of Local Fractional Partial Differential Equations Occurring in Physical Sciences, J. Comput. Nonlinear Dyn., 18 (2023), 031001.
[18]	D. Kumar, V. P. Dubey, S. Dubey, J. Singh, A. M. Alshehri, Computational analysis of local fractional partial differential equations in realm of fractal calculus, Chaos, Soliton. Fract., 167 (2023), 113009.
[19]	S. Noor, W. Albalawi, R. Shah, M. M. Al-Sawalha, S. M. Ismaeel, S. A. El-Tantawy, On the approximations to fractional nonlinear damped Burgers-type equations that arise in fluids and plasmas using Aboodh residual power series and Aboodh transform iteration methods, Front. Phys., 12 (2024), 1374481.
[20]	H. Yasmin, N. H. Aljahdaly, A. M. Saeed, R. Shah, Probing families of optical soliton solutions in fractional perturbed Radhakrishnan-Kundu-Lakshmanan model with improved versions of extended direct algebraic method, Fractal Fract., 7 (2023), 512.
[21]	P. Sunthrayuth, A. M. Zidan, S. W. Yao, M. Inc, The comparative study for solving fractional-order Fornberg-Whitham equation via $\rho$ -Laplace transform, Symmetry, 13 (2021), 784.
[22]	A. Saad Alshehry, M. Imran, A. Khan, W. Weera, Fractional view analysis of Kuramoto-Sivashinsky equations with non-singular kernel operators, Symmetry, 14 (2022), 1463.
[23]	H. M. Srivastava, H. Khan, M. Arif, Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions, Math. Methods Appl. Sci., 43 (2020), 199–212.
[24]	H. Yasmin, N. H. Aljahdaly, A. M. Saeed, Investigating symmetric soliton solutions for the fractional coupled konno-onno system using improved versions of a novel analytical technique, Mathematics, 11 (2023), 2686.
[25]	H. Huang, J. Shu, Y. Liang, MUMA: A multi-omics meta-learning algorithm for data interpretation and classification, IEEE J. Biomed. Health Inf., 28 (2024), 2428–2436. http://doi.org/10.1109/JBHI.2024.3363081 doi: 10.1109/JBHI.2024.3363081
[26]	C. Zhu, M. Al-Dossari, S. Rezapour, S. Shateyi, On the exact soliton solutions and different wave structures to the modified Schrodinger's equation, Results Phys., 54 (2023), 107037. http://doi.org/10.1016/j.rinp.2023.107037 doi: 10.1016/j.rinp.2023.107037
[27]	C. Zhu, M. Al-Dossari, N. S. A. El-Gawaad, S. A. M. Alsallami, S. Shateyi, Uncovering diverse soliton solutions in the modified Schrodingers equation via innovative approaches, Results Phys., 54 (2023), 107100. http://doi.org/10.1016/j.rinp.2023.107100 doi: 10.1016/j.rinp.2023.107100
[28]	C. Zhu, S. A. O. Abdallah, S. Rezapour, S. Shateyi, On new diverse variety analytical optical soliton solutions to the perturbed nonlinear Schrodinger equation, Results Phys., 54 (2023), 107046. http://doi.org/10.1016/j.rinp.2023.107046 doi: 10.1016/j.rinp.2023.107046
[29]	C. Zhu, S. A. Idris, M. E. M. Abdalla, S. Rezapour, S. Shateyi, B. Gunay, Analytical study of nonlinear models using a modified Schrodinger's equation and logarithmic transformation, Results Phys., 55 (2023), 107183. http://doi.org/10.1016/j.rinp.2023.107183 doi: 10.1016/j.rinp.2023.107183
[30]	Y. Kai, S. Chen, K. Zhang, Z. Yin, Exact solutions and dynamic properties of a nonlinear fourth-order time-fractional partial differential equation, Wave. Random Complex, 2022, 1–12. http://doi.org/10.1080/17455030.2022.2044541 doi: 10.1080/17455030.2022.2044541
[31]	Y. Kai, Z. Yin, Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation, Phys. Lett. A, 452 (2022), 128430. http://doi.org/10.1016/j.physleta.2022.128430 doi: 10.1016/j.physleta.2022.128430
[32]	S. S. Ray, R. K. Bera, Analytical solution of a fractional diffusion equation by Adomian decomposition method, Appl. Math. Comput., 174 (2006), 329–336.
[33]	B. K. Singh, P. Kumar, Fractional variational iteration method for solving fractionalpartial differential equations with proportional delay, Int. J. Differ. Equ., 2017 (2017), 5206380. http://doi.org/10.1155/2017/5206380 doi: 10.1155/2017/5206380
[34]	J. Chen, F. Liu, V. Anh, Analytical solution for the time-fractional telegraph equation by the method of separating variables, J. Math. Anal. Appl., 338 (2008), 1364–1377.
[35]	Y. Nikolova, L. Boyadjiev, Integral transforms method to solve a time-space fractional diffusion equation, Fract. Calculus Appl. Anal., 13 (2010), 57–68.
[36]	S. Mukhtar, M. Sohaib, I. Ahmad, A numerical approach to solve volume-based batch crystallization model with fines dissolution unit, Processes, 7 (2019), 453.
[37]	A. Elsaid, S. Shamseldeen, S. Madkour, Analytical approximate solution of fractional wave equation by the optimal homotopy analysis method, Eur. J. Pure Appl. Math., 10 (2017), 586–601.
[38]	R. K. Saxena, S. L. Kalla, On the solutions of certain fractional kinetic equations, Appl. Math. Comput., 199 (2008), 504–511.
[39]	A. Cetinkaya, O. Kymaz, The solution of the time-fractional diffusion equation by the generalized differential transform method, Math. Comput. Modell., 57 (2013), 2349–2354.
[40]	H. Yasmin, A. S. Alshehry, A. H. Ganie, A. Shafee, Noise effect on soliton phenomena in fractional stochastic Kraenkel-Manna-Merle system arising in ferromagnetic materials, Sci. Rep., 14 (2024), 1810.
[41]	M. M. Al-Sawalha, A. Khan, O. Y. Ababneh, T. Botmart, Fractional view analysis of Kersten-Krasil'shchik coupled KdV-mKdV systems with non-singular kernel derivatives, AIMS Mathematics, 7 (2022), 18334–18359. https://doi.org/10.3934/math.20221010 doi: 10.3934/math.20221010
[42]	A. A. Alderremy, N. Iqbal, S. Aly, K. Nonlaopon, Fractional series solution construction for nonlinear fractional reaction-diffusion Brusselator model utilizing Laplace residual power series, Symmetry, 14 (2022), 1944.
[43]	S. Alshammari, M. M. Al-Sawalha, R. Shah, Approximate analytical methods for a fractional-order nonlinear system of Jaulent-Miodek equation with energy-dependent Schrodinger potential, Fractal Fract., 7 (2023), 140.
[44]	E. M. Elsayed, R. Shah, K. Nonlaopon, The analysis of the fractional-order Navier-Stokes equations by a novel approach, J. Funct. Space., 2022 (2022), 8979447. https://doi.org/10.1155/2022/8979447 doi: 10.1155/2022/8979447
[45]	M. Alqhtani, K. M. Saad, W. Weera, W. M. Hamanah, Analysis of the fractional-order local Poisson equation in fractal porous media, Symmetry, 14 (2022), 1323.
[46]	M. A. E. Abdelrahman, M. A. Sohaly, Solitary waves for the modified Korteweg-de Vries equation in deterministic case and random case, J. Phys. Math., 8 (2017), 214. http://doi.org/10.4172/2090-0902.1000214 doi: 10.4172/2090-0902.1000214
[47]	M. A. E. Abdelrahman, M. A. Sohaly, Solitary waves for the nonlinear Schrodinger problem with the probability distribution function in the stochastic input case, Eur. Phys. J. Plus., 132 (2017), 339.
[48]	X. F. Yang, Z. C. Deng, Y. Wei, A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application, Adv. Differ. Equ., 1 (2015), 117–133.
[49]	S. Djilali, Threshold asymptotic dynamics for a spatial age-dependent cell-to-cell transmission model with nonlocal disperse, DCDS-B, 28 (2023), 4108–4143.
[50]	F. Z. Hathout, T. M. Touaoula, S. Djilali, Efficiency of Protection in the Presence of Immigration Process for an Age-Structured Epidemiological Model, Acta Appl. Math., 185 (2023), 3.
[51]	S. Bentout, S. Djilali, T. Kuniya, J. Wang, Mathematical analysis of a vaccination epidemic model with nonlocal diffusion, Math. Methods Appl. Sci., 46 (2023), 10970–10994. https://doi.org/10.1002/mma.9162 doi: 10.1002/mma.9162
[52]	S. Djilali, Y. Chen, S. Bentout Asymptotic analysis of SIR epidemic model with nonlocal diffusion and generalized nonlinear incidence functional, Math. Methods Appl. Sci., 46 (2023), 6279–6301.
[53]	A. H. Ganie, H. Yasmin, A. A. Alderremy, S. Aly, An efficient semi-analytical techniques for the fractional-order system of Drinfeld-Sokolov-Wilson equation, Phys. Scripta, 99 (2024), 015253.
[54]	M. Z. Sarikaya, H. Budak, H. Usta, On generalized the conformable fractional calculus, TWMS J. Appl. Eng.Math., 9 (2019), 792799.
[55]	D. Lu, Q. Shi, New Jacobi elliptic functions solutions for the combined KdV-mKdV equation, Int. J. Nonlinear Sci., 10 (2010), 320–325.

This article has been cited by:

1.	Musawa Yahya Almusawa, Hassan Almusawa, Dark and bright soliton phenomena of the generalized time-space fractional equation with gas bubbles, 2024, 9, 2473-6988, 30043, 10.3934/math.20241451
2.	Adel Lachouri, Naas Adjimi, Mohammad Esmael Samei, Manuel De la Sen, Non-separated inclusion problem via generalized Hilfer and Caputo operators, 2025, 10, 2473-6988, 6448, 10.3934/math.2025294

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1054) PDF downloads(55) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Analytical methods in fractional biological population modeling: Unveiling solitary wave solutions

Related Papers:

Abstract

1. Introduction

2. Methodology

3. Evaluation of problems

3.1. Problem 1

3.2. Problem 2

4. Results and discussion

5. Conclusions

Authors contributions

Use of AI tools declaration

Acknowledgments

Data availability

Funding

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Methodology

3. Evaluation of problems

3.1. Problem 1

3.2. Problem 2

4. Results and discussion

5. Conclusions

Authors contributions

Use of AI tools declaration

Acknowledgments

Data availability

Funding

Conflict of interest

References

AIMS Mathematics

Analytical methods in fractional biological population modeling: Unveiling solitary wave solutions

Related Papers:

Abstract

1. Introduction

2. Methodology

3. Evaluation of problems

3.1. Problem 1

3.2. Problem 2

4. Results and discussion

5. Conclusions

Authors contributions

Use of AI tools declaration

Acknowledgments

Data availability

Funding

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Methodology

3. Evaluation of problems

3.1. Problem 1

3.2. Problem 2

4. Results and discussion

5. Conclusions

Authors contributions

Use of AI tools declaration

Acknowledgments

Data availability

Funding

Conflict of interest

References