1.
Introduction
Cancer is one of the most frequently encountered diseases that can lead to the end of human life in spite of the advances in science and medicine. It is a multi-staged disease which occurs as a result of changes in DNA formation (mutation) of abnormal cells. Uncontrolled proliferation of the cells causes tumors and a great number cells mutate in the human body on a daily basis. While some of these mutated cells die, others continue to live and form cancerous cells. Cancer can occur when the immune system or other defensive mechanisms fail to protect the human body from these cells [1]. Cancer cells are different from normal cells due to their size, shape, number, differentiation, function, and ability to travel to distant tissues and organ systems [1]. The immune system recognizes cancer cells and tumors from their antigens [2].
Dendritic cells known as professional antigen-presenting cells, send tumor antigens to lymph nodes to activate T lymphocytes after recognizing cancer cells. CD4+T cells play a central role in the initiation and progression of immune responses [3] and also help CD8+T cells to activate and proliferate [4]. The basic mechanism of tumor immunity is to kill tumor cells by the help of CD8+T cells. Immune reactions that provide protection against tumors, are typically the task of CD8+T cells. CD4+T cells also play a major role in these tasks [3]. Human CD4+T cells can identify tissue-specific antigens, common tumor antigens and viral antigens caused by tumor transformation [3]. Another task of CD4+T cells is to produce IL-2 as a result of antigen stimulation response. IL-2 has a potent T cell growth factor effect and it has been reported that the application of IL-2 seemingly leads to curative and persistent regressions in cancer patients [5].
Recently, interest in fractional has increased in order to clarify real life problems because of memory and hereditary property [6,7,8,9,10,11,12,13,14]. One of the most common fractional operators is Caputo, Riemann-Liouville (RL). However, these operators are considered weakness due to singularity problems caused by their kernel function. As a result of this weakness, Atangana felt the need to define Atangana-Baleanu (AB) derivative in [15] and [16,17,18,19,20,21,22,23,24,25] are the some of the studies about AB derivative.
Mathematical modeling, known as the reinterpretation of real world problems with mathematical equations, has recently become one of the tools that scientists use to foresee the development of diseases that cause serious problems. [26,27,28,29,30] are some of the studies which attempt to show the relation between cancer and immune system by way of mathematical modeling.
The study is organized as: In section 2, some basic definitions and theorems to be used in study are briefly mentioned. In section 3, the existence and uniqueness of the solution of the fractional immune system-cancer model is given. The graphics of the numerical solution via predictor-corrector scheme is given in section 4 and comments is made on graphics. Lastly, we finalize our study in section 5. Briefly, the relationship between cancer cells and immune system cells will be examined with AB derivative and the effect of IL-2 and dendritic cells on cancer cells will be discussed using the integer form of model presented by Castiglione in [31].
Let us rearrange this model with fractional derivative:
with the initial conditions H(0)=0,C(0)=0,M(0)=1,D(0)=10,I(0)=0, where ABC0Dτt is AB derivative in Caputo sense and τ∈[0,1]. And H,C,M,D,I represent CD4+T (helper) cells, CD8+T (cytotoxic) cells, myeloid (cancer) cells, dendritic cells and IL-2, respectively.
2.
Basic definitions
In this part, some definitions and properties that will be helpful in this work is given.
Definition 2.1. Suppose that g∈H1(a,b), a<b be a function and τ∈[0,1]. The AB derivative in Caputo sense of order τ of g is given by [15]
where Eτ is the Mittag-Leffler function and F(τ) is a normalization function with F(0)=F(1)=1.
Definition 2.2. Assume that g∈H1(a,b), a<b be a function and τ∈[0,1]. The AB derivative in RL sense of order Eτ of g is given by [15]:
Definition 2.3. The fractional integral is given by [15]:
Theorem 2.1. [15] Let g on [a,b] is a continuous function. Given the following inequality holds on [a,b]:
where ‖g(t)‖=maxa≤t≤b|g(t)|.
Theorem 2.2. The AB derivative in Caputo and RL sense satisfy Lipschitz condition [15]:
and
Theorem 2.3. The fractional ordinary differential equation
has a unique solution given as [15]
3.
Existence and uniqueness
Let P=C(K)×C(K)×C(K)×C(K)×C(K) and C(K) be a Banach space of continuous R→R valued functions on the interval K with the norm
where ‖H‖ = sup{|H(t)|:t∈K}, ‖C‖=sup{|C(t)|:t∈K}, ‖M‖=sup{|M(t)|:t∈K}, ‖D‖ = sup{|D(t)|:t∈K}, ‖I‖=sup{|I(t)|:t∈K}.
For clarity, we rewrite the model (1.1) of the following form:
Using Theorem 2.3, the system (3.1) can be written as:
Theorem 3.1. If the following inequality holds
then the kernel N1 satisfies the Lipschitz condition and contraction.
Proof. Let H and H1 be two functions, then we have
Taking A1=b0ψ4+b0f0ψ4(ψ1+ω1)+c0 where D, H and H1 are bounded functions such that ‖D(t)‖≤ψ4, ‖H(t)‖≤ψ1, ‖H1(t)‖≤ω1 then we have
Hence, the Lipschitz condition is fulfilled for N1 and 0≤b0ψ4+b0f0ψ4(ψ1+ω1)+c0<1 implies N1 is also contraction.
Similarly, the other kernels N2, N3, N4 and N5 satisfy Lipschitz condition and contraction.
Consider the system (3.2) in the following recursive formula:
with the initial conditions
We find the difference between the successive terms in the expressions:
Notice that
Taking the norm on both sides of the Eq. (3.6) and applying triangular identity, we find
Because the kernel N1 satisfy Lipschitz condition proved in Eq. (3.4), we have
and
Analogously, we have the following results:
In the light of the results in hand, we give the below theorem.
Theorem 3.2. The fractional model given in (1.1) has a solution, if we can find t0 satisfying the equation
for i=1,2,3,4,5.
Proof. We know that H(t), C(t), M(t), D(t) and I(t) are bounded functions and satisfy Lipschitz condition. From the Eqs. (3.8) and (3.9), we obtain the succeeding relations:
Thus, the existence and continuity of the above solutions are proved. Our goal is to show that the above functions are solutions of Eq. (1.1), assume that
Then, we have
By continuing this method recursively, it gives at t0
As n approaches to ∞, ‖K1n(t)‖ tends to 0. In an analogous way, it can be shown ‖K2n(t)‖→0, ‖K3n(t)‖→0, ‖K4n(t)‖→0 and ‖K5n(t)‖→0.
It is another matter to demonstrate the uniqueness of the solutions of the Eq. (1.1). Suppose that there exist another set of solutions H1(t), C1(t), M1(t), D1(t) and I1(t), we find
Applying the norm to the Eq. (3.14) and because the kernel satisfies the Lipschitz condition, we find
This gives
Clearly H(t)=H1(t), if the following inequality holds
Using the same attitude, we obtain
4.
Numerical simulations
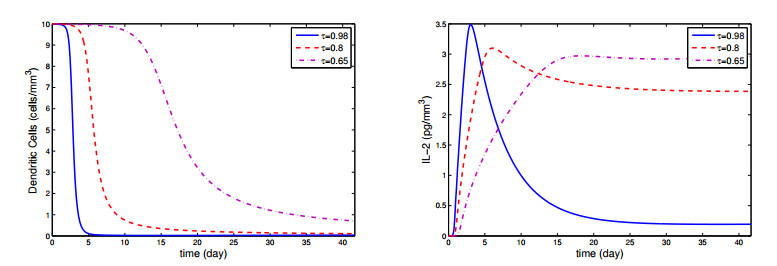
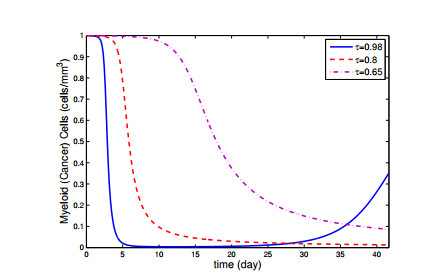
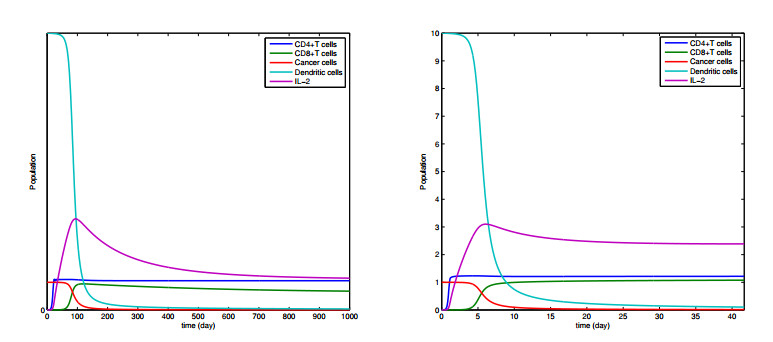
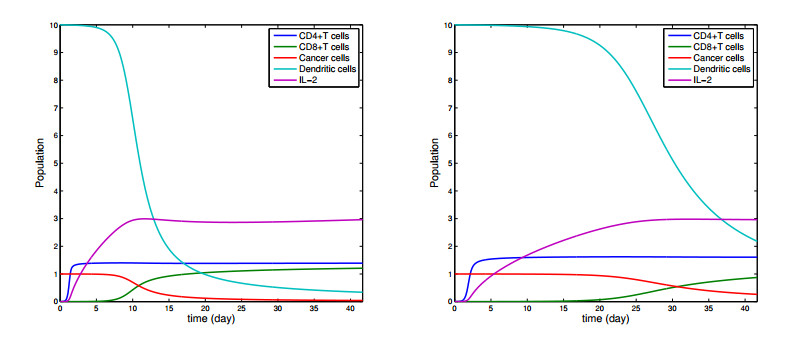
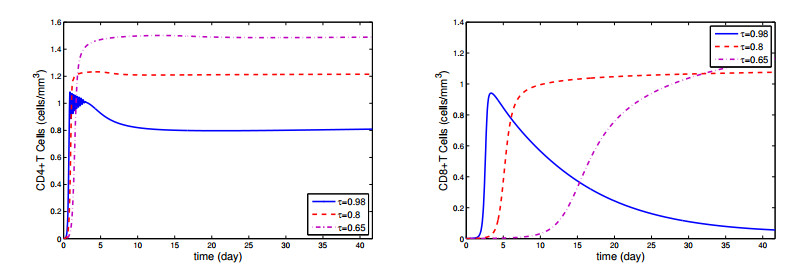
In this section, graphs obtained by using predictor-corrector numerical scheme given in [32] of fractional mathematical model in Eq. (1.1) is given. Our aim is to observe how cancer cells and immune system cells change as fractional order changes. In addition, the interaction between cancer cells and immune system cells can be observed by means of graphs. We use the initial conditions (0,0,1,10,0) for H,C,M,D,I, respectively and use parameters a0=10−4, b0=10−1, f0=1, c0=0.005, a1=10−4, b1=10−2, f1=1, c1=0.005, b2=0.02, f2=1, d2=0.1, d3=0.1, b4=10−2, e4=10−7, c4=10−2 given in [31]. Figures 1–3 represents that the action of the fractional cancer-immune system model constituent for distinct values of τ and it can be seen that as the fractional order τ is decreased, the number of helper, cytotoxic, dendritic cells and IL-2 are increased, while the cancer cells is declined. In other words, when τ=0.98, approximately 60 percent of cancer cells die, while τ=0.65, about 90 percent die. Moreover, Figures 4–5 represents that numerical simulations for the Eq. (1.1) at τ=0.9, τ=0.8, τ=0.7 and τ=0.6, respectively.
5.
Conclusions
Cancer is an issue that needs to be addressed when because of affects many people's lives directly and indirectly. How does the body respond to cancer? The answer to the question can be made more effective in the fight against cancer. So, the integer order cancer-immune system model given in [31] is studied in this paper. Firstly, the cancer-immune system model is modified by AB derivative and then the existence and uniqueness of numerical solution of this model is given. After obtaining graphs related to the model with predictor-corrector numerical method, these graphs is interpreted briefly it can be seen that as τ is increased, it is observed that immune system cells eliminate cancer cells less in these graphs. Apparently, because of the hereditary property of fractional derivative, the fractional derivative is more suitable for real life events.
Conflict of interest
The authors declare that no conflicts of interest in this paper.









 DownLoad:
DownLoad: