List of Abbreviations
The following abbreviations are used in this manuscript:
1.
Introduction and preliminaries
In science, convex functions have a long and distinguished history, and they have been the focus of study for almost a century. The rapid growth of convexity theory and applications of fractional calculus has kept the interest of a number of researchers on integral inequalities. Inequalities such as the H-H type, the Ostrowski-type, the H-H-M type, the Opial type, and other types, by using convex functions have been the focus of research for many years. The H-H inequality given in [1] has piqued the curiosity of most academics among all of these integral inequalities. Dragomir et al. [2] and Kirmaci et al. [3] presented some trapezoidal type inequalities and also some applications to special means. Following these articles, several mathematicians proposed new refinements of the Hermite-Hadamard inequality for various classes of convex functions and mappings such as quasi convex function [4], convex functions [5], m-convex functions [6], s-type convex functions of Raina type [7], σ-s-convex function [8] and harmonically convex functions [9]. Recently, this inequality was also investigated via different fractional integral operators, like Riemann-Liouville [10], ψ-Riemann-Liouville [11], Proportional fractional [12,13], k-Riemann-Liouville [14], Caputo-Fabrizio [15,16], generalized Atangana-Baleanu operator [17] to name a few.
It is important to emphasise that Leibniz and L'Hospital are credited with developing the idea of fractional calculus (1695). Other mathematicians, such as Riemann, Liouville, Letnikov, Erdéli, Grünwald, and Kober, have made significant inputs to the field of fractional calculus and its numerous applications. Many physical and engineering experts are interested in fractional calculus because of its behaviour and capacity to address a wide range of practical issues. Fractional calculus is currently concerned with the study of so-called fractional order integral and derivative functions over real and complex domains, as well as its applications. In many cases, fractional analysis requires the use of arithmetic from classical analysis to produce more accurate conclusions. Numerous mathematical models can be handled by differential equations of fractional order. Fractional mathematical models have more conclusive and precise results than classical mathematical models because they are particular examples of fractional order mathematical models. In classical analysis, integer orders do not serve as an adequate representation of nature. By using mathematical modelling, it is possible to identify the endemics' unique transmission dynamics and get insight into how infection impacts a new population. To enhance the actual phenomena to a higher degree of precision and accuracy, non-integer order fractional differential equations (FDEs) are applied. Additionally, [18,19,20,21,22] use and reference their utilization of fractional calculus. Other interesting results for fractional calclus can be found in [23,24,25]. However, fractional computation enables us to consider any number of orders and formulate far more measurable objectives. In recent years, mathematicians have become more and more interested in presenting well-known inequalities using a variety of novel theories of fractional integral operators. There are several different integral inequality results for fractional integrals. For generalizing significant and well-known integral inequalities, these operators are helpful. The Hermite-Hadamard integral inequality is a particular type of integral inequality. It is frequently used in the literature and outlines the necessary and sufficient conditions for a function to be convex. The Hermite-Hadamard inequalities were generalized by Sarikaya et al. [10] using Riemann-Liouville fractional integrals. Işcan [26] expanded Sarikaya et al. [10] 's findings to include Hermite-Hadamard-Fejer-type inequalities. By utilizing the product of two convex functions, Chen [27] produced fractional Hermite-Hadamard-type integral inequalities. Ögülmüs et al. [28] incorporated the Hermite-Hadamard and Jensen-Mercer inequalities to present Hermite-Hadamard-Mercer type inequalities for Riemann-Liouville fractional integrals. Motivated by the above articles, Butt et al. (see [29]), presented new versions of Jensen and Jensen-Mercer type inequalities in the fractal sense. New fractional versions of Hermite-Hadamard-Mercer and Pachpatte-Mercer type inclusions are established for convex [30] and harmonically convex functions [31] respectively. Latif et al. [32] established Hermite-Hadamard-Fejér type inequalities for convex harmonic and a positive symmetric increasing function. New refinements of Hermite-Mercer type inequalities are presented in [33], Mercer-Ostrowski type inequalities are presented in [34]. Further, the Hermite-Hadamard inequality is also generalized for convexity and quasi convexity [35] and differentiable convex functions [36]. For further information on other fractional-order integral inequalities, see the papers [37,38,39,40,41].
Definition 1.1. (see [42]) Let G:X→R be a function and X be a convex subset of a real vector space R. Then we say that the function G is convex if and only if the following condition:
holds true for all r,s∈X and Φ∈[0,1].
For further discussion, we first present the classical Hermite-Hadmard (H-H) inequality, which states that (see [1]):
If the function G:X⊆R→R is convex in X for r,s∈X and r<s, then
Definition 1.2. (see [43]) Let there be a function G:[r,s]→[0,∞) and it is symmetric with respect to r+s2, if
In 1906, Fejér [44] preposed the following weighted variant of Hermite-Hadamard inequality famously known as Hermite-Hadamard-Fejér inequality, given as
Theorem 1.1. Let there be a convex function G:[r,s]⊆R∖{0}→R with r<s. If D:[r,s]⊆R∖{0}→R be a convex symmetric and integrable function with respect to r+s2. Then
holds true.
Definition 1.3. (see [9]) Let G:X→R be a function and X be a subset of a real vector space R. Then we say that the function G is harmonically convex if and only if the following condition
holds true for all r,s∈X and Φ∈[0,1].
For further discussion, we first present the classical Hermite-Hadmard (H-H) inequality, which states that (see [9]):
If the function G:X⊆R→R is harmonically convex in X for r,s∈X and r<s, then
Definition 1.4. (see [45]) Let there be a function G:[r,s]→[0,∞) and it is harmonically symmetric with respect to 2rsr+s, if
In the year 2014, Chen and Wu [46] proposed the following weighted variant of Hermite-Hadamard inequality for harmonically convex function, given as
Theorem 1.2. Let there be a convex function G:[r,s]⊆R∖{0}→R with r<s. If D:[r,s]⊆R∖{0}→R be a convex symmetric and integrable function with respect to r+s2. Then,
holds true.
Definition 1.5. (see, for details, [10,47]; see also [48]) Let \(\mathscr{G} \in \mathcal{L} \left\lbrack \mathfrak{r}, \ \mathfrak{s} \right\rbrack\). Then, the Riemann-Liouville fractional integrals of the order α>0, are defined as follows:
and
respectively, where \(\Gamma\left(\alpha \right) = \int_{0}^{\infty}{\Phi^{\alpha - 1}e^{- \Phi}}{d\Phi}\) is the Euler gamma function.
Definition 1.6. (see, [49] for details) Let G∈L[r,s]. Then, the new left and right fractional integrals Iαr+ and Iαs− of order α>0 are defined as
and
respectively.
It should be noted that
Sarikaya et al. [37], in their article proved some interesting mid-point type Hermite-Hadamard inequalities. Here, we present one of his main results as follows:
Theorem 1.3. (see [37]) Let G:[r,s]⟶R be a convex function with 0≤r≤s. If G∈L[r,s], then the following inequality for Riemann-Liouville fractional integral operator holds true:
The major goal of this paper is to establish Fejér type fractional inequalities using differintegrals of the (r+s2) type for both convex and harmonically convex functions via a novel fractional integral operator. In order to derive those inequalities, first we prove two new lemmas i.e., Lemmas 2.1 and 3.1 for convex and harmonic convex functions respectively.
In this study, we used a new fractional integral operator to achieve more generalized results. This is caused by the exponential function that makes up the kernel of this fractional operator. Our results differ from prior generalizations in that they do not lead to the aforementioned fractional integral inequalities. Numerous experts have suggested utilizing different fractional integral operators to extend the Hermite-Hadamard and Fejér type inequalities, however, none of their findings exhibit an exponential property. This study generated interest in using an exponential function as the kernel to create more generalized fractional inequalities. Furthermore, the application of symmetric and harmonically symmetric functions to the main results gives the study of inequalities a new path. For other generalization regarding exponential kernel interested reader can see e.g., on distributed-order fractional derivative in [50]. There are many research gaps to be filled for integral inequalities involving fractional calculus for different types of convex functions, despite the fact that there exist many different forms of research on the growth of fractional integral inequalities. As a result, the main purpose of this research is to find new Hermite-Hadamard and Fejér type inequalities for positive symmetric functions using fractional integral operators.
Our present investigation is structured as follows. In Sections 2 and 3, we discuss two additional characteristics of the relevant fractional operator before proving some enhanced versions (mid-point types) of the Fejér and Hermite-Hadamard type inequalities for convex and harmonically convex functions respectively. Some applications are also taken into consideration in Section 4 to determine whether the predetermined results are appropriate. Section 5 explores a brief conclusion and possible areas for additional research that is related to the findings in this paper are discussed in Section 6.
2.
Improved Fejér type results for convex functions
In this section for simplicity, we denote ρc=1−αα(s−r). If α→1, then ρc=1−αα(s−r)→0.
Lemma 2.1. Let D:[r,s]⊆R∖{0}→R be a symmetric convex function with respect to r+s2. Then for α>0, the following equality holds true:
Proof. Since D:[r,s]⊆R∖{0}→R is integrable and symmetric to r+s2 we have D(r+s−x)=D(x). Also, Setting Φ=r+s−x and dΦ=−dx, we have
This led us to the desired equality.
First, we prove both the first and second kind Fejér type inequalities in a different approach. Then, we also prove the Hermite-Hadamard inequality using symmetric convex functions.
Theorem 2.1. Let there be a convex function G:[r,s]⊆R∖{0}→R with r<s. If D:[r,s]⊆R∖{0}→R be a convex symmetric and integrable function with respect to r+s2. Then for α>0, the following inequality holds true:
Proof. Using the convexity of G on [r,s], we have
Upon multiplication of both sides of the inequality (2.1) by e−1−αα(s−r)ΦD(Φs+(1−Φ)r) and then integrating the resultant over [0,12], we obtain
Since D is symmetric with respect to r+s2, we have D(x)=D(r+s−x).
Moreover, setting x=Φs+(1−Φ)r and dx=(s−r)dΦ in (2.2), we have
It follows from the above developments and Lemma 2.1 that,
This concludes the proof of the required result.
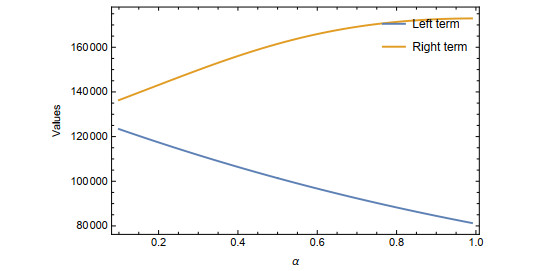
Example 2.1. Let G(m)=em, m∈[1,9] and D(m)=(5−m)2, is non-negative symmetric about m=5. Let 0<α<1, then
and
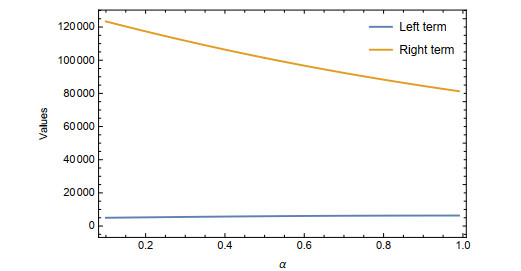
The graphical representation of Theorem 2.1 is shown in the graph below (see Figure 1) for 0<α<1:
Theorem 2.2. Let there be a convex function G:[r,s]⊆R∖{0}→R with r<s. If D:[r,s]⊆R∖{0}→R be a convex symmetric and integrable function with respect to r+s2. Then for α>0, the following inequality holds true:
Proof. Since G is convex function, we have
Multiplying both side of the above inequality (2.3) by e−1−αα(s−r)ΦD(Φs+(1−Φ)r) and upon integration of the obtained result over [0,12], one has
It follows
Furthermore, using the Lemma 2.1, we obtain
This concludes the proof of the desired result.
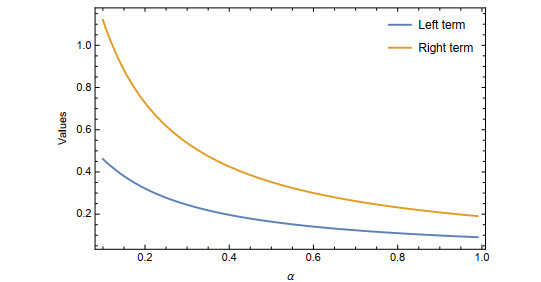
Example 2.2. Let G(m)=em, m∈[1,9] and D(m)=(5−m)2, is non-negative symmetric about m=5. Let 0<α<1, then
And
The graphical representation of Theorem 2.2 is shown in the graph below (see Figure 2) for 0<α<1:
Theorem 2.3. Let there be a convex function G:[r,s]⊆R∖{0}→R with r<s. Then for α>0, the following fractional integral inequality holds true:
Proof. By the hypothesis of convexity, we have
Upon multiplication of both sides of the inequality (2.5) by 2e−1−αα(s−r)Φ and then integrating the obtained result over [0,12], we have
Furthermore, let m=Φs+(1−Φ)r⟹dΦ=dms−r. Then inequality (2.6) gives
This concludes the proof of the first part of the inequality (2.4). To prve the next part of inequality, under the given hypothesis, we have
Upon multiplication of both sides of the inequality (2.8) by e−1−αα(s−r)Φ and integrating over [0,12], we have
Consequently, we obtain
Consequently, it follows from the above developments (2.7) and (2.9) that
This concludes the proof of the required result.
Remark 2.1. If one chooses α→1 i.e., ρc2→0, then
and hence Theorem 2.3 retrieves the classical Hermite-Hadamard inequality (1.1).
Example 2.3. Let G(m)=em, m∈[1,9] and 0<α<1, then
and
The graphical representation of Theorem 2.3 is shown in the graph below (see Figure 3) for 0<α<1:
3.
Improved inclusions via harmonically convex functions
The family of Lebesgue measurable functions is represented here by \(\mathcal{L} \left\lbrack \mathfrak{r}, \mathfrak{s} \right\rbrack \). In this section, for brevity we use, ρh=1−ααs−rrs wherever needed. If α→1, then ρh=1−ααs−rrs→0.
Lemma 3.1. Let D:[r,s]⊆R∖{0}→R be a harmonically symmetric and integrable function with respect to 2rsr+s. Then for α>0, the following equality holds true:
where K(x)=1x,x∈[1s,1r].
Proof. Let D be a harmonically symmetric function with respect to 2rsr+s. Then using the harmonically symmetric property of D, given as D(1Φ)=D(11r+1s−Φ) for α>0.
Consequently, it follows from the above developments that
where K(x)=1x,x∈[1s,1r].
Now, we use the above result to produce new Hadamard-Fejér type inequalities of both first and second kind for harmonically convex functions.
Let us begin with the Hadamard-Fejér type inequality of the first kind.
Theorem 3.1. Let there be a harmonically convex function G:[r,s]⊆R∖{0}→R with r<s. If D:[r,s]⊆R∖{0}→R be a harmonically symmetric and integrable function with respect to 2rsr+s. Then for α>0, the following inequality holds true:
Proof. Since G is harmonically convex function on [r,s], we have
Multiplying both side by 2e−1−ααs−rrsΦD(rsΦs+(1−Φ)r) and then integrating over [0,12], we find
Since, D is harmonically symmetric with respect to 2rsr+s i.e
Also, setting x=Φs+(1−Φ)rrs ⟹dΦ=rss−rdx the above developments proceed as follows:
From the above developments and Lemma 3.1, we have
This concludes the proof of the required result.
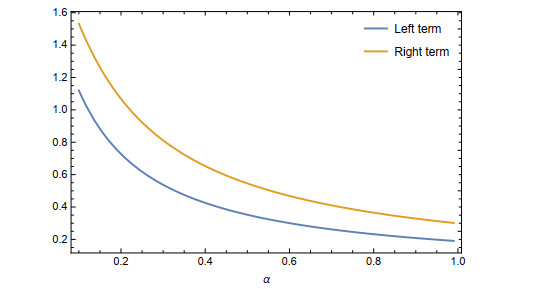
Example 3.1. Let G(m)=m2, m∈[1,4], D(m)=(5m−88m)2 and 0<α<1, then
and
The graphical representation of Theorem 3.1 is shown in the graph below (see Figure 4) for 0<α<1:
Now, we will establish the Fejér type inequality of the second kind.
Theorem 3.2. Let there be a harmonically convex function G:[r,s]⊆R∖{0}→R with r<s. If D:[r,s]⊆R∖{0}→R be a harmonically symmetric and integrable function with respect to 2rsr+s. Then for α>0, the following inequality holds true:
Proof. Since G is harmonically convex function
Multiplying both side by e−1−ααs−rrsΦD(rsΦs+(1−Φ)r) and then integrating the resultant over [0,12], we find
Setting x=Φs+(1−Φ)rrs and D(1x)=D(11r+1s−x) in (3.1), we have
Also,
From the above developments (3.2), (3.3) and Lemma 3.1, we have
This concludes the proof of the required result.
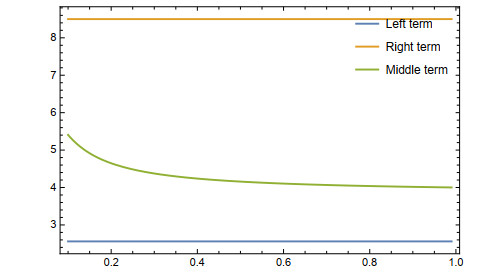
Example 3.2. Let G(m)=m2, m∈[1,4], D(m)=(5m−88m)2 and 0<α<1, then
and
The graphical representation of Theorem 3.2 is shown in the graph below (see Figure 5) for 0<α<1:
Theorem 3.3. Let there be a harmonically convex function G:[r,s]⊆R∖{0}→R with r<s. Then for α>0,
holds true.
Proof. Since G is harmonically convex function on [r,s], we have
Multiplying both side of the inequality (3.5) by 2e−1−ααs−rrsΦ and integrating over [0,12], we obtain
Let m=Φs+(1−Φ)rrs, then dm=s−rrsdΦ
This gives us the first part of the inequality (3.4). Now, for the next part, we use the hypotheses of harmonically convex function i.e.
Multiplying both side of the above inequality (3.7) by e−1−ααs−rrsΦ and then integrating the resultant over [0,1], we obtain
Consequently from the first inequality (3.6), we have
From the above developments (3.6) and (3.8), it follows
This concludes the proof of the required result.
Remark 3.1. If one chooses α→1 i.e., ρh2→0, then
and hence Theorem 2.3 retrieves the classical Hermite-Hadamard inequality (1.3) for harmonically convex function.
Example 3.3. Let G(m)=m2, m∈[1,4], K(m)=1m and 0<α<1, then
and
The graphical representation of Theorem 3.3 is shown in the graph below (see Figure 6) for 0<α<1:
4.
Applications
Example 4.1. Let Cn be the set of n×n complex matrices, Mn denote the algebra of n×n complex matrices, and M+n denote the strictly positive matrices in Mn. That is, for any nonzero u∈Cn, A∈M+n if ⟨Au,u⟩>0.
Sababheh [51], proved that G(κ)=∥AκXB1−κ+A1−κXBκ∥, A,B∈M+n,X∈Mn is convex for all κ∈[0,1].
Then, by using Theorem 2.3, we have
Example 4.2. The q-digamma(psi) function ψΦ given as (see [52]):
For Φ>1 and ζ>0, Φ-digamma function ψΦ can be given as:
If we set G(ζ)=ψ′Φ(ζ) in Theorem 2.3, then we have the following inequality.
Modified Bessel functions
Example 4.3. Let the function Jρ:R→[1,∞) be defined [52] as
Here, we consider the modified Bessel function of first kind given in
The first and second order derivative are given as
If we use, G(m)=J′ρ(m) and the above functions in Theorem 2.3, we have
5.
Concluding remarks
The use of fractional calculus for finding various integral inequalities via convex functions has skyrocketed in recent years. This paper addresses a novel sort of Fejér type integral inequalities. In order to generalize some H-H-F (Hermite-Hadamard-Fejér) type inequalities, a new fractional integral operator with exponential kernel is employed. New midpoint type inequalities for both convex and harmonically convex functions are studied. Applications related to matrices, q-digamma and modifed Bessel functions are presented as well.
6.
Future scopes
We will use our theories and methods to create new inequalities for future research by combining these new weighted generalized fractional integral operators with Chebyshev, Simpson, Jensen-Mercer Markov, Bullen, Newton, and Minkowski type inequalities. Quantum calculus, fuzzy interval-valued analysis, and interval-valued analysis can all be used to establish these kinds of inequalities. The idea of Digamma functions and other special functions will be integrated with this kind of inequality as the major focus. We also aim to find other novel inequalities using finite products of functions. In future, we will employ the concept of cr-order defined by Bhunia and Samanta [53] to present different inequalities for cr-convexity and cr-harmonically convexity [54].
Acknowledgments
This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation, (grant number B05F650018).
Conflict of interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.









 DownLoad:
DownLoad: