Modified nonmonotonic projection Barzilai-Borwein gradient method for nonnegative matrix factorization

1.   Introduction

The Cattaneo-Christov model marks a substantial improvement that is subject to the conventional Fourier ^[1] and Fick laws ^[2], which traditionally adopt that heat and mass flux respond instantaneously to mass and thermal gradients. These assumptions imply an infinite propagation speed for mass and thermal transfer, which is not realistic. The Cattaneo model ^[3] addresses this issue by introducing a thermal relaxation time that consequently acknowledges the restricted speed of heat diffusion. Christov ^[4] further refined this model by incorporating a derivative term to enhance its accuracy and predictive capabilities. By introducing this mathematical modification, Christov aimed to improve the model's ability to capture dynamic changes and respond more effectively to variations in the system. In fluid dynamics, the Cattaneo-Christov model enhances the precision of heat predictions, as noted by Yseen et al. ^[5]. In thermal systems, such as solar collectors and thermal insulators, this model improves our understanding of heat distribution, leading to greater efficiency ^[6]. Eid et al. ^[7] computationally analyzed fluid flow in a permeable medium under the Cattaneo-Christov model's influence. Mumtaz et al. ^[8] emphasized the significance of this model in concentration systems, mostly in biomedical and chemical uses, where it effectively represents the diffusivity and dispersal of fluid particles. This advanced modeling technique enhances the regulation of concentration gradients, leading to better performance in processes such as targeted drug delivery, chemical reactor optimization, and environmental pollutant monitoring. Unlike the traditional Fourier law, which has limitations in handling non-Fourier heat conduction, the Cattaneo-Christov model provides a more widespread framework for analyzing both concentration and thermal dynamics. Its ability to address these complexities makes it highly valuable in modern fluid dynamics and heat transfer studies. Rehman et al. ^[9] further reinforced its importance in improving industrial and scientific applications, paving the way for innovative technological advancements.

Magnetohydrodynamics (MHD) examine the performance of electrically conducted fluids influenced by magnetic fields. In this field, magnetic forces generate electric currents within the fluid, leading to interactions that affect the flow and thermal panels ^[10,11]. According to Ahmad et al. ^[12], when nanofluids move through a magnetic field, they encounter a Lorentz force, which alters their velocity and heat distribution. This force acts as a magnetic drag, reducing the movement of fluid perpendicular to the magnetic field lines. Consequently, the velocity panel converts to complicated form, often featuring regions of diminished speed and distinct flow configurations compared to cases without magnetic influence, as noted by Tarakaramu et al. ^[13]. MHD also has a profound impact on temperature distribution. Vinutha et al. ^[14] highlighted that interactions among fluid motion and magnetic fields induce Joule heating, where electrical resistance within the fluid converts kinetic energy into heat. This process raises the temperature in certain regions, leading to non-uniform thermal fields. In practical applications, MHD effects are connected to enhance efficiency in devices like MHD generators and pumps by regulating temperature gradients and controlling flow patterns. Obalalu et al. ^[15] discussed how these effects are employed to optimize thermal performance. These range from astro-physical studies to industrial phenomena comprising liquid metals and plasma. Algehyne et al. ^[16] focused on MHD fluid flow over an exponentially stretched surface while considering effects of chemical reactivity, further demonstrating the broad significance of MHD in scientific and engineering domains.

Nanofluid flow is the fluid motion comprising nanoparticles suspended within a base liquid. These nanoparticles, typically measured in nanometers, boost the thermal features of the fluid, as first identified by Choi ^[17]. Zafar et al. ^[18] explored advancements in the Das and Tiwari nanofluid flow model and its application across geometric configurations. Anjum et al. ^[19] conducted bio-convective simulations of three-dimensional nanofluid flow, considering the role of microorganisms. Mohite et al. ^[20] explored the relevance of nanofluid flow in many industrial and engineering applications as well as in bio-medicines. The performance of nanofluid flow is subjective to multiple elements, including nanoparticle numbers, size, and shape, as examined by Acharya et al. ^[21]. Further, Khan et al. ^[22] investigated nanofluid flow past a moving thin needle, incorporating dissipative effects, and discovered that increasing nanoparticle concentration improves thermal performance while reducing velocity. The collaboration among nanoparticles and the adjoining fluid affects viscosity and thermal conductivity, thereby influencing overall flow behavior and heat transfer efficiency, as demonstrated by Gowda et al. ^[23]. The existence of nanoparticles enhances the fluid's thermal performance, leading to more efficient heat transfer and a more uniform temperature distribution, which helps minimize thermal gradients ^[24]. However, the increased viscosity resulting from nanoparticles can slow the flow, particularly in boundary layer regions. Despite this, the improved thermal properties of nanofluids offset the reduction in velocity by enabling more effective heat dissipation. Due to these attributes, nanofluids are widely used in applications requiring precise thermal control, as they maintain efficient cooling even at lower flow speeds. Their ability to optimize heat transfer makes them indispensable in various high-performance thermal management systems.

A variable porous space is a medium where the proportion of void spaces, or porosity, changes across regions. Fluid flow in a variable porous space is a complex phenomenon influenced by spatial changes in porosity, permeability, and pressure gradients. In such a medium, the flow behavior deviates from classical Darcy's law due to variations in the pore structure, which may result from natural formations like sedimentary rocks or engineered materials such as functionally graded porous structures. Khan et al. ^[25] analyzed fluid flow incorporating binary diffusion using ANN approach with flow of fluid on a varying permeable sheet. Yadav et al. ^[26] investigated magnetohydrodynamic flow of fluid in a permeable medium with spatially varying porosity, concluding that the porous nature of materials directly regulates fluid motion. Wahid et al. ^[27] examined radiative nanofluid flow over a penetrable shrinking sheet, revealing that increasing radiation effects improved thermal distribution within the fluid. Variable porous media play a crucial role in many fields such as petroleum engineering, and hydrology as they influence the transport of oil, water, and impurities through geological formations, as observed by Shamshuddin et al. ^[28]. In these media, spatial porosity changes strongly affect fluid velocity and temperature distribution. Abbas et al. ^[29] demonstrated that higher porosity regions facilitate greater fluid movement, resulting in increased velocity, while lower porosity areas hinder flow and reduce velocity. Additionally, temperature distribution is impacted, with higher porosity regions supporting additional thermal transference causing unchanging thermal profile ^[30]. Further, Kodi et al. ^[31] examined MHD effects on fluid flow around a vertical cone surrounded by a porous medium, incorporating diffusive influences. Hussain et al. ^[32] studied the behavior of nanoparticles through a varying permeable space with a magnetic field.

Brownian motion denotes the random and irregular nanoparticles' motion mixed in a fluid, resulting from collisions with the surrounding fluid molecules. This process enhances particle dispersion and mixing, thereby improving thermal conductivity and ensuring a more augmented thermal panel, as highlighted by Thabet et al. ^[33]. Conversely, thermophoresis designates the migration of particles from hotter to cooler areas due to temperature gradients. Madhura and Babitha ^[34] explained that this phenomenon occurs because particles are subjected to diverse forces at variable heat, causing a net motion toward cooler regions. Both these phenomena (thermophoresis and Brownian motion) play main role in shaping the heat and concentration panels of nanofluids ^[35]. Brownian motion contributes to heat transfer by promoting continuous collisions between particles and fluid molecules, leading to an even distribution of thermal energy and improved thermal conductivity. In contrast, thermophoresis generates a concentration gradient as nanoparticles move toward cooler zones, creating an uneven particle distribution. Depending on nanoparticle concentration in specific regions, this movement can further influence thermal conductivity. The collective impact of thermophoresis and Brownian motion results in complicated interactions that affect both heat and particle distribution, as detected by Sundeep et al. ^[36]. These influences are significant in practical applications, particularly in optimizing nanofluids for heat transfer purposes. In cooling systems, Brownian motion enhances heat dissipation by boosting thermal conductivity ^[37]. Nevertheless, too much thermophoretic migration leads to particle accumulation in cold areas that potentially enhances nanofluid performance and stability ^[38]. Additional studies on this subject can be found in references ^[39,40].

Casson fluid is a non-Newtonian fluid categorized by its yield stress and viscosity, behaving as a solid below a certain shear stress threshold and flowing as a fluid above it. This rheological model was initially developed to describe the flow of blood and other bio-fluids but has since been applied to various industrial fluids like chocolate, ketchup, and certain polymers as studied by Kumar et al. ^[41]. Islam et al. ^[42] simulated computationally the transportation of mass and thermal flow for Casson fluid flow with sinusoidal constraints at borderlines. Mahmood et al. ^[43] examined augmented transportation phenomenon for Casson fluid flow on a radiative movable sheet with thermal slip constraints. The flow properties of Casson fluids are influenced by factors like particle concentration, temperature, and pressure as observed by Upreti et al. ^[44]. Under low shear rates, these fluids exhibit a high apparent viscosity, which decreases as the shear rate increases. This unique behavior enables Casson fluids to maintain stability under low-stress conditions while flowing readily when subjected to sufficient force, making them useful in applications requiring controlled flow properties. The velocity profiles of a Casson fluid is distinct due to its yield stress ^[45]. In regions where the applied stress is below the yield stress, the fluid acts like a solid, resulting in a plug flow region where the velocity gradient is zero. Beyond this region, the fluid begins to flow, and the velocity increases with distance from the solid boundary. This non-linear velocity distribution creates a steeper gradient near the wall compared to Newtonian fluids, indicating a higher shear rate near the boundary. The presence of yield stress also means that Casson fluids exhibits velocity slip at the boundary, which significantly impacts flow characteristics in confined spaces or porous media. Hussain et al. ^[46] examined thermal transportations for stagnant EMHD Casson fluid flow on a surface with impacts of thermal radiations.

Novelty of current work

● The literature lacks studies that examine the combined effects of an inclined magnetic field and variable porosity on Casson nanofluid flow on a convectively heated, dual-directional stretching surface. Researchers have primarily focused on Casson nanofluids flows with various flow conditions on stretching sheets with constant porosity. However, a comprehensive analysis of such flows integrating both an inclined magnetic field and variable porosity remains unexplored. This gap highlights the need for further investigation to understand the complex interactions of these factors on fluid dynamics and heat transfer characteristics.

● To fill this research gap, we seek to investigate the influence of Cattaneo-Christov heat and mass flux on Casson nanofluid flow, including the impact of an inclined magnetic field and varying porosity, on an elongating surface.

● The analysis also takes on convective boundary conditions, activation energy, chemical reaction, thermophoresis, and Brownian motion influences.

● The sheet's surface has variable porosity that is studied to clarify how changes in porosity influence the primary directional movement of the fluid.

● By means of the similarity transformations, the major equations are altered to a dimensionless form and numerically solved with a leveraging ANN technique.

Technical Specification of Physical Components

The technical specification of various components used in this work is illustrated as: The Cattaneo-Christov model is employed to analyze heat and mass transfer in the nanofluid system, incorporating thermal relaxation effects to extend Fourier's law. The working nanofluid consists of a base fluid as blood with suspended nanoparticles of gold enhancing thermal conductivity. We consider a variable porous space, where permeability varies spatially, affecting fluid resistance and heat dissipation. Inclined magnetic effects are modeled using an external magnetic field at an angle with inclination $\left( \gamma \right)$, modifying the Lorentz force and flow stability. A chemical reaction parameter accounts for species diffusion and reaction kinetics. Brownian motion of nanoparticles impacts heat and mass transfer, while thermophoresis effects nanoparticle distribution due to temperature gradients.

Main Goal/Research Questions

We aim to explore and answer key research questions, focusing on fundamental features of the topic:

➢ What are the effects of variable porous space on velocities in all directions?

➢ How the stretching ratio factor, magnetic factor, and Casson factor will affect the flow in primary and secondary directions?

➢ How heat and mass transfer in the nanofluid flow system is affected by Cattaneo-Christov flux model?

➢ How thermal distribution will vary with corresponding deviations in radiation, thermophoresis and Brownian motion factors.

➢ What are the impacts of thermophoresis factor, activation energy factor Schmidt number, chemical reactivity factor and Brownian motion factor on concentration panels?

Real World Applications

This study has significant real-world applications in biomedical engineering, industrial manufacturing, and thermal management systems. The analysis of gold blood-based Casson nanofluids can enhance targeted drug delivery, hyperthermia cancer treatments, and artificial blood substitutes, improving medical therapies. In industrial processes, the findings can optimize polymer extrusion, chemical reactors, and nano-coating technologies by improving heat and mass transfer efficiency. Additionally, the integration of machine learning enhances predictive modeling in fluid dynamics, benefiting applications in biotechnology, aerospace, and energy systems, where accurate control of nanofluid behavior is crucial for performance optimization.

2.   Formulation of the problem

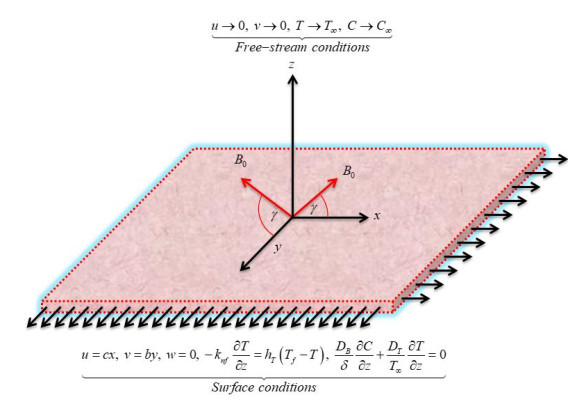
Take flow of gold-blood nanofluid on a convectively heated dual-directional elongating sheet with chemically reactive effects and activation energy. The surface of the sheet is elongated with velocities $u = cx$ and $v = by$ in x and y directions, respectively, keeping $b\, \, , \, \, c > 0$ as fixed numbers. The effects of the magnetic field used to the flow system with an inclination $\left( \gamma \right)$ along the z-axis, as portrayed in Figure 1. This study investigates heat and mass transfer in fluid flow by integrating the Cattaneo-Christov model while considering the influence of thermal radiation. The surface of the sheet is variably porous with thermophoresis and Brownian motion effects.

With the above stated suppositions, we have ^[47,48]:

With constraints at boundary ^[48]:

The transformable variables are given as ^[11,49]:

Thermo-physical features of nanofluid are illustrated as ^[48]:

The experimental values of thermo-physical features are given in Table 1.

In Eq (9), the interspace of nanoparticles is portrayed by $h$, and ${d_p}$ is used for the diameter of nanoparticles while their volume fraction is presented by $\varphi$.

Implementing Eq (7), we have

The constraints at the boundaries are

In the above equations, we have $\Pr = \frac{{{{\left( {\mu {C_p}} \right)}_f}}}{{{k_f}}} =$ Prandtl number, $Rd = \frac{{16{\sigma ^*}T_\infty ^3}}{{3{k^*}{k_f}}} =$ radiation factor, $\alpha = \frac{b}{c} =$ ratio factor, $Sc = \frac{{{v_f}}}{{{D_B}}} =$ Schmidt number, ${\gamma _2} = {\lambda _C}\, c =$ mass relaxation time factor, $B{i_T} = \frac{{{h_T}}}{{{k_f}}}\sqrt {\frac{{{\upsilon _f}}}{c}} =$ thermal Biot number, ${\gamma _1} = {\lambda _E}c =$ thermal relaxation time factor, $Da = \frac{{{\upsilon _f}}}{{\alpha {m^2}}} =$ variable porous media factor, $M = \frac{{{\sigma _f}B_0^2}}{{c{\rho _f}}} =$ magnetic factor, ${K_r} = \frac{{{K_r}^2}}{c} =$ chemical reactivity factor, $Nt = \frac{{{{\left( {\rho {C_p}} \right)}_{nf}}}}{{{{\left( {\rho {C_p}} \right)}_f}}}\frac{{{D_T}\left( {T - {T_\infty }} \right)}}{{{T_\infty }{\upsilon _f}}} =$ thermophoresis factor, $Nb = \frac{{{{\left( {\rho {C_p}} \right)}_{nf}}}}{{{{\left( {\rho {C_p}} \right)}_f}}}\frac{{{D_B}\left( {C - {C_\infty }} \right)}}{{{\upsilon _f}}} =$ Brownian motion factor and, $E = \frac{{{E_a}}}{{k{T_\infty }}} =$ activation energy factor.

2.1.   Interested quantities

The skin frictions in x and y-directions with Nusselt and Sherwood numbers are given as:

Using Eq (7), we get from Eq (15) that

With ${{Re} _x} = \frac{{{u_w}x}}{{{\upsilon _f}}}\, \, and\, \, {{Re} _y} = \frac{{{v_w}y}}{{{\upsilon _f}}}$ as local Reynolds numbers.

3.   Solution method

LMS-NNA is a sophisticated optimization technique designed for training artificial neural networks efficiently and accurately. It combines the gradient descent method, which adjusts the weights of the network to minimize the error between predicted and actual outputs, with the Gauss-Newton method, known for solving non-linear least squares problems. By merging these approaches, LMS-NNA provides a dynamic way to update the network's weights, transitioning smoothly between the stability of gradient descent when it is far from the solution and the faster convergence of Gauss-Newton as the solution nears optimality. This hybrid method is particularly effective in handling complex and large-scale neural networks, enabling faster and more precise training compared to standard optimization methods. As a result, it is extensively used in numerous applications, like pattern recognition and predictive modeling, where rapid and accurate convergence is crucial. This method is mathematically described as follows:

The sigmoid function is a bounded, smooth real-valued function characterized by a single inflection point and a derivative that is always non-negative. Its formula serves as an example of this type of function.

This function is incorporated into Eqs (17)−(20) so that we have

Above, $P, \, \, Q, \, \, M$ are component vectors described by ${P_i}, \, \, {Q_i}, \, \, {M_i}$. The number of neurons and the order of derivative are illustrated by $P, \, \, Q, \, \, M$. Equations (23)−(26) portray the Sigmoid function $f(\eta {M_i} + {P_i}_i) = \frac{1}{{1 + {e^{\eta {M_i} + {P_i}}}}}$ as the objective function and its higher order, which is of 3^rd order.

3.1.   Fitness function formulation

The MSE (mean squared error) is used as an error function that is given for the current model as follows:

Equation (27) illustrates the objective function in which $\chi$ corresponds with mean squared error that is the summation of ${\chi _1}, \, \, {\chi _2}, \, \, {\chi _3}$, and ${\chi _4}$. These values of ${\chi _1}, \, \, {\chi _2}, \, \, {\chi _3}$, and ${\chi _4}$ are evaluated through Eqs (28)−(31).

3.2.   Advantages and disadvantages

The Levenberg-Marquardt (LM) is a popular optimization technique used to train neural networks. Here are its key advantages and disadvantages.

3.2.1.   Advantages

● This algorithm is faster than standard gradient descent, especially for moderate-sized networks.

● It provides better optimization and often achieves lower error rates than other backpropagation methods.

● It performs well when dealing with networks of small to moderate size.

● It adapts between these two methods, improving both stability and speed.

● It works well with non-linear problems and avoids getting stuck in local minima as often as a simple gradient descent.

3.2.2.   Disadvantages

● The LM algorithm requires storing large Jacobian matrices, making it memory-intensive.

● As the network size increases, computational costs become very high.

● The effectiveness of the algorithm depends on the proper adjustment of the damping factor.

● It may not perform well when training data contains high levels of noise.

● Due to its high computational demands, it is impractical for very deep networks.

Figure 2 illustrates the neural network phenomenon.

4.   Results and discussion

In this work, we explore the behavior of nanofluid flow over a variable porous extending surface, considering the influence of an inclined magnetic field. We specifically examine how the size and spacing of nanoparticles impact the overall flow dynamics, heat transfer, and mass transport characteristics. To enhance the accuracy of thermal and mass diffusion analysis, the study integrates the Cattaneo-Christov heat and mass flux model, which accounts for relaxation time effects, improving upon the traditional Fourier and Fick's laws. Furthermore, the model includes the impact of chemical reactions and activation energy, which are crucial for understanding reaction kinetics in nanofluid transport. Additional effects such as Brownian motion and thermophoresis are also considered, as these play significant roles in nanoparticle dispersion and thermal conductivity enhancement. We solved the modeled equations using ANN. In the upcoming paragraphs, the discussion of ANN graphs and different flow distributions are presented.

4.1.   ANN graphs analysis

Figure 2 portrays the process for neural networks, using an algorithmic approach. The graphical depictions for statistical analysis of the LMS-NNA design regarding influences of distinct emerging factors on velocities, temperature, and concentration are portrayed in Figures 3−10. The illustration of MSE convergence is suggested in Figures 3(a)−10(a). The MSE values are closely monitored during the testing, training, and validation phases, providing a comprehensive understanding of the model's performance and convergence throughout these critical stages. The model's optimal performance is observed at certain epochs like 111,225,194,270,179,220,339, and 221. The traditional stages for addressing the gradient computation and validation checks in the LMS-NNA design are illustrated in Figures 3(b)−10(b). These visuals depict the sequential progression of the model as it undergoes adjustments to optimize performance. The gradient computation stage ensures that the model correctly updates its weights by evaluating the direction and magnitude of error reduction. Validation checks serve as an essential quality control mechanism, assessing the model's generalization ability and preventing overfitting by verifying its performance on unseen data. Each of these stages represents a fundamental aspect of the model's adaptive learning process, ensuring accurate and efficient optimization. The error histograms for all the scenarios are depicted in Figures 3(c)−10(c). These figures present visual representations that offer valuable insights into the convergence and accuracy of the suggested model. Additionally, these visuals provide a thorough examination of the model's precision, demonstrating how closely it lines up with expected conclusions. These diagrams provide a thorough understanding of the convergence behavior and accuracy displayed by fluid model during its assessment and simulation process. The function fitness for error analysis regarding the structure solution is covered in Figures 3(d)−10(d). These visuals suggest a thorough perception for the performance and maximization of the EA structure by illustrating the progression of the function's fitness during various phases. By depicting the progression of function fitness across stages of LMS-NNA design, the visuals help assess the effectiveness of the method in refining accuracy, minimizing errors, and maximizing performance. This comprehensive analysis enables a deeper understanding of how the structure evolves and adapts to achieve the best possible outcome. Figures 3(e)−10(e) illustrate the regression performance of the suggested model across cases (1−8). A consistent pattern emerges across all figures, with correlation values ('R') closely clustering near one for the training, testing, and validation phases. This near-unity alignment is a key finding, highlighting the exceptional accuracy of the LMS-NNA design in the suggested model.

4.2.   Analysis of velocity panels $\left\{ {f'\left( \eta \right)\, \, \& \, g'\left( \eta \right)} \right\}$

The effects of numerous factors on $\left\{ {f'\left( \eta \right)\, \, \& \, g'\left( \eta \right)} \right\}$ are portrayed in Figures 11−15. The effects of the stretching ratio factor $\left( \alpha \right)$ on $\left\{ {f'\left( \eta \right)} \right\}$ are portrayed in Figure 11(a) with a deteriorating behavior in $\left\{ {f'\left( \eta \right)} \right\}$ for growth in $\left( \alpha \right)$. As the stretching ratio factor $\left( \alpha \right)$ increases, the sheet elongates more rapidly in two directions (along x and y-axes). This causes the fluid near the surface to experience a stronger pull, causing a stretching-dominated flow. Consequently, the fluid's momentum near the surface becomes more aligned with the elongation direction, reducing the primary velocity $\left\{ {f'\left( \eta \right)} \right\}$. This happens because the stretching forces dominate the flow, slowing down the movement of fluid away from the surface (i.e., the primary flow). The effect reflects the competition between the stretching forces and the fluid's inherent tendency to flow in other directions. Figure 11(b) depicts the absolute error in $\left\{ {f'\left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( \alpha \right)$. These errors range from 10^-4 to 10^-7, as illustrated in Figure 11(b). This analysis emphasizes the computational discrepancies between the assessed and analytical results, providing valuable insights into the accuracy of the current model for the given problem.

The influences of magnetic factor $\left( M \right)$ on $\left\{ {f'\left( \eta \right)} \right\}$ are portrayed in Figure 12(a), with a declining behavior in $\left\{ {f'\left( \eta \right)} \right\}$ for growth in $\left( M \right)$. As $\left( M \right)$ increases in the fluid flow on a bidirectional elongating sheet, then $\left\{ {f'\left( \eta \right)} \right\}$ is reduced due to the magnetic field's opposing effect on the fluid motion. This phenomenon, known as the magnetohydrodynamic effect, generates a Lorentz force that acts against flow direction. Consequently, the fluid practices greater resistance to motion, particularly near the surface of the sheet. This increased resistance slows down the flow, causing a lessening in $\left\{ {f'\left( \eta \right)} \right\}$, which represents the flow along the main direction of movement. The magnetic field effectively dampens the fluid's momentum, decreasing the velocity profile. Figure 12(b) illustrates the absolute error in $\left\{ {f'\left( \eta \right)} \right\}$ for the given problem, specifically in relation to different values of the magnetic factor. This visual representation helps analyze how changes in the magnetic factor influence deviations in velocity, providing insights into the accuracy of the numerical or computational model used. By showcasing the absolute error, the figure highlights areas where discrepancies occur, enabling a better understanding of error distribution and potential improvements in the modeling process. The analysis, presented in this figure, is crucial for evaluating the impact of magnetic variations on fluid dynamics or structural behavior, ensuring that the proposed solution maintains precision across conditions. These errors range from 10^-4 to 10^-7, as illustrated in Figure 12(b).

The impacts of Casson factor $\left( \beta \right)$ on both velocities $\left\{ {f'\left( \eta \right)\, \, \& \, \, g'\left( \eta \right)\, } \right\}$ are portrayed in Figures 13(a) and 14(a) with a deteriorating behavior in $\left\{ {f'\left( \eta \right)\, \, \& \, \, g'\left( \eta \right)\, } \right\}$ for growth in $\left( \beta \right)$. As $\left( \beta \right)$ increases in the fluid flow on a bidirectional elongating sheet, the velocities $\left\{ {f'\left( \eta \right)\, \, \& \, \, g'\left( \eta \right)\, } \right\}$ decrease due to the fluid's non-Newtonian behavior. The Casson model describes fluids that exhibit yield stress, meaning the fluid resists motion until a certain stress threshold is exceeded. As $\left( \beta \right)$ grows, this threshold increases, making it harder for the fluid to start flowing. Consequently, the fluid experiences greater resistance, particularly near the sheet's surface in both the directions, resulting in a slower movement overall. This increased resistance reduces $\left\{ {f'\left( \eta \right)\, \, \& \, \, g'\left( \eta \right)\, } \right\}$, as the fluid's ability to flow is increasingly hindered by the higher Casson factor $\left( \beta \right)$, reflecting the thickening effect of the fluid under stress as portrayed in Figures 13(a) and 14(a). Figures 13(b) and 14(b) depict the absolute error in $\left\{ {f'\left( \eta \right)\, \, \& \, \, g'\left( \eta \right)\, } \right\}$ for the current problem regarding variations in $\left( \beta \right)$. These errors range from 10^-4 to 10^-7 in the case of $\left\{ {f'\left( \eta \right)} \right\}$, as illustrated in Figure 13(b), while in the case of $\, \left\{ {g'\left( \eta \right)} \right\}$, these errors expand on 10^-4 to 10^-8, as depicted in Figure 14(b).

The impacts of $\left( {Da} \right)$ on $\left\{ {f'\left( \eta \right)} \right\}$ are portrayed in Figure 15(a), with an augmenting behavior in $\left\{ {f'\left( \eta \right)} \right\}$ for growth in $\left( {Da} \right)$. The increase in $\left( {Da} \right)$ inside the fluid flow system means that the material through which the fluid flows become more permeable, enabling easier passage of fluid through its pores. On a bidirectional elongating sheet, this translates into a rise in primary velocity profiles $\left\{ {f'\left( \eta \right)} \right\}$ because the fluid encounters less confrontation when passing the porous medium. Consequently, the fluid moves faster both along and perpendicular to the sheet's stretching directions. This augmentation in velocity is also influenced by factors like the nature of the fluid, the sheet's elongation rates, and external forces; however, it primarily indicates reduced resistance in fluid flow due to higher porosity. Figure 15(b) illustrates the absolute error in $\left\{ {f'\left( \eta \right)} \right\}$ for the current problem, specifically considering the variations in $\left( {Da} \right)$. The graph provides a detailed comparison of the computational results by highlighting the deviation between benchmark solutions. As the porous factor changes, the figure captures how the error fluctuates across the domain, offering insights into the accuracy and reliability of the applied numerical method. The observed trends in the error distribution can be used to assess the sensitivity of the velocity profile to variations in the porous factor, which is crucial for optimizing computational models in porous media flow analysis. These errors range from 10^-4 to 10^-8 in the case of $\left\{ {f'\left( \eta \right)} \right\}$, as illustrated in Figure 15(b).

4.3.   Analysis of temperature distributions $\left\{ {\theta \left( \eta \right)} \right\}$

The effects of numerous factors on temperature distribution $\left\{ {\theta \left( \eta \right)} \right\}$ are portrayed in Figures 16−19. Figure 16(a) inspects the behavior of $\left\{ {\theta \left( \eta \right)} \right\}$ with deviations in $\left( {Rd} \right)$. Here, with the expansion in $\left( {Rd} \right)$, there is an upsurge in $\left\{ {\theta \left( \eta \right)} \right\}$. As $\left( {Rd} \right)$ upsurges on a bidirectional elongating sheet, the system absorbs more thermal energy from radiative heat transfer. This causes an upsurge in $\left\{ {\theta \left( \eta \right)} \right\}$, meaning the fluid's temperature rises more rapidly. Radiation supports heat transfer by emitting energy from the surface of the elongating sheet into the surrounding fluid, increasing the fluid's thermal energy. This effect is more significant as $\left( {Rd} \right)$ grows, enhancing the overall heat transfer rate and leading to higher temperatures within the fluid, especially near the sheet's surface, as shown in Figure 16(a). In cancer treatment, this principle is related to hyperthermia therapy, where targeted radiation is used to elevate temperatures in tumor tissues. By controlling radiation, the localized heating damage the cancer cells without harming the surrounding healthy tissues, making this a key technique in treatments like radiotherapy and thermal ablation. Figure 16(b) illustrates the absolute error in the temperature distribution $\left\{ {\theta \left( \eta \right)} \right\}$ for the current problem, considering variations in the radiation factor $\left( {Rd} \right)$. The error represents the difference between the computed and reference temperature values, indicating the accuracy of the numerical model. The error distribution provides insight into the model's sensitivity to radiative effects and helps in assessing the reliability of the thermal predictions. These errors range from 10^-4 to 10^-7 in the case of $\left\{ {\theta \left( \eta \right)} \right\}$, as illustrated in Figure 16(b).

Figure 17(a) illustrates the performance of $\left\{ {\theta \left( \eta \right)} \right\}$ for deviations in Brownian factor $\left( {Nb} \right)$. With expansion in $\left( {Nb} \right)$, there is an upsurge in $\left\{ {\theta \left( \eta \right)} \right\}$. Brownian motion is the erratic movement of tiny particles due to collisions with surrounding molecules, which leads to enhanced thermal interactions. This increased particle motion generates additional heat, causing a rise in the fluid's temperature. Consequently, the temperature profiles $\left\{ {\theta \left( \eta \right)} \right\}$ in the system are augmented as $\left( {Nb} \right)$ grows. This effect plays a significant role in nanofluid heat transfer, where the thermal energy distribution is influenced by the movement of nanoparticles within the fluid, causing enhanced heat transfer rates. In cancer treatment, this principle is applied in nanoparticle-based hyperthermia therapy. By injecting nanoparticles into tumor sites and using external energy sources, the nanoparticles exhibit Brownian motion, elevating local temperatures. This targeted heating destroys cancer cells by raising their temperature while minimizing damage to surrounding healthy tissue. Figure 17(b) portrays the absolute error in $\left\{ {\theta \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {Nb} \right)$. The error represents the difference between the computed and reference temperature values, indicating the accuracy of the numerical model. These errors range from 10^-3 to 10^-7 in the case of $\left\{ {\theta \left( \eta \right)} \right\}$, as illustrated in Figure 17(b).

Figure 18(a) inspects the performance of $\left\{ {\theta \left( \eta \right)} \right\}$ for deviations in thermophoresis factor $\left( {Nt} \right)$. With surge in $\left( {Nt} \right)$, there is an upsurge in $\left\{ {\theta \left( \eta \right)} \right\}$. When the factor $\left( {Nt} \right)$ increases, more particles move from hotter to cooler regions. The increase in $\left( {Nt} \right)$ leads to a rise in $\left\{ {\theta \left( \eta \right)} \right\}$ for fluid flow on the bidirectional elongating sheet because thermophoresis designates the movement of particles from a hot to a cooler region in the presence of a temperature gradient. As $\left( {Nt} \right)$ grows, more particles are moved from the hotter region towards cooler areas, reducing heat transfer from the surface of the sheet. This causes a higher accumulation of thermal energy near the sheet, effectively increasing the temperature of the fluid in proximity to it. Therefore, the thermal distribution $\left\{ {\theta \left( \eta \right)} \right\}$ rises due to the diminished cooling effect of particle migration. Figure 18(b) describes the absolute error in $\left\{ {\theta \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {Nt} \right)$. The error represents the difference between the computed and reference temperature values, indicating the accuracy of the numerical model. These errors range from 10^-2 to 10^-7 in the case of $\left\{ {\theta \left( \eta \right)} \right\}$, as illustrated in Figure 18(b).

Figure 19(a) inspects the performance of $\left\{ {\theta \left( \eta \right)} \right\}$ for deviations in the thermal Biot number $\left( {B{i_T}} \right)$. In this graph, it is seen that with an upsurge in $\left( {B{i_T}} \right)$, there is an upsurge in $\left\{ {\theta \left( \eta \right)} \right\}$. A higher $\left( {B{i_T}} \right)$ means a more efficient thermal exchange among the sheet's surface and the nearby fluid, resulting in greater heat retention and higher temperature near the surface. In cancer treatment, this principle is applicable in hyperthermia therapy, where elevated temperatures are used to damage the cancer cells. By manipulating factors like the Biot number, medical devices optimize heat distribution to target tumors effectively while minimizing damage to healthy tissues, enhancing the efficacy of treatments like radiofrequency or microwave-induced hyperthermia. Figure 19(b) portrays the absolute error in $\left\{ {\theta \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {B{i_T}} \right)$. The error represents the difference between the computed and reference temperature values, indicating the accuracy of the numerical model. These errors range from 10^-5 to 10^-7 in the case of $\left\{ {\theta \left( \eta \right)} \right\}$, as illustrated in Figure 19(b).

4.4.   Analysis of concentration distributions $\left\{ {\phi \left( \eta \right)} \right\}$

The effects of various factors on $\left\{ {\phi \left( \eta \right)} \right\}$ is portrayed in Figures 20−24. Figure 20(a) shows the behavior of $\left\{ {\phi \left( \eta \right)} \right\}$ for the reaction of deviations in Brownian number $\left( {Nb} \right)$. For a surge in $\left( {Nb} \right)$, there is a decline in $\left\{ {\theta \left( \eta \right)} \right\}$. As $\left( {Nb} \right)$ increases, the intensity of this random motion also grows, causing more frequent and widespread dispersal of particles throughout the fluid. This enhanced particle movement increases the overall concentration of particles in the fluid, resulting in an augmentation in $\left\{ {\phi \left( \eta \right)} \right\}$. Essentially, stronger Brownian motion promotes greater mixing and dispersion of particles, causing more uniform and heightened particle distribution within the fluid flow. Figure 20(b) describes the absolute error in $\left\{ {\phi \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {Nb} \right)$. The error represents the difference between the computed and reference temperature values, indicating the accuracy of the numerical model. These errors range from 10^-3 to 10^-7 in the case of $\left\{ {\phi \left( \eta \right)} \right\}$, as illustrated in Figure 20(b).

Figure 21(a) shows the performance of $\left\{ {\phi \left( \eta \right)} \right\}$ for the reaction of deviations in thermophoresis factor $\left( {Nt} \right)$. This graph shows that with the expansion in $\left( {Nt} \right)$, there is an augmentation in $\left\{ {\phi \left( \eta \right)} \right\}$. As $\left( {Nt} \right)$ increases, particles are more strongly influenced by these temperature differences. This results in the accumulation of particles in cooler areas, leading to an augmentation in $\left\{ {\phi \left( \eta \right)} \right\}$. In simple terms, the higher the thermophoretic force, the more significant the particle movement toward the cooler zones, enhancing the concentration of particles in specific regions of the fluid. This affects the overall distribution of particles within the flow field, which has implications for processes like heat and mass transfer. Figure 21(b) depicts the absolute error in $\left\{ {\phi \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {Nt} \right)$. The absolute error quantifies the deviation between the computed and reference concentration values, highlighting the accuracy of the numerical model. The error distribution helps assess the model's sensitivity to thermophoresis and provides insight into how well the numerical predictions capture the underlying physical mechanisms. These errors range from 10^-3 to 10^-6 in the case of $\left\{ {\phi \left( \eta \right)} \right\}$, as illustrated in Figure 21(b).

Figure 22(a) illustrates the performance of $\left\{ {\phi \left( \eta \right)} \right\}$ for the reaction of deviations in the chemical reactivity factor $\left( {Kr} \right)$. With an upsurge in $\left( {Kr} \right)$, there is a decline in $\left\{ {\phi \left( \eta \right)} \right\}$. As this factor increases, the chemical reactions become more intense, leading to a faster consumption or transformation of the reacting species. This results in a reduction in particle concentration as more particles are being used up or altered by the reactions. Consequently, the concentration profiles $\left\{ {\phi \left( \eta \right)} \right\}$ of the species diminish because the particles are being removed from the fluid more rapidly through these reactions. This process decreases the overall particle density in the fluid, especially in regions where the reactivity is higher. Figure 22(b) depicts the absolute error in $\left\{ {\phi \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {Kr} \right)$. These errors range from 10^-3 to 10^-6 in the case of $\left\{ {\phi \left( \eta \right)} \right\}$, as illustrated in Figure 22(b).

Figure 23(a) shows the performance of $\left\{ {\phi \left( \eta \right)} \right\}$ for the reaction of deviations in Schmidt number $\left( {Sc} \right)$. With an upsurge in $\left( {Sc} \right)$, there is a decline in $\left\{ {\phi \left( \eta \right)} \right\}$. For flow over the bidirectional elongating sheet, a higher $\left( {Sc} \right)$ implies that the concentration field diffuses more slowly than the velocity field. As a result, the concentration boundary layer gets thinner, causing a decline in $\left\{ {\phi \left( \eta \right)} \right\}$. Physically, this means that as the Schmidt number grows, the diffusion of mass in the fluid becomes more restricted, confining it closer to the sheet, while the velocity field spreads out more easily. Figure 23(b) portrays the absolute error in $\left\{ {\phi \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( {Sc} \right)$. These errors range from 10^-3 to 10^-7 in the case of $\left\{ {\phi \left( \eta \right)} \right\}$, as illustrated in Figure 23(b).

Figure 24(a) shows the performance of $\left\{ {\phi \left( \eta \right)} \right\}$ for deviations in the activation energy factor $\left( E \right)$. This graph shows that with an expansion in $\left( E \right)$, there is an upsurge in $\left\{ {\phi \left( \eta \right)} \right\}$. When $\left( E \right)$ increases for fluid flow on a bidirectional elongating sheet, it implies that more energy is needed for mass transfer or chemical reactions. As a result, higher energy barriers slow reaction rates, leading to an accumulation of the reactant species in the fluid. This accumulation augments the concentration profiles $\left\{ {\phi \left( \eta \right)} \right\}$ because less of the species is consumed or diffused from the surface of the sheet. Physically, this means that as the activation energy factor $\left( E \right)$ grows, species tend to remain in higher concentrations within the boundary layer, as the energy required for their diffusion or reaction is higher, leading to thicker concentration boundary layers. Figure 24(b) illustrates the absolute error in $\left\{ {\phi \left( \eta \right)} \right\}$ for the current problem regarding variations in $\left( E \right)$. These errors range from 10^-3 to 10^-7 in the case of $\left\{ {\phi \left( \eta \right)} \right\}$, as illustrated in Figure 24(b).

4.5.   Discussion of the tables

Table 1 depicts the experimental values of gold nanoparticles and blood. Table 2 offers an in-depth presentation of the computational data generated by the ANN model across several scenarios. This table provides critical information on the MSE recorded during three distinct phases of model development: Training, validation, and testing. The MSE is a key metric that measures the average squared difference between the predicted and actual values and is instrumental in assessing the ANN's predictive accuracy. Lower MSE values generally indicate a model that makes accurate predictions and generalize well to unseen data. In addition to MSE, the table highlights several other crucial metrics that contribute to the overall evaluation of the ANN model. These include network performance, which reflects the model's ability to minimize error across iterations, as well as the gradient and 'mu' parameter. The gradient measures how steeply the error changes with respect to adjustments in the model's weights, offering insight into how effectively the model is learning at each epoch. Table 2 also concludes that the model's optimal performance is observed at epochs 111,225,194,270,179,220,339, and 221. The 'mu' parameter, part of the Levenberg-Marquardt optimization algorithm used in many ANN models, helps control the transition between gradient descent and a more refined optimization process, balancing learning speed and stability. To validate the current results, a comparative analysis is conducted in Table 3. In this table, the results for heat transfer rate are compared with the established works of Gorla & Sadawi ^[51] and Hamad ^[52]. It is revealed in this table that a closed agreement exists amongst all the results that validate the results.

5.   Conclusions

In this study, we explore nanofluid flow on a bi-directional elongated plate. The surface of the sheet is characterized with variable porosity with inclined magnetic field effects, which is the main novelty of this work. We focus on how nanoparticle radius and spacing affect the overall flow dynamics. Additionally, we incorporate the Cattaneo-Christov heat and mass flux model effects to discuss the mass and thermal diffusions using flow conditions. The major equations are translated in dimensionless form and solved with ANNs. After a detailed discussion of the work, hawse highlight that:

● Primary velocity weakens with a surge in the stretching ratio factor and magnetic factor and is augmented with growth in a variable porous factor, where the AE varies in the range ${10^{ - 3}}$ to ${10^{ - 7}}$.

● Both velocities $\left\{ {f'\left( \eta \right)\, \, \& \, g'\left( \eta \right)} \right\}$ slow with the growth in the Casson factor.

● Thermal panels amplify with the escalation in thermophoresis, magnetic, radiation, and Brownian motion factors with AEs varying in the range ${10^{ - 3}}$ to ${10^{ - 7}}$.

● Concentration panels escalate with the augmentation in the thermophoresis factor and activation energy factor while they weaken with a surge in the Schmidt number, chemical reactivity factor, and Brownian motion factor, where the AE varies in the range ${10^{ - 4}}$ to ${10^{ - 6}}$.

● We conclude that the model's optimal performance is observed at epochs 111,225,194,270,179,220,339, and 221.

● For all the scenarios, the gradient values are associated at $9.97 \times {10^{ - 8}}$, $9.91 \times {10^{ - 9}}$, $9.92 \times {10^{ - 8}}$, $9.91 \times {10^{ - 8}}$, $9.95 \times {10^{ - 8}}$, $9.91 \times {10^{ - 8}}$, $9.92 \times {10^{ - 8}}$, and $9.91 \times {10^{ - 8}}$.

Future Direction of the Study: In future research, the impacts of Jeffery fluid will be incorporated to extend the study of non-Newtonian fluid behavior in the flow system. Additionally, the influence of microorganisms will be analyzed to model bio-convective effects in the nanofluid system.

Author contributions

Arshad Khan and Humaira Yasmin have modelled the problem in mathematical form. Rawan Bossly and Fuad S. Alduais have solved the problem by ANN approach. Fuad S. Alduais, Humaira Yasmin and Afrah Al-Bossly have prepared all the graphs. Arshad Khan, Fuad S. Alduais and Afrah Al-Bossly have written the original manuscript. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University Saudi Arabia (Grant No. KFU251351). This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1446).

Conflict of interest

The authors have no conflict of interest.