Forecasting the public financial budget expenditure in Dongguan with an optimal weighted combination Markov model

1.   Introduction

Hyperspectral images (HSI) can be derived from ordinary RGB cameras ^{[1,2,3,4,5,6]}. However, existing methods require detailed optical properties of the underlying camera, which can only be measured in a laboratory with expensive equipment, preventing ordinary users from using a plug-and-play webcam immediately.

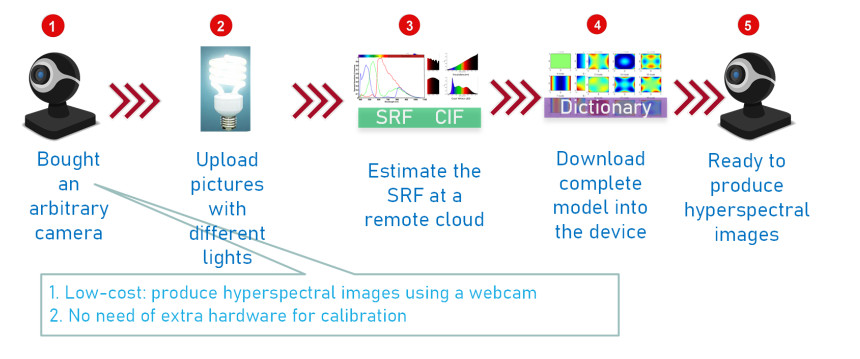
This study proposes a calibration-free and illumination-independent method, as shown in Figure 1, to facilitate ordinary users' instant use of an arbitrary camera. Our algorithm can transform an ordinary webcam into an expensive HSI camera without the help of additional hardware. Mathematically, the forward transformation, mapping from high-dimensional HSI images to low-dimensional RGB images, is relatively easy, compared to the reverse one, mapping from low- to high-dimensional.

Figure 1.  The setup and usage scenarios for any camera.

DownLoad: Full-Size Img PowerPoint

However, both the forward and reverse transformations involve a device-dependent response function for the underlying camera. In previous methods, the camera and light source must remain the same, and the spectral response function (SRF) of a camera and the current illuminating function (CIF) of the ambiance must be identified separately by specific equipment, such as standardized light sources, color-checkers, and spectrometers. The images used in the training database must match the same camera and light source. Such limitations prevent the algorithm from being plug-and-play.

Hyperspectral technology has been widely used in different fields ^[7]. Although HSI imaging possess tremendous advantages in wide fields of applications, the extremely high acquisition cost (USfanxiexian_myfh40 thousand or above) limits the suitable applications and usage scenarios. Existing computation methods converting RGB to HSI can significantly broaden the applicability of HSI.

In this study, a semi-finished model, independent of devices and illumination, is shipped with the installation package, as shown in the Model part of Figure 1. Before use, a setup step is performed without additional hardware to extract the SRF of the underlying camera, as shown in step 1 in Figure 1. During each usage, the ambient CIF must be estimated for each taken image, as shown in step 2 in Figure 1. The final reconstruction with SRF and CIF then projects RGB images to the device and illumination-independent HSI.

To accumulate sparse projection kernels of hyperspectral signatures in terms of many hyperspectral priors, we render the camera SRF through a most probable algorithm. As shown in Figure 2, at the setup step, two parametric tasks are accomplished automatically without the involvement of users. SRF and CIF are estimated by uploading random images taken by the target camera to the cloud. There is no need to involve a calibration step for ordinary users. We develop a triangular generative adversarial assimilation comprising two different methods in supervising and unsupervised learning, each with advantages, pulling each other up to make a high-precision reconstruction.

Figure 2.  During setup, two parametric tasks are accomplished automatically without the involvement of users. SRF and CIF are estimated by uploading random images taken by the target camera to the cloud.

DownLoad: Full-Size Img PowerPoint

2.   Relation to prior research

Despite the extensive studies in reconstructing HSI from RGB images, numerous challenges remain unsolved. This study seeks to close three research gaps. Existing studies require a laboratory-calibrated camera, and the training is only bound to that specific camera. Our results contribute to the online retrieval of SRF and the SRF independent training offline.

Much research has contributed to reverse mapping from the low-dimensional RGB space to the high-dimensional hyperspectral space ^[1,4,6,8,9]. However, gaps still exist.

The essence of the forward problem is a spatial convolution between incident image spectral and camera optics ^[10]. The properties of camera spectral response functions have been studied extensively ^[11]. The reverse mapping in algebraic or iterative approximation methods is sufficient as long as the camera response function can be correctly acquired before applying the algorithms ^[4,6]. The reverse mapping in kernel representation is prevalent and stable ^[1,8,9]. Statistical inference methods have been reported effective in enhancing the accuracy of the reverse mapping ^[2,3].

With the assistance of additional hardware, the recovered image can be more accurate ^[5,12,13,14]. However, such assistance does not fit the goal of this study. Therefore, the last piece of the puzzle for the HSI reconstruction is still acquiring camera response functions without the help of expensive instruments.

The second research gap leads to a challenge in algorithm design. Because the central part of the forward problem involves the convolution in the camera SRF, the training algorithm may only retrieve the function mapping if the SRF is determined at the training phase. On the other hand, estimating the SRF is difficult if we do not have the pairs of images with input RGB and output HSI ^[15]. Our problem is to retrieve the HSI without training pairs and a system model. The original generative adversarial network (GAN) requires a pair of images $(x, y)$ for discriminator $D$ and generator $G$ to evaluate $\min_G \max_D V(D, G) = \mbox{E}_{{{\bf x}}\approx p_{data}({{\bf x}})} \left[\log D(x|y) \right] + \mbox{E}_{{{\bf z}}\approx p_{z}({{\bf z}})} \left[\log 1-D(G(z|y)) \right]$. Thanks to modern progress of the maximum likelihood theorems and the sparse variation of the GAN, "double unknown retrieval" of those above has become possible ^[16,17,18]. One of the advantages of cycleGAN over standard GANs is that the training data need not be paired. This implies that, in our situation, only the images (RGB, HSI) are sufficient for estimating the output SRFs. The idea of conditional and cyclic adversarial networks with image-to-image translation has successfully solved the problem of double unknown retrieval ^[19].

When the training data are not completely paired, the latent space reconstruction becomes the key part of the double unknown retrieval ^[20,21,22]. Convolution particle filters have been proven effective in estimating unknown parameters in state-space ^[23].

The generative network synthesizes the SRFs based on a predictive distribution conditioned on the correctness of the recovery of the original RGB values ^[19,24]. When the projection to the latent space is not linear, some studies apply advanced algorithms to address the nonlinearity issue ^[25].

The third gap in the challenges of HSI reconstruction is the interference of versatile illumination conditions. Many studies tried to decouple the influence of illuminations. Despite the simplicity, an accurate spectral reflectance reconstruction must come with a spectral estimation of illumination ^[13]. Some solve the issue at the tristimulus value space (RGB or CIE XYZ) by collecting images of multi-conditional illumination ^[26,27,28]. On the other hand, CIE XYZ starts from the spectral response of illumination; and, nevertheless, they primarily focus on the color appearance for our bare eyes, not the spectral reflectance of objects. Therefore, a research gap exists in decoupling the influence of unknown illumination for spectral response estimation algorithms.

The sparse assimilation algorithm can reconstruct the parameters from limited observations ^[29]. However, most iterative algorithms are computationally intensive. Thus, they are not suitable for applying online and a tractable algorithm is needed for computational feasibility. We use hierarchical Bayesian learning and Metropolis-Hastings algorithms in the algorithm ^[30,31] to estimate joint probability densities. Therefore, this study exploits an assimilation method adapted to online computation.

3.   Methods

3.1.   Problem description

As shown in Figure 3, a camera with response function SRF $R_\phi(\lambda, i)$ takes a spectral reflectance input $h(j, \lambda)$ for wavelength $\lambda\in[1, N]$ and produces the tristimulus values $c(j, i)$ for $i\in[RGB]or [1,3]$, and the $j\in[1, n]$ is the $j$-th dataset pair in the database. The 24-patches' color-checker pixels have been arranged into a column vector for ease of dimension expression.

Figure 3.  The forward projection, dichromatic reflection model (DRM), from object reflectance to the RGB values.

DownLoad: Full-Size Img PowerPoint

The forward problem is stated as a dichromatic reflection model (DRM)

or,

where the matrix form is a collection of the indexes such that ${{\bf C}}_{n\times 3} = \{c(j, i)\}_{j\in[1, n], i\in [1,3]}$.

By the representation theorem, we can find coefficients $\tilde{w}(k, k')_{k, k'\in[1, m]} = \tilde{{{\bf W}}}$ for taking $m$ basis such that the RGB images ${{\bf C}}$ can be approximated by

The DRM (3.2) becomes

Therefore,

As discussed in the previous section, many methods exist to estimate the ill-posed back projection, but challenges still exist. Our problem is an inverse one. Given the tristimulus values ${{\bf C}}$, we want to reconstruct the ${{\bf H}}$. Because the dimension of ${{\bf H}}$ is much higher than that of ${{\bf C}}$, the inverse project is ill-posed. Our method requires no pre-built calibration and prevents over-fitting after training.

3.2.   Retrieving CIF from the white block

The CIF is estimated from the images of the white block of the color checker. The illumination light $e$ is converted to electric signals through the camera response $e_\phi$, and, therefore, $e(\lambda) = \sum_i e_\phi(\lambda, i)$. Utilizing the above-mentioned method, the CIF can be decomposed by a set of kernel functions. We have

where $b_k(\lambda)$ is the $k$-th basis for the CIF, and $\gamma_{i, k}$ is the coefficient.

3.3.   Retrieving SRF by cycleGAN

Classical generative adversarial network applications use neural networks entirely for classification and regression applications. Such modeling suffers from the convergence problem. In our method, we use optical models as generators and neural networks as discriminators to maximize the knowledge of prior model information for the stochastic process of Lambert reflectance (Eq 3.2), which is implemented through a Monte Carlo radiative simulation. Through collected priors, the discriminator can distinguish between successful or unsuccessful generations. Therefore, the cyclic iteration can converge fast and accurately estimate the latent sparse space with sparse converging metrics.

We hybridize a statistical generator and neural network discriminator to maximize the usage of prior model information for the stochastic process. Our generator can also take environment conditions as covariates in the random process and is robust to anti-symmetric station distribution.

A standard GAN comprises a generator $G$ and a discriminator $D$ ^[32]. The model $G$ and $D$ can be neural networks or any mathematical functions, as long as the optimization (3.7) with Lagrangian $\eta$ has solutions.

The standard loss functions have the form

The GAN used in this study is a type of cycleGAN, which contains 2 generators and 2 discriminators, as shown in Figure 4. Our cycleGAN takes two sets of images as input and obtains the output containing the corresponding SRF. The observation $Z$ contains the pair $C_3 = (R, G, B)$ and $H_{33}$ 33-band HSI images. The subscripts $3$ and $33$ represent the number of bands for the variables, and they can be ignored if the meaning is clear. The latent estimation represents the SRF $Z' = (R'_{33}, H'_{33}, C'_3)$. In the target domain, the $Z'$ is compared to a small set of collected SRFs $Z1 = R1_{33}$, which are only served as shape templates. The re-estimated image pairs are $Z'' = (C''_3, H''_{33})$, where $C''_3 = H'_{33}R'_{33}$, $H'_{33}$ is the coefficients of $G_{ZZ'}$, and $H''_{33}$ is the direct output of $G_{Z'Z}$.

Figure 4.  The generator and discriminator design in the cycleGAN. Systemically, we want to derive SRFs from the image pairs. Therefore, the observation $Z$ contains the pair $C_3 = (R, G, B)$ and $H_{33}$ 33-band HSI image. The latent estimation represents the SRF $Z' = (R'_{33}, H'_{33}, C'_3)$. In the target domain, the $Z'$ are compared to a small set of collected SRFs $Z1 = (R1_{33}, H_{33}, C_3)$, where the $R1_{33}$ are only served as shape templates. The re-estimated image pairs are $Z'' = (C''_3, H''_{33})$, where $C''_3 = H'_{33}R'_{33}$, $H'_{33}$ is the output of $G_{ZZ'}$, and $H''_{33}$ is the output of $G_{Z'Z}$. The models in the cycleGAN are $G_{ZZ'}$, $D_{Z'Z1}$, $G_{Z'Z}$ and $D_{ZZ''}$, respectively. When the cycleGAN converges, the error between $Z$ and $Z''$ will be minimized.

DownLoad: Full-Size Img PowerPoint

The models in the cycleGAN are $G_{ZZ'}$, $D_{Z'Z1}$, $G_{Z'Z}$, and $D_{ZZ''}$, respectively. The cycleGAN model takes $C_3$ and $H_{33}$ as input dataset. We first prepare a set of (RGB, HSI) pairs for different color patches and a known camera (e.g., CIE 1964). Because we expected the same color patch to produce the same HSI image through different cameras, we prepared additional image pairs by taking the image of the target unknown camera as RGB and the HSI of the known camera as the HSI. We also need small samples of normal SRFs $Z1 = R1_{33}$ as a target template to prevent multiple solutions that are dissimilar to normal SRFs.

The generator $G_{ZZ'}$ is a reverse model, which takes $Z = (H, C)$ in the source domain and outputs $Z' = (R', H', C')$ in the target domain. During the generation, $G_{ZZ'}$ synthesizes SRFs $Z' = R'$, which is equivalent to applying a perturbation $\Delta$ such that $R' = R\Delta$ without violating the modality (Eq 3.10) and positiveness (Eq 3.11) constraints.

where $i = \{1, 2, 3\}$ is the RGB channel, $m_i$ is a predefined mode number (peak location) for channel $i$, and $\lambda_k$ is the wavelength at each band. To integrate the constraints (3.10) to the loss function of the first discriminator $D(Z', Z1)$, the constraints can be written in a form of violation score.

where $\mbox{sgn}(s) = \{1, -1\}$ if $s > 0$ and $s\le 0$, respectively.

The synthesized SRFs $Z'$ will be rejected by $D_{Z' Z1}$ if they are dissimilar to normal SRFs $Z1 = R1_{33}$. The discriminator $D_{Z'Z1}$ is directly formed by a residual neural network (ResNet34). The network adds some jump connections that skip internal layers to avoid the vanishing gradient problem and the accuracy saturation problem. The construction of ResNet repeats a fixed pattern several times in which the strided convolution downsampler jumps, bypassing every 2 convolutions.

The $G_{Z'Z}$ is the forward model, which generates the re-estimated image pairs $Z'' = (C''_3, H''_{33})$. The $C''_3$ is directly applied to the estimated SRF $R'$ from the high-dimensional $H'_{33}$. The re-estimated RGB images are computed as $C''_3 = H'_{33}R'_{33}$, where $H'_{33}$ is the one of the output of $G_{ZZ'}$. The re-estimated HIS images $H''_{33}$ are the output of $G_{Z'Z}$ taking input from $C'_3$, another output of $G_{ZZ'}$.

Finally, a ResNet34 $D_{ZZ''}$, which takes the original images $Z$ and the re-estimated images $Z''$, rejects those having large errors. The discriminator $D_{Z'Z1}$ uses probability-based loss function, and $D_{ZZ''}$ uses a simple loss function in the mean squared error (mse) between the expected and predicted outputs.

The loss functions for the two discriminators are expressed in scores

where $p_d$ is the probability output of the discriminator $(Z^\prime, Z1)$, and $\eta_1$ and $\eta_2$ are the scaling factors controlling the involvement of the similarity and constraints, respectively. When the cycleGAN converges, the error scores (3.13) and (3.14) between $Z'$ and $Z1$, $Z$ and $Z''$, respectively, will be minimized (The convergence trend of the scores can be referred in Figure 9).

3.4.   Reconstructing HSI by back projection

To increase the accuracy of back projection, we use a kernel method to decompose the HSI and tristimulus RGB images. The estimated projection over the kernels can further minimize the reconstruction errors ^[33]. We decompose the HSI in the DRM (3.2) into a set of kernels $\psi(\lambda, \lambda')_{\lambda = 1, \cdots, N, \lambda' = 1, \cdots, N}$,

At the training stage, images are indexed by $j\in[1, m]$. We aim to find a set of kernels $\tilde{{{\bf H}}}(j) = \{ \tilde{h}(x, j, \lambda) \}_{x\in[1, n], \lambda\in[1, N]}$ that can span the tristimulus space.

$\tilde{{{\bf H}}}$ can be estimated by Yule-Walker equation ^[34] or a Nadaraya-Watson kernel estimator ^[35]. The kernels ${{{\bf \Psi}}}$ are chosen in the reproducing kernel Hilbert space, guaranteeing that the basis vectors exist ^[33].

By the representation theorem, the tristimulus values can be approximated by the transformed kernels $\sum_\lambda \tilde{h}(x, j, \lambda)R(\lambda, i)$ and the coefficients $\tilde{w}(x, x')_{x, x'\in[1, nm]} = \tilde{{{\bf W}}}$ such that

We decompose an RGB image by approximating

Together with the DRM (3.2), this implies that

Because the back projection $\tilde{{{\bf W}}}$ may not align with the direction of the covariance of ${{{\bf \Psi}}}(j){{\bf R}}$, we need to make additional assumptions in ${l}_1$ space. Assuming the tristimulus space is far smaller than one of the HSI space, the sparse partial least square regression partitions the space into two disjoint subspaces such that ${{{\bf H}}} = ({{{\bf H}}}_1, {{{\bf H}}}_2)$ spanned by relevant (${{{\bf H}}}_1$) and irrelevant variables (${{{\bf H}}}_2$) ^[36,37]. Such partition effectively isolates uncorrelated basis in the latent space.

We aim to find a set of coefficients that maximize the span of hyperspectral space and also try to avoid over-fitting. The goal is that

The challenge of the ill-posed problem is to invert a near-singular problem. The regularization methods in (3.19) with a positive perturbation in ${l}_1$ can suppress over-fitting effectively.

To avoid over-fitting, we further generalize the problem with an elastic net (3.19) in the Least Absolute Shrinkage and Selection Operator (Lasso) term ^[38] with Lasso penalty $\alpha$ with ${l}_1$ and ${l}_2$ norms, $||\cdot||_1$, $||\cdot||_2$.

Optimization (3.19) pushes the coefficients to zero if the covariates are insignificant due to the ${l}_1$ properties. The reconstruction efficiency increases when transformation manifests the sparsity properties ^[39]. The optimization (3.19) is regulated by the Lasso penalty ($\alpha = 1$) or the ridge penalty ($\alpha = 0$), and it takes advantage of the sparse ${l}_1$ norm in evaluating solutions for the ill-posed problem ^[40].

If $\alpha = 0$, the optimization in (3.19) reduces to an ordinary generalized matrix inverse, which serves as a comparison basis. The least-square estimation in the objective creates a significant variance when covariates exhibit multicollinearity.

Ridge regression performs optimization to compensate for the multicollinearity problem by finding a balance between variance and bias ^[41]. The ridge penalty effectively reduces the variance of the identified coefficients ^[42,43]. The experiments demonstrate that the lasso and ridge estimation effectively reconstruct the HSI without over-fit.

Due to the properties of the ${l}_1$ space, an optimization (e.g., $\min_{x} ||x||_1, \; \mbox{s.t.}\; (3.19)$) should possess minimal non-zero solutions, and yield strong reconstruction performance if several sparsity properties, such as restricted isometry and incoherence properties, are satisfied ^[39,40,44]. In our multivariate transformation matrix $\Psi_i$, the lasso penalty tends to reduce the coefficients of less important covariates to zero, thus generating more zero solutions and fitting our assumption about the hyperspectral space.

The ill-posed back projection from ${{\bf C}}$ to ${{\bf H}}$ still contains errors. We propose a machine learning model to further close the gap. In the training step, we aim to solve a model $g$ such that the error

is minimized. This study employs an ensemble of regression learners, including random forest regression, and supports vector regression.

At the query stage, we are ready to retrieve the HSI from the decomposition matrix $\tilde{{{\bf W}}}$ of the RGB images ${{\bf C}}_q$.

4.   Analysis

Our method is robust to a wide range of SRFs. An experiment is designed to prove our algorithm. The reconstructed HSIs by our method are almost identical between the measured SRF and the estimated SRF. Despite the quality of the SRF, the reconstructed HSIs are always of high quality.

4.1.   Retrieving algorithm in standard conditions

We first apply our algorithm in the standard CIE 1964 camera spectral response function (Figure 5 (a)). Our algorithm uses 33 bands from 400 nm to 720 nm. Based on the normal visible spectrum range, the 3-color images have been transformed into 33-color images. The reconstructed hyperspectral images match the original ground truth HSI closely (Figure 5 (b)).

Figure 5.  (a) The standard CIE 1964 camera spectral response function. (b) A sample of reconstructed HSIs in 460,550 and 620 nm bands using the standard CIE 1964 SRF. The entire HSI contains 33 bands from 400 nm to 720 nm. The errors between the original and the reconstructed images are insignificant according to the visual representation. Few pixels have errors approximating to 0.05. Please refer to Table 1 for the summarized root mean square errors. (image source: ^[45]).

DownLoad: Full-Size Img PowerPoint

4.2.   With known SRF and CIF (requiring a spectrometer)

To evaluate the effectiveness of our method, we designed the experiments to compare the results of standard laboratory camera calibration and ambient light conditions. We bought a low-cost camera (under USfanxiexian_myfh30) from the Internet and set-up for laboratory calibration. The environment should mimic the one that consumer users have. A Macbeth color-checker with 24 patches, in Figure 6 (c), was used. The spectral response $(\lambda)$ of light from these patches was measured by a spectrometer (PhotoResearchTM PR-670). The first two subgraphs (a) and (b) in Figure 6 show the light source and reflectance spectrum of patches and the blue patch of the color checker. As shown in the subgraph (d) in Figure 6, we fit the coefficients of the standard basis to estimate the actual SRF. With the measured SRF, we reconstruct a high-fidelity HSI in Figure 7. The error maps show small errors between the ground truth and reconstructed images. The quantitative errors are articulated in Table 1.

Figure 6.  (a) The spectral response of the light source illuminates the experiment. (b) The color checker. (c) The spectral response of the blue patch at the (1, 2) position of the color checker. (d) The fitted coefficients of the measured response.

DownLoad: Full-Size Img PowerPoint

Figure 7.  A sample of reconstructed HSI in 460,550 and 620 nm bands using the measured SRF. The entire HSI contains 33 bands from 400 nm to 720 nm. The errors between the original and the reconstructed images are insignificant based on the visual representation. Few pixels have errors approximating to 0.05. Please refer to Table 1 for the summarized root mean square errors.

DownLoad: Full-Size Img PowerPoint

Table 1.  Average prediction accuracy between the original and reconstructed HSI.

method	SRF	rmse	rrmse
ours	CIE	0.029766	0.069987
	Measured	0.037874	0.098941
	Generated	0.038611	0.12115
[1]	CIE	0.052838	0.1111
	Measured	0.04472	0.15981
	Generated	0.08846	0.16791
rmse=root mean squared error; rrmse=relative root mean squared error.

---

 | Show Table

DownLoad: CSV

4.3.   With unknown SRF and CIF

To achieve the goal of being calibration-free, autonomous generating of SRF should be implemented. Without any help of additional hardware, we iteratively generated an SRF by the cycleGAN (Figure 8). Through samples in the iteration in Figure 9, the cycleGAN converges promptly. Despite the slight non-smoothness in the spectral response in R-G-B bands, the reconstruction accuracy is still high. The error maps in Figure 10 still exhibit tiny errors.

Figure 8.  The generated SRF by our algorithm.

DownLoad: Full-Size Img PowerPoint

Figure 9.  (a) A sample of large error from the early iteration. (b) A sample of small error from the final iteration. (c) Score changes of (3.13) and (3.14) in the process of converging.

DownLoad: Full-Size Img PowerPoint

Figure 10.  A sample of reconstructed HSI in 460,550 and 620 nm bands using the generated SRF in Figure 8. The entire HSI contains 33 bands from 400 nm to 720 nm. The errors between the original and the reconstructed images are insignificant based on the visual representation. Not many pixels have errors approximating to 0.05. Please refer to Table 1 for the summarized root mean square errors.

DownLoad: Full-Size Img PowerPoint

As shown in Table 1, the generated SRFs by cycleGAN are accurate. The rmse (root mean squared error) and rrmse (relative root mean squared error) were 0.038 and 0.12, respectively. The convergence is relatively straightforward because the dimension in the latent space is the same as the HSI bands. The estimated SRFs are effective according to the low rmse, both by our kernel projection method or the dictionary learning method in ^[1].

To further visualize the performance of our reconstruction and generation algorithms, we show the original and the synthesized picture from the recovered HSI side-by-side in Figure 11. It is evident that the two pictures are almost identical, which implies that the reconstructed HSI is sufficiently accurate.

Figure 11.  Using the generated SRF in Figure 8, the HSI was reconstructed in Figure 10. For better illustration, the RGB images were compared side-by-side between the original picture (left) and the synthesized picture from the recovered HSI (right). The detailed error maps in HSI were shown in Figure 10.

DownLoad: Full-Size Img PowerPoint

4.4.   Discussion

The proposed method is superior to existing methods because it does not require laboratory measurement of SRF for a new camera. The experiments demonstrate that our automatic estimated SRFs are almost identical to the laboratory measurement.

Our generated SRFs are accurate and effective. The reconstructed HSIs with generated SRFs have low rmse, both by our kernel projection method and the existing method. We compared our result to an existing method ^[1] (Figure 12 and the second row of Table 1).

Figure 12.  The error maps by other projection method ^[1]. (a) The HSI by other methods with CIE SRF. (b) The HSI by other methods with measured SRF. (c) The HSI by other methods with our generated SRF.

DownLoad: Full-Size Img PowerPoint

Our learning process, however, has errors. The reconstructed HSIs from a 30-dollar webcam will not be as accurate as a 40-thousand-dollar camera. In Figure 10, the comparison of RGB shows a large 3% mse error. The maximal errors happened when the images appeared to be reflected by highlights. The highlighted parts are sensitive to unknown artifacts and cause the model confusion in the reconstruction process.

Fortunately, the target application scenarios mainly need cheap solutions and do not care much about accuracy. Moreover, noises, such as modeling errors and light source disturbance, influence the accuracy of SRF identification and HSI reconstruction.

5.   Conclusions

This research contributes to deep reverse analytics by integrating an automatic calibration procedure. This paper offers two contributions targeting HSI reconstruction. The estimated SRFs and CIFs match the results measured by the standard laboratory method, and the estimated HSIs achieve less than 3% errors in rmse. Therefore, our method possesses apparent advantages compared to other methods. Experimental results in real examples demonstrated the effectiveness of our method.

Limitations and future research

Our proposed algorithms work under several assumptions. We assume noise has no significant effect on the reconstruction process. In the future, we can use noise representation in the latent space. We will consider the spatial interaction effects resulting from the optical system in the future. In this study, we assume the exposure for each photo-transistor is independent. Therefore, we convert a picture to a 1D array in the model learning process to save computation time. In the future, we will use 2D array modeling.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the National Science and Technology Council, Taiwan, under Grant Numbers MOST 110-2622-E-992-026, MOST 111-2221-E-037-007, NSTC 112-2218-E-992-004, and NSTC 112-2221-E-153-004. The authors also thank Mr. Huang, Yuan's General Hospital (ST110006), and NSYSU-KMU Joint Research Project (#NSYSU-KMU-112-P10).

Conflict of interest

The authors have no competing interests to declare.