Chance-constrained approach for decentralized supply chain network under uncertain cost

1.   Introduction

As the market size grows and the competition intensifies, research on supply chain management is receiving great attention. Due to the increment in supply chain members, the traditional models based on one manufacturer and retailer cannot appropriately reflect the problems. The decentralized supply chain network considering different roles of decision-makers who independently make decisions is more suitable in this situation.

In ^[1], Nagurney et al. proposed an equilibrium model for a three-tier supply chain network. Since then, the supply chain network equilibrium model has been applied in many fields. For example, Nagurney et al. studied the electric supply chain network equilibrium model ^[2]. Yu and Nagurney proposed a supply chain network model for fresh produce^[3]. Because customers and regulators are paying more attention to environmental protection, Saberi et al. considered the environmental impact on the supply chain and proposed a multiperiod equilibrium model with freight carriers^[4]. Yang and Xu considered the carbon emission permits in a closed-loop supply chain network^[5]. Considering the huge impact of natural disasters, political and humanitarian disasters and health response disasters, Nagurney et al. considered the nongovernmental organizations in post-disaster humanitarian relief and developed a generalized supply network model^[6]. By considering the outbreak of the COVID-19 pandemic, Nagurney proposed a new equilibrium model to alleviate labor shortages in the supply chain network^[7].

In reality, a supply chain is usually affected by market fluctuation, disasters, etc., which is an inherent feature of supply chains. It will result in a suboptimal or even an infeasible solution if we do not pay enough attention to these uncertain parameters in decision-making^[8]. Interval optimization^[9,10,11,12], stochastic optimization^{[13,14,15,16]} and robust optimization^[17,18,19] are the main approaches for dealing with the uncertainty in many optimization problems.

For the interval optimization, Guo et al. studied the optimality conditions and duality theorems for interval-valued optimization problems based on the gH-symmetrical derivative^[20]. Treanţă introduced a new condition of generalized convexity such that all KT points are LU-optimal solutions in an interval-valued variational control problem^[21]. Guo et al. studied the properties of the symmetric gH-derivative and developed the Mond–Weir duality theory for a class of symmetric gH-differentiable interval-valued optimization problems^[9]. Treanţă established some characterization results for solutions associated with a class of interval-valued optimization problems with mixed constraints^[22].

For stochastic optimization in a supply chain network, Dong et al. considered the uncertain demand in an equilibrium model^[23]. Liu and Nagurney developed an equilibrium model under uncertain demand and cost^[24]. Xiao and Zhang proposed a decentralized equilibrium model under uncertain demand and considered the coordination of supply chain members^[25]. Zhou et al. incorporated retailers' dynamic loss-averse behaviors into an equilibrium model under uncertain demand^[26]. Wan et al. considered a polymorphic uncertain environment, including the uncertain demand, and got the deterministic equivalent formulation of the uncertain equilibrium model^[27].

When the exact distribution functions of uncertain parameters are difficult to be obtained for firms, robust optimization can be adopted to get a solution that is not sensitive to these uncertain parameters. For example, Golsefidi and Jokar proposed a robust optimization approach for the production-inventory-routing problem with simultaneous pickup and delivery^[17]. Kou and Wan developed a novel data-driven robust optimization model for solving multi-item newsboy problems by combining an absolute robust optimization with a data-driven uncertainty set^[28]. Robust optimization has been successfully applied in many fields, such as supply chain network design^[29], inventory problems^[17,18,28], vehicle routing problems^[17,18,19], location-allocation problems^[30], etc. However, only some researchers have applied it to the supply network equilibrium problem. Hirano and Narushima proposed a robust equilibrium model with uncertainties in the other players' strategies ^[31].

With the development of information technology and e-commerce, many retailers are providing consumers with multiple purchase channels. However, quantifying labor and transportation costs is one of the challenges in current supply chain management^[32]. Hence, the cost in a supply chain network is usually uncertain. However, most of the above literature only considers the uncertainty of demand, except ^[24] and ^[31]. The methods used to deal with the uncertain cost in ^[24] and ^[31] are the scenario-based method and robust method, respectively. The scenario-based method is only an approximate method, and the robust method is too conservative, which prevents the opportunity to gain more profit. The chance-constrained method is more accurate than the scenario-based method, and it can gain more profit under different risk attitudes than the robust method. It has been successfully applied in many fields, such as supply chain network design problems^[33,34], vehicle routing problems^[35], etc. Therefore, this paper evaluates a decentralized supply chain network under uncertain costs. A chance-constrained method is used to develop the equilibrium model for the first time.

The paper is organized as follows. Section 2 gives some notations for the problem studied in this paper, and the chance-constrained equilibrium model is reformulated as a variational inequality problem. The existence and uniqueness of the proposed chance-constrained equilibrium model are discussed in Section 3. The proposed chance-constrained equilibrium model is reformulated as a second-order cone complementarity problem, and the numerical results for four cases are discussed in Section 4. In Section 5, we conclude this paper.

2.   New equilibrium model of supply chain network with uncertain cost

In this section, we develop the chance-constrained supply chain network equilibrium model. The manufacturers, the retailers and the demand markets are analyzed respectively. The complete chance-constrained equilibrium model is constructed at last.

2.1.   Problem description

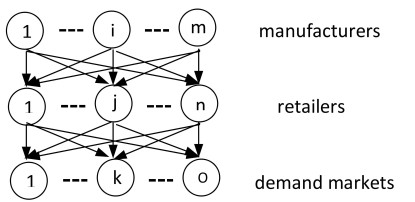
As shown in Figure 1, this paper considers a three-tier decentralized supply chain network with $m$ manufacturers, $n$ retailers and $o$ demand markets. The manufacturers produce products, and the retailers purchase products from manufacturers and sell these products to the demand markets. The manufacturers and the retailers decide the optimal number of products to maximize profits under the conditions of a competitive and uncertain environment. Suppose that the manufacturers and retailers cannot know the strategies of their competitors exactly, but that they can estimate the distributions of the competitor's strategies based on historical data.

2.2.   Notations

For Manufacturer $i \in {1, 2, \cdots, m}$, Retailer $j \in {1, 2, \cdots, n}$ and Market $k \in {1, 2, \cdots, o}$, the notations used in this paper are defined as follows:

● $q^{mr}_{ij}$: the number of products transacted between Manufacturer $i$ and Retailer $j$, and let $q^{mr}_{i\cdot} = (q^{mr}_{i1}, \cdots, q^{mr}_{in})^{T}$, $q^{mr}_{\cdot j} = (q^{mr}_{1j}, \cdots, q^{mr}_{mj})^{T}$, $q^{mr}_{-i\cdot} = ({q^{mr}_{1 \cdot}}^T, \cdots, {q^{mr}_{i-1 \cdot}}^T, {q^{mr}_{i+1 \cdot}}^T, \cdots, {q^{mr}_{m \cdot}}^T)^{T}$, $q^{mr}_{\cdot -j} = ({q^{mr}_{ \cdot 1}}^T, \cdots, {q^{mr}_{\cdot j-1}}^T, {q^{mr}_{\cdot j+1}}^T, \cdots, {q^{mr}_{ \cdot n}}^T)^{T}$;

● $q^{rd}_{jk}$: the number of products transacted between Retailer $j$ and Market $k$, and let $q^{rd}_{j\cdot} = (q^{rd}_{j1}, \cdots, q^{rd}_{jo})^{T}$, $q^{rd}_{\cdot k} = (q^{rd}_{1k}, \cdots, q^{rd}_{nk})^{T}$, $q^{rd}_{-j\cdot} = ({q^{rd}_{1 \cdot}}^T, \cdots, {q^{rd}_{j-1 \cdot}}^T, {q^{rd}_{j+1 \cdot}}^T, \cdots, {q^{rd}_{n \cdot}}^T)^{T}$, $q^{rd}_{\cdot -k} = ({q^{rd}_{ \cdot 1}}^T, \cdots, {q^{rd}_{\cdot k-1}}^T, {q^{rd}_{\cdot k+1}}^T, \cdots, {q^{rd}_{ \cdot o}}^T)^{T}$;

● $p_{k}$: the market price at Market $k$; $p = (p_{1}, \cdots, p_{o})^{T}$;

● $\rho^{mr}_{ij}$: the unit price of the product paid by Retailer $j$ to Manufacturer $i$; $\rho^{mr}_{i\cdot} = (\rho^{mr}_{i1}, \cdots, \rho^{mr}_{in})^{T}$; $\rho^{mr}_{\cdot j} = (\rho^{mr}_{1j}, \cdots, \rho^{mr}_{mj})^{T}$;

● $\rho^{rd}_{j}$: the unit price of the product paid by Market $k$ to Retailer $j$.

2.3.   Problem solved by the manufacturers

Similar to ^[1,31], the transaction cost between Manufacturer $i$ and Retailer $j$ is defined as $c_{ij}(q^{mr}_{ij})$, which is a convex function, and $i = 1, \cdots, m, j = 1, \cdots, n$.

If all manufacturers procure the raw materials from the same supplier, then their production costs will affect each other due to the competition. Hence, the production cost function of Manufacturer $i$ is related to its own decisions $q^{mr}_{i\cdot}$ and its competitors' decisions $q^{mr}_{-i\cdot}$. Therefore, we need the following assumption, similar to ^[31].

Assumption 1. The effect of competitors on Manufacturer $i$'s production cost is defined as the following function:

where $B_{il} = b_{il} E_n$, $l = 1, \cdots, n$, $b_{il}$ is a non-negative constant and $E_n \in \mathbb{R}^{n \times n}$ denotes a matrix in which all components are one.

For the above assumption, it is easy to find that, if the production of the other manufacturers increases, the production cost of Manufacturer $i$ also increases. Hence, this assumption can describe the competition between manufacturers properly. Then, the production cost function of Manufacturer $i$ can be defined as follows:

where $\hat{f}_i : \mathbb{R}^{n} \rightarrow \mathbb{R}$ is a convex, continuously differentiable function that does not depend on the other manufacturers' decisions.

In reality, Manufacturer $i$ cannot get an accurate value of $q^{mr}_{-i \cdot}$. According to the historical data, Manufacturer $i$ usually estimates $q^{mr}_{l \cdot}$ as $\tilde{q}^{mr}_{l \cdot}: = q^{mr}_{l \cdot} + M_{il} \tilde{u}_l (l = 1, \cdots, i-1, i+1, \cdots, m)$, where $\alpha S^{-1}_{il} = M_{il} \in \mathbb{R}^{n \times n}$ is a symmetric positive definite matrix, $S^{-1}_{il}$ is the variance-covariance matrix of historical data, $\alpha$ is a parameter that controls the degree of uncertainty and $\tilde{u}_l \in \mathbb{R}^{n}$ is a stochastic vector in which each element of it follows an independent standard normal distribution.

Based on the above definitions and assumptions, if a chance-constrained optimization method is adopted, then we can get the following proposition.

Proposition 1. The optimization model of Manufacturer $i$ is the following second-order cone optimization problem:

where $F^{-1}(\cdot)$ is the inverse function of the standard normal distribution function; $\epsilon$ measures the probability that this constraint will be violated.

Proof. When the estimation of $q^{mr}_{l \cdot}$ is stochastic, the stochastic optimization model of Manufacturer $i$ is

which equals

Manufacturer $i$ adopts the chance-constrained method to make decisions. If the manufacturer is willing to take certain risks to increase profits, then Model (2.2) equals

where the last constraint means that Manufacturer $i$ will violate this constraint in a probability $1 - \epsilon$ to increase profit. Due to each element of $\tilde{u}_l$ following an independent standard normal distribution, then we have

Hence,

where

Therefore, the last constraint of Model (2.3) is

Therefore, Model (2.3) equals Model (2.1).

Denote the feasible region of Model (2.1) as $S_M^{i}$. It is easy to prove that $S_M^{i}$ is a convex set and the objective function of Model (2.1) is concave with $q^{mr}_{i \cdot}$. Therefore, for a given ${q^{mr}_{-i \cdot}}^*$, the equilibrium condition for all manufacturers is as follows:

where

Model (2.4) implies that, if ${q^{mr}_{ij}}^* > 0$, then ${\rho^{mr}_{ij}}^* = \frac{\partial f_i ({q^{mr}_{i \cdot}}^*, {q^{mr}_{-i \cdot}}^*)}{\partial q^{mr}_{ij}} + \frac{d c_{ij} ({q^{mr}_{ij}}^*)}{d q^{mr}_{ij}}$, and if ${q^{mr}_{ij}}^* = 0$, then ${\rho^{mr}_{ij}}^* \leq \frac{\partial f_i ({q^{mr}_{i \cdot}}^*, {q^{mr}_{-i \cdot}}^*)}{\partial q^{mr}_{ij}} + \frac{d c_{ij} ({q^{mr}_{ij}}^*)}{d q^{mr}_{ij}}$.

2.4.   Problem solved by the retailers

The handling cost of Retailer $j$ may include the display and storage cost associated with the product, and it is not only related to its own decisions $q^{mr}_{\cdot j}$, but it is also related to its competitors' decisions $q^{mr}_{\cdot -j}$. Therefore, we need the following assumption, similar to ^[31].

Assumption 2. The effect of competitors on Retailer $j$'s handling cost is defined as the following function:

where $\Gamma_{jr} = \gamma_{jr} E_m$, $r = 1, \cdots, n$, $\gamma_{jr}$ is a non-negative constant and $E_m \in \mathbb{R}^{m \times m}$ denotes a matrix in which all components are one.

Then, the handling cost function of Retailer $j$ can be defined as follows:

where $\hat{h}_j : \mathbb{R}^{m} \rightarrow \mathbb{R}$ is a convex, continuously differentiable function that does not depend on the other retailers' decisions.

Similar to the situation of the manufacturers, Retailer $j$ cannot know the exact value of $q^{mr}_{\cdot -j}$. According to the historical data, Retailer $j$ usually estimates $q^{mr}_{\cdot r}$ as $\tilde{q}^{mr}_{\cdot r}: = q^{mr}_{\cdot r} + N_{jr} \tilde{v}_r (r = 1, \cdots, j-1, j+1, \cdots, n)$, where $N_{jr} \in \mathbb{R}^{m \times m}$ is a symmetric positive definite matrix, and $\tilde{v}_r \in \mathbb{R}^{m}$ is a stochastic vector in which each element of it follows an independent standard normal distribution.

Based on the above definitions and assumptions, if a chance-constrained method is adopted, we can get the following proposition.

Proposition 2. The optimization model of Retailer $j$ is the following second-order cone optimization problem:

where $F^{-1}(\cdot)$ is the inverse function of the standard normal distribution function; $\epsilon$ measures the probability that this constraint will be violated.

The proof of Proposition 2 is similar to that of Proposition 1. By defining a Lagrange multiplier $\xi \in \mathbb{R}^n_+$, denote

It is easy to prove that $S_R^{j}$ is a convex set and the objective function of Model (2.6) is concave with $q^{mr}_{\cdot j}$. Therefore, for a given ${q^{mr}_{\cdot -j}}^*$, the equilibrium condition for all retailers is as follows:

where

Model (2.7) implies that, if ${q^{mr}_{ij}}^* > 0$, then $\xi_{j}^* = {\rho^{mr}_{ij}}^* + \frac{\partial h_j ({q^{mr}_{\cdot j}}^*, {q^{mr}_{\cdot -j}}^*)}{\partial q^{mr}_{ij}}$, and if ${q^{mr}_{ij}}^* = 0$, then $\xi_{j}^* \leq {\rho^{mr}_{ij}}^* + \frac{\partial h_j ({q^{mr}_{\cdot j}}^*, {q^{mr}_{\cdot -j}}^*)}{\partial q^{mr}_{ij}}$. If ${q^{rd}_{jk}}^* > 0$, then ${\rho^{rd}_{j}}^* = \xi_{j}^*$, and if ${q^{rd}_{jk}}^* = 0$, then ${\rho^{rd}_{j}}^* \leq \xi_{j}^*$.

2.5.   Conditions for the demand markets

For Demand market $k$ $(k = 1, \cdots, o)$, define the following functions:

● $d_k(p)$: demand function of Demand market $k$,

● $g_{jk}(q^{rd}_{\cdot k}, q^{rd}_{\cdot -k})$: transaction cost between Demand market $k$ and Retailer $j$ $(j = 1, \cdots, n)$.

Then, similar to ^[1,31], the following conditions should be satisfied for Demand market $k$ at equilibrium:

and

These conditions correspond to the well-known spatial price equilibrium conditions. Equation (2.9) means that, if consumers in the Demand market $k$ purchase products from Retailer $j$, the sum of the price of the product and the transaction cost is equal to the price that consumers are willing to pay. Equation (2.10) means that, if the price that the consumers are willing to pay is positive, the demand of Demand market $k$ equals the total amount of products purchased from the retailers. Hence, we can get the following variational inequality for demand markets in equilibrium:

where $S_D : = \{({q^{rd}}^T, p^T)^T| q^{rd} \in \mathbb{R}_+^{n \times o}, p \in \mathbb{R}_+^{k}\}$.

2.6.   Equilibrium conditions of the supply chain

Theorem 1. The equilibrium conditions of the uncertain decentralized supply chain network are equivalent to the variational inequality problem:

Determine $({{q^{mr}}^*}^T, {{q^{rd}}^*}^T, {\xi^*}^T, {p^*}^T, {s^*}^T, {t^*}^T)^T \in K$ satisfying

where

Proof. By combining (2.4), (2.7) and (2.11), we can get the following equations.

● For variables $q^{mr}_{ij}, i = 1, \cdots, m, j = 1, \cdots, n$, we have

where the left-hand side of the equation is the first term in (2.12), the first term and the second term of the right-hand side of the equation is the first term in (2.4) and the first term in (2.7), respectively.

● For variables $q^{rd}_{jk}, j = 1, \cdots, n, k = 1, \cdots, o$, we have

where the left-hand side of the equation is the second term in (2.12), the first term and the second term of the right-hand side of the equation is the second term in (2.7) and the first term in (2.11), respectively.

The third term and the sixth term in (2.12) are the third term and the fourth term in (2.7), respectively. The fourth term in (2.12) is the second term in (2.11). The fifth term in (2.12) is the second term in (2.4).

Hence, the equilibrium conditions of the uncertain decentralized supply chain network are equivalent to the variational inequality problem (2.12).

We should notice that the proposed model is different from the robust equilibrium model of ^[31] in the following two aspects:

● First, the strategy adopted by decision-makers is different. In ^[31], the players use the minimax principle to make decisions, that is, to optimize the profit of the worst case. However, in this work, the players use the chance-constrained method to make decisions. That is, they are willing to take certain risks to increase profits. Therefore, the solution to the robust model of ^[31] is more conservative than the chance-constrained model proposed in this paper.

● Second, the feasible regions of these two models are different. There is an extra parameter $\epsilon$ in the proposed chance-constrained model. On the one hand, $\epsilon$ controls the size of the feasible region. The feasible region of the proposed model increases as $\epsilon$ decreases. On the other hand, $\epsilon$ reflects the risk attitude of decision-makers. A larger value of $\epsilon$ means that decision-makers are more conservative than a smaller value of $\epsilon$.

For simplification, the problem (2.12) is rewritten as follows:

Find $x^* \in K$ such that

where $x: = ({q^{mr}}^T, {q^{rd}}^T, \xi^T, p^T, s^T, t^T)^T$, $H(x): = (H^{q^{mr}}_{ij}, H^{q^{rd}}_{jk}, H^{\xi}_{j}, H^p_{k}, H^s_{il}, H^t_{jr})$ and the specific components of $H$ are given by (2.12).

3.   Existence and uniqueness of the equilibrium

Similar to the proofs of Theorems 4.1 and 4.2 in ^[31], we can easily obtain the following properties of the proposed chance-constrained equilibrium model.

Define a set $K^b$ as follows:

where $\beta_{v}$ is a vector with components $b_v$ $(v = 1, \cdots, 6)$, $b_v$ is sufficiently large and $K^b$ is not empty. As $K^b$ is compact, we have the following variational inequality problem:

Find $x^b \in K^b$ such that

has at least one solution. Then, we can obtain the next theorem similar to Theorem 4.1 in ^[31].

Theorem 2. (Existence) If there exist positive constants $R_1$, $N_1$, $R_2$ and $N_1$ that satisfy (3.2) and (3.3), the problem (2.14) has at least one solution:

Proof. Suppose that $x^b$ is a solution of (3.1), where $q^{mr} = {q^{mr}}^{b}, {q^{rd}} = {q^{rd}}^b, \xi = \xi^{b}, p = p^{b}, s = s^{b}$ and $t = t^{b}$. We assume that $\beta_v$ is a vector with components $b_v$ $(>N_v)((v = 1, \cdots, 6))$, where

Then, similar to the proof of Theorem 4.1 in ^[31], we can easily get that

● ${q^{mr}_{ij}}^b < b_1, i = 1, \cdots, m, j = 1, \cdots, n,$

● ${q^{rd}_{jk}}^b < b_2, j = 1, \cdots, n, k = 1, \cdots, o,$

● ${\xi_{j}}^b < b_3, j = 1, \cdots, n,$

● ${p_{k}}^b < b_4, k = 1, \cdots, o.$

Suppose that there exists a pair $(u, c)$ such that $s_{uc} = b_5$. For (2.12), if we let $q^{mr} = {q^{mr}}^{b}, {q^{rd}} = {q^{rd}}^b, \xi = \xi^{b}, p = p^{b}, s_{il} = s_{il}^{b}((i, l) \neq (u, c))$ and $t = t^{b}$, it follows that

However, if we let $s_{uc} < s_{uc}^b$, then (3.5) is not satisfied. Thus, it follows that $s_{uc} < b_5$.

Suppose that there exists a pair $(v, d)$ such that $t_{vd} = b_6$. For (2.12), if we let $q^{mr} = {q^{mr}}^{b}, {q^{rd}} = {q^{rd}}^b, \xi = \xi^{b}, p = p^{b}, s = s^{b}$ and $t_{jr} = t_{jr}^{b}$ $((j, r) \neq (u, c))$, it follows that

However, if we let $t_{vd} < t_{vd}^b$, then (3.6) is not satisfied. Thus, it follows that $t_{vd} < b_6$.

Hence, if there exist $R_1, N_1, R_2$ and $N_2$ that satisfy (3.2) and (3.3), then the variational inequality problem (3.1) has at least one solution, $x^b$, such that $x^b < \beta$, where $\beta: = (\beta_1^T, \beta_2^T, \beta_3^T, \beta_4^T, \beta_5^T, \beta_6^T)^T$. Therefore, by Theorem 2.2 in ^[31], the variational inequality problem (2.12) has at least one solution.

Define

To show the uniqueness of the equilibrium model, we need the following assumption.

Assumption 3. The function $g_{k}(q^{rd}_{\cdot k}, q^{rd}_{\cdot -k})$ $(k = 1, \cdots, o)$ and $-d(p)$ are monotone with $q^{rd}_{\cdot k}$ and $p$, respectively. In addition, either of $g_{k}(q^{rd}_{\cdot k})$, $-d(p)$, $\nabla_{q^{mr}_{i \cdot}} \hat{f}_i (q^{mr}_{i \cdot})$, $\nabla_{q^{mr}_{\cdot j}} \hat{h}_j (q^{mr}_{\cdot j})$ and $\frac{d c_{ij}(q^{mr}_{ij})}{dq^{mr}_{ij}}$ is strictly monotone with $q^{rd}_{\cdot k}, p, q^{mr}_{i \cdot}, q^{mr}_{\cdot j}$ and $q^{mr}_{ij}$, respectively.

Under Assumption 3, we can obtain the uniqueness of the proposed chance-constrained equilibrium model similar to Theorem 4.2 in ^[31].

Theorem 3. (Uniqueness) Let Assumption 3 hold. If the variational inequality problem (2.14) has at least one solution, then the solution is unique.

4.   Numerical experiments

4.1.   The solution method

Due to the non-differentiable functions in set $K$, the variational inequality problem (2.14) is difficult to solve. Hence, we reformulate it as a second-order cone complementarity problem.

The set $K$ can be written as

where $\sigma : = mn+no+n+o$ and $\mathcal{K}^{1+n}$ and $\mathcal{K}^{1+m}$ are $(1+n)$- and $(1+m)$-dimensional second-order cones, respectively.

Hence, we define

and

Then, similar to ^[31], the variational inequality problem (2.14) can be reformulated as the following mixed second-order cone complementarity problem:

where $v : = \sigma + m(m-1) + n(n-1)$ and $\tau : = \sigma + m(m-1)(n+1) + n(n-1)(m+1)$. Some algorithms have been developed to solve the mixed second-order cone complementarity problem, such as ^{[36,37,38,39]}. In this paper, the software ReSNA, based on a regularized and smoothing Newton algorithm^[39], is used to solve this problem and show the advantage of the proposed model.

4.2.   Numerical examples

To show the impacts of the uncertainty on the decisions and the profits of the supply chain members, we consider two manufacturers, two retailers and two demand markets in numerical experiments. According to ^[1,31], the cost functions are defined as follows:

The cost functions of manufacturers:

The cost functions of retailers:

The cost functions between manufacturers and retailers:

The cost functions between retailers and demand markets:

The demand functions:

We consider the following four cases to show the effects of uncertain parameters.

Case 1 There is no uncertainty for any decision-makers;

Case 2 Only Manufacturer 1 faces uncertainty, and the uncertain parameter is

Case 3 Only Retailer 1 faces uncertainty, and the uncertain parameter is

Case 4 Manufacturer 1 and Retailer 1 both face uncertainty. The uncertain parameters are

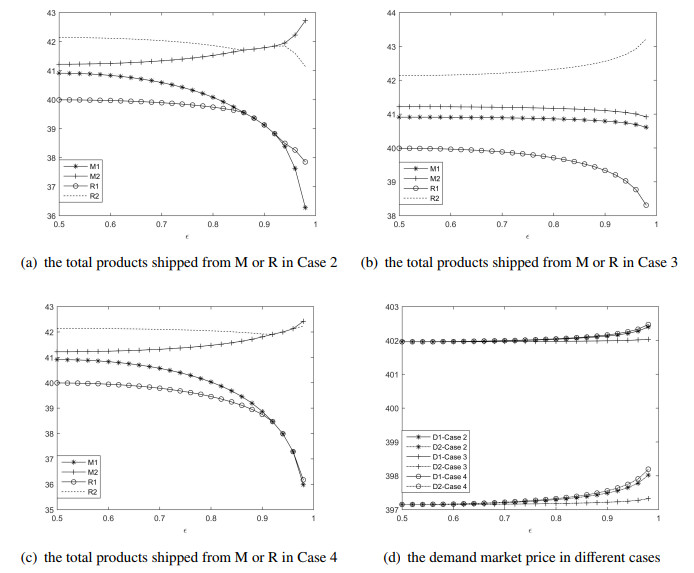
For simplicity, we denote "M1, M2, R1, R2, D1, D2" for two manufacturers, two retailers and two demand markets in all tables and figures, respectively. For Cases 2–4, set the uncertain parameters $\alpha = 1$ and risk attitude $\epsilon = 0.1$. The numerical solutions of the proposed equilibrium model for different cases are shown in Table 1.

From Table 1, we can find that the uncertainty of retailers and manufacturers has different effects on supply chain network members. In Case 1, the number of products shipped from Manufacturer 1 is $39.99 + 0.92 = 40.91$. In Case 2, the number of products shipped from Manufacturer 1 is $39.12 + 0.00 = 39.12$. Hence, the uncertainty of Manufacturer 1 may have a negative impact on Manufacturer 1's decision. Similarly, we can find that the uncertainty of Manufacturer 1 may positively impact Manufacturer 2's decision, which may be because Manufacturer 2 will compensate for the product decrease caused by Manufacturer 1. However, the uncertainty of Manufacturer 1 has a negative impact on all retailers' decisions.

Similarly, in Case 3, the uncertainty of Retailer 1 has a negative impact on Retailer 1 and all manufacturers' decisions. But, it has a positive impact on Retailer 2's decision. In Case 4, the uncertainty of Manufacturer 1 and Retailer 1 has a negative impact on Manufacturer 1 and all retailers' decisions. However, it only has a positive impact on Manufacturer 2's decision because the negative impact effect of Manufacturer 1 is less than the positive impact of Retailer 1. For the price of the demand market, the uncertainty of Manufacturer 1 and Retailer 1 will increase the price in all demand markets. However, the uncertainty of Manufacturer 1 has a greater impact on the price.

4.3.   Equilibrium solution under different risk attitudes

To confirm the conclusions from Table 1, we keep $\alpha = 1$ and vary the risk attitude $\epsilon$ from $0.5$ to $0.98$. Note that $\epsilon = 0.5$ corresponds to the situation of no uncertainty in the supply chain, with all of the uncertain parameters taking the mean values. Numerical solutions for different cases are shown in Figure 2.

From Figure 2, we can find that most of the conclusions we get from Table 1 still hold for varying values of $\epsilon$, except for the conclusion we get from Case 4. The combined impact of the uncertainty of Manufacturer 1 and Retailer 1 results in the total amount of product decreasing for $\epsilon \in [0.5, 0.92]$ and increasing for $\epsilon \in [0.92, 0.98]$.

We also find that, for small $\epsilon$, the change of all supply chain members' decisions is insignificant. However, for larger $\epsilon$, a small change in $\epsilon$ will significantly change all decisions, which means that all decision-makers should be careful to trade-off their risk attitude and decisions, especially when they are risk-averse.

4.4.   Effects of the risk attitude on the profits

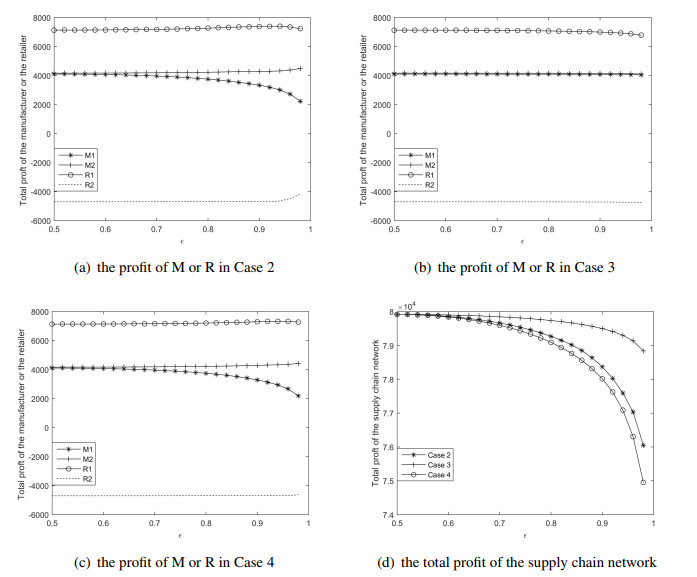
In this subsection, we will analyze the effects of the risk attitude on profits. The profits of all decision-makers in different cases are shown in Figure 3.

From Figure 3, we can find that, in Cases 2 and 4, the risk attitude of Manufacturer 1 positively impacts the profits of Manufacturer 2 and Retailer 2. However, it has a negative impact on Manufacturer 1 and Retailer 1's profits. In Case 3, the risk attitude of Retailer 1 has a small impact on all supply chain members' profits. But, the total profit is decreasing in all cases.

Similar to the situation in Figure 2, we also find that, for small $\epsilon$, the change in each member's profit is small. But, for larger $\epsilon$, a small change in $\epsilon$ will significantly change each member's profits, which means that all supply chain members should carefully trade-off their risk attitude and decisions, especially when risk-averse.

4.5.   Comparison between chance-constrained method and robust method

This subsection compares the chance-constrained equilibrium model proposed in this paper and the robust equilibrium model proposed in ^[31].

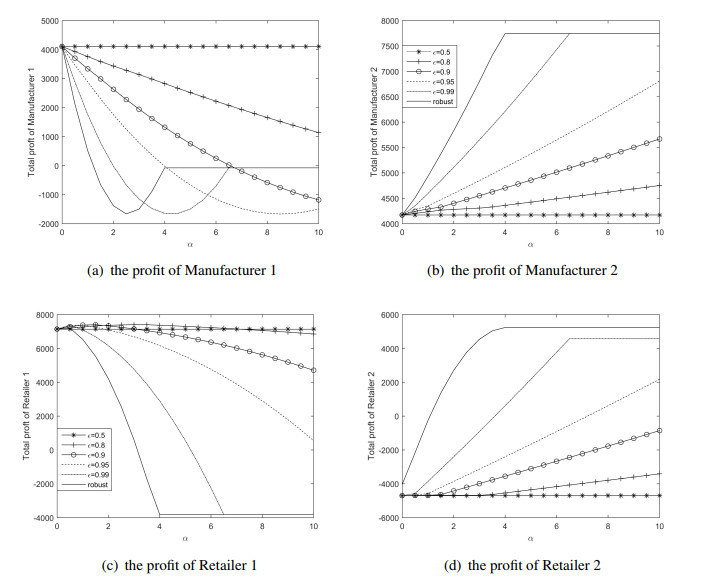
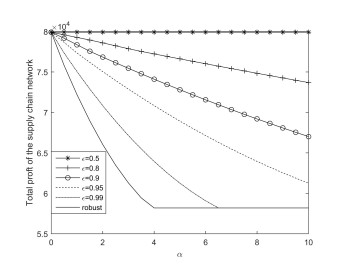
We only analyze Case 2 in this subsection. Furthermore, according to the 3$\sigma$ principle in the normal distribution, the parameter controls the magnitude of the uncertainty set in the robust model and equals three times the standard deviation of the stochastic parameter in the chance-constrained model. The results of the chance-constrained model and robust model are shown in Figures 4 and 5.

From Figure 5, we find that the total profit of all decision-makers will decrease as the uncertainty parameters $\alpha$ and risk attitude $\epsilon$ increase, which shows that, even though the uncertainty of Manufacturer 1 has a negative impact on the total profit, the profit can still increase if the supply chain members' risk attitude is high. The same conclusions hold for Manufacturer 1 when $\alpha \leq 2.5$ (see Figure 4). But, for Manufacturer 2 and Retailer 2, their profits will increase as the uncertainty parameters $\alpha$ and risk attitude $\epsilon$ increase (see Figure 4). Hence, the supply chain members' profits will increase if their risk attitudes increase and they are positively affected by the uncertainty. The profits of the supply chain members will decrease if their risk attitudes increase and they are negatively affected by the uncertainty.

By comparing the chance-constrained and robust model, we can find that, when the supply chain members can estimate the distributions of the competitors' strategies by using historical data, we can get the equilibrium decisions under different risk attitudes. But, the difference in decisions under different risk attitudes is significant. For example, when $\alpha \geq 6.5$ and $\epsilon = 0.99$, Manufacturer 1 will decide to exit the market, while Manufacturer 1 will continue operating for another value of $\epsilon$. However, Manufacturer 1 will enter the market when $\alpha \geq 4.5$ in the robust decision strategy. Hence, when the supply chain members can estimate the distributions of the competitors' strategies, it is appropriate to adopt the chance-constrained method.

5.   Conclusions

This paper has presented a chance-constrained equilibrium model for a decentralized and uncertain supply chain network. When supply chain members can estimate the distributions of competitors' strategies, a chance-constrained strategy is used to make decisions. The existence and uniqueness properties of the proposed chance-constrained equilibrium model are discussed under some mild assumptions. Moreover, we have reformulated the proposed model as a second-order cone complementarity problem to solve it. Some numerical experiments were conducted to analyze the proposed model. This study can be extended in several directions. In addition to cost uncertainty, demand uncertainty and polymorphic uncertainty in ^[27] can also be considered. Moreover, a model which can control the degree of robustness or a distributionally robust supply chain network equilibrium model should also be studied further.

Acknowledgments

The authors are very grateful to the editors and referees for their constructive advice.

This work was financially supported by the Science and Technology Planning Project of Guangzhou, China (Grant No. 202102020600), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2022A1515110315), the Natural Science Foundation of China (Grants No. 71901074, 11801105) and the Guangxi Science and Technology Project (Grant No. Guike AD19245106).

Conflict of interest

The authors declare that there is no conflict of interest.