On $\mathcal{A B C}$ coupled Langevin fractional differential equations constrained by Perov's fixed point in generalized Banach spaces

1.   Introduction

For centuries, infectious diseases have ranked with wars and famine as major challenges to human progress and survival ^[1]. The spread of infectious diseases in populations and how to control and eliminate them from the populations are important and necessary subjects. Mathematical models are introduced to study what happens when an infection enters in a population, and under which conditions the disease will be wiped out from population or persist in population. Therefore, mathematical epidemic models have been a popular topic for many years (see ^[2,3,4,5] and the references therein).

In general, the dynamics of epidemic are a highly transited topic of investigation from the epidemiological point of view. There are virous families of models depending on the assumption on the mechanisms of propagation. For example, there are susceptible-infected-susceptible (SIS) models which have been used to model nonlinear incidence rates and double epidemic hypotheses ^[6], susceptible-infected-recovered (SIR) models which are employed to consider the awareness of the presence of a disease ^[7], susceptible-exposed-infected-recovered (SEIR) models that predict the propagation of epidemics with nonlocal reaction functions^[8], susceptible-exposed-infected-quarantined-recovered (SEIQR) models used to account for adjusted incidence and imperfect vaccinations ^[9], and so on. Among the variety of epidemic models, {the SIR model can be seen as the basis, over which more complex and realistic models have been built. Hence, SIR epidemic models have been extensively investigated by ecologists and mathematicians in ^{[10,11,12,13,14]} and the references therein. The literatures mentioned above investigate bifurcation phenomena as one systemic parameter varies. However, they do not consider the analysis of codimention-two bifurcation for epidemic models.

Most Researchers often study bifurcation phenomena as one systemic parameter varies. In fact, many practical models contain several systemic parameters. Complicated bifurcations such as codimension-two bifurcations likely occur when more than one systemic parameter is varied at the same time. Codimension-two bifurcations, also known as double crises, occur when different codimension-one bifurcation intersect in the two-dimensional plane of the systemic parameters. Many literatures consider the codimention-two bifurcations for different fields. Luo et al. ^[15] consider 1:2 resonance bifurcation of a vibroimpact system. In ^[16], Yuan and Yang investigate the complex dynamics of a discrete predator-prey system, and show that the system undergoes flip bifurcation, Neimark-Sacker bifurcation and codimension-two bifurcation associated with 1:2 resonance. Ruan and Wang ^[17] discuss Bogdanov-Takens bifurcation of a continuous epidemic model with a nonlinear incidence rate. Yi et al.^[18] derive the conditions for existence of codimension-one bifurcations (fold bifurcation, flip bifurcation and Neimark-Sacker bifurcation) and present the condition for the occurrence of codimension-two bifurcation (fold-flip bifurcation). Ren and Yu ^[19] study the codimension-two bifurcations of a discrete information diffusion model. The epidemic model is usually a high-dimensional and complex system, including many parameters and variables. Therefore, it is quite natural to ask how the parameters affect the dynamics of the model, what may happen and what match rules about parameters are when two or many parameters change simultaneously, which are what we concern. In our problem, we will study the codimension-two bifurcations of a discrete SIR epidemic model.

Hu et al. ^[20] study a continuous-time SIR epidemic model as following

where $S(t), \; I(t), \; R(t), \; N(t)$ denote the numbers of susceptible, infective, recovered individuals, total numbers of the individuals at time $t$, respectively; $A$ is the recruitment rate of the population, $d$ is the natural death rate of the population, $r$ is the recovery rate of the infective individuals, and $\lambda$ stands for the bilinear incidence rate.

We can get the following discrete-time epidemic model by the Euler scheme.

where $h$ is the step size and all the parameters are positive. As the first two equations of model (1.2) about $(S_{n}, I_{n})$ not including $R_{n}$, and the third equation is the linear equation of $R_{n}$. Therefore, the dynamical behaviors of model (1.2) are equivalent to the dynamical behaviors of the following model

which only includes $S_{n}$ and $I_{n}$.

For simplicity, we rewrite the above system in the form

Hu et al. have algebraically shown that the system undergoes Flip bifurcation and Neimark-Sacker bifurcation, they also show that discrete-time epidemic models can produce a more richer set of dynamic patterns than those observed in continuous-time models. Motivated by the above works, the aim of this paper is to show that system (1.4) undergoes 1:2, 1:3 and 1:4 strong resonances, which provide the sights to the complex dynamics of action potential. In this paper, we choose $h$ and $\lambda$ as perturbation parameters to analyze the codimension-two bifurcations numerically and analytically. All of these studies were previously not considered in the work of Hu et al. In fact, the problem considered in the paper and the obtained results can be seen as a beneficial extension of ^[20].

The remainders of the paper are organized as follows. In Section 2, we present the existence and local stability of fixed points for map (1.4). In Section 3, we show that there exist some values of parameters such that map (1.4) undergoes codimension-two bifurcations. In Section 4, we give some numerical simulations, which not only validate the effectiveness of the theoretical analysis, but also prove that the alternation of the periodic and chaotic motions in two-dimensional parameter space with the system parameter changing. The last section is devoted to the conclusion.

2.   Stability analysis at fixed points

We first discuss the existence and stability of the positive fixed points of model (1.4). The basic reproductive rate of model (1.4) is $R_{0} = A \lambda / d(d+r)$, which is the average number of secondary infections generated by an initial population of infected individuals over their lifetimes. If $R_{0} < 1$, the model (1.4) has an unique fixed point $E_{0}(\frac{A}{d}, 0)$; If $R_{0} > 1$, the model (1.4) has two fixed points: $E_{0}(\frac{A}{d}, 0)$ and $E_{1}(x_{1}, y_{1})$, where

By using the Jacobian matrix and some mathematical calculations, we find that $E_{0}$ does not come into being any codimension-$2$ bifurcation. For $E_{1}$, its Jacobian matrix evaluated is given by

The corresponding characteristic equation at $E_{1}(x_{1}, \; y_{1})$ is given by

where

According to the Lemma 1 in Ren and Yu ^[19], we state the following proposition about stability criterion of $E_{1}(x_{1}, y_{1})$.

Proposition 2.1. Suppose that the fixed point $E_{1}$ of system (1.4) exists. Then it is

(I) Sink if one of the following conditions holds:

(I.1) $G^{2}-4H\geq0$ and $h < (-G-\sqrt{G^{2}-4H})/H;$

(I.2) $G^{2}-4H < 0$ and $h < -G/H;$

(II) Source if one of the following conditions holds:

(II.1) $G^{2}-4H\geq0$ and $h > (-G+\sqrt{G^{2}-4H})/H;$

(II.2) $G^{2}-4H < 0$ and $h > -G/H;$

(III) Saddle if the following conditions hold:

$G^{2}-4H\geq0$ and $(-G-\sqrt{G^{2}-4H})/H < h < (-G+\sqrt{G^{2}-4H})/H;$

(IV) Non-hyperbolic if one of the following conditions holds:

(IV.1) $G^{2}-4H\geq0$ and $h = (-G\pm\sqrt{G^{2}-4H})/H;$

(IV.2) $G^{2}-4H < 0$ and $h = -G/H.$

The non-hyperbolic case of fixed point can result in bifurcations and chaos, and the chaos of epidemics can cause the population to run a higher risk of extinction due to the unpredictability ^[21,22]. Further, the theoretical proofs can provide strong evidences for the existence and characteristic of the bifurcations. Therefore, it is important and necessary to give a detailed analysis about the bifurcations. Thus, we focus on the parametric conditions of non-hyperbolic case. Let $\rho_{1, 2}$ be two eigenvalues of Jacobian matrix J. It follows that $\rho_{1} \rho_{2}$ = 1, and that implies that $\rho_{1, 2} = e^{\pm i\theta_{0}}$ for some real number $\theta_{0}$. If $\rho_{1, 2}^{k} = 1$ for $k = 1, 2, 3, 4$, system (1.4) may exhibit more complicated dynamical behaviors, namely, chaos and codimension-2 bifurcations. As a matter of fact, we can get the following conditions for the strong resonances. Thus, we define three bifurcation sets

at which 1:2, 1:3 and 1:4 resonances will occur, respectively.

3.   Codimension-two bifurcation analysis

In this section, we will give attention to recapitulate the codimension-two bifurcation of system (1.4) around $E_{1}$. Parameters $h, \; \lambda$ are chosen as the bifurcation parameters.

3.1.   1:2 strong resonance at $E_{1}$

We first consider $A, \; d, \; r$ as fixed parameters $\lambda, \; h$ as free parameters. The system (1.4) has a 1:2 strong resonance at $E_{1}(x_{1}, \; y_{1})$. Let $u = x-x_{1}, \; v = y-y_{1}$, then $(x_{1}, y_{1})$ is converted to the origin point $(0, 0)$, and the system (1.4) can be changed into

Let

Let us consider an inverse transaction

The system (3.1) can be expressed as

with

Introduce the non-singular linear coordinate transformation

Map (3.2) can be uniquely represented as

where

Then we take

with

The normal form for 1:2 resonance can be achieved as follows

where

Based on the results given in ^{[23,24,25,26]}, We have the following theorem which gives parametric conditions at 1:2 resonance point.

Theorem 3.1. Assume that $C(\bar{h}, \bar{\lambda}) \neq0$ and $D(\bar{h}, \bar{\lambda})+3C(\bar{h}, \bar{\lambda})\neq0$. Then model (1.4) undergoes a 1:2 strong resonance bifurcation at $E_{1}$ when parameters vary in a small neighbourhood of $F_{12}$. If we further assume $C(\bar{h}, \bar{\lambda}) < 0$ (resp., $C(\bar{h}, \bar{\lambda}) > 0$), then $E_{1}$ is a saddle (resp., elliptic). $D(\bar{h}, \bar{\lambda})+3C(\bar{h}, \bar{\lambda})$ determines the bifurcation scenarios near the 1:2 point. Moreover, model (1.4) has the following bifurcation behaviors:

(I) There is a pitchfork bifurcation curve $PF = \{(\theta_{1}, \theta_{2}):\theta_{1} = 0\},$ and there exists nontrivial fixed point for $\theta_{1} < 0;$

(II) There is a non-degenerate Neimark-Sacker bifurcation curve $H = \{(\theta_{1}, \theta_{2}):\theta_{1} = -\theta_{2}+O((|\theta_{1}|+|\theta_{2}|)^{2}), \theta_{1} < 0\};$

(III) There is a heteroclinic bifurcation curve $HL = \{(\theta_{1}, \theta_{2}):\theta_{1} = -\frac{5}{3}\theta_{2}+O((|\theta_{1}|+|\theta_{2}|)^{2}), \theta_{1} < 0\}.$

3.2.   1:3 strong resonance at $E_{1}$

Based on the analysis given in Section 2, we take parameters $(A, \; d, \; r, \; \tilde{h}, \; \tilde{\lambda})$ from $F_{13}$. We can also transform $E_{1}$ into the origin and expand the model as the same as system (3.1). The Jacobian matrix at $E_{1}$ is shown as

J has two eigenvalues $\lambda_{1, 2} = \frac{-1\pm\sqrt{3}i}{2}.$ We can easily derive the corresponding eigenvalues $q(\tilde{h}, \tilde{\lambda})\in \mathbb{C}^{2}$, and the adjoint eigenvector $p(\tilde{h}, \tilde{\lambda})\in \mathbb{C}^{2}$ as follows:

For any vector $Z = (u, \; v)^{T}\in\mathbb{R}^{2}$, which can be represented in the form $Z = zq+\bar{z}\bar{q}$, we can make the system (3.1) written in the following complex form:

where

In order to eliminate some quadratic terms, we introduce the following transformation

where $h_{jk}$ with $j+k = 2$ will be determined later. Under the transformation (3.7) and its inverse transformation, model (3.6) can be transformed as

where

Take

To further annihilate some cubic terms, we take the transformation

Using (3.9) and its inverse transformation, we can obtain

where

Let

Thus the normal form for 1:3 resonance is derived.

where

Let

Applying the above results and the analyses in the references (see ^{[23,24,25,26]}), we obtain the following theorem regarding the system (3.10).

Theorem 3.2. Assume that $C_{1}(\tilde{h}, \tilde{\lambda})\neq 0$ and $Re D_{1}(\tilde{h}, \tilde{\lambda})\neq 0$. Then system (1.4) undergoes a 1:3 strong resonance bifurcation at $E_{1}$. $Re D_{1}(\tilde{h}, \tilde{\lambda})\neq 0$ determines the stability of the bifurcation invariant closed curve. Moreover, model (1.4) admits a number of the following complex codimension$-$one bifurcation curves:

(I) There is a non-degenerate Neimark-Sacker bifurcation at trivial fixed point $P_{0}$ of (3.10);

(II) There is a saddle cycle of period three corresponding to saddle $P_{k}(k = 1, \; 2, \; 3)$ of (3.10);

(III) There is a homoclinic structure formed by the stable and unstable invariant manifolds of the period three cycle intersecting transversally in an exponentially narrow parameter region.

3.3.   1:4 strong resonance at $E_{1}$

In this Section, we analyze the 1:4 strong resonance with arbitrary parameters $(A, \; d, \; r, \; \hat{h}, \; \hat{\lambda})\in F_{14}$. We can also transform $E_{1}$ into the origin and expand the model as the same as system (3.1). The Jacobian matrix for $(\hat{h}, \hat{\lambda})$ at $E_{1}$ is

From Section 2, we know that $J$ has two eigenvalues $\lambda_{1, 2} = \pm i$. We can obtain the corresponding eigenvector $q(\hat{h}, \hat{\lambda})\in\mathbb{C}^{2}$ and the adjoint eigenvector $p(\hat{h}, \hat{\lambda})\in\mathbb{C}^{2}$ as following.

For any vector $Z = (u, v)^{ T }\in\mathbb{R}^{2},$ which can be represented in the form $Z = zq+\bar{z}\bar{q}$, we can make the system (3.1) written in the following complex form:

where

Similar as in Section 3.2, we can transform (3.11) into the following form by (3.7) and its inverse transformation

Let

By (3.9) and its inverse transformation, (3.12) can be changed into

where

Take

Thus we can get the normal form at 1:4 resonance point as

where

Let $C_{1}(\hat{h}, \hat{\lambda}) = -4i C(\hat{h}, \hat{\lambda}), \; D_{1}(\hat{h}, \hat{\lambda}) = -4i D(\hat{h}, \hat{\lambda}).$ If $D_{1}(\hat{h}, \hat{\lambda})\neq0,$ we denote $B(\hat{h}, \hat{\lambda}) = \frac{ C_{1}(\hat{h}, \hat{\lambda})}{|D_{1}(\hat{h}, \hat{\lambda})|}.$

Applying the above discussions and the results given in ^{[23,24,25,26]}, we can obtain the following results.

Theorem 3.3. Assume that $ReB(\hat{h}, \hat{\lambda})\neq 0$ and $ImB(\hat{h}, \hat{\lambda})\neq 0$. Then map (1.4) has a 1:4 strong resonance bifurcation at $E_{1}$. $B(\hat{h}, \hat{\lambda})$ determines the bifurcation scenarios near $E_{1}$. Near the equilibrium $E_{1}$, there exist two-parameter families of equilibria of order four bifurcation from $E_{1}$, and one of them is unstable, or attractive or repelling invariant circles, which depends on the choices of parameters $\lambda$ and $h$. Moreover, there are many complex codimension$-$one bifurcation curves of map (3.13) in a sufficiently small neighborhood of $(\hat{h}, \hat{\lambda})$.

(I) There is a Neimark-Sacker bifurcation curve at trivial fixed point $P_{0}$ of (3.13). Furthermore, if $\lambda = -i$, there is an invariant circle; if $\lambda = i$, the invariant circle will disappear;

(II) There are eight non-trivial fixed point $S_{k}, \; P_{k}(k = 1, \; 2, \; 3, \; 4)$ if $|B(\hat{h}, \hat{\lambda})| > 1$. The eight non-trivial fixed point appear or disappear in pairs via the fold bifurcation at the corresponding parameter values;

(III) There are Neimark-Sacker bifurcations at $P_{k}(k = 1, \; 2, \; 3, \; 4)$. Moreover, four small invariant circles bifurcate from $P_{k}(k = 1, \; 2, \; 3, \; 4)$, then disappear at homoclinic loop bifurcation curve.

4.   Numerical simulations

In this section, we will give the bifurcation diagrams, largest Lyapunov exponents, phase portraits and two-parameter space diagrams, in addition to confirming the results of our analysis, more behavior is extracted from the model (1.4) by using numerical simulations. The bifurcation parameters are considered in the following three cases, respectively:

Case (i): From $R_{0} > 1$ we find $0.23 < \lambda < 1$ if there is 1:2 strong resonance at $E_{1}$. Let $A = 1.2, \; d = 0.4, \; r = 0.24$. Then $\bar{h} = 8.0594, \; \bar{\lambda} = 0.2647$ and $J(E_{1})$ has eigenvalues $\rho_{1, 2} = -1$. We get an unique fixed point $E_{1}(2.4178, 0.3639)$ and obtain $C(\bar{h}, \bar{\lambda}) = -25.7506, \; D(\bar{h}, \bar{\lambda})+3C(\bar{h}, \bar{\lambda}) = -0.8093$. From Theorem $3.1$, we can obtain that the conditions for the 1:2 strong resonance are satisfied.

Figure 1 gives the phase portraits with different $\bar{h}$ varying in a neighborhood of $\bar{h} = 8.0594$. We can observe that an invariant curve bifurcates from $E_{1}$ causing by Neimark-Sacker bifurcation at $\bar{h} = 8.0594, \; \bar{\lambda} = 0.2647$.

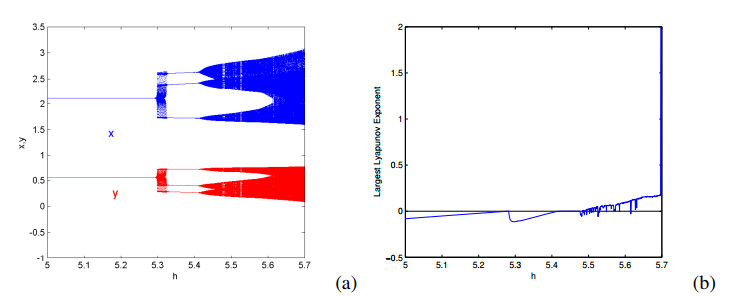
Case (ii): Combining the theoretical analysis and numerical results, we find $0.21 < \lambda < 0.55$ if there is 1:3 strong resonance at $E_{1}$. Let $A = 1.2, \; d = 0.4, \; r = 0.24$. Then $\tilde{h} = 5.2805, \; \tilde{\lambda} = 0.303$ and J has two eigenvalues $\rho_{1, 2} = e^{\pm \frac{2\pi}{3}i}$. We have an unique fixed point $E_{1}(2.1122, 0.5549)$ and get $C_{1}(\tilde{h}, \tilde{\lambda}) = -130.9-47.479i, \; Re D_{1}(\tilde{h}, \tilde{\lambda}) = -139.41$. From Theorem 3.2, we obtain that $E_{1}$ is a 1:3 resonance point.

Figure 2(a) shows bifurcation diagram in $(h, x), \; (h, y)$ space when $\tilde{h}$ vary in a neighborhood of $\tilde{h} = 5.2805$. The corresponding largest Lyapunov exponent is given in Figure 2(b), which is shown to confirm the periodic motion and chaotic motion. Figure 2 shows that system (1.4) has chaotic and periodic behaviors near 1:3 resonance point. Figure 2(b) shows that some Lyapunov exponents are negative, which implies there exists stable fixed point or stable periodic window; the others are positive, which means that there exists chaotic region.

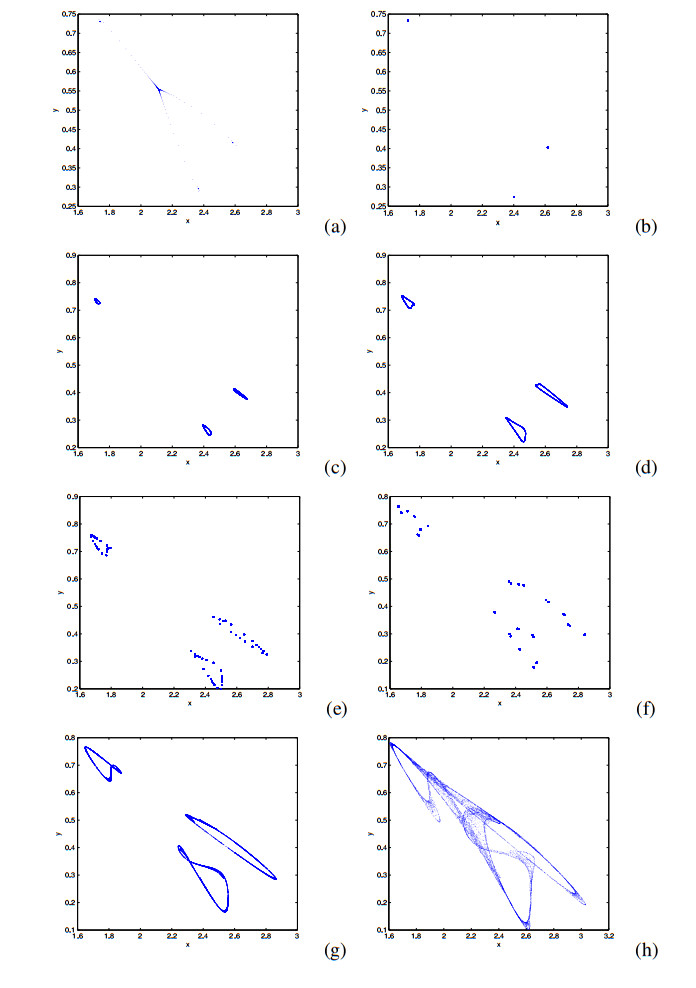
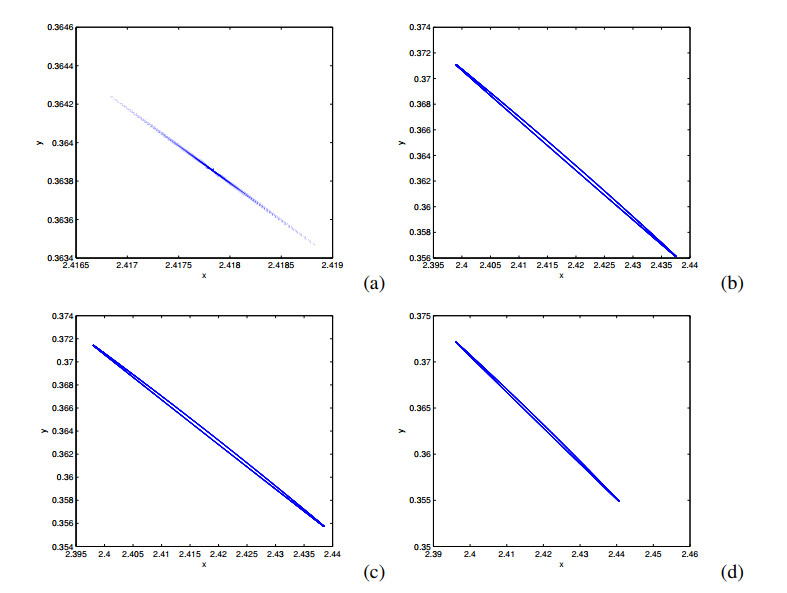
The phase portraits which are associated with Figure 2 are depicted in Figure 3(a)–(h). We observe that there exist period 3 orbit, quasiperiodic orbit, attracting $3-$point cycle, chaos and three curves caused by Neimark-Sacker bifurcation near 1:3 resonance point. In reality, the occurrence of invariant curve also shows the coexistence of susceptibles and infectives. The phase diagrams in Figure 3 also show how the system enters the chaos.

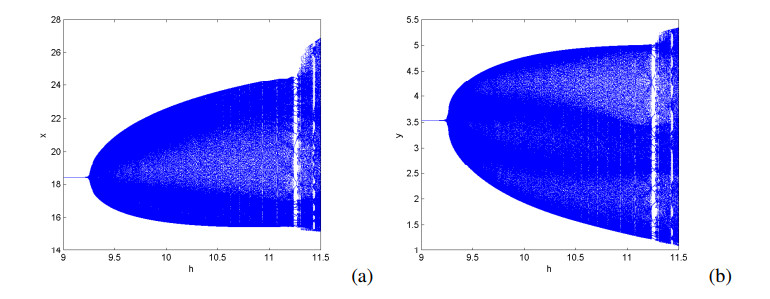
Case (iii): Combining the theoretical analysis and numerical results, we find $0.013 < \lambda < 0.037$ if there is 1:4 strong resonance at $E_{1}$. Let $A = 4, \; d = 0.15, \; r = 0.2$. Then $\hat{h} = 9.1864, \; \hat{\lambda} = 0.019$. We get an unique fixed point $E_{1}(18.3727, 3.5546)$, and obtain $ReB(\hat{h}, \hat{\lambda}) = 0.2251\neq 0, \; ImB(\hat{h}, \hat{\lambda}) = -0.0037\neq 0$. By Theorem 3.3, it is easy to derive that $E_{1}$ is a 1:4 resonance point.

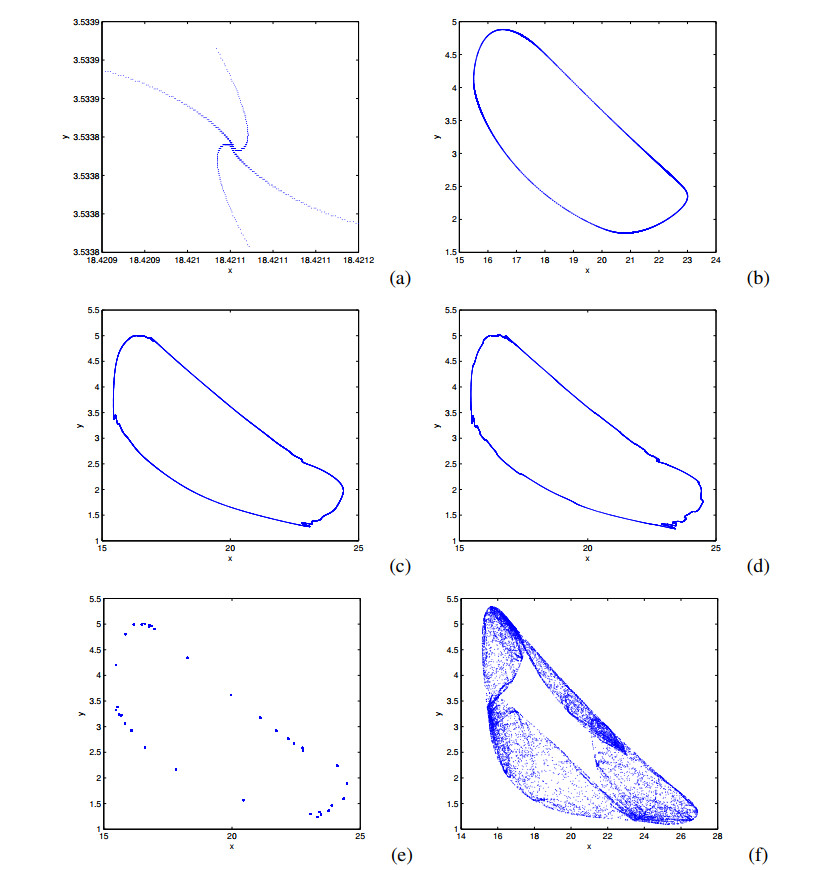
Figure 4 shows the bifurcation diagrams in $(h, x)$ space and $(h, y)$ space with varying $\hat{h}$ in range $9 < h < 11.5$. The phase portraits near $E_{1}$ for different $\hat{h}$ are shown in Figure 5(a)–(f). From which, we can observe invariant circle, Neimark-Sacker bifurcation curve, quasi-period orbits and attracting chaotic set near 1:4 resonance point. This is entirely consistent with the results we obtained analytically. Numerical results illustrate that the theoretical analyses are effective.

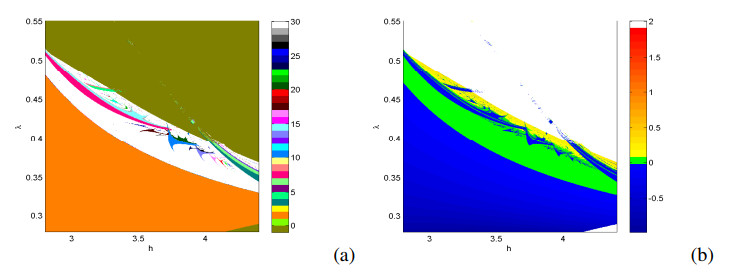
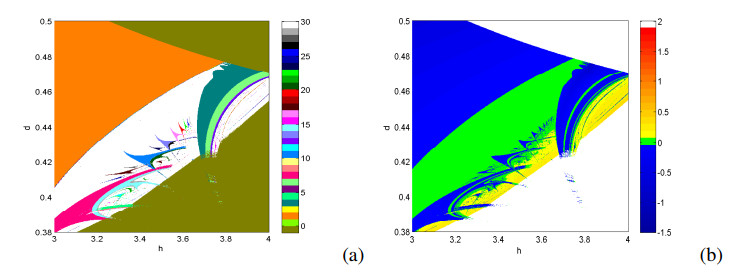
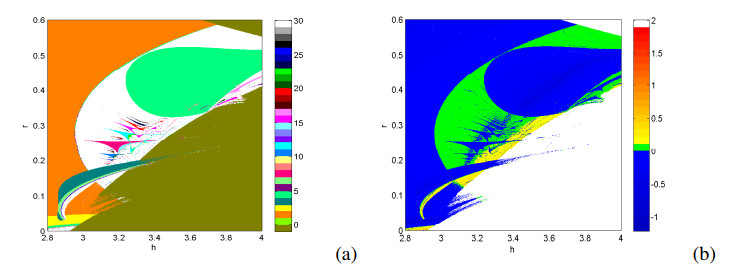
As we show, all our analytical predictions have excellent argument with the numerical results. And the above numerical simulations revel the dynamical behaviors of model (1.4) from the one-parameter bifurcation point of view. While chaos does not appear simply via a period doubling sequence. The bifurcation sequence is much more complex. It is very difficult to study this sequence from the one-parameter bifurcation point of view. Hence we imbed this one-parameter sequence into the $(h, \lambda)$-parameter space. Figure 6 shows a group of typical scenario of the parameter plane $(h, \lambda)$ for model (1.4), while holding all other parameters constant: $A = 1.2, \; d = 0.4, \; r = 0.24$. It is an isoperiodic diagram obtained by discretizing the parameter interval in a grid of $1000\times1000$ points equally spaced, which is generated numerically by using a method based on that described in ^{[27,28,29,30]}. For each point $(h, \lambda)$, an orbit of initial condition $(x_{0}, y_{0}) = (1.4222, 0.9861)$ converges to a chaotic, or to a quasiperiodic, or to a periodic attractor, or to an attractor at infinity (an unbounded attractor). If the trajectory initialized in $(x_{0}, y_{0})$ converges to infinity, that is diverges, which is described by dark green in Figure 6(a). As is well known, quasiperiodic solutions arise after a Neimark-Sacker bifurcation, which is not easy to obtain by isoperiodic diagram. Thus, the quasiperiodic regions are identified by Lyapunov phase diagram of Figure 6(b). Figure 6(b) represents Lyapunov phase, colorbar is associated with the magnitude of the largest Lyapunov exponent. In fact, Figure 6(a) and (b) are two complementary ways phase diagrams.

As shown in Figure 6, the periodic windows and the intermittent chaotic responses generate alternately. These phase diagrams unfold the detailed dynamics characteristics of the model (1.4). In this figure, it is obviously observable that periodic response alternates with chaotic response to produce some fractal structures. Compared to the codimension one bifurcation diagram, Figure 6 contains more information.

There are many parameters having a deterministic effect on the transitions of attractors in epidemic model. A natural question now is to ask, what relations of these parameters are? To this end, we extend a number of phase diagrams of other parameter combinations shown in Figures 7 and 8, where the color representations are as the same as Figure 6. There also exist chaotic regions embedded in period areas. We can also explore the alternation of the periodic and chaotic motion with the parameter changing.

5.   Conclusions

This paper investigates codimension-two bifurcations associated with 1:2, 1:3 and 1:4 strong resonances of a discrete-time SIR epidemic model. Our work can be seen as an extension of ^[20]. Although it is a simple discrete epidemic model, we find that there are many complex and abundant dynamical behaviors. The main results are included in Theorems 3.1–3.3. There are actually three types of codimension-two bifurcations including 1:2, 1:3 and 1:4 strong resonances. We realize that parameters $\lambda$ and $h$ have tremendous effect on the models equilibrium points. The numerical simulations represented in Section 4 show that the discrete epidemic model has plentiful kinetic characteristics. Good correlation between the numerical and theoretical results is found. Furthermore, the dynamic characteristics of the model in two-dimensional parameter space are analyzed, and the results show that we can more clearly and directly observe the chaotic phenomena, periodic phenomena. The results obtained in this paper are interesting and useful and may be applied to a variety of the life systems.

Acknowledgments

This work was partially supported by Tarim University President Fund (TDZKSS201904) and by Key Laboratory of Agricultural Engineering in Southern Xinjiang of Tarim University (TDNG20180301).

Conflict of interest

All authors declare no conflict of interest.