Risk-seeking insider trading with partial observation in continuous time

1.   Introduction

In Kyle's insightful pioneering paper ^[4], he gave a dynamic model of insider trading where a risk-neutral insider received a liquidation value of a fundamental asset, and found that at the market equilibrium, the insider slowly released her/his private information to obtain profit and incorporated all of the private information into market price at the end of trading. In fact, different agents have different risky preferences, which is an important factor in affecting the market equilibrium. In most cases, investors are assumed to be risk-averse by many researchers. Baruch ^[1] used an exponential utility to study risk-averse insider trading. Immediately afterward, Cho ^[2] selected the same utility function in a risk-averse insider trading market. Actually, there is much literature on risk-averse models ^[6,8,12].

However, the risk-seeking insider does exist in the actual trading process, due to the temptation of very high profits. For example, Tang et al. ^[5] gave an empirical research on CEO aggressive insider trading behavior and social media presence, and found that the aggressive insiders are risk-seeking. Moreover, Gong and Zhou ^[3] considered a multi-stage model of risk-seeking insider trading where they first maximized the risky profit, and then maximized the guaranteed profit.

Recently, Zhou ^[13] investigated a linear strategy equilibrium of continuous-time insider trading where market makers were allowed to know partial information on the risky asset, and pointed out that there was no equilibrium in a Cournot competition when two insiders adopted a linear strategy. Subsequently, Xiao and Zhou ^[9,10] expanded Zhou's model ^[13] and continued to study insider trading at a random deadline with partial observation.

In this paper, inspired by the literature above, we will continue to study a continuous-time insider trading model, in which an insider is risk-seeking and market makers are allowed to have partial information on the value of a risky asset, and establish the uniqueness and existence of linear Bayesian equilibrium. It shows that at the equilibrium, the market liquidity in our model is a monotonically increasing function of time, which contrasts to those in insider trading with a risk-averse insider ^[2,6].

The rest of the paper is as follows. In section two, a risk-seeking insider trading model with partial observation is introduced. Section three gives some necessary conditions of the linear Bayesian equilibrium. The main conclusions in this paper are contained in section four, including the existence and uniqueness of the linear Bayesian equilibrium. In section five, we get some numerical simulations for the equilibrium, and conclusions are drawn in section six.

2.   The model

We assume that all of random variables in this paper come from a common filtered probability space $(\Omega, {\cal F}, \{{{\cal{F}}_t}\}_{t\geq 0}, {\bf P})$ satisfying the usual conditions.

In a market, there is a risky asset traded in a finite time interval [0, 1], whose liquidation value $v$ is normally distributed with a mean of zero and variance $\sigma_v^2$. There are three representative agents in the market:

$({\rm{i}})$ an insider, who gets the perfect knowledge of the liquidation value $v$ and submits her/his order $x_{t}$, as in the form:

where $\beta$ is a deterministic measurable function, called trading intensity ^[4];

$({\rm{ii}})$ liquidity traders, who have no information on the value $v$ of the risky asset and submit total order $z_t$ evolving as the dynamics ^[2]:

where the constant $\sigma_z > 0$ and $B_{z}$ is a standard Brownian motion independent of $v$;

$({\rm{iii}})$ market makers, who collect the total orders

and observe a signal of the value $v$ as

with the random variable $\epsilon$ normally distributed as $N(0, \sigma_{\epsilon}^{2})$ and independent of $v$ and $B_{zt}$, and according to the trading volume $y_t$ and the signal $u$, set the market a local linear price $p$ satisfying

where $\lambda$ is a deterministic measurable function, called price pressure ^[1].

Roughly speaking, the insider's profit from time $t$ to one is given by

As a risk-seeking insider, she/he has an exponential utility function from time $t$ to one in the form

To ensure the well-posedness, the following three technical conditions must be guaranteed, $\int_0^1\beta_t^2dt < \infty,$ $\int_0^1\lambda_t^2dt < \infty$ and $E (\exp^{\int_t^1\beta_s(v-p_s)^2ds}) < \infty$. Next, we will give the concept of an equilibrium in our model.

Definition 2.1. A risk-seeking linear Bayesian equilibrium is a pair of $(\beta, \lambda)$ such that

($i$) maximization of utility: for the given $\lambda$, the function $\beta$ maximizes

where the insider's information field ${\cal F}^I_{t} = \sigma\{v\}\vee\sigma\{p_s, 0\leq s\leq t\}$ for $t\in[0, 1)$, and

($ii$) market efficiency: for the given $\beta$, the function $\lambda$ satisfies

where ${\cal F}_t^{M} = \sigma\{y_s, 0\leq s \leq t\}\bigvee \sigma\{u\}$ for $t\in[0, 1)$.

3.   Necessary condition for market efficiency

Unquestionably, the signal-observation system for market makers is given by

where $\xi_{t} = \begin{pmatrix} y_{t} \\ u \end{pmatrix}$, $\xi_{0} = \begin{pmatrix} 0 \\ v+\epsilon \end{pmatrix}$, $A_{0} = \begin{pmatrix} -p_t\beta_{t} \\ 0 \end{pmatrix}$, $A_{1} = \begin{pmatrix} \beta_{t} \\ 0 \end{pmatrix}$, $A_{2} = \begin{pmatrix} \sigma_{z} & 0 \\ 0 & 0 \end{pmatrix}$, $B_t = \begin{pmatrix} B_{zt} \\ 0 \end{pmatrix}$.

By Theorem 12.1 in ^[7] and Lemma 3.1 in ^[9], we obtain

where $\lambda_t = \frac{\Sigma_{t}\beta_{t}}{\sigma_{z}^{2}}$, and

where $\Sigma_{t} = E[(v-p_t)^{2}]$ with $\Sigma_0 = \frac{\sigma_{\epsilon}^{2}\sigma_{v}^{2}}{\sigma_{v}^{2}+\sigma_{\epsilon}^{2}}$, which is called residual information ^[4].

4.   Existence and uniqueness of linear Bayesian equilibrium

We now turn to investigate the risk-seeking linear Bayesian equilibrium.

Let $(\beta, \lambda)$ be a linear Bayesian equilibrium. From Definition 2.1, the insider's value function is given by for $t\in[0, 1]$

where ${\cal U}(t, \beta)$ is the collection of all these functions $\tilde{\beta}$ such that $\tilde{\beta}_s = \beta_s$ for $0\leq s\leq t$, and the two conditions for (4.1) are needed

Of course, the first is obvious, and the second can be inferred by (3.2), (3.3) and the equality $\lim_{t\to 1_{-}}\Sigma_{t} = 0$.

The following conclusion is the stochastic version on Bellman's principle of optimality for above insider trading problem.

Proposition 4.1. Given $t\in [0, 1)$, for $\hat{t}\in [t, 1]$

Proof. From (4.1), we have

□

By the dynamic programming principle, the insider's optimal condition is portrayed as follows.

Proposition 4.2. If the value function of insider is determined by Proposition 4.1, then the Hamiton-Jacobi-Bellman ($HJB$ for short) equation will be given by

Proof. Applying $It\hat{o}s$ formula to the difference $V(\hat{t}, v-p_{\hat{t}})- V(t, v-p_{t})$, and as $\hat{t}-t\rightarrow o$, the limit of

is equal to $\beta_t{{(v-p_{t})}}^{2}$. Then, using the $HJB$ equation ^[11], the conclusion holds. □

Proposition 4.3. If the value function satisfies (4.5), then it will be given by

where

the two constants $c_1$ and $c_2$ satisfy the following two equations, respectively

and

Proof. We know that (4.5) is equivalent to the following two equations:

The second equation of (4.7) can be viewed as an ordinary differential equation with respect to $p_t$, which has a solution of the form

where $g(t)$ is a deterministic function on [0, 1].

Substituting (4.8) into the first equation of (4.7), we can obtain the equation

which is equivalent to

Taking expectation for the above equation, the following two equations hold:

Then, by the first equation of (4.9),

where $\frac{1}{\lambda_{0}} = c_1$ is some constant real number. We now bring (4.10) into the second equation of (4.9)

where $g_{0} = c_2$ is some constant real number. According to the boundary conditions in (4.2), the constant $c_{1}$ can be solved by the following system:

Namely,

by (4.10), we assert

and

□

Theorem 4.1. There is a unique linear equilibrium $(\beta, \lambda)$ satisfying

At the equilibrium, the residual information $\Sigma_{t}$ at time t is

and the insider's total ex ante utility

where

and

Proof. By the optimal filtering theorem ^[7], we have

Taking (4.10) into (4.14), we have

Again, together with (4.14), we obtain

By the properties of expectation and the expression of $c_{2}$

where

The proof is complete. □

Corollary 4.1. At the equilibrium $(\beta, \lambda)$ in Theorem 4.1, the following results hold:

(i) As the time goes by, both the optimal trading intensity and the market liquidity increase, while the residual information decreases.

(ii) Given a fixed time, the less partial observation accuracy, then the weaker the optimal trading intensity is, while the stronger both the market liquidity and the residual information are.

Proof. Omitted. □

5.   Numerical simulation

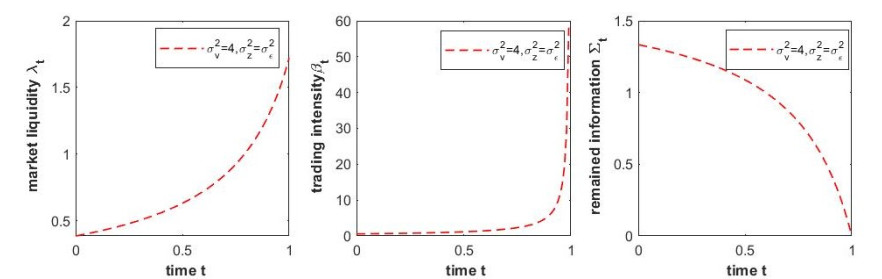
In Corollary 4.1, we gave some theoretical characteristics of the equilibrium. Next, we will give numerical simulations on the equilibrium. First of all, we assume $\sigma_v^2 = 4$.

In Figure 1, as time $t$ goes by, insider's private information slowly releases even time close to zero. Beside that, we find that the private information is released slowly at the beginning and rapidly at the end, which explains why the trading intensity will be strong at last. Different from risk-aversion, the market liquidity increases with time going by when the insider is risk-seeking. According to the views of economics, as the market liquidity becomes strong, the market activity will increase, and the market price will remain relatively stable. Moreover, it is beneficial for market makers to obtain more sample information and contribute to market auction; that is, the risk-seeking insider can make the market more active.

Next, we will give numerical simulations on partial observation accuracy as given below.

In Figure 2, as the accuracy of partial observations decreases, the residual information of market increases. Therefore, the more residual information for the insider, then the weaker the trading intensity, such that the insider can obtain higher profits, corresponding to case (ⅱ) in Corollary 4.1.

6.   Conclusions

In this paper, we established the uniqueness and existence of the linear Bayesian equilibrium for a continuous-time insider trading model, in which an insider is required to be risk-seeking and the market makers can observe partial signals on the risky asset.

It shows that at the equilibrium, (ⅰ) as time goes by, both the market liquidity and the trading intensity increased quickly in the later trading and the residual information decreased slowly at the beginning. In fact, the characteristic of market liquidity indicated that the insider was willing to trade, and that they had a stronger desire to trade when there was less residual information, and (ⅱ) the residual information and the partial observation accuracy have a relative relationship. In other words, the worse the partial information on the risky asset received by market makers, the more residual information relatively the insider owns. Further, the market liquidity decreased if market makers observed more accurate information on the risky asset.

We remarked that our model extended Kyle's version (1985) ^[4] from the risk-seeking perspective. In Kyle's model, the market liquidity was always a constant, while the market liquidity was a decreasing function of time in the models of risk-aversion ^[1,2,6]. In contrast to those in the above models ^[1,2,4,6], the market liquidity in our model was an increasing function of time. This indicates that the insider was eager to trade in the latter. Generally speaking, it is beneficial for market development when the insider increases appropriately for her/his risk appetite behavior, and the insider should try their best to avoid private information exposure. In the future, we will try to study a risk-seeking insider trading model with memory, which will be a challenging research.

Use of AI tools declaration

The author declares that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Supported by Guizhou QKZYD[2022]4055, the innovative exploration and new academic seedling project of Guizhou University of Finance and Economics (No. 2022XSXMB25).

Thanks to Professor Yonghui Zhou, who carefully revised our manuscript, and provided many suggestions and assistance on the review comments.

Conflict of interest

The author declares no conflict of interest in this paper.