Electroencephalogram based face emotion recognition using multimodal fusion and 1-D convolution neural network (ID-CNN) classifier

1.   Introduction

Over the past few decades, relentless research in quantum computing (QC) has borne fruit in the form of remarkable advancements in the QC industry. These developments have garnered significant attention from both academic ^[1,2,3] and industrial ^[4,5,6,7] spheres, establishing QC as a focal point of contemporary research and development. QC, which harnesses the principles of superposition, entanglement, and parallelism to perform computations, promises substantial advantages over classical computing in specific problem domains such as discrete logarithm calculation, integer factorization, eigenvalue estimation, and problems involving fractals and fractional calculus ^[8,9,10]. The proliferation of various quantum algorithms ^{[11,12,13,14]} has further accelerated the expansion of QC applications across diverse fields.

However, the current state of QC devices has yet to reach the level of practical, large-scale quantum computers and quantum networks due to scalability and error correction issues. These challenges remain significant obstacles in QC research. To address this gap, there has been a surge in research and development aimed at emulating quantum algorithms using classical computing resources ^[15]. These QC emulators serve a critical role in bridging the gap until fully operational QC devices become available. More in detail, QC emulators enable rapid experimentation and prototyping of quantum circuits, algorithms, and applications. Traditionally, classical QC emulators have relied on large-scale, resource-intensive, and expensive emulation platforms ^[16,17]. In contrast, contemporary QC emulators are increasingly utilizing Field-Programmable Gate Arrays (FPGAs) for more efficient, scalable, and cost-effective hardware-accelerated quantum algorithm emulation ^{[12,15,18,19]}. The inherent cost-effectiveness, high performance, and reconfigurability of FPGAs make them an attractive choice for this purpose.

Despite these advantages, significant challenges remain in implementing FPGA-based QC emulators, mainly due to the limited resources of FPGAs relative to the high demands of QC emulators. Quantum states and operations in quantum computers, represented as vectors and matrices, respectively, scale exponentially with the number of qubits ^[20]. This exponential growth necessitates substantial computational resources for storage and processing, making it impractical for low-performance (low-end) FPGAs. While high-performance (high-end) FPGAs with extensive resources are available, they are costly and still have limited capacity. { Furthermore, as the advancement of various quantum algorithms is expected to extend QC applications into low-power, low-performance devices such as IoT end nodes, embedded systems, and wearable devices, current FPGA-based QC emulators, which are typically used as accelerator modules in systems with external high-performance CPUs and large memories, are not suitable for these compact devices. These devices require a compact, standalone solution that can execute QC without relying on external CPUs or large memory resources. Therefore, research focused on creating a fully self-contained system, integrating a CPU, memory, peripherals, and a QC-specific accelerator into a single compact platform, is essential to meet these requirements.}

To address these challenges, the goal of this paper is to propose resource optimization techniques for QC emulators and to realize a standalone QC emulator on FPGAs by applying these techniques. To achieve the goal, we first select Grover's quantum algorithm ^[21] as the target application, as it is expected to be highly active in embedded systems among the various existing QC algorithms. Grover's algorithm performs unstructured data searches on quantum computers. In contrast to classical computers, where searching a dataset of size $N$ requires $O(N)$ function calls, Grover's algorithm on a quantum computer can accomplish the search in $O(\sqrt{N})$ calls. This represents a quadratic reduction in the number of operations compared to classical computers, making it the most optimal search algorithm ^[22]. Therefore, this algorithm is expected to significantly enhance the utility of quantum computers by enabling the search of large datasets that are impractical for classical computers, such as finding specific shapes or features within fractal structures and accelerating calculations for finding specific solutions in fractional calculus using quantum algorithms ^{[10,23,24,25,26,27]}.

Next, in this study, we develop optimization techniques to emulate Grover's algorithm with minimal resources. Based on the fact that the fast searching efficiency of the Grover's algorithm is proportional to the size of the system implementing the algorithm, the resource optimization algorithm makes a significant contribution to enhancing the performance of the emulator by enabling the implementation of the largest possible Grover's algorithm system using limited resources. Specifically, Grover's search progresses by repeatedly applying a specific operation, represented by matrix $G$, to an initial state vector. We discovered that by leveraging the characteristics of $G$, we can reduce both the computational load and resource requirements when emulating Grover's algorithm. First, $G$ represents real-number operations, ensuring that the resulting values remain real for initial state vectors within the real range. Additionally, $G$ can be decomposed into the product of an Oracle matrix and a Diffusion matrix. The application of the diffusion matrix to any vector can be computed using simpler basic operations rather than full matrix-vector multiplication. Furthermore, the vector resulting from repeated applications of $G$ can have a dominant basis state close to 1, allowing for approximate probability calculations. Alongside these Grover-specific optimizations, we propose overall optimization techniques that include the application of fixed-point representation to further reduce the emulator's resource demands. Ultimately, the optimization techniques tailored to Grover's algorithm are realized through the synergistic combination of four detailed steps.

Finally, we design a hardware IP, termed the Grover accelerator, to incorporate the proposed optimization techniques and develop a system-on-chip (SoC) platform to achieve the targeted standalone Grover's algorithm emulator on FPGAs. We designed the Grover accelerator to perform the algorithm approximately 191 times faster than a software implementation for a 4-qubit system. By integrating this accelerator with a RISC-V processor, we developed the emulator and programmed it onto a high-performance and resource-rich Kintex Ultrascale+ FPGA. As a result, while traditional methods could implement a maximum of 4-qubit emulators on this FPGA, our optimized techniques enabled the implementation of a 6-qubit emulator. Additionally, we programmed the emulator on a low-performance and resource-limited Arty A7 FPGA. The results showed that, compared to the traditional method's limit of a 2-qubit emulator, our optimization techniques enabled the implementation of up to a 4-qubit emulator, thereby demonstrating the superior resource-saving effectiveness of the proposed techniques.

The remainder of the paper is organized as follows. Section 2 introduces the fundamental concepts of QC states and operations, and based on these, briefly explains the principles of the Grover's algorithm. Section 3 proposes resource optimization techniques for emulation derived from the operational characteristics of the Grover's algorithm. Section 4 describes in detail the design and implementation of the hardware emulator applying the proposed techniques. Section 5 evaluates the resource-saving superiority and performance enhancement of the proposed techniques using various developed FPGA prototype emulators. Section 6 is dedicated to providing the conclusions of this study.

2.   Quantum computing and quantum search algorithm: a preliminary

2.1.   Qubit and quantum gate

Just as classical computing uses bits as the basic unit of information, QC uses quantum bits, or qubits, as their fundamental unit. However, while a bit in a classical computer can only be in one of two states, 0 or 1, a qubit can exist in both the states $|0\rangle$ and $|1\rangle$, which are called basis states of the single qubit quantum system, simultaneously. This phenomenon is known as superposition in QC and is a key property that gives quantum computers their superiority over classical computers. The superposed state of a qubit can be represented as a column vector $|\psi\rangle$ with $|0\rangle$ and $|1\rangle$ as basis states:

where $\alpha$ and $\beta$ are arbitrary complex numbers such that the sum of the squares of their Euclidean norm is equal to 1.

The state of a system comprising multiple qubits can also be defined. When $n$ qubits are arranged in sequence to form a single system, each qubit can be in one of two basis states, $|0\rangle$ and $|1\rangle$. Consequently, the total number of basis states for the system defined by $n$ qubits is $N = 2^n$. The general expression representing the superposition of all basis states in such a system is given by:

where $\alpha_0, \alpha_1, \ldots, \alpha_{N-1}$ are complex numbers that satisfy $\sqrt{\sum_{i = 0}^{N-1}{\|\alpha_i\|^2}} = 1$.

Meanwhile, the coefficients ($\alpha_i$) of each basis state in the system represent the probability of measuring that specific basis state. When a system in a superposition of multiple basis states is measured, it 'collapses' to one of the basis states. That is, the state of the system is randomly determined to be one of the possible basis states. The probability of each basis state $|i\rangle{}\ (i = 0, 1, \ldots{} N-1)$ being determined from an arbitrary state $|\psi{}\rangle{}$ is given by $|\langle{}i|\psi{}\rangle{}|^{2}$, where $\langle{}i|\psi{}\rangle{}$ represents the inner product between $|i\rangle{}$ and $|\psi{}\rangle{}$. If the coefficient $\alpha_{i}$ is known, the same probability can be calculated by squaring the amplitude of the coefficient, which is $\|\alpha{}_{i}\|^{2}$, the Euclidean norm of $\alpha_{i}$. Thus, the probability can be expressed as shown below:

Therefore, due to the properties of probabilities, the following equation is satisfied:

Next, the basic operations applied to qubits in QC can be represented by unitary matrices. Therefore, the result of applying an operation to a system in a specific state can be calculated as a matrix-vector multiplication. Table 1 shows some of the commonly used basic operations for one and two qubits along with their matrix representations.

If $U_i$ denotes a single-qubit quantum gate applied to the $i$-th qubit ($i = 1, 2, \ldots, n$), the matrix representation $U$ of the operation on an $n$-qubit system, resulting from the simultaneous application of $U_1, U_2, \ldots, U_n$ to the $n$ qubits, is obtained using the Kronecker product as follows:

2.2.   Grover's quantum searching algorithm

Grover's algorithm performs data search on a quantum computer to find the value of $x$ that satisfies $f(x) = 1$ for a given function $f(x)$, as follows:

where $s$ is the unique value that satisfies $f(s) = 1$.

In a system of $n$ qubits, the $G$ operation is repeatedly applied $k$ times to the initial state where all basis states are uniformly superposed. Here, $k$ is determined by $n$ and is derived from the following equation:

where the notation $\lfloor{} \rceil{}$ means the number rounded to the nearest integer. As a result, the coefficient of the basis state $|s\rangle$ corresponding to the value $x$ that satisfies $f(x) = 1$ ($x = s$) becomes large, while the coefficients of the other basis states approach zero. Therefore, by measuring the state of the system after completing the Grover iterations, the value of $x$ that satisfies $f(x) = 1$ can be obtained with very high probability.

Next, the operations of Grover's algorithm can be expressed as follows ^[28]:

where $|0^{n}\rangle$ denotes the basis state where all $n$ qubits of the system are in the $|0\rangle$ state, and $H^{\otimes n}$ represents the operation of applying the Hadamard gate $H$ to all $n$ qubits simultaneously.

The $G$ operation consists of the Oracle gate, represented by $Z_{f}$, and the Diffusion gate, represented by $H^{\otimes n}Z_{or}H^{\otimes n}$. The Oracle gate inverts the phase of the basis state $|s\rangle$ for which $f(s) = 1$, while the Diffusion gate inverts the coefficients of all basis states about the average of the coefficients. The operation of the Oracle gate $Z_{f}$ can be expressed as follows:

{In addition, the operation of the Diffusion gate $H^{\otimes n}Z_{or}H^{\otimes n}$ can be expressed with the notation $|n\rangle{}$ which refers to a uniform superposition state. Specifically, it represents an equal superposition of all computational basis states, where each basis state $|i\rangle{}$ ($i = 0, 1, \ldots, N-1$) is included with an equal probability amplitude. Mathematically, this can be written as:}

where $|0^{n}\rangle{}$ represents the quantum state in which all $n$ qubits are in $|0\rangle{}$ states. With this notation, and $\langle{}n| = |n\rangle{}^{\dagger{}}$, where $\dagger{}$ means conjugate transpose, the equation for the Diffusion gate is given as follows:

3.   Resource optimization techniques for the Grover's algorithm emulator

The parallel hardware computation structure of FPGAs is well-suited to mimic the natural parallelism arising from the superposition and entanglement phenomena in quantum mechanics. Additionally, the high cost-efficiency and reconfigurability of FPGAs provide a foundation for extending the realm of QC into the domain of embedded systems. However, as the number of qubits in the quantum computer being emulated increases, the number of basis states that the emulator must store and process grows exponentially. Consequently, the traditional approach of representing quantum states and operations as vectors and matrices becomes highly constrained within the resource limits of an FPGA.

To address this issue, we propose techniques to optimize resources and reduce computational overhead for FPGAs, specifically targeting Grover's algorithm. The proposed techniques consist of four detailed sub-techniques.

3.1.   Efficient real number representation

In a quantum system, the coefficients of the superposed basis states are generally expressed in the complex number domain. To represent these coefficients as complex numbers in a QC emulator, register blocks must be allocated to store the real and imaginary parts of the coefficients, which are represented as real numbers. This doubles the consumption of register resources compared to using real numbers alone. Consequently, the required register resource amount for the emulator also doubles.

Additionally, the number of real number operations required for addition and multiplication of complex numbers is greater than for operations involving real numbers only. In the case of complex addition, as shown in Figure 1a, two real additions are required: one for the real parts and one for the imaginary parts. For complex multiplication, calculating the real and imaginary parts requires two real multiplications and one real addition for each part, as illustrated in Figures 1b and 1c. When calculating the real part, the real and imaginary parts of one complex number are each multiplied by the corresponding parts of the other complex number. For the imaginary part, each part of one complex number is multiplied by the counterpart of the other complex number. The resulting pairs of real numbers from these multiplications are then added (or subtracted) to produce the final real and imaginary parts of the complex multiplication result.

ADD_Original and MULT_ORIGINAL in Algorithm 1 are algorithms for complex-based addition and multiplication. We can clearly confirm that ADD_Original requires 2 real number additions, while MULT_ORIGINAL requires 4 real number multiplications and 2 real number additions. The correctness of Algorithm 1 is as follows:

Theorem 1. Correctness of Algorithm 1

Let $\alpha = \alpha_{Re} + i\alpha_{Im}$ and $\beta = \beta_{Re} + i\beta_{Im}$ be two complex numbers where $\alpha_{Re}, \alpha_{Im}, \beta_{Re}, \beta_{Im} \in \mathbb{R}$. $\text{ADD_ORIGINAL}$ and $\text{MULT_ORIGINAL}$ correctly computes the addition and multiplication of two complex numbers in terms of their real and imaginary parts.

Proof. For addition, let $\psi = \alpha + \beta$. The real and imaginary parts of the sum are computed as:

ADD_ORIGINAL correctly performs this computation by independently summing the real and imaginary parts. Therefore, the correctness of the addition is guaranteed by the definition of complex number addition.

For multiplication, let $\psi = \alpha \cdot \beta$. Using the formula for complex multiplication:

MULT_ORIGINAL correctly computes these values by performing two real multiplications and one real addition for each part, following the standard procedure for complex number multiplication.

Thus, the algorithm follows the mathematically correct method for complex number addition and multiplication, ensuring that the results are correct. □

To perform operations on coefficients expressed as complex numbers in the emulator, more operations and thus more clock cycles are required compared to real number operations. Arranging the real number operation hardware in parallel to reduce clock cycles increases the resource requirements of the FPGA, which is not suitable for the design of the compact emulator targeted in this paper. Specifically, in the case of Grover's algorithm, the coefficients of the states remain real throughout all operations. The complex coefficients only have phases of 0 or $\pi$, which can be represented as the sign of the real-valued coefficients ^[29]. Therefore, the imaginary part of the coefficients can be disregarded in Grover's search. This is possible because the basic operations constituting the $G$ operation of Grover's algorithm-$H$ (cf. Table 1), $Z_{or}$ in Eq (2.12), and $Z_{f}$ in Eq (2.9)-all have real matrix coefficients. As a result, reducing the coefficients to real numbers in the emulator for Grover's algorithm does not lead to any loss of information.

Therefore, to achieve resource optimization for the emulator, we propose adopting a real representation of the coefficients of the basis states, considering the characteristics of Grover's algorithm. Unlike an universal QC emulator, which allocates register blocks for both the real and imaginary parts of each coefficient and performs complex arithmetic, we propose excluding the imaginary part registers and retaining only the real parts. ADD_PROPOSED and MULT_PROPOSED in Algorithm 2 demonstrate addition and multiplication performed solely with real numbers. The correctness of Algorithm 2 can be stated as follows:

Theorem 2. Correctness of Algorithm 2

Let $\alpha$ and $\beta$ be real numbers. $\text{ADD_PROPOSED}$ and $\text{MULT_PROPOSED}$ correctly computes the addition of real numbers $\alpha + \beta$ and the multiplication of real numbers $\alpha \times \beta$, respectively.

Proof. ADD_PROPOSED adds $\alpha$ and $\beta$ directly as $\psi = \alpha + \beta$, and MULT_PROPOSED multiplies $\alpha$ and $\beta$ directly as $\psi = \alpha \times \beta$. Since the addition and multiplication of real numbers are well-defined operations in $O(1)$, these prove the correctness of the addition and multiplication operation in Algorithm 2. □

ADD_PROPOSED requires only a single real addition, and MULT_PROPOSED requires only one real multiplication, significantly reducing the computational load compared to ADD_ORIGINAL and MULT_ORIGINAL. While both Algorithms 1 and 2 have a time complexity of $O(1)$, the proposed method focuses not on reducing time complexity, but rather on minimizing the number of fundamental operations required for each arithmetic task, thereby reducing the overall computational load of the emulator. This approach not only reduces the hardware resources needed for arithmetic units but also shortens the execution time of the emulator's operations without consuming additional hardware resources like registers. By using real arithmetic for all operations in Grover's algorithm, we aim to achieve faster execution times while maintaining the integrity of the basis state information, without increasing the use of resources such as arithmetic units and registers.

3.2.   Fixed-point expression

Applying the proposed Efficient Real Number Representation, we can consider representing the coefficients using single precision floating-point format ^[30], as shown in Figure 2. However, floating-point arithmetic incurs significant overhead. When performing operations between two floating-point numbers, normalization must adjust the mantissa and exponent of the operands to enable the operation. Additionally, exceptions must be handled, and the result must be appropriately rounded according to the standard. More specifically, Algorithm 3 presents the algorithms for Floating-point addition (FLOAT_ADD) and multiplication (FLOAT_MULT) for the coefficients of the quantum state. The following theorem proves correctness of Algorithm 3:

Theorem 3. Correctness of Algorithm 3

Addition: Let $a$ and $b$ be two floating-point numbers represented by their sign, exponent, and mantissa:

Theorem 3.1. FLOAT_ADD correctly computes the addition of floating-point numbers $a + b$.

Proof. The algorithm extracts the sign, exponent, and mantissa for $a$ and $b$, aligning the exponents by shifting the mantissa of the smaller exponent:

or vice versa. The mantissas are added or subtracted depending on the signs of $a$ and $b$:

After normalization (shifting the mantissa and adjusting the exponent if necessary), the result is obtained. Since addition of floating-point numbers is well-defined, this proves the correctness of the algorithm for floating-point addition.

Multiplication: Let $a$ and $b$ be two floating-point numbers.

Theorem 3.2. FLOAT_MULT correctly computes the multiplication of floating-point numbers $a \times b$.

Proof. The sign of the result is calculated as:

where $\oplus$ represents the XOR operation. The exponents are added:

and the mantissas are multiplied:

Normalization ensures the mantissa is adjusted so that the most significant bit is set. In case of overflow, the mantissa is shifted and the exponent incremented. The final result is formed by combining the sign, exponent, and mantissa. Thus, Algorithm 3 correctly computes the multiplication of floating-point numbers, proving its correctness for floating-point multiplication.

Through Algorithm 3, we can observe that floating-point operations involve several steps, including the manipulation of exponents and mantissas, normalization, and rounding. In addition to multiple real number additions, comparison operations for conditional branches (if-else) and bit shifts are also required during this process. This ultimately leads to increased execution time and resource demands for the emulator.

As an alternative, a fixed-point representation of real numbers can be adopted. In fixed-point representation, the bit string used to represent an integer (excluding the sign bit, $S$) is divided into an integer part ($int.$) and a fractional part ($fraction$) to represent real numbers. Given the total number of bits allocated for $int.$ and $fraction$, the range and resolution of the represented real numbers are determined by the number of bits assigned to each part. Allocating more bits to $int.$ allows for representing a wider range of real numbers, while allocating more bits to $fraction$ allows for representing real numbers with higher resolution. These two aspects are in a trade-off relationship, so bits are assigned appropriately to each part based on the needs. Then, from Eq (2.3), we know that the absolute value of the coefficient of a basis state in a QC emulator is less than or equal to 1. Therefore, only one bit may be enough for $int.$ to represent the coefficient in fixed-point format, allowing relatively more bits to be allocated to $fraction$. Consequently, representing coefficients in fixed-point format can allow for storing and processing them with high accuracy without loss of information within the representable range of real numbers.

Meanwhile, fixed-point representation can have significant advantages over floating-point representation, especially for multiplication by powers of two. Multiplication is an operation that causes considerable overhead in hardware design. The simplest serial multiplier requires $i$ clock cycles to perform addition operations for multiplying $i$-bit integers. To optimize execution time of such multiplier, the hardware complexity of the multiplier must be increased. Multiplication of real numbers represented in floating-point format also involves integer multiplication to obtain the mantissa, along with additional hardware and clock cycles for normalization, rounding, and exception handling. Thus, multiplication of floating-point numbers is evidently a high-overhead operation.

As an alternative, we can consider replacing the multiplication of arbitrary integers by powers of two with bit-shift operations. The bit-shift operation shifts the bit string stored in a register block left or right by a certain distance $l$, resulting in multiplying (left shift) or dividing (right shift) the integer represented by the bit string by $2^l$. Bit-shift operations are implemented very simply through wiring changes and can be completed within a single clock cycle, thus offering high execution speed.

Finally, we propose applying fixed-point representation to express coefficients in the emulator and replacing multiplications by powers of two with bit-shift operations during the $G$ operations. Specifically, as shown in Figure 3, the emulator represents coefficients by allocating 1 bit each to $S$ and $\text{Int.}$, and the remaining 30 bits to the fractional part. This approach ensures high resolution of $2^{-30} (\approx 10^{-9}$) while reducing the computational overhead compared to floating-point representation. Algorithm 4 presents the proposed fixed-point addition (FIXED_ADD) and multiplication (FIXED_MULT_2_EXP) algorithms. The proof of the algorithm is as follows:

Theorem 4. Correctness of Algorithm 4

Addition: Let $a$ and $b$ be real numbers.

Theorem 4-1. FIXED_ADD correctly computes the fixed-point addition of real numbers $a$ and $b$.

Proof. The algorithm converts the real numbers $a$ and $b$ to fixed-point representations, $fixed_a = \left\lceil a \times 2^{30} \right\rceil$ and $fixed_b = \left\lceil b \times 2^{30} \right\rceil$. The fixed-point representations are then added directly as:

Since addition of fixed-point numbers is equivalent to integer addition after scaling, the algorithm correctly computes the addition of the real numbers $a$ and $b$ in fixed-point form.

Multiplication: Let $a$ be a real number and $2^k$ represent a power of two.

Theorem 4-2. FIXED_MULT_2_EXP correctly computes the fixed-point multiplication of $a$ and $2^k$.

Proof. The algorithm first converts the real number $a$ to a fixed-point representation:

It then multiplies by $2^k$ using a bit-shift operation, which is equivalent to multiplying by a power of two:

This correctly computes the multiplication of $a$ by $2^k$ in fixed-point representation. Since bit-shift operations are computationally efficient, the algorithm correctly performs the multiplication with minimal computational complexity.

From Algorithm 4, fixed-point operations only require a single real number operation, making them significantly more resource-efficient compared to the number of operations required in Algorithm 3. Similar to the Real Number Representation method introduced earlier, while the complexity of both Algorithms 3 and 4 is $O(1)$, the aim of the proposed Fixed Point Expression method is not to reduce time complexity but to lower the number of basic operations required for each computation. This approach is intended to reduce the overall computational load of the emulator when performing these operations repeatedly.

3.3.   Matrix-vector multiplication decomposition

Matrix-vector multiplication is another well-known overhead-intensive operation. For the emulation of an $n$-qubit QC with $N = 2^n$ distinct states, the multiplication of an $N \times N$ matrix by an $N \times 1$ vector required for a single quantum gate involves $N^2$ real multiplications and $N(N-1)$ real additions. Notably, as $n$ increases, $N$ grows exponentially, leading to a single quantum gate operation exhibiting a complexity of $O(2^{2n})$. This complexity is calculated under the assumption that real multiplications have a complexity of $O(1)$ compared to additions, implying that the actual computational overhead will escalate even more sharply. Furthermore, in the case of Grover's algorithm, the $G$ operation composed of four quantum gates must be repeated $k$ times as per Eq (2.7), further increasing the total computational complexity of the emulator.

In Algorithm 5, CONV_MATRIX_VECTOR_MULT demonstrates the matrix-vector multiplication algorithm for a single G operation, the correctness of which can be proven as follows:

Theorem 5. Correctness of the conventional matrix-vector multiplication in the G operation

Proof. Let $M$ be an $N \times N$ matrix representing an arbitrary single quantum gate, where $N = 2^n$, and let $v$ be an $N \times 1$ vector representing the quantum state. The matrix-vector multiplication is defined as:

The matrix-vector multiplication proceeds by iterating over each row $i$ of the matrix and computing the dot product of the $i$-th row of $M$ with the vector $v$. Specifically, for each $i$, we compute:

This is a well-defined operation in linear algebra and ensures that the multiplication of the matrix $M$ with the vector $v$ produces the expected output vector. Each element $result[i]$ is the result of summing the products of corresponding elements from row $i$ of the matrix and the vector $v$. By iterating through all $N$ rows, CONV_MATRIX_VECTOR_MULT correctly computes the result of the matrix-vector multiplication. Thus, the algorithm satisfies the correctness condition for matrix-vector multiplication. □

As shown in Algorithm 5, CONV_MATRIX_VECTOR_MULT requires matrix-vector multiplication for the three basic quantum gates (two Hadamard gates and one $Z_{or}$) that make up the G operation. As a result, the total number of real addition and multiplication operations required is $3N(N-1)$ and $3N^2$, respectively, and this computational load increases exponentially with the number of qubits, i.e., the complexity is $O(N^2)$. In other words, implementing a general-purpose emulation framework based on matrix-vector multiplication on a standalone FPGA-based QC emulator is almost impossible.

As an alternative, we leverage the properties of the diffusion matrix in Grover's algorithm to express matrix-vector multiplication as a datapath model ^[31], thereby decomposing the complex matrix-vector multiplication into simpler operations. The diffusion gate in the $G$ operation can be expanded as Eq (2.11). Using this equation, the application of the $G$ operation to an arbitrary state $|\psi\rangle$ can be decomposed as follows:

where, $|\phi{}\rangle{} = Z_{f}|\psi{}\rangle{} = \begin{bmatrix} \beta_{0} & \ldots{} & \beta_{N-1} \end{bmatrix}^{T}$.

In Eq (3.1), the first term on the right-hand side can be computed through accumulation ($\sum_{i = 0}^{N-1}\beta_{i}$) and bit-shift ($2^{-n+1}$), followed by subtraction with the second term (i.e., $-\begin{bmatrix} \beta_{0} & & \ldots{} & & \beta_{N-1} \end{bmatrix}^{T}$) to ultimately obtain the set of coefficients for $G|\psi\rangle$. Therefore, the matrix multiplication $H^{\otimes n}Z_{or}H^{\otimes n}$ required to emulate the diffusion gate can be decomposed into basic operations, as shown in Figure 4. These decomposed basic operations consist solely of real additions and bit-shifts. As discussed in Section 3.2, additions and bit-shifts for fixed-point real numbers are less demanding in terms of computational requirements and hardware resources compared to multiplications.

Finally, Algorithm 5's PROPOSED_DECOMP_G_OPERATION presents the proposed algorithm for a single G operation. The correctness of this algorithm can be stated as follows:

Theorem 6. Correctness of the proposed decomposition in the G operation

Proof. In the conventional matrix-vector multiplication for Grover's algorithm, the $G$ operation requires multiplying an $N \times N$ matrix by an $N \times 1$ vector, which results in $N^2$ real multiplications and $N(N-1)$ real additions. Given that $N = 2^n$ for an $n$-qubit quantum system, the computational complexity is $O(2^{2n})$. The proposed decomposition leverages the structure of the $G$ operation to reduce the computational load. Instead of performing direct matrix-vector multiplication, the algorithm computes the sum of all vector elements and then adjusts each element accordingly.

Let $v[i]$ be the $i$-th element of the input vector. The decomposition works as follows:

(1). Compute the accumulator:

This requires $N$ real additions.

(2). For each $v[i]$, compute:

This involves one division and $N$ real subtractions.

As a result, the total number of operations consists of i) $N$ real additions for the accumulator, ii) one division, and iii) $N$ real subtractions. This reduces the complexity from $O(N^2)$ of CONV_MATRIX_VECTOR_MULT to $O(N)$, as the proposed decomposition avoids the need for $N^2$ multiplications and $N(N-1)$ additions. Thus, the correctness of the proposed decomposition is proven, and the significant reduction in computational complexity is established. □

Through Algorithm 5, we can confirm that it requires only $2N$ addition operations and a single bit shift, which demonstrates significant resource savings and execution speed improvements compared to CONV_MATRIX_VECTOR_MULT. Therefore, for the purpose of achieving the compact emulator we aim for, we propose a matrix-vector multiplication decomposition based on Eq (3.1).

3.4.   Resource-efficient measurement approximation

The Grover's algorithm is completed by measuring the state of the system after iterative $G$ operations. To emulate the measurement of the system state, we need to square the coefficients of each basis state according to Eq (2.3) to obtain the cumulative distribution of measurement probabilities for all basis states. However, due to limited FPGA resources, performing parallel multiplication for the coefficients of $N$ basis states in the emulator is highly constrained. To tackle this issue, we propose an approximation method for squaring the coefficient values and their cumulative distribution. This approach achieves acceptable error levels while consuming fewer FPGA resources and computational requirements.

3.4.1.   Approximation of the probability of measuring the state

For a function $f(x)$ with a single solution $s$, the coefficients of the state $|s\rangle$ become close to 1 after repeated $G$ operations. The probability of measuring the state $|s\rangle$, that is, the approximate squared Euclidean norm of the coefficients of the state $|s\rangle$, $\widetilde{\|\alpha_{s}\|^2}$, can be obtained through linear approximation as follows:

This approximation can be computed using only bit-shift and subtraction operations.

After repeated $G$ operations, the coefficients $\alpha_{\omega}$ (where $\omega \neq s$) of the remaining $N-1$ basis states $|\omega\rangle$, which are not in the state $|s\rangle$, approach 0 and have the same value. Therefore, using Equations (2.4) and (3.2), the probability of the state $|\omega\rangle$ can be obtained as follows:

However, this requires division by $N-1$. In general, the integer division is an overhead-intensive operation. Therefore, we need to reduce the overhead by division, which can be done by following approximation:

where, $p = 1, 2, 3, \ldots$ is an arbitrary approximation order that determines the degree of approximation. Since $N = 2^n$, division by $N^i$ can be replaced with a bit-shift operation. Thus, by using the above approximation, we replace division operations with bit-shift and addition operations, thereby reducing computational overhead.

Meanwhile, the relative error $\epsilon_r$ when using this approximation can be obtained through the following equations:

In a 4-qubit emulation ($N = 16$) using an approximation of $p = 3$, $\epsilon_r$ becomes 0.4%.

3.4.2.   Construction of cumulative probability distribution

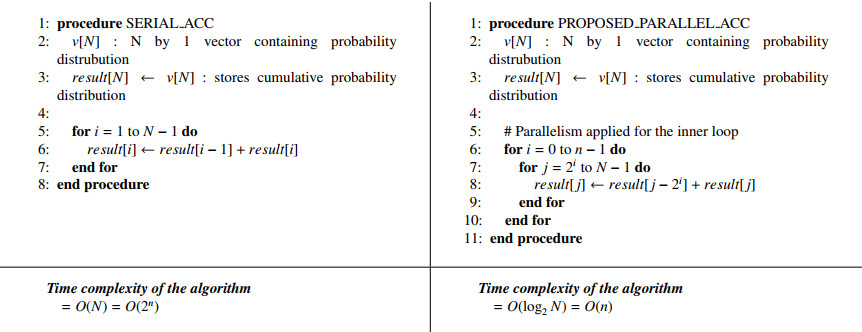
To emulate the measurement based on the previously calculated probability of measuring the state $|s\rangle$, a weighted random number generator that generates random numbers according to a probability distribution formed based on the input weights is required. This random number generator operates by obtaining the cumulative probability distribution from the array of probabilities received as input. For this purpose, we can consider serial accumulation performed over $N-1$ clock cycles, as shown in Figure 5. However, as the number of qubits increases, the number of clock cycles required for accumulation increases exponentially, making effective measurement emulation difficult.

To address this issue, we propose a parallel accumulation method and architecture as shown in Figure 6, and apply it to the emulation of measurement operations. The proposed parallel accumulation is performed over a total of $\log N ( = n)$ stages for $N$ basis states, with operations at each stage conducted in parallel. More specifically, during the $k$-th stage ($k = 0, 1, \ldots, n-1$), the values stored in the registers containing the coefficients of all basis states are updated as follows:

$(1)$ The value of the $i$-th register ($i = 2^{k}, 2^{k}+1, 2^{k}+2,$$\ldots, N-1$) is updated by adding the value of the $(i - 2^k)$-th register to it, respectively, and storing the result back in the $i$-th register. This is performed in parallel for all possible $i$ values at the given stage.

$(2)$ Once a stage is completed, the registers corresponding to the coefficients of the $0$-th basis state to the $(2^{k+1}-1)$-th one will contain their respective cumulative probability values. By repeating this process up to the $(n-1)$-th stage, all registers will eventually contain the cumulative probability values for their respective basis states.

Algorithm 6 presents the SERIAL_ACC and PROPOSED_PARALLEL_ACC algorithms for serial accumulation and the proposed parallel accumulation, respectively. The correctness of each algorithm can be proven as follows:

Theorem 7. Correctness of SERIAL_ACC in Algorithm 6

Proof. Let $v[i]$ be the probability distribution at index $i$, where $0 \leq i < N$. SERIAL_ACC computes the cumulative probability distribution, which is defined as:

The algorithm starts with $result[0] = v[0]$, and for each subsequent index $i$, it adds $result[i-1]$ to $result[i]$:

This operation correctly computes the cumulative sum of the distribution up to the $i$-th index. Since each index $i$ is processed sequentially, the correctness is guaranteed by induction: - Base Case: $i = 0$, $result[0] = v[0]$, which is trivially correct. - Inductive Step: Assume the algorithm correctly computes $result[i-1] = \sum_{j = 0}^{i-1} v[j]$ for $i-1$. Then, $result[i] = result[i-1] + v[i] = \sum_{j = 0}^{i} v[j]$, proving the inductive step. Thus, the algorithm computes the cumulative probability distribution correctly for all indices. □

Theorem 8. Correctness of PROPOSED_PARALLEL_ACC in Algorithm 6

Proof. PROPOSED_PARALLEL_ACC computes the cumulative probability distribution using parallel processing. The algorithm uses the following parallel step:

The algorithm ensures that for every step, it updates the cumulative sum by adding the corresponding previous sums from earlier stages. The correctness can be proven by induction on $i$: i) Base Case: For $i = 0$, each $result[j]$ is updated with $result[j-1]$, which mimics the behavior of the serial algorithm, ensuring the correctness for the first step, and ii) Inductive Step: Assume the cumulative sum is correctly computed for the $i$-th step. For the $(i+1)$-th step, the algorithm updates each $result[j]$ by adding $result[j-2^{i+1}]$ to the current $result[j]$. This process continues for all steps until the final cumulative sum is achieved for all indices.Therefore, the algorithm correctly computes the cumulative probability distribution in parallel. □

SERIAL_ADD operates by sequentially adding the value of each previous register to the next register, consuming a total of $N-1$ clock cycles as it iterates through the for loop. This results in a time complexity of $O(N) = O(2^n)$. As the number of qubits, $n$, increases, the clock cycles required for SERIAL_ADD grow exponentially, leading to a significant increase in overall execution time. In contrast, PROPOSED_PARALLEL_ACC executes the inner loop in parallel, completing the operation in just $n$ clock cycles. With a time complexity of $O(\log_{2}{N}) = O(n)$, this algorithm is far more efficient than SERIAL_ADD, and as the number of qubits increases, the difference in the number of clock cycles required by the two algorithms becomes even more pronounced. In addition, based on the cumulative probability distribution stored in the registers, a weighted random number generator (WRNG) can be used to emulate the measurement.

4.   Emulator design and implementation

4.1.   Architecture and design automation

To implement the Grover's quantum algorithm emulator on standalone FPGAs, we have designed a RISC-V SoC platform based on the architecture depicted in Figure 7. The RISC-V core used is the ORCA core ^[32], which is well-regarded for its low power consumption, making it suitable for IoT/ edge devices. The architecture includes several key components: a 256K SRAM as the main memory, Flash memory for non-volatile storage, a lightweight Network-on-Chip ($\mu$NoC ^[33]) for system interconnect, a control module for boot and reset functions, and standard external I/O interface modules such as UART, SPI, and I$^{2}$C. For the RTL design of the SoC platform, we utilized the EDA tool RISC-V eXpress (RVX)^[34], which is widely used for the lightweight RISC-V processor development ^{[35,36,37,38,39]}, and engineered the emulator to operate at a clock frequency of 50MHz. Most importantly, we have developed a dedicated hardware, the Grover Accelerator, which incorporates the proposed resource optimization techniques for Grover's algorithm processing, and embedded it into the SoC platform as shown in the figure.

Based on the developed SoC platform, we have modified RVX to develop QC Emulator eXpress (QEX), which automatically generates the RTL code of the emulator according to the target number of qubits. QEX accepts the number of qubits for the target emulator as an input parameter $\texttt{NUM_QUBIT}$ from the user and automatically generates the emulator RTL code. More specifically, once $\texttt{NUM_QUBIT}$ is defined, QEX first determines the number of blocks for the register $amp\_state$ to store the coefficients of the basis states processed by the emulator and the number of iterations of the diffusion gate operation. These are defined as local parameters $\texttt{NUM_STATE}$ and $\texttt{MAX_ITERATION}$, respectively. QEX then configures the registers and computation units of the Grover Accelerator according to these parameter values. Subsequently, QEX generates the RTL code of the SoC platform depicted in Figure 7 and provides it as an output to the user.

Additionally, we have developed a C-language API for the Grover Accelerator in the emulator. This API consists of two main commands: i) the $\texttt{set_oracle}$ command, which sets the $s$ value indicating which {basis's} phase the Oracle should invert before executing the algorithm, and ii) the $\texttt{activate_grover}$ command, which sends the activation signal to the Grover Accelerator to start the algorithm. The emulator operates by storing an application, implemented using this API, in the SRAM as instructions, which are then executed by the ORCA core. Upon completion of the emulation, the Grover Accelerator returns the results of the Grover search to the ORCA core, allowing the user to verify the success of the Grover search.

4.2.   Grover Accelerator

First, we designed a finite state machine (FSM) that uses the basic operational steps of the Grover's algorithm, described in Section 2.2, as its states to facilitate the operating mechanism of the Grover accelerator. Figure 8 illustrates this FSM, which consists of five states: IDLE, INIT, ORACLE, DIFFUSION, and MEASURE. The DIFFUSION state is further divided into two sub-states: DIFF_mac and DIFF_sub. Each state of the FSM executes the operations using the proposed optimization techniques introduced in Section 3. The transitions between the states of the FSM are triggered by the activation commands received from the ORCA core via an API or the iteration count of the $G$ operation, provided that specific conditions are met.

In this section, we provide a detailed explanation of each state, using a 2-qubit target emulation as an example to facilitate understanding. We also include register-level circuit diagrams corresponding to the operations performed in each state, as shown in Figure 9. Based on this example, readers can extend the emulation to an $n$-qubit target, applying operations to $N = 2^n$ registers.

INIT In this state, initialization for performing the Grover's algorithm is carried out. Upon receiving the $\texttt{Activate_grover}$ command, as shown in Figure (9a), all elements of amp_state are initialized to the value corresponding to the initial state of the Grover's algorithm, $|n\rangle{} = H|0^{n}\rangle{}$. At this stage, all elements of amp_state have equal positive values, which, due to the characteristic of QC expressed in Equation (2.4), is $1/\sqrt{N}$.

Calculating this initial value requires the computation of a square root, which is a computationally expensive operation. Therefore, it is necessary to replace it with a lighter computation. For this purpose, we express the initial value $1/\sqrt{N} = 1/\sqrt{2^{n}}$ in terms of $n$ as follows:

Using Eq (4.1), we can determine $1/\sqrt{N}$ by dividing a constant by a power of 2, where the constant and exponent depend on whether $n$ is even or odd. Based on this, we derived the following algorithm to define the initialization value $\texttt{init_coefficient}$ for amp_state relative to $\texttt{NUM_QUBIT}$.

In the above conditional statement, it is determined whether $\texttt{NUM_QUBIT}$ is even or odd. If $\texttt{NUM_QUBIT}$ is even, the bit string $\texttt{0x4000_0000}$, representing 1 in the fixed point representation proposed in the optimization technique (cf. Figure 3), is bit-shifted by $\texttt{NUM_QUBIT}$ / 2 to calculate $\texttt{init_entry}$. Conversely, if $\texttt{NUM_QUBIT}$ is odd, the bit string $\texttt{0x2D41_3CCE}$, representing $1/\sqrt{2}$, is bit-shifted by ($\texttt{NUM_QUBIT}$ - 1) / 2 to calculate $\texttt{init_entry}$.

ORACLE Before the Grover Accelerator starts executing the algorithm, the value of the basis state $s$ whose phase will be inverted by the Oracle is pre-set. When the $\texttt{set_oracle}$ command is received via the API, the input value is stored in the func_table register within the Accelerator, which holds the value of $s$.

In the ORACLE state, the operation described by Equation (2.9) is performed using the value stored in func_table. This process is illustrated in Figure 9b. As a result of this operation, the value of each element in amp_state is set according to the following algorithm:

DIFFUSION This state completes one $G$ operation by performing the diffusion operation after the Oracle operation. The Diffusion operation, as shown in Figure 4, involves three steps: 1) accumulation, 2) bit-shift, and 3) subtraction. We divided these operations into two stages: 1) and 2) are executed in the DIFF_mac stage, while 3) is executed in the DIFF_sub stage.

More specifically, in the DIFF_mac stage, as illustrated in Figure 9c, all elements of amp_state are accumulated, and then this value is multiplied by $2^{-n+1}$ and stored in the acc_result register. The multiplication by $2^{-n+1}$ is replaced by a bit-shift operation to reduce overhead. In the subsequent DIFF_sub stage, each element of amp_state is subtracted from acc_result, and the results are updated back into amp_state. This process is depicted in Figure 9d.

Ultimately, the Diffusion operation is represented by the following algorithm and is implemented in the RTL design of the Grover Accelerator.

Iteration of ORACLE and DIFFUSION In Grover's algorithm, the $G$ operation is repeated a specific number of times $k$, as defined in Equation (2.7). The Grover Accelerator includes a register, iteration, to store the count of Oracle and Diffusion executions. The value of iteration is initialized to 0 and increments by 1 with each $G$ operation. When this value equals the predefined local parameter $\texttt{MAX_ITERATION}$, the $G$ operations are completed, and the process moves to the MEASURE stage.

The $\texttt{MAX_ITERATION}$ corresponds to the value of $k$ in Eq (2.7). Calculating this requires a square root computation with respect to $N$, similar to the $\texttt{init_entry}$ in the INIT state. Hence, using a similar approach to Equation (4.1), the value of $k$ is expressed as a function of $n$ as follows:

In this equation, the constants $\frac{\pi{}}{4} \times 2^{32}$ and $\frac{\pi{}\sqrt{2}}{4} \times 2^{32}$ are represented as $\texttt{0x0_C90F_DAA2}$ and $\texttt{0x1_1C58_31AC}$, respectively. Based on these constants, we derive the algorithm for $\texttt{MAX_ITERATION}$ as follows:

MEASURE To perform the measurement operation on amp_state after completing the $G$ operations for $\texttt{MAX_ITERATE}$ iterations, we designed a weighted random number generator (WRNG) module. This module takes amp_state as input, squares each element, and accumulates these values to create a cumulative distribution of measurement probabilities for the basis states. The cumulative distribution is then used as weights to generate a random number, i.e., the measurement result of the quantum state.

The WRNG module calculates the measurement probabilities of the basis states using the optimization techniques based on the two linear approximation formulas (3.2) and (3.5) introduced in Section 3.4. To function correctly, the module must determine whether each element of amp_state corresponds to the $|s\rangle$ state or the $|\omega{}\rangle$ state, based on the {Oracle} function $f(x)$ defined in Eq (2.6), where $f(s) = 1$ and $f(\omega{}) = 0$. The appropriate linear approximation formula is then applied to calculate the measurement probability of each state, and these probabilities are stored in the acc_state register.

To determine whether each element of amp_state is in the $|s\rangle$ or $|\omega{}\rangle$ state, we compare the coefficient value stored in each element of amp_state to a fixed threshold value stored in the $\texttt{THRESHOLD}$ constant. For a given $s \in \{0, 1, \ldots, N-1\}$, if the value stored in the $s$-th element of amp_state is greater than $\texttt{THRESHOLD}$, the corresponding basis state is identified as the $|s\rangle$ state, and the value of $s$ is stored in the s_value register. The linear approximation formula (3.2) for the measurement probability of the $|s\rangle$ state is then applied, using bit-shift and subtraction operations to compute the square of amp_state[s]. This value is stored in the $s$-th element of acc_state.

For all $\omega{} (\omega{} = 0, 1, \ldots, N-1 \text{ and } \omega{} \neq s_value)$, the linear approximation formula (3.5) for the measurement probability of the $|\omega{}\rangle$ state is applied, using bit-shift and subtraction operations to approximate the square of $\textit{amp_state[$\omega{}$]}$. This approximated value is then stored back in the $\omega{}$-th element of amp_state. The degree of approximation $p$ in the linear formulas is controlled by the $\texttt{APRX_ORDER}$ constant.

The process of determining whether each state is $|s\rangle$ or $|\omega{}\rangle$, approximating their measurement probabilities, and storing them in ${acc\_state}$ is implemented in the WRNG module using the following algorithm:

By executing this algorithm, the measurement probabilities stored in acc_state are accumulated and stored again in acc_state using the parallel accumulation technique described in Figure 6. In this technique, at the $k$-th stage, the value of each element at index $i$ ($i = 2^{k}, 2^{k}+1, 2^{k}+2, \ldots, N-1$) in acc_state is incremented by the value of the element at index $i-2^{k}$, progressively completing the values of elements from index $0$ to $2^{k+1}-1$ in $\texttt{acc_state}$. This process is repeated incrementally for $k$ from $0$ to $NUM\_QUBIT-1$, resulting in the final cumulative probability values stored in all elements of acc_state. The series of processes to accumulate and store the values in acc_state is implemented as a nested loop, with $k$ and $i$ serving as the indices of the outer and inner loops, respectively. The following algorithm is implemented for the WRNG module's cumulative probability calculation:

5.   Evaluation

We designed and FPGA-prototyped emulators targeting various numbers of qubits, including the Grover Accelerator, using the developed QEX. For FPGA prototyping, we selected the Kintex Ultrascale+ board ^[40], representing resource-rich consumer FPGAs, and the Arty A7 board ^[41], representing low-performance FPGAs suitable for IoT devices or embedded systems. Figure 10 shows the emulators prototyped and operating on these boards.

To demonstrate the superiority of the proposed optimization techniques in terms of resource consumption reduction, we designed baseline emulators using conventional matrix-vector multiplication-based universal QC ^[18,42] and prototyped them on the same FPGA boards. All prototype emulators share the same core (i.e., RISC-V ORCA core), memory, NoC, etc., except for the Grover Accelerator. For reference, Table 2 reports the resource consumption of these components in the Kintex Ultrascale+ board-based prototype emulators.

In this study, we emphasize the importance of analyzing the differences in resource utilization between the conventional method and our proposed approach based on actual synthesis results rather than theoretical estimations. This is primarily due to the inherent challenges in theoretically analyzing the resource usage of synthesized RTL code. As outlined in Section 3.3, the computational complexity of matrix-vector multiplication is $O(N^{2}) = O(2^{2n})$, which means that for every increment of 1 in $n$, the computational load increases fourfold. Consequently, the hardware resources required to handle this load in parallel are expected to increase by the same factor. However, actual hardware resource usage during synthesis is influenced by internal algorithms used by the synthesis tools to optimize resource allocation, making it difficult to accurately predict resource consumption solely through theoretical analysis. In this study, we generated the RTL code for the emulator's basic components using RVX and synthesized the entire emulator using Vivado ^[43]. Vivado optimally synthesizes RTL code while considering timing constraints, power consumption, and available resources on the target FPGA board. However, since the optimization algorithms used by Vivado are proprietary and play a crucial role in determining the final resource usage, theoretical analysis alone is not sufficient. Therefore, we developed emulators for various numbers of qubits, synthesized them on FPGA, and empirically analyzed the actual resource consumption as the number of qubits in the quantum system increased.

Meanwhile, on the emulators synthesized with varying numbers of qubits, the application of the proposed optimization techniques may cause errors in the amplitudes of the quantum states, depending on the number of qubits. The maximum error for each case, with different numbers of qubits, is presented in Table 3. The Real Number Representation and Matrix-Vector Multiplication Decomposition techniques are optimizations that leverage the matrix operation characteristics of Grover's algorithm, ensuring that no errors occur as a result. In contrast, rounding errors may arise in the Fixed-Point Expression due to the limited number of fractional bits, as discussed in Section 3.2, with a rounding error value of $2^{-30} \approx{} 10^{-9}$. However, this impact is negligible compared to the approximation error resulting from the probability of measuring the state in Section 3.4.1, which is on the order of $N^{-p} = 2^{-np}$. In the emulators targeting quantum systems with qubits ranging from $n = 2$ to $n = 6$, using an approximation order of $p = 2$ provides a reasonable approximation without burdening the computation, and the approximation error is no greater than $2^{-12}$. In comparison, the rounding error is insignificant. Furthermore, as the number of qubits increases, this approximation error decreases exponentially, showing an acceptable error rate even as the scale of the quantum system being emulated grows.

Table 4 shows the FPGA resource consumption results for the baseline emulators and the proposed emulators prototyped on the Kintex Ultrascale+ board. The table indicates that for the baseline emulator, when the target qubit count reaches five, the LUT consumption exceeds three times the available FPGA resources, making synthesis infeasible. Thus, only emulators targeting up to four qubits can be prototyped. In contrast, the proposed emulator, even targeting six qubits, consumes resources within the FPGA's capacity. This significant resource saving is attributed to the proposed optimization techniques, achieving up to 95.48% reduction in LUT resource consumption.

Next, Table 5 reports the resource consumption results for emulator prototypes using the Arty A7 board. For the baseline emulator, the LUT resource consumption exceeds the Arty A7's capacity when targeting three qubits, making implementation impossible. Therefore, only up to two-qubit emulators can be prototyped. However, the proposed emulator can be synthesized for up to four qubits, demonstrating that the proposed techniques yield excellent results even on low-performance FPGAs.

In addition, we also conducted additional experiments to evaluate the performance of the Grover Accelerator, the core hardware IP of the emulator we developed. We performed experiments comparing three cases: i) executing the Grover's algorithm using general QC with ORCA core only (sw_naive), ii) executing the Grover's algorithm with the proposed optimization techniques (sw_Grover_optimized), and iii) executing the Grover's algorithm using the Grover Accelerator (hw_Grover_Accelerator). All software was coded in C language. Detailed descriptions of each case are as follows:

- sw_naive: Uses software-based matrix-vector multiplication to calculate state values on a RISC-V based platform without the Grover Accelerator, employing the matrix representation of $H^{\otimes{}n}$ gates and performing the Grover's algorithm.

- sw_Grover_optimized: Executes the Grover's algorithm with the proposed optimization techniques (Fixed-point expression, reduced matrix-vector multiplication) applied to sw_naive.

- hw_Grover_Accelerator: Executes the Grover's algorithm on an emulator equipped with the Grover Accelerator, with all proposed optimization techniques applied.

We measured the execution time for each case on emulators targeting two to four qubits, with the time measured as the number of clock cycles until emulation completion. Table 6 reports the results. The table shows that sw_naive takes significantly longer than the other cases for all qubit counts, indicating poor practicality for emulation due to hundreds to thousands of times longer execution times compared to optimized versions. Examining hw_Grover_Accelerator, which is the main focus of this paper, we see a substantial reduction in execution time compared to all sw_Grover_optimized results. Unlike the substantial increase in execution time for sw_Grover_optimized as the qubit count increases, hw_Grover_Accelerator shows less than double the increase. For four-qubit emulation, hw_Grover_Accelerator performs 191 times faster than sw_Grover_optimized. This efficiency is achieved by shifting the increased computational overhead from 'execution time' to 'hardware resources', allowing the Grover Accelerator to handle increased computations by increasing the number of parallel operation units, thus preventing exponential increases in execution time. In conclusion, these experimental results confirm that the proposed optimization techniques not only reduce resource consumption but also significantly enhance performance through optimized hardware design.

6.   Conclusions

Despite the significant interest in quantum computing (QC) and its vast potential across various fields, the current state of research and development is constrained by the limited practicality of large-scale quantum computers. To address the shortcomings of QC research and development based on large-scale quantum computers, FPGA-based QC emulators were introduced. However, the high resource demands of these emulators remain a significant barrier. To overcome this issue, we proposed optimization techniques focused on Grover's algorithm, one of the most well-known QC algorithms, to significantly reduce resource requirements and enable standalone FPGA implementations of QC emulators. We designed the Grover Accelerator that incorporates the proposed resource optimization techniques and integrated it with a RISC-V SoC platform, achieving significant performance enhancements and resource reductions. The optimized emulator was implemented to operate standalone on both high-performance Kintex Ultrascale+ and low-performance Arty A7 FPGAs. Through resource consumption and performance comparisons with conventional QC emulators, we demonstrated the efficacy and superiority of our developed emulator.

Author contributions

Seonghyun Choi: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing-original draft, Writing-review and editing, Funding acquisition; Woojoo Lee: Conceptualization, Methodology, Software, Validation, Writing-original draft, Writing-review and editing, Supervision, Project administration, Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported in part by Korea Institute for Advancement of Technology(KIAT) grant funded by the Korea Government(MOTIE) (P0017011, HRD Program for Industrial Innovation), in part by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. RS-2024-00345668), and in part by the Chung-Ang University Graduate Research Scholarship Grants in 2024.

Conflict of interest

The authors declare no conflicts of interest.