1.
Introduction
Water pollution is a pressing global issue, and one of the most common contaminants in wastewater originates from synthetic dyes (15-20% v/v) [1,2]. The improper disposal of synthetic dyes from industries poses a serious threat to water quality, and one of the dyes frequently found in wastewater from batik and cardboard industries in Indonesia is methylene blue (MB).Subsequently, high concentrations of this type of dyes have adverse effects on the environment and living organisms due to the toxicity, inertness, and carcinogenic properties [5,6,7,8,9]. As a result, when it infiltrates the human body, it accumulates in the liver, potentially leading to liver cancer. The presence of MB in water can hinder the penetration of sunlight into the water, disrupting the photosynthetic activities of the aquatic ecosystem[1,10]. This disruptionalso affects the reduction of oxygen demand in the water. Therefore, it is important to remove dye substances from wastewater before discharging into natural water bodies to safeguard the environment and human health.
The removal of MB dye from industrial wastewater can be achieved through various processes, including physical methods (adsorption and filtration), chemical purification (photocatalysis and oxidation), or biological degradation[4,11]. Among these methods, adsorption is the most common method for mitigating the toxicity of liquid effluents[1,8,12,13,14,15] Commercially, activated carbon, silica gel, and zeolite are commonly used as adsorbents [1].More research has been carried out in order to develop cost-effective techniques of eliminating contaminants from wastewater [16]. According to many studies, low-cost adsorbents will bring economic benefits [17]. Adsorption studies employing agricultural products and their co-products to remove dyes from wastewater have gained a lot of attention in the previous decade[18,19,20]. To remove contaminants from aqueous solutions, agricultural products and their co-products can be used in place of commercially available activated carbon. These items are widely available and simple to obtain. Agricultural and forestry waste contains a high concentration of cellulose, hemicellulose, and lignin. The surface contains a large number of active groups such as hydroxyl, carbonyl, amino, carboxyl, methyl, and so on.[1,17,21].Various kinds of adsorbents with low costs have been developed to remove dyes from industrial wastewater such as coconut leaves [22], tea powder [23], water hyacinth [24], banana stem [25], maize stem [26], potato peel [27], orange peel [28] papaya peel fiber [29], moss [30], watermelon rind [31], and bagasse[32].
In a recent study, focused on the optimization of using waste wood powder (Cedrus atlantica) as an adsorbent in the degradation of MB [33]explored various extraction methods, including hydrodistillation, Soxhlet, maceration, and ultrasonic for the effectiveness in adsorbing MB. Among these, the most effective adsorbent was found to be the residual wood powder obtained after maceration, with an adsorption capacity of 98.42%. The amount adsorbed (Qads = 7.84 mg/g) approached powdered activated carbon used as a reference (Qads = 9 mg/g). Furthermore, this study evaluated the performance of another forest waste as an attractive adsorbent, namely nipa(Nypafruticans), as a promising adsorbent, and the result is shown in Table 1.
Nipa is a type of palm that grows in mangrove environments or tidal areas near the coast. In Southeast Asia, the leaves are highly valued for the use in roofing, thatching for walls, and flooring materials [34]. The plant thrives in river estuaries and brackish water environments, where saltwater and freshwater mix. In some island nations, nipa has been introduced to control coastal erosion [35,36]. Various parts of nipa, includingfrond, husks, shells, and leaves (Figure 1), contain cellulose (28.9-48.2 wt%), hemicellulose (26.4 wt%), and lignin (17.8 wt%) [37,39].
The feasibility of using nypa and its derivatives as adsorbents has been thoroughly studied. One notable success was the use of nypa palm shell (NPS) waste as a renewable precursor for producing highly porous activated carbon through direct NaOH activation was successful.Thecharacterization results showed the conversion of NPS into activated carbon with a high Hg2+ adsorption capacity of 227.86 mg/g [40]. Additionally, the conversion of nipafrond into an adsorbent for heavy metal lead (Pb) pollution has also been successfully studied. The results showed a maximum metal adsorption rate of 99.29% for 80-mesh particle size with a contact time of 100 minutes. The adsorption mechanism is closely in line with the Langmuir isotherm equation with R2 = 0.9998 [38].These findings show that nipa frond have a high absorption capacity, motivating researchers to investigate maximizing the use of nipa frond as adsorbents in wastewater treatment. This optimization study applies a response surface methodology (RSM) approach to evaluate MB adsorption, a degrading process not previously investigated by other researchers. The use of nipa frond as adsorbents has various advantages, including simple and low-cost material preparation and abundant availability.
2.
Materials and methods
Nipa frond was collected from the coastal area of PortPelindo, North Aceh, Aceh Province, Indonesia. MB (E.MERCK with a high purity of ≥89%), and hydrochloric acidwasalsoobtained. The chemical materials were obtained online and delivered from Sigma-Aldrich Pte. Ltd., USA.
2.1. Preparation of nipa frond
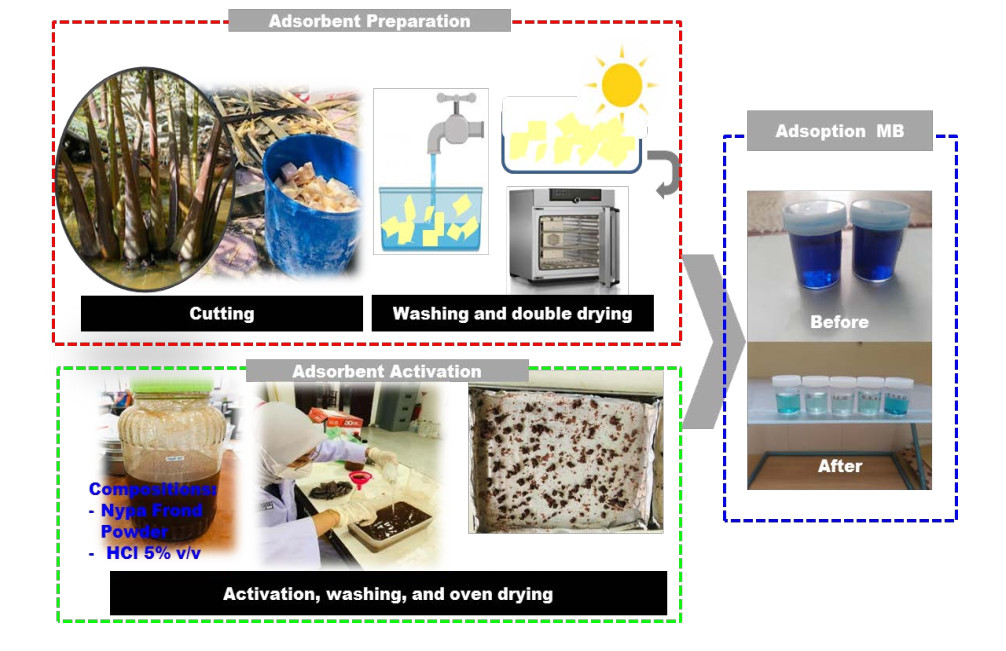
A total of 10 kg nipafrond was cleaned and reduced in size to approximately 5 x 5 cm. The frond pieces were sun-dried and further dried in an oven dryer at 105 ℃ (Memmert oven) until a constant mass was achieved. The dried frond was ground into a fine powder and sieved (100 mesh). Unactivatednipa frond powder was tested for functional groups using Fourier transform infrared (FT-IR, Shimadzu, Prestige21).In general, the adsorption process is presented in Figure 2.
2.2. Activation of nipafrond
A total of 100 g of nipa frond powder was soaked in a 5% v/v HCl solution for 24 hours, and the mixture was separated using filter paper (Whatman No.1). The residue was washed until it reached a pH of 7 (Horiba pH meter) and dried at 105℃ (oven dryer) for 48 hours. Activated nipa frond powder was tested for functional groups using FT-IR.
2.3. MB adsorption
Adsorbent was added to MB aqueous solution with a concentration of 50 mg/L, using varying amounts of 2, 3, and 4 g. The mixture was shaken at 150 rpm for different time intervals of 80, 90, and 100 minutes. This treatment was performed for both unactivated and activated adsorbents. The mixture was then separated, and the filtrate was analyzed using UV-Vis spectrophotometer (653 nm), FT-IR, as well as the adsorption capacity and percentage were calculated.
2.4. Response surface method optimization experiment design
Statistical experimental design is an efficient method for conducting experiments and obtaining valid and objective conclusions by analyzing the data. It has two primary applications, including identifyingthe factors influencing the experiment and determining the optimal conditions[10].In this study, Design Expert 13.0 software (Stat-Ease Inc., Minneapolis, MN, USA) is used for regression and graphical data analysis. RSM is applied to examine response patterns and determine the best combinations of variables expected to yield optimal conditions. This study includes 2 independent variables, A (contact time) and B (adsorbent mass), and 2 response variables, response variable 1 (adsorption capacity) and response variable 2 (adsorption percentage). Table 2 shows the experimental design for this study.
3.
Results and discussion
3.1. Characteristics of nipafrond with XRD, BET, and FT-IR
To determine the functional groups present in nipa frond, activated and non-activated fronds were characterized using FT-IR. Additionally, to determine the content of natural and activated adsorbents from nipa frond, characterization was conducted using X-ray fluorescence (XRF).The characterization results of nipa frond using XRF are presented in Table 3. It is evident that both natural and HCl-activated nipa frond primarily consist of Ca and K, along with trace amounts of other metals. According to XRF characteristics, the natural nipa with a value of 398% has the same K content as HCl-activated nipa, which is also 398%. This shows that there is no increase or decrease in K content between natural and HCl-activated nipa. The activation process cannot improve the content of K and Ca, which means it does not expand the pore structure of nipa or increase the pore volume. This is because the original pore structure of nipa frond already has an optimal structure before activation. Therefore, for this nipa frond adsorbent, HCl activation does not significantly change the size of its pores.
Table 4 shows the surface area, pore volume, and pore diameter of natural nipa powder and HCl-activated nipa. According to BET analysis, activated nipa shows a decrease in specific surface area, pore volume, and micropores. This is because the activation process by HCl does not lead to a change in the value of compounds in nipa. This result is consistent with XRF data, where K content in natural nipa is 398% and K content in activated nipa is also 398%. Subsequently, efficient adsorbent requires a large surface area because many adsorption processes occur on the surface. A large specific surface area provides more active sites and greater surface reactivity with pollutant molecules
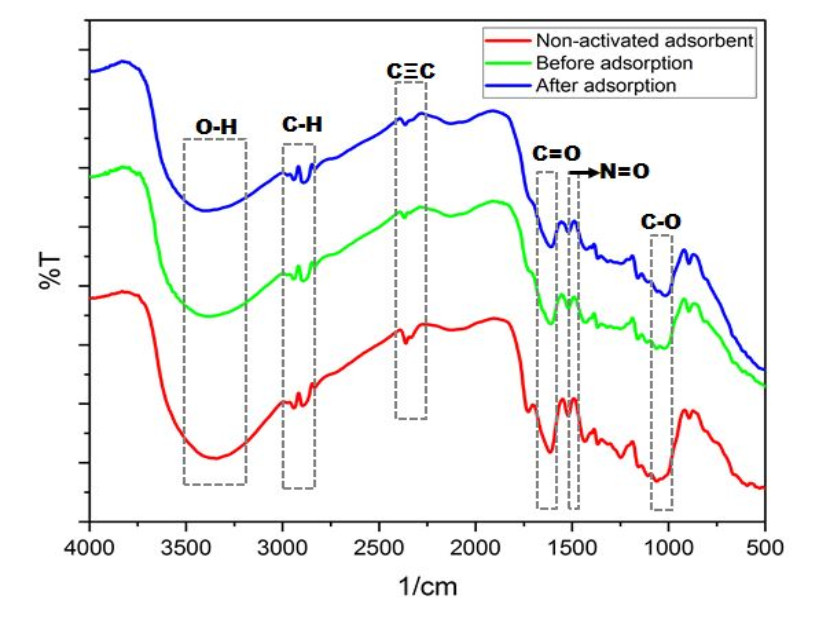
The analysis of functional groups of nipa frond adsorbent was carried out using FT-IR, as shown in Figure 3. The absorption bands of O-H functional groups in non-activated nipa frond adsorbent, activated nipa, and after adsorption were observed at wavelengths 3342.64, 3350.65, and 3414.00 cm-1, respectively. This is in line with previous investigation, which shows that O-H groups are typically found in the absorption range of 3000-3700 cm-1. There is an increase in the wave number due to the vibration of hydrated OH groups resulting from the addition of HCl groups to activated adsorbent, leading to a sharper peak in activated adsorbent [48]. Furthermore, other functional groups found include C-H, C = O, C-O, C≡C, and N = O, each with the respective wavelengths, as summarized in Table 5.
The peaks at 2941.44 and 2893.22 cm-1 indicate the presence of CH2 absorption by aliphatic compounds. The appearance of peaks at wavelengths 1728.22 and 1608.63 cm-1 suggests absorption from the C = O aldehyde group. while peaks at 1062.78 and 1020.3cm-1 identify the presence of carboxylic acid and alcohol in the nipafrond adsorbent, respectively before and after adsorption. The observed peaks are similar to those found in other studies on forest waste [18,33].The FTIR spectrum of the nipafrond adsorbent after MB adsorption shows a decrease in intensity across all bands. The changes observed in the spectrum suggest the possible involvement of adsorbate molecules adsorbed onto the adsorbent surface. These interactions can lead to changes in the vibration and rotation of molecules, resulting in shifts in the infrared spectrum.
3.2. Adsorbateconcentrationanalysis (UV-Vis)
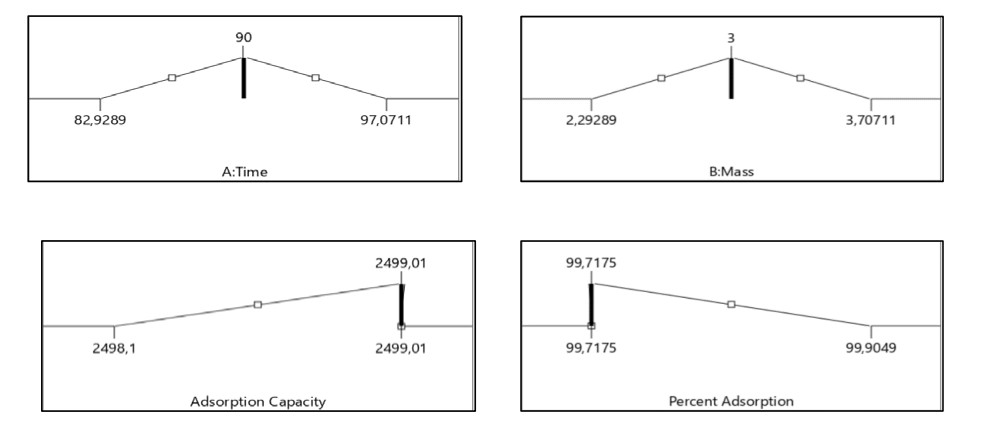
Table 2 showsthe final concentration of MB with an initial concentration (Co) of 50 ppm. The highest concentration after adsorption (Ce) is found at a contact time of 82.9289 minutes with a mass of 3.70711 g, resulting in a Ce of 0.1412 ppm. The lowest concentration after adsorption (Ce) is observed at a contact time of 90 minutes with a mass of 2 g, resulting in a Ce of 0.0475 ppm. The optimum point, as shown in Figure 4, is characterized by an increase in adsorbent mass, leading to an expansion of the particlesurface area. However, after the optimum time, there is a decrease in MB concentration, attributed to the fact that not all active sites are occupied by adsorbate. Active sites in large quantities require more time to attain equilibrium[49]. Generally, a longer contact time between adsorbent and adsorbate results in increased adsorbate adsorption, leading to a reduction in the adsorbateconcentration. The contact time for nipa frond in adsorbing MB shows a significant decrease in concentration at 100 minutes. After passing the optimum time, the active surface of adsorbent was fully occupied by adsorbate particles, thereby increasing the adsorption time, which only has a slight effect on the final concentration or will tend to remain constant[50]. This is because a longer contact time between adsorbent and adsorbate allows the formation of more bonds between adsorbent particles and MB [51,52].
3.3. ANOVA in regression model
The validation of the prediction results against the experimental data in Table 6 shows that the error percentage at each point is small. Therefore, it can be concluded that the model obtained from Equations 1 and 2 effectively establishes the relationship between the independent and dependent variables. This validation of the prediction results against the experimental data is one of the methods to show the validity of the proposed model.
To assess the modelsignificance, a probability value below 0.05 is typically considered significant, while a probability value (Prob > F) exceeding 0.1 suggests that the model is not significant. The ANOVA for the model and variable A shows a probability value (Prob > F) greater than 0.1 as shown in Tables 8 and 9. This suggests that the quadratic model and variable A only have a small influence on absorption capacity and percentage. However, variable A is retained in the model due to its potentially significant influence on absorption capacity.
3.4. Model feasibility test
Tables 10 and 11 show the feasibility test for MB absorption capacity and percentage models by activated nipa frond adsorbent. An analysis of response surface optimization methods results in a third-order regression equation with a quadratic model.
Subsequently, the accuracy of the model canbe determined by the R-squared (R2) of 0.8099 and 0.9080. As R2 approaches 1, the model becomes more reliable for predicting the response. In the sum of squares test, a model is considered suitable when the difference between Adjadjusted(adj)R2 and Predprediction (pred) R2 is less than 0.2. Based on the results showing Adj R2 of 0.6742 and 0.8422 as well as Pred R2 of -0.3516 and 0.3456, this model is not suitable as the difference between Adj R2 and Pred R2 is greater than 0.2. Additionally, a model is deemed good when the ratio of Adeq Precision is greater than 4. According to the table, the ratio of Adeq Precision is 6.2002 and 11.3611, which is adequate, showing that this model can be used.
The equation obtained for absorption capacity with activated adsorbent is as follows:
The equation for absorption percentagewith activated adsorbent is as follows:
3.5. Optimization conditions and MB adsorption isotherms
The parameters assigned to each independent and dependent variable yield an optimal range value from the study carried out. The parameters and boundary conditions for each independent and dependent variable are shown in Table 10.
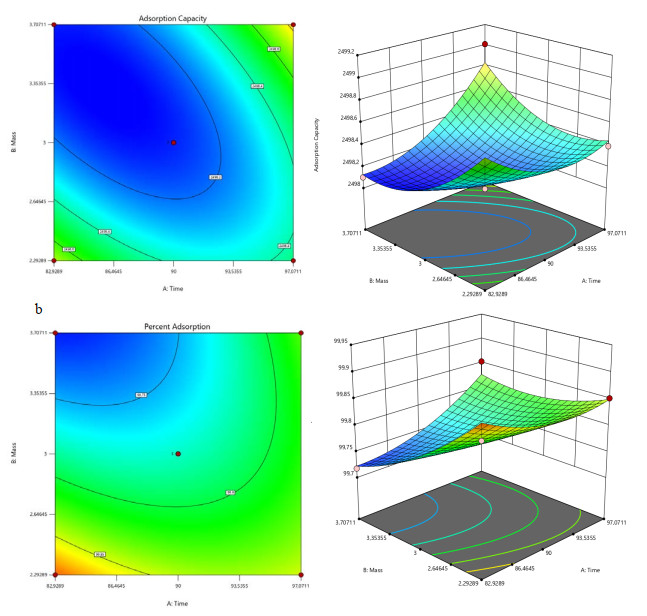
Based on the optimization results shown in Table 11 and Figures 5a, b, the combination of independent variable levels that provides an optimal response is at 83.1145 minutes and 3.7071 g mass with a desirability value of 0.974. The desirability value shows the optimization objective function, indicating the program ability to fulfill criteria based on the set parameters for the final product. A desirability value approaching 1 signifies an increasingly perfected program ability to generate a good product [53]. However, the optimization objective is not to achieve a desirability value of 1 but rather to identify the optimal conditions that balance all the objective functions [25].
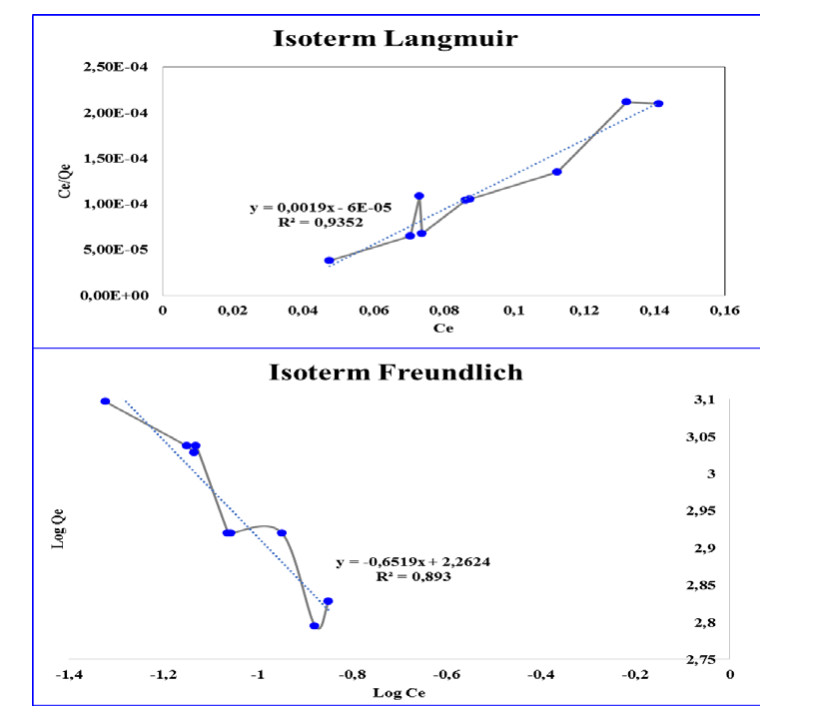
Figure 7 shows the curves of the Langmuir and Freundlich isotherm patterns derived from Y = 0.0019x-6E-05 and Y = -0.6519x+2.2624 respectively. These equations are used to compute the slope and intercept values to determine the magnitudes of the constants KL, RL, and qmax. Subsequently, KL represents the Langmuir isotherm constant (L/mg), while the constant for the Freundlich equation is KF and 1/n. The Langmuir isotherm equation constant is KL = -31.67 L/mg with a correlation coefficient (R2) of 0.9352, RL = -0.00063 L/g, and qmax = -16666.67 mg/g, respectively. Meanwhile, the parameters obtained from the Freundlich isotherm include a correlation coefficient (R2) of 0.893, a slope value (1/n) of -1.5339, and an intercept value (KF) of 0.354 L/mg.
The Langmuir and Freundlich equation curves show different linearizations, showing that MB adsorption usingactivated nipa frond adsorbent follows the Langmuir isotherm model. This is evidenced by a well-fitted linearization graph with a determination coefficient (R) close to or equal to 1. Subsequently, the linearity value for the Langmuir isotherm is higher compared to the Freundlich isotherm, suggesting that the Langmuir isotherm model is more suitable for characterizing MB adsorption mechanism usingactivated nipa frond adsorbent. This suggests that the adsorption primarily occurs on the surface layer of adsorbent(monolayer).
4.
Conclusions
In conclusion, the potential of nipa frond adsorbent in absorbing MB dye was extensively examined. The optimum absorption capacity for activated adsorbent occurred at a contact time of 97.0711 minutes and a mass of 3.70711 g, namely 2499 mg/g. The adsorption using activated adsorbent was in line with the Langmuir isotherm equation with an R2 of 0.9352. According to the test results, the determination coefficient R-square was 0.9352 (93.52%). The ability of the independent variables influenced the dependentvariable by 93.52%, while the remaining 6.48% (1-0.9352) was explained by other variables.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors are grateful to LPPM of Malikussaleh University for financial support through the
research project PNBP, No. 40/PPK-2/SWK-II/AL.04/2023.
Conflict of interest
The authors declare that we have no competing interests.









 DownLoad:
DownLoad: