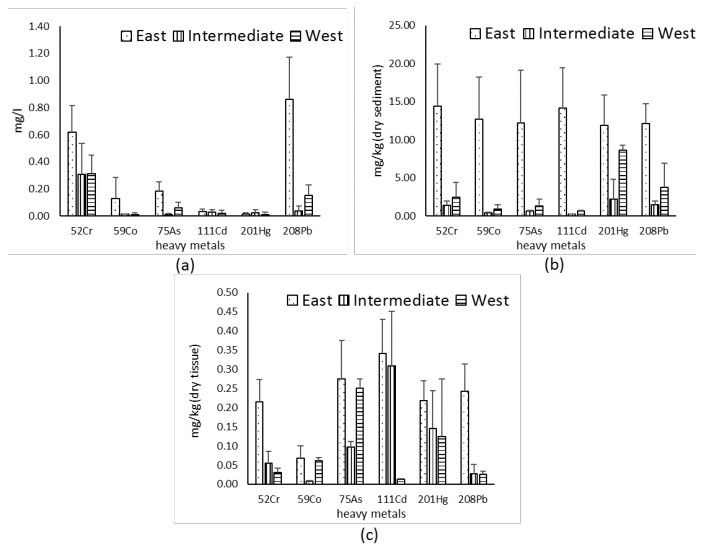
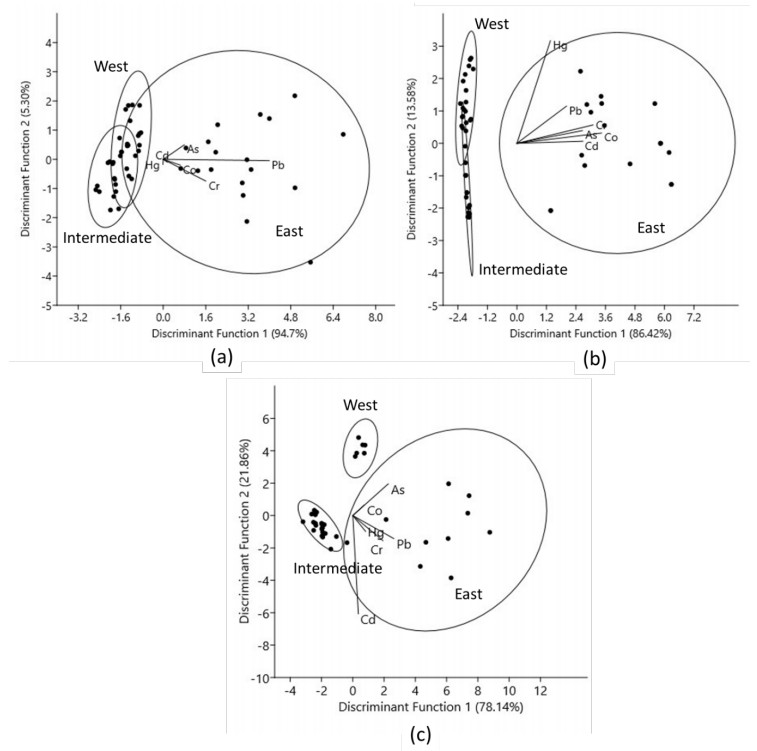
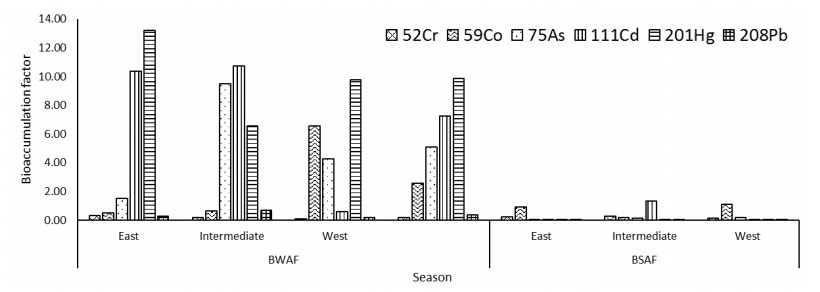
A problem of food safety may rise in benthic estuary organisms such as the bivalve mollusc of Anadara granosa, as dangerous metals in environment may accumulate in their soft tissue. Fluctuation of accumulation may also happen, as there are factors that influence the amount of pollutants in water environment. This research aimed to analyze the seasonal pattern (Indonesian east, intermediate, and west monsoon season) of heavy metals (Cr, Co, As, Cd, Hg and Pb) accumulation factor in the soft tissue A. granosa and evaluate the use of mollusc as bio-indicator in metals pollution. The study had been done on the estuary of Tanjung Balai, North Sumatra, Indonesia. Heavy metal from water, sediment, and soft tissue of A. granosa were extracted by microwave digestion and analyzed by ICP-MS (Inductively Coupled Plasma-Mass Spectrometer). Result of the study showed that the heavy metals accumulation in the soft tissue of A. granosa was as follow Cd > As > Hg > Pb > Cr > Co and between 0.01–0.31 mg/kg. The concentration may consider as safe, which is below the maximum allowable limits for marine products. Meanwhile, a significant (P < 0.05) heavy metals contamination was detected higher in the beginning east monsoon season. Thus, temporal variation should be considered in food safety monitoring program on fisheries products, which usually only collected once per year. Moreover, BWAF (bio-water accumulation factor) was detected significantly (P < 0.05) higher than BSAF (bio-sediment accumulation factor). The results also showed only Cr and Pb had a significant relation (P < 0.05) between their accumulation in environment and in the mollusc. Therefore, environmental parameters need to take into account when using bivalves as indicator of heavy metal pollution since seasonality could affect the absorption of heavy metals.
1.
Introduction
Energy is an integral part of every country's economic development. Electricity is an incredibly flexible energy source that fuels the efficiency of almost any sector of the economy. Pakistan's disastrous energy failure policies have left the nation with a severe power catastrophe, suffering economic damages throughout the last twenty years. Hence, understanding the energy consumption and real GDP is very important to improve its financial growth and development process from a policy perspective.
Over three decades after [1], seminal work reaffirming the causal link between energy consumption and real production, the causal path between these factors remains uncertain [2,3]. Several earlier empirical studies discovered that electricity consumption Granger-causes real GDP, such as [4,5,6], although other studies claimed that electricity consumption does not Granger-causes real GDP [7,8]. On the other hand, some studies (e.g., [9,10,11,12] specify the number of explanations why recent research on the link between electricity and economic growth has contradictory findings. According to these researches, the existing electricity demand model focused only on observed variables, economic development, and energy price, and neglects the non-observable elements. Electricity consumption often depends on non-observable variables such as energy conservation, technical advances, and customer preference. Because electricity demand is considered a derived output, energy consumption relies on electrical appliances usage and capital stock. Appropriately, such findings indicate other exogenous factors aside from economic variables such as income and price (e.g., energy consumption factors, technological change, and customer preference) should be incorporated for modeling electricity demand. argued that capturing the impact of un-observable factors through a simple timing pattern is impractical [13]. Dimitropoulos et al. (2004), Dilaver and Hunt (2011), Hunt and Ninomiya (2003) and Hunt (2003) stated that the method Structural Time Series Modeling (STSM) was established by [15,16] is an adequate approach to capture the results of non-observable variables (trends in energy usage, technical changes, and customer fondness) effectively [9,12,13,14]. Furthermore, Harvey et al. (2004) claimed that time series is broken down into non-observed patterns and other abnormal elements in the STSM technique and that these are not identified [17]. The stochastic process, also regarded as the Underlying Energy Demand Trend (UEDT), incorporates not just exogenous technological advancement but other significant social and economic implications as for customers’ expectations, resource-saving scientific changes.
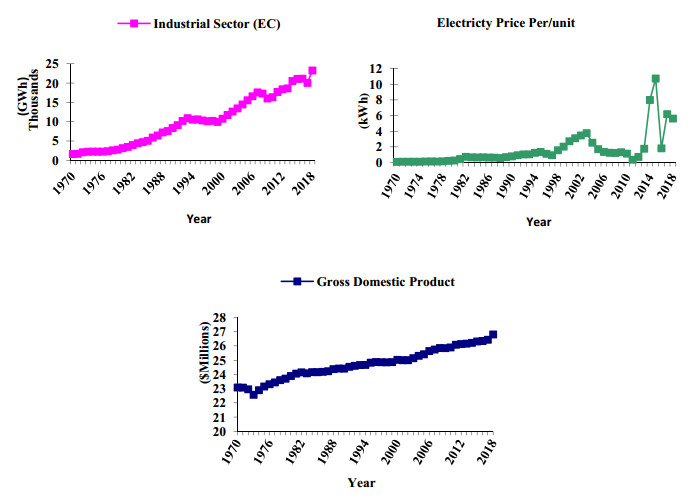
The uninterrupted provision of electricity is the critical factor to flourish in the industrial sector. It plays an indispensable role, as this sector is the engine of economic growth in Pakistan. However, Pakistan has faced a severe electricity crisis, directly and indirectly, involving all economic sectors, particularly concerning the changing energy structure. In the past, energy shortage and inefficiencies’ posed damages to the economy. The government launched various plans during 2013–2018 to fix the energy crisis for ensuring the smooth distribution of energy supply. These schemes added a total power of 12,230 MW to the national energy system [18]. Electricity consumption patterns evidenced that there was no substantial change in electricity demand. The household’s electricity consumption pattern indicated a slight decrease from 51% in 2018 to 48% in 2019. The industrial sector also revealed an increasing electricity consumption trend of 25% in 2018 and 27% in 2019; however, commercial consumption remained unchanged from 2018 to 2019. The agriculture sector consumption also declined by 1% from 10% in 2018 to 9% in 2019. The surge in industrial sector electricity consumption shows a positive sign that market was recovering from the earlier economic damages but still needs improvement in other sectors. Figure 1 shows a comparison of electricity consumption patterns from July 2018 to March 2019 fiscal year.
Several past studies evaluated the indispensable role of electricity consumption in Pakistan and applied linear and nonlinear conceptual models to report agammaegate demand for electricity consumption and quantify it [3,6,19,20,21]. The past literature findings specified that real wages, real substitute and actual electricity rates, temperature, and stochastic patterns appear to be critical determinants of Pakistan's agammaegate and sectoral electricity demand. The factors mentioned above evidenced that Pakistan has to develop an appropriate and well-designed economic model linked to electricity rate, consumption, and economic growth indicators. Figure 2 indicates the rising trends in electricity consumption and GDP while prices fluctuate from 1998 to 2018 due to government subsidy for the industrial boost in Pakistan.
The study's inspiration and contribution consist of a review of Pakistan's energy demand and supply and its effects on Pakistan's economy. Comparison to prior research, the present study provides fascinating and real contributions. First, we find limited studies that address all the variables related to the industrial sector in Pakistan. Second, the current research explores the relationship between electricity consumption, price, and real GDP of Pakistan's industrial sector using data from the 1960–2018 time series. Third, the study employs the unit root test, Johansen co-integration, Vector Error Correction Model (VECM), impulse response function, and variance decomposition tests, and offers more fruitful inferences. By comparison, within a VECM system, we research the variables' relationships. It helps us determine whether there is a long-term (or co-integrating) link between the variables and investigate their existence. Fourth, the study results would help formulate energy generation and consumption policies while also articulating an ambitious power rationing strategy to minimize economic loss due to energy shortages. Finally, similar studies are based on flawed data, but specific data from Pakistan's industrial sector is considered in this study. This novelty has created a gap between earlier research.
The remainder of the study organized as follows: the next section 2 presents the literature review, and section 3 parades econometric material and methods. Section 4 shows the results and discussion, while section 5 provides conclusions and policy implications.
2.
Literature review
Several studies have been done over the last few years, examining the relationship between an economy's electricity demand and economic progress. As of now, the relationship between energy use and financial growth is recorded significantly by [4,22,23,24]. Thus, our analysis estimates electricity consumption (EC) prices and gross domestic product (GDP) from the literature context. Followed Chen and Fang (2018) investigated the co-integrating and Granger causal relationships between economic development, industrial energy use, and human resources in China using a panel of 210 prefectural cities for the 2003–2012 period [25], also Cialani and Mortazavi (2018) examined the energy demand and its determinants after the liberalization of the power markets in 29 European countries [26]. Based on panel data from 1995–2015 for these countries and using a dynamic partial adjustment model, market elasticity is calculated for both residential and industrial demand for electricity. They discovered short-run and long-run causation of EC to GDP and inferred that a lack of energy could harm economic growth (EG). The causality evidence found from energy use to EG confirms the result of [28,29,30,31], whereas the causality findings from economic progress to electricity use are aligned with [27,28,29,30,31]. Moreover, another critical study by [32] enquired about the effect of power consumption, using yearly data for the period 1971–2012, on GDP, labor, and capital stocks. The Structural Vector Self-Regression (SVAR) method analysis shows that labor demand rises with economic growth. Conversely, Nazlioglu et al. (2014) inspected the causal association between Turkey's energy and financial development between 1967 and 2007 [33]. They use three investigative econometrics methods to achieve this objective: the bounds testing method to co-integration, the linear and the nonlinear Granger causality test. The analysis of co-integration indicates that in the long run, co-integrated relationship. Further, Al-bajjali and Yacoub (2018) inspected determinants of electricity consumption from 1986–2015, focused on six independent variables by employed VECM for analysis; the results confirmed that GDP, urbanization, and agammaegate water consumption, are essential and positively related electricity consumption [34].
Similarly, Ghafoor et al. (2016) studied that energy shortages have caused economic losses of between 2% and 3% of Pakistan's GDP [35]. Further, Sidique (2014) used the Granger causality test of Hsiao and reported that the effect of EC on EG is strong and highly meaningful [36]. However, Shahbaz and Hooi (2012) utilized the Autoregressive Distributed Lag (ARDL) model and found the bidirectional causality between EC and EG [37]. Additionally, Javid and Qayyum (2014) utilized the structural time series and found a growing EC pattern in the rural, industrial, and housing sectors [38]. Jamil and Ahmad (2010) presented Johansen cointegration and VECM Granger causality tests and noticed one-way causation flowing from EG to EC [39]; Khan and Abbas (2016) implemented a panel cointegration study, and calculated electricity demand in agricultural and industrial sectors are more resilient to reform [40]. The Autoregressive Integrated Moving Average (ARIMA) models were applied by [41] and observed that EC has a clear interaction with EG. They stated that the ARIMA model was the best in the forecast and indicated that schemes' productivity would be improved by increasing energy usage.
Lin and Yousaf (2021) measured the electricity consumption in Pakistan between 1989 and 2018 using the index decomposition. The findings indicate that the economic structure's impact was the key driving force in Pakistan's increasing overall electricity usage [42]. Recently Lin and Yousaf (2020) implemented the MARKAL model and measured the supply, demand, and diversity of primary energy supplies [43]. The findings suggested that the availability of primary energy decline slightly. These analyses investigated the correlation between EG and EC, the short-term causal relationship, long-run, and regression-related tests among the parameters. The result showed that the scarcity of electricity could damage the economy of Pakistan. The outcomes are varied, according to early findings. In particular, all research on Pakistan's electricity use and economic growth relationships indicates no consent on the direction of causality among these variables. The EC, therefore, plays a vital role in Pakistan's cultural identity of economic and financial growth. Structural transition and with up-gradation might be a little more specific in this case. Therefore, the characteristics and distinctions in energy use within the multiple segments need to be addressed. Lin and Yousaf (2020) indicated that it is possible to achieve optimum production by rising capital and energy technologies [44]. The different studies' findings are inconsistent, or even substantially contradictory, partially due to variations in methods or data length. They reviewed previous studies and their findings from the causal relationship between energy consumption and economic growth reported in Table 1. Whereas we find various studies evaluating the causal association between energy and economic development in Pakistan, no research explicitly examined the relationship between energy consumption, price, and GDP growth in the industrial sector. However, these variables are used in different aspects, methodology, and duration. This research extends the relevant literature on electricity by defining the industrial sector causality path between electricity consumption, prices, and real GDP.
Therefore, this study aims to capture a comprehensive view, based on the most up-to-date database, of the differentiation indices of electricity consumption (EC), price, and GDP of the industrial sector in Pakistan from 1970 to 2018. Nevertheless, no consideration was given to studying the modeling techniques of electricity consumption of Pakistan in general. We may examine the efficacy of the past policies by observing the EC, price, and GDP link. In formulating future policies, a greater understanding of how the EC is evolving in Pakistan is also crucial. This analysis allows us to use the VECM in combination with the variance decomposition method to determine the influence of selected variables that affect EC in Pakistan over the time defined.
3.
Econometric material and methods
3.1. Data collection
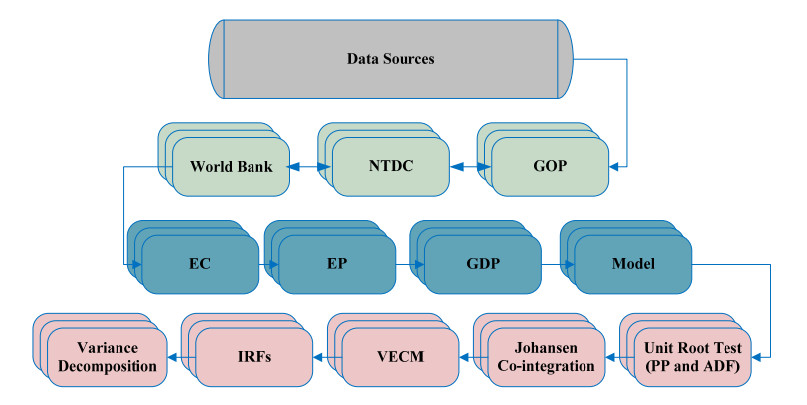
The research investigates the relationship between electricity consumption, electricity prices, and the GDP of Pakistan's industrial sector. The study used time series secondary data based on yearly observation, covering five decades approximately from 1970–2018, exhibits in Table 2. The electricity will measure in Gigawatt hour (GWh). Because electricity has been a public enterprise in Pakistan, instead of being regulated by the market, the electricity price is cross-subsidizing in all sectors. We use the average price of electricity, while real GDP uses a proxy of industrial value-added taken by the world bank's most authentic source, National Transmission & Despatch Company (NTDC) and Government of Pakistan (GOP) official websites. Figure 3 depicts the diagram of the variables.
3.2. Model selection and estimation
3.2.1. Stationarity diagnostics
The cointegration test allows the series under examination to be non-stationary in the same integration order to evaluate the long-term relationship between variables. The model forecasts that price is a significant factor in demanding electricity. Our empirical research implements the extensively employed method to maximum likelihood by Johansen for the analysis. The first step is to check all the variables for their stationarity., and two following tests are widely prominent [57,58], to detect the integration in all series, which stated in Eq 1:
where, yt denotes a series and ut expresses error terms. Appropriate lags of Δyt are incorporated the whiten the errors. According to the Schwarz Bayesian criterion (SBC), the lag length is chosen, later checking for the serial correlation of first and higher-order in residuals. For the H0 null hypothesis test in Eq 1 is ‘d,’ which = 0, against the one-tailed, and alternative, which is negative. The stationarity of yt would not be rejected If δ result results significantly negative. Modeling associations among non-stationary features essentially prerequisite their differencing to make stationarity. For several years, most of the long-run economic relationship lost due to differences; therefore, extensive data needed at level variable for the conservation of the long-run. Meanwhile prevents chosen variables from being spuriously regressed. A long-run equilibrium relationship among non-stationary time series data exists as indicated by economic theories. If variables are I(1), so the co-integration approach will be applied in the long-run. Augmented Dickey-Fuller (ADF) and Phillips–Perron (PP) unit root tests are the primary step to move into the co-integration model.
3.2.2. Johansen cointegration test
Following [59] and [60], a demand-side model was used to investigate the industrial sector's reaction to unanticipated electricity consumption shock electricity prices and GDP. Impulse response function assessment ensures a systematic long-run relationship to determine the underlying predictor and does not wander much farther away from one another. The Johansen-Juselius cointegration technique is favored over the Engle and Granger two-step cointegration process for estimating long-term relationships in multivariate condition. Since if we regress Y on X in the former model, the outcomes would vary from regressing X on Y. In comparison, the Engle-Granger technique is a two-step procedure and the second step would therefore be influenced by an error happening in the first step. The technique proposed by [61] for maximum likelihood is reflected in the following VAR model:
where Xt is an (n × 1) economic time series vector. A1, A2, ..., the (n × n) coefficient matrices are represented by Ap and εt is an (n × 1) vector with zero mean and constant variance error terms. We notice two test statistics for the estimation of cointegrating vectors, i.e., likelihood ratio or trace statistics, under the Johansen-Juselius methodology, and maximal eigenvalue statistics, as follows:
trace statistics are used to test the null hypothesis that the number of cointegrating vectors is less or equal to r, whereas max statistics evaluate the null hypothesis that cointegrating vectors are equal to r. These measures are focused on drawing parallels, and both λtrace and λmax statistics would be weak if characteristic roots are near to 0, and there will be less support for long-term series relationships.
3.2.3. Vector error correction model
One of the Granger interpretation theorem's ramifications is that Granger causality occurs at least in one direction if the series has a cointegrating relationship, which indicates if a conditional variable strengthens the predictor variables prediction when shown in the model [61,62]. The popular meaning of lagging independent terms is investigated under the Vector Autoregression (VAR) concept of Granger causality. The causal relationship is calculated under a VECM that differs between short-and long-term casualties while the sequence is co-integrated. Important terminology for error correction leads to long-term Granger causality, while the general sense of lagged independent variables is an example of short-term Granger causality. In addition, the corrections to the long-run equilibrium suggested in Eqs 2–4 are summarized:
where EC,EP,andGDP represents electricity consumption, electricity price, and real GDP. Correspondingly, ‘α’ is the intercept ‘n’ is the number of lags, ‘Δ’ is the 1st difference, the joint consequence of lags β1i,γ1i,δ1i, β2i,γ2i,δ2i and β3i,γ3i,δ3i in Eqs 2–4, respectively, while ui,t For (i=1,2,3) are residuals, and the Error Correction Terms (ECT) specified by ECTr,t−1 and 'ϕ' is the adjustment of model speed towards equilibrium. For example, scale and the statistical significance of the one-period lag ECTr,t−1 coefficient determines how quick the disequilibrium in EC,EPandGDP are corrected to return to the equilibrium. All the variables are used in the natural logarithmic form. A series of short-run changes slowly rectify the divergence from the long-run equilibrium. The size and statistical significance of the ECT is a measure of the degree to which the left side variable returns to its long-run equilibrium in reaction to the random shocks of each equation for each short-run cycle, while the error correction model via the ECT provides another method for the detection of Granger causality that can be avoided in standard Granger and Sim study. The actual regression coefficients are generally hard to read in a VAR system. These are then represented by techniques connected with VAR models, i.e., impulse response functions and decomposition methods of variance. Impulse response function in earlier researches has been utilized widely for policy evolution. Energy sector reform appraisal analyses include [63,64,65,66]. Causation from EPtoEC and GDPtoEP can be tested similarly from Eqs 4–6, respectively. As explained above, whereas the existence of causality indicated by co-integration, VECM confirms the direction of causality among the variables. In addition, in [67], the error correction model makes it possible to differentiate between long-term and short-term causality in contrast to returning the missing information to the system due to the terminology of error correction. Figure 4 demonstrates the graphical representation of the study framework.
4.
Results and discussions
Firstly, the stationarity check of all variables to be conducted, which is necessary to prevent the spurious regression. The H0 considered as non-stationary series (has unit root). All variables should be stationery earlier containing in the model. Across all variables, the ADF and PP tests suggest the presence of unit root at a 5% significance level, indicating that any statistical inferences in levels from the series would be invalid [68]. Though the non-stationarity hypothesis was discarded in its first difference for all the series, electricity consumption, electricity prices, and real GDP were integrated with order one or I(1) as a whole shown in Table 3. All variables are integrated with order one, a necessary condition of the process variables co-integration relationship.
After the first condition has been met, we step into the next process to determine whether there is a long-run relationship among the variables. Therefore, Johansen and Juselius (1990), Johansen (1988) maximum likelihood method applied to find the co-integration, which consists of the two following estimations: trace(λ−trace)andmaximumeigenvalue(λ−max)statistics [61,62]. The H0 is rejected against the H1 at a 5% level. Hence, it is confirmed that there is a long-run relationship exists in two variables in line with [34,53]. The illustration of unrestricted co-integration outcomes shown in Table 4.
We proceed to the VECM estimate, as defined by Eqs 4–6, drawing inferences for each variable within the sample on the direction of causality and the exogenity or endogeneity. The result of the VECM is exhibited in Table 5. All variables are projected at a one-period lag. The term error-correction depends on the previous period deviation from long-run equilibrium (the error) affects the explanatory variables short-run dynamics. Hence, the coefficient of ECT, ϕ, is the speed of adjustment; it measures the speed at which explained variables return towards equilibrium after a change in the other variables [69].
ECT's coefficient is negative in all variables and found significant at the 5% level, where a 1% increase in electricity price decreases electricity consumption by 0.13%, as well a 1% increase in GDP increase EC by 0.09%. While a 1% upsurge in electricity consumption decreases electricity price by 0.19%, if GDP increase by 1%, then electricity price decreases by 0.16%. However, a 1% increase in electricity consumption increases GDP by 0.15%, and electricity prices have an insignificant effect on GDP. The study in line with [37,70,71,72] reported similar results in Pakistan's case between energy use and economic development and energy consumers, except exogenous energy prices. Additionally, our results are similar to those of [73] for China and [74] for Turkey. These findings indicate that the key factors for Pakistan's economic progress are energy use and price. The overall vector error-correction models confirm that the industrial sector energy management could be viable. Since our study is limited to the use of electricity instead of the total use of electricity, Our findings do not merely contradict with the results in the [39] and [75] that shows energy shortages in Pakistan could affect economic growth, as causality varies from short- and long-term energy consumption to GDP. Our findings also vary from those reported in [76], which also considers the existence of unidirectional causality at the agammaegate level from electricity consumption to GDP. There could be several factors for the discrepancy in their outcomes, such as various data periods included in the research and econometric methods Granger causality form of Hsiao. Our findings show that as real economic growth rises, the electricity demand increases and distributors need to boost their capacity to maintain an adequate supply. While the increase in price decreases electricity consumption, that can decrease the productivity of the industrial sector. However, electricity consumption reflects positively in economic growth that could be considered for the policymakers.
4.1. Impulse responses functions (IRFs)
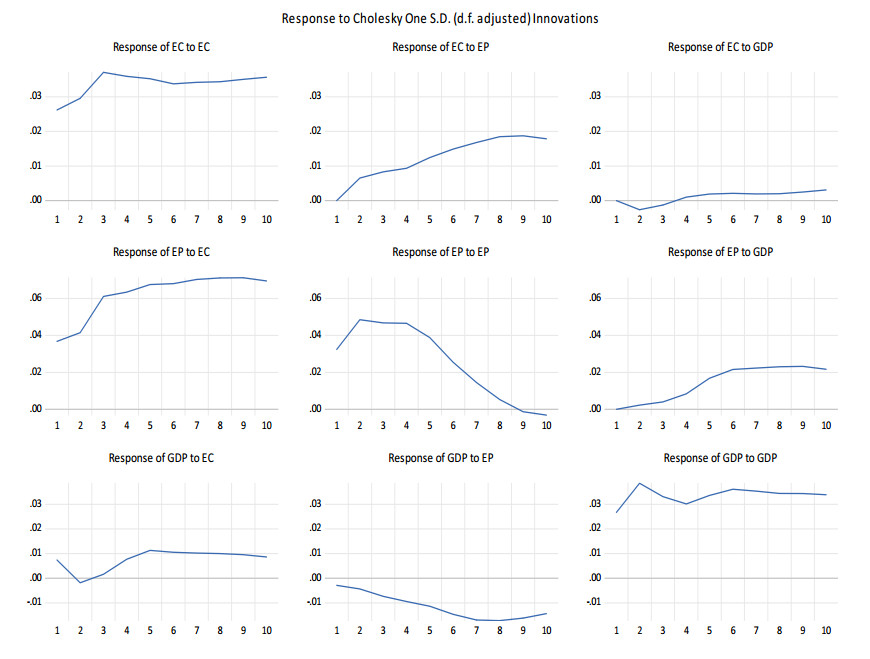
In the vector error correction model, the IRF tracks the predictor variables' response to an unexpected shock or novelty. In this study, we calculated IRFs for sector-specific EC, EP, and GDP. IRF outcomes for the industrial sector is seen in Figure 5.
To determine how a shock affects alternative variables and how long the effect lasts, we use the generalized variable impulse responses proposed by [77] and [78] for ten years, the impulse responses from the variables given. Illustration Figure 5 shows shock in EC, EP, and GDP separately. If one standard deviation is positively shocked at electricity price, then electricity consumption is continually rising, and the GDP decline declined about two years afterward, it is continuously increasing and shows a positive long-run relationship. However, in response to electricity price positive shock increasing electricity consumption two years, then even continuously, electricity price positive shock increases GDP for three years then stable, which shows the long-run relationship. If one standard deviation shock in electricity consumption, then GDP upwards about five years after that constantly. However, the shock in electricity price declined GDP about seven years later; it seems steady.
4.2. Variance decomposition analysis
Until now, the research has been limited to in-samples. Furthermore, to assess the comparative importance of the causality check's findings, we are now carrying out variance decomposition analyses. Because it is well renowned, the variance decomposition effects rely on ordering the variables necessary to recognize the structural VAR from the projected modified form VAR approach. In literature, the normal method is to propose the most credible order driven by economic concept and confirm the outcomes' robustness by inverting the ordering see, for example, [39,79]. For short, we are considering three years and for the long-run eight years in all models.
Table 6 depicts the findings of variance decompositions for the model (EC, EP, and GDP). In the short-run, electricity consumption analysis causes a 96.07% variation in electricity consumption shock fluctuation. Further shock to electricity price influences 3.66% in electricity consumption fluctuation, whereas GDP affects 0.27% in response to electricity consumption change. To check the long-run shock to electricity consumption causes 87.97% variation of the fluctuation is self-explained—however, electricity prices and GDP effects by 11.78% and 0.25%, respectively.
Table 7 illustrates the outcomes of variance decompositions for the model (EP, EC, and GDP). The short-run shock to electricity price causes a 44.97% variation of the electricity price fluctuation is generally self-explained. Further shock to electricity consumption influences 54.86% in the fluctuation of electricity prices. At the same time, GDP affects 0.17% to electricity prices. The long-run shock to electricity price causes a 24.15% variation of the fluctuation is self-explained—however, electricity consumption and GDP effects by 71.39% and 4.46%, respectively.
Table 8 demonstrates the effects of variance decompositions for the model (GDP, EP, and EC). The short-run shock to GDP causes 95.87% variation of the fluctuation in GDP, usually is self-explained. Further shock to electricity consumption influences 1.78% in the fluctuation of GDP. However, electricity price affects 2.35% to GDP. However, the long-run shock to GDP causes 84.54% variation of the fluctuation is self-explained. But electricity consumption and electricity prices effects by 5.25% and 10.21% respectively.To summarize, the by-and-large findings of the variance decomposition endorse the results achieved by the VECM model. The primary effect that energy usage is influenced by electricity prices, whereas output and electricity consumption also positively affect real GDP.
4.3. Discussions
Pakistan's electricity generation from 1987 to 2019 was revised monthly at an average of 5,955 GWh. In 2018, the data hit an all-time peak of 16,946 GWh and a historic low of 2,313 GWh in 1989. The findings indicate that model coefficients met all predictions, and the electricity price is a reliable mediating component for the industrial sector that revealed a 1% change in electricity price decreases electricity consumption by 0.13%. The study found that as the rise in industrial electricity prices raised firms' energy costs, it could push firms to pursue technological innovation and enhance production performance. By reducing their conflicting duties, the institutional setup of energy divisions needs to be standardized. For instance, the NEPRA electricity regulator's role to advise the government on secure and reliable ways to meet electricity demands at manageable rates should be fulfilled as per law. As well a 1% change in GDP increase EC by 0.09%. Disagammaegated power use and economic development analyses would make it more useful for authorities to devise a robust energy-saving and environmental degradation strategy. The findings show the industries in which economic development over long periods is related to energy consumption. A 1% upsurge in electricity consumption decreases electricity price by 0.19%, which is quite useful for policymakers that managing industrial electricity prices can enhance manufacturing productivity. These prediction findings were correlated with related studies in the existing literature to demonstrate the accuracy of the present analysis. The findings differ from various studies focused on energy factors using different models and periods, such as [12,80,81,82,83,84,85]. In Pakistan's case, many studies concluded differently, such as [3,88–92]; however, none of them focused on these factors. The novel findings can be beneficial for the sustainable energy policy as per Pakistan's industrial sector's potential.
5.
Conclusions and policy implications
The current electricity provision rates in Pakistan are considered unsustainable due, in particular, to poor infrastructure. The widespread blackouts throughout the country have incredibly adverse effects on Pakistan's economic growth and social lives. The current study contributes to the emerging energy literature by investigating the causal link in the industrial sector in Pakistan between electricity consumption, prices, and GDP, by using a neoclassical development system. The empirical analysis was conducted using data for the period 1970–2018. The indication of co-integration between variables showed the long-run relationship. It ensures a short-term fluctuation in electricity consumption and GDP, which ultimately returns to long-run equilibrium. Most of the coefficients lagged in our analysis are significant at a 5% level except for GDP electricity prices. The outcomes show a causal relationship from electricity consumption to price and GDP that impact is long-term in the industrial sector, which is the foremost determinant of Pakistan's economic change.
5.1. Recommendations and policy implications
Pakistan is a country where a lack of electricity and the electricity sector work bare capacity margin. Based on our findings obtained in this study. More interest should be given to policy recommendations as follows: (a) 1% rise in the price of energy reduces electricity usage by 0.13%, and a 1% increase in GDP raises EC by 0.09%. The result implies that the key driver is the energy price, which indicates an inverse impact on electricity usage that is visa-versa with the costs of industrial production. Also, an increase in EC was positively affecting GDP. The government should invest more in power projects to maintain energy demands and supply, which is beneficial for economic growth and boosts industrial productivity. (b) While a 1 percent rise in energy demand reduces electricity by 0.19%, the price of electricity reduces by 0.16 percent if GDP increases by 1 percent. (c) However, an increase in energy consumption by 1% raises GDP by 0.15%. The empirical results further suggest that electricity prices are the main factor in the use of industrial electricity. The findings suggest that officials should focus on relevant legislation, subsidy reforms, and tax relief in the industrial sector. Moreover, it will attract the business community; foreign investors also provide employment opportunities and boost Pakistan's GDP growth. As a whole, electricity consumption is essential for long-term economic stability and growth in the industrial sector. We suggest that infrastructure planning and investments are vital to meeting the growing electricity demand. Whereas any policies to ease the electricity market should stimulate productivity, the invention in generation and supply, resulting in lesser prices as autonomous suppliers, can stabilize the fluctuation that may positively affect the long term. Finally, we propose that planning and investing in infrastructure growth is essential to meeting the growing electricity demand.
5.2. Research limitations
We have some limitations concerning our studies. Based on the findings of multiple literature pieces, this study selects energy consumption, price, and GDP as useful for the industrial sector. This research was carried out in the industrial sector's specific context, so other Pakistan sectors need to be investigated.
Conflict of interest
The authors declare no conflict of interest.
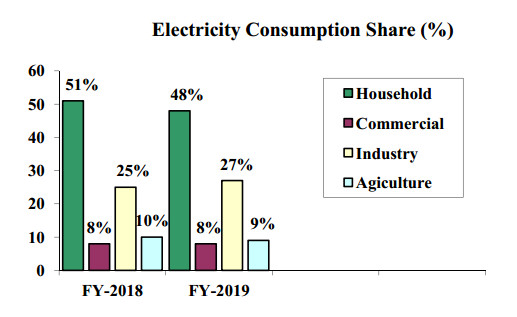









 DownLoad:
DownLoad: