A special class of triple starlike trees characterized by Laplacian spectrum

1.   Introduction

All graphs mentioned in this paper are finite, undirected and simple. Let $\Gamma = (V(\Gamma), E(\Gamma))$ be a graph of order $n$ with vertex set $V(\Gamma) = \{v_1, v_2, \dots, v_n\}$ and edge set $E(\Gamma) \subseteq \binom{V(\Gamma)}{2}$. The adjacency matrix of a graph $\Gamma$, denoted by $A(\Gamma) = (a_{i, j})$ is a square matrix of order $n$ such that $a_{i, j} = 1$ if two vertices $v_i$ and $v_j$ are adjacent and $0$ otherwise. Let $d_i = d_{v_i}$ be the degree of a vertex $v_i$ in $\Gamma$. The Laplacian matrix and the signless Laplacian matrix are defined as $L(\Gamma) = D(\Gamma)-A(\Gamma)$ and $Q(\Gamma) = D(\Gamma)+A(\Gamma)$ respectively, where $D(\Gamma)$ is the diagonal matrix with diagonal entries $\{d_1, d_2, \dots, d_n\}$ and all others entries are zeros ^[9]. We know that the matrices $A(\Gamma)$, $L(\Gamma)$ and $Q(\Gamma)$ are real symmetric, their eigenvalues are real. So, we assume that $\mu_1\geq \mu_2 \geq \dots \geq \mu_n$, $\lambda_1\geq \lambda_2\geq \dots \geq \lambda_n$, and $\sigma_1\geq \sigma_2\geq \dots \geq \sigma_n$ are the adjacency, Laplacian, and signless Laplacian eigenvalues of $\Gamma$, respectively. The multiset of eigenvalues of $A(\Gamma) \ (\text{or} \ L(\Gamma), \ Q(\Gamma))$ is called the adjacency (or Laplacian, signless Laplacian) spectrum of the graph $\Gamma$. If two non-isomorphic graphs share the same adjacency (or Laplacian, signless Laplacian) spectrum then we call graphs are cospectral. A graph $\Gamma$ is said to be determined by the adjacency spectrum (abbreviated to DAS) if there is no non-isomorphic graph which have same adjacency spectrum. Similarly, we can define DLS graph for the Laplacian matrix $L(\Gamma)$ and DQS graph for the singless Laplacian matrix $Q(\Gamma)$.

In 1956, Günthard and Primas ^[6] raised a question "which graphs are determined by their spectrum" in context of Hückels theory. Basically this problem originates from Chemistry and generally seem to be very difficult. On this problem, Dam and Haemers ^[24] presented a survey and proposed the modest shape of this problem that is "which trees are determined by their spectrum". Many researcher have been established results on the graphs DAS, DLS and DQS and some of these results can be found in ^{[1,2,21,23,24,25]}, in ^{[1,5,11,12,13,14,21,22,26,27,29]} and in ^{[3,4,13,16,17,20,28]} respectively.

A tree $T_{n'}$ of order $n'$ is a connected graph without cycle. A vertex $v\in V(T_{n'})$ is called large if $d_{v}\geq3$. A tree having one, two or three large vertices is called starlike, double starlike or triple starlike tree, respectively.

We denote by $T_{n'}(p, q)$, $n'\geq2$ and $p, q\geq1$, one special double starlike tree (of order $n'$) obtained by joining $p$ pendent vertices to an end vertex of a path of length $n$ and joining $q$ pendent vertices to another one. In 2009 Liu et al. ^[11] studied the Laplacian spectrum of $T_{n'}(p, q)$, for $q = p$ they showed that $T_{n'}(p, q)$ can be determined by its Laplacian spectrum. In 2010 Lu et al. ^[14] showed that for $q = p-1$, $T_{n'}(p, q)$ can be determined by its Laplacian spectrum. In ^[15], the authors proved that $T_{n'}(p, q)$ can be completely determined by its Laplacian spectrum.

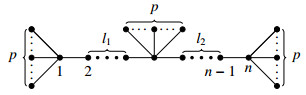
Let $P_{n}$ be a path of length $n$, where $n\geq 5$, attach $p$ pendent vertices to an end vertex of $P_{n}$, $p$ pendent vertices to another end vertex and $p$ pendent vertices to any vertex $v\in V(P_{n})$ which is at distance at least two from the end vertices of $P_{n}$ where $p\geq 2$, by this way we obtain a special triple starlike tree as shown in Figure 1 (or Figures 2 and 3). We denote the aforementioned tree by $T_{n'}(p, p, p)$. Note that the order $n'$ of $T_{n'}(p, p, p)$ is $n+3p$, where $l_1+l_2 = n-3$ see Figure 1. In this paper we show that $T_{n'}(p, p, p)$ can be determined by its Laplacian spectrum or more precisely, any graph that is determined by its degree sequence is determined by its Laplacian spectrum.

2.   Preliminaries

In this section, we present some known results that play an important role in the results of next section.

Lemma 1. ^[19,24] Let $\Gamma$ be a graph. Then the following items are determined by spectrum of adjacency or Laplacian matrix.

1). The number of vertices in $\Gamma$.

2). The number of edges in $\Gamma$.

3). Whether $\Gamma$ is regular.

4). Whether $\Gamma$ is regular with any fixed girth.

For adjacency matrix, the following quantities are determined by its spectrum.

5). Whether $\Gamma$ is bipartite or not.

6). The number of closed walks of any length.

For Laplacian matrix, the following quantities are determined by its spectrum.

7). The number of components.

8). The number of spanning trees.

9). The sum of the squares of degrees of vertices.

Lemma 2. ^[7] Let $T_{n}$ be a tree of order $n$ and ${\frak{L}}(T)$ be its line graph. Then $\lambda_i(T) = \mu_i({\frak{L}}(T))+2$, where $1\leq i \leq n$

Lemma 3. ^[8,10] For a graph $\Gamma$ with a non-empty vertex set $V(\Gamma)$ and non-empty edge set $E(\Gamma)$, let $\it{\Delta}(\Gamma)$ be the maximum vertex degree of $\Gamma$. Then we have the following inequality.

where $m_{v_i}$ denotes the average of the degrees of the vertices adjacent to a vertex $v_i$ in $\Gamma$.

3.   Determination of $T_{n'}(p, p, p)$ by Laplacian spectrum

In this section, first we establish the following two lemmas which will be used in our main result.

Lemma 4. Let ${\Gamma}^{'}$ and $\Gamma = T_{n'}(p, p, p)$, where $n' = n+3p$ with $n\geq5$ and $p\geq2$ are cospectral graphs with respect to the Laplacian matrix. Then ${\Gamma}^{'}$ has $t_{p+2} = 1$, $t_{p+1} = 2$, $t_{2} = n-3$, and $t_{1} = 3p$, where $t_i$ is number of the vertices of degree $i$ in ${\Gamma}^{'}$.

Proof. Given that the graphs ${\Gamma}^{'}$ and $\Gamma$ are cospectral with respect to the Laplacian matrrix. Then by 1, 2, 7, and 8 of Lemma 1, the graph ${\Gamma}^{'}$ is a tree with $|V({\Gamma}^{'})| = n+3p$ and $|E({\Gamma}^{'})| = n+3p-1$. From Lemma 3, we have $p+3\leq \mu_1\leq p+4-\frac{2}{p+3}$, which implies the maximum degree in the graph ${\Gamma}^{'}$ is at most $p+2$. Now, assume that the graph ${\Gamma}^{'}$ has $t_i$ vertices of degree $i$, for $i = 1, 2, \dots, {\Delta}^{'}$, where ${\Delta}^{'}\leq p+2$ is the maximum degree of ${\Gamma}^{'}$. The following equations follow from $1$, $2$, and $9$ of Lemma 1.

Then

The line graphs of $\Gamma$ and $\Gamma^{'}$ have same spectrum with respect to the adjacency matrix, by Lemma 2. Hence, from $6$ of Lemma 1, they have same number of triangles (closed walk of length three). Therefore,

First we show that there is only one vertex of degree $p+2$, $i.e.$, $t_{p+2} = 1$. If $t_{p+2} = 0$, $i.e.$, ${\Delta}^{'} < p+2$

$i.e.,$

By Eq (3.4), $p\leq 0$ which is a contradiction.

If $t_{p+2}\geq 2$, $i.e.,$ there are at least two vertices of degree $\Delta = p+2$, then we have

$i.e.,$

This is a contradiction, hence $t_{p+2} = 1$.

Second we prove that $t_{p+1} = 2$. If $t_{p+1}\geq 3$, $i.e.$, there are at least three vertices of degree $p+1$, then we have

$i.e.,$

This is a contradiction, so $t_{p+1}\leq 2$.

If $t_{p+1} = 0$, $i.e.,$ there is no vertex of degree $p+1$, then we have

$i.e.,$

$i.e.,$

$i.e.,$

$i.e.,$

By Eq (3.4), $3p^2+p-2 \leq 3p^2-p$, $i.e., \; 2p-2\leq 0$, a contradiction.

If $t_{p+1} = 1$, $i.e.,$ one vertex of degree $p+1$, then

$i.e.,$

$i.e.,$

$i.e.,$

$i.e.,$

By Eq (3.4), $3p^2-1\leq 3p^2-p$, $i.e., \; p-1\leq 0$, a contradiction. Thus $t_{p+1} = 2$.

For each $i = 3, 4, \dots, p$, $t_i = 0$ from Eq (3.4). Finally, Eqs (3.1) and (3.2), immediately yield $t_1 = 3p$ and $t_2 = n-3$. This finishes the proof.

Lemma 5. Let ${\Gamma}^{'}$ be any tree of order $n+3p$, where $n\geq5$ and $p\geq2$, such that $t_{p+2} = 1$, $t_{p+1} = 2$, $t_2 = n-3$, and $t_1 = 3p$. Then ${\Gamma}^{'}$ is isomorphic to $\Gamma = T_{n'}(p, p, p)$.

Proof. It is clear that there exists $2$, $p+2$, $2p$, and $n-5$ vertices of degree $p+2$, $p+1$, $p$, and $2$, respectively in the line graph ${\frak{L}}(\Gamma)$. Here, we divide the proof into two main cases.

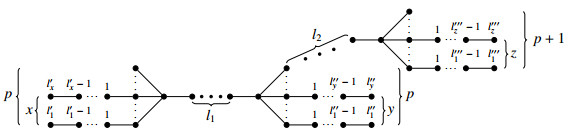
Case 1. When two vertices of degree $p+1$ are joined by a path of length $l_1+1$, $(l_1\geq0)$ and one vertex of them joined by a path of length $l_2+1$, $(l_2\geq0)$ with a vertex of degree $p+2$. Without loss of generality, suppose that there exist $p-x$, $p-y-1$, and $p+1-z$ vertices of degree $1$ which are adjacent to the vertex of degree $p+1$, $p+1$, and $p+2$, respectively in the graph ${\Gamma}^{'}$ as shown in Figure 4. Where $0\leq x \leq p$, $0\leq y\leq p-1$, and $0\leq z\leq p+1$. Therefore, we have

where $l_0^{'} = l_0^{''} = l_0^{'''} = 0$. That is

For the values of $l_1$, $l_2$, there exits four different shape of the graph ${\Gamma}^{'}$. Let $t^{'}_i$ be the number of the vertices of degree $i$. Clearly, there exists $t^{'}_1 = x+y+z$, $t^{'}_2 = n-i-x-y-z$, $t^{'}_p = 2p-x-y-1$, $t^{'}_{p+1} = p+j+x+y-z$, $t^{'}_{p+2} = k+z$, $t^{'}_{2p} = r$, $t^{'}_{2p+1} = s$, and $t^{'}_l = 0$ for $l = 3, 4, \dots, p-1$ and $p+2 < l < 2p$ in the line graph ${\frak{L}}({\Gamma}^{'})$, where the values of $i$, $j$, $k$, $r$ and $s$ are listed in Table 1 corresponding to each shape of ${\frak{L}}({\Gamma}^{'})$.

From $2$ and $5$ of Lemma 1, the line graphs ${\frak{L}}(\Gamma)$ and ${\frak{L}}({\Gamma}^{'})$ have the same number of edges and closed walks of length $4$, respectively. Clearly, they have the same number of $4$-cycles $2\binom{p+1}{4}+\binom{p+2}{4}$. Hence the line graphs ${\frak{L}}(\Gamma)$ and ${\frak{L}}({\Gamma}^{'})$ have the same number of induced paths of length 2. Then we have

$i.e.,$

Since $p\geq 2$, $0\leq x\leq p$, $0\leq y\leq p-1$, and $0\leq z\leq p+1$. For each case of $l_1$ and $l_2$ that mentioned in Table 1 and take corresponding values of $i, j, k, r, s$. It is easy to check that the Eq (3.7) is not equal to zero, which is a contradiction.

Case 2. When a vertex of degree $p+2$ joined with two vertices of degree $p+1$ by paths of length $l_1+1$, $(l_1\geq0)$ and $l_2+1$, $(l_2\geq0)$, respectively. Without loss of generality, suppose that there exits $p-x$, $p-x$ and $p-z$ vertices of degree 1 which are adjacent to vertex of degree $p+1$, $p+1$, and $p+2$ respectively in the graph $\Gamma^{'}$ as shown in Figure 5. Where $0\leq x, y, z \leq p$. Therefore, we have same two equations as Eqs (3.5) and (3.6).

For the values of $l_1$, $l_2$, there exits three different shape of the graph $\Gamma^{'}$. Clearly, there exits $t^{'}_1 = x+y+z$, $t^{'}_2 = n-i-x-y-z$, $t^{'}_p = 2p-x-y$, $t^{'}_{p+1} = p+j+x+y-z$, $t^{'}_{p+2} = k+z$, $t^{'}_{2p+1} = r$ and $t^{'}_l = 0$, for $l = 3, 4, \dots, p-1$ and $p+2 < l < 2p+1$ in the line graph ${\frak{L}}(\Gamma^{'})$. Where values of $i$, $j \; k$, and $r$ are listed in Table 2 corresponding to each shape of ${\frak{L}}(\Gamma^{'})$.

By same argument that we used in first case, we have

$i.e.,$

Since $p\geq 2$ and $0\leq x, y, z\leq p$. For first two cases of $l_1$ and $l_2$ that mentioned in Table 2 and take their corresponding values of $i, j, k, r, s$. It is easy to check that the Eq (3.8) is not equal to zero, a contradiction. For the last case $l_1, l_2\geq1$, we obtained $(x+y+z)p-(x+y) = 0$, so $x = y = z = 0$. By Eq (3.6), we have $l_1+l_2 = n-3$. Thus all the vertices of degree $1$ adjacent to the two vertices of degree $p+1$ and one vertex of degree $p+2$. Hence, $\Gamma^{'}$ is isomorphic to $\Gamma$.

Now, we ready to prove our main result.

Theorem 6. The tree $T_{n'}(p, p, p)$, where $n' = n+3p$ with $n\geq 5$ and $p\geq2$, is determined by its Laplacian spectrum.

Proof. The proof of this result immediately follows from Lemmas 4 and 5.

Acknowledgments

The authors are grateful to the editor and anonymous referees for their comments and suggestions to improve quality of this article. The research of Muhammad Ajmal was supported by Post Doctoral Research Fellowship at Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing, China.

Conflict of interest

The authors declare that they have no conflict of interest.