1.
Introduction
Time-delay is well known as the source of instability, degradation of quality, and vibration in dynamic systems [1,2,3,4,6,5,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. The delay is ineluctable for almost all systems with input-process-output and feedback structures, so the stability analysis of the time-delay systems (TDSs) is the prerequisite before the systems can be operated. From the perspective of the frequency domain analysis, the linear systems are asymptotically stable if and only if the spectrum (system poles) lies in the left half plane. Since the spectrum for TDSs ˙x(t)=Ax(t)+Adx(t−h) is {s:det(sI−A−Ade−sh)=0}, the infinite dimensional states (poles) exist. For this reason, because it is very difficult to solve the matter of the stability for TDSs in analytical methods, various methods [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] for the problem have been studied by using the numerical method based on the Lyapunov stability theorem. According to the Lyapunov stability theorem, the system is asymptotically stable if there exists the Lyapunov function V(x(t)):Rn→R such that V(x)>0 for all x≠0 and ˙V(x)<0. When considering this, the structure of V(x) is not fixed. This means that the effectiveness of the analysis method is affected by the structure of V(x). As a result, this is the open problem in the TDSs.
In general, stability analysis for TDSs can be divided into two types: delay-dependent and delay-independent analysis. In general, the former containing information about the time delay value is less conservative than the latter, especially if the time delay value is small. Then, many researchers have proposed various delay-dependent stability criteria for TDSs. In this regard, recently, Zhang et al. [23] proposed delay-dependent-matrix-based reciprocally convex inequality and estimation approaches were introduced in [23] for stability analysis with time-varying delays of linear systems. Through the augmented L-K functional approach, Park et al. [24] studied the stability problem for linear systems with time-varying delays. In [25], by developing the delay-product-type L-K functional, new delay-dependent stability criteria were proposed. In [26], the double integral inequality and the L-K functional were proposed based on the second-order derivative. By introducing appropriate intermediate polynomial, some novel delay-product types of inequality-based functions were constructed in [27]. In [28], the stability criterion specified as a negativity condition for a quadratic function parameterized by the delay was presented.
From the above considerations, it makes sense to inquire the following thing: "Considering the AFBI-inspired Lyapunov-Krasowskii function, can the feasible areas of stability criteria be improved?". Before we ask the answer to the question, the following facts should be minded through [12]: when examining the conservatism of stability criteria, two momentous indicators exist. One is to find the maximum value of delay bound for guaranteeing asymptotic stability of systems. The other is to reduce the number of the decision variables, in the other words, the computational burdens, while keeping the maximum value of the delay binding the same. In particular, many studies have focused on the former. In this work, prioritizing the former, the main goal in this paper is to propose a stability criterion which provides the delay bounds for guaranteeing asymptotic stability of TDSs as large as possible. In addition, an improved stability criterion obtained by the augmented zero equality approach is also proposed, taking into account both the former and the latter.
From the discussions so for, novel delay-dependent stability criteria for linear systems with time-varying delays are proposed. The highlight of this paper can be summarized:
● Some novel L-K functionals which provide more cross terms among the components of the augmented vector are proposed in Theorem 1. Among them, newly constructed L-K functional inspired by AFBI is included.
● From the relationships of the elements of the augmented vectors, one augmented zero equality is established and Finsler's lemma with the newly constructed zero equality are applied to the derived stability condition. As a result, both reducing of the number of decision variables and extending the feasible region will be done in Theorem 2 comparing with Theorem 1.
Through the simulation of numerical examples, the advantages, effectiveness and superiorities of the proposed theorems are illustrated.
Notations. Rn and Rm×n denote, respectively, n-vectors with the l2-norm ‖⋅‖ and m×n matrices. Sn (Sn+) is the sets of n×n symmetric (positive definite) matrices. In and 0m⋅n are, respectively, the n×n identity matrix and the m×n zero matrix. col{⋯} stands for the column vector. Sym{X} is the sum of X and its transpose. X[α] means the sum of a constant matrix X1 and a linear matrix αX2 for all real scalars α. The symmetric terms will be denoted by ⋆ when necessary.
2.
Problem formation
Consider linear systems as follows
where χ(t) is an initial function, x(t) is the state vector in Rn, A and Ad are system matrices in Rn×n. The time-delay function ν(t) is considered to meet the following conditions:
where νm>0, μu≥0 and μl are known scalar values.
To derive the stability criteria for the system (2.1), the following useful lemmas are employed.
Lemma 1. [13] For matrix H∈Sn+ and vector f:[a,b]→Rn, the following inequality holds:
where scalars a<b and semi-positive integers k, l, for i=0,1,…,l, and other notations were defined at the work [13].
Remark 1. Lemma 1 with k=0 and l=1 is WBI [14] and with k=0 and l=2 is corresponded to AFBI [15].
Lemma 2. [29] For matrices M1, M2 ∈Sn+ and a constant α∈(0,1), if there exist matrices S1, S2 ∈Sn+, F1, F2 ∈Rn×n such that
for all α=0,1, then the following inequality holds:
Lemma 3. [30] For v∈Rn, F∈Sn, G∈Rm×n such that rank{G}<n, the following formulas are equivalent:
3.
Main results
In this section, by the use of LMI framework, new two stability conditions for the system (2.1) are introduced. To simplify matrix representation, the block entry matrices can be expressed as ϑi=[0n⋅(i−1)n,In,0n⋅(16−i)n]T∈R16n×n for i=1,2,…,16, ϑ0=016n⋅n.
The following theorem is the stability criterion of system (2.1).
Theorem 1. The system (2.1) with the condition (2.2) is asymptotically stable when obtaining matrices R∈S7n+, Gi∈S6n+ (i=1,2,3), Q∈S2n+, W∈Sn+, Sj∈S6n+, Pj∈Sn, Fj∈R6n×6n (j=1,2), ϝk∈Rn×16n (k=1,2,3,4) that satisfies the following LMIs :
with several notations
Proof. Let us choose the following L-K functional candidate:
where
Here, the vectors ϖ(t), ϕ(s), β(b,s), ρ1(t) and ρ2(t) are defined as
The time-derivative of Vi (i=1,2,…,4) can obtained as
where
So, it can be arranged that:
Calculating the time-derivative of V5 leads to
Consider two zero equalities:
with symmetric matrices P1 and P2.
Adding the equalities (3.15) and (3.16) to (3.14), we can obtain that:
Using Lemma 1 with k=0 and l=2, integral terms of ˙V5 can be bounded as
where ρ3(t)=∫tt−ν(t)ϕ(s)ds−2ν(t)ξ2ν(t),0(ϕ(u)), ρ4(t)=∫tt−ν(t)ϕ(s)ds−6ν(t)ξ2ν(t),0(ϕ(u))+12ν2(t)ξ3ν(t),0(ϕ(v)), and, in the same way, we get
Thus, from (3.14)–(3.19), ˙V5 has the following bound as
Then, by utilizing Lemma 2 with the conditions (3.5) and (3.6), ˙V5 can be rebounded as
Note that, from Lemma 1 with k=0 and l=2, ˆV is always positive if the W is the positive definite matrix. By taking the time-derivative of ˆV, it can be deduced that:
where
Introducing the free weighting matrices ϝi (i=1,2,3,4), we have
The above zero equalities (3.23)–(3.26) can be combined as
From (3.9)–(3.27), ˙V(t) can be bounded as
Thus, a sufficient stability condition is organized as
By Lemma 3 (i) and (ii), (3.29) is the same as (Γ⊥)T(Ψ[ν(t),˙ν(t)]−Ω[ν(t)])Γ⊥<0. From the convexity of ν(t)∈[0,νm] and ˙ν(t)∈[μl,μu], if the LMIs (3.1)–(3.4) are satisfied with (3.5) and (3.6), then inequality (3.29) holds. This means that Theorem 1 guarantee the asymptotic stability of the system (2.1).
Remark 2. In Theorem 1, from V1 to V4 in (3.8), new combination of the state vectors are considered, which provides more cross terms in LMIs for stability condition of system (2.1). Inspired by AFBI [15], one newly constructed L-K functional ˆV in (3.8) is introduced for the first time. As an outcome of the time-derivatives of ˆV, ζT(t)Ψ6[ν(t)]ζ(t) is added in stability condition. Through the comparison of the obtained maximum delay bounds provided by Theorem 1 with the existing works for the same numerical example, it will be verified that the proposed L-K functional can reduce the conservatism of stability conditions.
Finally, based on Theorem 1, a further advanced outcome is introduced in Theorem 2.
Theorem 2. The system (2.1) with the condition (2.2) is asymptotically stable when obtaining matrices R∈S7n+, Gi∈S6n+ (i=1,2,3), Q∈S2n+, Pj∈Sn, W∈Sn+, Sj∈S6n+, Fj∈R6n×6n (j=1,2) that satisfies the following LMIs with (3.5) and (3.6):
where
Proof. From Theorem 1, a stability condition without considering (3.23)–(3.26) for system (2.1) can be written by
Note that the four zero equations:
Above zero equations and Γ are incorporated into one augmented zero equality as
By Lemma 3 (ⅰ) and (ⅲ), for a matrix Z with an appropriate dimension, (3.34) can be expressed as
Since above inequality (3.40) is affinely dependent on ν(t) and ˙ν(t), if the following four inequalities hold for ν(t) and ˙ν(t),
then system (2.1) is asymptotically stable. By Lemma 3 (ⅱ) and (ⅲ), the feasibility of (3.41) can be checked from (3.30)–(3.33). Other terms are omitted because they are very similar to those in Theorem 2.
Remark 3. In Theorem 1, through new L-K functionals and the equalities (3.23)–(3.26), the improved result was obtained. However, in this case, the free weighting matrices ϝi(i=1,2,3,4) contained in (3.27) result in a large amount of computation for the result. Therefore, the authors proposed the augmented zero approach to remove the free weighting matrices in Theorem 2. This approach reduces the amount of computation because it eliminates the free weight matrices. It also helps to obtain a less conservative result than Theorem 1.
Remark 4. In the very recent works [25,26,27,28], various L-F functionals and mathematical techniques are utilized to obtain the maximum allowable bound that guarantees the stability of the systems. In particular, the stability of the system was studied through the non-convex matrix inequality conditions [31,32]. However, in this work, through the augmented zero equality approach, both important things are met when analyzing the stability of a time delay system. One is to find the maximum delay bound ensuring the asymptotic stability of the system. The other is to reduce the number of decision variables, that is, the computational burden. Thus, via numerical examples, the superiority and effectiveness of the proposed idea presented in Theorems 1 and 2 will be verified.
4.
Numerical examples
This section shows the superiority of the proposed results through numerical examples listed in Table 1. Within Table 2 for Example 1, the most recent results are compared with those obtained in Theorems 1 and 2. First, it can be checked that Theorem 1 provides wider delay bounds than the existing works [20,21,22,23,24,25,26,27]. This means the newly proposed L-K functionals in Theorem 1 plays a key role to enlarge the feasible region of stability condition. Also, Theorem 2 provides better results than Theorem 1 as well as other results. Now, let us look at the result listed in Table 2 for Example 1. Theorem 1 gives better results than most of the results listed in the Table 2, but Theorem 2 is superior to all of those methods. Thus, from Tables 2, 3 and 4, one can see that the stability results based on AFBI give reinforced ones for the three representative examples mentioned in a great number of papers for checking the conservatism of stability criteria for systems (2.1). Furthermore, in Table 4, Theorem 2 provides remarkable improved results. Note that, one can easily confirmed that while Examples 1 and 2 is delay-dependent stable, Example 3 is delay-independent stable. Here, in case of the delay-dependent stable, the value of the delay bound is finite as the value of the analytic bound. As is well known, the analytic bounds of stability for Examples 1 and 2 are 6.1725 and π, respectively. When μu=μl=0 in Theorem 2, 6.1689 and 3.1366 can be obtained, respectively. This means that, because the bounds obtained by Theorem 2 are less than the analytic bounds, Theorem 2 provides the reasonable results. Therefore, the obtained results listed in Examples 1, 2 and 3 are reasonable.
Example 4. Consider the metal cutting process [33]:
where m is the mass of the roll, c is the damping coefficient, k is the stiffness coefficient, F is the stiffness coefficient of the contact, ν(t) is the roll rotation time, and y(t) is displacement of the roll. By defining x(t)=col{y(t),˙y(t)} and setting m=1, k=1, F=2, c=0.5, the above equation (4.1) can be written as
By applying Theorems 1 and 2 in this work, the maximum allowable delay bounds with various μu(=−μl) are listed in Table 5. It can be confirmed that Theorem 2 is less conservatism than Theorem 1.
5.
Conclusion
Novel delay-dependent stability criteria for systems with time-varying delays were introduced. To achieve less conservatism, the new augmented L-K functional including the function on the basis of AFBI was proposed to extend the feasible region of stability criteria. Through several numerical examples, it can be seen that the improvements in the proposed criteria for existing outcomes were shown. Based on the proposed idea, the authors will focus on extending the proposed idea to various applications such as stability analysis for the single switch positive system or the discrete-time single switch positive system, and so on [34,35,36].
Acknowledgments
This research was supported by Chungbuk National University Korea National University Development Project (2020).
Conflict of interest
The authors declare no conflict of interest.









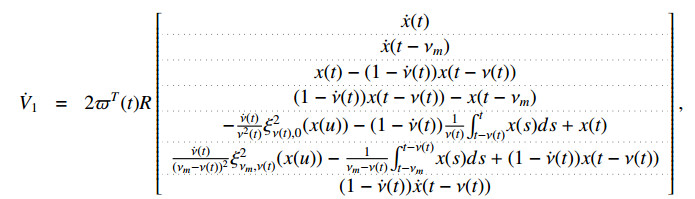
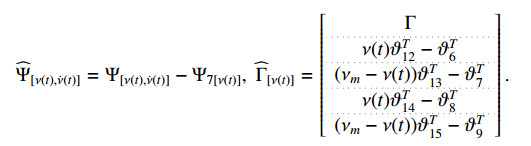
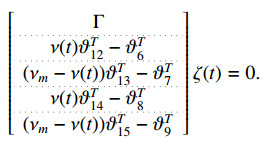
 DownLoad:
DownLoad:



