Forming localized waves of the nonlinearity of the DNA dynamics arising in oscillator-chain of Peyrard-Bishop model

1.   Introduction

In the past few years, investigations of complex dynamical networks (CDNs) have drawn much attention from scholars due to their applications in real-world schemes such as the World Wide Web, electric power grids, food webs, and so on ^[1,2,3]. Complex networks comprise a vast multitude of interconnected nodes and edges that depict the dynamic behaviors exhibited by various individuals and capture the relationships between them. Synchronization is a common and significant collective phenomenon observed in complex networks. It refers to the gradual convergence of node trajectories toward a shared state over time, despite varying initial conditions and interactions between nodes. This convergence of node states forms the basis of synchronization analysis in complex networks ^[4]. There are two types of synchronization: Internal synchronization and external synchronization. External synchronization refers to synchronization between nodes in different networks while ignoring synchronization between nodes within the same CDNs. On the other hand, internal synchronization involves adjusting the movements of two or more nodes to achieve a shared behavior. Various studies have focused on internal synchronization, such as finite-time synchronization ^[8], cluster synchronization ^[9], projective synchronization ^[10], lag synchronization ^[11], and more. Therefore, investigating internal synchronization is an important issue. Dynamic systems in the real world are commonly acknowledged for their intricate, uncertain, and nonlinear characteristics, making them challenging to control or manipulate. The fuzzy logic theory is an intriguing and efficient approach to addressing the complexities of analyzing and synthesizing such complex nonlinear systems. Among the various fuzzy methods, the Takagi-Sugeno (T-S) fuzzy model ^[5] is an effective tool that merges principles from linear and fuzzy theories to resolve control problems in nonlinear systems. By utilizing fuzzy membership functions, these linear subsystems are integrated. Consequently, the author merged the T-S fuzzy model with complex networks to study the synchronization challenge described in the references ^[6,7].

It is widely recognized that in complex networks, the nodes must share information with their neighboring nodes through an information channel. Nevertheless, time delay is an unavoidable consequence caused by long-distance communication, transmission rate, and transmission blockage. This time delay has significant implications for the instability of complex networks and the decline in system performance, as highlighted in previous studies ^[12,13,14]. Nevertheless, these sources only considered scenarios where neighboring nodes were either fully connected or completely disconnected. However, in many realistic networks, incomplete information is commonly encountered. For instance, research ^[15] discovered that only $5%$ of all excitatory synapses in the human brain network, connecting cortical regions, can transmit information. Additionally, references ^[16,17] established that the transmitter cannot receive information from all users' information channels. Hence, it becomes essential to investigate and analyze the problem of partial coupling in CDNs, which has been explored in reference ^[18]. Scholars in ^[19,20,21] have examined a different form of connection called distributed coupling. The spatial nature of complex networks introduces variations in axon sizes and the length of parallel paths. It is crucial to account for the continuous distributed coupling delay when representing such networks. This consideration brings the model closer to real-world scenarios and aids in addressing practical issues more effectively. Previous research on synchronizing CDNs with time-varying delays primarily assumes that differentiable functions can represent these delays. However, this article focuses on CDNs that incorporate continuous time-varying non-differentiable delays.

When all nodes within a network cannot synchronize independently, it presents a challenge to devise a practical controller capable of achieving network synchronization. CDNs can utilize various control schemes, such as pinning control ^[22,23], impulsive control ^[17], intermittent control ^[24,25], and adaptive control ^[26,27]. Nevertheless, due to frequent perturbations in the controller gain and potential actuator deterioration, inaccuracies inevitably arise in the controller's operation. Therefore, researchers have explored nonfragile controllers, which are precise controllers capable of tolerating acceptable faults in the controller's functioning, and this area of study has been investigated by several researchers ^{[28,29,30,31,32,33,34]}. For example, in ^[33] a non-fragile controller was utilized to tackle the synchronization problem in discrete-time CDNs with interval time-varying delays. The investigation in reference ^[31] focused on the problem of achieving exponential synchronization in CDNs with time-varying coupling delays by integrating non-fragile control with sampled-data control. In a subsequent study, the authors in reference ^[29] presented a method for achieving non-fragile synchronization in CDNs with hybrid delays and stochastic disturbance using sampled-data control. Following that, concern ^[34] addressed the issue of attaining $H_\infty$ performance synchronization in a specific class of T-S fuzzy complex dynamical networks with hybrid coupling delays. The hybrid delay in this context encompassed both discrete-time coupling and distributed coupling delays. In contrast to these references, this paper adopts a combination of interval time-varying delays, which include discrete-time coupling delay, partial coupling delay, and distributed coupling delay. Consequently, the problem of researching synchronization in CDNs with hybrid time-varying delays poses a significant challenge.

However, during the actual control process, certain unavoidable uncertainties, external disturbances, or changes in control parameters may occur, leading to a decline in the performance of complex networks and even jeopardizing their stability. In such cases, the dissipativity theory, which is based on the energy properties of dynamic systems, offers valuable tools for system analysis. Dissipative systems especially posit that the energy dissipated within a dynamic system is always less than the energy supplied from an external source. Recently, researchers have applied dissipative analysis to address the impact of external disturbances in dynamical systems ^[35,36]. Additionally, in ^{[4,37,38,39,40]}, the notion of extended dissipativity performance was introduced as a comprehensive framework that unifies various robust performance measures such as $H_\infty$, $L_2 - L_\infty$, passivity, and dissipativity performances. These robust performances are achieved by appropriately tuning the weighting parameters in the extended dissipativity criteria. Despite these developments, to our knowledge, there have yet to be any reports on the extended dissipativity analysis of T-S fuzzy CDNs with mixed interval time-varying delay. Inspired by earlier research, we aim to conduct an extended dissipativity analysis of the conceded CDNs framework with hybrid interval time-varying delays.

The main findings of this paper, drawn from the discussions mentioned earlier, can be summarized in the following aspects:

● For the first time, we conducted a novel study exploring the extended dissipative performance and non-fragile control concerning the synchronization of T-S fuzzy complex dynamical networks. These networks incorporate interval discrete and distributed coupling time-varying delay, which may involve non-differentiable functions and the lower bound of the delays is not limited to zero.

● Compared with the model of the complex dynamical networks with coupling delays presented in references ^[20,41], we opted for a T-S fuzzy complex dynamical networks model with a combination of hybrid coupling delays. This includes partial coupling delay, distributed coupling delay, and discrete-time coupling delay. Furthermore, we employed a regrouping approach to handle these coupling delays efficiently to replace the Kronecker product, thus avoiding complex calculations.

● We have developed a synchronization criterion for hybrid delayed CDNs, utilizing a non-fragile state-feedback control design to assess the extended dissipativity performance. To make a comparison with the controller designed in ^[34], we utilized a single free-matrix parameter $F$ in Eq (3.17) instead of the two parameters used in the zero equation. Importantly, we were able to achieve this without introducing any additional variables.

● We can achieve a less conservative condition by creating multiple integral Lyapunov functionals and employing more stringent scaling methods, an integral inequality based on Jensen's inequality, Wirtinger's inequality, and various mathematical techniques. Furthermore, our findings can be used to validate Chua's circuit system.

The remaining sections are structured as follows: Section 2 presents the model description and some preliminary concepts. Section 3 discusses the results of the extended dissipative synchronization under the non-fragile control. Section 4 provides two simulation examples to demonstrate the feasibility and validity of our obtained results. Finally, in Section 5, we present the overall conclusion of our main work.

Notation: $\mathbb{R}^{m\times n}$ and $\mathbb{R}^n$ correspond to the collection of all real matrices with dimensions $m \times n$ and the n-dimensional Euclidean space, respectively. The symbol $X^T$ denotes the transpose of the matrix $X$. The notation $diag\{\dots\}$ indicates the formation of a block diagonal matrix. The symbol $*$ is used to denote symmetry. $col\{\dots\}$ denotes a column vector. In a matrix $X$, the expression $X > 0$ signifies that $X$ is positive definite. $sym\{X\}$ denotes $X + X^T.$ The space $\mathcal{L}^n_{2} [0, \infty)$ is the Hilbert space containing square-integrable functions defined over the interval $[0, \infty)$.

2.   Preliminaries

This paper studies T-S fuzzy complex dynamical networks involving hybrid coupling delays. Within the network, every T-S fuzzy node is equipped with $d^{th}$ plant rules:

Plant Rule d: IF $\chi_{1}(t)$ is $\psi_{d1}, \; \chi_{2}(t)$ is $\psi_{d2}, \dots, \; \chi_{p}(t)$ is $\psi_{dp}.$

Then,

where $\chi_{1}(t), \dots, \chi_{p}(t)$ are the premise variables$; \psi_{d1}, \dots, \psi_{dp}$ are the fuzzy sets identified by their membership values, $d\in\{1, 2, \dots, r\}, r$ denotes the number of fuzzy rules$; x_{i}(t) = col\{x_{i1}(t), x_{i2}(t), \dots, x_{in}(t)\}\in\mathbb{R}^{n}$ denotes the state vector of the $i^{th}$ node$; z_{i}(t)\in\mathbb{R}^{n}$ represents output of each node$; A_{d} = diag\{a_{d1}, a_{d2}, \dots, a_{dn}\}, B_{d} = \left[b_{dij}\right]_{n\times n}\in\mathbb{R}^{n\times n}$ and $\Im = diag\{\Im_{1}, \Im_{2}, \dots, \Im_{n}\}$ are given constant matrices. The function $f(x_{i}(t)) = col\{f_{1}(x_{i1}(t)), f_{2}(x_{i2}(t)), \dots, f_{n}(x_{in}(t))\}\in\mathbb{R}^{n}$ is a continuous nonlinear function with a global Lipschitz condition. $c_{i} > 0, (i = 1, 2, 3)$ is the constant coupling strength. $\mathcal{F} = \left[\mathcal{F}_{ij}\right]_{N\times N}$ is the outer coupling matrix, if there is a connection from node $j$ to node $i,$ then the coupling $\mathcal{F}_{ij}\not = 0(j\not = i);$ otherwise, $\mathcal{F}_{ij} = 0$ and the diagonal elements $\mathcal{F}_{ii} = - \sum\limits_{j = 1, j\not = i}^{N}\mathcal{F}_{ij}; \; \Upsilon_{dij} = diag\{\Upsilon^{1}_{dij}, \Upsilon^{2}_{dij}, \dots, \Upsilon^{n}_{dij}\}$ is an inner coupling matrix with $\Upsilon^{l}_{dij} = 0$ or $1. \; \Upsilon^{l}_{dij}$ denotes the information transmission of channel, if the $l^{th}$ channel of state node $j$ can be connected to node $i,$ then $\Upsilon^{l}_{dij} = 1;$ otherwise, $\Upsilon^{l}_{dij} = 0.$ The real function $\gamma(t)$ and $\varsigma_{i}(t)$ ($i = 1, 2$) represent the interval discrete and distributed time-varying delays, respectively. These delays adhere to the conditions $0 \leq \gamma_{1} \leq \gamma(t) \leq \gamma_{2}$ and $0 \leq \varsigma_{1} \leq \varsigma_{1}(t) \leq \varsigma_{2}(t) \leq \varsigma_{2}$, where $\gamma_{1}$, $\gamma_{2}$, $\varsigma_{1}$ and $\varsigma_{2}$ are known real constants. Using the weighted average defuzzifier, the complex dynamical networks system can be described as follows:

where $\chi(t) = col\{\chi_{1}(t), \chi_{2}(t), \dots, \chi_{p}(t)\}$ defines the normalized membership function that satisfies the condition:

where $\eta_{d}(\chi(t))$ denotes the membership grade of $\chi_{i}(t)$ in $\rho_{d}$. As mentioned in the fuzzy sets definition, it is presumed that $\eta_{d}(\chi(t))\geq 0, \sum\limits_{d = 1}^{r}\rho_{d}(\chi(t)) = 1.$

Assume that $s(t) = col\{s_{1}(t), s_{2}(t), \dots, s_{n}(t)\}$ represents the state of isolated nodes and satisfies the following:

Consider $\nu_i(t)$ as the output of an isolated node, defined as $\nu_{i}(t) = \Im s_{i}(t)$. The output error $\tilde{z}_{i}(t)$ can be represented as $\tilde{z}_{i}(t) = z_{i}(t) - \nu_{i}(t)$ for $i = 1, 2, \dots, N.$ Moreover, to address the issue of partial couplings, researchers have adopted the regrouping method to investigate the impact of channels on T-S fuzzy CDNs. Let $\mathcal{G}_{dij}^{l} = \mathcal{F}_{ij}\Upsilon_{dij} = diag\Big\{ g_{dij}^{1}, g_{dij}^{2}, \dots, g_{dij}^{n}\Big\}(i\not = j)$ and $\mathcal{G}^{l}_{dii} = - \sum\limits_{j = 1, j\not = i}^{N}\mathcal{G}^{l}_{dij} = diag\Big\{g^{1}_{dii}, g^{2}_{dii}, \dots, g^{n}_{dii}\Big\}.$

The error system is defined as $e_{i}(t) = x_{i}(t)-s(t)$, where $e_{i}(t) = col\{e_{i1}, e_{i2}(t), \dots, e_{in}(t)\}.$ Subsequently, according to $(2.2)$, it can be inferred that the error system can be represented as:

where $f(e_{i}(t)) = col\{f_{1}(e_{i1}(t)), f_{2}(e_{i2}(t)), \dots, f_{n}(e_{in}(t))\}\in\mathbb{R}^{n}$ with $f(e_{i}(t)) = f(x_{i}(t))-f(s(t)), \tilde{z}_{i}(t)$ as the output for $i^{th}$ node.

Based on the regrouping method, the matrix $\mathcal{G}^{l}_{dij}\in\mathbb{R}^{N\times N}$ for the $l^{th}$ channel can be described as follows:

Let $e_{l}(t) = col\{e_{1l}(t), e_{2l}(t), \dots, e_{Nl}(t)\}$ be the error state vector of $l^{th}$ channel, and the synchronization error system can be established as below:

where $u^{d}_{l}(t)\in\mathbb{R}^{N}$ represents the control input of the $l^{th}$ channel, and

The main objective of this paper is to attain extended dissipative synchronization to the target node $s(t)$ in T-S fuzzy CDNs with hybrid coupling delays by the non-fragile controller. The controller is defined as follows:

where $K^{d}_{l} = diag\Big\{k^{d}_{1l}, k^{d}_{2l}, \dots, k^{d}_{Nl} \Big\}$ is the control gain matrix. Moreover, the perturbed matrix $\Delta K(t)$ can be expressed as the norm-bounded additive in the following form

where $C_{l}$ and $E_{l}$ are fixed matrices provided and $D_{l}(t)\in\mathbb{R}^{n\times n}$, where $l = 1, 2, \dots, n,$ is a time-varying unknown matrix that satisfies the condition $D^T_{l}(t)D_{l}(t)\leq I.$

Remark 1. The controller application introduces perturbations in the controller gains, which could cause system errors or adjustments made to modify the controller gains. Hence, creating a controller system that remains unaffected by these fluctuations becomes essential. The non-fragile controller embodies precision and insensitivity to permissible operational errors of the controller, a topic that has garnered significant focus in previous studies ^{[28,29,30,31,32,33,34]}. Given these aspects, the rationale for exploring the adoption of a non-fragile state feedback controller becomes apparent.

Next, the paper will utilize various definitions, assumptions and lemmas to demonstrate the proof of the theorem.

Assumption 1. ^[42] Each component of the nonlinear function $f(x_{i}(t))$ satisfies a global Lipschitz condition, acquired through the following way:

where $j = 1, 2, \dots, n,$ and $L_{j}$ is a positive constant.

Remark 2. This study deals with several communication restrictions within T-S fuzzy complex dynamical networks. A decoupling approach is employed to explore the communication channel challenge in the analyzed system rather than relying on the Kronecker product. This shift significantly diminishes the computational load, especially when dealing with large-scale CDNs.

Definition 1. The T-S fuzzy complex dynamical networks $(2.1)$ with $\omega(t) = 0$ is said to be asymptotic synchronization if

Definition 2. ^[39] If matrices $\Theta_1, \Theta_2, \Theta_3$ and $\Theta_4$ are given, where $\Theta_1, \Theta_3$ and $\Theta_4$ are real symmetric, system $(2.7)$ is considered to be extended dissipative when, for any nonnegative time $t_{f}$ and all $\omega(t)\in\mathcal{L}_{2}[ 0, \infty)$, the following inequality holds:

where $\mathcal{J}(t) = \tilde{z}^T(t)\Theta_{1}\tilde{z}(t) + 2\tilde{z}^T(t)\Theta_{2}\omega(t) + \omega^T(t)\Theta_{3}\omega(t).$

In this paper, the general assumptions regarding $\Theta_{1}, \Theta_{2}, \Theta_{3}$ and $\Theta_{4}$ are applied consistently.

Assumption 2. ^[39] The real symmetric matrices $\Theta_{1}, \Theta_{2}, \Theta_{3}$ and $\Theta_{4}$ satisfy the following conditions:

(1) $\Theta_{1}\leq 0, \Theta_{3} > 0\; \text{and}\; \Theta_{4}\geq 0;$

(2) $(\Vert \Theta_{1}\Vert + \Vert \Theta_{2}\Vert)\cdot\Vert \Theta_{4}\Vert = 0.$

Remark 3. The concept of extended dissipativity performance introduced in Definition 2 encompasses various performance measures as specific instances, achieved by adjusting the weighting matrices $\Theta_1, \Theta_2, \Theta_3$ and $\Theta_4,$ in the following ways:

● When $\Theta_1 = -I, \Theta_2 = 0, \Theta_3 = \delta^{2}I$ and $\Theta_4 = 0,$ Definition 2 simplifies to the $H_\infty$ performance.

● If $\Theta_1 = 0, \Theta_2 = 0, \Theta_3 = \delta^{2}I$ and $\Theta_4 = I,$ Definition 2 transforms into the $L_2-L_\infty$ performance.

● In the case of $\Theta_1 = 0, \Theta_2 = I, \Theta_3 = \delta I$ and $\Theta_{4} = 0,$ Definition 2 represents passivity performance.

● When $\Theta_{1} = Q, \Theta_{2} = S, \Theta_{3} = R-\delta I$ and $\Theta_4 = 0,$ Definition 2 corresponds to (Q, S, R)-dissipativity performance.

Lemma 1. ^[34] For a matrix $\mathcal{P} > 0$ and a vector function $\psi(t), t\in[a, b],$ the inequality is formulated as follows:

where

Lemma 2. ^[43] For a matrix $\mathcal{M} > 0,$ the following inequality holds:

Lemma 3. ^[43] (Jensens Inequality) For a matrix $\mathcal{Q} > 0$ and a continuously differentiable function $\psi(t) : [a, b] \rightarrow \; \mathbb{R}^{n}$, the following statement is true:

Lemma 4. ^[44] For a matrix $\mathcal{T} > 0,$ constant $\gamma_{1}\leq\gamma(t)\leq\gamma_{2}$ and a function $\dot{x}(t): [-\gamma_{2}, \gamma_{1}]\rightarrow \mathbb{R}^{n}$ such that the following integration is well defined, then the following inequality holds:

Lemma 5. ^[29] Given matrices $\mathcal{H}$ and $\mathcal{N}$, and a matrix $\mathcal{F}(t)$ that satisfies $\mathcal{F}(t)\mathcal{F}^{T}(t)\leq I$, for any positive value of $\epsilon$, the following statement is true:

3.   Main results

In this section, we present certain notations to aid in expressing matrices and vectors more conveniently. The notations are described below:

3.1.   Non-fragile synchronization analysis

We will introduce a novel sufficient synchronization criterion for the analyzed complex dynamical networks $(2.1)$ when $\omega_{l}(t) = 0.$

Theorem 1. Given positive scalar $\epsilon$ and nonnegative scalars $\gamma_1, \gamma_2, c_{i}, (i = 1, 2, 3),$ if there exists positive matrices $P_{il}\in\mathbb{R}^{N\times N}, (i = 1, 2, 3), \; Q_{il}\in\mathbb{R}^{N\times N}, (i = 1, 2, 3, 4), \; R_{l}\in\mathbb{R}^{N\times N}$ and any matrices $\Lambda_{1l}, \Lambda_{2l}\in\mathbb{R}^{N\times N}, F_{l} = diag\bigg\{F_{1}, F_{2}\dots, F_{N}\bigg\}, \Gamma = diag\bigg\{\Gamma_{1}, \Gamma_{2}\dots, \Gamma_{N}\bigg\}\; ,l = 1, 2, \dots, n,$ such that the LMIs hold as follows:

where

then, the error system $(2.7)$ achieves asymptotic synchronization. Additionally, the control gain can be determined as $K_{l}^{d} = (F_{l}^{T})^{-1}\Gamma$.

Proof. The candidate Lyapunov functional for system $(2.7)$ is formulated as follows:

where

By computing the time derivative of $V(t),$ we have

By using Lemma 1, we gained:

$\dot{V}_{4}$ can be calculated as follows:

By utilizing Lemma 2, we have

$\dot{V}_{5}$ can be calculated as follows:

After utilizing Lemma 3, we gain

$\dot{V}_{6}$ can be calculated as follows:

By applying Lemma 4, we have

Based on the error system (2.7), we can deduce that for any suitable matrix $F_{l},$ the following equation is true:

Then, by combining $(3.6)$–$(3.18),$ we get

where

By using Lemma 5,

By utilizing the Schur complement, we can derive $\Omega < 0$ from (3.2), which in turn ensures $\dot{V}(t) < 0.$ According to the Lyapunov stability theory, the T-S fuzzy complex dynamical network $(2.1)$ can achieve asymptotic synchronization. This concludes the proof. □

3.2.   Non-fragile extended dissipative synchronization analysis

We conduct an extended dissipative performance analysis of the considered CDNs $(2.1)$ under various initial conditions, where $\omega_{l}(t)\not = 0$ and $\omega_{l}(t)\in\mathcal{L}_{2}[0, \infty)$.

Theorem 2. Given positive scalar $\epsilon$ and nonnegative scalars $\gamma_1, \gamma_2, c_{i}, i = 1, 2, 3, \; \Theta_{i}\; (i = 1, 2, \dots, 4)$ satisfying Assumption $2,$ if there exists positive matrices $P_{il}\in\mathbb{R}^{N\times N}, (i = 1, 2, 3), \; Q_{il}\in\mathbb{R}^{N\times N}, (i = 1, 2, 3, 4), \; R_{l}\in\mathbb{R}^{N\times N}$ and any matrices $\Lambda_{1l}, \Lambda_{2l}\in\mathbb{R}^{N\times N}, F_{l} = diag\bigg\{F_{1}, F_{2}\dots, F_{N}\bigg\}, \Gamma = diag\bigg\{\Gamma_{1}, \Gamma_{2}\dots, \Gamma_{N}\bigg\}\; ,l = 1, 2, \dots, n,$ such that the LMIs hold as follows:

where

Then, the error system (2.7) is extended dissipative, with all other parameters unchanged as described in Theorem 1.

Proof. By applying the Schur complement and Lemma 5, it is clear that $(3.22)$ is equivalent to

where

$\tilde{\Omega} = \hat{\Pi}^{(2)} + n\tilde{e}^T_{1}F^T_{l}\Lambda^{-1}_{1l}F_{l}\tilde{e}_{1}+n\tilde{e}^T_{2}F^T_{l}\Lambda^{-1}_{2l}F_{l}\tilde{e}_{2} + (\tilde{e}_{1}+\tilde{e}_{2})^T\left(F^T_{l}C_{l}D_{l}(t)E_{l}\right)\tilde{e}_{1} +\tilde{e}^T_{1}\left(E^T_{l}D^T_{l}(t)C^T_{l}F_{l}\right)(\tilde{e}_{1}+\tilde{e}_{2}).$

From (3.19), we have

and it is clear that

where $\mathcal{J}(t)$ is provided in Definition 2.

Then, we have

By integrating both sides of inequality $(3.28)$ from $0$ to $t \; (t\geq 0)$, we obtain the following result:

Our attention is specifically directed toward two cases: $\Theta_{4} = 0$ and $\Theta_{4}\geq 0$. The rationale behind this focus is that the extended dissipative performance can encompass the conditions of strictly $(Q, S, R)$-dissipativity, $H_{\infty}$ and passive performance when $\Theta_{4} = 0$ or the $L_{2} - L_{\infty}$ performance when $\Theta_{4} > 0$.

Taking $\Theta_{4} = 0$ into account, the inequality (3.29) implies the following:

Simultaneously, in the case where $\Theta_{4} > 0$ as indicated in Assumption 2, this implies that the matrices are $\Theta_{1} = 0$, $\Theta_{2} = 0$ and $\Theta_{3} > 0$. Consequently, for $t\in[0, t_{f}]$, the inequality (3.29) leads to the following chain of relations: $\int_{0}^{t_{f}}\mathcal{J}(s)ds\geq\int_{0}^{t}\mathcal{J}(s)ds\geq e^T_{l}(t)P_{1l}e_{l}(t)$. Subsequently, utilizing (3.23), we can deduce the following expression:

By combining (3.30) and (3.31), system (2.1) is extended dissipative synchronization. This concludes the proof. □

Remark 4. To make a comparison with the controller designed in ^[34], we utilized a single free-matrix parameter $F$ in Eq (3.17) instead of the two parameters used in the zero equation in ^[34]. Importantly, we were able to achieve this without introducing any additional variables.

Remark 5. Employing multiple integral components within the Lyapunov function addresses the challenges of mixed interval time-varying delays. This paper introduces a less conservative stability criterion using auxiliary function-dependent integral inequalities and mathematical approaches. In real-world scenarios, if the system possesses initial energy, this energy will progressively diminish as time elapses, ultimately guiding the system toward a state of equilibrium. However, determining the energy function of the system can be inconvenient. Consequently, Lyapunov introduced the function $V(x, t),$ serving as an energy representation known as the Lyapunov equation.

Remark 6. The external disturbance $\omega(t)$ can generally impact the system's stability. Various robust performance measures, including $H_\infty, L_{2}-L_{\infty},$ passivity, and dissipativity, are utilized to assess system stability. These measures offer improved ways of gauging stability. By adjusting weighting matrices and scalars, extended dissipative performance can be transformed into four standard individual performance criteria, enhancing the comprehensiveness and generality of system analysis. A recent study ^[34] established $H_\infty$ synchronization conditions for uncertain CDNs with hybrid delays using inequalities such as Jensens inequality and Wirtinger inequality. However, there has been no prior investigation into the extended dissipativity criteria through a synchronization approach in T-S fuzzy CDNs.

4.   Simulation examples

This section will present two simulation examples to showcase reduced conservatism and validate the proposed method.

Example 1. Let us examine the T-S fuzzy complex dynamical networks with four nodes. Each node has three information vectors, and the membership functions are $\rho_{1}(\chi(t)) = \sin^{2}\frac{t}{4}$ and $\rho_{2}(\chi(t)) = \cos^{2}\frac{t}{4}.$ The following network parameters are provided:

The diagonal matrix $\Upsilon_{1ij}$ represents the channel matrix associated with Rule 1 and is defined as follows:

Additionally, in the context of Rule 2, the diagonal matrix $\Upsilon_{2ij}$ is defined as follows:

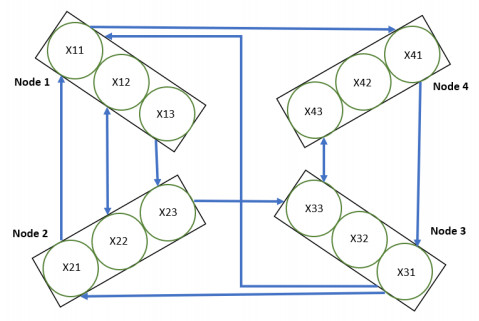
Figure 1 illustrates the information pathways of the network for Rule 1. It uses two-way arrows $(i \leftrightarrow j)$ to indicate the activation of information channels between node i and j and one-way arrows $(i \rightarrow j)$ to represent the activation of information channels from node $i$ to $j.$

Next, a decoupling method addresses the partial coupling between linked nodes. The $N \times N$ matrix $\mathcal{G}^{l}_{1}, (l = 1, 2, 3)$ represents the $l^{th}$ channel within a network of $N$ nodes, following the guidelines of Rule 1. It can be readily observed that:

Figure 2 depicts the network's channel configuration according to Rule 2. Using a similar analysis as mentioned earlier, the computation of matrix $\mathcal{G}^{l}_{2} (l = 1, 2, 3)$ is determined as follows:

The nonlinear function $f(x_{i}(t))$ is chosen as:

It is possible to determine that any element $f_l(x_{il}) (l = 1, 2, 3; i = 1, 2, 3, 4)$ meets the Lipschitz condition with $L_l = 1.$

In this case, we take $\omega(t) = 0,$ and the uncertain parameter matrices are taken as: $C_{l} = diag\{0.1, 0.1, 0.1, 0.1\}, \; E_{l} = diag\{0.2, 0.2, 0.2, 0.2\}$ and $D_{l}(t) = diag\{\sin t, \sin t, \cos t, \sin t\}.$ Moreover, $c_{1} = c_{2} = c_{3} = 1, \gamma(t) = 0.2 \vert\tanh{t}\vert, \; \varsigma_{1}(t) = 0.1+0.1\sin{t}$ and $\varsigma_{2}(t) = 0.2\sin{t},$ which means $\gamma_{1} = 0.1$ and $\gamma_{2} = 0.2, \sigma_{1} = 0.1, \sigma_{2} = 0.2$.Then, the non-fragile control matrices can be calculated as:

In the given example, we set the initial conditions as follows: $x_{1}(0) = \left[-1, 1.5, 3\right]^T, \; x_{2}(0) = \left[2.5, -1.2, 1\right]^T\; x_{3}(0) = \left[3.5, -1, 0.5\right]^T, \; x_{4}(0) = \left[-2, -3, 4\right]^T,$ and $s(0) = \left[3.7, 2.4, -1.3\right]^{T}.$ Based on the observation from Figure 3, it is evident that the error system (2.7) cannot achieve synchronization without using a non-fragile controller. However, Figure 4 illustrates that the trajectory of the error system converges toward zero. The application of the non-fragile controller enables the error to converge to zero, facilitating synchronization in the T-S fuzzy complex dynamical networks. The control input $u(t)$ for the synchronization system is depicted in Figures 5 and 6, where the trajectories converge to zero. To provide more evidence of the effectiveness of the proposed approach, we define $e(t) = \sqrt{ \sum\limits_{i = 1}^{4}\Vert x_{i}(t)-s(t)\Vert^2}$ as the overall synchronization error between the network and the target node. Figure 7 demonstrates that the trajectories of the synchronization error can reach a convergence to 0.

Remark 7. We choose continuous time-delay functions, denoted as $\gamma(t),$ which fulfill the criterion $\gamma_{1} \leq \gamma(t) \leq \gamma_{2}.$ In the context of Example 1, we adopt the specific function $\gamma(t) = 0.2\vert \tanh{t}\vert.$ As illustrated in Figure 8, the time-delay functions $\gamma(t)$ that we employ are continuous and adhere to the condition $\gamma_{1} \leq \gamma(t) \leq \gamma_{2}.$ Notably, our chosen delay function is not required to be differentiable. This contrasts with prior research ^{[4,6,8,34,39]}, where the time-delay function was consistently differentiable.

Example 2. To implement the networks in practical applications, Chua's circuit system is carefully chosen as the isolated node within the networks to demonstrate the effectiveness of the outcome. This can be explained as follows:

where $\sigma_{1} = 10, \sigma_{2} = 14.87, \varphi(s_{1}(t)) = \eta_{1}s_{1}(t) + 0.5(\eta_{1}-\eta_{2})(\vert s_{1}(t) + 1\vert-\vert s_{1}(t) - 1\vert), \; \eta_{1} = -1.27$ and $\eta_{2} = -0.68.$ Let $s(t) = \left[s_{1}(t), s_{2}(t), s_{3}(t)\right]^{T}$. As a result, the function $f(s(t))$ can be expressed as the following matrix equation:

The example focuses on five nodes, where the outer coupling matrix and channel matrices are given as follows:

from which one has $\mathcal{G}^{k} = \mathcal{F} (k = 1, 2, 3).$

Additionally, we consider the perturbation $\omega(t) = 1/(10t^2 + 1),$ and the uncertain parameter matrices are provided as follows: $C_{l} = \text{diag}\{1, 1, 1, 1, 1\}, E_{l} = \text{diag}\{0.3, 0.3, 0.3, 0.3, 0.3\}, D_{l}(t) = \text{diag}\{\sin t, \sin t, \sin t, \cos t, \sin t\}$ and $\hat{\Im} = \text{diag}\{0.1, 0.1, 0.1, 0.1, 0.1\}.$ Furthermore, we set $c_{1} = 0, c_{2} = 1, c_{3} = 0, \gamma(t) = 0.04, \varsigma_{1} = \varsigma_{2} = 0$ and the performance index for $H_{\infty}$ performance is $\delta = 0.3.$ By utilizing Theorem 2, we can derive the non-fragile control matrices as shown below:

We select matrices corresponding to each scenario outlined in Table 1 to investigate the extended dissipative behavior. We employed this approach to examine and analyze the extended dissipativity performance in this particular case. Using the Matlab control toolbox, we solved the LMIs stated in Theorem 2. The solutions obtained, ensuring extended dissipative synchronization, are presented in Table 2, encompassing the optimal minimum value $\gamma$ and the maximum value $\alpha.$

In the given illustration, we consider the initial conditions: $x_{1}(0) = [4, 4, 2]^T, x_{2}(0) = [3, -0.7, 1.5]^T, x_{3}(0) = [2.8, 2.8, -1]^T, x_{4}(0) = [2.9, -0.7, 5.7]^T$ and $x_{5}(0) = [1, 2, 3]^T$ along with $s(0) = [1, -1, 0]^T$. In the context of the non-fragile controller, Figure 11 visually demonstrates the convergence of the synchronization error system (2.7) toward zero. Conversely, Figure 10 highlights that the error system (2.7) cannot accomplish synchronization unless a non-fragile controller is utilized. The control input $u_{i}(t)$, where $(i = 1, 2, 3, 4, 5)$, is depicted in Figure 12 and consistently exhibits zero trajectories. Furthermore, Figure 9 graphically represents the chaotic behavior of Chua's circuit.

Remark 8. This study introduces a novel criterion for achieving non-fragile control in T-S fuzzy complex networks. Innovative and practical scaling techniques are also applied to address derivatives within the multi-integral Lyapunov functional. Compared with ^[29,34], we observe that the convergence speed of the state trajectory of the error system under a non-fragile controller in Figure 11 is faster than the findings in ^[29,34]. In summary, the method proposed in this study offers a combination of reduced computational complexity and less conservatism.

Remark 9. In the past few years, there has been a significant surge in fascination with the management and synchronization of chaotic behaviors in dynamic systems. Chaotic systems exhibit complex behaviors characterized by distinct traits, including their high sensitivity to minor variations in initial conditions and the confinement of their trajectories within phase space. Researchers have delved into the control of chaos within nonlinear systems like Chua's, Lur'e, and Chen's systems. Consequently, Chua's circuit is utilized as unforced, isolated nodes in (2.7) to illustrate its effectiveness through a practical example.

5.   Conclusions

This article has focused on achieving extended dissipative synchronization in T-S fuzzy complex dynamical networks, considering interval hybrid coupling delays and additional disturbances. To begin with, a non-fragile controller was formulated to address the challenge of extended dissipative synchronization. Subsequently, developing a multi-integral Lyapunov functional and applying a mathematical method established novel synchronization criteria for the studied system, ensuring the desired extended dissipative behavior. Finally, the proposed methodology's simulation results validated the synchronization criterion's rationality. Future research might extend these findings to singular systems featuring hybrid time-varying delays.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the Fundamental Fund of Khon Kaen University. The research on Novel non-fragile extended dissipative synchronization of T-S fuzzy complex dynamical networks with interval hybrid coupling delays by Khon Kaen University has received funding support from the National Science, Research and Innovation Fund or NSRF.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.