Rate of convergence of Euler approximation of time-dependent mixed SDEs driven by Brownian motions and fractional Brownian motions

1.   Introduction

In this paper, we consider the following time-dependent mixed stochastic differential equations(SDEs) involving independent Brownian motions and fractional Brownian motions(fBms) with Hurst parameter $H\!\in\!(\frac{1}{2}, 1)$, defined on the complete probability space $(\Omega, \mathcal F, \{\mathcal F_t\}_{t\in[0, T]}, P)$,

where $X_0$ is $\mathcal F_0$-measurable random variable, the stochastic integral with respect to Brownian motion $W = \{W_t:t\in[0, T]\}$ and fBm $B^H = \{B_t^H:t\in[0, T]\}$ are interpreted as Itô and pathwise Riemann-Stieltjes integral respectively. $a, b, c:\Omega\times[0, T]\times\mathbb R\rightarrow\mathbb R$ are measurable functions such that all integrals on the right hand side of (1.1) are well defined.

On one hand, SDEs driven only by Brownian motions has long history. We can refer to the monograph ^[1]. On the other hand, the increasing interest of SDEs driven only by fBms is motivated by their applications in various fields of science such as physics, chemistry, computational mathematics, financial markets e.t. (see ^[2,3,4]). In particular, for $H > \frac{1}{2}$ the increments of fBm are positively correlated and moreover the generalized spectral density behaves like $\lambda^{-2H+1}$. The two properties have recently led to applications of them in various fields, which include the noise simulation in electronic circuits ^[5], the modelling of the subdiffusion of a protein molecule ^[6], the pricing of weather derivatives ^[7] and so on.

Recently, mixed stochastic models containing both Brownian motions and fBms gained a lot of attention, e.g. ^{[8,9,10,11,12]}. They allow us to model systems driven by a combination of random noises, one of which is white and another has a long memory. The motivation to consider such equations comes from some financial applications, where Brownian motion as a model is inappropriate because of the lack of memory, and fBm with $H > \frac{1}{2}$ is too smooth. A model driven by both processes is free of such drawbacks. For example, in financial mathematics, the underlying random noise includes a "fundamental" part, describing the economical background for a stock market, and a "trading" part, coming from the randomness inherent for the stock market. In this case, the fundamental part of the noise should have a long memory, while the second part is likely to be a white noise.

The existence and uniqueness for the solutions of mixed SDEs is discussed by an extensive literature (see ^[9,13,14]). However, the solution of (1.1) is rarely analytically tractable, so it is important to consider certain numerical methods to solve it. Euler approximation used in this paper usually is most popular and probably simplest among all methods of approximation of SDEs. There have been several works devoted to Euler approximation of mixed SDEs (see ^[13,15,16]). Guerra and Nualart ^[13] established the global existence and uniqueness for the solutions of multidimensional time-dependent mixed SDEs under the assumption that $W$ and $B^H$ are independent. The proof relied on an estimate for Euler approximation of them, which was obtained by using fractional calculus and Itô integration. Mishura and Shevchenko ^[16] considered the following mixed SDEs involving both standard Brownian motions and fBms with Hurst parameter $H > \frac{1}{2}$,

Under the boundedness of $a(t, x), b(t, x), c(x)\; (c(x) > 0)$ together with their partial derivatives in $x$, and $(2H-1)$-Hölder continuity of $a(t, x)$ and $b(t, x)$ in $t$, they showed that the mean-square rate of convergence for Euler approximation of (1.2) was $O(\delta^{\frac{1}{2}\wedge(2H-1)})$, where $\delta$ is the mesh of the partition of $[0, T]$. We can also find that a faster convergent rate $O(\delta^{\frac{1}{2}})$ can be deduced if we apply the modified Euler method (see ^[15]).

However, there is an obstacle to discuss mixed SDEs because of the different machinery behind Itô integral with respect to $W$ and Riemann-Stieltjes integral with respect to $B^H$, particularly in the multidimensional and time-dependent cases. Exactly, the former integral is treated usually in a mean-square sense, while the latter is understood in a pathwise sense and all estimates are pathwise with random constants. Therefore, it is very hard to analyze with standard tools of stochastic analysis. This forces us to consider very smooth coefficients and to make delicate estimates on a suitable space. For example, the measurable space $\mathcal W_0^{\alpha, \infty}([0, T])$ with the following norm was introduced in ^[17],

The method of dealing with mixed SDEs in $\mathcal W_0^{\alpha, \infty}([0, T])$ does solve a lot of questions (see ^{[9,11,13,14,18,19]}).

The aim of this paper is to prove that the rate of convergence of Euler approximation of (1.1) is $O(\delta^{\frac{1}{2}\wedge(2H-1)})$ in probability in the space of $\mathcal W_0^{\alpha, \infty}([0, T])$ (see Remark 7). Meanwhile, we also get that, for any fixed $\varepsilon > 0$, there exist a positive constant $C_{\varepsilon}$ and a subset $\Omega_{\varepsilon}$ of $\Omega$ with $P(\Omega_{\varepsilon}) > 1-\varepsilon$ such that

where $C$ is a general positive constant independent of $\delta$ and $\varepsilon$ (see Corollary 3). Unsurprisingly, the rate of convergence appears to be equal to the worst of the rates for corresponding "pure" equations (see ^[18,20]). Our approach is different from ^[18,20] in the sense that we combine pathwise approach with Itô integration in order to handle both types of integrals by using the Garsia-Rademich-Rumsey inequality. The proof of our result combines the techniques of Malliavin calculus with classical fractional calculus. The main ideas are to estimate the pathwise Riemann-Stieltjes integral by a random constant with moments of any order (see (2.3) and (2.5) and to express it as the sum of a Skorohod integral plus a correction term which involves the trace of the Malliavin derivative (see (2.11) and (2.13).) One can read Remark 10 for details. To the best of our knowledge, up to now, there is no paper which investigates the rate of convergence of Euler approximation of (1.1). We here make a first attempt to research such problem.

The rest of this paper is organized as follows. Several important functional space and some elements of fractional calculus and Malliavin calculus on an interval are give in Section 2. Section 3 contains the results concerning the rate of convergence for Euler scheme associated to (1.1). We first give our assumptions and some priori estimates, and then prove the rate of convergence is $O(\delta^{\frac{1}{2}\wedge(2H-1)})$ in probability. In Section 4, we give a numerical example and in Section 5, we summarize the work done in this paper and look forward to the next stage of our work. Finally, in Section 6, we prove the bounded estimation (3.5) and recall a couple of technical results.

2.   Preliminaries

Let $(\Omega, \mathcal F, \{\mathcal F_t\}_{0\leq t\leq T}, P)$ be a complete probability space equipped with a filtration $\{\mathcal F_t\}_{0\leq t\leq T}$ satisfying standard assumptions, i.e., it is increasing and right-continuous while $\mathcal F_0$ contains all $P$-null sets. Denote by $W = \big\{W_t: t\in[0, T]\big\}$ Brownian motions and $B^H = \big\{B_t^H: t\in[0, T]\big\}$ fractional Brownian motions (fBms) with Hurst parameter $H\in(1/2, 1)$. Both are defined on $(\Omega, \mathcal F, \{\mathcal F_t\}_{0\leq t\leq T}, P)$, where $\mathcal F_t = \sigma\{X_0, W_s, B_s^H|s\in[0, t]\}$. As we know, they are mean zero centered Gaussian processes with covariance kernels $R(s, t) = \min\{s, t\}$ and $R_{_H}(s, t) = \frac{1}{2}\left(s^{2H}+t^{2H}-|t-s|^{2H}\right)$ for any $s, t\in[0, T]$ respectively. fBm is different from Brownian motion, it is neither a semimartingale nor a Markov process. Moreover, it holds $(\mathbb E |B_t-B_s|^2)^{1/2} = |t-s|^H, \; s, t\in[0, T],$ and almost all sample paths of $B^H$ are Hölder continuous of any order $\mu\in(0, H)$. Now, let us briefly recall the Malliavin calculus, fractional calculus and three important functional spaces.

2.1.   Three important functional spaces

1. The space of $\beta$-Hölder continuous functions: $\mathcal C^\beta([0, T])$.

Let $\beta\in(0, 1)$. For a function $f:[0, T]\rightarrow\mathbb R, \; \|f\|_{0, T, \beta}$ denotes the $\beta$-Hölder norm of $f$ on $[0, T]$, that is,

If $\|f\|_{0, T, \beta} < \infty$, then we say $f\in \mathcal C^\beta([0, T]).$

2. The functional space: $\mathcal W^{\alpha, 1}([0, T])$. (see ^[11])

Consider the fixed interval $[0, T]$ and $\alpha\in(1-H, 1/2)$. We denote by $\mathcal W^{\alpha, 1}([0, T])$ the space of measurable functions $f$ on $[0, T]$ such that

It is useful for us to estimate the pathwise Riemann-Stieltjes integral with respect to fBm. (see (2.3) and (2.5)

3. The functional space: $\mathcal W_0^{\alpha, \infty}([0, T])$. (see ^[13])

Definition 2.1. Let $\alpha\in(0, 1/2)$. For any measurable function $f:[0, T]\rightarrow\mathbb R$, define

If $\|f\|_{\alpha, \infty} < \infty$, then we say $f\in\mathcal W_0^{\alpha, \infty}([0, T])$.

Remark 2.1. $\mathcal W_0^{\alpha, \infty}([0, T])$ is called Besov space (see ^[11], ^[18]). Moreover, given any $\varepsilon$ such that $0 < \varepsilon < \alpha$, there exists the following inclusions (see ^[13]):

where $\mathcal C_\infty^\alpha([0, T])$ denotes the space of $\sup$ and $\alpha$-Hölder continuous functions $f:[0, T]\rightarrow\mathbb R$, equipped with the norm $\|f\|_{\infty, 0, T, \alpha}: = \sup\limits_{0\leq t\leq T}|f_t|+\sup\limits_{0\leq s < t\leq T}\frac{|f_t-f_s|}{|t-s|^\alpha}.$ In particular, both the fractional Brownian motion $B^H$ with $H > 1/2$, and the standard Brownian motion $W$, have their trajectories in $\mathcal W_0^{\alpha, \infty}([0, T])$.

2.2.   Elements of fractional calculus

Due to the fact that fBm is neither a semi-martingale nor a Markov process, Itô's stochastic calculus is not fit for it. In this subsection, we show the definitions of the generalized fractional integrals and derivative operators (see ^[21]) before introducing the pathwise Riemann-Stieltjes integral with respect to fBm.

For $p\geq 1$ and $a, b\in\mathbb R$ with $a < b$, we denote by $\mathcal L^p(a, b)$ the space of Lebesgue measurable functions $f:[a, b]\rightarrow\mathbb R$ satisfying

If $f\in\mathcal L^1(a, b)$ and $0 < \alpha < 1$, the left-sided and right-sided fractional Riemann-Liouville integrals with respect to $f$ of order $\alpha$ are defined by, for almost all $t\in(a, b)$,

and

where $\Gamma(\alpha) = \int_0^\infty r^{\alpha-1}e^{-r}dr$ is the Gamma function. Let $I_{a+}^\alpha(\mathcal L^p)$ (resp. $I_{b-}^{1-\alpha}(\mathcal L^q)$) be the image of $\mathcal L^p(a, b)$ by the operator $I_{a+}$ (resp. $I_{b-}^{1-\alpha}$). Suppose that $\lim\limits_{\varepsilon\downarrow 0}f(a+\varepsilon)$ and $\lim\limits_{\varepsilon\downarrow 0}g(b-\varepsilon)$ exist, moreover,

where $p\geq 1, q\geq 1, \frac{1}{p}+\frac{1}{q}\leq 1, 0 < \alpha < 1, f_{a+}(t) = f_t-\lim\limits_{\varepsilon\downarrow 0}f(a+\varepsilon)\text{ and } g_{b-}(t) = \lim\limits_{\varepsilon\downarrow 0}g(b-\varepsilon)-g_t$, then the fractional (Weyl) derivatives are defined by, for almost all $s\in(a, b)$,

and

Remark 2.2. From ^[13], we can see $I_{a+}^\alpha(D_{a+}^\alpha f_{a+}) = f_{a+}$ for any $f_{a+}\in I_{a+}^\alpha(\mathcal L^p(a, b))$ and $I_{b-}^{1-\alpha}(D_{b-}^{1-\alpha} g_{b-}) = g_{b-}$ for any $g_{b-}\in I_{b-}^{1-\alpha}(\mathcal L^q(a, b))$. Moreover, from ^[11], we also see $D_{a+}^\alpha f_{a+}\in\mathcal L^p(a, b)$ and $D_{b-}^{1-\alpha} g_{b-}\in\mathcal L^q(a, b)$.

Now we can construct the pathwise Riemann-Stieltjes integral with respect to fBm. If $f\in\mathcal C^\lambda([a, b])$ and $g\in\mathcal C^\mu([a, b])$ with $\lambda+\mu > 1$, then, from the classical paper ^[22] by Young, the Riemann-Stieltjes integral $\int_a^bfdg$ exists. Furthermore, Zähle ^[23] provided an explicit expression for it in terms of fractional derivatives as follows.

Proposition 2.1. Suppose that $f\in\mathcal C^{\lambda}([a, b])$ and $g\in\mathcal C^{\mu}([a, b])$ with $\lambda+\mu > 1.$ Let $\lambda > \alpha$ and $\mu > 1-\alpha.$ Then the pathwise Riemann-Stieltjes integral $\int_a^bf_sdg_s$ exists and it can be expressed as

We know that the fBm $B^H$ is $\nu$-Hölder continuous for $\forall \nu \in(0, H)$. Therefore, for $f\in\mathcal C^\beta([a, b])$ and $1-H < \alpha < \beta < 1$, we can express the pathwise Riemann-Stieltjes integral with respect to fBm according to (2.1) as

where $B_{b-}^H(s) = B^H(b)-B^H(s).$

Remark 2.3. (see ^[24]) For any $\alpha\in(1-H, 1)$, it follows from ^[21] that $D_{b-}^{1-\alpha}B_{b-}^H(x)\in\mathcal L^\infty(a, b)$. Therefore, for any $f\in I_{a+}^\alpha(\mathcal L^1(a, b))$, (2.2) still holds.

The stochastic integral (2.2) admits the following estimate (see ^[11]): for $\alpha\in(1-H, 1/2)$ and $t\in[0, T]$, there exists a random variable $\psi(\omega, \alpha, t)$ with finite moments of any order such that, for any determination or random function $f\in\mathcal W^{\alpha, 1}([0, T]),$

Moreover, from the classical Garsia-Rodemich-Rumsey inequality (see (1.2) of ^[25]), we can choose $\psi(\omega, \alpha, t)$ as

where $C_{\alpha, H, \theta}$ is a constant depending on the underlying arguments, $\theta < \alpha+H-1$. Without loss of generality we can assume that $\theta = (\alpha+H-1)/2$ (see, for example, ^[17]). It is easily obtained from (2.4) that $\psi(\omega, \alpha, t)$ is continuous in $t$ and $\psi(\omega, \alpha, t)\leq\psi(\omega, \alpha, T)$ for all $\omega, \alpha$ and $t\in[0, T].$

Also we need the following inequality from Proposition 4.1 in ^[17]: for any $\alpha\in(1-H, 1/2), 0\leq s\leq t\leq T$ and $f\in\mathcal W^{\alpha, 1}([0, T]),$ we have

Particularly, for any $\eta\in(0, H)$, there exists some constant $C_\eta$ depending on $\eta$ such that

Again applying the Garsia-Rademich-Rumsey inequality to $W_t$ and $\int_s^tb(u, X_u)dW_u$, for any $\eta\in(0, 1/2)$, one can deduce

and

where

and

respectively, $C_\eta, K_\eta$ are both constants depending on $\eta$.

2.3.   Elements of Malliavin calculus

Let $\Im$ be the set of step functions on $[0, T]$ and consider the Hilbert space $\mathcal H$ defined as the closure of $\Im$ with respect to the scalar product $\langle 1_{[0, t]}, 1_{[0, s]}\rangle_\mathcal H = R_{_H}(s, t)$ for $s, t\in[0, T]$. The mapping $1_{[0, t]}\mapsto B_t^H$ can be extended to an isometry between $\mathcal H$ and its associated Gaussian space. This isometry will be denoted by $\phi\mapsto B^H(\phi)$. Note that

where

and

here $c_{_H} = \left(\frac{H(2H-1)}{\mathbf{B}(2-2H, H-\frac{1}{2})}\right)^{\frac{1}{2}}$ and $\mathbf{B}$ denotes the Beta function. Moreover, we have $\mathcal L^{1/H}([0, T])\subset \mathcal H$ and in particular

for $\varphi, \psi\in\mathcal L^{1/H}(0, T)$

For $n\geq 1$, let $F = f(B_{t_1}, \cdots, B_{t_n})$ be smooth and cylindrical random variables with $t_i\in[0, T]$ for $i = 1, \cdots, n$ and $f$ being bounded and smooth. Then, the derivative operator $D$ in the Sobolev space $\mathbb D^{1, 2}$ is defined by

In particular $D_sB_t^H = 1_{[0, t]}(s)$. As usual, $\mathbb D^{1, 2}$ is the closure of the set of smooth random variables with respect to the norm$\|F\|_{1, 2}^2 = \mathbb E|F|^2+\mathbb E\|D.F\|_{\mathcal H}^2$

If $F_1, F_2\in\mathbb D^{1, 2}$ such that $F_1$ and $\|DF_1\|_{\mathcal H}$ are bounded, then $F_1F_2\in\mathbb D^{1, 2}$ and

Moreover, recall also the following chain rule: For $F\in\mathbb D^{1, 2}$ and $g\in\mathcal C^1(\mathbb R)$ with bounded derivative we have $g(F)\in\mathbb D^{1, 2}$ and

The divergence operator, or Skorohod integral operator $\delta,$ is the adjoint of the derivative operator and we have the duality relationship $\mathbb E [F\delta(u)] = \mathbb E \langle DF, u\rangle_\mathcal H$ for every $F\in\mathbb D^{1, 2}$ and $u\in Dom(\delta).$ We should also note that, for $1/2 < H < 1$,

Here, $\mathcal L^p(\Omega, \mathcal H)$ denotes the space of stochastic functions with finite $p-$order moment.

If $(u_t)_{t\in[0, T]}$ is a stochastic process with Hölder continuous sample paths of order $\beta > 1-H,$ then the Riemann-Stieltjes integral with respect to $B^H$ is well defined. If $u$ moreover satisfies $u_t\in\mathbb D^{1, 2}$ for all $t\in[0, T]$ and

then the relation

holds, here $\alpha_{_H} = H(2H-1).$ Set $p > \frac{1}{H}$, from Remark 5 of ^[26], for the Skorohod integral of the process $\{u_t: t\in[0, T]\}$, we have the inequality

Remark 2.4. Due to Hölder inequality, it can be obtained from (2.12) that

3.   Euler approximation

For any $n\in\mathbb N$, consider the isometric partition of $[0, T]$: $\{0 = t_0 < t_1 < \cdots < t_n = T, \; \delta = \frac{T}{n}\}, \; t_k = k\delta, \; k = 0, 1, \ldots, n$. Define $\tau_t: = \max\{t_k:t_k < t\}$ and $n_t: = \max\{k:t_k < t\}$. The Euler approximation of (1.1) is expressed as

or, in the integral form,

3.1.   Assumptions

Throughout this paper, we denote by $C$ the generic positive constants independent of $\delta$ and $\omega$. Their values are not important for us and maybe different from line to line. The mixture of Itô integral and pathwise Riemann-Stieltjes integral makes things a lot harder, forcing us to consider very smooth coefficients. Specifically, in this paper, besides the independence of $W$ and $B^H$, we suppose the coefficients of (1.1) satisfy the following hypotheses almost surely.

$\textbf{(Hab)}$: The coefficients $a(t, x), b(t, x)$ together with their partial derivatives in $x$ are bounded. Moreover, $a(t, x)$ and $b(t, x)$ are $\beta$-Hölder continuous in $t$. That is, there exist two constants $C > 0$ and $\beta\in\big(\frac{1}{2}\vee(2H-1), 1\big]$ such that

$(1).$ $|a(t, x)|+|b(t, x)|\leq C$;

$(2).$ $|a_x(t, x)|+|b_x(t, x)|\leq C;$

$(3).$ $|a(t, x)-a(s, x)|+|b(t, x)-b(s, x)|\leq C|t-s|^\beta.$

$\textbf{(Hc)}$: The coefficient $c(t, x)$ is continuously differentiable in $x$. Moreover, there exist two constants $C > 0$ and $\beta\in\big(\frac{1}{2}\vee(2H-1), 1\big]$ such that

$(1).$ $|c(t, x)|+|c_x(t, x)|\leq C;$

$(2).$ $|c(t, x)-c(s, x)|+|c_x(t, x)-c_x(s, x)|\leq C|t-s|^\beta;$

$(3).$ $|c_x(t, x)-c_x(t, y)|\leq C|x-y|.$

Note that the above assumptions (2) of (Hab) and (1) of (Hc) imply the Lipschitz continuity, that is, there exists some constant $C > 0$ such that, for any $t\in[0, T]$ and $x, y\in\mathbb R$,

Remark 3.1.

1. As was stated in ^[13], under the assumptions (Hab) and (Hc), the main SDEs (1) has a unique solution $\{X(t), t\in[0, T]\}$ in the space of $\mathcal W_0^{\alpha, \infty}([0, T])$ with $\alpha\in(1-H, 1/2)$.

2. Even if, instead of the boundedness of $a(t, x)$, we assume that the coefficient $a(t, x)$ is linear growth, all results in this paper are still true.

3.2.   Some lemmas

Now, we are going to formulate some useful properties of the Euler approximation $\{X_t^\delta, t\in[0, T]\}$. For this, we need some additional notations. Denote $\psi_{t}: = \psi(\omega, \alpha, t)\vee 1, \phi_{t}: = \phi(\omega, \eta, t)\vee\phi_{_b} (\omega, \eta, t)\vee 1$ and $\xi_{t}: = \psi_{t}\vee\phi_{t}$. Obviously, $\xi_{t}$ is non-deceasing in $t$, that is, for any $t\in[0, T]$, $\xi_{t}\leq \xi_{_{T}} = \psi_{_T}\vee\phi_{_T}$ holds almost surely. Moreover, $\xi_{t}$ has finite moments of any order. For any $R > 1$, define a stopping time $\pi_{_R}: = \inf\left\{t:\xi_{t}\geq R\right\}\wedge T.$ Let $\Omega_{_R} = \{\omega:\pi_{_R} = T\}$. By Lemma 4.4 in ^[11], $\mathbb P(\pi_{_R} < T)$ tends to 0 as $R\rightarrow\infty$ if assumptions (Hab) and (Hc) hold.

Our first result is Hölder continuity for the processes $\{X_t\}_{t\in[0, T]}$ and $\{X_t^\delta\}_{t\in[0, T]}$ defined in (1.1) and (3.1) respectively.

Lemma 3.1. If the coefficients of (1.1) satisfy the conditions (Hab)(1)(2) and (Hc), then, for any $1-H < \alpha < \frac{1}{2}$, it has a unique solution $X$ such that $\{X_t\}_{t\in[0, T]}\in\mathcal W_0^{\alpha, \infty}([0, T], \mathbb R)$ almost surely. Moreover, for any $0 < \eta < \frac{1}{2}$ and $0\leq s\leq t\leq T$, there exists some constant $C > 0$ such that

Proof. It follows from ^[13] that, for any $1-H < \alpha < \frac{1}{2}$, there exists a unique solution $\{X_t\}_{t\in[0, T]}$ of (1.1) belonging to $\mathcal W_0^{\alpha, \infty}([0, T])$ almost surely. Now, we estimate (3.2). From (2.8) and the condition (1) of (Hab) we immediately get

Using the estimation (2.5) and for $s, t\in[0, T]$, we have

By exchanging the order of integration and choosing $0 < \eta < \frac{1}{2}-\alpha$, for $s, u\in[0, T]$, we have

Consequently, Lemma 6.3 implies that

Therefore,

which completes the proof.

Remark 3.2. A similar proof to Lemma 3.1, we also have

Then, we prove the boundedness of the processes $\{X_t\}_{t\in[0, T]}$ and $\{X_t^\delta\}_{t\in[0, T]}$.

Lemma 3.2. Let $\mathbb E|X_0|^{p} < \infty$ for $p\geq 1$. If the assumptions (Hab) and (Hc) hold, then, for any $1-H < \alpha < \frac{1}{2}$, there exists a constant $C > 0$ such that $\mathbb E[\sup\limits_{t\in[0, T]}\|X_t\|_\alpha^{p}]\leq C$ and $\mathbb E[\sup\limits_{t\in[0, T]}\|X_t^\delta\|_\alpha^{p}]\leq C$, where $\{X_t\}_{t\in[0, T]}$ and $\{X_t^\delta\}_{t\in[0, T]}$ are the solutions of (1.1) and Euler (3.1) respectively.

Proof. It can be directly derived from Theorem 4.2 of ^[11] that $\mathbb E[\sup\limits_{t\in[0, T]}\|X_t\|_\alpha^{p}]\leq C$. Hence we just need to show $\mathbb E[\sup\limits_{t\in[0, T]}\|X_t^\delta\|_\alpha^{p}]\leq C$. Write

where

It follows easily from (1) of (Hab) and $1-H < \alpha < \frac{1}{2}$ that $J_1(t)\leq C.$

We estimate $J_{31}(t)$ by using (2.3). From the definition of $\tau_t$ and Euler equation (3.1), we have

In order to estimate $J_{311}(t)$ and $J_{312}(t)$, we need the following difference

In fact, (3.3) can be easily derived from (2.6) and (2.7).

If one takes $\eta\in\left(0, \frac{1}{2}-\alpha\right)$, it is obviously that $J_{311}(t)\leq C\xi_{_{t}}.$

Note that the area of $\{0\leq s\leq t; 0\leq r\leq\tau_s\}$ is equivalent to the area of $\{0\leq r\leq\tau_t; \tau_r+\delta\leq s\leq t\}$. So, by exchanging the order of integration of $J_{312}$, we have

where we use the difference (3.3) and the following inequality (see (4.15) of ^[17])

Evidently, $J_{313}(t)\leq \int_0^t\|X_s^\delta\|_\alpha ds.$

Now, we estimate $J_{32}(t)$ by using (2.5) and the following estimation

From the definition of $\tau_t$ and Euler equation (3.1), we have

It is obvious that

From (3.3) and $0 < \eta < \frac{1}{2}-\alpha$, we estimate $J_{321}(t)$ and $J_{322}(t)$.

Exchanging the order of integration of $J_{322}(t)$, we have

Further, noting that $0 < \alpha < \frac{1}{2}$ and then using (3.4), we have

Summing up all the above estimations, we obtain

So, it follows from Lemma 6.3 that

For each $p\geq1, \omega\in \Omega, \text{ and } \alpha\in(1-H, \frac{1}{2})$, we take into account that the right-hand side of the above inequality does not depend on $t$ and arrive at

Therefore,

Taking into account that $1 < \frac{1}{1-\alpha} < 2$, we apply Fernique theorem (see (24) in ^[11]) and obtain that

Our next step is to estimate $\mathbb E[J_{21}^{2p}]$ with the help of the Doob martingale inequality.

Applying (2.8) to $J_{22}^{2p}$ and noting that $0 < \eta < \frac{1}{2}-\alpha$, one can easily obtain

Finally, because $\phi_t$ and $\psi_t$ have bounded moments of $p$-order, we get

where the constant $C$ depends on $\alpha$ and $p$, but is independent of $\delta$ and $\omega$.

As a result of Lemma 3.2, one can easily get the following corollary.

Corollary 3.1. Let $\mathbb E|X_0|^{p} < \infty$ for $p\geq 1$. If assumptions (Hab) and (Hc) hold, then there exists a constant $C > 0$ such that

where $\{X_t\}_{t\in[0, T]}$ and $\{X_t^\delta\}_{t\in[0, T]}$ are the solutions of (1.1) and Euler (3.1) respectively.

Thirdly, we are ready to prove that the moments of the Malliavin derivative of Euler approximation (3.1) is bounded. We refer the reader to Nualart and Saussereau ^[27] for results on Malliavin regularity of the solutions of stochastic differential equations.

Lemma 3.3. Let $t\in(t_k, t_{k+1}]$, i.e., $\tau_t = t_k$, $X_{\tau_t}^\delta$ be the solution of Euler (3.1) at the point $t_k, \; k = 0, 1, \cdots, n$. If the assumptions (Hab) and (Hc) hold and $X_0$ is independent of $B^H$ with $\mathbb E[|X_0|^{p}] < \infty$ for $p\geq 1$, then, there exist some positive constant $C$ such that $\mathbb E[\sup\limits_{t\in[0, T]}|D_sX_t^\delta|^{p}]\leq C$ for any $s > \tau_t$ and some constant $M_{_{p, R}}$ dependent on $p$ and $R$ such that $\mathbb E[\sup\limits_{t\in[0, T]}|D_sX_{\tau_t\wedge\pi_{_R}}^\delta|^{p}]\leq M_{_{p, R}}$ for any $s\in[0, \tau_t]$, here, for any fixed $R > 1$, the stopping time $\pi_{_R} = \inf\left\{t:\xi_{t}\geq R\right\}\wedge T.$

Proof. If $s > t$ then it is clear that $D_sX_t^\delta = 0$.

Thanks to (2.9), (2.10) and the independence of $W$ and $B^H$, if $\tau_t < s\leq t$ then we have

By the boundedness of $c(t, x)$, we have $\mathbb E[\sup\limits_{t\in[0, T]}|D_sX_t^\delta|^{p}]\leq C$ for any $s > \tau_t$.

If $s\in[0, \tau_t]$ then we have

From Lemma 2.3 of ^[14] and the boundedness of $a_x(t, x)$, $b_x(t, x)$ and $c_x(t, x)$, for any $s$ belonging to the interval $[0, T]$, we obtain

For any $s\in[0, \tau_t]$, note that the equation

is true. Therefore, we have the following corollary by Lemma 3.3 and Cauchy-Schwarz type inequality.

Corollary 3.2. If the conditions of Lemma 3.3 are satisfied, then, for any $s\in[0, \tau_t]$, we have

and

3.3.   Main result

The aim of this subsection is to estimate the rate of convergence of Euler (3.1) to the solution of (1.1).

Theorem 3.1. Suppose that $X_0$ is a random variable independent of $W$ and $B^H$ with $\mathbb E|X_0|^4 < \infty$. If assumptions (Hab) and (Hc) are satisfied then we have

for any $\gamma < \min\{\frac{1}{2}, 2H-1\}$, $\varepsilon > 0$ and $\alpha \in\left(1-H, \frac{1}{2}\right)$. Here, $\{X_t\}_{t\in[0, T]}$ and $\{X_t^\delta\}_{t\in[0, T]}$ are the solutions of (1.1) and Euler (3.1) respectively and $n = \frac{T}{\delta}$.

Remark 3.3. Theorem 3.1 shows that the rate of convergence for Euler (3.1) is equal to $\gamma$ ($\gamma < \min\{\frac{1}{2}, 2H-1\}$) in probability with the norm $\sup\|\cdot\|_\alpha$, i.e. in the sense of probability, we can establish an estimate for the error of $|X_t-X_t^\delta|$ with the norm $\sup\|\cdot\|_\alpha$ in certain Besov space $\mathcal W_0^{\alpha, \infty}([0, T])$ (see Definition 2.1), exactly,

for any $\varepsilon > 0$ and any sufficiently small $\rho > 0$, there exists $\delta_0 > 0$ and $\Omega_{\varepsilon, \delta_0, \rho}$ such that $P(\Omega_{\varepsilon, \delta_0, \rho}) > 1-\varepsilon$ and for any $\omega\in\Omega_{\varepsilon, \delta_0, \rho}, \delta < \delta_0$,

here $\alpha \in\left(1-H, \frac{1}{2}\right)$, $C(\omega)$ does not depend on $\delta$ and $\varepsilon$ (but depends on $\rho$).

Proof. of Theroem 3.1. Fix an arbitrary $\varepsilon > 0$ and any $R > 1$. As mentioned previously, $\pi_{_R} = \inf\{t:\xi_{t}\geq R\}\wedge T$. Consider

For the second term on the right hand side of (3.6), applying Chebyshev's inequality, we have

Now, we estimate (3.7). According to Definition 2.1, for any $t\in[0, T]$, we have

In turn, $I_1(t)$ can be estimated as

From Corollary 3.1, we have

From Doob martingale inequality and Corollary 3.1, we have

Estimate $I_{13}(t)$ by dividing it into three parts.

Taking into account the estimation (2.3) and the definition of stopping time $\pi_{_R}$, we have

Noting that $1-H < \alpha < \frac{1}{2}$ and $c(t, x)$ is Lipschitz continuous, we have

Using Lemma 6.2, Lemma 3.1 and $1-H < \alpha < \frac{1}{2}$, we have

where $C_{_R} = CRe^{CR^{\frac{1}{1-\alpha}}}$, $\gamma = \frac{1}{2}-\eta-\alpha > 0$ only if we take $\eta\in(0, \frac{1}{2}-\alpha)$.

Estimate $I_{132}(t)$ and $I_{133}(t)$ by the relation between the pathwise Riemann-Stieltjes integral and the Skorohod integral with respect to fBm. Firstly,

From the estimation (2.13), Lemma 3.2 and 3.3, Corollary 3.1 and 3.2, we have

Similarly to the estimation of $I_{1321}(t)$,

Secondly,

Further we apply (2.13) and Lemma 3.3 to $I_{1331}(t)$,

Similar to the estimation of $I_{1331}(t)$, we have

Summing up all the estimations (3.9)-(3.20), we obtain

Next step, we consider $I_2(t)$.

As regards $I_{21}(t)$, we estimate it in the following way:

Choosing $\varrho$ such that $\alpha < \varrho < \frac{1}{2}$, by Hölder inequality, Lipschitz continuity of $a(t, x)$ and exchanging the order of integration, we have

By a similar discussion to $I_{211}(t)$, one can easily get

and

Similar to the estimation of $I_{21}(t)$, we estimate $I_{22}(t)$ by dividing it into three parts as well,

From Hölder inequality, Burkhölder-Davis-Gundy inequality and then exchanging the order of integration, we get

A similar discussion to $I_{221}(t)$, one can easily get

and

Now we go on with the term $I_{23}(t)$ including fBm.

With the help of the estimation (2.5) and the definition of stopping time $\pi_{_R}$, we have

By exchanging the order of the integration we have

Here we use the following estimation (see (4.15) of ^[17]):

According to Lemma 6.2, $I_{2312}(t)$ admits the following estimation:

here $\alpha < \varrho < \frac{1}{2}$.

By Hölder inequality and exchanging the order of the integration, we have

and

According to Remark 3.2, similar to the above estimation, we have

where $C_{_R} = CRe^{CR^{\frac{1}{1-\alpha}}}$ (see (3.14)), $\alpha < \varrho < \frac{1}{2}$, $\gamma = \frac{1}{2}-\eta-\alpha > 0$ only if we take $\eta\in(0, \frac{1}{2}-\alpha)$.

Then we estimate $I_{232}(t)$. (2.11) implies

According to (2.13), Corollary 3.1 and 3.2 as well as Lemma 3.3, we have

and

Finally, we estimate $I_{233}(t)$. (2.11) implies

From the estimation (2.13) and Lemma 3.3, we have

and

Summing up all estimations (3.22)-(3.43), we have

Then, taking into account (3.21) and (3.44), we obtain

Evidently, the above estimation can be written as

Therefore, Lemma 6.3 yields

Plugging (3.45)) into (3.7), we arrive at

Passing to the limit as $n\rightarrow\infty$, we prove that the right hand side of (3.6) approaches 0.

Then (3.6) gives

Letting $R\rightarrow\infty$, by Lemma 4.4 of ^[11], we obtain

Corollary 3.3. If the conditions of Theorem 3.1 are satisfied, then, for any fixed $\varepsilon > 0$, there exist a positive constant $C_{\varepsilon}$ and a subset $\Omega_{\varepsilon}$ of $\Omega$ with $P(\Omega_{\varepsilon}) > 1-\varepsilon$ such that

and

where $C_\varepsilon = C\exp\left\{C\varepsilon^{\frac{8}{2\alpha-1}}\cdot\exp\left(C\varepsilon^{\frac{1}{2\alpha-1}}\right)\right\}$ and $C$ is a general positive constant independent of $\delta$ and $\varepsilon$.

Proof. For any fixed $\varepsilon > 0$, let $R = \frac{2\mathbb E\xi_{_T}}{\varepsilon}$, $\pi_\varepsilon = \inf\left\{t:\xi_t\geq \frac{2\mathbb E\xi_{_T}}{\varepsilon}\right\}\wedge T$ and $\Omega_\varepsilon = \{\omega:\pi_\varepsilon = T\}$. We have $P(\Omega_\varepsilon) > 1-\varepsilon$. In fact,

(3.48) can be derived from (3.45) immediately, and (3.49) can be from Lemma 3.2 and $P(\Omega/\Omega_\varepsilon) < \varepsilon$.

Remark 3.4. In ^[28], it is proved that, for some equation with $b(t, x) = 0$ and $c(t, x) = c(x)$, the error $n^{2H-1}(X_t-X_t^\delta)$ almost surely converges to some stochastic process, i.e., as $n\rightarrow\infty$,

In ^[29], it is shown that, for the Itô-SDEs with $b(t, x) = b(x)$ and $c(t, x) = 0$, the error $n\mathbb E|X_t-X_t^\delta|^2$ converges to some stochastic process, i.e., as $n\rightarrow\infty$,

with another Brownian motion $B$, which is independent of the Brownian motion $W$, and

The above facts mean that the estimation of the rate of convergence in Theorem 3.1 is sharp.

Remark 3.5. In this paper we have restricted ourselves to the case of a scalar SDEs. This is only to keep our notations and computations relatively simple but the theory developed above can certainly be generalized to the multidimensional case without any difficulty. Moreover, instead of fractional Brownian motion one can take any process, which is almost surely Hölder continuous with Hölder exponent $\lambda > \frac{1}{2}$.

Remark 3.6. The proof of our main result combines the techniques of Malliavin calculus with classical fractional calculus. The main idea is to estimate the path-wise Riemann Stieltjes $\int_0^tc(s, X_s)dB_s^H$ flexibly by (2.3) or (2.11). Specifically,

(1) We estimate $I_{131}(t)\; (\text{and } I_{231}(t))$ by the properties of fractional calculus instead of Malliavin calculus, i.e., by $(2.3)\; (\text{and } (2.5))$ instead of $(2.11)\; (and(2.13))$. It is because we can hardly establish the boundedness of the Malliavin derivative $D_sX_t$ for any $s\leq t$, and the estimation for the second moment of the difference between $D_sX_t$ and $D_sX_t^\delta$ for any $s\leq t$. Indeed, for analyzing both of them, we need also the second Malliavin derivative and then the third Malliavin derivative etc., however, there is not closable formulas for them.

(2) However, we estimate $I_{132}(t), I_{133}(t)\; (and I_{232}(t), I_{233}(t))$ by $(2.11)\; (and (2.13))$ instead of $(2.3)\; (and (2.5))$ because we have little idea how to process the second term generated by $(2.3)$ and $(2.5)$. For example, it is very difficult to estimate the upper bound of the following expression:

4.   A numerical example

Let us consider the following mixed SDE driven by both Brownian motion and fractional Brownian motion,

Here $\mu, \sigma$ are nonzero constants. Mixed SDE (4.1) has the explicit solution (see ^[30])

For any $N\in\mathbb N$, consider the isometric partition of $[0, T]$: $\{0 = t_0 < t_1 < \cdots < t_N = T, \; \delta = \frac{T}{N}\}$. Define $\tau_t: = \max\{t_k:t_k < t\}$. The Euler approximation of (4.1) is expressed as

or, in the integral form,

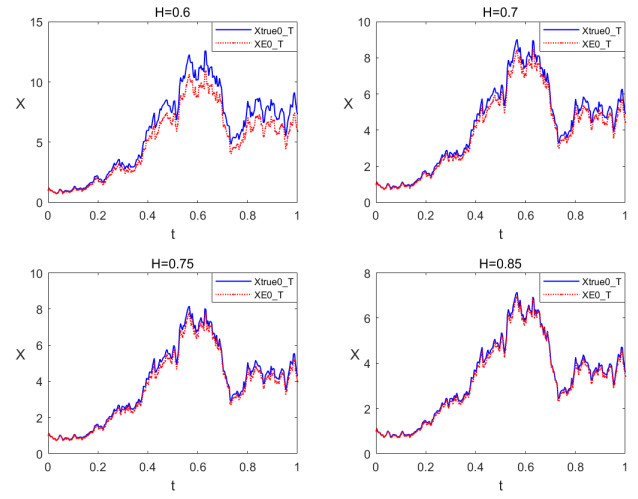
In the M-file EulerMSDE.m we set the initial state of the random number generator to be 100 with the command randn('state', 100) and consider (4.1) with $\mu = 2, \sigma = 1, T = 1$ and $X_0 = 1$. We compute a discretized Brownian motion and fBm path over $[0, T]$ with $N = 2^8$ and evaluate the solutions in (4.2) as Xtrue0$\_$T, and then apply Euler approximation using a stepsize $\delta$. The Euler solution is stored in the 1-by-$(N+1)$ array XE0$\_$T. The $\sup\|\cdot\|_\alpha$-error and the constant $C(\omega)$ in Remark 7 computed as XEerrsup and Comega respectively in the M-file EulerMSDE.m. In order to compare different convergent cases, we set $H = 0.6, 0.7, 0.75, 0.85, \alpha = 0.75-0.5H$ and $\rho = \gamma = \min\{0.5, 2H-1\}/2$. We get the following numerical results:

From the Table 1, we can see the larger $H$, the smaller XEerrsup and Comega, i.e. the larger $H$, the smaller error and dominated constant $C(\omega)$. From the Figure 1, we can see the larger $H$, the better the convergence, moreover, the two graphs of $H = 0.75$ and $H = 0.85$ are very similar. These are consistent with our conclusion because the rate of convergence is less than $\min\{0.5, 2H-1\}$. (see Theorem 3.1)

5.   Conclusions

The following time-dependent mixed stochastic differential equation driven by both Brownian motion and fBm is considered in this paper.

We obtain that the Euler approximation has the convergent rate $O(\delta^{\frac{1}{2}\wedge(2H-1)})$ with the norm $\|\cdot\|_\alpha$ (see Definition 2.1) in probability. We also show that it has the rate of convergence $\delta^{1\wedge(4H-2)}$ in the sense of Besov type norm on some subsets of $\Omega$ with probability close to one. Meanwhile, on the complement of above subsets, the error of Euler (3.1) can be small enough correspondingly in the same norm (see Corollary 3.3). We mention that it is also true for the result of Corollary 3.3 in the sense of mean-square norm if $1\wedge(4H-2)$ is replaced by $\frac{1}{2}\wedge(2H-1)$.

On one hand, as we known, the mean-square rate of convergence for 'pure' SDE driven by single Brownian motion is $O(\delta^{\frac{1}{2}})$ (see ^[20]) and by single fractional Brownian motion is $O(\delta^{2H-1})$ (see ^[18]). For the mixed SDEs, we can only obtain the worst convergent rate of those of 'pure' SDEs because their estimates for 'pure' equations are sharp (see ^[20,28]).

On the other hand, Mishura and Shevchenko ^[16] researched the Euler approximation of the following one-dimensional mixed SDEs,

They derived the mean-square rate of convergence $O(\delta^{\frac{1}{2}\wedge(2H-1)})$. In ^[15] the authors also find that a faster rate of convergence $O(\delta^{\frac{1}{2}})$ to (5.1) can be obtained if one uses the modified Euler method. In a forthcoming paper we will study, whether the rate of convergence of (modified) Euler approximation to (1.1) is $O(\delta^{\frac{1}{2}\wedge(2H-1)})$ with P-a.s. ($O(\delta^{\frac{1}{2}})$ with mean-square norm).

6.   Appendix

In this section, we prove the bounded estimation (3.5) and recall two results from ^[17].

Lemma 6.1. Given $\alpha, \beta(1 > \beta > \alpha), T$ and any $t\in[0, T], n\in\mathbb N$, consider the isometric partition of $[0, T]$: $\{0 = t_0 < t_1 < \cdots < t_n = T\}.$ Let $\delta = \frac{T}{n}$ and $\tau_t: = \max\{t_k:t_k < t\}$(see Euler equation (3.1), then we have

here the constant $C$ is independent of $n$ and $\delta$.

Proof. From the primary inequality $(a+b+c)^\beta\leq C_0(a^\beta+b^\beta+c^\beta), \; a\geq 0, b\geq 0, c\geq 0, \beta > 0$, we have

For $\beta > \alpha$, we have

Exchanging the order of integration, we have

Let $C = C_0(C_1+C_2+C_3)$, we complete the proof.

Lemma 6.2. (The modification of Lemma 7.1 of ^[17]) Let $c:[0, T]\times\mathbb R\rightarrow\mathbb R$ be a function such that $c(t, x)$ satisfies the assumption (Hc), then, for all $x_1, x_2, x_3, x_4\in\mathbb R$, we have

The following lemma is a generalization of Gronwall lemma.

Lemma 6.3. (Lemma 7.6 of ^[17]) Fix $0\leq \theta < 1, a, b\geq 0$. Let $x:[0, \infty)\rightarrow[0, \infty)$ be a continuous function such that for each $t$

Then

where $\Gamma$ is the Gamma function, $c_{_\theta}$ and $d_{_\theta}$ are positive constants depending only on $\theta$ (as an example, one can set $c_{_\theta} = 2(\Gamma(1-\theta))^{1/(1-\theta)}$ and $d_{_\theta} = \frac{4\Gamma(1-\theta)}{1-\theta}e^2$).

Acknowledgement

The authors are very grateful to Professor Guiwu Hu for his support and encouragement in making this work possible. We also would like to thank the referees for the careful reading of the manuscript and for their valuable suggestions. This work is supported by Project of Department of Education of Guangdong Province (No.2018KTSCX072) and Guangdong University of Finance & Economics, Big data and Educational Statistics Application Laboratory (No.2017WSYS001).

Conflict of interest

The authors declare that they have no conflict of interest.