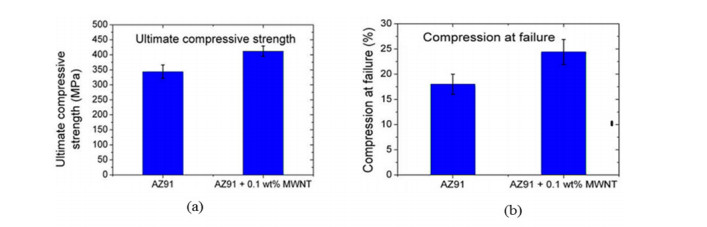
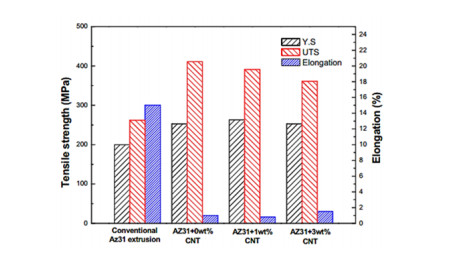
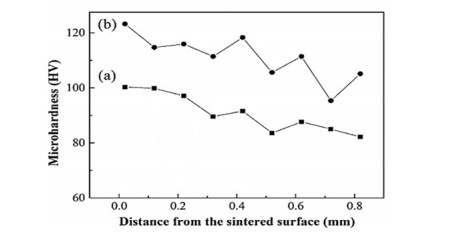
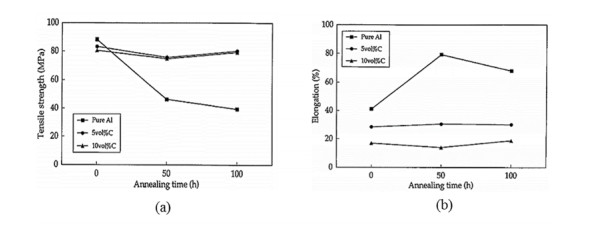
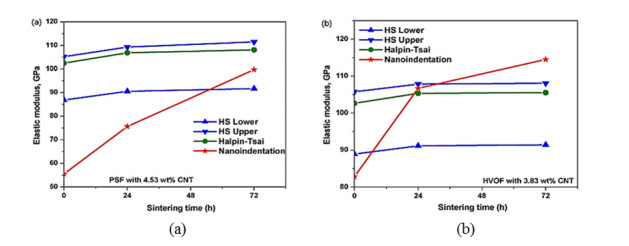
Lightweight materials characterized by low density, high strength to weight ratio, low porosity, high corrosion resistance with improved mechanical, thermal, electrical properties are now extensively used in many engineering applications ranging from the deep sea to aerospace. Besides, the materials must be multifunctional comprises a fast and economic manufacturing technique. Metallic matrix CNTs composites such as Mg/CNTs and Al/CNTs have such the aforementioned quality. However, Mg/CNTs and Al/CNTs has some specific advantages and disadvantages that restrict their applicability. To harvest the dual benefit of Mg/CNTs and Al/CNTs, bimetallic matrix Mg-Al/CNTs may be prospected. Mg-Al bimetallic combination for alloying has substantial mechanical properties with heavy amalgamation. Therefore, interdisciplinary research on reinforcement, compacting, bonding, dispersion of CNTs in the bimetallic matrix, microstructure and defect analysis will open the door for producing new class of composite materials. In this work, various Mg/CNTs, Al/CNTs, Mg-Al composites have been studied to find the prospect of Mg-Al/CNTs composites. The worthwhile accomplishment of the reviews will provide the knowledge of fabrication for CNTs reinforced bimetallic Mg-Al based lightweight composites and understand its mechanical behaviors.
1.
Introduction
Hepatitis B, a viral liver infection caused by the hepatitis B virus (HBV), is a major threat to public health and security around the whole world. HBV can cause both acute and chronic hepatitis. Acute hepatitis B refers to the virus infection less than half a year and part of the patients can recover and get lifetime immunity. The disease course of chronic hepatitis B can be quite long, and it can lead to severe liver disease such as cirrhosis and liver cancer [1]. Globally 257 million people were living with chronic hepatitis B infection, which resulted in estimated 887,000 deaths in 2015. According to the latest fact sheets released by the World Health Organization (WHO), 296 million people were living with chronic hepatitis B infection in 2019, and there are 1.5 million new infections each year [2]. Worldwide, hepatitis B resulted in an estimated 820,000 deaths in 2019, mostly from cirrhosis and hepatocellular carcinoma (primary liver cancer) [2]. Hence, hepatitis B epidemic is still a major global health problem.
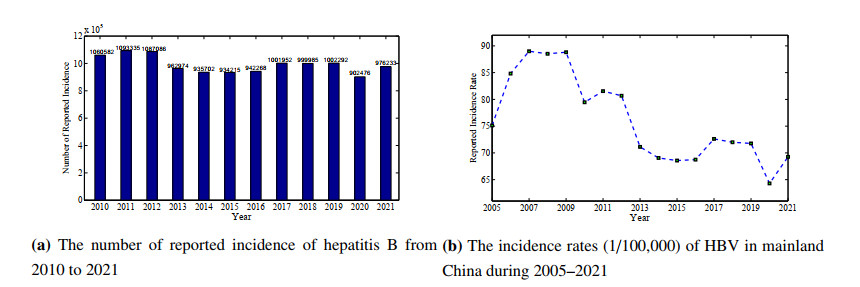
In China, hepatitis B is one of the top three infectious diseases reported by the Chinese Center for Disease Control and Prevention (CDC) [3]. Based on the sero-epidemiological investigation of hepatitis B in 1992, about 9.75% of the general population in China was chronic HBV carriers. That is, around 130 million people of mainland China were carriers of HBV in the 1990s [1]. Then an effective and national vaccination program has been conducted by the government, especially the hepatitis B planned immunization for newborn babies and children. The sero-epidemiological survey in 2006 showed about 7.18% of the population was hepatitis B carriers, and the number of hepatitis B carriers was reduced by 30 million [3]. Lately in 2014, an epidemiology survey of people younger than 29 reported that the HBV infection rates were 0.32% among the group of children aged one to four, 0.94% in the group aged 5 to 14, and 4.18% in the group aged 15 to 29, respectively. The government of mainland China has achieved remarkable results in the prevention and treatment of hepatitis B. Nevertheless, the epidemic situation remains to be severe and complicated. At present there are 80 million HBV carriers in mainland China, among whom 28 million carriers need immediate medical treatment. During the past decade, the number of reported incidence of hepatitis B is around one million each year (Figure 1(a)). The incidence rates of hepatitis B in mainland China from 2005 to 2021 are presented in Figure 1(b), and the incidence rates varied from 89.00 per 100,000 in 2007 (the highest during 2005–2021) to 64.29 per 100,000 in 2020 (the lowest during 2005–2021).
The incidence of hepatitis B is different among regions, and it could be influenced by various factors such as vaccination and economy. Figure 2 displays the hepatitis B incidence rates in 31 provinces and municipalities of mainland China, and the data in 2007 and 2020 are chosen and displayed. The figure shows that the incidence decreased for most provinces (22 of 31), especially for Ningxia, Gansu, Henan, Xinjiang and Qinghai. This strongly reveals that the immunization program with hepatitis B vaccine is successful in most provinces, and the achievement is remarkable for western areas in China. However, it should be pointed out, in 2020, the incidence varied from 6.15 per 100,000 in Beijing to 150.99 per 100,000 in Qinghai. There is still a gap between the impoverished west and the prosperous east.
In the last three decades, the research on hepatitis B has attracted more and more attention from the perspective of epidemiology and biomathematics. For instance, in 1991, Anderson and May used a simple mathematical model to study the impacts of carriers on the transmission of HBV [4]. Zhao et al. [5] studied the dynamics of HBV transmission and proposed vaccination strategy to prevent the prevalence in the population. In 2010, Zou et al. [1] formulated a high dimensional deterministic model to analyze the transmission dynamics of HBV infection in China. Then in 2015 Zou et al. [6] investigated the sexual transmission dynamics of HBV in China. Zhang et al. [7] proposed a four dimensional HBV epidemic model involving an exponential birth rate and vertical transmission, and fitted the parameters to the public data in Xinjiang, China. Recently Din and Li [8] analyzed a stochastic hepatitis B epidemic model with vaccination effect and showed a case study for Pakistan. For more mathematical epidemic models on HBV infection, one can refer to [9,10,11,12] and the references therein.
Besides the classical compartmental models for hepatitis B epidemic, a vibrant field of research on the virus transmission dynamics has emerged and developed rapidly [12]. The modeling approaches usually incorporate the interaction among intracellular viral dynamics, multicellular infection process, and immune responses [13,14,15,16]. For instance, Wang et al. [13] formulated a multi-scale computational model of SARS-CoV-2 infection using a combination of differential equations and stochastic modeling, and revealed heterogeneity among COVID-19 patients. Rihan and Alsakaji [14] analyzed a stochastic delay HBV infection model with cell-to-cell transmission and cytotoxic T lymphocytes (CTLs) immune response. Recently Mohajerani et al. [17] proposed a multiscale modeling of HBV capsid assembly pathways, by constructing Markov state models and employing transition path theory.
When an infectious disease breaks out in one area, the center for disease control and prevention will release authoritative information through the mass media at the first moment, including the potential risk of the disease and prevention measures [18]. Media coverage helps to raise public health awareness, increase vaccine rates and reduce the spread of infections. Recently, a number of epidemic models have taken into account the influence of media coverage on the spread of infectious disease [19,20,21,22,23]. Their study suggests that media coverage is critical in disease eradication [19,20]. There are different forms of function to represent the effect of media coverage in epidemic models. Let S and I denote the number of the population that are susceptible and infectious respectively, and let β be the transmission rate. Cui et al. [19] used the exponential function βexp(−mI)SI to denote the incidence rate with media coverage, where m>0. In another work [20], the incidence rate incorporating media coverage takes the form: (β−β2f(I))SI, where β>β2 and the function f(I) satisfies f(0)=0, f′(I)≥0, limI→+∞f(I)=1. In the present paper, similar to the approach in the previous literatures [21,24,25], we adopt the most common form f(I)=Ib+I, where b is a half saturation constant.
Furthermore, the transmission of HBV is disturbed by various random factors in the environment, such as population mobility and unpredictable exposure to infections. An increasing number of researchers have formulated stochastic hepatitis B epidemic models considering environmental noise [8,10,11]. In fact, environment disturbances have an important effect on the evolution of infectious diseases [26,27,28,29,30], and Gaussian white noise is usually selected as an appropriate representation of environmental fluctuations [31]. For instance, Wang et al. [28] and Meng et al. [29] proved that a large disturbance of white noise can lead infectious diseases to extinction. A large number of works also indicate that stochastic disturbance can suppress disease outbreak [18,26].
In the present paper, motivated by the above discussion, we formulate and investigate a stochastic hepatitis B model with media coverage and saturated incidence rate. We obtain a sufficient condition for the extinction of the disease, and prove that the stochastic system has a unique stationary distribution under certain conditions. Moreover, as a case study, we utilize our model for fitting the available data of mainland China from 2005 to 2021. Based on our simulation result, the incidence rate of hepatitis B in China will remain around 50–60 per 100,000 in the long term.
The paper is organized as follows. In Section 2, we present the model formulation. In Section 3, the existence and uniqueness of positive solution is proved for the stochastic model. In Section 4, we obtain a sufficient condition for the extinction of the disease. In Section 5, the sufficient condition on the existence of stationary distribution is obtained, which indicates that all the compartments will be persistent. Moreover, we provide an estimation of lower bound of the expectation for the number of infected cases. In Section 6, numerical simulations are conducted to illustrate our theoretical results. As a case study, we fit our model to the available HBV data of mainland China from 2005 to 2021.
2.
Model formulation
Recently, Khan et al. [10] proposed a stochastic model for the transmission of HBV. In their work, the population is divided into four compartments: susceptible humans S; acute HBV infections I1; chronical HBV infections I2; and recovered population R. They further assumed: (i) the contact of susceptible individuals with acutely and chronically infected hepatitis B individuals primarily causes acutely infected species; (ii) the transmission coefficient β is subject to random fluctuation, that is, βi→βi+ηi˙Bi(t) for i=1,2, where Bi(t) is standard Brownian motion with Bi(0)=0 and with the noise intensity η2i>0. Then the stochastic hepatitis B epidemic model in [10] was presented as follows
where Λ is the recruitment rate of the population, μ0 is the natural mortality rate, μ1 is the disease mortality rate, and υ represents the vaccination rate of hepatitis B. Moreover, βi (i=1,2) represent the transmission rate of hepatitis B, γ is the moving rate of acutely infected humans to chronic stage, and γi (i=1,2) denote the recovery rates of acutely and chronically infected hepatitis B individuals, respectively.
In the above model, the authors chose bilinear incidence rate, that is, βSI. As a matter of fact, the transmission of infectious diseases is complicated, and nonlinear incidence rates have been wildly utilized in epidemic model [26,29]. In 1978, to describe the phenomenon that incidence is increasing and the population is saturated with the infective, Capasso and Serio [32] proposed a saturated incidence rate βSI1+αI. Then such saturated incidence has been extensively used in epidemic models. For instance, Khan and Zaman [33] and Liu et al. [11] have formulated hepatitis B epidemic models with saturated incidence rate. In addition, as discussed in the introduction part, we also incorporate the impact of media coverage by using the function f(I)=Ib+I. Consequently, based on the deterministic part of model (2.1), we obtain the hepatitis B model with media coverage and saturated incidence rate as follows
where the forms SIi1+αiIi (i=1,2) represent the saturated incidence rates of acute and chronical infections, and the forms Iibi+Ii (i=1,2) denote the media coverage functions. Moreover, βi1 (i=1,2) represent the transmission rates for acute and chronical infections, and βi2 (i=1,2) denote the maximal reduced contact rates by mass media alert for acute and chronical infections, respectively. Recall that βi1>βi2 (i=1,2).
Furthermore, the disease transmission and biological populations are inevitably affected by environment noises. There are different approaches to add random perturbations to biological systems. The transmission rates βi (i=1,2) are assumed to be disturbed by Gaussian white noise in model (2.1). In this article, following the approach in [8,11,34,35], we assume that the environmental white noise is proportional to each state variable S(t),I1(t),I2(t) and R(t). Finally we extend model (2.2) to the following stochastic model
where Bi(t) (i=1,2,3,4) are independent standard Brownian motions with Bi(0)=0, and σ2i>0 (i=1,2,3,4) denote the intensities of white noise.
Throughout the paper, let (Ω,F,{Ft}t≥0,P) be a complete probability space with a filtration {Ft}t≥0 satisfying the usual conditions (i.e., it is increasing and right continuous while F0 contains all P-null sets), then Bi(t) (i=1,2,3,4) are defined on this complete probability space. We also introduce the following notations: Rd+={(x1,x2,...,xd)∈Rd:xi>0,i=1,2,...,d}, a∧b=min{a,b}, a∨b=max{a,b}, ⟨f⟩=1t∫t0f(r)dr.
3.
Existence and uniqueness of the positive solution
Since S,I1,I2 and R in system (2.3) denote the number of individuals, they should be nonnegative from the viewpoint of biology. We first introduce some basic definitions that will be used in the reminder of the article [36]. In general, let X(t) be a homogeneous Markov process in the d-dimension Euclidean space Rd described by the stochastic differential equation
then the diffusion matrix is defined as
Furthermore, the differential operator L is defined by
where V(x) is an arbitrary twice continuously differential real-value function.
In this section, we obtain the following theorem which guarantees the existence and uniqueness of positive solution for system (2.3).
Theorem 3.1. For any initial value (S(0),I1(0),I2(0),R(0))∈R4+, there is a unique positive solution (S(t),I1(t),I2(t),R(t)) for system (2.3) on t≥0 and the solution will remain in R4+ with probability one, namely, (S(t),I1(t),I2(t),R(t))∈R4+ for all t≥0 almost surely.
Proof. Since the coefficients of system (2.3) are locally Lipschitz continuous in R4+, then for any initial value (S(0),I1(0),I2(0),R(0))∈R4+, there exists a unique positive solution (S(t),I1(t),I2(t),R(t)) on t∈[0,τe), where τe is the explosion time [37]. Thus, it suffices to verify S(t), I1(t), I2(t) and R(t) do not explode to infinity in a finite time, that is, τe=∞ a.s. Let k0>0 be sufficiently large such that S(0), I1(0), I2(0) and R(0) all lie within the interval [1k0,k0]. For each integer k≥k0, define the stopping time
and throughout this paper we set inf∅=∞ (as usual ∅ is the empty set). Clearly, τk is increasing as k→∞. Let τ∞=limk→∞τk, then τ∞≤τe a.s. Thus, τ∞=∞ a.s. implies τe=∞ a.s. Now we state that τ∞=∞. If this assertion is false, then there is a pair of constants T>0 and ϵ∈(0,1) such that
Thus there exists an integer k1≥k0 such that
Define a C2-function V:R4+→R+ by
where a and b are positive constants to be determined later. The nonnegativity of this function can be obtained from
Apply Itô's formula [37] to V, and we obtain
where
Choose a=min{μ0β11,μ0+μ1β21} and b=μ0b1α1β12, then
and
where K is a positive number. Thus, according to Eq (3.3), one can get
Let k≥k1 and integrate the above inequality from 0 to τk∧T, then we have
Taking the expectation of both sides of Eq (3.4) yields
Set Ωk={ω∈Ω:τk=τk(ω)≤T} for k≥k1, then we have P(Ωk)≥ϵ by (3.2). Note that for every ω∈Ωk, at least one of S(τk,ω),I1(τk,ω),I2(τk,ω) and R(τk,ω) equals to either k or 1k, So V(S(τk,ω),I1(τk,ω),I2(τk,ω),R(τk,ω)) is no less than either
Thus, one can obtain
It then follows from Eq (3.5) that
where IΩk(ω) is the indicator function of Ωk. Taking k→∞ will induce ∞>V(S(0),I1(0),I2(0),R(0))+KT≥+∞, and it is a contradiction. Hence, we must have τ∞=∞ a.s.
The conclusion is confirmed.
4.
Extinction
In this section, we mainly discuss the extinction of hepatitis B under some conditions. To begin with, we present the following theorem.
Theorem 4.1. If min{μ0,μ1}>(σ21∨σ22∨σ23∨σ24)2, then the solution (S(t),I2(t),Sh(t),Ih(t)) of system (2.3) has the following properties
and
The proof is similar to those in [38] and hence is omitted here.
It is easy to compute that the deterministic system (2.2) admits a disease-free equilibrium point E0(Λμ0+υ,0,0,Λυμ0(μ0+υ)). For the stochastic system (2.3), we obtain a sufficient condition on the extinction of disease in the following theorem.
Theorem 4.2. Let (S(t),I1(t),I2(t),R(t)) be a solution of system (2.3) with initial value (S(0), I1(0), I2(0), R(0))∈R4+. If Rs0:=4Λ(2β11−β12+2β21−β22)μ0(σ22∧σ23)<1 and min{μ0,μ1}>(σ21∨σ22∨σ23∨σ24)2 hold, then the disease will tend to extinction with probability one, and the solution of system (2.3) satisfies
Proof. Denote
and applying Itô's formula to lnQ yields
Integrate inequality (4.1) from 0 to t and divide by t on both sides, then we get
According to system (2.3), we have
Integrate the above inequality form 0 to t and divide by t on both sides, then
Furthermore, it follows from Theorem 4.1 that
Therefore,
Take the superior limit on both sides of inequality (4.2), then we have
Consequently,
which implies that
On the other hand, according to Eq (4.3), we have
According to Theorem 4.1 and Eq (4.7), we obtain
The conclusion is confirmed.
Remark 1. According to the expression of Rs0, it is clear that the value of Rs0 decreases with the increase of σ2,3, β12 and β22. Since βi2 (i=1,2) represent the maximal reduced contact rates by mass media, the media coverage plays an important role in disease eradication.
5.
Stationary distribution and persistence
In this section, we focus on the existence of stationary distribution for system (2.3). From the biological point of view, stationary distribution can be interpreted as a weak stability of the system, and the disease will be persistent in the time mean sense. We first present a fundamental lemma.
Lemma 5.1. ([39]) The Markov process X(t), the solution of system (3.1), has a unique ergodic stationary distribution π(⋅), if there exists a bounded domain D⊂Rd with regular boundary Γ and
(C.1) there is a positive number M such that ∑di,j=1aij(x)ξiξj≥M|ξ|2, x∈D, ξ∈Rd,
(C.2) there exists a nonnegative C2-function V such that LV is negative for any x∈Rd∖D. Then
for all x∈Rd, where f(⋅) is a function integrable with respect to the measure π.
Define
Theorem 5.2. If ˆRs0>1, then there exists a unique stationary distribution for system (2.3) and it has the ergodic property.
Proof. We will prove the theorem by verifying the conditions in Lemma 5.1. The diffusion matrix of model (2.3) is given by
Apparently, the matrix A is positive definite for any compact subset of R4+, so the condition (C.1) in Lemma 5.1 holds.
Define V1=−lnS, then
Define
where a1,a2,c1,c2 and c3 are positive constants to be chosen later. By the use of Itô's formula, we obtain
Choose
and
It follows from inequality (5.1), that
Define
then by inequality (5.2) one can derive
where
and
Define
where θ is a positive constant that is less than one. Thus, we obtain
and
where
Define a C2-function ˜V:R4+→R by
Choose a positive constant M such that
where
It is easy to check that
here, Dn=(1n,n)×(1n,n)×(1n,n)×(1n,n). Thus one can see that there exists at least one minimum point (S∗,I∗1,I∗2,R∗) for the function ˜V(S,I1,I2,R). Define a nonnegative C2-function V:R4+→R+ by
According to inequalities (5.3)–(5.7), we obtain
Now we denote a bounded closed set as follows
where ϵ>0, and we choose ϵ sufficiently small such that the following conditions hold in the set R4+∖Dϵ
where D,F,G,H,J are all positive constants which will be determined later. Hence, R4+∖Dϵ can be divided into the following ten domains,
Obviously, R4+∖Dϵ=D1ϵ⋃D2ϵ⋃D3ϵ⋃D4ϵ⋃D5ϵ⋃D6ϵ⋃D7ϵ⋃D8ϵ⋃D9ϵ⋃D10ϵ. Our next task is to verify LV≤−1 on R4+∖Dϵ.
Case 1. If (S,I1,I2,R)∈D1ϵ, then
where
According to inequality (5.9), we obtain that LV≤−1 for all (S,I1,I2,R)∈D1ϵ.
Case 2. If (S,I1,I2,R)∈D2ϵ, then
It then follows from inequality (5.9) that LV≤−1 for all (S,I1,I2,R)∈D2ϵ.
Case 3. If (S,I1,I2,R)∈D3ϵ, then
Combining inequalities (5.8) and (5.10) we derive that LV≤−1 for all (S,I1,I2,R)∈D3ϵ.
Case 4. If (S,I1,I2,R)∈D4ϵ, then
By inequality (5.9), one can derive that LV≤−1 for all (S,I1,I2,R)∈D4ϵ.
Case 5. If (S,I1,I2,R)∈D5ϵ, then
Combining with inequality (5.9), we obtain that LV≤−1 for all (S,I1,I2,R)∈D5ϵ.
Case 6. If (S,I1,I2,R)∈D6ϵ, we have
According to inequality (5.9), we can deduce that LV≤−1 for all (S,I1,I2,R)∈D6ϵ.
Case 7. If (S,I1,I2,R)∈D7ϵ, we have
where
Combining with inequality (5.11), we can derive that LV≤−1 for all (S,I1,I2,R)∈D7ϵ.
Case 8. If (S,I1,I2,R)∈D8ϵ, then
where
By virtue of inequality (5.12), we obtain that LV≤−1 for all (S,I1,I2,R)∈D8ϵ.
Case 9. If (S,I1,I2,R)∈D9ϵ, then
where
By virtue of inequality (5.13), we can conclude that LV≤−1 for all (S,I1,I2,R)∈D9ϵ.
Case 10. If (S,I1,I2,R)∈D10ϵ, then
where
Together with inequality (5.14), one can obtain that LV≤−1 for all (S,I1,I2,R)∈D10ϵ.
Combining inequalities (5.15)–(5.24), we finally get a sufficiently small ϵ such that LV≤−1 for all (S,I1,I2,R)∈R4+∖Dϵ. Therefore the condition (C.2) of Lemma 5.1 holds. According to Lemma 5.1, system (2.3) has a unique stationary distribution and it has the ergodic property.
The conclusion is confirmed.
Consequently, we provide an estimation of lower bound for the expectation of infective population in the following theorem.
Theorem 5.3. Let (S(t),I1(t),I2(t),R(t)) be a solution of system (2.3) for any initial value (S(0), I1(0), I2(0), R(0))∈R4+. If ˆRs0>1, then
where λ2=max{c3α2γμ0+μ1+γ2+a2α1γμ0+γ+γ1,a2α1γ2μ0+γ+γ1}.
Proof. Recall the function V2 in the proof of Theorem 5.2
Apply Itô's formula to V2, then by inequality (5.2) we have
Integrate the inequality (5.26) from 0 to t and divide by t on both sides, then we obtain
where
According to the strong law of large numbers [37] and Theorem 4.1, it then follows that
Therefore,
namely, lim inft→∞⟨I1+I2⟩≥(μ0+γ+γ1+σ222)(ˆRs0−1)λ2a.s.
Remark 2. From the viewpoint of biology, the existence of stationary distribution indicates that all the compartments will be persistent in the time mean sense. As is discussed in [40], the lower bound for the expectation of infective populations in Theorem 5.3 clearly shows that the disease will prevail if ˆRs0>1.
6.
Numerical simulations and a case study of China
In this section, we provide some numerical simulations for system (2.3) to illustrate the feasibility of our theoretical results. Applying Milstein's higher order method [41] to system (2.3), we obtain the corresponding discretization equation as follows
where Δt>0, and ξk,ηk,ζk,ςk (k=1,2,...n) are independent Gaussian random variables N(0,1), and σ2i>0 (i=1,2,3,4) are the intensities of white noise.
First of all, take the data of hepatitis B of mainland China as a case study. We have provided the reported incidence rates (1/100, 000) of HBV in mainland China during 2005–2021 in Figure 1(b). Besides, the incidence rates of hepatitis B in 31 provinces are displayed in Figure 2. By comparing Figure 1(c) in [1] and Figure 2 (the data of 2007), one can see that the reported incidence rates of HBV were taken as acute incidence rates therein. It is reasonable because the clinical difference between acute and chronic HBV infections depends on the length of infection, and acute hepatitis B usually refers to the virus infection less than six months. Therefore, inspired by the method in [1], we simulate the reported incidence rates in Figure 1(b) by computing the percentage of acute infection. In the process of model fitting, we first fix the initial values such that the percentage of acute infection is close to the incidence rate 75/100, 000. Then similar to the approaches in Table 3 of [8], we fix a relatively large value of the parameter Λ. The rest of the parameters are estimated and selected partially according to the values in Table 1 of [1]. More specifically, we choose the initial value (S(0),I1(0),I2(0),R(0)) as (5000,0.4,20,10), and the parameters in model (2.3) are taken as
Then we compute the percentage of acute HBV infection by Eq (6.1), and compare it with the incidence rates of HBV in mainland China during 2005–2021. The simulation is displayed in Figure 3(a), which shows that stochastic model fits the data well by selecting appropriate parameter values. The long-term solution is given in Figure 3(b), and one can see that the incidence rate of HBV in China will remain around 50–60 per 100,000 in the long term.
More simulations are conducted to illustrate our theoretical results. Firstly, let the initial value (S(0),I1(0),I2(0),R(0))=(0.9,0.4,0.2,0.1), and we choose the parameter values in the stochastic model (2.3) as follows
It is easy to compute that
Thus, the condition of Theorem 4.2 is satisfied and the disease will tend to extinction. The numerical simulation is depicted in Figure 4.
Then we fix the same initial value (S(0),I1(0),I2(0),R(0))=(0.9,0.4,0.2,0.1), and the parameter values in the stochastic model (2.3) are taken as
One can compute that
Therefore, the condition of Theorem 5.2 is satisfied, and system (2.3) has a stationary distribution. The numerical simulation is shown in Figures 5 and 6, which indicates that the system will be persistent in mean and the disease will prevail.
7.
Conclusions and discussion
Since most realistic systems are disturbed by various stochastic factors, in this paper, we have investigated a stochastic HBV transmission model with media coverage and saturated incidence rate. To begin with, we prove the existence and uniqueness of global positive solution of system (2.3). Then we prove that hepatitis B will tend to extinction if Rs0<1 and min{μ0,μ1}>(σ21∨σ22∨σ23∨σ24)2, while system (2.3) has a unique ergodic stationary distribution if ˆRs0>1. According to the expression of Rs0 and ˆRs0, the noise intensities and mass media alert are crucial factors in the disease control. We also obtain an estimation of lower bound of the expectation for the number of infectious cases. Moreover, as a case study, we fit our stochastic model to the data of reported incidence rates of HBV in mainland China, and it is anticipated that the incidence rate of HBV in China will remain around 50–60 per 100,000 for a long time to come.
It should be mentioned that the present HBV transmission model is formulated from a standard SIR epidemic model. This modeling method often divides the total population into several compartments under the assumption that individuals are homogeneous [42]. In other words, our modeling approach is conducted on the single spatial scale, without the consideration of human behavior, contact heterogeneity, and population spatial or social structure [12]. In recent years, multiscale models have been introduced to improve the modeling of disease transmission [43]. Guo et al. [42] developed a heterogeneous graph modeling approach to describe the dynamic process of influenza virus transmission. Since the outbreak of coronavirus disease 2019 (COVID-19) throughout the world, the modeling of SARS-CoV-2 dynamics has further motivated the trends on multiscale modeling [44,45], from the small scale of the virus itself and cells to the large scale of individuals and further up to the collective behavior of populations [46]. For instance, Hayden et al. [47] extended a classical SIR model to a SIRC model by considering the coronavirus concentration in the air (denoted by C). The researchers proposed multi-scale epidemic models by linking the disease transmission to information dissemination dynamics [48] and to the behavior change dynamics [49]. Such multiscale modeling approaches provide important insights into HBV transmission dynamics.
Some interesting research topics deserve further consideration. In stochastic epidemic modeling, Gaussian white noise has been usually adopted to represent environment disturbances and to reflect the fluctuations of disease transmission. Meanwhile different types of noise has also been investigated in the literatures [50,51,52,53,54]. For instance, Lévy noise is introduced to represent some abrupt environmental shocks and disasters [53], and telephone noise (also known as telegraph noise or burst noise) can be regarded as instantaneous transitions between different regimes [54]. We hope to formulate more realistic models considering different types of noise in future research.
Acknowledgement
The authors are grateful to the anonymous referees for their valuable comments and suggestions which led to the improvement of this paper.
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: