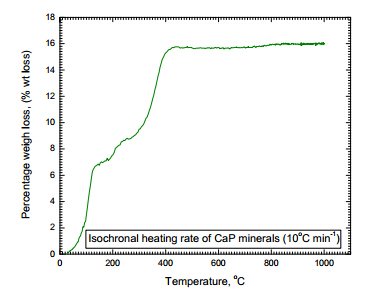
Tooth sensitivity is a common occurrence and it is caused by acid induced erosion of enamel surface. In this investigation we report the results of calcium phosphate based minerals which are irradiated with lasers ex vivo for the analysis of photo activated densification of minerals. The photo-activation in these minerals may primarily arise from the absorption centres, namely OH- and rare-earth (RE)3+ ion dopants (e.g. Er3+ ions) incorporated during synthesis. The loss of hydroxyl group from mineral is characterized using the thermogravimetric technique. The microstructural changes under the conditions of continuous wave (CW) and pulsed laser irradiation are reported together with the measured temperature rise. The preliminary data on surface hardness of occluded dentine with photo-activated calcium phosphate minerals are also reported, for aiming an eventual hardness value of 3300 MPa which is known for natural enamels.
1.
Introduction
Modeling derivative products in mathematical finance usually starts with a system of stochastic differential equation that correspond to state variables like stock, interest rate and volatility. For financial analysts, economic auditors and risk managers in financial organizations, securities analysis is very important, thus in last decades they have tried to design new models that help to change markets react and solve some problems in the market. Modeling challenges has created a common link between applied mathematicians and financial researchers as the production of knowledge in this area [4,15].
As an important model in the original Black–Scholes option valuation theory the volatility and the interest rate are both assumed constant. A popular expansion of the Black–Scholes model has been proposed by Heston. This expansion allows also for correlation between the volatility and the asset price, so that one can capture skewness effects [16]. In addition to the volatility the values of many practically important securities are sensitive to interest rates, necessitating the construction of interest rate models [17].
Consider an agent who at each time has a portfolio valued at $ X(t). $ This portfolio invests in a money market account paying a constant rate of interest $ r, $ and in a stock modeled by the geometric Brownian motion,
Suppose at each time $ t, $ the investor holds $ \Delta(t) $ shares of stock. The position $ \Delta(t) $ can be random but must be adapted to the filtration associated with the Brownian motion $ W(t), t\geq0. $ The remainder of the portfolio value, $ X(t)-\Delta(t) S(t), $ is invested in the money market account [12].
In addition to, we consider the following model which presents the system of three SDEs which they have composed from different assets called hybrid model. The asset price model in following can be viewed as an extension of the popular Heston stochastic volatility model where the interest rate is not constant but also follows a stochastic process, described here by the Hull–White model.
In this model for $ 0 < \tau\leq T $ with $ T > 0 $ the given maturity time of an option. The stocks process $ S_\tau, V_\tau, $ and $ R_\tau $ denote random variables that represent the asset price, its variance, and the interest rate, at time $ \tau $respectively. The variance process $ V_\tau $ was proposed by Heston and interest rate process $ R_\tau, $ by Cox, Ingersoll and Ross in Eq.(1.2). Parameters $ k, \eta, \delta_1, \delta_2, $ and $ a, $ are given positive real numbers and $ dW_{\tau}^1, dW_{\tau}^2, dW_{\tau}^3 $ are Brownian motions with given correlation factors $ \rho_1, \rho_2, \rho_3\in[-1, 1]. $ Also $ b, $ is a given deterministic positive function of time which can be chosen such that to match the current term structure of interest rates [12,13].
The introduction of Legendre wavelet method for the variational problems by Razzaghi and Yousefi in 2000 and 2001 [3,11,14], several works applying this method were born. The Legendre wavelets method (LWM) is transformed a boundary value problem (BVP) into a system of algebraic equations [14]. The unknown parameter of this system is the vector that its components are the decomposition coefficients of the BVP solution into Legendre wavelets basis. In this paper we apply the multi- Legendre wavelet method to solve B-S and HCIR partial differential equations.
This paper is organized as follows: In section 2, PDE models of Black-Scholes equation and Heston-Cox-Ingersoll-Ross equation have derived from SDE models, Section 3 has described properties and formulation of Legendre wavelet and Multi-dimensional Legendre Wavelet, Section4, metodology of multi-dimensional LWM is applied on PDEs that use in section 2. In section 5, numerical results and figures are presented and section 6, Conclusion is used to review.
2.
Deriving PDE models of B-S and HCIR
In his section we discuss about the B-S PDE model and HCIR PDE model that they have derived from SDE models [1,2,19].
Theorem 2.1. (Ito-Doeblin formula for Brownian motion). Let $ f (t, x) $ be a function for which the partial derivatives $ f_{t}(t, x), f_{x}(t, x) $ and $ f_{xx}(t, x) $ are defined and continues and let $ W(t) $ be a Brownian motion. Then for every $ T\geq0, $
Proof: see [6].
Remark 2.1: In the Ito- Doeblin formula we can write in differential form [6],
But
And the Ito- Doeblin formula in differential form simplifies to
Definition 2.1: let $ W(t), t\geq0 $ be a Brownian motion and let $ F(t), t\geq0 $ be an associated filtration. An Ito process as the form following
Where $ X(0) $ is nonrandom and $ \triangle(u) $ and $ \theta(u) $ are adapted stochastic process.
Lemma 2.1: the quadratic variation of the Ito process Eq.(2.5) is
Proof: see [6].
Definition 2.2: let $ X(t), t\geq0 $ be an Ito process as described in Definition 2.1 and let $ \Gamma(t), t\geq0 $ be an adapted process. We define the integral with respect to an Ito process,
Theorem 2.2. (Ito-Doeblin formula for an Ito process). Let $ X(t), t\geq0 $ be an Ito process as described in Definition 2.1 and let $ f(t, x) $ be a function for which the partial derivatives $ f_{t}(t, x), f_{x}(t, x) $ and $ f_{xx}(t, x) $ are defined and continues. Then for every $ T \geq0, $
We may rewrite Eq.(2.8),
proof: See [6].
A SDE has defined as te following
The functions $ \beta(u, X(u)) $ and $ \gamma(u, X(u)) $ called drift and diffusion respectively. Where $ t\geq0 $ final goal in these problems is to find a stochastic proces$ X(T) $ which is governed by
Under conditions of the functions $ \beta(u, x) $ and $ \gamma(u, x) $ there exists a unique process $ X(T), T\geq t $ Satisfying Eq.(2.11) and Eq.(2.12) and generally this is a SDE form of following
Where $ a(u), b(u), \delta(u) $ and $ \gamma(u) $ are non-random functions of time and we permit on the right- hand side of Eq.(2.10) is the randomness inherent in the solution $ X(u) $ and in the driving Brownian motion $ W(u). $Then the stochastic differential equation for geometric Brownian motion is
The rate of change $ \frac{dS}{S}, $ can be decomposed in to two parts in Eq.(2.14): One is deterministic, the other one is random.
The deterministic part can be modeled by $ \frac{dS}{S} = \mu dt, $ where $ \mu $ is a measure of the growth rate of the asset and random part modeled by a Brownian motion $ \delta dW(t) $ that $ \delta $ is the variance of the return and is called the volatility. The overall asset price model is then given by
Eq.(2.15), is a SDE and it can be expressed as follows
An important lemma for finding their solution is the following Ito lemma.
Lemma 2.2: Suppose $ S(t) $ satisfies the stochastic differential Eq.(2.16), and $ u(S, t) $ is a smooth function. Then $ u(S(t), t) $ satisfies the following stochastic differential equation [8].
By expanding Eq.(2.17) with applying different variables in Ito lemma to earn B-S PDE and HCIR PDE equations, as following Black-Scholes PDE equation [1].
Option transaction contract is divided into different types which the most important types are call option and put option. call option contract means that buyer have to buy the certain asset with given price in certain time, as the same way the put option contract leads to sale of asset with given price and certain time by seller. Maturity validity includes American option and European option [5]. Where $ W(t), $ is a standard Brownian motion. We also assume that interest rate are constant so that one unit of currency invested in the cash account at time $ 0 $, will be worth
at time $ t. $ We will value of call option or put option at time $ t. $ By Ito Lemma we know that,
Let us now consider a self-financing trading strategy where at each time $ t, $ we hold units $ x_{t}, $ of the cash account and $ y_{t}, $ units of the stock. Then $ p_{t}, $ value of this strategy satisfies,
We will choose $ x_{t} $ and $ y_{t} $ in such a way that the strategy replicates the value of the option the self-financing assumption implies that
Note that Eq.(2.20) is consistent with our earlier definition of financing. In particular gains or losses on the portfolio are due entirely to gain or losses in the underlying securities i.e. the cash account and stock and not due to change in holding $ x_{t}, $ and $ y_{t}. $
Returning to our derivation, we can equate times in Eq.(2.18), to obtain
If we set
that $ C $ and $ P $ are call option and put option in finance, the interval value of strategy, then it must be the case that
since call option or put option have the same dynamics this is true by construction after we equate terms in Eq.(2.19), with the corresponding terms in Eq.(2.22).
Substituting Eq.(2.22) into Eq.(2.19), we obtain the Black-Scholes PDE
In order to solve Eq.(2.23), boundary conditions must be provided in the case of call option or put option.
By applying system of Eq.(1.1) in Eq.(2.17), for construction of PDE model we need part of deterministic section of a stochastic differential equation model as,
Heston-Cox-Ingersoll-Ross PDE equation [6,7,8,9],
By Eq.(2.25) we are obtained PDE model of the HCIR equation.
3.
Construction of multi-dimensional Legendre wavelet
In this study Legendre wavelet well-addressed in [5,10,18], are employed.The wavelet basis is constructed from a single function, which is called the mother wavelet. These basis functions are called wavelets and they are an orthonormal set. One of the most important wavelets is Legendre wavelets. The Legendre wavelets are obtained from Legendre polynomials. In the past decade special attention has been given to applications of wavelets. The main characteristic of Legendre wavelet is that it reduces to a system of algebraic equation.
The function $ \psi (x) \in L^2 (R) $ is a mother wavelet and $ \psi (x)_{uv} = \vert u\vert ^\frac{-1}{2}\psi(\frac{x-v}{u}) $ which $ u, v\in R $ and $ u\neq 0 $ is a family of continuous wavelets. If we choose the dilation parameter $ u = a^{-n} $ and the translation parameter$ v = ma^{-n} b $ where $ a > 1, b > 0, n $ and $ m $ are positive integer, we have the discrete orthogonal wavelets set.
The Legendre wavelet is constructed from Legendre function [4,15]. One dimension Legendre wavelets over the interval $ [0, 1] $ are defined as,
With $ n = 1, 2..., 2k-1, m = 0, 1, 2, ..., M-1. $ In Eq.(3.1) $ P_{m} $ are ordinary Legendre functions of order defined over the interval [-1, 1]. Legendre wavelet is an orthonormal set as,
The function $ f(x) \in L^{2}([0, 1] \times [0, 1]), $ may be expanded as the following,
Now we defined four dimensions Legendre wavelets in $ L^{4} ([0, 1]\times[0, 1]\times[0, 1]\times[0, 1]), $ as the form
that
Four dimensions Legendre wavelets are orthonormal set over $ [0, 1]\times[0, 1]\times[0, 1]\times[0, 1]. $
The function $ u(x, y, z, q)\in L^{4}([0, 1]\times[0, 1]\times[0, 1]\times[0, 1]), $ can be expanded as fallows
Where
The truncated version of Eq.(3.6), can be expressed as the following,
Where $ C $ and $ \Psi (x, y, z, q), $ are coefficients matrix and wavelets vector matrix, respectively. The dimensions of those are $ \lbrace\prod _{i = 1}^{4}(2^{k_{i}-1}M_{i})\rbrace\times1, $ and are given as the form
and also
The integration of the product of four Legendre wavelet function vectors is obtained as
Where $ I, $ is diagonal unit matrix.(All of procedures in section 3, are established)
Lemma 3.1: if $ h\in C ([0, T], L^{2}[0, 1]) $ then the functions $ C_{n, m}(t) $ are continuous on $ [0, 1] $ [13].
Lemma 3.2: if $ h\in C^{1} ((0, T), L^{2}[0, 1]) $ then the function $ C_{n, m}(t) $ coefficient belong to $ C^{1} (0, T), $ furthermore if $ \frac{\partial h}{\partial t} \in L^{2}((0, T), L^{2}[0, 1]) $ then,
Proof: see [13].
3.1. Operational matrix of integration
The integration matrix for one variable $ x, $ define as follows
In which
$ P_{x}, $ is a $ 2^{k_{1}-1}2^{k_{2}-1}2^{k_{3}-1}2^{k_{4}-1} M_{1}M_{2}M_{3}M_{4}\times 2^{k_{1}-1}2^{k_{2}-1}2^{k_{3}-1}2^{k_{4}-1} M_{1}M_{2}M_{3}M_{4} $ matrix and $ L, F $ and $ O, $ are $ 2^{k_{1}-1} \times M_{1} \times2^{k_{2}-1} \times M_{2} \times 2^{k_{3}-1} \times M_{3}\times 2^{k_{4}-1} \times M_{4} $ matrices [14]. (In case of two variables Eq.(3.10), is established clearly).
Theorem 3.1. A function $ f(x, y, z, l) \in L^{4}([0, 1)\times [0, 1)\times[0, 1)\times[0, 1)) $ is with bounded second derivative say $ \vert f^{\prime\prime }(x, y, z, l) \leq M, $ can be expanded as an infinite sum of Legendre wavelets and the series converges uniformly to the function $ f(x, y, z, l) $ that is [15],
Proof:
we have proved this theorem for multi-dimension states as following,
Now let,
then,
with get out the constants as followes
and polynomials are substituted
Constants in terms of polynomials are calculated with the others,
that,
Using integration properties as following,
Upper bounds are noted as,
Now $ (2m_{1}-1)^{2} < (2m_{1}+3)^{2}, $ and $ (2m_{1}+1)^{2} < (2m_{1}+3)^{2}, $ then
Therefore we have,
Thus the series $ \sum _{n_{1} = 1}^{\infty}\sum _{m_{1} = 0}^{\infty} \sum _{n_{2} = 1}^{\infty}\sum _{m_{2} = 0}^{\infty}\sum _{n_{3} = 1}^{\infty}\sum _{m_{3} = 0}^{\infty}\sum _{n_{4} = 1}^{\infty}\sum _{m_{4} = 0}^{\infty}c_{n_{1, .., 4}, m_{1, .., 4}}, $ is ab-solute convergent, it follows that
convergence to the function $ f(x, y, z, l), $ uniformly.
Notice: This result for two dimensions in theorem $ (3.1), $ is calculated as upper bound,
4.
Methodology for B-S and HCIR PDEs
In this methodology section, the Black-Scholes model for American put problem have used in the form of moving-boundary problem.
Lemma 4.1: For American options, we have [5,6]
ⅰ) The optimal exercise time for American call option is $ T $ and we have
ⅱ) The optimal exercise time for American put option as earlier as possible, i.e. $ t $ and we have
ⅲ) The put-call parity for American option:
As a consequence,
Letting $ S $ be the price of an asset $ A $ at time $ t $ the American early exercise constraint leads to the following model for the value $ P(S, t) $ of an American put option to sell the asset $ A. $
Where $ S(\overline{t}) $ represent the free boundary. The parameters $ \delta, r $ and $ E $ represent the volatility of the underlying asset, the interest rate, and the exercise price of the option. And the partial differential equation (PDE) associated with Eq.(2.25) for the fair values of European- style options forms a time- dependent connection- diffusion- reaction equation with mixed spatial- derivative terms.
On the unbounded three- dimensional spatial domain $ S > 0, v > 0, r > 0 $ with $ 0 < t\leq T. $ $ u(S, v, r, t) $ denotes the fair value of a European- style option if at the time $ \tau = T-t $ the asset price, its variance, and the interest rate be equal to $ S, v $ and $ r $ respectively. Eq.(4.2) is known as the Heston- Cox- Ingersoll- Ross (HCIR) PDE. This equation usually appears with initial and boundary conditions which are determined by the specific option under consideration. Initial conditions in European call options equation is usually as follows,
With a given strike price $ k > 0. $
In this methodology section the Eq.(4.1) and Eq.(4.2), have been solved using two dimensional and four dimensional Legendre wavelets respectively,
First we assume for B-S PDE,
With boundary condition $ P(S, 0) = \beta_{1} (S, t), $ and $ \frac{\partial P(S, 0)}{\partial t} = \beta_{2}(S, t). $
Those coefficients of $ \alpha_{i} $ the same parameters and variables which be in Eq.(4.1), in practice they will be calculate with this technique in follow.
Integrating (4.4) with respect to second variable over $ [0, t], $ we get
And also
We have also
Substituting Eqs.(4.4) to (4.8) in Eq.(4.1), we obtain
The solution of B-S PDE, $ P(S, t) $ can be calculate when Eq.(4.9) can be solved For unknown coefficients of the vector $ C(S, t). $
Let for HCIR PDE in Eq.(4.2), we assume as following,
Also with boundary condition
and
Parameters of Eq.(4.2), by using method as following,
Integrating right hand side in Eq.(4.10), with respect to differential equations over [0, t] we get As well as
We have
And also
Substituting (4.11) to (4.14) in (48), we obtain
This system can be solved for unknown coefficients, which are calculated,
5.
Numerical results
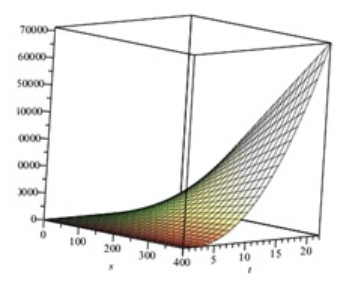
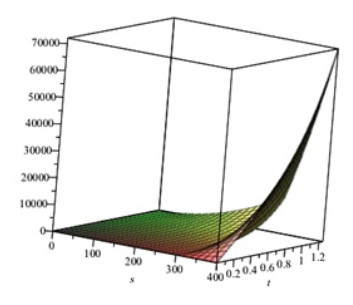
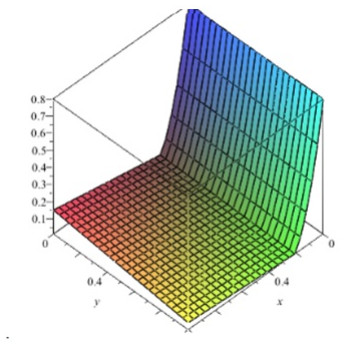
In this section, values of parameters are used in B-S PDE model (Figure 1): $ k_{1} = k_{2} = 1, r = 0.2, E = 0.2, \delta = 0.001, $ and HCIR PDE model (Figures 2 and 3): $ k = 0.1, \eta = 0.12, \rho_{12} = 0.6, \rho_{13} = 0.2, \rho_{23} = 0.4, \delta_{1} = 0.04, \delta_{2} = 0.03, $ respectively. Appling values of parameters in models, numerical results are calculated. Due to the accuracy and convergence of spectral method which has been reviewed in $ [0, 1], $ the numerical results obtained from this method can be assured. Therefore it can be used for future scams to compare with the same methods.
By choosing $ M = 2, 4 $ and $ k = 1 $ in Eq.(2.23) and $ M = 1, 2 $ in Eq.(2.25) the models are solved from the coefficients vector of C that was found. Then the results were compared by Adomian decomposition method (ADM), as a semi-analytical method [20,21]. Tables 1 and 2 give values of pricing options solutions in B-S and HCIR models.
6.
Conclusion
The multi-dimensional Legendre wavelet method has been applied to solve the Black-Scholes and Heston-Cox-Ingersoll-Ross models which these PDE equations have been derived from stochastic differential equations by using one of the important stochastic calculous Lemma named Ito. Generally the present method (LWM) reduces the partial differential equation into a set of algebraic equation and it can be useful in high degree derivatives problems, therefore considering the properties and using structure of LWM leads to save the time. Multi- dimensional Legendre wavelet is orthonormal set and its integration of the product is a diagonal matrix as in the case of the one dimension Legendre wavelet. In addition the Theorem 3.1 has been proved in paper which it could be determine an upper bound for coefficients of vector $ C $. Also in this work results of LWM have been compared with the Adomian Decomposition Method (ADM) as a semi-analytical method and they have been shown for different parameters in Tables 1–2 and Figures 1–3, finally.
Conflict of interest
The authors declare that there is no conflicts of interest in this paper.









 DownLoad:
DownLoad: