1. Introduction

The majority of the engineering materials such as metallic alloys, ceramics, composites and granular media are heterogeneous in nature. Such materials possess complex microstructures spanning a wide spectrum of length scales, which determine their macroscopic properties and performance [1, 2, 3, 4]. The growing dem and s in global sustainability, national security, and renewable energy have raised great challenges in the design and development of multifunctional materials that can achieve optimal performance under extreme conditions [5, 6]. The success of such a mission strongly relies on our ability to characterize and modify material properties and behaviors under a myriad of external stimuli. This in turn depends on our intrinsic underst and ing and knowledge of complex microstructures and how they evolve under various conditions, which make it extremely important to accurately characterize and model material microstructures.

Advances in experimental methods, analytical techniques, and computational approaches, have now enabled the development of three dimensional (3D) structural analyses [7]. The study of 3D microstructures under an external stimulus (e.g., stress, temperature, environment) as a function of time (4D) is particularly exciting. Examples include an underst and ing of time-dependent deformation, crack initialization and propagation, phase transformations, compositional evolution, magnetic domain separation, etc. Furthermore, advances in 3D and 4D computational tools and structure analysis methods have enabled the analysis of large experimental data sets, as well as simulation and prediction of material behavior [8, 9, 10].

On the experimental side, x-ray tomography has become an extremely attractive, non-destructive technique for characterizing microstructures in 3D and 4D [11, 12, 13, 14, 15, 16, 17, 18, 19]. The use of high brilliance and partially coherent synchrotron light allows one to image multi-component materials from the sub-micrometer to nanometer range. In a typical tomography experiment, 2D projections are obtained at small angular increments, from which tomographic reconstruction techniques such as the filtered-back-projection algorithm (FBP) [11] can be employed to generate a grayscale image of the material microstructure. However, the FBP reconstruction method usually requires a very large number of projections to render a raw 3D image, and further segmentation and thresholding analysis are needed to resolve details of individual material phases and produce accurate digital representations of the microstructure in 3D. These strongly limit its application in characterizing rapidly evolving materials (i.e., 4D materials science). Alternative reconstruction methods that directly render accurate 3D or 4D microstructure models from limited tomography data (e.g., a very small number of projections) without segmentation are thus highly desirable.

For system with low adsorption contrast between the phases, such as a polycrystalline material, x-ray tomography cannot sufficiently resolve the 3D phase morphology (e.g., the distribution of grain orientations). In such cases, a common practice is to use serial sectioning to reconstruct the 3D material from 2D electron-back-scattered-diffraction (EBSD) micrographs of the material’s surfaces [20, 21]. This technique, which involves extensive surface polishing, image smoothing and image alignment, is extremely time consuming and tedious. Thus, developing efficient statistical morphological descriptors [3, 22, 23] that capture the key structural features of the materials from a h and ful of 2D images and that enable one to reconstruct accurate 3D virtual microstructure models from such limited information will significantly improve the efficiency in characterizing polycrystalline materials.

In this paper, we present a general computational framework that enables one to generate realistic 3D microstructure models from limited morphological information, such as limited angle tomographic projections and 2D micrographs, via stochastic optimization. This framework is based on the stochastic microstructure reconstruction procedure originally devised by Yeong and Torquato [24, 25], and further generalized by Jiao, Stillinger and Torquato [26, 27, 28]. Specifically, we consider that the 3D microstructure is represented as a 3D array, whose entries indicate the local state of that voxel (e.g., the phase the voxel belongs to). The limited structural data obtained in various experiments correspond to different mathematical transformations of the 3D array (see Sec. 2 for details). Thus, generating or reconstructing the 3D material structure from such limited data can be formulated as an inverse problem in which one recovers the original 3D array, given the transformation and the resulting data. The utility of our general framework is illustrated by reconstructing a polycrystalline microstructure from 2D EBSD micrographs and a binary metallic alloy from limited angle projections.

The rest of the paper is organized as follows: In Sec. 2, we present the general mathematical formulation for the reconstruction framework and a stochastic procedure for solving the general inverse problem. In Sec. 3, we illustrate the utility of the framework by reconstructing a polycrystalline microstructure from 2D EBSD micrographs and a binary metallic alloy from limited angle projections. In Sec. 4, we provide concluding remarks.

2. Inverse Microstructure Reconstruction

Accurate rendition of 3D microstructure is long st and ing in computational materials. A variety of reconstruction schemes have been developed that enable one to generate material microstructure models from limited structural information. Examples of such schemes include the Gaussian r and om field method [29], phase recovery method [30], multi-point reconstruction method [31], and raster-path method [32], to name but a few. The Gaussian r and om field method [29] was originally devised to reconstruct realizations of statistically homogeneous and isotropic r and om media from the associated two-point correlation functions (see Sec. 2.1 for definitions and discussion of the correlation functions). The phase recovery method enables one to take into account the full vector information contained in the two-point statistics associated with the material, and thus allows the reconstructions of complex anisotropic microstructure and polycrystalline materials [30]. The multi-point reconstruction method was originally developed for the reconstruction of porous geomaterials from 2D images [31]. Instead of using two-point statistics associated with the entire 2D microstructure, this method incorporates all n-point statistics within a smaller window containing portions of the 2D microstructure. The recently developed raster-path method allows one to employ the multi-point statistics in a much more efficient way [32]. Specifically, instead of extracting the statistics from the 2D microstructure, a cross-correlation function is introduced to directly compare a reconstructed portion of the material to the target 2D image.

All of the aforementioned reconstruction methods require specific structural information as input and thus, are system dependent. Another widely-used reconstruction method is the stochastic optimization procedure devised by Yeong and Torquato [24, 25]. In its original implementation, the Yeong-Torquato (YT) procedure enables one to incorporate an arbitrary number of correlation functions of any type (see Sec. 2.1 for details) into the reconstructions, which is formulated as an inverse optimization problem. Although the correlation functions are a special type of structural information, we will see in the subsequent section that this procedure can be generalized to incorporate a wide class of different types of structural information, as long as a mathematical transformation that maps the material microstructure to the given information can be defined.

2.1. Mathematical formulation

Consider a digitized representation of a 3D material by a 3D array M, whose entry value M_ijk indicates the local state of that voxel (e.g., the phase that the voxel belongs to). An experiment performed to probe the material microstructure generates a set of structural data, which we noted by D. In general, a mathematical transformation F can be defined, which maps the 3D array to the structural data set, i.e.,

D = F { M }

(1)

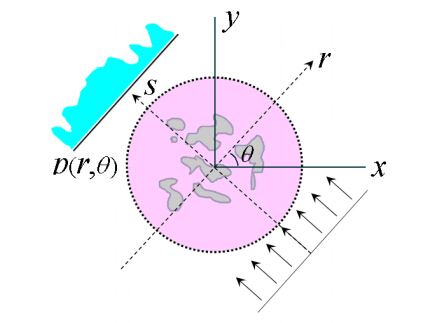
In the case of x-ray tomography, the structural data D are 2D projections of the original 3D microstructure from different angles. The 3D material can be completely determined once the attenuation coefficient associated with every voxel (i.e., the phase associated with that voxel) is known. Thus, the entries of the 3D array representing the material M are the attenuation coefficient values associated with different phases in the material. The intensity of the projection (i.e., the value of an entry of D) associated with angle θ at position r is given by,

$${\bf{D}} (r,\theta ) = {I_0}\exp \left[ { - \int {{\bf{M}} (x,y,z) d{\bf{s}}} } \right]$$

(2)

where I₀ is initial intensity of the incident rays without attenuation and s is the path along which the ray travels (see Figure 1). Given a sufficient number of 2D projections (acquired with small angle increments, typically several thous and projections over an interval from 0 to π) , computed tomographic reconstruction techniques, such as filtered-back-projection method, can be employed to directly inverse the integral transformation in Eq. (2) to recover the 3D distribution of the attenuation coefficients (i.e., material phases) , and thus, the 3D microstructure. However, such methods could not lead to accurate reconstructions when only limited angle projection data (e.g., a h and ful of projections) are available.

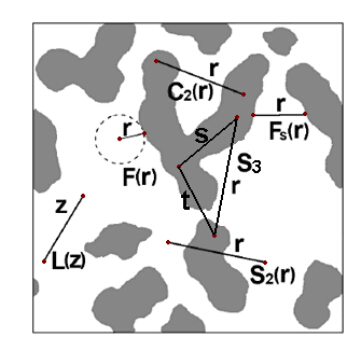
In the case of 2D micrographs, the structural data set D contains spatial statistics sampled from the micrographs which are assumed to be representative of the original 3D microstructure M. Specifically, spatial correlation functions associated with the material’s phases can be used as D for 3D reconstructions. Examples of such statistical structural descriptors include the st and ard n-point correlation functions S_n [3], which provides the probability of finding a particular n-point configuration (i.e., a polyhedron with n vertices) in the bulk phase of interest. The surface correlation functions F_s [3, 33] are associated with the probability of finding an n-point configuration with a subset of points falling on to the surface, while the others lie in the bulk of the phase of interest. The lineal-path function L [3, 34] gives the probability of finding a line segment of a specific length entirely lying in the phase of interest. The pore-size function F [3, 35, 36] provides statistics of the size of the largest spherical region centered at a r and omly selected point in the phase of interest that entirely lie in this phase. The functions L and F respectively contain linear and spherical topological connectedness information of the phases of interest, which can be obtained from the 2D micrograph. The n-point cluster function C_n, [3, 37] is associated with the probability of finding a particular n-point configuration in the same cluster of the phase of interest, and thus, contain complete topological connectedness information of the phases of interest. However, C_n for a 3D material cannot be obtained from 2D micrographs. Figure 2 schematically illustrates the probability interpretation of the aforementioned st atistical microstructural descriptors. Detailed discussion of these correlation functions can be found in Ref. [3]. It is noteworthy that these descriptors have been employed to successfully model [38, 39] and design [40, 41] engineering materials.

For a general heterogeneous material, the microstructure M can be represented as a collection of binary arrays M ⁽ⁱ⁾ , in which the voxels associated with phase i possess a value of 1 and 0 otherwise. For statistically homogeneous and isotropic microstructures, the two-point correlation function S₂ (r) associated with phase i, which is the probability of finding two points separated by distance r both falling into phase i, can be obtained as follows:

$${S_2} (r) = \frac{1}{{4\pi }}\int {\left[ {\frac{1}{V}\int {{M^{ (i) }} ({\bf{x}}) {M^{ (i) }} ({\bf{x}} + {\bf{r}}) d{\bf{r}}} } \right]} d\Omega$$

(3)

where V is volume of the material and Ω is the solid angle in 3D. For such materials, it has been shown that S₂ (r) sampled from 2D images or slices is representative of the full 3D microstructure, and thus, can be used to reconstruct the 3D material microstructure. Similarly, the surface correlation functions F_s, lineal-path function L and pore-size function F sampled from 2D micrographs can also be used as structural data for 3D reconstruction, i.e., we have D = { S_n, F_s, L, F }.

2.2. Stochastic optimization for reconstruction

To reconstruct 3D microstructure M from the limited data set D and the associated transformation F, we generalize the Yeong-Torquato (YT) procedure [24, 25] originally devised to generate virtual 3D microstructures from a specific set of correlation functions discussed in Sec. 2.1. In particular, the reconstruction problem is formulated as an “energy” minimization problem, with the energy functional E defined as the squared “difference” between the available data set D and a corresponding set D* measured from a trial microstructure M*:

E = | D - D* |2

(4)

where D = F { M } and D* = F { M* }. The squared difference can be defined as the sum of squared differences between corresponding data points in D and D*. For example, in the case that the data set contains the spatial correlation functions, i.e., D = { $\overline {{f^\alpha }} (r)$}, the energy has the following form:

$$E = {\sum\limits_\alpha {\sum\limits_r {\left[ {{f^\alpha } (r) - \overline {{f^\alpha }} (r) } \right]} } ^2}$$

(5)

where $\overline {{f^\alpha }} (r)$ is a target correlation function of type α and ${f^\alpha } (r)$ is the corresponding function associated with a trial microstructure.

The simulated annealing method [45] is usually employed to solve the aforementioned minimization problem. Specifically, starting from an initial trial microstructure M_o (i.e., old microstructure) which contains a fixed number of voxels for each individual phase consistent with the volume fraction of that phase, two r and omly selected voxels associated with different phases are exchanged to generate a new trial microstructure M_n. The transformation F is applied to both M_o and M_n to obtain the associated data set D_o and D_n, which are then compared to the experimentally measured structural data D. The energies E_old and E_new, which are associated with the old and new trial microstructures, repressively, are then evaluated using Eq. (4). The energy values determine whether the new trial microstructure should be accepted or not via the probability:

$${p_{acc}} (old \to new) = \min \left\{ {1,{\rm{ }}\exp \left ( {\frac{{{E_{old}}}}{T}} \right) /\exp \left ( {\frac{{{E_{new}}}}{T}} \right) } \right\}$$

(6)

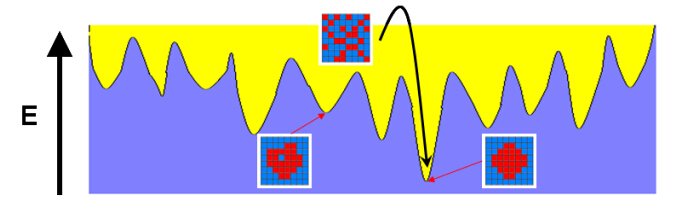
where T is a virtual temperature that is chosen to be initially high and slowly decreases according to a cooling schedule [24, 25]. Initially, T is chosen to be high in order to allow a sufficiently large number of “up-hill” (energy increasing) trail microstructures. As T gradually decreases, the “up-hill” moves become less favorable. This procedure significantly decreases the chances that the final microstructure gets stuck in a shallow local energy minimum, as illustrated in Figure 3. In practice, it is usually extremely difficult for the system to converge to the global minimum. Thus, the annealing process is considered complete if E is smaller than a prescribed tolerance, e.g., E* = 10^-6 here.

In general, an extremely large number of trial microstructures need to be searched during the reconstruction, and for each trial microstructure M* the associated structural data D* need to be computed by performing the transformation on M* in order to evaluate the energy. Therefore, efficient methods have been devised to re-compute D* of a new trial microstructure from that of the old trial microstructure, using the fact that only a single pair of voxels are switched to generate the new microstructure from the old one and thus, only a small portion of D* is affected [28, 43, 44].

3. Illustrative Examples

In this section, we demonstrate the utility of our general framework by employing it to reconstruct 3D solder materials from limited structural information. Specifically, we will reconstruct the 3D polycrystalline microstructure of a portion of a pure tin joint from 2D electron back scattered tron back scattered diffraction (EBSD) experimendiffractionmicrographs and reconstruct a 3D lead-tin alloy from limited angle projections.

3.1. Reconstructing polycrystalline microstructure from 2D micrographs

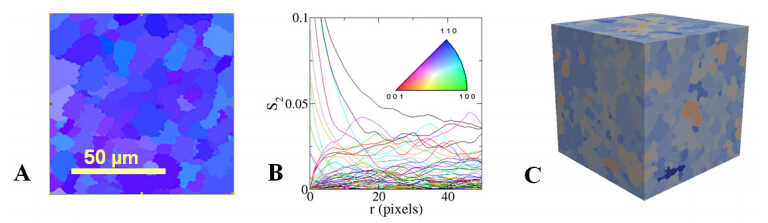
Tin has been widely used as solider materials in electronic packaging [45]. Due to heterogeneous cooling and the existence of intermetallic particles, a pure tin solder joint usually processes a polycrystalline microstructure. The physical properties of the joint are largely determined by the grain size distribution and the grain orientations. Such structural information can be obtained via electron back scattered diffraction (EBSD) experiments (see Fig.ure 4A). However, the EBSD imaging technique only allows one to probe essentially the surface of the material sample. Therefore, serial sectioning is required to acquire successive 2D images at different depth of the polycrystalline structure. A final reconstruction can be obtained by carefully stacking these 2D images via image alignment.

Our framework provides an alternative approach to generate virtual 3D polycrystalline structure models from single or a few EBSD images of the material surface. Specifically, the almost continuous distribution of grain orientations is “coarsened” such that the polycrystalline microstructure is represented as a multiphase structure, with each phase associated with a narrow range of orientation values. In practice, the original colored EBSD image is converted to a gray-scale image, which is then thresholded according to the gray value of each pixel to produce a multiphase material structure for further analysis. The morphology of each phase includes compact regions (i.e., grains) that are associated with a specific narrow range of orientations. The two-point correlation functions S₂ associated with the individual phases are computed (see Figure 4B). Under the assumption that the structure is statistically homogeneous and isotropic, the sampled S₂ from 2D images are representative of the full 3D microstructure (i.e., the morphology of different grains) and thus, can be used to generate 3D reconstructions.

Figure 4C shows the reconstructed 3D polycrystalline material (i.e., a multiphase structure) using S₂ of the phases, including both the autocorrelation functions (i.e., spatial correlations within each phase) and cross-correlation functions (i.e., spatial correlations between different phases). The reconstruction process is terminated when the energy E is smaller than 10^-4, which means that the sum of squared difference between the target and reconstructed correlation functions are small than 10^-4. Therefore, the target and reconstructed correlation functions are virtually identical to one another and thus, cannot be distinguished on the plot scale in Figure 4B. The reconstruction statistically reproduces the key structural features including the size and shape of the grains and the orientation correlation between neighboring grains (i.e., the cross-correlation functions) , as can be seen by comparing the surfaces of the 3D virtual microstructure to the target 2D image. These results suggest that S₂ alone would be sufficient to model this polycrystalline material as a multiphase structure. We emphasize that a quantitative comparison between the reconstructions and experimentally obtained 3D structure is necessary to definitely ascertain the accuracy of the reconstructions. However, the latter is currently not available.

3.2. Reconstructing binary metallic alloy from limited angle projections

Conventional tomography reconstruction algorithms such as the filtered-back-projection method usually require an extremely large number of 2D projections as input, and can only yield a gray-scale image, for which extensive post-processing including image segmentation is required to generate a 3D microstructure model. On the other h and , our framework only requires a h and ful of projections (usually 20 ~ 40) and can directly produce an accurate 3D microstructure without post-processing.

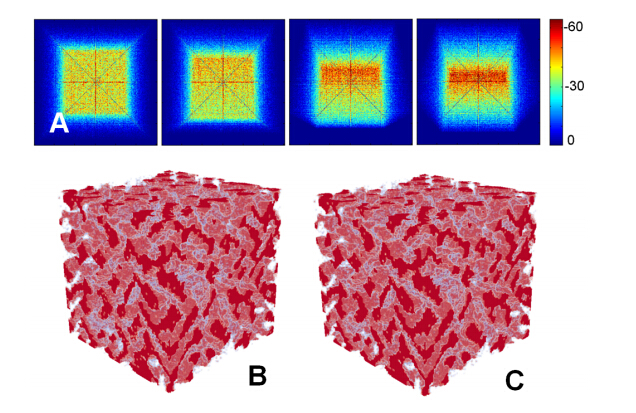
Figure 5B shows a 3D lead-tin alloy microstructure, which is our target system. The 2D projections associated with the binary structure at selected angles in cone-beam geometry are shown in Fig. 5A. We note that these simulated projections are obtained by sending virtual rays through the material in vacuum and recording the total attenuation values on a virtual detector. Thus, the projection intensity corresponds to the value of the total attenuation at that point. Figure 5C shows the reconstructed alloy microstructure using 30 projections associated with angles evenly distributed over the interval [0, π], which is visually indistinguishable from the target microstructure. Quantitative comparisons between the target and reconstructed microstructure indicate that there are less than 3% of mis-placed voxels in the reconstruction. These results clearly demonstrate the accuracy and robustness of our stochastic reconstruction framework using limited-angle projections.

4. Concluding Remarks

We have presented a general computational framework that enables one to generate realistic 3D microstructure models from limited morphological information via stochastic optimization. In our framework, the 3D microstructure is represented as a 3D array, whose entries indicate the local state of that voxel. The limited structural data obtained in various experiments correspond to different mathematical transformations of the 3D array. Thus, generating or reconstructing the 3D material structure from such limited data can be formulated as an inverse problem in which one recovers the original 3D array, given the transformation and the resulting data. A general stochastic microstructure reconstruction procedure has been provided which evolves a trial microstructure to minimize the difference between the corresponding structural data and the experimental structural data, such that the final reconstructed microstructure possesses the target experiment data. The utility of our general framework has been illustrated by reconstructing a polycrystalline microstructure from 2D EBSD micrographs and a binary metallic alloy from limited angle projections, which also demonstrated the versatility and robustness of our procedure.

Although only limited-angle 2D projections and 2D micrographs were used as limited structural data to illustrate our general framework, it is straightforward to apply the framework to reconstruct 3D materials from other limited data. For example, stochastic optimization procedures have been successfully applied to study the phase separation of a fluid in nano-porous materials from limited small-angle x-ray scattering (SAXS) data [46].

Importantly, our computational framework also has ramifications in 4D materials science (e.g., charactering microstructural evolution over time). Since only limited structural information is required for our reconstruction procedure, the time needed for accquring structural data in experiments can be significantly reduced (e.g., accquring 2000 tomography projections vs. 20 projections). This enables one to increase the temporal resolution and thus, to study rapidly evolving materials. In addition, characterizing of the evolution of grain orientation distributions and associated structural features in a 3D polycrystalline material [47, 48] is almost not possible to achieve using serial sectioning method. However, one can model such process from the limited structural information contained in the 2D micrographs using our framework. We will report the applications of our framework in 4D materials science in future publications.

Acknowledgements

The author is very grateful to Hechao Li for his help with creating Figure. 5. This work was supported by the Division of Materials Research at National Science Foundation under award No. DMR-1305119. The author also thanks Arizona State University for the generous start-up package.