Geotechnical characterization of index and deformation properties of Stockholm clays

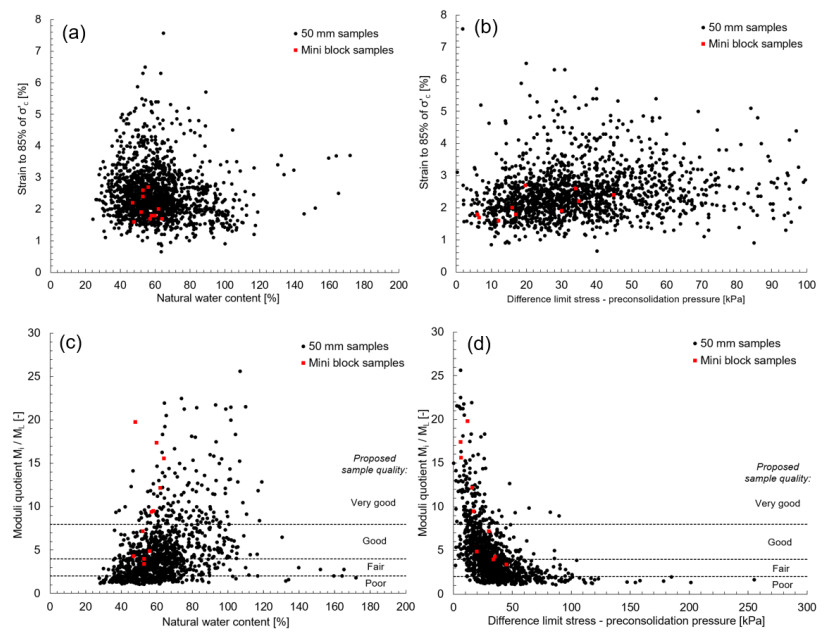
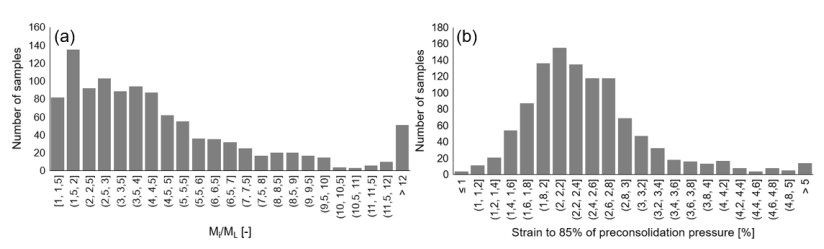
1.   Introduction

In the mid-19th century, the English physician John Snow ^[9] refused to accept the theories of cholera infection prevailing at that time. Both the sharing of clothing and transmission through the air seemed to him to be insufficient explanations for what was happening in London, under an epidemic that was undermining the entire population of any social class. He established a famous practical example of spatial epidemiology, measuring the distances of each patient to the nearest water source.

Not only Covid-19 ^[11,22], but many other infectious diseases ^[6] are forcing us, in general, to rethink new techniques for describing and discovering spatial epidemiology, that is, "the description and analysis of geographic variations in disease with respect to demographic, environmental, behavioral, socioeconomic, genetic, and infectious risk factors" ^[10]. To this end, we can draw on data that reflect human behavior in terms of spatial location and movement. In particular, geolocation data ^[24], which includes geographical location information associated with the hosting device (e.g., mobile phone), is key for modeling the spread and evolution of infectious diseases in space and time.

Using this kind of data, we cannot only track the movement patterns of individuals, but also derive general mobility patterns for the population over time. They give insight into, e.g., "the prediction of future moves, detecting modes of transport, mining trajectory patterns and recognizing location-based activities" ^[13]. That is, geolocation data is key data computational spatial empidemiologic models and simulations.

The idea that a microscopic coronavirus in the city of Wuhan has caused an economic crisis in Europe reminds us of Edward Lorenz's famous speech at MIT, where he raised how the flapping of a butterfly in Brazil could cause a tornado in Texas. That is, the well-known butterfly effect and its repercussions on chaos theory.

In this work, data about spatial population movement such as geolocation data are used as key sources of insight in the way infectious diseases spread in space and time among individuals. To this end, this work proposes a mathematical foundation following an inverse methodology on the chaotic bases ^[18] since it raises the search of the starting attractor or "patient zero". This procedure collects the ideas of reverse engineering, as a way of establishing the unknown initial parameters of a problem whose solutions and effects are known.

In particular, tracking and analyzing population movements are key to get insights about patterns of propagation of environmentally-transmitted pathogens. For example in the case of Covid-19, "[...] changing geography of migration, the diversification of jobs taken by migrants, the rapid growth of tourism and business trips, and the longer distance taken by people for family reunion are what make the spread of COVID-19 so differently from that of SARS" ^[19].

To this end, we introduce a graph-based approach to model population movements in space and time, including a health status of individuals that allows us to classify risks for individuals as well as spatial locations and temporal periods.

The main methods to be used will be differential geometry of curves adapted to the symptomatology of the disease and graph theory for its representation and monitoring ^[16]. In its inverse reasoning, we can establish algorithms that, e.g., facilitate finding a "patient zero", classify possible originators of the contagion ^{[1,3,12,17,20]}, or classify spatial locations with respect to the spread of pathogens.

2.   Concept

As a key source of human mobility patterns, we consider mobile phone location data. The high penetration of mobile phones in the population allows a very representative survey of mobility dynamics ^[14].

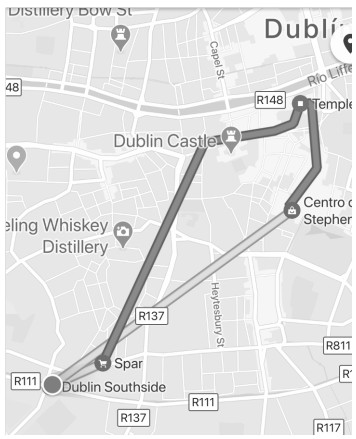
The trajectories on which we base the monitoring of population movements are those recorded by the smartphones devices with GPS. We know that both smartphones and social networks ^[23] have the ability to store the paths followed by their owners, just as telephone companies can track that path followed by their customers ^[7,8]. This information is collected both by these devices and by the telephone companies, and can be represented geospatially by the different navigation systems. As an example we can see the path followed by an smartphone and represented in Figure 1 using Google Maps software:

Definition 2.1. For every patient $P$ we distinguish three disjointed and sequential time intervals (as can be seen in the medical graphs in Figure 2) that we will note by:

1. $H$: where the person is "healthy". In the timeline it will be distinguished by a simple line and during this interval ^[5] (before infection) the value of the state variable will be $1$.

2. $C$: where the person is "contagious" (incubation period). This interval or latency period will be estimated, given the patient's symptoms, based on the maximum and minimum time it could take to become "ill". It will be represented by a double line and its state variable will be $2$. Currently this period is from 0 to 7 days aproximately.

3. $I$: where the patient is "ill". It will be represented by a triple line, together with the previous one completes the incubation time ^[21] and its state variable will be $3$.

Definition 2.2. To establish the path we use the notation of differential geometry by using Cartesian coordinates, incorporating the state variable over time $\rho(t)\in\{1, 2, 3\}$ remaining:

and whose graph is represented in Figure 3.

Definition 2.3. We will say that a contagion has occurred if, given two patients $P_i$ and $P_j$ it is fulfilled:

● the paths cross in a sufficiently close environment, i.e. there is a maximum transmission distance $M$ such that:

To simplify the calculation, without loss of generality, we will consider that this distance $M$ is null, or what is the same, they are in the same place. With this we have:

● one patient's status must be "contagious" and the other patient's status must be "ill", i.e., $t\in C$ for $P_i$ and $t\in I$ for $P_j$ or vice versa. This is simplified as $\rho_i(t) \cdot \rho_j(t) = 6$ (product of a state that is "contagious" by another "ill").

We will note the contagion between both patients as $P_i \sim P_j$.

Notation 2.4. The point of infection of each patient $P$ will be identified with the symbol $\otimes$ and its coordinates will be $\vec{\otimes} = (x, y, n, t)$ where:

● $x$ and $y$ are the cartesian coordinates of the place of infection

● $n$ is the variable where the number of infections produced in this place is accumulated.

● $t$ is the variable that indicates the furthest moment in which the contagion occurred in this place.

It can be seen in the contagion graph of Figure 4 that a different situation occurs at each confluence $\otimes_i$ since in

$\otimes_1$ Both patients are healthy

$\otimes_2$ The second patient $P_2$ has been infected by the first $P_1$

$\otimes_3$ The first patient $P_1$ is still "healthy" after meeting the second $P_2$ who is ill. They may not have coincided in time at this intersection and the first one was not in a "contagious" state.

$\otimes_4$ Here both patients are already "ill"

3.   Modelization

Procedure 3.1 (Intersections analysis). Given two different paths, $\vec{\alpha}_i$ and $\vec{\alpha}_j$, these can be subdivided into segments, being considered therefore as polygonal ^*. Hence, the analysis of intersections is restricted to the calculation of common points between two segments of different paths ^[16]. Let us consider the segments between points:

^*A polygonal sufficiently close to the curve is considered. Its existence is assured by Schoenflies theorem for polygonal Jordan curves. This concept also appears in the formulation of the length of a parametric curve, making use of the approximations by sufficiently small segments and its use in the Riemann integral.

1. We check for the existence of temporal (one-dimensional) intersection, that is, time concurrence:

2. We check for geometric (two-dimensional) intersection:

(a) It can be done by solving the system, as long as it is well-conditioned:

If there are $0\le\lambda\le1$ and $0\le\mu\le1$ that fulfill both equations or are collinear, that is:

where contagion could occur if they are coincidental:

In any other situation, as there are no points in common between the segments, the minimum distances between each point and the opposite segment are calculated. Finally, it is checked whether the minimum of them is below the maximum transmission distance, so that there is a possibility of contagion (as Figure 5):

In this case the execution time for $n$ segments would be

(b) Or using Bentley's & Ottmann algorithm ^[4], whose execution time for $n$ segments with $s$ points of intersection is

Procedure 3.2 (Establishing Contagion). The big data algorithm must fulfill the following phases:

1. Analyze the intersections of patient trajectories by pairs ($\vec{\alpha}_i$ and $\vec{\alpha}_j$) where contagion may occur ^[15]:

2. In each analysis, establish the possible point of contagion (if any) and increase both its contagion index and its most remote time variable in which a contagion occurred

3. Patients are classified according to the sum of the indexes of all the points of contagion contained in their trajectory. In this way, we will order the patients from the one that has caused the most infections to the one that has caused the least.

4. Patients are classified according to the lowest value of $t$ contained in their points of contagion. With this we can establish patient zero.

With this procedure, we calculate the distribution of contagion points of known patients $\vec{\otimes}_k$, and the final number of contagions in each one of them $\vec{\otimes}_k$, which gives us an image of the city as shown in Figure 6:

4.   Inverse graph

Once the possible cut-off points between known patient routes have been established, we ask ourselves whether there are any undetected patients who can be deduced from the possible points of contagion. This question involves a probabilistic analysis of what the possible path of the unknown patient would look like.

Let us suppose that there is an unknown patient that has been causing an uncontrolled contagion, which we will call $P_x$.

1. If the contagion has occurred at an intersection $\vec{\otimes}_{ij}$ of two "contagious" patients $P_i$ and $P_j$, that is, $\rho_i(t) \cdot \rho_j(t) = 4$, it could be that:

(a) one of them was already really ill: This forces a recalculation of the $C$ and $I$ intervals for both. In this case, if the one who was already ill had been $P_i$, he must have been previously infected by a stranger, and therefore there was a cross with $P_x$. Similarly for $P_j$.

(b) neither of them infected the other: In this case there is a coincidence of the path of both with the one of $P_x$ at the point of infection.

In both cases we assign a new contagion in the point $\vec{\otimes}_{ij}$, although in the first assumption we also know that there is some point in the path of $P_i$ or $P_j$ in the state $C$ where it must have crossed with that of $P_x$ in the state $I$. Therefore, if we call $t(\vec{\otimes}_{ij}, C_i^0)$ and $t(\vec{\otimes}_{ij}, C_j^0)$ the time from the crossing point to the place where $P_i$ and $P_j$ met $P_x$ respectively, which are $C_i^0$ and $C_j^0$, then the crossing probabilities (CP) with $P_x$ of each interval are set as:

where $[C_i]$ and $[C_j]$ are the times at which $P_i$ and $P_j$ have been contagious.

2. If the infection has occurred in the $C$ range of any patient $P_i$, the path of $P_x$ matches that of $P_i$ with $\rho_i(t) = 2$ and $\rho_x(t) = 3$. In this case it is known that there is some point in the path of $P_i$ in the state $C$ where it should have crossed with that of $P_x$ in the state $I$. Here the probability of the whole $C$ interval is equal to $1$.

The zone graph, in these cases, is represented by Figure 7

Procedure 4.1 (Inverse graphs by big data). The big data algorithm will then be based on finding, of all existing paths of citizens that go through this area, those that achieve a higher sum of probabilities at the intersections of the $N$ intervals of known contagion ^[12].

1. To do this, the route followed by each citizen's smartphone $P_x$ is analysed and its intersections with the probable paths, assuming that this citizen was permanently ill:

2. This would cause a contagion at each intersection and would add probabilities to its final value.

3. Those candidates with the highest score will be studied to see if they are carriers or not. A new set of patients will be deducted from the patients prior to the existing ones. Using the procedure recursively, we will reach patient zero.

5.   Analysis of algorithm

After the theoretical development of the Inverse Graph method, the general geolocation algorithm has been programmed using a Computer Algebra System (CAS) as MatLab ^†. The developed algorithm has a quadratic execution time, i.e. $\Theta (n^2)$ and its pseudo-code ^‡ would be as follows:

^†Algorithms and functions programmed in MatLab version R2020b and tested on a MacBook with processor 1.3 GHz Intel Core m7

^‡All that appears between braces are comments

begin      Read kml compress files from Google Maps timeline for each

         user $i$. Build matrix $M_i$ of coordinates and its convex hull.

         Analyzes only disjunct concentrations of convex hulls (Figure 8)

$M = [];$ for i:1:users do $M = [M; M_i]$ end for

Times = intervals(M);      {Build matrix time interval for all users}

I = sort(Times)      {Sort the intervals as a function of time}

point = []; inter = size(I, 1);

for j = 2:inter

     for i = 1:j-1      {Check the space-time match}

         if fit(Times(i), Times(j))

             point = cuts(I, Times, M);      {Found intersection points}

         end if

     end for

  end for

end

Next Table 1 and Figures below (Figures 9 and 10) show execution times (in seconds) and the number of contact points that occurred between different people, based on user graph intersections for the last twelve days, with an average of 388 vertexes at their polygonal paths for each user

6.   Conclusions

The capacity of Big Data to solve the problem will depend on the reduction that is made on the population to be analyzed for the search of the patient zero ^[20].

This reduction is conditioned by the need for temporal and geometric coincidence of the routes with those of the probable intervals. Therefore, it is a priority to establish the condition of temporal coincidence, which will considerably reduce the set of candidates (Figure 11), and then analyze the intersections in the plane.

7.   Future work

7.1.   Matrix representation

Each element $a_{ij}$ of a dispersed matrix of contagions $A = (a_{ij})$ would represent with values 0 or 1 the possibility that the patient $P_i$ has infected the patient $P_j$, with $i, j \in \{1, \dots, N\}$

With this representation the rows $i$, whose sum of terms is greater $\sum\limits_{j = 1}^N a_{ij}$, will correspond to the index of the most dangerous patients. The number of infections of the most dangerous patient will be indicated by

7.2.   Markov chains

The application of Markov Chains on arrays, whose elements represent the mesh of an area, will allow us to see to which position each individual moves in a unit of time and to which state of health he can evolve ^[3,17].

7.3.   Artificial Intelligence

Neural networks can provide a trained system for the pre-selection of possible candidates for asymptomatic or unknown patients ^[1].

Ackowledgements

We thank the support of this paper from University of Málaga and CBUA (funding for open access charge: Universidad de Málaga / CBUA) and we thank also the anonymous reviewers whose suggestions helped improve and clarify this manuscript.. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflict of interest

The authors declare that there are no conflicts of interest.