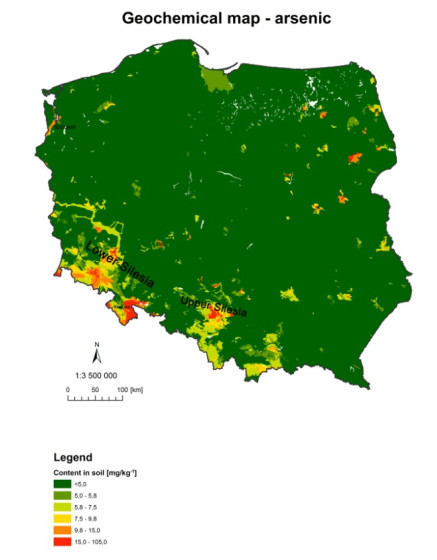
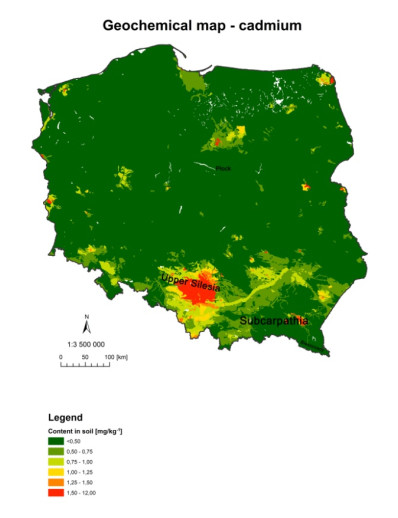
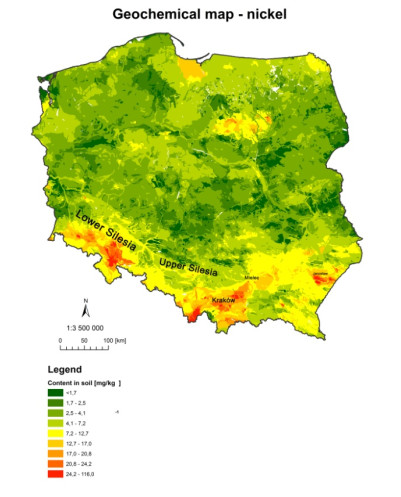
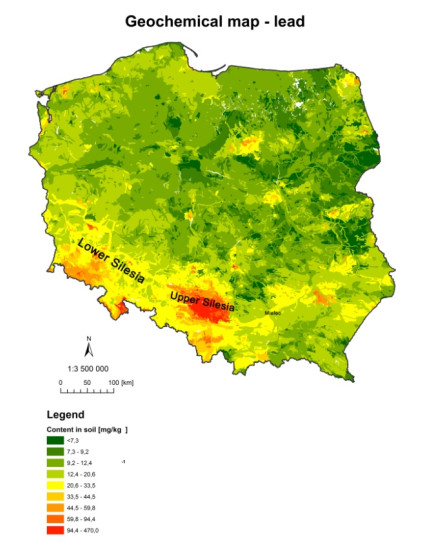
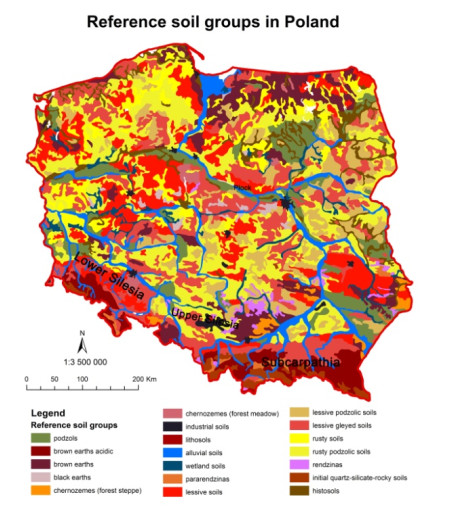
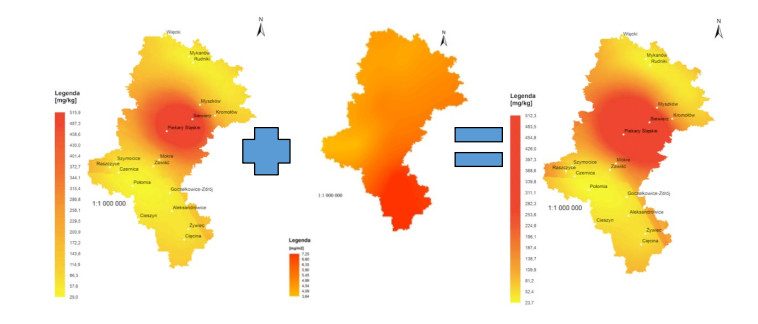
The increasing number of spatial data sets permits their application for minimising the duration and cost of such research. An example of such application is geostatistical modelling. Data on the quality of atmospheric air can be used for the assessment of the quality of soil in a given area. The objective of the study was an attempt to apply geostatistical methods in the estimation of the degree of soil contamination with selected heavy metals resulting from deposition from atmospheric air. This paper uses data obtained from the State Environmental Monitoring (data on the quality of atmospheric air) and other collections of publicly available spatial data for the purpose of analysis of the state of quality of soils in the province of Silesia in Poland. Conducted analyses revealing that contamination with lead in atmospheric air in the Silesian voivodeship considerably exceeds acceptable values, and the load of lead deposition is largely transferred to the soil. The paper also presents geochemical maps necessary to understand sources of soil contamination, including their natural content.
1.
Introduction
The rapid development of e-commerce platforms in recent years has led to more and more large online capital flows and offline commodity flows, which have resulted in not only an increasingly rapid rate of product updating but also environmental pollution, resource waste, and other problems. With the advancement of the global low-carbon economy, there is an increasing demand for remanufacturing and low-carbon technologies by enterprises. As a result, closed-loop supply chain is gradually becoming an important mode of operation in the context of a low-carbon circular economy. The closed-loop supply chain (CLSC) is developed from the traditional forward supply chain by adding the reverse logistics of recycling and remanufacturing of used products [1]. As an important operation mode of enterprises, CLSC can save resources through the recycling of used products, and is an important way to achieve the development of a green economy with a low carbon cycle [2]. The CLSC operation mode can bring good economic benefits for enterprises [3]. Specifically, an enterprise can establish a good image and improve market competitiveness by recycling used products. In addition, the recycling and remanufacturing activities can reduce carbon emissions and save costs. For example, Bosch can save 40% of costs annually through recycling and remanufacturing activities, and reduce 23,000 tons of carbon dioxide emissions [4,5]. Through recycling and remanufacturing activities, Kodak can save 40%–60% [6] and IBM saves up to 80% [7] of production costs.
In essence, CLSC involves the incorporation of a reverse feedback process into the conventional forward supply chain, thereby establishing a complete, closed-loop system. At its core, CLSC operates as a feedback system that encompasses the entire lifecycle of products, spanning from resource extraction and production to consumption, and ultimately to the recycling and renewal of resources, through both forward delivery and reverse recycling processes [8]. CLSC members are committed to recycling and reusing used products, obtaining the surplus value of the used products, reducing production cost, and achieving the cyclic flow of resources, which will help indirectly reduce negative impacts on the environment [9]. Since pricing decisions are also pivotal in shaping the overall operational efficiency of CLSC, it has received extensive attention from scholars [10]. Vorasayan et al. analyzed the effect of changes in the returned product quality and refurbishment cost on the pricing decision [11]. Thereafter, the pricing strategies of the CLSC have been extensively explored [12,13,14], focusing on various aspects such as incentive strategies, product quality, power asymmetry, and demand uncertainty. Existing studies have discussed pricing strategies, reverse logistics, and remanufacturing in CLSC, but most of them have ignored a key reality: there is a significant difference in consumer acceptance of new and remanufactured products, especially in the context of the gradual increase in low-carbon awareness. To enhance the acceptance of remanufactured products in the market [15,16], this study introduces low-carbon technologies in the hope of increasing consumer demand for remanufactured products by reducing carbon emissions.
While it is true that low-carbon technologies can increase the demand for remanufactured products, many companies are reluctant to actively participate in carbon reduction activities due to concerns about high investment costs [17]. To address this issue, this paper proposes a program where retailers and manufacturers share the investment costs of low-carbon technologies. Based on the literature discussing recycling activities [18,19], a differential response is constructed in which the manufacturer is responsible for product recycling, and the retailer and the manufacturer share the costs of recycling and low-carbon technology development. Unlike traditional studies, this paper focuses on analyzing cost-sharing mechanisms and pricing strategies under different power structures to find out the optimal decision-making of supply chain members with product differentiation and the way to maximize the overall profit.
Based on the above discussion, this paper addresses the following questions for a dynamic supply chain with product differentiation:
(1) What are the equilibrium pricing strategies and low-carbon technology levels of CLSC members under different power structures?
(2) How does the retailer's optimal cost-sharing ratio affect the pricing decision under different power structures?
(3) How do substitutability coefficients and low-carbon preferences affect pricing strategies? Under which power structure is the system profit maximized?
To solve the above questions, we construct a CLSC consisting of a manufacturer and a retailer, since most of the literature assumes no difference between new and used products and does not consider the dynamic characteristics in the selling and recycling activities of used and end-of-life products. Therefore, this study presents a differential game model that captures the dynamic demand patterns specific to both new and remanufactured products. The focus of this study is a CLSC comprising a manufacturer and a retailer, which jointly bear the costs associated with remanufacturing and the low-carbon technology investment. With the differential game model, this study investigates the pricing strategies within three distinct game scenarios: the manufacturer-dominated Stackelberg game, the Nash game, and the retailer-dominated Stackelberg game. In addition, the effects of substitutability coefficient, low-carbon preference, and power structures on pricing decisions are analyzed. Furthermore, the optimal profits attainable within the CLSC system are examined under varying power structures. The main contributions of this study are as follows:
(1) For the first time, we incorporate a dynamic perspective into a CLSC study of low-carbon technology R & D and cost-sharing mechanisms under different power structures.
(2) We innovatively construct a differential response model that covers the dynamic demand for both new and remanufactured products. This model accurately determines the optimal pricing strategy, the level of low-carbon technology upgrading, and predicts market demand for new and remanufactured products under the three different power structures.
(3) We reveal how substitutability coefficients and consumers' low-carbon preferences profoundly affect the formulation of pricing strategies in the context of different power structures. In addition, we clarify how the retailer optimizes its cost-sharing ratio to maximize its own benefits under different power structures.
(4) In this paper, we explore in depth the optimal power structure configuration corresponding to the maximization of the overall profit of the CLSC system.
The above contributions not only fill the research gap in resource recycling and reuse in supply chain management but also provide a new perspective on the research of the low-carbon economy. Moreover, they show how enterprises can achieve a balance between economic and environmental benefits through a CLSC. This is a key challenge under the current dual pressures of market competition and environmental protection.
This study is organized as follows: Section 2 is the literature review; Section 3 describes the problems and basic assumptions; Section 4 shows the model construction and solution under different power structures; Section 5 is about numerical simulation; Section 6 presents the conclusions and prospects.
2.
Literature review
The literature related to this study focuses on three areas: the pricing decision problem, the cost sharing and power structure problem, and the application of differential games in CLSC. Table 1 sets out a comparison between previous literature and our work.
Currently, many scholars have profoundly studied pricing decisions in CLSC. Liu et al. explored the pricing strategies that took into account different reverse channels, quality uncertainty, and socially responsible investment behaviors [20,21,22]. But, the above studies do not consider the recovery cost, and all assume that the remanufacturing cost is zero. In fact, these costs affect the pricing decisions of CLSC members. Herein, we add the investment cost of low-carbon technology to the above costs, and study the pricing strategies of CLSC under the sharing of the recycling cost of the remanufacturing process and the investment cost of low-carbon technology between the manufacturer and the retailer.
Meanwhile, the current society presents a diversified CLSC dominance situation that involves a model where large-scale manufacturers like Volkswagen and first automobile works dominate the market, and a model where large-scale retailers such as Wal-Mart, Carrefour, and Gome dominate the market. There is also a model in which electronic equipment manufacturers and Jingdong, Suning, and other retailers dominate the market simultaneously, which is also known as an evenly matched model [23]. Different power structures determine different decision-making orders of CLSC members, which will impact the pricing decision-making results of the whole CLSC and the benefit distribution structure of CLSC members in different ways [24]. Wei et al. studied the optimal decision-making problem of CLSC with symmetric and asymmetric information structures under manufacturer-led or retailer-led scenarios [25]. Results show that firms in the leadership of the supply chain have the advantage of obtaining higher profits under both symmetric and asymmetric information. Under varying power structures, some researchers studied the optimal pricing strategies, remanufacturing strategies, and coordination mechanisms within CLSC [17,26,27]. Nevertheless, the dynamic factors in product sales and waste product recycling activities were not considered in their research. In reality, the favorable reputation of an enterprise throughout its operations can be translated into consumers' positive perception of the product as a potential value, thereby influencing the sales and recycling of the product in subsequent periods [28]. If it is seen as a static state, the resulting strategy is only the company's local short-term optimal strategy, rather than the global optimal strategy. Therefore, given the dynamic influence of members' decisions, it is more suitable to investigate the effects of low-carbon technology and cost burdens under varying power structures from a dynamic perspective.
There is an extensive body of research on dynamic characteristics-based analyses of CLSC [29,30]. For instance, Ma et al. constructed a dynamic differential equation for product goodwill and explored its influence on the decision-making processes of each participant within a CLSC [31,32,33]. Yang et al. built a dynamic differential equation for carbon emission reduction and thereby investigated the emission reduction decision-making of the manufacturer [34,35,36]. Ma et al. established a dynamic differential equation for carbon emission reduction by considering the product quality and the dynamic differential equation of product greenness and compared the dynamic pricing model with the static pricing model [37]. Nonetheless, the existing literature fails to differentiate between new and remanufactured products. In contrast, this study proposes a differential game model with product differentiation that captures dynamic demand patterns specific to new and remanufactured products. Moreover, the supply chain includes a manufacturer and a retailer who share the costs of remanufacturing and investing in low-carbon technologies. Finally, we give the optimal cost-sharing ratio for the retailer under different power structures to maximize its own benefit.
3.
Model description and assumptions
This study focuses on the continuous time t→[0,+∞), and is aimed to analyze the decisions related to pricing and low-carbon technology within CLSC under distinct power structures (Figure 1). The production of new products and the recycling and remanufacturing activities of used products are handled by the manufacturer. Additionally, the manufacturer conducts research and development to enhance the low-carbon technology used in remanufacturing processes. Simultaneously, the retailer assumes the role of selling both new and remanufactured products to consumers and collaborates with the manufacturer in sharing the recycling price and the investment cost associated with low-carbon technology within the recycling and remanufacturing activities.
Table 2 shows the specific symbols and corresponding meanings of relevant parameters. The notation πji denotes the profit by member i within the CLSC. i∈{m,r,T} represents the manufacturer, the retailer, and the CLSC system, respectively. j∈{MLM,NM,RLM} represents the manufacturer-dominated Stackelberg game, the Nash game, and the retailer-dominated Stackelberg game, respectively.
The basic assumptions of the CLSC model are specified below:
Assumption 1. Both parties are rational economic people, and all decisions are made from rational principles.
Assumption 2. Under the assumption of zero inventory cost and out-of-stock cost for both the manufacturer and the retailer, and considering an infinite time horizon, it is assumed that they share the same discount rate at any given point in time.
4.
Model construction and analysis
We develop three models for decentralized decision-making: the Nash game (a market game without a leader), the Stackelberg game where the manufacturer dominates, and the Stackelberg game where the retailer dominates. Within these three decentralized decision-making models, both the retailer and the manufacturer exhibit risk-neutral and rational behavior, and their objectives are to maximize their profits throughout the decision-making procedure.
The demands for new and remanufactured products are denoted as QN and QR, respectively, and satisfy the following differential equations
Where the demand naturally decreases over time. Meanwhile, the prices of both new and remanufactured products influence their respective demands. Specifically, as the price of a particular product increases, its demand tends to be suppressed. Correspondingly, when the price of new products rises, consumers are more likely to purchase remanufactured goods, and vice versa. Additionally, higher wholesale prices negatively affect retailers' procurement of similar products. An increase in the level of low-carbon technology can increase the recognition of remanufactured products. Therefore, it positively affects the change in demand for remanufactured products. At the same time, the research and development cost of low-carbon technology is highly correlated with its level, which is set as a quadratic function in this paper, i.e.,
For convenience, the time variable t is omitted below. The necessary theorem on the existence of equilibrium solutions for differential games (Theorem 2.4.2) please refer to [39].
4.1. Manufacture-led model (MLM)
Manufacturer, as the core company in a CLSC, enjoys leadership over the supply chain. In this scenario, the manufacturer first decides on the wholesale price of products ωN and ωR, and low-carbon technology level E. The retailer then gives the retail price of products pN and pR, based on the manufacturer's decisions. The profit functions for each side are as follows:
Based on the above decision sequence, each equilibrium solution is found according to the principle of backward derivation, as in Proposition 1.
Proposition 1. The optimal equilibrium strategies under the MLM model are given by
where
and
Proof. The Hamiltonian function for the follower is obtained as
where β1,β2 are the adjoint variables of the corresponding state variables. The HJB equations are obtained by taking a first-order partial derivative for pN,pR, respectively,
The adjoint variables satisfy the following adjoint equations
And the limiting transversality conditions
Then, in order not to violate the transversality condition, we choose a set of stable solutions
The definition of a stable solution is one solution that satisfies
and is itself a solution of the adjoint equation. Substituting Eq (4) into Eq (3), we obtain
We can obtain
where
Substituting Eq (5) into the leader's objective function yields the leader's Hamiltonian function
The HJB equations are obtained by taking a first-order partial derivative for ωN,ωR,E, respectively
Similarly, in order not to violate the transversality conditions, we choose a set of stable solutions. Then
According to Eq (6), the constant adjoint variables
and
are obtained,
Substituting Eq (8) into Eq (7), we can obtain
where
Plugging Eq (9) into Eq (5)
In order to find the Stackelberg solutions, it is necessary to solve QN,QR. Therefore, by substituting pMLM∗N,pMLM∗R,ωMLM∗N,ωMLM∗R into (1), we obtain
When the autonomy equations are stable,
Then the equilibrium solutions for the demand for the new and remanufactured products are
The Stackelberg solutions for the manufacturer and retailer control variables are obtained
4.2. Nash model (NM)
The Nash game, a leaderless market game, assumes that both parties make decisions at the same time, but the manufacturer decides on the wholesale price of the products ωN and ωR, and the level of low-carbon technology E, and the retailer decides on the retail price of the products pN and pR. The profit functions for each side are as follows:
Proposition 2. The optimal equilibrium strategies under the NM model are given by
where
and
Proof. The Hamiltonian functions for manufacturer and retailer, respectively, are as follows:
The HJB equations are obtained by taking a first order partial derivative for ωN,ωR,E and pN,pR,
The adjoint variables satisfy the following adjoint equations:
And the limiting transversality conditions
In order not to violate the transversality condition, we choose a set of stable solutions
Substituting Eq (11) into Eq (10), we obtain
We can obtain
and
In order to find the Nash solutions, it is necessary to solve QN,QR. Therefore, by substituting pMLM∗N,pMLM∗R,ωMLM∗N,ωMLM∗R,E into Eq (1), we get
When the autonomy equations are stable,
Then the optimal demands for the new and remanufactured products are
And the Nash equilibrium for the manufacturer and retailer control variables are obtained
4.3. Retailer-led model (RLM)
The retailer, as the core company in a CLSC, enjoys leadership over the supply chain. In this scenario, the retailer first decides the retail price of the products pN and pR. The manufacturer then gives the wholesale price of the product ωN and ωR, and the level of low-carbon technology E, based on the retailer's decision. The profit functions for each side are as follows:
Proposition 3. The optimal equilibrium strategies under the MLM model are
where
and
Proof. Similar to the proof of Proposition 1.
5.
Numerical analysis
In order to be more intuitive and thorough for more in-depth research and analysis, we conduct simulations to explore the impacts of cost-sharing coefficient, product substitutability, and consumers' low-carbon preference on pricing decisions. The parameters in this section include
5.1. Optimal cost-sharing ratios under different power structures
In addition to the manufacturer benefiting from recycling, recycling is also a profitable endeavor for the retailer. Therefore, the retailer is actively involved in cost-sharing, both in terms of recycling costs for the manufacturer and investment costs for low-carbon technology, thus incentivizing recycling. Therefore, it is necessary to investigate the optimal cost-sharing ratio for retailers under different power structures to maximize the retailer's profits. The parameters in this section are
As demonstrated in Figure 2, the optimal cost-sharing ratio is exclusively present within the RLM model. Conversely, in both the NM and MLM models, the retailer achieves maximum profit without engaging in cost-sharing measures, and the profits decrease as the cost-sharing ratio increases. Under the RLM model, the retailer's profit and its cost-sharing ratio are in an inverted U-shaped curve, as the retailer has the optimal cost-sharing ratio of 0.8, at which the retailer's profit reaches 14.75, which is much higher than the profit under the NM and MLM models. Therefore, as the retailer's power increases, its profit also rises. To maximize their profits, the retailer must establish the most suitable cost-sharing ratio based on their levels of power within the CLSC.
5.2. Impact of cost-sharing ratios on pricing decisions
Within this subsection, the impact of cost-sharing ratios on the equilibrium solution of members within a CLSC is analyzed under varying power structures. This analysis is visually represented in Figures 3–5. As shown in Figure 3, there is
and the low-carbon technology level under the NM and MLM models slowly increase as b rises, indicating the cost-sharing mechanism can improve the low-carbon technology level of remanufacturing. However, the low-carbon technology level under the RLM model is decreasing on the whole, and falls to 0 at φ = 0.21. Therefore, when the retailer possesses greater power within the CLSC, the corresponding consequence is a lower level of low-carbon technology for the manufacturer.
The retail price of new products under the RLM model is consistently higher than under the NM and MLM models regardless of the values of φ (Figure 4). As φ increases, under both the RLM and NM models, the retail price of new products rises, albeit at different rates. Specifically, the retail price rises gradually under the NM model, while it escalates more rapidly under the RLM model. In the MLM model, the retailer's retail prices are slowly decreasing, and there is a threshold point between the RLM and NM models at
When at
the retail price of a new product in the MLM model is slightly higher than in the NM model, while the opposite is true at
This result indicates that as the retailer's power in the CLSC increases, the retail price of the new products rises, because the retailer transfers its inputs for cost-sharing in the recycling and remanufacturing process to the new product. As shown in Figure 5, the retail price of remanufactured products decreases under all three models regardless of the values of φ, and changes in the order of
When the manufacturer and retailer simultaneously make their pricing strategies, the retail price of the remanufactured product is higher, but the price decreases as power shifts to the retailer (Figure 5).
The wholesale price of new products is minimally affected by the sharing ratio in both the NM and MLM models (Figure 6). The wholesale price gradually decreases in the MLM model, while it slowly increases in the NM model. At higher sharing ratios, there is
When dominance shifts from the manufacturer to the retailer, the retailer's bargaining power is intensified, while the manufacturer's wholesale price increases. Under all three models, the wholesale price of remanufactured products decreases as the sharing ratio increases:
and an increased sharing of investment in recycling activities by retailers, manufacturers demonstrates their willingness to lower the wholesale price of remanufactured products as a means to support retailer (Figure 7).
5.3. Impact of substitutability coefficient, and low-carbon preference on pricing decisions
The substitutability coefficient of the product and the consumers' low-carbon preference under the Nash game little affect the retail price of a new product, which fluctuates between 1.297 and 1.400 with a relatively small range as the two parameters change (Figure 8). In the manufacturer-dominated Stackelberg game, the substitutability coefficient positively impacts the retail price of new products, while low-carbon preference has a negative impact, resulting in a decrease. Compared to the previously mentioned games, the retailer-dominated Stackelberg game results in a higher retail price for new products. The highest retail price is attained when both the substitutability coefficient and low-carbon preference are at larger values.
Figure 9 illustrates that the wholesale price of a new product follows a downward trend as the substitutability factor increases under the Nash game. Conversely, when low-carbon preference increases, the wholesale price shows an upward trend. In the manufacturer-dominated Stackelberg game, the impact of both parameters on the wholesale price of a new product is in line with their impact on the retail price. In the context of the retailer-dominated Stackelberg game, the wholesale price of the new products fluctuates between 1.050 and 1.500 with the change of the two parameters, which is a wider range of fluctuation than the two games mentioned above.
5.4. Optimal profit under different power structures
To further refine the presentation of our model results and minimize the impact of parameter selection, we conducted additional simulations using randomly generated parameters. Ensuring that all parameter values remained meaningful in practice, we generated 500 different parameter sets to analyze the variations in total supply chain profit under different cost-sharing ratios across the three power structures. The total supply chain profit, defined as the sum of the manufacturer's and retailer's profits, is denoted by the subscript T. The results are presented in Table 3 and Figure 10. The findings reveal that when the cost-sharing ratio is low, the MLM structure has a higher probability of achieving greater total profit compared to NM and RLM, while the likelihood of NM outperforming RLM remains relatively low. As the cost-sharing ratio increases, the advantage of MLM becomes more evident. When the ratio reaches around 0.8, the probability of MLM's total profit exceeding that of RLM reaches its peak. At the same time, the chance of NM achieving higher profits than RLM also increases significantly.
This indicates that, with a reduced cost burden, the manufacturer can allocate more resources to low-carbon technology development and product innovation. Their technological advantage in both new and remanufactured products enables the supply chain to maintain high operational efficiency. This insight also highlights that, although the manufacturer bears sole responsibility for the recovery process, their ability to optimize the remanufacturing workflow and control costs is stronger, ensuring a high level of profitability across the entire supply chain.
6.
Discussion and conclusions
6.1. Discussion
This study offers valuable insights into the management of CLSC with product differentiation, particularly within the context of a low-carbon economy. Unlike previous research that primarily focused on static models, we combine product differentiation and dynamic game theory to provide a more detailed understanding of long-term strategic interactions among supply chain participants. Our findings demonstrate that integrating low-carbon technologies and cost-sharing mechanisms can significantly enhance both environmental sustainability and economic efficiency. By offering new theoretical perspectives, this study contributes to the field of sustainable supply chain management.
Theoretically, this study advances the development of CLSC management with product differentiation. Our model highlights how different power structures, such as manufacturer-led and retailer-led scenarios, impact the optimal level of low-carbon technology and cost-sharing strategies. This deepens our understanding of strategic decision-making in the supply chain.
From a practical perspective, our findings offer actionable insights for policymakers and industry leaders. By implementing the cost-sharing mechanisms and low-carbon technologies proposed in this paper, companies can strengthen their sustainability practices while simultaneously improving their economic performance. This has the potential to drive significant progress toward achieving environmental goals.
Specifically, the impact of this research extends beyond the specific context of CLSC. By proposing a model that integrates low-carbon technologies and cost-sharing mechanisms, we provide a framework that can be adapted to various industries facing similar sustainability challenges. This approach not only aids in policy development but also offers guidance for practitioners in balancing economic and environmental objectives.
6.2. Conclusions
This paper constructs a differential game model for new and remanufactured products concerning dynamic pricing and low-carbon technology decision-making in CLSC. It fills the gap left by previous studies, which failed to distinguish between new and remanufactured products and primarily relied on static models. By introducing dynamic game analysis, we investigate the pricing strategies and low-carbon technology levels under three power structures: manufacturer-dominated, retailer-dominated, and Nash games.
The results of the study show that there are significant differences in the decision-making behaviors of manufacturers and retailers under different power structures, particularly in terms of cost-sharing mechanisms. Compared with the static model, this study demonstrates, for the first time, the long-term effect of the manufacturer reducing the wholesale price of remanufactured products for the retailer after the retailer bears more costs, using a dynamic model. This plays a positive role in the overall coordination of the supply chain. The problem of "free-riding", which occurs in some studies, is resolved.
In addition, we find that an increase in the level of low-carbon technology contributes to the growth of the market for remanufactured products. However, if the level of low-carbon technology is too high, it may undermine the competitiveness of new products, especially if it leads to manufacturer-led price reductions for new products. Therefore, the control of low-carbon technology needs to be moderate to balance the market share between old and new products. This finding addresses gaps in existing studies.
Through the quantitative analysis of numerical simulation, we find that the retailer-dominated Stackelberg game maximizes profit for the retailer and that there exists an optimal cost-sharing ratio. Compared with previous studies, we not only extend the applicability of the game model but also provide a new quantitative benchmark for power structures and profit distribution in the supply chain, particularly in the context of low-carbon technologies and cost-sharing mechanisms.
In conclusion, the research in this paper provides a theoretical basis and practical guidance for the strategic management of CLSC with product differentiation in the context of a low-carbon economy. It also proposes an effective cost-sharing mechanism and power structure selection strategy by comparing different game structures.
Author contributions
Jun Wang: designed project, provided figures and revised the manuscript; Dan Wang: designed the project, wrote the first draft and revised the manuscript; Yuan Yuan: conceptualized and supervised the project, revised the manuscript, and acquired funding. All authors have read and approved the final version of the manuscript for publication.
Acknowledgments
The authors would like to thank the reviewer for their valuable comments. This work was supported by the Natural Science Foundation of Jilin Province, under grant number. 20230101288JC.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: