1. Introduction
The bacterium Escherichia coli is commonly found in the intestine of warm-blooded organisms. Most of its strains are harmless and are a beneficial part of the gut fauna. Pathogenic E. coli strains, in particular O157:H7, cause illness in humans. Scallan et al. [12] indicate that a significant part of all cases of acquired food-borne illness in the U.S.A. is caused by the pathogenic strains of E. coli. These strains are primarily transmitted from cattle to humans by consumption of meat and especially under-cooked ground beef, although infection can also occur after consumption of dairy products [15,16] or from other sources.
In the western world, most meat production is concentrated in large meat processing plants, and any outbreak of E. coli contamination may affect many people over a wide area. In addition to the health hazard, outbreaks cause large economic losses and have a negative impact on the beef industry. The existing food safety regulations in Canada and the U.S.A. require the removal of all production and raw sources associated with an identified contamination event. This leads to the recalling of large amounts of beef, much of it likely uncontaminated, and consequently big losses for the beef industry. The goal of this paper is to present a probabilistic model for estimation of the likelihood that sequential batches of ground beef produced in a large plant are contaminated with pathogenic E. coli given that one batch is contaminated.
E. coli and its impact on human health have being studied extensively in the last several decades. There is a large body of literature dealing with risk assessment for E. coli in ground beef and burgers in different countries [4,6,7,8,13]. A risk assessment model for E. coli O157:H7 in ground beef and beef cuts in Canada is presented in [14]. The difficulties in risk assessment of contamination stems from the fact that it depends on many factors, such as production conditions in the meat processing plants, distribution networks, cooking methods, etc. In [17], using data from a large E.coli outbreak in the U.S.A., possible sources of contamination are investigated. The main method used in these studies is statistical analysis of empirical data.
Stochastic models for outbreak and transmission of E. coli O157:H7 infection in cattle, are presented in [18] and [20].
Most of the existing deterministic mathematical models about E. coli, published in recent years, are devoted to the study of the bacterium itself, rather than the study of the illness caused by it or the estimation of the risk of contamination [5,10,11].
The sources of contamination by pathogenic E. coli in a beef-packing plant has been studied by Aslam et al. [1,2] and Bell [3]. E. coli in meat products, originates mainly from the hides of the incoming animals and is transferred to the trimmings, and subsequently the ground beef, during the dressing of carcasses and carcass breaking. There are still uncertainties regarding the exact relationship between the E. coli found on skinned carcasses and that found on meat at later stages of processing. In recent years, in order to reduce the number of bacteria on the skinned carcasses, North American beef processing plants have implemented different decontamination treatments, such as treatments with antimicrobial solutions and pasteurization. The effect of these treatments was investigated in [19]. Although this study found that these treatments significantly reduce the risk of contamination, the hazard can not be completely removed. Also, there are still no effective methods for quickly screening large amounts of ground beef in big production facilities. All of these uncertainties justify using probabilistic methods for control and estimation of E. coli contamination in the production of ground beef.
2. Materials and methods
The context of this model is a large ground beef production facility. Given that a particular batch of ground beef has been identified as contaminated, this model assigns probabilities of contamination due to the same origin for the other batches in the production cycle. A preliminary, less general, version of this model was presented in a short conference proceedings [9].
2.1. Basic assumptions
The primary assumption is that the contamination is due to the presence of the contaminant on a single carcass. Typically, only a portion of the carcass, often part of the fat layer, would be contaminated, but the model treats all portions of this one carcass as contaminated. Spread of the contaminant in the production process is assumed to be due to division and dispersion of the contaminated carcass portions; transfer via physical contact with other pieces and machinery surfaces is assumed to be negligible. Further, due to the temperature at which production occurs, it is assumed that the contaminant does not grow appreciably.
Ground beef is produced in batches. Each batch has input from several raw sources, typically one or more "lean" fresh sources and "fat" fresh sources, but also often frozen sources and other sources such as Boneless Lean Beef Trimmings (BLBT), also called Lean Finely Textured Beef (LFTB), which is extracted from trimmings via a centrifuge at temperatures around 38 C. BLBT is usually free of bacterial contamination since it is typically treated to kill bacteria before being used. The meat in a batch is well-mixed and ground together, so that, if any contamination is present on any of the raw source material that is input to the batch, the entire batch is deemed to be contaminated.
As a carcass is processed, parts of it are trimmed off and put into raw source bins to be used as input to the ground beef batches. Typically a carcass gets spread over a region in the raw source. The size of this region and the probability of a piece of the carcass being present at any point in that region is highly dependent on the production process. If carcasses are spread across sources, measures of carcass overlap between any two sources are necessary for the model.
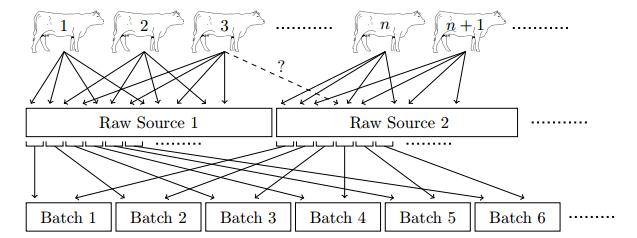
Some simplifying assumptions are made regarding how carcasses are spread in a particular raw source and how a raw source is used in ground beef production, as illustrated in Figure 1:
● For each raw source, every carcass is the same. The number of pieces contributed by each carcass, the various masses of those pieces, and the manner of the spread of those pieces throughout a region of the raw source, are the same for each carcass present in the raw source.
● Material within a raw source is ordered and used as input to the ground beef production batches in that order.
● The carcasses are sequentially processed. The regions of a raw source through which pieces from sequential carcasses are spread overlap one another but are shifted forward in the ordering. (Boundary effects for carcasses near the beginning and end of the raw source do alter the spread distributions of pieces from these carcasses; see Section 2.2.)
The second assumption allows us to define a "mass location" in each raw source; mass from a particular raw source used in batch number b comes from locations just prior to those for the mass from the same source used in batch number b+1. In other words, the carcass pieces are points and the production geometry is linear. Although these assumptions are likely not valid for a real production facility, they are useful simplifying assumptions for the modelling process. The likely mixing that occurs within the raw source can be partly accommodated by the carcass piece distribution that is adopted in the model. If there is heterogeneity of the carcasses within the source and this aspect was deemed important, then detailed information about the character of this heterogeneity would be required before it could be built into the model.
Suppose there are B batches of ground beef produced in a production cycle and S raw sources used as input to these batches. Not all sources need be used in all batches. It is assumed that a particular batch of ground beef has been identified as being contaminated. This batch is referred to as the "hot" batch, and it is identified as batch number h. The origin of this contamination is due to a single hot raw source and in turn, to a single hot carcass in this raw source.
The following subsections describe in detail how carcasses are spread in a raw source, which determines their likelihood of appearing in a given batch of ground beef, and how, given a particular hot batch h, the model computes 1) the probability that any particular source is the hot source, 2) the probability that a particular carcass in the hot source is the hot carcass, and 3) the probability that the hot carcass is also present in other batches. These probabilities are then combined in Equation (13), at the end of this section, to determine the probability that other batches are contaminated. Table 1 lists the symbols used in the model.
Table 1. List of Symbols.
| S |
Total number of raw sources. |
| B |
Total number of ground beef batches. |
| h |
The contaminated (hot) batch. |
| Cs |
Number of carcasses in raw source s. |
| ps |
Number of pieces supplied by each carcass in raw source s. |
| as |
Average size of pieces from each carcass in raw source s. |
| Ms |
Total mass in raw source s. |
| x |
Mass location in raw source. |
| μc |
Mid point of piece distribution for carcass c (in source s). |
| Fs |
Base probability density function for piece distribution in source s. |
| Gsc(x) |
Probability density function for piece distribution for carcass c in source s. |
| Qsc(R) |
Probability that a piece from carcass c is located in region R in source s. |
| K |
Half the number of piece-wise linear segments of Fs. |
| Ni |
Boundaries of piece-wise linear segments of Fs, measured in number of carcasses from centre, μc, of distribution. |
| H±i |
Values of Fs at boundary Ni, approaching from the left, −, or the right, +. |
| msb |
Mass from source s input to batch b. |
| Msb |
Mass from source s input to batches 1 through b−1. |
| Bsb |
Interval of mass locations in source s input to batch b. |
| Asc(Bsb) |
Probability that carcass c is absent from the set Bsb, that is, carcass c contributes no pieces to batch b through source s. |
| fs |
Fraction of fat in raw source s. |
| gs |
Relative susceptibility to contamination factor for source s. |
| Vs1s2 |
Fraction of carcasses present in both raw sources s1 and s2. |
2.2. Spread of carcasses in a raw source
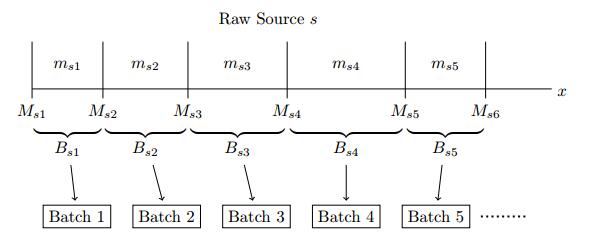
It is assumed that each carcass present in a particular raw source s contributes ps pieces and that the average mass of these pieces is as. Let Cs be the total number of carcasses in the raw source, then the total mass in the raw source is Ms=Cspsas. The pieces from each carcass are distributed throughout this raw source as illustrated in Figure 2 and described below.
For all pieces from a particular carcass c, the "centre" of the piece distribution is located in the source at the mass location
|
μc=(c−12)psas,c∈Z,1≤c≤Cs=Mspsas.
|
(1)
|
Thus the carcass centres are spread evenly across the source. Let Fs be the common base probability density function for all pieces from all carcasses in raw source s. Then, excluding boundary effects, the probability density function for pieces from carcass c in this raw source would be Fs(x−μc), where x is the mass location in the source. However, since the source is finite, carcasses with centres near the boundary would typically have Fs being nonzero beyond the beginning or end of the source. To prevent this, the distribution function is reflected at the boundaries (x=0 and x=Ms) and added to the base. Therefore, the probability density function for pieces from carcass c in source s is
|
Gsc(x)=Fs(x−μc)+Fs(−x−μc)+Fs(−x−μc+2Ms),x∈[0,Ms].
|
(2)
|
The first term on the right side of (2) is just the base probability function shifted to the centre, μc, for this carcass; the second and third terms are the reflections around x=0 and x=Ms, respectively. For carcasses near the middle of the raw source, the reflection terms will not contribute anything unless the breadth of the base probability function Fs is very large. In addition, Fs(x) is restricted to be zero for |x|>Ms, so that a single reflection at each end incorporates all of the support of Fs. For each piece from carcass c the probability that it is located between mass locations x1 and x2 is
|
Qsc([x1,x2])=∫x2x1Gsc(x)dx.
|
(3)
|
More generally, define Qsc(R) for some set R as the integral of Gsc(x) over R.
The above assumptions put some restrictions on the density function Fs. In particular, the total expected mass of all carcasses in a particular set must add to the size of the set. That is, for any set R⊆[0,Ms],
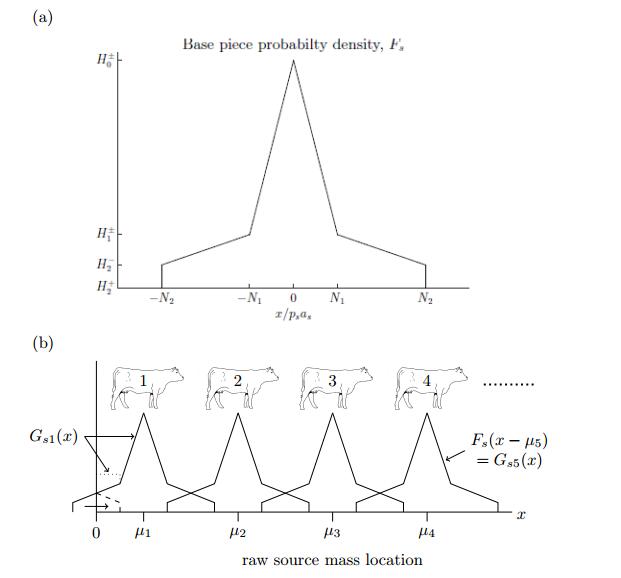
A number of functions Fs may satisfy this constraint, but here only a class of even (around 0), piece-wise linear functions, where each piece has a length being a multiple of psas, is considered. An example of such a function is shown in Figure 2(a). In the following, a technical description of this class of functions is given. A function Fs in this class may be defined in terms of parameters K, N, and H as below, where the subscript s on the these parameters has been suppressed for readability:
|
Fs(x)={(|x|psas−Ni−1)H−i+(Ni−|x|psas)H+i−1Ni−Ni−1if Ni−1≤|x|psas<Ni,1≤i≤K,0if |x|psas≥NK,
|
(4)
|
where the Ni are integers (number of carcasses) satisfying 0=N0<N1<N2<⋯<NK≤Cs, and H±i≥0, 0≤i≤K, are the limiting values of Fs at Nipsas from the left (−) and right (+), respectively. Necessarily, H−0=H+0 and H+K=0. Also, Fs must itself be a valid probability density, hence
|
K∑i=1(Ni−Ni−1)psas(H−i+H+i−1)=1.
|
This is just the statement that the area under Fs must equal one. This class of functions includes the uniform distribution, obtained with K=1, and H±0=H−1=12N1psas. If the parameters are chosen such that H−i=H+i, 1≤i≤K, then the function Fs is continuous. Each raw source s may have a different distribution function Fs, and thus a different set of parameters K, N, and H.
The realized distribution of pieces from a particular carcass is dependent on the locations of all other pieces from all carcasses, because piece locations cannot overlap. In particular, the locations of pieces from a given carcass c are not independent selections from the density function Gsc(x), nor are they only dependent on previous selections for the same carcass. However, assuming independence greatly simplifies the selection modelling and should introduce minimal error especially when there are a large number of carcasses. Independent selection is therefore employed in this model.
2.3. Probability of carcass presence in given batches
The probability that a carcass c from source s is input to batch b is computed as follows. The mass in each raw source is labeled according to the sequential batches for which it is used. Let msb be the mass input from source s to batch b, and let Msb be the mass input from source s to batches prior to batch b, that is, Msb=∑b−1i=1msi. The range of mass locations in raw source s that are input to batch b is then the interval
see Figure 3. For source s, denote the probability of carcass c being absent from the set Bsb as Asc(Bsb). Since the selection of the ps pieces for carcass c is modelled as being independent of the selection of other pieces, Asc is given by
|
Asc(Bsb)=(1−Qsc(Bsb))ps.
|
(6)
|
Therefore, the probability of carcass c from source s being present in batch b is
|
Prob(c from s in b)=1−Asc(Bsb).
|
(7)
|
Consider two batches, h and j, that receive input from the same source s, and a particular carcass c from that source. The probability that this carcass has at least one piece that is input to batch h and at least one that is input to batch j is
|
Prob(c from s in h&j)=1−[Asc(Bsh)+Asc(Bsj)−Asc(Bsh∪Bsj)].
|
(8)
|
The last term is present because it is included in both the previous terms but should only be counted once.
2.4. Identification of the hot source
The contamination in the hot batch, h, may be due to any of the raw sources that provided input to this batch, and these raw sources may have varying degrees of relative susceptibility to being contaminated. It is known that the contamination is often carried on the fat, so the fraction of fat, fs, in raw source s is an important factor. However, even sources with the same fat content may have differing likelihood of being contaminated. For example, a frozen source may be much less likely to be contaminated than a fresh source. To account for these differences, a relative susceptibility factor, gs, must be assigned to each source by the user. The absolute size of these factors is not important, only their sizes relative to one another. Thus if the user specifies g1=0.5, g2=1.0, and g3=1.5, then source 2 is twice as likely to be contaminated than source 1, source 3 is three times more likely to be contaminated than source 1 and 1.5 times more likely to be contaminated than source 2.
The probability that raw source s is the origin of the contamination in batch h is taken as
|
Prob(s is hot |h)=gsfsmsh∑Si=1gifimih.
|
(9)
|
Equation (9) is simply a weighted fractional contribution of mass from source s to the hot batch h. The larger the fraction of mass from source s in batch h, the more likely the contamination came from source s. The weighting is the product of the fat fraction fs and the susceptibility factor gs.
2.5. Identification of the hot carcass
Given that batch h is the hot batch and assuming the contamination is due to a single hot carcass in raw source s (which contributes mass to batch h) then, with no additional information, the probability that a particular carcass is the hot one is simply the relative probability of that carcass being present in batch h:
|
Prob(c from s is hot |h)={Prob(c from s in h)∑Csk=1Prob(k from s in h)if msh>0,0if msh=0.
|
(10)
|
The right side of the above is computed using (7).
2.6. Presence of the hot carcass in other batches
Assuming that a particular carcass c is the hot carcass and that this carcass contaminated batch h via input from source s, then the final step is to compute the probabilities that this carcass is also present in each of the other batches. It is possible that a particular carcass may be present in more than one raw source. This could occur, for example, in a production facility where certain trim from each carcass is placed in one raw source, and other trim from the same carcass, is placed in another source. Presence of carcass c from source s in another batch j, may therefore be due to either input from the same source or input from pieces of the same carcass present in another source.
The model presented here uses a conditional probability of carcass overlap. The probability that carcass c1 from source s1 is the same as carcass c2 from source s2, given that c1 from source s1 is in the hot batch h, is denoted
|
Prob(c1 from s1≡c2 from s2|c1 from s1 in h).
|
This probability must be assigned by the user. If sufficiently detailed information on the trimming process were available, this probability could reflect that, giving different values for different carcasses within each raw source. Without such detailed information, a more coarse approximation of this probability can be assigned using a measure of source overlap, Vs1s2, defined as the number of carcasses present in both sources divided by the total number of distinct carcasses in both sources. If n carcasses are present in both sources s1 and s2, then this overlap fraction is
which may be re-arranged for n giving
The probability of carcass overlap can then be approximated by the probability of selecting one of these n carcasses from source s1 and then selecting the exact same carcass from source s2:
|
Prob(c1 from s1≡c2 from s2|c1 from s1 in h)=(nCs1)(1Cs2)=Vs1s2(Cs1+Cs2)(1+Vs1s2)Cs1Cs2.
|
(11)
|
This coarse approximation, due to lack of further detail, disregards the condition that carcass c1 from source s1 is in batch h.
The probability that carcass c is present in batch j given that carcass c from source s is present in the hot batch h can now be determined. This probability is computed as one minus the product of the probabilities that carcass c is not in batch j via equivalence with any other carcass from any other source:
|
Prob(c in j|c from s in h)=1−Prob(c not in j|c from s in h)=1−S∏i=1Ci∏k=1[1−Prob((c from s≡k from i)&(k from i in j)|c from s in h)]=1−[1−Prob(c from s in h&j)Prob(c from s in h)]S∏i=1i≠sCi∏k=1[1−Prob(c from s≡k from i|c from s in h)Prob(k from i in j)]
|
(12)
|
In the last pair of lines of the above equation the factor with i=s is separated out from the i product since its product over k collapses to a single factor. Also the conditional probability rule
|
Prob(A|B)=Prob(A&B)/Prob(B)
|
has been used in this factor. Equation (12) may be computed using Equations (7), (8), and (11).
2.7. Probability of other batches being contaminated
The probability that batch j is also contaminated given that batch h is contaminated is then found by 1) summing over all raw sources, computing the probability that that source is hot, 2) summing over all carcasses in that source, computing the probability that that carcass is hot, and 3) multiplying by the probability that that carcass is also present in batch j.
|
Prob(j hot |h is hot)=S∑s=1Prob(s is hot |h)×Cs∑c=1[Prob(c from s is hot |h)Prob(c in j|c from s in h)]
|
(13)
|
This expression can be evaluated using (1)-(12).
3. Results and discussion
The following two examples illustrate the above model. The first is a synthetic full set of data for a fictitious beef processing plant, the second is based on a partial data set from genetic typing experiments done at an actual production plant. The data for this final example are used to provide estimates for the spread of a carcass within a raw source and to inform the model about masses of raw source input to batches. Unfortunately, it is not possible to directly verify the model with data since a processing facility clearly cannot deliberately contaminate their ground beef supply with E. coli. However, further experiments would be beneficial to help determine the spread of carcasses within a raw source, which will depend very much on the processes in place at any given facility.
3.1. Synthetic data
These data are fictitious but based on typical values one might encounter in a large ground beef production facility. In this example, there are a total of S=7 sources (three frozen lean, two fresh lean, and two fresh fat), and a total of B=14 one-tonne batches of ground beef are produced. Relevant information for the sources is provided in Table 2. The carcass overlap fractions between different sources were taken as zero except for the following overlap between the fresh sources:
Table 2. Model parameters for the raw sources in the synthetic data set.
| Source |
gs |
fs |
ps |
as (kg) |
N1s |
Cs |
Ms (kg) |
| Ⅰ(frozen lean) |
0.2 |
0.05 |
25 |
0.5 |
15 |
160 |
2000 |
| Ⅱ (frozen lean) |
0.2 |
0.09 |
25 |
0.5 |
15 |
160 |
2000 |
| Ⅲ (frozen lean) |
0.2 |
0.07 |
25 |
0.5 |
15 |
160 |
2000 |
| Ⅳ(fresh lean) |
0.8 |
0.10 |
20 |
0.25 |
20 |
500 |
2500 |
| Ⅴ (fresh lean) |
0.8 |
0.08 |
20 |
0.25 |
20 |
600 |
3000 |
| Ⅵ (fresh fat) |
1.0 |
0.40 |
40 |
0.2 |
30 |
250 |
2000 |
| Ⅶ (fresh fat) |
1.0 |
0.45 |
40 |
0.2 |
30 |
250 |
2000 |
|
V45=0.001V46=0.02V47=0.005V56=0.007V57=0.01V67=0.001
|
The uniform distribution for F (K=1, H±0=H−1=1/(2N1spsas)) was used for all raw sources in this example. The mass from each source used in each batch is provided in Table 3.
Table 3. Source input mass, msb, (kg) and total fat percentage for the synthetic data set.
|
Source |
|
|
frozen lean |
fresh lean |
fresh fat |
|
| Batch |
Ⅰ |
Ⅱ |
Ⅲ |
Ⅳ |
Ⅴ |
Ⅵ |
Ⅶ |
fat % |
| 1 |
312 |
|
|
136 |
|
552 |
|
25 |
| 2 |
384 |
|
|
52 |
|
564 |
|
25 |
| 3 |
114 |
|
|
404 |
|
260 |
222 |
25 |
| 4 |
262 |
|
|
239 |
|
231 |
268 |
25 |
| 5 |
201 |
205 |
|
89 |
|
293 |
212 |
25 |
| 6 |
320 |
180 |
|
292 |
|
100 |
108 |
15 |
| 7 |
407 |
105 |
|
284 |
|
|
204 |
15 |
| 8 |
|
390 |
|
456 |
|
|
154 |
15 |
| 9 |
|
300 |
|
205 |
325 |
|
170 |
15 |
| 10 |
|
209 |
|
211 |
543 |
|
37 |
10 |
| 11 |
|
293 |
|
132 |
536 |
|
39 |
10 |
| 12 |
|
318 |
94 |
|
540 |
|
48 |
10 |
| 13 |
|
|
479 |
|
454 |
|
67 |
10 |
| 14 |
|
|
701 |
|
226 |
|
73 |
10 |
Before displaying the final results, we first illustrate some of the intermediate model computations for this example. The probability that a particular source is the hot source given that batch h is hot, is determined by Equation (9). Given the values in Tables 2 and 3, this probability is easily computed and is reported in Table 4 for each source and each batch being the hot batch. As can be seen from this table, the fresh fat sources typically have the highest probability of being the hot source, followed by the fresh lean sources. This is due to both the fact that the contamination factor gs in Table 2 is highest for the fat sources, and also because the fat content fs in these sources is highest. For example, if Batch 11 is the hot batch, the probability that Source Ⅶ is the hot raw source from which the contaminated carcass came is above 25% even though Source Ⅶ only contributed 39 out of 1,000 kg to the batch.
Table 4. Probability (%) that sources are hot, given hot batch h, for the synthetic data set. Prob(s1 is hot |h) is computed from Equation (9) and the data from Tables 2 and 3. Blank entries indicate zero probability due to no mass input.
|
Source |
| hot |
frozen lean |
fresh lean |
fresh fat |
| Batch |
Ⅰ |
Ⅱ |
Ⅲ |
Ⅳ |
Ⅴ |
Ⅵ |
Ⅶ |
| 1 |
1.3 |
|
|
4.6 |
|
94.0 |
|
| 2 |
1.6 |
|
|
1.8 |
|
96.6 |
|
| 3 |
0.5 |
|
|
13.6 |
|
43.8 |
42.1 |
| 4 |
1.1 |
|
|
8.2 |
|
39.4 |
51.4 |
| 5 |
0.9 |
1.6 |
|
3.2 |
|
52.0 |
42.3 |
| 6 |
2.7 |
2.7 |
|
19.7 |
|
33.8 |
41.1 |
| 7 |
3.4 |
1.6 |
|
18.9 |
|
|
76.2 |
| 8 |
|
6.2 |
|
32.3 |
|
|
61.4 |
| 9 |
|
4.5 |
|
13.8 |
17.5 |
|
64.2 |
| 10 |
|
5.2 |
|
23.4 |
48.2 |
|
23.1 |
| 11 |
|
7.8 |
|
15.6 |
50.7 |
|
25.9 |
| 12 |
|
9.1 |
2.1 |
|
54.7 |
|
34.2 |
| 13 |
|
|
10.2 |
|
44.1 |
|
45.7 |
| 14 |
|
|
17.2 |
|
25.3 |
|
57.5 |
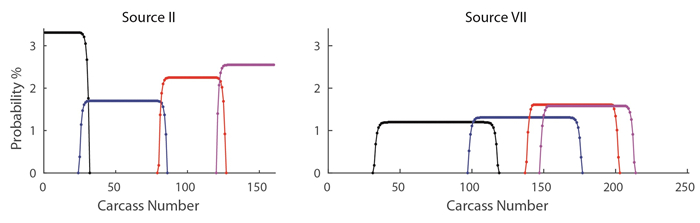
The probability that a particular carcass within a raw source is the contaminated carcass given that batch h is the hot batch is given by Equation (10) and computed using Equations (1)-(7). For this example, using the uniform distribution as indicated, the results of this calculation for several hot batches h and Sources Ⅱ and Ⅶ are shown in Figure 4. Note from this figure that as the hot batch number increases, the carcass numbers with nonzero probability of being the hot carcass also shift to the right. The flat section of each probability curve is due to the fact that the chosen carcass distribution functions for this example are fairly narrow, and hence most of the central mass contributed to the batch from this source has the same probability of being contaminated. Wider curves correspond to batches that take larger amounts of mass from the source. Results for other sources and other hot batches are similarly computed.
The probability that a particular carcass from a particular raw source that is present in batch h is also present in batch j is given by (12). Consider carcass number 100 in Source Ⅵ. From Tables 2 and 3 this source consists of 250 carcasses comprising 2000 kg, about the second quarter of which is input to Batch 2. It is not difficult to show given the piece distribution function, that if there were no overlap of carcasses between sources, this carcass would only be present in Batch 2. However, since Source Ⅵ overlaps with Sources Ⅳ, Ⅴ, and Ⅶ in this example (V46, V56, and V67 are nonzero), there will be nonzero probability of this carcass appearing in other batches. Figure 5 displays this probability. Since V46 is considerably larger than either V56 or V67, the nonzero probability of carcass 100 from Source Ⅵ being present in other batches is larger for the batches to which Source Ⅳ contributes significantly, namely Batches 3, 4 and 6 through 11.
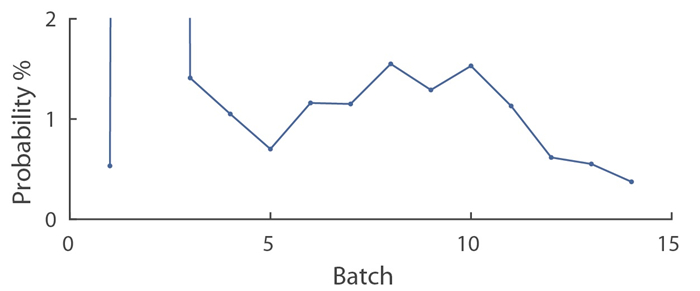
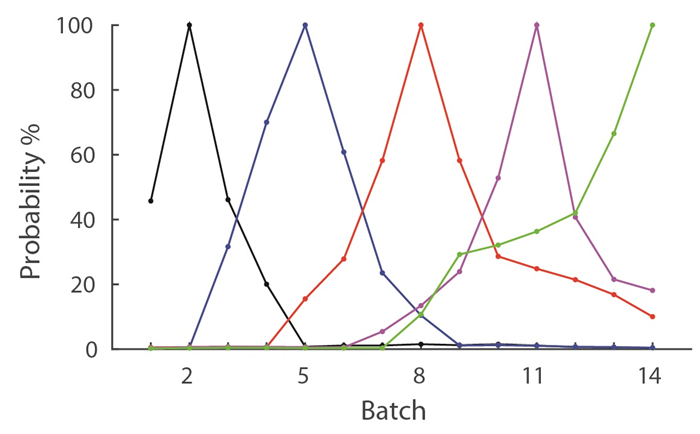
Using the full model, and letting each batch be the hot batch in turn, probabilities of contamination for each batch were computed. Complete results are given in Table 5 and a selection of these are plotted in Figure 6.
Table 5. Probability of contamination for each batch in percent. Each column corresponds to a different hot batch.
|
hot batch |
| Batch |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| 1 |
100 |
46 |
3 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
| 2 |
60 |
100 |
33 |
12 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
| 3 |
4 |
46 |
100 |
63 |
32 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
| 4 |
1 |
20 |
75 |
100 |
70 |
40 |
16 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
| 5 |
1 |
1 |
32 |
63 |
100 |
78 |
41 |
16 |
1 |
1 |
1 |
1 |
0 |
0 |
| 6 |
1 |
1 |
1 |
29 |
61 |
100 |
63 |
28 |
10 |
1 |
0 |
0 |
0 |
0 |
| 7 |
1 |
1 |
1 |
10 |
23 |
44 |
100 |
58 |
31 |
7 |
5 |
4 |
1 |
0 |
| 8 |
1 |
1 |
1 |
1 |
10 |
20 |
61 |
100 |
56 |
14 |
13 |
15 |
15 |
11 |
| 9 |
1 |
1 |
1 |
1 |
1 |
8 |
35 |
58 |
100 |
48 |
24 |
26 |
29 |
29 |
| 10 |
1 |
1 |
1 |
1 |
1 |
1 |
16 |
29 |
62 |
100 |
53 |
28 |
31 |
32 |
| 11 |
1 |
1 |
1 |
1 |
1 |
1 |
11 |
25 |
43 |
47 |
100 |
50 |
35 |
36 |
| 12 |
1 |
1 |
1 |
1 |
1 |
1 |
7 |
21 |
39 |
20 |
41 |
100 |
56 |
42 |
| 13 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
17 |
34 |
18 |
22 |
47 |
100 |
67 |
| 14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
27 |
14 |
18 |
27 |
57 |
100 |
The likelihood of other batches being contaminated is highly dependent on the source input. In the example, if one of the early batches is the hot batch, then the likelihood of contamination is large only for batches near the hot batch. Conversely, if one of the last batches is the hot batch, then a greater number of other batches have large probability of being contaminated. This is due to the source configuration shown in Tables 2 and 3. Since the contamination is most likely to be carried in the fatty sources (Ⅵ and Ⅶ) followed by the lean fresh sources (Ⅳ and Ⅴ), the distribution of these sources across the batches is a primary contributor to the contamination probability distribution. The other two factors that were found to be very important were the values of N1s and Vs1s2. If these spread indicators were small, then the contamination was much more confined to nearby batches to the hot batch. The overall result then, is the obvious observation that if one wishes to restrict contamination, then one should restrict the spread of each carcass within the raw source, and restrict the spread of the raw source across batches. In other words, try to make it so that one carcass is present in as few batches as possible.
3.2. Real data
These data are from genetic typing experiments performed at an industrial ground beef production facility in 2012. The primary goal of these experiments was to see if genetic typing could be used to accurately determine the number of carcasses present in a ground beef batch and to estimate the amount of overlap of genetic material from batch to batch. Samples of beef were taken from the final ground beef product and genetically analyzed to determine the number of different "profiles" (or distinct animals) present. These profiles were then compared against the profiles found from sampling other batches and the number of shared samples was reported. In addition, this data set provides some information on the sources input to each batch but only partial information on mass amounts. The company where these genetic typing experiments were performed has not provided permission to be named and the experimental results are not publicly available, hence these data are provided without reference.
Although these experiments were not designed specifically to help construct and validate this model, they do provide some information that can be utilized. Our model requires a knowledge of the spread of a carcass across a raw source, but the samples for these data were taken from the final ground beef batches, not raw sources. Therefore these data do not distinguish spread differences between raw sources. Nonetheless, the information available is used to estimate the spread of carcasses in all sources assuming all sources have identical spreads.
There were eight raw sources: four frozen lean, two fresh lean, and two fresh fat. In this experiment 30 of 45 sequential batches were sampled and genetically profiled. Table 6 gives the number of distinct genetic profiles in each batch and the number that match profiles from other batches. The data in this table are interpreted as the weighted average of the conditional probability that a particular carcass is present in batch j given that it is present in batch h, the weights being the probability that that carcass is present in h. That is, if Tjh is the entry from row j and column h of the table (although the table does not show the bottom triangle, it is symmetric so that Tjh=Thj), then
Table 6. Number of profiles (on the diagonal) and profile matches between batches.
| Batch |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
15 |
16 |
20 |
21 |
22 |
23 |
27 |
28 |
29 |
30 |
33 |
40 |
41 |
42 |
43 |
44 |
45 |
| 1 |
87 |
7 |
15 |
12 |
4 |
7 |
2 |
2 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 2 |
|
56 |
10 |
2 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
| 3 |
|
|
64 |
6 |
0 |
2 |
4 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
| 4 |
|
|
|
61 |
4 |
8 |
3 |
4 |
0 |
2 |
2 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
|
|
|
|
57 |
14 |
1 |
4 |
2 |
1 |
4 |
3 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 6 |
|
|
|
|
|
62 |
5 |
6 |
3 |
3 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
2 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
| 7 |
|
|
|
|
|
|
66 |
12 |
6 |
4 |
3 |
3 |
0 |
0 |
0 |
0 |
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
| 8 |
|
|
|
|
|
|
|
50 |
3 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
| 9 |
|
|
|
|
|
|
|
|
56 |
9 |
6 |
5 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
| 10 |
|
|
|
|
|
|
|
|
|
50 |
4 |
4 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
| 11 |
|
|
|
|
|
|
|
|
|
|
58 |
9 |
2 |
0 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 12 |
|
|
|
|
|
|
|
|
|
|
|
61 |
3 |
1 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
2 |
0 |
0 |
0 |
2 |
2 |
0 |
0 |
| 13 |
|
|
|
|
|
|
|
|
|
|
|
|
67 |
3 |
1 |
0 |
0 |
1 |
0 |
0 |
2 |
2 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
11 |
0 |
3 |
2 |
2 |
1 |
0 |
4 |
1 |
0 |
2 |
0 |
0 |
0 |
0 |
2 |
| 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
0 |
6 |
3 |
2 |
0 |
1 |
3 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
7 |
7 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
| 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
11 |
4 |
0 |
2 |
3 |
0 |
5 |
0 |
0 |
1 |
0 |
0 |
0 |
| 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
3 |
1 |
2 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
2 |
1 |
1 |
1 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
| 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
3 |
4 |
2 |
2 |
4 |
0 |
0 |
0 |
0 |
1 |
| 28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
3 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
| 29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
10 |
5 |
1 |
1 |
0 |
0 |
0 |
0 |
| 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
0 |
1 |
1 |
0 |
0 |
1 |
| 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53 |
5 |
4 |
4 |
8 |
3 |
| 41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
7 |
3 |
6 |
8 |
| 42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
27 |
13 |
5 |
| 43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
15 |
11 |
| 44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
14 |
| 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
TjhThh=#matched profiles in batches h and j#profiles in batch h=∑Ss1=1∑Cs1c1=1Prob(c1 from s1 in h)Prob(c1 in j|c1 from s1 in h)∑Ss1=1∑Cs1c=1Prob(c1 from s1 in h).
|
(14)
|
The above can be calculated using (7) and (12). Since the data are limited, providing only information on carcass spread through sums of the sources rather than spread in individual sources, in order not to have too many parameters, the spread in all sources is assumed to be described by the same two-piece (K=2) continuous (H−1=H+1, H±2=0) distribution function F. The data indicated that there were four suppliers from whom Source Ⅰ, Sources Ⅱ-Ⅳ, Sources Ⅴ-Ⅵ, and Sources Ⅶ-Ⅷ originated, respectively. For this reason, only source pairs Ⅱ and Ⅲ, Ⅱ and Ⅳ, Ⅲ and Ⅳ, Ⅴ and Ⅵ, and Ⅶ and Ⅷ were allowed to have overlap of carcasses, and the overlap fraction was assumed the same for Ⅱ and Ⅲ, Ⅱ and Ⅳ, and Ⅲ and Ⅳ. The number of pieces, p, and the average piece mass, a, were also taken as the same for each source. The parameters a, p, H, N, and V were chosen so that the computed values from the right side of (14) were as close as possible to the data values from the left side of (14) using a sum of squared differences as the minimization function. These results are shown in Table 7. The best fit to the data indicated that each carcass in a raw source contributes 8 pieces of average size 0.1 lbs. (0.045 kg) to that source, totalling 0.8 lbs (0.364 kg). The carcass distributions are concentrated fairly tightly around their centres, but with long, low tails. Over 94% of the carcass distribution lies within about 26 carcasses (21 lbs., 9.545 kg) on either side of its centre, with the remaining spreading out as far as 6202 carcasses (4,962 lbs., 2,255 kg). These parameters for the carcass distributions were used in all eight of the model's raw sources.
Table 7. Fit carcass distribution parameters for the combined raw sources. The overlap fractions V24 and V34 are equal to V23.
| p |
a (kg) |
N1 |
N2 |
H±0 |
H±1 |
V23 |
V56 |
V78 |
| 8 |
0.045 |
27 |
6383 |
4.351×10−2 |
1.177×10−5 |
0.08 |
0 |
0.20 |
The data from Table 6 indicate profile matches between Batches 1-10 and 23-45 even though Table 8 shows there are no common raw sources for these two sets of batches. Consequently, there must be some overlap of carcasses across raw sources. The fitted overlap fractions indicate a substantial carcass overlap in Sources Ⅱ-Ⅳ (three of the frozen lean sources) and between Sources Ⅶ and Ⅷ (the two fresh fat sources), but no overlap between Sources Ⅴ and Ⅵ (the two fresh lean sources).
Table 8. Estimated source input mass, msb, (kg) for real data set.
|
Source |
|
frozen lean |
fresh lean |
fresh fat |
| Batch |
Ⅰ |
Ⅱ |
Ⅲ |
Ⅳ |
Ⅴ |
Ⅵ |
Ⅶ |
Ⅷ |
| 1-10 |
355 |
355 |
|
|
264 |
|
255 |
|
| 11-13 |
|
355 |
355 |
|
264 |
|
255 |
|
| 14-17 |
|
355 |
355 |
|
132 |
132 |
255 |
|
| 18-20 |
|
355 |
355 |
|
|
264 |
255 |
|
| 21-22 |
|
355 |
355 |
|
|
264 |
|
255 |
| 23-40 |
|
|
709 |
|
|
264 |
|
255 |
| 41-45 |
|
|
|
709 |
|
264 |
|
255 |
Unfortunately, in the data available to us, only the mass input from each raw source to the first batch was recorded as well as an indication (without mass amounts) of which raw sources were used in subsequent batches from which samples were taken. Based on this, the mass input was estimated as shown in Table 8 for all 45 batches. No further information about the raw sources was provided by this data set even though much of it would have been available to have been recorded. The remaining parameters needed for our model have been estimated (or derived from previous assumptions) and are given in Table 9. Of the remaining parameters, the susceptibility, gs, and the fat content, fs, were given reasonable but arbitrary values and so that the fat content of the ground beef batches was about 10%. The mass of each source, Ms, and the number of carcasses in each source were calculated using the assumed mass inputs of Table 8 and the estimated values of p and a from Table 7.
Table 9. Estimated and derived model parameters for the raw sources.
| Source |
gs |
fs |
Cs |
Ms (kg) |
| Ⅰ (frozen lean) |
0.2 |
0.05 |
1,950 |
3,545 |
| Ⅱ (frozen lean) |
0.2 |
0.05 |
4,290 |
7,800 |
| Ⅲ (frozen lean) |
0.2 |
0.05 |
9,360 |
17,018 |
| Ⅳ (frozen lean) |
0.2 |
0.05 |
1,950 |
3,545 |
| Ⅴ(fresh lean) |
0.8 |
0.10 |
2,175 |
3,955 |
| Ⅵ (fresh lean) |
0.8 |
0.10 |
4,350 |
7,909 |
| Ⅶ (fresh fat) |
1.0 |
0.24 |
2,800 |
5,091 |
| Ⅷ (fresh fat) |
1.0 |
0.24 |
3,500 |
6,364 |
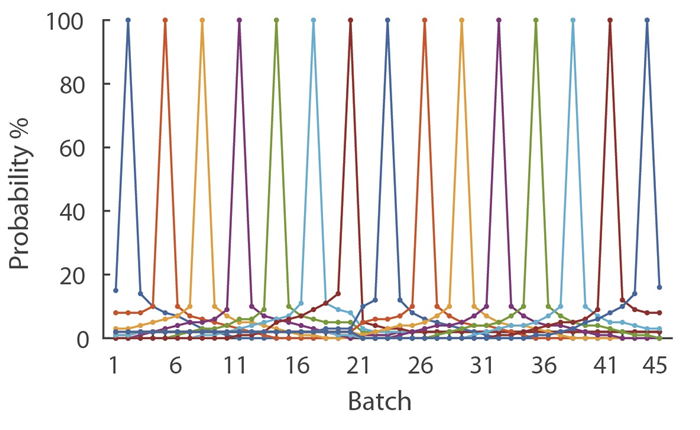
Complete results are given in Tables 10 and 11 and a selection of these are plotted in Figure 7. As can be seen in these tables, the probability of contamination of batches immediately adjacent to the hot batch is typically about 10-15%. Batches further away have a decreasing chance of contamination but the probability does not drop to zero until about 8-10 batches away from the hot batch. This is primarily due to the spread distribution of carcasses in the raw sources, which, as noted above, is very concentrated near the centre. The fresh fat source changes from Source Ⅶ for batches 1-20 to Source Ⅷ for batches 21-45, as shown in Table 8. Since much of the contamination probability is due to these fat sources (high in fat fs and relatively high susceptibility factors gs, Table 9), there is a noticeable asymmetric effect when the hot batch is near this switch. When batch 20 is the hot batch, batches prior to 20 show greater probability of also being contaminated than do batches after 20. This effect is present to a lesser degree when the hot batch is number 17, 18, or 19. Similarly, when the hot batch is 21, batches after 21 show a greater probability of contamination than those prior, and this effect is also seen to a lesser degree for hot batches 21, 22, and 23. There is also evidence of "long-range" contamination spread. As shown in Tables 10 and 11 and indicated in their captions, Batches 21-45 have a small (about 2%) probability of contamination when the hot batch is in the range 1-20, and similarly Batches 1-20 have a small probability of contamination when the hot batch is in the range 21-45. This long-range contamination spread is primarily due to the carcass overlap probability between Sources Ⅶ and Ⅷ, V78=0.2. As mentioned above, Source Ⅶ is input to the first 20 batches and Source Ⅷ to Batches 21-45. Since these sources have a relatively high probability of being contaminated, their overlap causes long-range contamination spreading.
Table 10. Probability of contamination for Batches 1-24 in percent for hot batches (columns) 1-20. Batches 25-45 (not shown) all had probability of contamination of 2 percent for hot Batches 1-20.
|
hot batch |
| Batch |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 1 |
100 |
15 |
12 |
10 |
8 |
6 |
5 |
3 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
16 |
100 |
14 |
10 |
8 |
7 |
5 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
12 |
14 |
100 |
12 |
8 |
7 |
5 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
10 |
10 |
12 |
100 |
10 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
9 |
8 |
8 |
11 |
100 |
10 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 6 |
7 |
7 |
7 |
7 |
10 |
100 |
10 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 7 |
5 |
5 |
5 |
6 |
7 |
10 |
100 |
10 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
| 8 |
3 |
3 |
4 |
5 |
6 |
7 |
10 |
100 |
10 |
7 |
5 |
5 |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
| 9 |
2 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
100 |
10 |
6 |
5 |
5 |
3 |
3 |
2 |
1 |
0 |
0 |
0 |
| 10 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
100 |
9 |
6 |
6 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
| 11 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
5 |
6 |
9 |
100 |
10 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
1 |
| 12 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
5 |
6 |
10 |
100 |
10 |
6 |
6 |
5 |
4 |
2 |
2 |
1 |
| 13 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
100 |
9 |
6 |
6 |
5 |
3 |
3 |
2 |
| 14 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
3 |
4 |
6 |
6 |
9 |
100 |
10 |
7 |
6 |
5 |
5 |
5 |
| 15 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
100 |
10 |
7 |
7 |
6 |
6 |
| 16 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
100 |
11 |
8 |
8 |
7 |
| 17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
11 |
100 |
11 |
9 |
9 |
| 18 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
2 |
3 |
5 |
7 |
8 |
11 |
100 |
13 |
11 |
| 19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
2 |
5 |
6 |
7 |
9 |
13 |
100 |
14 |
| 20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
5 |
6 |
7 |
8 |
11 |
14 |
100 |
| 21 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
4 |
4 |
5 |
| 22 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
4 |
4 |
| 23 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
| 24 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
Table 11. Probability of contamination for Batches 1-4 and 16-45 in percent for hot batches (columns) 21-45. Batches 5-15 (not shown) all had probability of contamination of 2 percent for hot batches 21-45.
|
hot batch |
| Batch |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
| 2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
| 3 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 4 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| ⋮ |
| 16 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 17 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 18 |
4 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
| 19 |
4 |
4 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
| 20 |
5 |
4 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
| 21 |
100 |
14 |
10 |
9 |
7 |
5 |
4 |
3 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 22 |
14 |
100 |
12 |
9 |
7 |
6 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 23 |
10 |
12 |
100 |
12 |
8 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 24 |
9 |
9 |
12 |
100 |
11 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 25 |
7 |
7 |
8 |
11 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 26 |
6 |
6 |
6 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 27 |
4 |
4 |
5 |
6 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 28 |
3 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 29 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 30 |
1 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 31 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 32 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
| 33 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
| 34 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
| 35 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
1 |
0 |
| 36 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
4 |
4 |
3 |
2 |
1 |
1 |
| 37 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
5 |
4 |
3 |
2 |
2 |
| 38 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
10 |
7 |
5 |
5 |
4 |
3 |
3 |
| 39 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
10 |
100 |
11 |
6 |
6 |
5 |
5 |
5 |
| 40 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
4 |
4 |
5 |
7 |
11 |
100 |
9 |
6 |
6 |
6 |
7 |
| 41 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
4 |
5 |
5 |
6 |
9 |
100 |
12 |
9 |
8 |
8 |
| 42 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
4 |
5 |
5 |
6 |
12 |
100 |
13 |
10 |
10 |
| 43 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
9 |
12 |
100 |
14 |
12 |
| 44 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
5 |
6 |
8 |
10 |
14 |
100 |
16 |
| 45 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
5 |
6 |
8 |
9 |
12 |
16 |
100 |
4. Conclusions
We believe that the proposed model may help to reduce economic losses in the beef industry. To our knowledge, this is a novel method for estimating of the probability of E. coli contamination in the production of ground beef. Most of the input to the model is easily obtained from production records, or easily estimated (such as the average size of pieces). The most difficult input values to estimate are the within-source spread parameters, K, L, and H±, and the across-source overlap parameters Vs1s2. However, some knowledge of these values could be obtained through detailed observations of the plant processes or by using genetic sampling experiments in the raw sources as well as the final ground beef product. The model has been implemented in C and is available on the author's web site http://www.uoguelph.ca/awillms/grbeefcontam/. A useful next step would be to use an innocuous surrogate for pathogenic E. coli that could be applied to pieces from a particular carcass and then identified in the final product batches. This would allow for better determination of carcass spread within a raw source and would provide data for direct validation of the model.
As a general statement, results from this model indicate that to restrict the spread of E. coli contamination, ground beef production processes should be designed to restrict the spread of pieces from a single carcass within a raw source, and limit the number of batches to which a given raw source provides input.
Acknowledgments
The authors would like to thank the unnamed company for use of the genetic data from their production plant and the company and individuals responsible for collecting those data. The first author was supported by a grant from the Applied Livestock Genomics Program of Genome Alberta.









 DownLoad:
DownLoad: