Allelic Interaction between <em>CRELD1</em> and <em>VEGFA</em> in the Pathogenesis of Cardiac Atrioventricular Septal Defects

Jennifer K. Redig; Gameil T. Fouad; Darcie Babcock; Benjamin Reshey; Eleanor Feingold; Roger H. Reeves; Cheryl L. Maslen; Jennifer K. Redig; Gameil T. Fouad; Darcie Babcock; Benjamin Reshey; Eleanor Feingold; Roger H. Reeves; Cheryl L. Maslen

doi:10.3934/genet.2014.1.1

AIMS Genetics

2014, Volume 1, Issue 1: 1-19. doi: 10.3934/genet.2014.1.1

Previous Article Next Article

Research article

Allelic Interaction between CRELD1 and VEGFA in the Pathogenesis of Cardiac Atrioventricular Septal Defects

1.
Department of Molecular and Medical Genetics, Oregon Health & Science University, Portland, OR 97239, USA;
2.
Current address, Hume Center for Writing and Speaking, Stanford University, Stanford, CA 94305, USA;
3.
Current address, Biotron Laboratories, West Centerville, UT 84014, USA;
4.
Department of Biomedical Engineering, Oregon Health & Science University, Portland, OR 97239, USA;
5.
Knight Cardiovascular Institute, Oregon Health & Science University, Portland, OR 97239, USA;
6.
Department of Human Genetics, Graduate School of Public Health, University of Pittsburgh, Pittsburgh PA 15261, USA;
7.
Department of Physiology and the Institute for Genetic Medicine, Johns Hopkins University School of Medicine, Baltimore, MD 21205, USA

Received: 01 February 2014 Accepted: 11 March 2014 Published: 27 March 2014

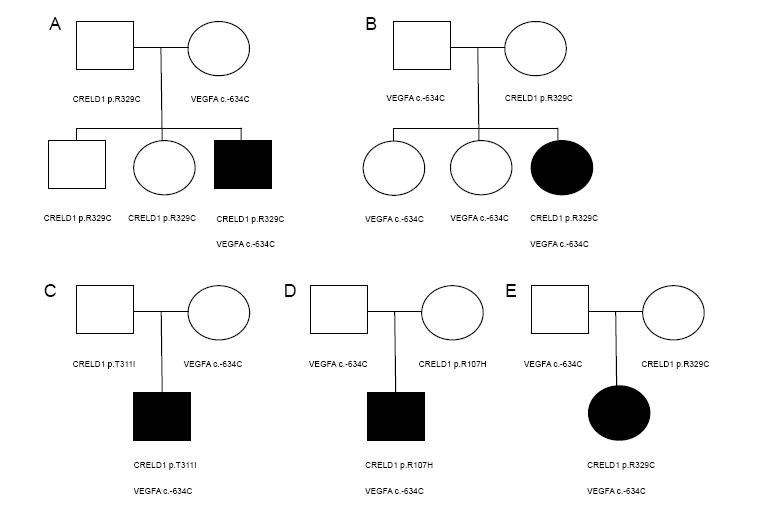
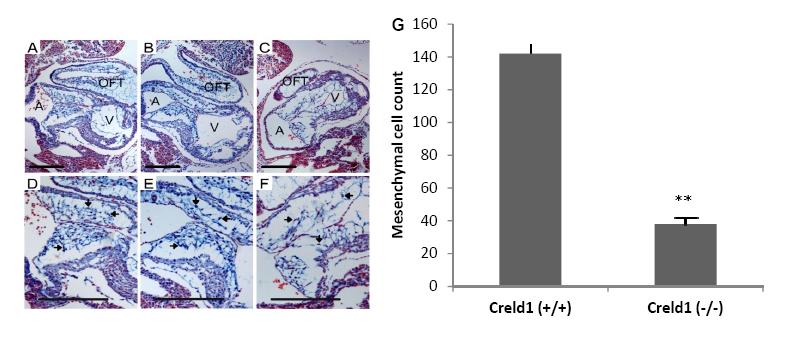
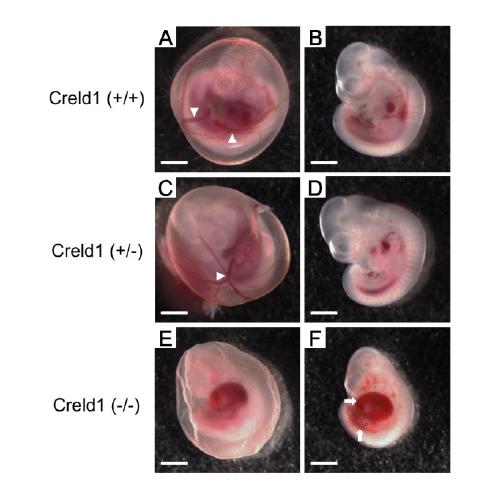
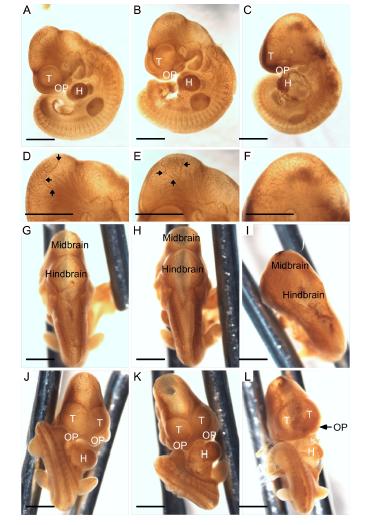
Atrioventricular septal defects (AVSD) are highly heritable, clinically significant congenital heart malformations. Genetic and environmental modifiers of risk are thought to work in unknown combinations to cause AVSD. Approximately 5–10% of simplex AVSD cases carry a missense mutation in CRELD1. However, CRELD1 mutations are not fully penetrant and require interactions with other risk factors to result in AVSD. Vascular endothelial growth factor-A (VEGFA) is a well-characterized modulator of heart valve development. A functional VEGFA polymorphism, VEGFA c.-634C, which causes constitutively increased VEGFA expression, has been associated with cardiac septal defects suggesting it may be a genetic risk factor. To determine if there is an allelic association with AVSD we genotyped the VEGFA c.-634 SNP in a simplex AVSD study cohort. Over-representation of the c.-634C allele in the AVSD group suggested that this genotype may increase risk. Correlation of CRELD1 and VEGFA genotypes revealed that potentially pathogenic missense mutations in CRELD1 were always accompanied by the VEGFA c.-634C allele in individuals with AVSD suggesting a potentially pathogenic allelic interaction. We used a Creld1 knockout mouse model to determine the effect of deficiency of Creld1 combined with increased VEGFA on atrioventricular canal development. Morphogenic response to VEGFA was abnormal in Creld1-deficient embryonic hearts, indicating that interaction between CRELD1 and VEGFA has the potential to alter atrioventricular canal morphogenesis. This supports our hypothesis that an additive effect between missense mutations in CRELD1 and a functional SNP in VEGFA contributes to the pathogenesis of AVSD.

Keywords:

congenital heart disease,
genetic modifier

Citation: Jennifer K. Redig, Gameil T. Fouad, Darcie Babcock, Benjamin Reshey, Eleanor Feingold, Roger H. Reeves, Cheryl L. Maslen. Allelic Interaction between CRELD1 and VEGFA in the Pathogenesis of Cardiac Atrioventricular Septal Defects[J]. AIMS Genetics, 2014, 1(1): 1-19. doi: 10.3934/genet.2014.1.1

Related Papers:

[1]	Maysaa Al-Qurashi, Saima Rashid, Fahd Jarad, Madeeha Tahir, Abdullah M. Alsharif . New computations for the two-mode version of the fractional Zakharov-Kuznetsov model in plasma fluid by means of the Shehu decomposition method. AIMS Mathematics, 2022, 7(2): 2044-2060. doi: 10.3934/math.2022117
[2]	M. Ali Akbar, Norhashidah Hj. Mohd. Ali, M. Tarikul Islam . Multiple closed form solutions to some fractional order nonlinear evolution equations in physics and plasma physics. AIMS Mathematics, 2019, 4(3): 397-411. doi: 10.3934/math.2019.3.397
[3]	Harivan R. Nabi, Hajar F. Ismael, Nehad Ali Shah, Wajaree Weera . W-shaped soliton solutions to the modified Zakharov-Kuznetsov equation of ion-acoustic waves in (3+1)-dimensions arise in a magnetized plasma. AIMS Mathematics, 2023, 8(2): 4467-4486. doi: 10.3934/math.2023222
[4]	Aslı Alkan, Halil Anaç . The novel numerical solutions for time-fractional Fornberg-Whitham equation by using fractional natural transform decomposition method. AIMS Mathematics, 2024, 9(9): 25333-25359. doi: 10.3934/math.20241237
[5]	M. Hafiz Uddin, M. Ali Akbar, Md. Ashrafuzzaman Khan, Md. Abdul Haque . New exact solitary wave solutions to the space-time fractional differential equations with conformable derivative. AIMS Mathematics, 2019, 4(2): 199-214. doi: 10.3934/math.2019.2.199
[6]	Baojian Hong, Jinghan Wang, Chen Li . Analytical solutions to a class of fractional coupled nonlinear Schrödinger equations via Laplace-HPM technique. AIMS Mathematics, 2023, 8(7): 15670-15688. doi: 10.3934/math.2023800
[7]	Sumbal Ahsan, Rashid Nawaz, Muhammad Akbar, Saleem Abdullah, Kottakkaran Sooppy Nisar, Velusamy Vijayakumar . Numerical solution of system of fuzzy fractional order Volterra integro-differential equation using optimal homotopy asymptotic method. AIMS Mathematics, 2022, 7(7): 13169-13191. doi: 10.3934/math.2022726
[8]	Volkan ALA, Ulviye DEMİRBİLEK, Khanlar R. MAMEDOV . An application of improved Bernoulli sub-equation function method to the nonlinear conformable time-fractional SRLW equation. AIMS Mathematics, 2020, 5(4): 3751-3761. doi: 10.3934/math.2020243
[9]	Azzh Saad Alshehry, Naila Amir, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon . On the solution of nonlinear fractional-order shock wave equation via analytical method. AIMS Mathematics, 2022, 7(10): 19325-19343. doi: 10.3934/math.20221061
[10]	Ali Khalouta, Abdelouahab Kadem . A new computational for approximate analytical solutions of nonlinear time-fractional wave-like equations with variable coefficients. AIMS Mathematics, 2020, 5(1): 1-14. doi: 10.3934/math.2020001

Abstract

1. Introduction

In recent decades, importance of fractional order models is well disclosed fact in many fields of engineering and science. Numerous fractional order partial differential equations(FPDEs) have been used by many authors to describe various important biological and physical processes like in the fields of chemistry, biology, mechanics, polymer, economics, biophysics control theory and aerodynamics. In this concern, many researchers have studied various schemes and aspects of PDEs and FPDEs as well, see ^{[1,2,3,4,5,6,7,8,9,10]}. However, the great attention has been given very recently to obtaining the solution of fractional models of the physical interest. Keeping in views, the computation complexities involved in fractional order models is very crucial and is the difficulty in solving these fractional models. Some times, the exact analytic solution of each and every FPDE can not be obtained using the traditional schemes and methods. However, there exists some schemes and methods, which have been proved to be efficient in obtaining the approximation to solution of the fractional order problems. Among them, we bring the attention of readers to these methods and schemes ^{[11,12,13,14,15,16,17,18,19,20,21]} which are used successfully. These methods and schemes have their own demerits and merits. Some of them provide a very good approximation with convenient way. For example, see the methods and schemes in the articles ^{[22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]}.

The main aim of this work is to develop a new procedure which is easy with respect to application and more efficient as compare with existing procedures. In this concern, we introduced asymptotic homotopy perturbation method (AHPM) to obtain the solution of nonlinear fractional order models. It is a new version of perturbation techniques. In simulation section, we have testified our proposed procedure by considering the test problems of non linear fractional order Zakharov-Kuznetsov $ ZK(m, n, r) $ equations of the form ^[11,12]

$\begin{equation} \begin{split}& \frac{{{\partial ^\alpha }u(x, y, t)}}{{\partial {t^\alpha }}} + {a_0}{\left( {{u^m(x, y, t)}} \right)_x} + {a_1}{\left( {{u^n(x, y, t)}} \right)_{xxx}} + {a_2}{\left( {{u^r(x, y, t)}} \right)_{yyx}} = 0, 0 \lt \alpha \le 1. \end{split} \end{equation}$ $

(1.1)

Where $ a_0 $, $ a_1 $, $ a_2 $ are arbitrary constants and $ m, n, r $ are non zero integers. If $ \alpha = 1, $ then equation (1.1) becomes classical Zakharov-Kuznetsov $ ZK(m, n, r) $ equation given as:

$\begin{equation} \begin{split}& \frac{{{\partial}u(x, y, t)}}{{\partial {t }}}+ {a_0}{\left( {{u^m(x, y, t)}} \right)_x} + {a_1}{\left( {{u^m(x, y, t)}} \right)_{xxx}} + {a_2}{\left( {{u^r(x, y, t)}} \right)_{yyx}} = 0. \end{split} \end{equation}$ $

(1.2)

The ZK equation has been firstly modelized for depicting weakly nonlinear ion-acoustic waves in strongly magnetized lossless plasma ^[40]. The ZK equation governs the behavior of weakly nonlinear ion-acoustic waves in plasma comprising cold ions and hot isothermal electrons in the presence of a uniform magnetic field ^[41,42].

The plan of the rest paper is as follows: Section 2 provides theory of the AHPM; Section 3 provides implementation of AHPM. Finally, a brief conclusion and the further work has been listed.

2. Basic idea of AHPM

Here, we provide that the Caputo type fractional order derivative will be used throughout this paper for the computation of derivative.

Let us consider the nonlinear problem in the form as

$\begin{eqnarray} T\left( {u(x, y, t)} \right) + g(x, y, t) = 0, \end{eqnarray}$ $

(2.1)

$\begin{eqnarray} B\left( {u\left( {x, y, t} \right), \frac{{\partial u\left( {x, y, t} \right)}}{{\partial t}}} \right) = 0. \end{eqnarray}$ $

(2.2)

Where $ T\left({u\left({x, y, t} \right)} \right) $ denotes a differential operator which may consists ordinary, partial or space- fractional or time-fractional differential derivative. $ T\left({u\left({x, y, t} \right)} \right) $ can be expressed for fractional model as follows:

$\begin{eqnarray} \frac{{{\partial ^\alpha }u(x, y, t)}}{{\partial {t^\alpha }}} + N\left( {u(x, y, t)} \right) + g(x, y, t) = 0 \end{eqnarray}$ $

(2.3)

subject to the condition

$\begin{eqnarray} B\left( {u\left( {x, y, t} \right), \frac{{\partial u\left( {x, y, t} \right)}}{{\partial t}}} \right) = 0, \end{eqnarray}$ $

(2.4)

where the operator $ \frac{{{\partial ^\alpha }}}{{\partial {t^\alpha }}} $ denotes the Caputo derivative operator, $ N $ is non linear operator and $ B $ denotes a boundary operator, $ u\left({x, y, t} \right) $ is unknown exact solution of Eq. (2.1), $ g\left({x, y, t} \right) $ denotes known function and $ x, y $ and $ t $ denote special and temporal variables respectively. Let us construct a homotopy $ \Phi (x, y, t;p):\Omega \times \left[{0, 1} \right] \to R $ which satisfies

$\begin{eqnarray} \frac{{{\partial ^\alpha }\Phi (x, y, t;p)}}{{\partial {t^\alpha }}} + g(x, y, t) - p\left[ {N\left( {\Phi (x, y, t;p} \right)} \right] = 0, \end{eqnarray}$ $

(2.5)

where $ p \in \left[{0, 1} \right] $ is said to be an embedding parameter. At this phase of our work it is pertinent that our proposed deformation Eq. (2.5) is an alternate form of the deformation equations as

$\begin{eqnarray} \left( {1 - p} \right)\left[ {L\left( {\Phi (x, y, t;p)} \right) - L\left( {{u_0}(x, y, t)} \right) + g(x, y, t)} \right] + p\left[ {T\left( {\Phi (x, y, t;p} \right) + g(x, y, t)} \right] = 0, \end{eqnarray}$ $

(2.6)

$\begin{eqnarray} \left( {1 - p} \right)\left[ {L\left( {\Phi (x, y, t;p)} \right) - L\left( {{u_0}(x, y, t)} \right)} \right] = hp\left[ {T\left( {\Phi (x, y, t;p} \right) + g(x, y, t)} \right] \end{eqnarray}$ $

(2.7)

and

$\begin{eqnarray} \left( {1 - p} \right)\left[ {L\left( {\Phi (x, y, t;p)} \right) + g(x, y, t)} \right] - H\left( p \right)\left[ {T\left( {\Phi (x, y, t;p} \right) + g(x, y, t)} \right] = 0. \end{eqnarray}$ $

(2.8)

in HPM, HAM, OHAM proposed by Liao in ^[43], He in ^[44] and Marinca in ^[45] respectively.

Basically, according to homotopy definition, when $ p = 0 $ and $ p = 1 $ we have

$ \Phi \left( {x, y, t;p} \right) = {u_0}\left( {x, y, t} \right), \phi \left( {x, y, t;p} \right) = u\left( {x, y, t} \right). $

Obviously, when the embedding parameter $ p $ varies from $ 0 $ to $ 1 $, the defined homotopy ensures the convergence of $ \phi \left({x, y, t;p} \right) $ to the exact solution $ u\left({x, y, t} \right) $. Consider $ \phi \left({x, y, t;p} \right) $ in the form

$\begin{eqnarray} \Phi \left( {x, y, t;p} \right) = {u_0}\left( {x, y, t} \right) + \sum\limits_{i = 1}^\infty {{u_i}\left( {x, y, t} \right)} {p^i} \end{eqnarray}$ $

(2.9)

and assuming $ N\left({\Phi \left({x, y, t;p} \right)} \right) $ as follows

$\begin{eqnarray} N\left( {\Phi \left( {x, y, t;p} \right)} \right) = {B_1}{N_0} + \sum\limits_{i = 1}^\infty {\left( {\sum\limits_{m = 0}^i {{B_{i + 1 - m}}{N_m}} } \right)} {p^i}, {{B_1} + {B_2} + {B_3} + ...} = -1. \end{eqnarray}$ $

(2.10)

Where

$\begin{eqnarray} {B_i} = {B_i}(x, y, t, {c_i}), for , i = 1, 2, 3, \dots. \end{eqnarray}$ $

(2.11)

are arbitrary auxiliary functions, will be discussed later. Thus, if $ p = 0 $ and $ p = 1 $ in Eq. (2.5), we have

$ \frac{{{\partial ^\alpha }u(x, y, t)}}{{\partial {t^\alpha }}} + f\left( x \right) = 0, \ \text{and}\ \frac{{{\partial ^\alpha }u(x, y, t)}}{{\partial {t^\alpha }}} + N\left( {u(x, y, t)} \right) + g(x, y, t) = 0, $

respectively.

It is obvious that the construction of introduced auxiliary function in Eq. (2.10) is different from the auxiliary functions that are proposed in articles ^[43,44,45]. Hence the procedure proposed in our paper is different from the procedures proposed by Liao, He, Marinca in aforesaid papers ^[43,44,45] as well as Optimal Homotopy perturbation method (OHPM) in ^[46].

Furthermore, when we substitute Eq. (2.9) and Eq. (2.10) in Eq. (2.5) and equate like power of $ p $, the obtained series of simpler linear problems are

$\begin{equation*} \begin{split}& {p^0}: \frac{{{\partial ^\alpha }{u_0}(x, y, t)}}{{\partial {t^\alpha }}} + g = 0, \\& {p^1}: \frac{{{\partial ^\alpha }{u_1}(x, y, t)}}{{\partial {t^\alpha }}} = {B_1}{N_0}, \\& {p^2}: \frac{{{\partial ^\alpha }{u_2}(x, y, t)}}{{\partial {t^\alpha }}} = {B_2}{N_0} + {B_1}{N_1}, \\& {p^3}: \frac{{{\partial ^\alpha }{u_3}(x, y, t)}}{{\partial {t^\alpha }}} = {B_3}{N_0} + {B_2}{N_1} + {B_1}{N_2}, \\& \vdots\\& {p^k}: \frac{{{\partial ^\alpha }{u_k}(x, y, t)}}{{\partial {t^\alpha }}} = \sum\limits_{i = 0}^{k - 1} {{B_{k - i}}{N_i}}. \end{split} \end{equation*}$ $

We obtain the series solutions by using the integral operator $ {J^\alpha } $ on both sides of the above each simple fractional differential equation. The convergence of the series solution Eq. (2.9) to the exact solution depends upon the auxiliary parameters (functions) $ {B_i}(x, y, t, {c_i}) $. The choice of $ {B_i}(x, y, t, {c_i}) $ is purely on the basis of terms appear in nonlinear part of the Eq. (2.1). The Eq.(2.9) converges to the exact solution of Eq. (2.1) at $ p = 1 $:

$\begin{eqnarray} \widetilde u(x, y, t) = {u_0}(x, y, t) + \sum\limits_{k = 1}^\infty {{u_k}(x, y, t;{c_i}), \ i = 1, 2, 3, \dots}. \end{eqnarray}$ $

(2.12)

Particularly, we can truncate the Eq. (2.12) into finite m-terms to obtain the solution of nonlinear problem. The auxiliary convergence control constants $ {c_1}, {c_2}, {c_3}, \dots $ can be found by solving the system

$\begin{eqnarray} R\left( {\partial {x_1}, \partial {y_1}} \right) = R\left( {\partial {x_2}, \partial {y_2}} \right) = R\left( {\partial {x_3}, , \partial {y_3}} \right) = \dots = R\left( {\partial {x_m}, , \partial {y_m}} \right) = 0, \partial {x_i}, \partial {y_i} \in \left[ {a, b} \right]. \end{eqnarray}$ $

(2.13)

It can be verified to observe that HPM is only a case of Eq. (2.5) when $ p = -p $ and

$\begin{eqnarray*} N\left( {\Phi \left( {x, y, t;p} \right)} \right) = {N_0} + \sum\limits_{i = 1}^\infty {{N_i}{p^i}}. \end{eqnarray*}$ $

The HAM is also a case of Eq. (2.5) when $ p = ph $ and

$\begin{eqnarray*} N\left( {\Phi \left( {x, y, t;p} \right)} \right) = {N_0} + \sum\limits_{i = 1}^\infty {{N_i}{p^i}}. \end{eqnarray*}$ $

The OHAM is also another case when

$\begin{eqnarray*} {B_{k - 1}} = {B_{k - 2}} + {h_k}\left( {t, {c_j}} \right) + \sum\limits_{i = 0}^{k - 2} {{h_{\left( {_{k - (i + 1)}} \right)}}\left( {t, {c_j}} \right)} {B_i}, \ \text{and}\ {h_k}\left( {t, {c_j}} \right) = {c_k} \end{eqnarray*}$ $

in Eq. (2.10), we obtain exactly the series problems which are obtained by OHAM after expanding and equating the like power of $ p $ in deformation equation. Furthermore, concerning the Optimal Homotopy Asymptotic Method (OHAM) mentioned in this manuscript and presented in ^[45], that the version of OHAM proposed in 2008 was improved in time and the most recent improvement, which also contains an auxiliary functions, are presented in the papers ^[47,48]. We also have improved the version of OHAM by introducing a very new auxiliary function in Eq. (2.10). Our method proposed in this paper uses a very new and more general form of auxiliary function

$ N\left( {\phi \left( {x, y, t;p} \right)} \right) = {B_1}{N_0} + \sum\limits_{i = 1}^\infty {\left( {\sum\limits_{m = 0}^i {{B_{i + 1 - m}}{N_m}} } \right)} {p^i} $

which depends on arbitrary parameters $ {B_1}, {B_2}, {B_3}, \dots $ and is useful for adjusting and controlling the convergence of nonlinear part as well as linear part of the problem with simple way.

3. Applications

In this portion, we apply AHPM to obtain solution of the following problems to show the accuracy and appropriateness of the new procedure for to solve nonlinear problems.

Problem 3.1. Let us consider FZK$ (2, 2, 2) $ in the form:

$\begin{eqnarray} \frac{{{\partial ^\alpha }u(x, y, t)}}{{\partial {t^\alpha }}} + {\left( {{u^2}(x, y, t)} \right)_x} + \frac{1}{8}{\left( {{u^2}(x, y, t)} \right)_{xxx}} + \frac{1}{8}{\left( {{u^2}(x, y, t)} \right)_{yyx}} = 0, {\mkern 1mu} {\mkern 1mu} 0 \lt \alpha \le 1, \end{eqnarray}$ $

(3.1)

subject to the condition

$\begin{equation*} u\left( {x, y, 0} \right) = \frac{4}{3}k{\sinh ^2}\left( {x + y} \right). \end{equation*}$ $

When $ \alpha = 1 $. Then the exact solution of Eq. (3.1):

$\begin{equation*} u\left( {x, y, t} \right) = \frac{4}{3}k{\sinh ^2}\left( {x + y-kt} \right). \end{equation*}$ $

As in Eq. (3.1), the non linear part

$\begin{equation*} N\left( {u(x, y, t)} \right) = {\left( {{u^2}(x, y, t)} \right)_x} + \frac{1}{8}{\left( {{u^2}(x, y, t)} \right)_{xxx}} + \frac{1}{8}{\left( {{u^2}(x, y, t)} \right)_{yyx}}. \end{equation*}$ $

Now, follow the procedure of AHPM, we obtain series of the simpler linear problems as:

Zero order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_0}}}{{\partial {t^\alpha }}} = 0, {u_0} = \frac{4}{3}k{\sinh ^2}\left( {x + y} \right). \end{eqnarray}$ $

(3.2)

First order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_1}}}{{\partial {t^\alpha }}} = {B_1}{N_0}, {u_1} = 0. \end{eqnarray}$ $

(3.3)

Second order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_2}}}{{\partial {t^\alpha }}} = {B_2}{N_0} + {B_1}{N_1}, {u_2} = 0. \end{eqnarray}$ $

(3.4)

Third order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_3}}}{{\partial {t^\alpha }}} = {B_3}{N_0} + {B_2}{N_1} + {B_1}{N_2}, {u_3} = 0. \end{eqnarray}$ $

(3.5)

Fourth order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_4}}}{{\partial {t^\alpha }}} = {B_4}{N_0} + {B_3}{N_1} + {B_2}{N_2} + {B_1}{N_3}, {u_4} = 0 \end{eqnarray}$ $

(3.6)

and so on.

Solving the above equations, the respective solutions from Eqs. (3.2)–(3.6) are given as follow:

$\begin{eqnarray} {u_0}\left( {x, y, t} \right) = \frac{4}{3}k{\sinh ^2}(z) \end{eqnarray}$ $

(3.7)

$\begin{eqnarray} {u_1}\left( {x, y, t} \right) = {B_1}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} \end{eqnarray}$ $

(3.8)

$\begin{eqnarray} {u_2}\left( {x, y, t} \right) = {B_2}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} + \frac{{64}}{{27}}{B_1}^2{k^3}\left[ {13\cosh\left( {2z} \right) - 70\cosh\left( {4z} \right) + 75\cosh\left( {6z} \right)} \right] \frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}, \end{eqnarray}$ $

(3.9)

$\begin{array}{l} {u_3}\left( {x, y, t} \right) = \\ {B_3}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} + \frac{{64}}{{27}}{B_1}{B_2}{k^3}\left[ {13\cosh \left( {2z} \right) - 70\cosh \left( {4z} \right) + 75\cosh \left( {6z} \right)} \right]\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}\\ + {B_1}\frac{{64}}{{81}}{k^3}\left[ \begin{array}{l} {B_2}\left( {39\cosh \left( {2z} \right) - 210\cosh \left( {4z} \right) + 225\cosh \left( {6z} \right)} \right)\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}\\ + {B_1}^2k\left( {\begin{array}{*{20}{l}} {160\sinh \left( {2z} \right) + 320\sinh \left( {4z} \right) - 2400\sinh \left( {6z} \right)}\\ { + 3400\sinh \left( {8z} \right)} \end{array}} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{2\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}}\\ + {B_1}^2k\left( {\begin{array}{*{20}{l}} { - 768\sinh \left( {2z} \right) + 9120\sinh \left( {4z} \right) - 26400\sinh \left( {6z} \right)}\\ { + 20400\sinh \left( {8z} \right)} \end{array}} \right)\frac{{{t^{3\alpha }}}}{{\Gamma \left( {3\alpha + 1} \right)}}{\rm{ }} \end{array}$ \right] \end{array}$

(3.10)

$\begin{array}{l} {u_4}\left( {x, y, t} \right) = \\ {B_4}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} + \frac{{64}}{{27}}{B_1}{B_3}{k^3}\left[ {13\cosh \left( {2z} \right) - 70\cosh \left( {4z} \right) + 75\cosh \left( {6z} \right)} \right]\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}} + {B_2}\frac{{64}}{{81}}{k^3}\\ \left[ {\begin{array}{*{20}{l}} {{B_2}\left( {39\cosh \left( {2z} \right) - 210\cosh \left( {4z} \right) + 225\cosh \left( {6z} \right)} \right)\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}}\\ { + {B_1}^2k\left( {\begin{array}{*{20}{l}} {160\sinh \left( {2z} \right) + 320\sinh \left( {4z} \right) - }\\ {2400\sinh \left( {6z} \right) + 3400\sinh \left( {8z} \right)} \end{array}} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{2\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}}}\\ { + {B_1}^2k\left( {\begin{array}{*{20}{l}} { - 768\sinh \left( {2z} \right) + 9120\sinh \left( {4z} \right) - }\\ {26400\sinh \left( {6z} \right) + 20400\sinh \left( {8z} \right)} \end{array}} \right)\frac{{{t^{3\alpha }}}}{{\Gamma \left( {3\alpha + 1} \right)}}} \end{array}} \right] + {B_1}\frac{{64}}{{243}}{k^3}\\ \left[ \begin{array}{l} {B_1}^3{k^2}\left( {1022400\cosh \left( {6z} \right) - 15200\cosh \left( {4z} \right) - 2502400\cosh \left( {8z} \right) + 1768000\cosh \left( {10z} \right)} \right)\\ \frac{{2\Gamma \left( {2\alpha } \right){t^{4\alpha }}}}{{\alpha {{\left( {\Gamma \left( \alpha \right)} \right)}^2}\Gamma \left( {4\alpha + 1} \right)}} + {B_1}^3{k^2}\left( {\begin{array}{*{20}{l}} {85248\cosh \left( {2z} \right) - 1816320\cosh \left( {4z} \right) + 9878400\cosh \left( {6z} \right)}\\ { - 18278400\cosh \left( {8z} \right) + 10608000\cosh \left( {10z} \right)} \end{array}} \right)\\ \frac{{{t^{4\alpha }}}}{{\Gamma \left( {4\alpha + 1} \right)}} + {B_3}\left( {117\cosh \left( {2z} \right) - 630\cosh \left( {4z} \right) + 675\cosh \left( {6z} \right)} \right)\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}} + {B_1}^3{k^2}\\ \left( {\begin{array}{*{20}{l}} { - 56640\cosh \left( {2z} \right) + 119040\cosh \left( {4z} \right) + 496800\cosh \left( {6z} \right)}\\ { - 2121600\cosh \left( {8z} \right) + 2340000\cosh \left( {10z} \right)} \end{array}} \right)\frac{{\Gamma \left( {3\alpha + 1} \right){t^{4\alpha }}}}{{\Gamma \left( {\alpha + 1} \right)\Gamma \left( {2\alpha + 1} \right)\Gamma \left( {4\alpha + 1} \right)}}\\ + {B_1}{B_2}k\left( {\begin{array}{*{20}{l}} {1440\sinh \left( {2z} \right) + 2880\sinh \left( {4z} \right) - 21600\sinh \left( {6z} \right)}\\ { + 30600\sinh \left( {8z} \right)} \end{array}} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{3\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}}\\ + {B_1}{B_2}k\left( {\begin{array}{*{20}{l}} { - 4608\sinh \left( {2z} \right) + 54720\sinh \left( {4z} \right) - 158400\sinh \left( {6z} \right)}\\ { + 122400\sinh \left( {8z} \right)} \end{array}} \right)\frac{{{t^{3\alpha }}}}{{\Gamma \left( {3\alpha + 1} \right)}} \end{array}$ \right] \end{array}$

(3.11)

so on $\dots$.

In similar way, we can compute the solution of the next simpler linear problems which are difficult to compute by using OHAM procedure. we choose $ {{B_1} = {c_1}, B_2} = {c_2}, {B_3} = {c_3}, {B_4} = {c_4} $ and consider

$\begin{eqnarray} \widetilde u(x) = {u_0}(x) + {u_1}(x, {c_1}) + {u_2}(x, {c_1}, {c_2}) + {u_3}(x, {c_1}, {c_2}, {c_3})+{u_4}(x, {c_1}, {c_2}, {c_3}, {c_4}) . \end{eqnarray}$ $

(3.12)

The residual:

$\begin{eqnarray} R\left( {\widetilde u\left( {x, y, t} \right)} \right) = \frac{{{\partial ^\alpha }\widetilde u\left( {x, y, t} \right)}}{{\partial {t^\alpha }}} + {\left( {{{\widetilde u}^2}(x, y, t)} \right)_x} + \frac{1}{8}{\left( {{{\widetilde u}^2}(x, y, t)} \right)_{xxx}} + \frac{1}{8}{\left( {{{\widetilde u}^2}(x, y, t)} \right)_{yyx}}. \end{eqnarray}$ $

(3.13)

We obtain number of optimal values of auxiliary constants by using the Eq. (2.13) and choose those optimal values whose sum is in $ \left[{- 1, } \right.\left. 0 \right) $. Now, substituting the optimal values of auxiliary constants (from the Table 1) into the Eq. (3.12), we obtain the AHPM solutions for different values of $ \alpha $ at $ k = 0.001 $

Table 1. The auxiliary control constants for the problem 3.1.

$ Aux. Const. $	$ \alpha=1 $	$ \alpha=0.75 $	$ \alpha=0.67 $
$ c_1 $	$ -0.03206298594 $	$ 0.02857059949 $	$ 0.02811316381 $
$ c_2 $	$ -0.05626044816 $	$ -0.09201640919 $	$ -0.09255449827 $
$ c_3 $	$ -0.03255192821 $	$ 0.23864503710 $	$ 0.24163106460 $
$ c_4 $	$ 0.09230916402 $	$ -0.58155364530 $	$ -0.59008434920 $
$ c_1+c_2+c_3+ c_4 $	$ -0.0286 $	$ -0.4064 $	$ -0.4129 $

| Show Table

DownLoad: CSV

If $ \alpha = 1, $ then we have

$\begin{equation*} \begin{split}& \widetilde u\left( {x, y, t} \right)\\& = 6.67{e^{ - 4}}\cosh(2z) - 1.5{e^{ - 36}}\cosh(2x - 2y) + 1.52{e^{ - 10}}{t^2}\cosh(2z) - 8.2{e^{ - 10}}{t^2}\cosh(4z) - 9.82{e^{ - 19}}{t^4}\\& \cosh(2z)- 1.96 {e^{ - 17}} {t^4}\cosh(4z) - 3.44 {e^{ - 16}}{t^4}\cosh(8z) + 9.74{e^{ - 15}}{t^3}\sinh(2z) - 2.7 {e^{ - 13}}{t^3}\sinh(4z) -\\& 7.91 {e^{ - 13}}{t^3}\sinh(8z) + 2.45{e^{ - 16}}{t^4}\cosh(10z)+ 8.79{e^{ - 10}}{t^2}\cosh(6z) + 1.56{e^{ - 16}}{t^4}\cosh(6z) + 8.85{e^{ - 13}}{t^3}\\& \sinh(6z) + 1.02{e^{ - 7}}t\sinh(2z) - 1.27{e^{ - 7}}t\sinh(4z) - 6.67{e^{ - 4}}. \end{split} \end{equation*}$ $

If $ \alpha = 0.75, $ then we have

$\begin{equation*} \begin{split}& \widetilde u\left( {x, y, t} \right) \\& = 6.67{e^{ - 4}}\cosh(2z) - 1.5{e^{ - 36}}\cosh(2z) - 9.63{e^{ - 19}}{t^3}\cosh(2z) - 5.12{e^{ - 17}}{t^3}\cosh(4z) + 4.09{e^{ - 10}}{t^{3/2}}\\& \cosh(2z) - 7.79{e^{ - 16}}{t^3}\cosh(8z) - 2.2{e^{ - 9}}{t^{3/2}}\cosh(4z) + 1.57{e^{ - 6}}{t^{3/4}}\sinh(2z) - 1.97{e^{ - 6}}{t^{3/4}}\sinh(4z) \\& + 2.65{e^{ - 14}}{t^{9/4}}\sinh(2z)- 6.14 {e^{ - 13}}{t^{9/4}} \sinh(4z) - 1.74 {e^{ - 12}}{t^{9/4}}\sinh(8z) + 5.34 {e^{ - 16}}{t^3}\cosh(10z) +\\& 3.66 {e^{ - 16}}{t^3}\cosh(6z) + 2.36 {e^{ - 9}}{t^{3/2}}\cosh(6z) + 1.98{e^{ - 12}}{t^{9/4}}\sinh(6z) - 6.67{e^{ - 4}}. \end{split} \end{equation*}$ $

If $ \alpha = 0.67, $ then we have

$\begin{equation*} \begin{split}& \widetilde u\left( {x, y, t} \right) \\& = 6.67{e^{ - 4}}\cosh(2z) - 1.5{e^{ - 36}}\cosh(2x - 2y) - 8.33{e^{ - 19}}{t^{67/25}}\cosh(2z) - 7.12{e^{ - 17}}{t^{67/25}}\cosh(4z) - \\& 1.05{e^{ - 15}}{t^{67/25}}\cosh(8z) + 4.57 {e^{ - 10}}{t^{67/50}}\cosh(2z) - 2.46 {e^{ - 9}}{t^{67/50}}\cosh(4z) + 1.63 {e^{ - 6}}{t^{67/100}}\sinh(2z)\\& - 2.03 {e^{ - 6}}{t^{67/100}}\sinh(4z)+ 3.45 {e^{ - 14}}{t^{201/100}}\sinh(2z) - 7.54 {e^{ - 13}}{t^{201/100}}\sinh(4z) - 2.1 {e^{ - 12}}{t^{201/100}}\\& \sinh(8z) + 7.09 {e^{ - 16}} {t^{67/25}}\cosh(10z) + 4.97 {e^{ - 16}}{t^{67/25}}\cosh(6z) + 2.64 {e^{ - 9}}{t^{67/50}}\cosh(6z) +2.41 {e^{ - 12}}\\& {t^{201/100}}\sinh(6z) - 6.67{e^{ - 4}}. \end{split} \end{equation*}$ $

Tables 2 and 3 show the AHPM solution, VIM solution, exact solution and absolute error of AHPM solution. It is obvious from Tables 2 and 3 that AHPM solution results are more accurate to the exact solution results as compare with VIM ^[11] solution results. The AHPM solution, exact solution and absolute error of AHPM solution are plotted for different values of $ \alpha $, $ x $, $ y $ and $ t $ in Figures 1 and 2. The curves of AHPM and exact solution are exactly matching as compare with homotopy perturbation transform method (HPTM)^[12]. It is obvious from the Tables 2 and 3, Figures 1 and 2, that the AHPM solution of the problem 3.1 is in very good agreement with exact solution.

Table 2. Solution of the problem 3.1 for various values of $ \alpha $, $ x $, $ y $ and $ t $ at $ k = 0.001 $.

$ x $	$ y $	$ t $	VIM ^[1] ($ \alpha=0.67 $)	AHPM ($ \alpha=0.67 $)	VIM ^[1] ($ \alpha=0.75 $)	AHPM ($ \alpha=0.75 $)
$ 0.1 $	$ 0.1 $	$ 0.2 $	$ 5.312992862e-5 $	$ 0.000053661825095 $	$ 5.325267164e-5 $	$ 0.000053719590053 $
		$ 0.3 $	$ 5.285029317e-5 $	$ 0.000053541299605 $	$ 5.297615384e-5 $	$ 0.000053602860321 $
		$ 0.4 $	$ 5.260303851e-5 $	$ 0.000053433636044 $	$ 5.272490734e-5 $	$ 0.000053495694982 $
$ 0.6 $	$ 0.6 $	$ 0.2 $	$ 2.953543396e-3 $	$ 0.0029991909006 $	$ 2.964363202e-3 $	$ 0.0030049612043 $
		$ 0.3 $	$ 2.928652795e-3 $	$ 0.0029871641418 $	$ 2.939926307e-3 $	$ 0.0029932937681 $
		$ 0.4 $	$ 2.905913439e-3 $	$ 0.0029764476067 $	$ 2.917239345e-3 $	$ 0.002982607386 $
$ 0.9 $	$ 0.9 $	$ 0.2 $	$ 1.045289537e-2 $	$ 0.011096367296 $	$ 1.064555345e-2 $	$ 0.011161869914 $
		$ 0.3 $	$ 0.990546789e-2 $	$ 0.010960230827 $	$ 1.017186398e-2 $	$ 0.011029208413 $
		$ 0.4 $	$ 0.927982231e-2 $	$ 0.010839735959 $	$ 0.960539982e-2 $	$ 0.010908463773 $

| Show Table

DownLoad: CSV

Table 3. Solution and absolute error of the problem 3.1 for various values of $ x $, $ y $ and $ t $ at $ k = 0.001, \alpha = 1 $.

$ x $	$ y $	$ t $	VIM ^[1]	AHPM	Exact	VIM ^[1]	AHPM Error
$ 0.1 $	$ 0.1 $	$ 0.2 $	$ 5.355612471e-5 $	$ 0.00005403406722 $	$ 5.393877159e-5 $	$ 3.83e-7 $	$ 9.53e-8 $
		$ 0.3 $	$ 5.331384269e-5 $	$ 0.000054026996643 $	$ 5.388407669e-5 $	$ 5.7e-7 $	$ 1.43e-7 $
		$ 0.4 $	$ 5.307396595e-5 $	$ 0.000054019939232 $	$ 5.382941057e-5 $	$ 7.55e-7 $	$ 1.91e-7 $
$ 0.6 $	$ 0.6 $	$ 0.2 $	$ 2.991347666e-3 $	$ 0.0030365547595 $	$ 3.036507411e-3 $	$ 4.52e-5 $	$ 4.73e-8 $
		$ 0.3 $	$ 2.969760240e-3 $	$ 0.0030358658613 $	$ 3.035778955e-3 $	$ 6.6e-5 $	$ 8.69e-8 $
		$ 0.4 $	$ 2.948601126e-3 $	$ 0.0030351876618 $	$ 3.035050641e-3 $	$ 8.64e-5 $	$ 1.37e-7 $
$ 0.9 $	$ 0.9 $	$ 0.2 $	$ 1.102746671e-2 $	$ 0.011526053047 $	$ 1.153697757e-2 $	$ 5.1e-4 $	$ 1.09e-5 $
		$ 0.3 $	$ 1.073227877e-2 $	$ 0.011518772848 $	$ 1.153454074e-2 $	$ 8.02e-4 $	$ 1.58e-5 $
		$ 0.4 $	$ 1.035600465e-2 $	$ 0.011511900292 $	$ 1.153210438e-2 $	$ 0.00118 $	$ 2.02e-5 $

| Show Table

DownLoad: CSV

Figure 1. AHPM solution, exact solution and absolute error of AHPM solution of Problem 3.1 at $ \alpha $ = 1 and $ t $ = 0.5 when $ k $ = 0.001.

DownLoad: Full-Size Img PowerPoint

Figure 2. AHPM solution of the Problem 3.1 for various values of $ x $ and $ y $ at $ t $ = 0.5 when $ k $ = 0.001.

DownLoad: Full-Size Img PowerPoint

Problem 3.2. Now, we consider FZK$ (3, 3, 3) $ in the form:

$\begin{eqnarray} \frac{{{\partial ^\alpha }u(x, y, t)}}{{\partial {t^\alpha }}} + {\left( {{u^3}(x, y, t)} \right)_x} + 2{\left( {{u^3}(x, y, t)} \right)_{xxx}} + 2{\left( {{u^3}(x, y, t)} \right)_{yyx}} = 0, {\mkern 1mu} 0 \lt \alpha \le 1, \end{eqnarray}$ $

(3.14)

subject to condition

$ u\left( {x, y, 0} \right) = \frac{3}{2}k\sinh \left( {\frac{1}{6}\left( {x + y} \right)} \right). $

When $ \alpha = 1 $. Then the exact solution of equation (3.14):

$ u\left( {x, y, t} \right) = \frac{3}{2}k\sinh \left( {\frac{1}{6}\left( {x + y-kt} \right)} \right). $

As in Eq. (3.14), the non linear part:

$ N\left( {u(x, y, t)} \right) = {\left( {{u^3}(x, y, t)} \right)_x} + 2{\left( {{u^3}(x, y, t)} \right)_{xxx}} + 2{\left( {{u^3}(x, y, t)} \right)_{yyx}}. $

Now, follow the procedure of AHPM, we obtain series of the simpler linear problems as follow:

Zero order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_0}}}{{\partial {t^\alpha }}} = 0, {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {u_0} = \frac{3}{2}k\sinh \left( {\frac{1}{6}\left( {x + y} \right)} \right). \end{eqnarray}$ $

(3.15)

First order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_1}}}{{\partial {t^\alpha }}} = {B_1}{N_0}, {u_1} = 0. \end{eqnarray}$ $

(3.16)

Second order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_2}}}{{\partial {t^\alpha }}} = {B_2}{N_0} + {B_1}{N_1}, {u_2} = 0. \end{eqnarray}$ $

(3.17)

Third order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_3}}}{{\partial {t^\alpha }}} = {B_3}{N_0} + {B_2}{N_1} + {B_1}{N_2}, {u_3} = 0. \end{eqnarray}$ $

(3.18)

Fourth order problem:

$\begin{eqnarray} \frac{{{\partial ^\alpha }{u_4}}}{{\partial {t^\alpha }}} = {B_4}{N_0} + {B_3}{N_1} + {B_2}{N_2} + {B_1}{N_3}, {u_4} = 0. \end{eqnarray}$ $

(3.19)

The respective solutions of the Eqs. (3.15)–(3.19) are given as follow:

$\begin{eqnarray*} {u_0}\left( {x, y, t} \right) & = & \frac{3}{2}k\sinh \left( {{ {1 \over 6}}z} \right), \\ {u_1}\left( {x, y, t} \right) & = & {B_1}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}}, \\ {u_2}\left( {x, y, t} \right) & = & {B_2}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} + \frac{3}{{32}}{k^5}{B_1}^2\left[ \begin{array}{l} 801{{\sinh }^3}\left( {{ {1 \over 6}}z} \right) + 765{{\sinh }^4}\left( {{ {1 \over 6}}z} \right)\\ + 127\sinh \left( {{ {1 \over 6}}z} \right)\end{array} \right]\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}, \end{eqnarray*}$ $

$\begin{eqnarray*} \begin{array}{l} {u_3}\left( {x, y, t} \right) = {B_3}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} + \frac{3}{{32}}{k^5}{B_1}{B_2}\left[ {801{{\sinh }^3}\left( {{ {1 \over 6}}z} \right) + 765{{\sinh }^4}\left( {{ {1 \over 6}}z} \right) + 127\sinh \left( {{ {1 \over 6}}z} \right)} \right]\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}\\ + {B_1}\frac{3}{{8192}}{k^5}\left[ \begin{array}{l} {B_2}\left( {1120\sinh \left( {{ {1 \over 6}}z} \right) - 9936\sinh \left( {{ {1 \over 2}}z} \right) + 12240\sinh \left( {{ {5 \over 6}}z} \right)} \right)\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}\\ {B_1}^2{k^2}\left( \begin{array}{l} 1350\cosh \left( {{ {1 \over 2}}z} \right) + 2770\cosh \left( {{ {1 \over 6}}z} \right) - 29070\cosh \left( {{ {5 \over 6}}z} \right)\\ + 32886\cosh \left( {{ {7 \over 6}}z} \right)\end{array} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{3\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}}\\ {B_1}^2{k^2}\left( \begin{array}{l} 56079\cosh \left( {{ {1 \over 2}}z} \right) - 4155\cosh \left( {{ {1 \over 6}}z} \right) - 182835\cosh \left( {{ {5 \over 6}}z} \right) \\ + 155295\cosh \left( {{ {7 \over 6}}z} \right)\end{array} \right)\frac{{{t^{3\alpha }}}}{{\Gamma \left( {3\alpha + 1} \right)}} \end{array} \right] \end{array}, \end{eqnarray*}$ $

$\begin{eqnarray*} \begin{array}{l} {u_4}\left( {x, y, t} \right) = \\ {B_4}{N_0}\frac{{{t^\alpha }}}{{\Gamma \left( {\alpha + 1} \right)}} + \frac{3}{{32}}{k^5}{B_1}{B_3}\left[ {801{{\sinh }^3}\left( {{ {1 \over 6}}z} \right) + 765{{\sinh }^4}\left( {{ {1 \over 6}}z} \right) + 127\sinh \left( {{ {1 \over 6}}z} \right)} \right]\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}} + {B_2}\frac{3}{{8192}}{k^5}\\ \left[ \begin{array}{l} {B_2}\left( {1120\sinh \left( {{ {1 \over 6}}z} \right) - 9936\sinh \left( {{ {1 \over 2}}z} \right) + 12240\sinh \left( {{ {5 \over 6}}z} \right)} \right)\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}\\ {B_1}^2{k^2}\left( \begin{array}{l} 1350\cosh \left( {{ {1 \over 2}}z} \right) + 2770\cosh \left( {{ {1 \over 6}}z} \right) - 29070\cosh \left( {{ {5 \over 6}}z} \right)\\ + 32886\cosh \left( {{ {7 \over 6}}z} \right)\end{array} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{3\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}}\\ {B_1}^2{k^2}\left( \begin{array}{l} 56079\cosh \left( {{ {1 \over 2}}z} \right) - 4155\cosh \left( {{ {1 \over 6}}z} \right) - 182835\cosh \left( {{ {5 \over 6}}z} \right) \\ + 155295\cosh \left( {{ {7 \over 6}}z} \right)\end{array} \right)\frac{{{t^{3\alpha }}}}{{\Gamma \left( {3\alpha + 1} \right)}} \end{array} \right] + {B_1}\frac{1}{{131072}}{k^5}\\ \left[ \begin{array}{l} {B_1}^3{k^3}\left( {937040\cosh \left( {{ {1 \over 3}}z} \right) - 36000\cosh \left( {{ {2 \over 3}}z} \right) + 16083360\cosh \left( {{ {4 \over 3}}z} \right)} \right)\frac{{\Gamma \left( {3\alpha + 1} \right){t^{4\alpha }}}}{{\Gamma \left( {\alpha + 1} \right)\Gamma \left( {2\alpha + 1} \right)\Gamma \left( {4\alpha + 1} \right)}}\\ + {B_3}\left( { - 476928\sinh \left( {{ {1 \over 2}}z} \right) + 53760\sinh \left( {{ {1 \over 6}}z} \right) + 587520\sinh \left( {{ {5 \over 6}}z} \right)} \right)\frac{{{t^{2\alpha }}}}{{\Gamma \left( {2\alpha + 1} \right)}}\\ + {B_1}^3{k^4}\left( \begin{array}{l} 552744\sinh \left( {{ {1 \over 2}}z} \right) + 1771470\sinh \left( {{ {3 \over 2}}z} \right) - 63900\sinh \left( {{ {1 \over 6}}z} \right) \\ - 275400\sinh \left( {{ {5 \over 6}}z} \right) - 1479870\sinh \left( {{ {7 \over 6}}z} \right) \end{array} \right)\frac{{\Gamma \left( {3\alpha + 1} \right){t^{4\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {4\alpha + 1} \right)}}\\ + {B_1}^3{k^4}\left( \begin{array}{l} - 2349000\sinh \left( {{ {1 \over 2}}z} \right) + 39956490\sinh \left( {{ {3 \over 2}}z} \right) - 21300\sinh \left( {{ {1 \over 6}}z} \right)\\ + 23555880\sinh \left( {{ {5 \over 6}}z} \right) - 57758778\sinh \left( {{ {7 \over 6}}z} \right) \end{array} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{4\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {4\alpha + 1} \right)}}\\ + {B_1}^3{k^4}\left( \begin{array}{l} 2948400\sinh \left( {{ {1 \over 2}}z} \right) + 33461100\sinh \left( {{ {3 \over 2}}z} \right) - 540600\sinh \left( {{ {1 \over 6}}z} \right)\\ + 9510480\sinh \left( {{ {5 \over 6}}z} \right) - 39704364\sinh \left( {{ {7 \over 6}}z} \right) - 10167120\cosh \left( z \right) \end{array} \right)\frac{{\Gamma \left( {3\alpha + 1} \right){t^{4\alpha }}}}{{\Gamma \left( {\alpha + 1} \right)\Gamma \left( {2\alpha + 1} \right)\Gamma \left( {4\alpha + 1} \right)}}\\ + {B_1}^3{k^4}\left( \begin{array}{l} - 24230988\sinh \left( {{ {1 \over 2}}z} \right) + 188683425\sinh \left( {{ {3 \over 2}}z} \right) + 903510\sinh \left( {{ {1 \over 6}}z} \right) + \\ 147146220\sinh \left( {{ {5 \over 6}}z} \right) - 300495825\sinh \left( {{ {7 \over 6}}z} \right) \end{array} \right)\frac{{{t^{4\alpha }}}}{{\Gamma \left( {4\alpha + 1} \right)}}\\ + {B_1}{B_2}{k^2}\left( \begin{array}{l} 5383584\cosh \left( {{ {1 \over 2}}z} \right) - 398880\cosh \left( {{ {1 \over 6}}z} \right) - 17552160\cosh \left( {{ {5 \over 6}}z} \right) \\+ 14908320\cosh \left( {{ {7 \over 6}}z} \right) \end{array} \right)\frac{{{t^{3\alpha }}}}{{\Gamma \left( {3\alpha + 1} \right)}}\\ + {B_1}{B_2}k\left( \begin{array}{l} 1399680\sinh \left( z \right) - 108160\sinh \left( {{ {1 \over 3}}z} \right) - 576000\sinh \left( {{ {2 \over 3}}z} \right) \end{array} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{3\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}}\\ + {B_1}{B_2}{k^2}\left( \begin{array}{l} 129600\cosh \left( {{ {1 \over 2}}z} \right) + 265920\cosh \left( {{ {1 \over 6}}z} \right) - 2790720\cosh \left( {{ {5 \over 6}}z} \right) \\+ 3157056\cosh \left( {{ {7 \over 6}}z} \right) \end{array} \right)\frac{{\Gamma \left( {2\alpha + 1} \right){t^{3\alpha }}}}{{{{\left( {\Gamma \left( {\alpha + 1} \right)} \right)}^2}\Gamma \left( {3\alpha + 1} \right)}} \end{array} \right] \end{array} \end{eqnarray*}$ $

and so on.

In similar way, we can compute the solution of the next simpler linear problems. We choose $ {{B_1} = {c_1}, B_2} = {c_2}, {B_3} = {c_3}, {B_4} = {c_4} $ and consider

$\begin{eqnarray} \widetilde u(x) = {u_0}(x) + {u_1}(x, {c_1}) + {u_2}(x, {c_1}, {c_2}) + {u_3}(x, {c_1}, {c_2}, {c_3})+{u_3}(x, {c_1}, {c_2}, {c_3}, {c_4}). \end{eqnarray}$ $

(3.20)

We compute the residual;

$\begin{equation*} R\left( {\widetilde u\left( {x, y, t} \right)} \right) = \frac{{{\partial ^\alpha }\widetilde u(x, y, t)}}{{\partial {t^\alpha }}} + {\left( {{{\widetilde u}^3}(x, y, t)} \right)_x} + 2{\left( {{{\widetilde u}^3}(x, y, t)} \right)_{xxx}} + 2{\left( {{{\widetilde u}^3}(x, y, t)} \right)_{yyx}}. \end{equation*}$ $

We obtain number of optimal values of auxiliary constants by using the Eq. (2.13) and choose those optimal values whose sum is in $ \left[{- 1, } \right.\left. 0 \right) $. Now, substituting the optimal values of auxiliary constants (from Table 4) into the Eq. (3.20), we obtain the AHPM solutions for different values of $ \alpha $ at $ k = 0.001. $

Table 4. The auxiliary control constants for the problem 3.2.

$ Aux. Const. $	$ \alpha=1 $	$ \alpha=0.75 $	$ \alpha=0.67 $
$ c_1 $	$ -0.5877657093 $	$ -0.6018150968 $	$ -0.2216842316 $
$ c_2 $	$ -0.1517357373 $	$ -0.1655454563 $	$ -1.594288158 $
$ c_3 $	$ -0.3855312838 $	$ -0.3415880346 $	$ 5.172517408 $
$ c_4 $	$ 0.1250311669 $	$ 0.10894720410 $	$ -4.35654487 $
$ c_1+c_2+c_3+ c_4 $	$ -1.0000 $	$ -1.0000 $	$ -1.0000 $

| Show Table

DownLoad: CSV

If $ \alpha = 1, $ then we have

$\begin{equation*} \begin{split}& \widetilde u\left( {x, y, t} \right) = \\& 1.5 {e^{ - 3}}\sinh \left( {0.17z} \right) - 1.3 {e^{ - 21}}{t^3}\cosh \left( {0.5z} \right) - 6.2 {e^{ - 16}}{t^2}\sinh \left( {0.5z} \right) - 6.4 {e^{ - 28}}{t^4}\sinh \left( {0.5z} \right) - 3.4 {e^{ - 21}} {t^3}\\& \cosh \left( {1.2z} \right) - 1.4{e^{ - 21}}{t^3}\cosh \left( {1.2z} \right) - 2.1{e^{ - 26}}{t^4}\sinh \left( {1.2z} \right) + 1.8{e^{ - 24}}{t^4}\cosh \left( {1.3z} \right) + 1.1{e^{ - 25}}{t^4}\cosh \left( {0.33z} \right) \\& - 2.2{e^{ - 23}}{t^3} \cosh \left( {0.17z} \right) - 4.1 {e^{ - 27}}{t^4}\cosh \left( {0.67z} \right) - 8.9{e^{ - 24}}{t^3}c\cosh \left( {0.17z} \right) + 1.4{e^{ - 20}}{t^3}\sinh \left( {0.33z} \right) + 2.3\\& {e^{ - 17}}{t^2}\sinh \left( {0.17z} \right) + 7.7{e^{ - 20}}{t^3}\sinh \left( {0.67z} \right) + 4.6 {e^{ - 17}}{t^2}\sinh \left( {0.17z} \right) - 4.3 {e^{ - 29}}{t^4}\sinh \left( {0.17z} \right) + 1.4 {e^{ - 26}}{t^4}\\& \sinh \left( {1.5z} \right) + 5.3 {e^{ - 21}}{t^3} \cosh \left( {0.83z} \right) + 5.1 {e^{ - 16}} {t^2} \sinh \left( {0.83z} \right) + 8.4 {e^{ - 27}} {t^4} \sinh \left( {0.83z} \right) + 2.5 {e^{ - 16}} {t^2}\\& \sinh \left( {0.83z} \right) - 1.2 {e^{ - 24}}{t^4}\cosh \left( z \right) - 1.9 {e^{ - 19}}{t^3}\sinh \left( z \right) - 3.8 {e^{ - 10}}t\cosh \left( {0.17z} \right)(9.0{\cosh ^2}\left( {0.17z} \right) - 8) + 3.1\\& {e^{ - 17}}{t^2}\sinh \left( {0.17z} \right)(800.0{\sinh ^2}\left( {0.17z} \right) + 766 {\sinh ^4}\left( {0.17z} \right) + 133). \end{split} \end{equation*}$ $

If $ \alpha = 0.75, $ then we have

$\begin{equation*} \begin{split}& \widetilde u\left( {x, y, t} \right) = \\& 1.5{e^{ - 3}}\sinh \left( {0.17z} \right) - 3.3{e^{ - 21}}{t^{2.25}}\cosh \left( {0.5z} \right) - 3.3{e^{ - 27}}{t^3}\sinh \left( {0.5z} \right) - 9.1{e^{ - 16}}{t^{1.5}}\sinh \left( {0.5z} \right) - 8.3{e^{ - 21}}{t^{2.25}}\\& \cosh \left( {1.2z} \right) - 3.6{e^{ - 21}}{t^{2.25}}\cosh \left( {1.2z} \right) - 8{e^{ - 26}}{t^3}\sinh \left( {1.2z} \right) + 5.6{e^{ - 24}}{t^3}\cosh \left( {1.3z} \right) + 3.3{e^{ - 25}}{t^3}\cosh \left( {0.33z} \right) \\& - 8.2{e^{ - 24}}{t^{2.25}}\cosh \left( {0.17z} \right) - 1.3{e^{ - 26}}{t^3}\cosh \left( {0.67z} \right) - 3.5{e^{ - 24}}{t^{2.25}}\cosh \left( {0.17z} \right) + 3.1 {e^{ - 20}}{t^{(2.25}}\sinh \left( {0.33z} \right)\\& + 3.9 {e^{ - 17}}{t^{1.5}}\sinh \left( {0.17z} \right) + 1.6 {e^{ - 19}}{t^{2.25}}\sinh \left( {0.67z} \right) - 7.8 {e^{ - 29}}{t^3}\sinh \left( {0.17z} \right) + 6.3{e^{ - 17}} {t^{1.5}} \sinh \left( {0.17z} \right) + \\& 5.5 {e^{ - 26}}{t^3}\sinh \left( {1.5z} \right) + 13 {e^{ - 21}}{t^{2.25}}\cosh \left( {0.83z} \right) + 3.4{e^{ - 26}}{t^3}\sinh \left( {0.83z} \right) + 11.2 {e^{ - 16}}{t^{1.5}}\sinh \left( {0.83z} \right) - 3.5\\& {e^{ - 24}} {t^3}\cosh \left( z \right) - 4 {e^{ - 19}} {t^{2.25}}\sinh \left( z \right) - 4.1 {e^{ - 10}} {t^{0.75}}\cosh \left( {0.17z} \right) (9{\cosh ^2}\left( {0.17z} \right) - 8) + 4.7 {e^{ - 17}}{t^{1.5}}\\& \sinh \left( {0.17z} \right) (800{\sinh ^2}\left( {0.17z} \right) + 766{\sinh ^4}\left( {0.17z} \right) + 133). \end{split} \end{equation*}$ $

If $ \alpha = 0.67, $ then we have

$\begin{equation*} \begin{split}& \widetilde u\left( {x, y, t} \right) = \\& 1.5 {e^{ - 3}} \sinh \left( {0.17z} \right) - 2.6 {e^{ - 21}}{t^{2.01}} \cosh \left( {0.5z} \right) - 9.3 {e^{ - 29}}{t^{2.68}}\sinh \left( {0.5z} \right) - 5.3 {e^{ - 15}}{t^{1.34}}\sinh \left( {0.5z} \right) - \\& 3.3{e^{ - 21}}{t^{2.01}}\cosh \left( {1.2z} \right) - 5.8{e^{ - 21}}{t^{2.01}} \cosh \left( {1.2z} \right) - 2.1{e^{ - 27}}{t^{2.68}} \sinh \left( {1.2z} \right) + 1.4{e^{ - 25}}{t^{2.68}}\cosh \left( {1.3z} \right)\\& + 7.9 {e^{ - 27}}{t^{2.68}}\cosh \left( {0.33z} \right) + 1.6 {e^{ - 24}} {t^{2.01}}\cosh \left( {0.17z} \right) - 3.0 {e^{ - 28}} {t^{2.68}}\cosh \left( {0.67z} \right) + 2.7 {e^{ - 24}} {t^{2.01}}\\& \cosh \left( {0.17z} \right) + 4.7 {e^{ - 20}}{t^{2.01}}\sinh \left( {0.33z} \right) + 9.9 {e^{ - 16}}{t^{1.34}} \sinh \left( {0.17z} \right) + 2.5 {e^{ - 19}}{t^{2.01}} \sinh \left( {0.67z} \right) - 1.4\\& {e^{ - 30}}{t^{2.68}}\sinh \left( {0.17z} \right) - 3.9 {e^{ - 16}} {t^{1.34}}\sinh \left( {0.17z} \right) + 1.4 {e^{ - 27}}{t^{2.68}}\sinh \left( {1.5z} \right) + 10 {e^{ - 21}}{t^{2.01}}\cosh \left( {0.83z} \right)\\& + 9.0{e^{ - 28}}{t^{2.68}}\sinh \left( {0.83z} \right) - 4.3{e^{ - 15}}{t^{1.34}} \sinh \left( {0.83z} \right) + 1.1{e^{ - 14}} {t^{1.34}} \sinh \left( {0.83z} \right) - 8.6{e^{ - 26}}{t^{2.68}} \cosh \left( z \right) \\& - 6.1{e^{ - 19}}{t^{2.01}} \sinh \left( z \right) - 4.2{e^{ - 10}}{t^{0.67}} \cosh \left( {0.17z} \right) (9{\cosh ^2}\left( {0.17z} \right) - 8) - 5.8{e^{ - 17}}{t^{1.34}}\sinh \left( {0.17z} \right)\\& (800{\sinh ^2}\left( {0.17z} \right) + 766{\sinh ^4}\left( {0.17z} \right) + 133). \end{split} \end{equation*}$ $

Tables 5–7 show the AHPM solution, VIM solution, exact solution and absolute error of AHPM solution. The AHPM solution, exact solution and absolute error of AHPM solution are plotted for different values of $ \alpha $, $ x $, $ y $ and $ t $ in Figures 3 and 4. It is obvious from the Tables 5–7, Figures 3 and 4, that the AHPM solution of the problem 3.2 is in very good agreement with exact solution.

Table 5. Solution of the problem 3.2 for varios values of $ \alpha $, $ x $, $ y $ and $ t $ at $ k = 0.001 $.

$ x $	$ y $	$ t $	VIM ^[1] ($ \alpha=0.67 $)	AHPM ($ \alpha=0.67 $)	VIM ^[1] ($ \alpha=0.75 $)	AHPM ($ \alpha=0.75 $)
$ 0.1 $	$ 0.1 $	$ 0.2 $	$ 5.000911707e-5 $	$ 0.000050009117063 $	$ 5.000913646e-5 $	$ 0.000050009136457 $
		$ 0.3 $	$ 5.000907252e-5 $	$ 0.000050009072517 $	$ 5.000909264e-5 $	$ 0.000050009092629 $
		$ 0.4 $	$ 5.000903274e-5 $	$ 0.000050009032711 $	$ 5.000905240e-5 $	$ 0.00005000905238 $
$ 0.6 $	$ 0.6 $	$ 0.2 $	$ 3.020038072e-4 $	$ 0.00030200380721 $	$ 3.020038341e-4 $	$ 0.00030200383392 $
		$ 0.3 $	$ 3.020037458e-4 $	$ 0.00030200374584 $	$ 3.020037735e-4 $	$ 0.00030200377354 $
		$ 0.4 $	$ 3.020036910e-4 $	$ 0.000302003691 $	$ 3.020037181e-4 $	$ 0.00030200371809 $
$ 0.9 $	$ 0.9 $	$ 0.2 $	$ 4.567801693e-4 $	$ 0.00045678016935 $	$ 4.567802061e-4 $	$ 0.00045678020615 $
		$ 0.3 $	$ 4.567800847e-4 $	$ 0.00045678008481 $	$ 4.567801231e-4 $	$ 0.00045678012298 $
		$ 0.4 $	$ 4.567800092e-4 $	$ 0.00045678000927 $	$ 4.567800467e-4 $	$ 0.0004567800466 $

| Show Table

DownLoad: CSV

Table 6. Solution and absolute error of the problem 3.2 for various values of $ x $, $ y $ and $ t $ at $ k = 0.001 $ and $ \alpha = 1 $.

$ x $	$ y $	$ t $	VIM ^[1]	AHPM	Exact
$ 0.1 $	$ 0.1 $	$ 0.2 $	$ 5.000918398e-5 $	$ 0.000050009183981 $	$ 4.995923204e-5 $
		$ 0.3 $	$ 5.000914609e-5 $	$ 0.000050009146085 $	$ 4.993421817e-5 $
		$ 0.4 $	$ 5.000910820e-5 $	$ 0.000050009108189 $	$ 4.990920434e-5 $
$ 0.6 $	$ 0.6 $	$ 0.2 $	$ 3.020038992e-4 $	$ 0.0003020038994 $	$ 3.019530008e-4 $
		$ 0.3 $	$ 3.020038472e-4 $	$ 0.00030200384719 $	$ 3.019274992e-4 $
		$ 0.4 $	$ 3.020037950e-4 $	$ 0.00030200379498 $	$ 3.019019978e-4 $
$ 0.9 $	$ 0.9 $	$ 0.2 $	$ 4.567802964e-4 $	$ 0.00045678029634 $	$ 4.567281735e-4 $
		$ 0.3 $	$ 4.567802242e-4 $	$ 0.00045678022442 $	$ 4.567020404e-4 $
		$ 0.4 $	$ 4.567801525e-4 $	$ 0.00045678015251 $	$ 4.566759074e-4 $

| Show Table

DownLoad: CSV

Table 7. AHPM solution and exact solution and absolute error of AHPM solution of the problem 3.2 for various values of $ \alpha $, $ x $, $ y $ and $ t $ at $ k = 0.001 $.

$ x $	$ y $	$ t $	AHPM ($ \alpha=0.67 $)	AHPM ($ \alpha=0.75 $)	AHPM ($ \alpha=1 $)	Exact ($ \alpha=1 $)	Error
$ 1 $	$ 1 $	$ 0.2 $	$ 0.00050931053201 $	$ 0.0005093105733 $	$ 0.0005093106745 $	$ 0.00050925803257 $	$ 5.26e-8 $
		$ 0.4 $	$ 0.00050931035239 $	$ 0.00050931039427 $	$ 0.00050931051311 $	$ 0.00050920522983 $	$ 1.05e-7 $
		$ 0.6 $	$ 0.00050931020147 $	$ 0.00050931023732 $	$ 0.00050931035172 $	$ 0.00050915242765 $	$ 1.58e-7 $
		$ 0.8 $	$ 0.00050931006661 $	$ 0.00050931009319 $	$ 0.00050931019033 $	$ 0.00050909962604 $	$ 2.11e-7 $
		$ 1 $	$ 0.00050930994256 $	$ 0.00050930995788 $	$ 0.00050931002895 $	$ 0.00050904682499 $	$ 2.63e-7 $
$ 5 $	$ 5 $	$ 0.2 $	$ 0.003829187741 $	$ 0.0038291908792 $	$ 0.00382919857 $	$ 0.0038290737537 $	$ 1.25e-7 $
		$ 0.4 $	$ 0.0038291740912 $	$ 0.0038291772737 $	$ 0.0038291863046 $	$ 0.003828936676 $	$ 2.5e-7 $
		$ 0.6 $	$ 0.0038291626226 $	$ 0.0038291653465 $	$ 0.0038291740396 $	$ 0.0038287996024 $	$ 3.74e-7 $
		$ 0.8 $	$ 0.0038291523746 $	$ 0.0038291543934 $	$ 0.003829161775 $	$ 0.0038286625332 $	$ 4.99e-7 $
		$ 1 $	$ 0.0038291429482 $	$ 0.003829144112 $	$ 0.0038291495107 $	$ 0.0038285254682 $	$ 6.24e-7 $
$ 10 $	$ 10 $	$ 0.2 $	$ 0.020993470055 $	$ 0.020993944094 $	$ 0.02099510678 $	$ 0.020996261505 $	$ 1.15e-6 $
		$ 0.4 $	$ 0.020991408888 $	$ 0.020991888681 $	$ 0.02099325193 $	$ 0.020995559858 $	$ 2.31e-6 $
		$ 0.6 $	$ 0.020989679031 $	$ 0.020990088717 $	$ 0.020991398624 $	$ 0.020994858233 $	$ 3.46e-6 $
		$ 0.8 $	$ 0.020988134787 $	$ 0.020988437313 $	$ 0.020989546856 $	$ 0.020994156633 $	$ 4.61e-6 $
		$ 1 $	$ 0.020986715582 $	$ 0.02098688854 $	$ 0.020987696623 $	$ 0.020993455055 $	$ 5.76e-6 $

| Show Table

DownLoad: CSV

Figure 3. AHPM solution, exact solution and absolute error of AHPM solution of Problem 3.2 at $ \alpha $ = 1 and $ t $ = 0.2 when $ k $ = 0.001.

DownLoad: Full-Size Img PowerPoint

Figure 4. AHPM solution, exact solution and absolute error of AHPM solution of Problem 3.2 at $ \alpha $ = 1 and $ k $ = 0.0001.

DownLoad: Full-Size Img PowerPoint

4. Discussion and conclusions

In this article, asymptotic homotopy perturbation method (AHPM) is developed to solve non-linear fractional models. It is a different procedure from the procedures of HAM, HPM and OHAM. The two special cases, $ ZK(2, 2, 2) $ and $ ZK(3, 3, 3) $ of fractional Zakharov-Kuznetsov model are considered to illustrate a very simple procedure of the homotopy methods. The numerical results in simulation section of AHPM solutions are more accurate to the exact solutions as comparing with fractional complex transform (FCT) using variational iteration method (VIM). In the field of fractional calculus, it is necessary to introduce various procedures and schemes to compute the solution of non-linear fractional models. In this concern, we expect that this new proposed procedure is a best effort. The best improvement and the application of this new procedures to the solution of advanced non-linear fractional models with computer software codes will be our further consideration.

Acknowledgments

The authors would like to thank anonymous referees for their careful corrections to and valuable comments on the original version of this paper.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	Hoffman JIE, Kaplan S (2002) The incidence of congenital heart disease. J Am Coll Cardiol 39: 1890-1900. doi: 10.1016/S0735-1097(02)01886-7
[2]	Blue GM, Kirk EP, Sholler GF, et al. (2012) Congenital heart disease: current knowledge about causes and inheritance. Med J Aust 197: 155-159. doi: 10.5694/mja12.10811
[3]	Boening A, Scheewe J, Heine K, et al. (2002) Long-term results after surgical correction of atrioventricular septal defects. Eur J Cardiothorac Surg 22: 167-173. doi: 10.1016/S1010-7940(02)00272-5
[4]	Stulak JM, Burkhart HM, Dearani JA, et al. (2010) Reoperations after repair of partial atrioventricular septal defect: a 45-year single-center experience. Annals of Thoracic Surgery 89: 1352-1359. doi: 10.1016/j.athoracsur.2010.01.018
[5]	Ackerman C, Locke AE, Feingold E, et al. (2012) An excess of deleterious variants in VEGF-A pathway genes in Down-syndrome-associated atrioventricular septal defects. Am J Hum Genet 91: 646-659.
[6]	Maslen CL, Babcock D, Robinson SW, et al. (2006) CRELD1 mutations contribute to the occurrence of cardiac atrioventricular septal defects in Down syndrome. Am J Med Genet A 140: 2501-2505.
[7]	Robinson SW, Morris CD, Goldmuntz E, et al. (2003) Missense mutations in CRELD1 are associated with cardiac atrioventricular septal defects. American Journal of Human Genetics 72: 1047-1052. doi: 10.1086/374319
[8]	Li H, Cherry S, Klinedinst D, et al. (2012) Genetic Modifiers Predisposing to Congenital Heart Disease in the Sensitized Down Syndrome Population. Circ Cardiovasc Genet 5: 301-308. doi: 10.1161/CIRCGENETICS.111.960872
[9]	de Vlaming A, Sauls K, Hajdu Z, et al. (2012) Atrioventricular valve development: new perspectives on an old theme. Differentiation 84: 103-116. doi: 10.1016/j.diff.2012.04.001
[10]	Snarr BS, Wirrig EE, Phelps AL, et al. (2007) A spatiotemporal evaluation of the contribution of the dorsal mesenchymal protrusion to cardiac development. Dev Dyn 236: 1287-1294. doi: 10.1002/dvdy.21074
[11]	Dor Y, Camenisch TD, Itin A, et al. (2001) A novel role for VEGF in endocardial cushion formation and its potential contribution to congenital heart defects. Development 128: 1531-1538.
[12]	Dor Y, Klewer SE, McDonald JA, et al. (2003) VEGF modulates early heart valve formation. Anat Rec A Discov Mol Cell Evol Biol 271: 202-208.
[13]	Stankunas K, Ma GK, Kuhnert FJ, et al. (2010) VEGF signaling has distinct spatiotemporal roles during heart valve development. Developmental Biology 347: 325-336. doi: 10.1016/j.ydbio.2010.08.030
[14]	Stevens A, Soden J, Brenchley PE, et al. (2003) Haplotype analysis of the polymorphic human vascular endothelial growth factor gene promoter. Cancer Res 63: 812-816.
[15]	Watson CJ, Webb NJ, Bottomley MJ, et al. (2000) Identification of polymorphisms within the vascular endothelial growth factor (VEGF) gene: correlation with variation in VEGF protein production. Cytokine 12: 1232-1235. doi: 10.1006/cyto.2000.0692
[16]	Vannay A, Vasarhelyi B, Kornyei M, et al. (2006) Single-nucleotide polymorphisms of VEGF gene are associated with risk of congenital valvuloseptal heart defects. American Heart Journal 151: 878-881. doi: 10.1016/j.ahj.2005.10.012
[17]	Smedts HP, Isaacs A, de Costa D, et al. VEGF polymorphisms are associated with endocardial cushion defects: a family-based case-control study. Pediatric Research 67: 23-28.
[18]	Miquerol L, Langille BL, Nagy A (2000) Embryonic development is disrupted by modest increases in vascular endothelial growth factor gene expression. Development 127: 3941-3946.
[19]	Gale NW, Dominguez MG, Noguera I, et al. (2004) Haploinsufficiency of delta-like 4 ligand results in embryonic lethality due to major defects in arterial and vascular development. Proc Natl Acad Sci USA 101: 15949-15954. doi: 10.1073/pnas.0407290101
[20]	Pierpont MEM, Markwald RR, Lin AE (2000) Genetic aspects of atrioventricular septal defects. American Journal of Medical Genetics 97: 289-296. doi: 10.1002/1096-8628(200024)97:4<289::AID-AJMG1279>3.0.CO;2-U
[21]	Zhian S, Belmont J, Maslen CL (2012) Specific association of missense mutations in CRELD1 with cardiac atrioventricular septal defects in heterotaxy syndrome. Am J Med Genet A 158A: 2047-2049. doi: 10.1002/ajmg.a.35457
[22]	Enciso JM, Gratzinger D, Camenisch TD, et al. (2003) Elevated glucose inhibits VEGF-A-mediated endocardial cushion formation: modulation by PECAM-1 and MMP-2. Journal of Cell Biology 160: 605-615. doi: 10.1083/jcb.200209014
[23]	Rupp PA, Fouad GT, Egelston CA, et al. (2002) Identification, genomic organization and mRNA expression of CRELD1, the founding member of a unique family of matricellular proteins. Gene 293: 47-57. doi: 10.1016/S0378-1119(02)00696-0
[24]	Camenisch TD, Molin DG, Person A, et al. (2002) Temporal and distinct TGFbeta ligand requirements during mouse and avian endocardial cushion morphogenesis. Developmental Biology 248: 170-181. doi: 10.1006/dbio.2002.0731
[25]	Camenisch TD, Schroeder JA, Bradley J, et al. (2002) Heart-valve mesenchyme formation is dependent on hyaluronan-augmented activation of ErbB2-ErbB3 receptors. Nature Medicine 8: 850-855.

This article has been cited by:

1.	ZAIN UL ABADIN ZAFAR, ZAHIR SHAH, NIGAR ALI, EBRAHEEM O. ALZAHRANI, MESHAL SHUTAYWI, MATHEMATICAL AND STABILITY ANALYSIS OF FRACTIONAL ORDER MODEL FOR SPREAD OF PESTS IN TEA PLANTS, 2021, 29, 0218-348X, 2150008, 10.1142/S0218348X21500080
2.	D. Gopal, S. Saleem, S. Jagadha, Farooq Ahmad, A. Othman Almatroud, N. Kishan, Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation, 2021, 60, 11100168, 1861, 10.1016/j.aej.2020.11.034
3.	Jiabin Xu, Hassan Khan, Rasool Shah, A.A. Alderremy, Shaban Aly, Dumitru Baleanu, The analytical analysis of nonlinear fractional-order dynamical models, 2021, 6, 2473-6988, 6201, 10.3934/math.2021364
4.	Alamgeer Khan, Muhammad Farooq, Rashid Nawaz, Muhammad Ayaz, Hijaz Ahmad, Hanaa Abu-Zinadah, Yu-Ming Chu, Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods, 2021, 19, 2391-5471, 134, 10.1515/phys-2021-0015
5.	Haji Gul, Sajjad Ali, Kamal Shah, Shakoor Muhammad, Thanin Sitthiwirattham, Saowaluck Chasreechai, Application of Asymptotic Homotopy Perturbation Method to Fractional Order Partial Differential Equation, 2021, 13, 2073-8994, 2215, 10.3390/sym13112215
6.	Muhammad Farooq, Hijaz Ahmad, Dilber Uzun Ozsahin, Alamgeer Khan, Rashid Nawaz, Bandar Almohsen, A study of heat and mass transfer flow of a variable viscosity couple stress fluid between inclined plates, 2024, 38, 0217-9849, 10.1142/S0217984923502317
7.	Murugesan Manigandan, Saravanan Shanmugam, Mohamed Rhaima, Elango Sekar, Existence of Solutions for Caputo Sequential Fractional Differential Inclusions with Nonlocal Generalized Riemann–Liouville Boundary Conditions, 2024, 8, 2504-3110, 441, 10.3390/fractalfract8080441
8.	Razia Begum, Sajjad Ali, Nahid Fatima, Kamal Shah, Thabet Abdeljawad, Dynamical behavior of whooping cough SVEIQRP model via system of fractal fractional differential equations, 2024, 12, 26668181, 100990, 10.1016/j.padiff.2024.100990

Reader Comments

Your name:*

Email:*
© 2014 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Genetics

Metrics

Article views(5317) PDF downloads(1073) Cited by(12)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Genetics

Allelic Interaction between CRELD1 and VEGFA in the Pathogenesis of Cardiac Atrioventricular Septal Defects

Related Papers:

Abstract

1. Introduction

2. Basic idea of AHPM

3. Applications

4. Discussion and conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Basic idea of AHPM

3. Applications

4. Discussion and conclusions

Acknowledgments

Conflict of interest

References

AIMS Genetics

Allelic Interaction between CRELD1 and VEGFA in the Pathogenesis of Cardiac Atrioventricular Septal Defects

Related Papers:

Abstract

1. Introduction

2. Basic idea of AHPM

3. Applications

4. Discussion and conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Basic idea of AHPM

3. Applications

4. Discussion and conclusions

Acknowledgments

Conflict of interest

References