1.
Introduction
In this paper, we consider the following initial-boundary value problem
and its corresponding steady-state problem
where Ω⊂Rn (n≥1 is an integer) is a bounded domain with boundary ∂Ω and u0∈H10(Ω); the parameters p and σ satisfy
(1) was called homogeneous (inhomogeneous) pseudo-parabolic equation when σ=0 (σ≠0). The concept "pseudo-parabolic" was proposed by Showalter and Ting in 1970 in the paper [20], where the linear case was considered. Pseudo-parabolic equations describe a variety of important physical processes, such as the seepage of homogeneous fluids through a fissured rock [1], the unidirectional propagation of nonlinear, dispersive, long waves [2,23], and the aggregation of populations [17].
The homogeneous problem, i.e. σ=0, was studied in [3,4,5,7,9,10,13,15,16,21,24,25,26,27,28,29]. Especially, for the Cauchy problem (i.e. Ω=Rn and there is no boundary condition), Cao et al. [4] showed the critical Fujita exponent pc (which was firstly introduced by Fujita in [8]) is 1+2/n, i.e. if 1<p≤pc, then any nontrivial solution blows up in finite time, while global solutions exist if p>pc. In [28], Yang et al. proved that for p>pc, there is a secondary critical exponent αc=2/(p−1) such that the solution blows up in finite time for u0 behaving like |x|−α at {|x|→∞} if α=(0,αc); and there are global solutions for for u0 behaving like |x|−α at {|x|→∞} if α=(αc,n). For the zero Dirichlet boundary problem in a bounded domain Ω, in [13,25,26], the authors studied the properties of global existence and blow-up by potential well method (which was firstly introduced by Sattinger [19] and Payne and Sattinger [18], then developed by Liu and Zhao in [14]), and they showed the global existence, blow-up and asymptotic behavior of solutions with initial energy at subcritical, critical and supercritical energy level. The results of [13,25,26] were extended by Luo [15] and Xu and Zhou [24] by studying the lifespan (i.e. the upper bound of the blow-up time) of the blowing-up solutions. Recently, Xu et al. [27] and Han [9] extended the previous studies by considering the problem with general nonlinearity.
Li and Du [12] studied the Cauchy problem of equation in (1) with σ>0. They got the critical Fujita exponent (pc) and second critical exponent (αc) by the integral representation and comparison principle. The main results obtained in [12] are as follows:
(1) If 1<p≤pc:=1+(2+σ)/n, then every nontrivial solution blows up in finite time.
(2) If p>pc, the distribution of the initial data has effect on the blow-up phenomena. More precisely, if u0∈Φα and 0<α<αc:=(2+σ)/(p−1) or u0 is large enough, then the solution blows up in finite time; if u0=μϕ(x), ϕ∈Φα with αc<α<n, 0<μ<μ1, then the solution exists globally, where μ1 is some positive constant,
and
Here BC(Rn) is the set of bounded continuous functions in Rn.
In view of the above introductions, we find that
(1) for Cauchy problem in Rn, only the case σ≥0 was studied;
(2) for zero Dirichlet problem in a bounded domain Ω, only the case σ=0 was studied.
The difficulty of allowing σ to be less than 0 is the term |x|σ become infinity at x=0. In this paper, we consider the problem in a bounded domain Ω with zero Dirichlet boundary condition, i.e. problem (1), and the parameters satisfies (3), which allows σ to be less than 0. To overcome the singularity of |x|σ at x=0, we use potential well method by introducing the |x|σ weighed-Lp+1(Ω) space and assume there is a lower bound of σ, i.e,
for n≥3.
The main results of this paper can be summarized as follows: Let J and I be the functionals given in (12) and (13), respectively; d be the mountain-pass level given in (14); Sρ and Sρ be the sets defined in (20).
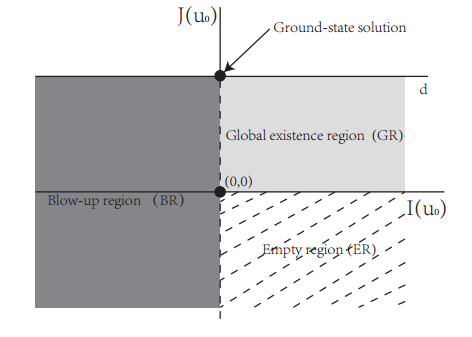
(1) (the case J(u0)≤d, see Fig. 1) If u0∈H10(Ω) such that (I(u0),J(u0)) is in the dark gray region (BR), then the solution blows up in finite time; if u0∈H10(Ω) such that (I(u0),J(u0)) is in the light gray region (GR), then the solution exists globally; if u0∈H10(Ω) such that (I(u0),J(u0))=(0,d), then u0 is a ground-state solution and (1) admits a global solution u≡u0; there is no u0∈H10(Ω) such that (I(u0),J(u0)) is in the dotted part (ER).
(2) (the case J(u0)>d) If u0∈Sρ for some ρ≥J(u0)>d, then the solution exists globally and goes to 0 in H10(Ω) as times goes to infinity; if u0∈Sρ for some ρ≥J(u0)>d, then the solution blows up in finite time.
(3) (arbitrary initial energy level) For any M∈R, there exits a u0∈H10(Ω)) satisfying J(u0)=M such that the corresponding solution blows up in finite time.
(4) Moreover, under suitable assumptions, we show the exponential decay of global solutions and lifespan (i.e. the upper bound of blow-up time) of the blowing-up solutions.
The organizations of the remain part of this paper are as follows. In Section 2, we introduce the notations used in this paper and the main results of this paper; in Section 3, we give some preliminaries which will be used in the proofs; in Section 4, we give the proofs of the main results.
2.
Notations and main results
Throughout this paper we denote the norm of Lγ(Ω) for 1≤γ≤∞ by ‖⋅‖Lγ. That is, for any ϕ∈Lγ(Ω),
We denote the |x|σ-weighted Lp+1(Ω) space by Lp+1σ(Ω), which is defined as
where
By standard arguments as the space Lp+1(Ω), one can see Lp+1σ(Ω) is a Banach space with the norm ‖⋅‖Lp+1σ.
We denote the inner product of H10(Ω) by (⋅,⋅)H10, i.e.,
The norm of H10(Ω) is denoted by ‖⋅‖H10, i.e.,
An equivalent norm of H10(Ω) is ‖∇(⋅)‖L2, and by Poincaré's inequality, we have
where λ1 is the first eigenvalue of −Δ with zero Dirichlet boundary condition, i.e,
Moreover, by Theorem 3.2, we have
Then we let Cpσ as the optimal constant of the embedding H10(Ω)↪Lp+1σ(Ω), i.e.,
We define two functionals J and I on H10(Ω) by
and
By (3) and (10), we know that J and I are well-defined on H10(Ω).
We denote the mountain-pass level d by
where N is the Nehari manifold, which is defined as
By Theorem 3.3, we have
where Cpσ is the positive constant given in (11).
For ρ∈R, we define the sub-level set Jρ of J as
Then, we define the set Nρ:=N∩Jρ. In view of (15), (12), (17), we get
For ρ>d, we define two constants
and two sets
Remark 1. There are two remarks on the above definitions.
(1) By the definitions of Nρ, λρ and Λρ, it is easy to see λρ is non-increasing with respect to ρ and Λρ is non-decreasing with respect to ρ.
(2) By Theorem 3.4, we have
Then the sets Sρ and Sρ are both nonempty. In fact, for any ϕ∈H10(Ω)∖{0} and s>0,
So,
In this paper we consider weak solutions to problem (1), local existence of which can be obtained by Galerkin's method (see for example [22,Chapter II,Sections 3 and 4]) and a standard limit process and the details are omitted.
Definition 2.1. Assume u0∈H10(Ω) and (3) holds. Let T>0 be a constant. A function u=u(x,t) is called a weak solution of problem (1) on Ω×[0,T] if u(⋅,t)∈L∞(0,T;H10(Ω)), ut(⋅,t)∈L2(0,T;H10(Ω)) and the following equality
holds for any v∈H10(Ω) and a.e. t∈[0,T]. Moreover,
Remark 2. There are some remarks on the above definition.
(1) Since u(⋅,t)∈L∞(0,T;H10(Ω))↪L2(0,T;H10(Ω)), ut(⋅,t)∈L2(0,T;H10(Ω)), we have u∈H1(0,T;H10(Ω)). According to [6], u∈C([0,T];H10(Ω)), then (23) makes sense. Moreover, by (10), all terms in (22) make sense for u∈C([0,T];H10(Ω)) and ut∈L2(0,T;H10(Ω)).
(2) Denote by Tmax the maximal existence of u, then u(⋅,t)∈L∞(0,T;H10(Ω))∩C([0,T];H10(Ω)), ut(⋅,t)∈L2(0,T;H10(Ω)) for any T<Tmax.
(3) Taking v=u in (22), we get
where ‖⋅‖H10 is defined in (7) and I is defined in (13).
(4) Taking v=ut in (22), we get
where J is defined in (12).
Definition 2.2. Assume (3) holds. A function u∈H10(Ω) is called a weak solution of (2) if
holds for any v∈H10(Ω).
Remark 3. There are some remarks to the above definition.
(1) By (10), we know all the terms in (26) are well-defined.
(2) If we denote by Φ the set of weak solutions to (2), then by the definitions of J in (12) and N in (15), we have
where J′(ϕ)=0 in H−1(Ω) means ⟨J′(ϕ),ψ⟩=0 for all ψ∈H10 and ⟨⋅,⋅⟩ means the dual product between H−1(Ω) and H10(Ω).
With the set Φ defined above, we can defined the ground-state solution to (2).
Definition 2.3. Assume (3) holds. A function u∈H10(Ω) is called a ground-state solution of (2) if u∈Φ∖{0} and
With the above preparations, now we can state the main results of this paper. Firstly, we consider the case J(u0)≤d. By the sign of I(u0), we can classify the discussions into three cases:
(1) J(u0)≤d, I(u0)>0 (see Theorem 2.4);
(2) J(u0)≤d, I(u0)<0 (see Theorem 2.5);
(3) J(u0)≤d, I(u0)=0. In this case, by the definition of d in (14), we have u0=0 or J(u0)=d and I(u0)=0. In Theorem 2.6, we will show problem (1) admits a global solution u(⋅,t)≡u0.
Theorem 2.4. Assume (3) holds and u=u(x,t) is a weak solution to (1) with u0∈V, then u exists globally and
where
In, in addition, J(u0)<d, we have the following decay estimate:
Remark 4. Since u0∈V, we have I(u0)>0. Then it follows from the definitions of J in (12) and I in (13) that
So the equality (28) makes sense.
Theorem 2.5. Assume (3) holds and u=u(x,t) is a weak solution to (1) with u0∈W. Then Tmax<∞ and u blows up in finite time in the sense of
where
and Tmax is the maximal existence time of u. If, in addition, J(u0)<d, then
Remark 5. There are two remarks.
(1) If J(ϕ)<0, then we can easily get from the definitions of J and I in (12) and (13) respectively that I(ϕ)<0. So we have ϕ∈W if J(ϕ)<0.
(2) The sets V and W defined in (29) and (31) respectively are both nonempty. In fact for any ϕ∈H10(Ω)∖{0}, we let
Then (see Fig. 2)
(a) f(0)=f(s∗4)=0, f(s) is strictly increasing for s∈(0,s∗3), strictly decreasing for s∈(s∗3,∞), lims↑∞f(s)=−∞, and
(b) g(0)=g(s∗3)=0, g(s) is strictly increasing for s∈(0,s∗1), strictly decreasing for s∈(s∗1,∞), lims↑∞g(s)=−∞, and
(c) f(s)<g(s) for 0<s<s∗2, f(s)>g(s) for s>s∗2, and
where
So, {sϕ:s∗1<s<s∗3}⊂V, {sϕ:s∗3<s<∞}⊂W.
Theorem 2.6. Assume (3) holds and u=u(x,t) is a weak solution to (1) with u0∈G. Then problem (1) admits a global solution u(⋅,t)≡u0(⋅), where
Remark 6. There are two remarks on the above theorem.
(1) Unlike Remark 5, it is not easy to show G≠∅. In fact, if we use the arguments as in Remark 5, we only have J(s∗3ϕ)≤d and I(s∗3ϕ)=0 (see Fig. 2 and (33)). In Theorem 2.7, we will use minimizing sequence argument to show G≠∅.
(2) To prove the above Theorem, we only need to show G is the set of the ground-state solution of (2), which is done in Theorem 2.7.
Theorem 2.7. Assume (3) holds and let G be the set defined in (34), then G≠∅ and G is the set of the ground-state solution of (2).
Secondly, we consider the case J(u0)>d, and we have the following theorem.
Theorem 2.8. Assume (3) holds and the initial value u0∈H10(Ω) satisfying J(u0)>d.
(i): If u0∈Sρ with ρ≥J(u0), then problem (1) admits a global weak solution u=u(x,t) and ‖u(⋅,t)‖H10↓0 as t↑∞.
(ii): If u0∈Sρ with ρ≥J(u0), then the weak solution u=u(x,t) of problem (1) blows up in finite time.
Here Sρ and Sρ are the two sets defined in (20).
Next, we show the solution of the problem (1) can blow up at arbitrary initial energy level (Theorem 2.10). To this end, we firstly introduce the following theorem.
Theorem 2.9. Assume (3) holds and u=u(x,t) is a weak solution to (1) with u0∈ˆW. Then
and u blows up in finite time in the sense of
where
and Tmax is the maximal existence time of u.
By using the above theorem, we get the following theorem.
Theorem 2.10. For any M∈R, there exists u0∈H10(Ω) satisfying J(u0)=M such that the corresponding weak solution u=u(x,t) of problem (1) blows up in finite time.
3.
Preliminaries
The following lemma can be found in [11].
Lemma 3.1. Suppose that 0<T≤∞ and suppose a nonnegative function F(t)∈C2[0,T) satisfies
for some constant γ>0. If F(0)>0, F′(0)>0, then
and F(t)↑∞ as t↑T.
Theorem 3.2. Assume p and σ satisfy (3). Then H10(Ω)↪Lp+1σ(Ω) continuously and compactly.
Proof. Since Ω⊂Rn is a bounded domain, there exists a ball B(0,R):={x∈Rn:|x|=√x21+⋯x2n<R}⊃Ω.
We divide the proof into three cases. We will use the notation a≲b which means there exits a positive constant C such that a≤Cb.
Case 1. σ≥0. By the assumption on p in (3), one can see
Then we have, for any u∈H10(Ω),
which, together with (37), implies H10(Ω)↪Lp+1σ(Ω) continuously and compactly.
Case 2. −n<σ<0 and n=1 or 2. We can choose r∈(1,−nσ). Then by Hölder's inequality and
for any u∈H10(Ω), we have
which, together with (38), implies H10(Ω)↪Lp+1σ(Ω) continuously and compactly.
Case 3. (p+1)(n−2)2−n<σ<0 and n≥3. Then there exists a constant r>1 such that
By the second inequality of the above inequalities, we have
So,
Then by Hölder's inequality, for any u∈H10(Ω), we have
which, together with (39), implies H10(Ω)↪Lp+1σ(Ω) continuously and compactly. Here ωn−1 denotes the surface area of the unit ball in Rn.
Theorem 3.3. Assume p and σ satisfy (3). Let d be the constant defined in (14), then
where Cpσ is the positive constant defined in (11).
Proof. Firstly, we show
where N is the set defined in (15) and
By the definition of N in (15) and s∗ϕ in (41), one can easily see that s∗ϕ=1 if ϕ∈N and s∗ϕϕ∈N for any ϕ∈H10(Ω)∖{0}.
On one hand, since N⊂H10(Ω) and s∗ϕ=1 for ϕ∈N, we have
On the other hand, since {s∗ϕϕ:ϕ∈H10(Ω)∖{0}}⊂N, we have
Then (40) follows from the above two inequalities.
By (40), the definition of d in (14), the definition of J in (12), and the definition of Cpσ in (11), we have
Theorem 3.4. Assume (3) holds. Let λρ and Λρ be the two constants defined in (19). Here ρ>d is a constant. Then
Proof. Let ρ>d and Nρ be the set defined in (18). By the definitions of λρ and Λρ in (19), it is obvious that
Since Nρ⊂N, it follows from the definitions of d, J, I in (14), (12), (13), respectively, that
which implies
On the other hand, by (8) and (18), we have
Combining the above two inequalities with (43), we get (42), the proof is complete.
Theorem 3.5. Assume (3) holds and u=u(x,t) is a weak solution to (1). Then the sets W and V, defined in (31) and (29) respectively, are both variant for u, i.e., u(⋅,t)∈W (u(⋅,t)∈V) for 0≤t<Tmax when u0∈W (u0∈V), where Tmax is the maximal existence time of u.
Proof. We only prove the invariance of W since the proof of the invariance of V is similar.
For any ϕ∈W, since I(ϕ)<0, it follows from the definition of I (see (13)) and (11) that
which implies
Let u(x,t) be the weak solution of problem (1) with u0∈W. Since I(u0)<0 and u∈C([0,Tmax),H10(Ω)), there exists a constant ε>0 small enough such that
Then by (24), ddt‖u(⋅,t)‖2H10>0 for t∈[0,ε], and then by (25) and J(u0)≤d, we get
We argument by contradiction. Since u(⋅,t)∈C([0,Tmax),H10(Ω)), if the conclusion is not true, then there exists a t0∈(0,Tmax) such that u(⋅,t)∈W for 0≤t<t0, but I(u(⋅,t0))=0 and
(note (25) and (46), J(u(⋅,t0))=d cannot happen). By (44), we have u(⋅,t)∈C([0,Tmax),H10(Ω)) and u(⋅,t0)∈¯W, then
which, together with I(u(⋅,t0))=0, implies u(⋅,t0)∈N. Then it follows from the definition of d in (14) that
which contradicts (47). So the conclusion holds.
Theorem 3.6. Assume (3) holds and u=u(x,t) is a weak solution to (1) with u0∈W. Then
where W is defined in (31) and Tmax is the maximal existence time of u.
Proof. Let N−:={ϕ∈H10(Ω):I(ϕ)<0}. Then by Theorem 3.5, u(⋅,t)∈N− for 0≤t<Tmax.
By the proof in Theorem 3.3,
where we have used I(u(⋅,t))<0 in the last inequality. Since I(u(⋅,t))<0, we get from (41) that
Then
and (48) follows from the above inequality.
Theorem 3.7. Assume (3) holds and u=u(x,t) is a weak solution to (1) with u0∈ˆW. Then I(u(⋅,t))<0 for 0≤t<Tmax, where Tmax is the maximal existence time of u and ˆW is defined in (36)
Proof. Firstly, we show I(u0)<0. In fact, by the definition of J in (12), u0∈ˆW, and (8), we get
which implies
Secondly, we prove I(u(⋅,t))<0 for 0<t<Tmax. In fact, if it is not true, in view of u∈C([0,Tmax),H10(Ω)), there must exist a t0∈(0,Tmax) such that I(u(⋅,t))<0 for t∈[0,t0) but I(u(⋅,t0))=0. Then by (24), we get ‖u(⋅,t0)‖2H10>‖u0‖2H10, which, together with u0∈ˆW and (8), implies
On the other hand, by (24), (12), (13) and I(u(⋅,t0))=0, we get
which contradicts (49). The proof is complete.
4.
Proofs of the main results
Proof of Theorem 2.4. Let u=u(x,t) be a weak solution to (1) with u0∈V and Tmax be its maximal existence time. By Theorem 3.5, u(⋅,t)∈V for 0≤t<Tmax, which implies I(u(⋅,t))>0 for 0≤t<Tmax. Then it follows from (25), (12) and (13) that
which implies u exists globally (i.e. Tmax=∞) and
Next, we prove ‖u(⋅,t)‖H10 decays exponentially, if in addition, J(u0)<d. By (24), (13), (11), (50), (16) we have
which leads to
The proof is complete.
Proof of Theorem 2.5. Let u=u(x,t) be a weak solution to (1) with u0∈W and Tmax be its maximal existence time.
Firstly, we consider the case J(u0)<d and I(u0)<0. By Theorem 3.5, u(⋅,t)∈W for 0≤t<Tmax. Let
For any T∗∈(0,Tmax), β>0 and α>0, we let
Then
and (by (24), (12), (13), (48), (25))
Since I(u(⋅,t))<0, it follow from (24) and the first equality of (54) that
Then
By (6), Schwartz's inequality and Hölder's inequality, we have
which, together with the definition of F(t), implies
Then it follows from (54) and the above inequality that
In view of (55), (56), and (57), we have
If we take β small enough such that
then F(t)F″(t)−p+12(F′(t))2≥0. Then, it follows from Lemma 3.1 that
Then for
we get
Minimizing the above inequality for α satisfying (59), we get
Minimizing the above inequality for β satisfying (58), we get
By the arbitrariness of T∗<Tmax it follows that
Secondly, we consider the case J(u0)=d and I(u0)<0. By the proof of Theorem 3.5, there exists a t0>0 small enough such that J(u(⋅,t0))<d and I(u(⋅,t0))<0. Then it follows from the above proof that u will blow up in finite time. The proof is complete.
Proof of Theorems 2.6 and 2.7. Since Theorem 2.6 follows from Theorem 2.7 directly, we only need to prove Theorem 2.7.
Firstly, we show G≠∅. By the definition of d in (14), we get
Then a minimizing sequence {ϕk}∞k=1⊂N exists such that
which implies {ϕk}∞k=1 is bounded in H10(Ω). Since H10(Ω) is reflexive and H10(Ω)↪Lp+1σ continuously and compactly (see (10)), there exists φ∈H10(Ω) such that
(1) ϕk⇀φ in H10(Ω) weakly;
(2) ϕk→φ in Lp+1σ(Ω) strongly.
Now, in view of ‖∇(⋅)‖L2 is weakly lower continuous in H10(Ω), taking lim infk↑∞ in the equality ‖∇ϕk‖2L2=‖ϕk‖p+1Lp+1σ (sine ϕk∈N), we get
We claim
In fact, if the claim is not true, then by (61),
By the proof of Theorem 3.3, we know that s∗φφ∈N, which, together with the definition of d in (14), implies
where
On the other hand, since s∗φφ∈N, we get from the definitions of J in (12) and I in (13), s∗φ∈(0,1), ‖∇(⋅)‖L2 is weakly lower continuous in H10(Ω), (60) that
which contradicts to (63). So the claim is true, i.e.
which, together with H10(Ω) is uniformly convex and ϕk⇀φ in H10(Ω) weakly, implies ϕk→φ strongly in H10(Ω). Then by (60), J(φ)=d, which, together with (62) and the definition of G in (34), implies φ∈G, i.e., G≠∅.
Second, we prove G⊂Φ, where Φ is the set defined in (27). For any φ∈G, we need to show φ∈Φ, i.e. φ satisfies (26). Fix any v∈H10(Ω) and s∈(−ε,ε), where ε>0 is a small constant such that ‖φ+sv‖p+1Lp+1σ>0 for s∈(−ε,ε). Let
Then I(τ(s)(φ+sv))=0. So by the definition of N in (15), the set
is a curve on N, which passes φ when s=0. The function τ(s) is differentiable and
where
Since (62), we get τ(0)=1 and
Let
Since τ(s)(φ+sv)∈N for s∈(−ε,ε), τ(s)(φ+sv)|s=0=φ, ϱ(0)=J(φ)=d, it follows from the definition of d that ϱ(s) (s∈(−ε,ε)) achieves its minimum at s=0, then ϱ′(0)=0. So,
So, φ∈Φ, i.e. G⊂Φ. Moreover, we have G⊂(Φ∖{0}) since φ≠0 for any φ∈G.
Finally, in view of Definition 2.3 and J(φ)=d (∀φ∈G), to complete the proof, we only need to show
In fact, by the above proof and (27), we have G⊂Φ∖{0}⊂N. Then, in view of the definition of d in (14), i.e.,
and J(φ)=d for any φ∈G, we get (66). The proof is complete.
Proof of Theorem 2.8. Let u=u(x,t) be the solution of problem (1) with initial value u0 satisfying J(u0)>d. We denote by Tmax the maximal existence of u. If u is global, i.e. Tmax=∞, we denote by
the ω-limit set of u0.
(i) Assume u0∈Sρ={ϕ∈H10(Ω):‖ϕ‖H10≤λρ,I(ϕ)>0} (see (20)) with ρ≥J(u0). Without loss of generality, we assume u(⋅,t)≠0 for 0≤t<Tmax. In fact it there exists a t0 such that u(⋅,t0)=0, then it is easy to see the function v defined as
is a global weak solution of problem (1), and the proof is complete.
We claim that
Since I(u0)>0, if the claim is not true, there exists a t0∈(0,Tmax) such that
and
which together with the definition of N in (15) and the assumption that u(⋅,t)≠0 for 0≤t<Tmax, implies u(⋅,t0)∈N. Moreover, by using (68), similar to the proof of (46), we have J(u(⋅,t0))<J(u0), i.e. u(⋅,t0)∈JJ(u0) (see (17)). Then u(⋅,t0)∈NJ(u0) (since NJ(u0)=N∩JJ(u0)) and then ‖u(⋅,t0)‖H10≥λJ(u0) (see (19)). By monotonicity (see Remark 1) and ρ≥J(u0), we get
On the other hand, it follows from (24), (68) and u0∈Sρ that
which contradicts (70). So (67) is true. Then by (24) again, we get
which implies u exists globally, i.e. Tmax=∞.
By (24) and (67), ‖u(⋅,t)‖H10 is strictly decreasing for 0≤t<∞, so a constant c∈[0,‖u0‖H10) exists such that
Taking t↑∞ in (24), we get
Note that I(u(⋅,s))>0 for 0≤s<∞, so, for any sequence {tn} satisfying tn↑∞ as n↑∞, if the limit limn↑∞I(u(⋅,tn)) exists, it must hold
Let ω be an arbitrary element in ω(u0). Then there exists a sequence {tn} satisfying tn↑∞ as n↑∞ such that
Then by (71), we get
As the above, one can easily see
which implies ω∉NJ(u0). In fact, if ω∈NJ(u0), by (19), λJ(u0)≤‖ω‖H10, a contradiction. Since NJ(u0)=N∩Ju0 and ω∈JJ(u0), we get ω∉N. Therefore, by the definition of N in (15) and (73), ω=0, then it follows from ‖u(⋅,t)‖H10 is strictly decreasing and (72) that
(ⅱ) Assume u0∈Sρ={ϕ∈H10(Ω):‖ϕ‖H10≥Λρ,I(ϕ)<0} (see (20)) with ρ≥J(u0). We claim that
Since I(u0)<0, if the claim is not true, there exists a t0∈(0,Tmax) such that
and
Since (75), by (44) and u∈C([0,Tmax),H10(Ω)), we get
which, together with the definition of N in (15), implies u(⋅,t0)∈N. Moreover, by using (75), similar to the proof of (46), we have J(u(⋅,t0))<J(u0), i.e. u(⋅,t0)∈JJ(u0) (see (17)). Then u(⋅,t0)∈NJ(u0) (since NJ(u0)=N∩JJ(u0)) and then ‖u(⋅,t0)‖H10≤ΛJ(u0) (see (19)). By monotonicity (see Remark 1) and ρ≥J(u0), we get
On the other hand, it follows from (24), (75) and u0∈Sρ that
which contradicts (77). So (74) is true.
Suppose by contradiction that u does not blow up in finite time, i.e. Tmax=∞. By (24) and (74), ‖u(⋅,t)‖H10 is strictly increasing for 0≤t<∞. If the limit limt↑∞‖u(t)‖H10 exists, i.e. there exists a constant ˜c∈[‖u0‖H10,∞) such that
Taking in (24), we get
Note for , so, for any sequence satisfying as , if the limit exists, it must hold
Let be an arbitrary element in . Then there exists a sequence satisfying as such that
Since is strictly increasing, exists and
Then by (78), we get
By (24), (25) and (74), one can easily see
which implies . In fact, if , by (19), , a contradiction. Since and , we get . Therefore, by the definition of in (15) and (80), . However, this contradicts . So blows up in finite time. The proof is complete.
Proof of Theorem 2.9. Let be a weak solution of (1) with and be its maximal existence time, where is defined in (36). By Theorem 3.7, we know that for . Then by (8) and (24), we get
The remain proofs are similar to the proof of Theorem 2.9. For any , and , we consider the functional again (see (52)). We also have (53), (54), but there are some differences in (55), in fact, by (81) and (25), we have
We also have (56) and (57). Then it follows from (56), (57) and (82) that
If we take small enough such that
then . Then, it follows from Lemma 3.1 that
Then for
we get
Minimizing the above inequality for satisfying (84), we get
Minimizing the above inequality for satisfying (58), we get
By the arbitrariness of it follows that
Proof of Theorem 2.10. For any , let and be two arbitrary disjoint open domains. Let , extending to by letting in , then . We choose large enough such that
For such and , we take a (which is extended to by letting in i.e. ) such that
where (see Remark 5)
which can be done since
and can be chosen such that .
By Remark 5 again,
By (87) and (86), we can choose such that satisfies . Letting , since and are disjoint, we get
and (note (85))
Let be the weak solution of problem (1) with initial value given above. Then by Theorem 2.9, blows up in finite time.









 DownLoad:
DownLoad: