1.
Introduction
Oceangoing shipping transports a significant amount of different goods across the globe, which supports the development of the global economy [1,2,3,4,5,6,7,8]. In these years, sustainable shipping has also become an important issue because of the air emissions released by ships, which adversely impact the marine environment [9,10,11,12,13]. To guarantee maritime safety and protect the marine environment, PSC is an international regime to inspect foreign visiting ships. It is designed to ensure that foreign visiting ships are seaworthy and comply with required international conventions, such as the international convention for the safety of life at sea (SOLAS) and the international convention for the prevention of pollution from ships (MARPOL). When a ship is selected to be inspected, the port state control officer (PSCO) first conducts an initial inspection, including the first impression of the ship, certificate check, and walking around to check the overall ship conditions. During a PSC inspection, conditions that do not comply with the relevant conventions are denoted as deficiencies. When the deficiencies identified are too many or severe, the PSCO will detain the ship until these deficiencies are rectified.
To achieve uniform and efficient PSC inspections, regional Memorandum of Understandings (MoUs) on PSC are established through cooperation among their members. The goal of MoUs on PSC is to verify that the foreign visiting ships meet the international conventions' requirements through a harmonized system of PSC, which allows for information sharing [14]. By the end of 2018, nine MoUs on PSC had been signed worldwide. And the inspection results, including the deficiencies identified and the detention outcome, combined with ship information, are recorded in the database of MoUs on PSC.
One of the essential issues faced by PSC authorities is how to select ships for PSC inspections. Port states recognize that inspecting all foreign visiting ships would be impractical due to the resources it would take and unnecessary because not all ships are substandard. Therefore, port states started to select foreign visiting ships to inspect according to the features of ships. Taking Tokyo MoU as an example, it introduced a ship selection scheme in 2014, namely NIR, to evaluate the risk level of one ship, as shown in Table 1 [15]. It considers seven features related to the characteristics and historical inspection records of a ship, including ship type, ship age, ship flag performance, ship recognized organization (RO) performance, ship company performance, the number of deficiencies within the previous 36 months, and the number of detentions within the previous 36 months. Each candidate value of a certain feature is assigned a fixed weighting point, and a ship's risk level is determined by the sum of seven features' weighting points. Based on the total points, all ships are divided into three types: high-risk ship (HRS) (whose total weighting points is at least 4), standard-risk ship (SRS) (whose total weighting points is at most 3 and who does not meet all the criteria of low-risk ships), and low-risk ship (LRS) (whose total weighting points is at most 3 and who meets all the criteria for low-risk ships, including white ship flag performance, high ship RO performance, high ship company performance, 5 or fewer deficiencies within the previous 36 months, and no detention within the previous 36 months); this scheme is easy to understand and implement. Thanks to the implementation of the NIR, maritime security, pollution prevention, and working conditions have all been improved [16].
Regarding the weighted-sum method of the NIR, the assumption is that ships with values attached with higher weighting points should have more deficiencies. For example, ships in high-risk types (i.e., chemical tankers, gas carriers, oil tankers, bulk carriers, etc.) are supposed to have higher numbers of deficiencies and thus have more chances to be inspected. However, by analyzing the dataset containing PSC inspection records that we collect (more information with respect to this dataset will be introduced in Section 3.2), we find that foreign visiting ships in low-risk ship types have a higher average number of deficiencies (4.02), while ships in high-risk ship types have a lower average number of deficiencies (3.77). A possible explanation for this finding is that those ships in high-risk types are registered under white flags to evade inspection, or the ages of these ships are young. Because the total weighting points of ships under white flags and at young ages are relatively low, even if those ships are in high-risk types, they are not likely to be inspected. Therefore, selected ships in high-risk types might have lower numbers of deficiencies compared with ships in low-risk types. This finding indicates that the NIR's weighted-sum method, which is based on the assumption that the values of the selected seven features are linear to the risk level of ships (i.e., the number of deficiencies) might not be reasonable. If the weighted-sum method does not consider the correlations of pairwise features among selected features, its effectiveness might be compromised. Therefore, the weighting method should not be established based on the linear total score of all considered features but consider a more comprehensive manner, such as considering the compound influence of pairwise features.
The paper aims to investigate the correlations of pairwise features among selected features of the NIR and further investigate the plausibility of the NIR's weighted-sum method. We require that when we classify ships according to the values of a certain feature, the values of the remaining features of ships should be identical. According to the NIR, the average number of deficiencies of ships in high-risk values of a certain feature is assumed to be higher than the average number of deficiencies of ships in low-risk values of that feature. However, if the relationship reverses (i.e., the average number of deficiencies for ships in high-risk values is lower than that for ships in low-risk values) when the values of remaining features are identical, a paradox with respect to the NIR appears, which is termed Simpson's paradox. If Simpson's paradox exists, we further explore which feature flips the effect. By investigating Simpson's paradox and analyzing the causes, we answer the question of whether it is reasonable to follow NIR's weighted-sum method to select ships for inspection.
The contributions of the paper are as follows. First, the methodology used in our research identifies possible paradoxes of the NIR by analyzing a PSC dataset. To the best of our knowledge, identifying Simpson's paradox by finding correlations of pairwise features among selected features of the NIR has not been considered in previous relevant research. Therefore, our research is the first one to examine the plausibility of the NIR. Second, based on the correlations of pairwise features revealed in this paper, we conclude that the values of selected features of NIR are nonlinear to the risk level of ships. Different from previous studies that propose machine learning (ML) models to invent a brand-new ship selection scheme that requires great technological transformations, we mainly focus on diagnosing the intrinsic issues with respect to the current NIR, leading to managerial insights and suggestions that are easier to operate and implement for efficient and effective ship selections in PSC.
The remainder of this paper is organized as follows. Section 2 reviews the relevant literature. Section 3 presents a detailed description of our methods and materials. Section 4 shows the results. Finally, Section 5 concludes this study.
2.
Literature review
2.1. Studies on PSC inspection
A recent literature review classified the large body of literature on PSC into four main categories: targeted features influencing PSC inspection results, inspected ship selection scheme, PSC inspection effects, and suggestions for MoU management [17]. In this study, we focus on the literature about features influencing PSC inspection results and inspected ship selection schemes.
For targeted features influencing PSC inspection results, several studies arrived at the conclusion that generic features, including ship age, ship flag, and ship type, were main determinants of ship deficiencies and detention [18,19,20]. As for non-generic features, Knapp and Franses [21] claimed that inspection areas and different backgrounds of inspectors would influence the inspection results. Ravira and Piniella [22] and Graziano et al. [23] both concluded that the professional profile of PSC inspectors might affect inspection results. These papers all used statistical models to analyze data and find out the determinant features of PSC inspection results.
For ship selection scheme, relevant studies used ML models to select ships to be inspected or predict the number of deficiencies and detentions of foreign visiting ships. Xu et al. [24] introduced a risk assessment system based on a support vector machine (SVM) to classify foreign visiting ships as either high-risk or low-risk according to the target factors. Yang et al. [25] combined the Bayesian network model with the game model between PSC port authorities and ship owners to present an optimal PSC inspection scheme. In addition, several studies developed new ship selection models to predict the deficiencies and detentions of ships. Wang et al. [26] proposed a BN model to predict the number of ship deficiencies and compared it with the current NIR's ship selection scheme in the Tokyo MoU, demonstrating the superiority of the BN model. Based on the static risk factors adopted by the NIR, Dinis et al. [27] developed a BN-based ship risk assessment model and conducted a quantitative assessment of the predictive validity of the model using historical PSC inspection records. Yan et al. [28] proposed a random forest-based model to predict the probability of ship detention. In a recent study, Yan and Wang [29] further proposed an anomaly detection model for ship detention prediction. These studies used ML models for ship selection in PSC inspections, which can identify substandard ships more efficiently and accurately.
2.2. Studies on the Simpson's paradox in operations management
Simpson first described the paradox in 1951 [30]. It is a statistical phenomenon that causes a potential bias in certain data analyses. The paradox occurs when a relationship between two variables reverses when a third variable, called a confounding variable, is introduced. The literature on Simpson's paradox has focused on explaining the phenomenon, specifying its magnitude [31,32], the conditions where it vanishes [33], and its frequency [34]. The implications of Simpson's paradox on managerial decision-making have been considered in operations management. Sunder [35] considered the paradox in the context of the allocation of indirect costs in the logistics system, which sharpened our intuition through deriving new rules of thumb. Mehrez et al. [36] discussed the paradox in the case of efficiency measures for firms or decision-making units. This research reminded us to exercise caution when developing models to deal with different technologies. Curley and Browne [37] observed the paradox in the background of on-time rate for delivery companies, where the judged relationship between two variables (e.g., company and performance) differs depending on whether that relationship is viewed within subcategories of a third variable (e.g., package size) or in the aggregate. Melumad and Ziv [38] looked at the relationship between product quality and increased production and found that under certain conditions, each individual firm's average quality decreased while the overall market average quality increased.
In summary, relevant studies have proposed ML models to improve the accuracy and efficiency of ship selection for PSC. Nevertheless, the NIR (i.e., weighted-sum method) is still in effect for Tokyo MoU. Although most existing studies propose new methods, they do not investigate the internal reasons for the drawbacks of the current weighted-sum method of the NIR. Therefore, our research studies the correlations between selected features of the NIR and investigates whether there are paradoxes with respect to the NIR, aiming to diagnose for the current scheme and provide suggestions for PSC authorities.
3.
Methods and materials
3.1. Methods
In this article, we aim to investigate the correlations of pairwise features among selected features of the NIR by studying whether ships with high-risk values of a certain feature have more deficiencies. To achieve this aim, we compare the average number of deficiencies of two categories divided by a splitting value of a certain feature. To examine the effect of a certain feature, we require that when we classify ships according to the values of a certain feature, the values of the remaining features of ships in these two subcategories should be identical. For example, ship age and ship flag performance are two features that affect the overall points of a visiting ship. If we first divide ships into two categories according to their ship flag performance, the total number of deficiencies, the total number of ships, and the average number of deficiencies, of the two categories are shown in Table 2. To examine the effect of ship flag performance on the number of deficiencies, we then require that the ships in these two categories have an identical range of ship age (i.e., above 12 or below 12). Therefore, by further stratifying the data, because we can divide ship age into two different range levels, we could get the corrected data, namely four subcategories, as shown in Table 3. Then pairwise comparisons of ships under the identical range level of age but with different values of the ship flag performance are conducted.
As shown in Tables 2 and 3, assume that we obtain the following results:
where Eq (1) indicates that the average number of deficiencies of ships under the black flag state is higher than that of ships under the white flag and grey flag when we do not require that the ships in each category have an identical range of ship age. However, Eqs (2) and (3) indicate that the average number of deficiencies of ships under the black flag states appear to be smaller than that of ships under the white flag and grey flag when we require that the ships in a subcategory should age below 12 or above. It means the relationship between the average number of deficiencies of ships and ship flag performance reverses after we divide the dataset into four subcategories by introducing a confounding feature ship age. The phenomenon observed is generally termed Simpson's paradox. In this paradox, we assume that the ship flag is the basic categorical feature, the average number of deficiencies is the outcome, and the ship age is the introduced categorical confounding feature that causes the paradox. The reason for this Simpson's paradox may be that the ages of ships under the black flag state are younger, so selected ships under the black flag state have lower average numbers of deficiencies.
Since the NIR considers seven features, the influence of ship selection features on the ship conditions (deficiencies and detentions) is complex, and the categorical confounding features that may cause the paradox might be a combination of the other features. Therefore, we consider situations where the ships in the two subcategories only have different values in one basic categorical feature, and the values of the remaining introduced categorical confounding features are identical. The classification of values of seven features according to the NIR is shown in Table 4. Then, we choose one feature as the basic categorical feature, group ships with identical values of remaining features into different subcategories, and conduct the analysis with subcategory data. The data analysis procedures for calculating the average number of deficiencies are shown in Algorithm 1, where the notation used is listed in Table 5.
3.2. Materials
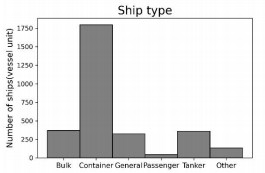
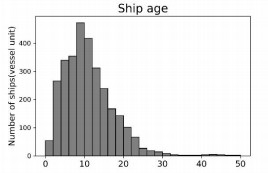
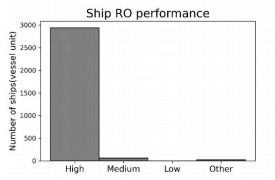
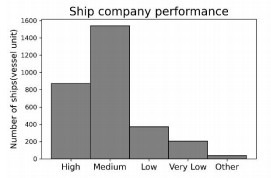
We collect PSC inspection records during January 2015 to December 2019 period at the Hong Kong port from the database of Tokyo MoU1. Data records with incomplete information are omitted, and we finally obtain 3026 PSC inspection records to be analyzed in this paper. The information we need comes from each PSC inspection record, including seven features that the NIR focuses on (i.e., ship type, ship age, ship flag performance, ship RO performance, ship company performance, the number of deficiencies within previous 36 months, and the number of detentions within previous 36 months) and the number of deficiencies identified. The distributions of the seven features over the 3026 cases are shown in Table 6. It is noticeable that the 3026 records do not have low and very low ship RO performance states. Because all ships in the dataset do not have to add points with respect to their ship RO performance, we ignore this feature in the following analysis.
1 https://www.tokyo-mou.org/inspections_detentions/psc_database.php
4.
Results
Based on the method described in Section 3.1, we classify ships according to the values of a certain basic categorical feature by restricting that the values of remaining confounding features are identical. Because we select six features of the NIR's ship selection scheme, for each feature, the whole dataset could be divided into 32 (25) subcategories. In each subcategory, the values of all other features except for the chosen basic categorical feature are the same, so we can analyze whether there exists Simpson's paradox for this basic categorical feature in this subcategory. For each subcategory of one certain basic categorical feature, we can divide the subcategory into two groups according to the risk value of the basic categorical feature. We compute the average number of deficiencies in each group and display it in a histogram. The left red side of the histogram is the average number of deficiencies of ships with the high-risk value of the basic categorical value, while the right green side of the histogram is that of ships with the low-risk value. If the left value of the histogram is smaller than the right value, Simpson's paradox exists because this finding violates the assumption that ships with high-risk values should have more deficiencies than those with low-risk values. Then we present each subcategory as a branch. The 32 branches construct a decision tree, and the leaf node of each branch shows the histogram mentioned above. By doing this for each feature, we obtain six decision trees in total, and further select the branch with Simpson's paradox in each decision tree by blue boxes, as shown in Figures 1–6. In addition, we select the branches with Simpson's paradox and show them in the table, as shown in Tables 7–12. In each table, we analyze which categorical confounding features cause Simpson's paradox.
In each decision tree, we classify ships according to the values of one basic categorical feature, the values of the remaining confounding features of the ships are identical in the same branch. According to Figures 1–6, we find 23, 11, 16, 8, 12 and 10 cases of Simpson's paradox in six trees, respectively. Tables 7–12 show the average numbers of deficiencies of the branches showing Simpson's paradox.
Table 7 shows that, when we choose ship type as the basic categorical feature, there are 13 cases with other flag state performance and 12 cases with fewer than 5 deficiencies identified within previous 36 months where Simpson's paradox occurs. This result indicates that ship flag performance and the number of deficiencies within previous 36 months are two confounding features that are coupled with ship type. Table 8 shows that, when we choose ship age as the basic categorical feature, there are 6 cases under other flags and 6 cases with fewer than 3 detentions identified within previous 36 months where Simpson's paradox occurs. This result indicates that ship flag performance and the number of detentions within previous 36 months are two confounding features that are coupled with ship age. Table 9 shows that, when we choose ship flag performance as the basic categorical feature, there are 9 cases with ship age below 12 years old and 10 cases with fewer than 5 deficiencies identified within previous 36 months where Simpson's paradox occurs. This result indicates that ship age and ship company performance are two confounding features that are coupled with ship flag performance. Table 10 shows that, when we choose ship company performance as the basic categorical feature, there are 5 cases with ship age below 12 years old and 5 cases with high or medium ship company performance where Simpson's paradox occurs. This result indicates that ship age and the number of deficiencies within previous 36 months are two confounding features that are coupled with ship company performance. In Table 11, because all the numbers of cases with low-risk values of each confounding feature do not exceed half of the total 12 cases, it is hard to tell which features are coupled with the number of deficiencies within previous 36 months. Table 12 shows that, when we choose the number of detentions within previous 36 months as the basic categorical feature, there are 6 cases with ship age below 12 years old where Simpson's paradox occurs, which indicates that ship age is coupled with the number of detentions within previous 36 months. This result may indicate that because young ships are assumed to have less possibility of being detained, shipping companies may neglect these ships, resulting in more deficiencies detected in official PSC inspections. At last, Figure 7 displays the correlation of pairwise features among six features based on the above results.
Based on our results, we find that the selected features are nonlinear to the risk level of a ship, so the simple weighted-sum method could not identify ships' conditions accurately. The PSC authorities can consider improving the ship selection scheme of NIR by reformulating a scoring system that considers the correlations between pairwise features. Based on the decision rules revealed in this paper, port states should pay attention to certain ship features when scoring ships. For example, for features such as ship age, ship flag performance, and ship company performance, even if one of them of a ship is in high-risk values, it does not indicate that this ship is supposed to have a large number of deficiencies. The reason is that those features are coupled with three other features (see Figure 7), respectively. For example, although some ships are registered under black flags, their ages might be below 12 years old, or their ship company performance is high or medium, leading to a lower average number of deficiencies. However, for features such as the number of detentions within previous 36 months, they can reflect the actual condition of a ship because there is only one feature coupling to them. Therefore, these features should be given more attention during inspections. In addition, when developing advanced models for calculating ship risk level, e.g., statistical and ML models, the correlations between pairwise features can be further considered in the modeling procedures.
5.
Conclusions
Certain selection features, such as the ship's flag, age, and type, are believed to directly influence how well a ship is likely to be operated. Currently, the ship selection method widely adopted by PSC authorities regulated by Tokyo MoU is the NIR's simple weighted-sum scheme. This paper aims to investigate the plausibility of the NIR's weighted-sum method; that is, investigating whether there are paradoxes with respect to it. If Simpson's paradox exists, we could further explore which feature flips the effect. By observing the results, we find that many features selected by the NIR are coupled. Ship age, ship flag performance, and ship company performance are all coupled with three other features, respectively. Ship type and the number of deficiencies within previous 36 months are coupled with two other features, respectively. The number of detentions within previous 36 months is coupled with only one feature.
The results of this study indicate that selected features of the NIR are nonlinear to the risk level of ships, so the weighted-sum method should be improved according to their nonlinear relationships. The finding suggests that PSC authorities should pay attention to certain features like ship age, ship flag performance and ship company performance, since none of them could reflect the condition of the ship directly and there exist at least three pairwise correlations between each of them and other features. If we apply the nonlinear models which consider the correlations between the features (e.g., ML models) to evaluate a ship's risk level, the models can achieve better effectiveness in ship selection in PSC than the linear model (i.e., the weighted-sum method). Although this paper is the first study to examine the plausibility of the NIR, we do not quantitatively analyze the impact of compounding features on the final ship selection results. In the future, more advanced analytics techniques should be investigated for ship selection in PSC inspection based on the findings discovered in this paper, such as machine learning [39,40], online learning [41], prediction and optimization[42,43,44], evolutionary algorithms [45,46], multi-objective optimization [47], parameter control [48], and scheduling and routing [49], which have been applied as powerful solution approaches in many other domains.
Acknowledgments
The authors thank the four reviewers for their valuable comments.
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: