A mosquito population replacement model consisting of two differential equations

1.   Introduction

Dengue fever, also known as breakbone fever, is an acute infectious disease caused by dengue viruses, transmitted through bites of infected mosquito vectors, and characterized by fever, nausea, vomiting, joint and muscle pain, and internal bleeding, etc. The main vectors of dengue include Aedes aegypti and Aedes albopictus. The global incidence of dengue places half of the world's population at risk, and affects more than 100 countries around the world. Traditional methods aiming to kill mosquitoes by spraying insecticide and removing breeding sites have only short-term effect due to the emergence of insecticide resistance ^[1] and the continual creation of ubiquitous water containers. What makes things even worse is antibody-dependent enhancement phenomenon between different dengue serotypes, which halted the application of dengue vaccines ^[2].

To date, the World's Mosquito Program's Wolbachia method is helping communities around the world prevent the spread of mosquito-borne disease. As one of the most common bacterial endosymbionts on the planet, Wolbachia was first identified in 1924 but little research was ever conducted until in 1971 when its role in cytoplasmic incompatibility (CI for abbreviation hereafter) was revealed. CI refers to embryonic mortality in crosses between an infected male and an uninfected female, thereby bringing fitness advantage to infected females over uninfected females. Unfortunately, Wolbachia does not occur in Aedes aegypti and although there are two natural Wolbachia strains in Aedes albopictus, they do not induce CI. The groundbreaking work on establishing stable Wolbachia strain in Aedes aegypti was accomplished in 2005 through microinjection ^[3]. After that, various Wolbachia strains have been established in Aedes albopictus, which can block partially or completely the replication of dengue viruses in mosquitoes. Nowadays, two innovative strategies aiming to control mosquito and mosquito-borne diseases have been carried out in recent years. One is named as population replacement which targets to replace the wild mosquito population with the infected one by releasing both infected females and males. And the other is called population suppression which is devoted to eradicating wild mosquito vectors through CI by releasing only infected males.

As a natural, sustainable and affordable solution to control the mosquito-borne diseases, field trials for both population replacement and population suppression have been carried out. In 2011, Wolbachia-infected female and male mosquitoes were released in Cairns, Northern Australia for the first time, and successfully invaded two natural Aedes aegypti populations, reaching near-fixation in a few months ^[4]. Over decades, population replacement strategy has also been deployed as a practical approach to dengue suppression in Asia, Latin America and Oceania. Since March 2015, by combining the incompatible and sterile insect techniques (IIT-SIT), Wolbachia-infected male mosquitoes have been released on Shazai Island and Dadaosha Island, south of Guangzhou city. The implementation of IIT-SIT from 2015 to 2017 enabled near-elimination of wild-type Aedes albopictus field populations ^[5].

These successful field trials demonstrate the feasibility of area-wide application of Wolbachia release for control of vector mosquitos. Mathematical modeling and analysis on Wolbachia spread dynamics in mosquito populations can be traced back to half a century ago, when Caspari and Watson ^[6] was motivated by the evolutionary importance of CI in mosquitoes. Since that, various mathematical models for the spread of Wolbachia infection have been developed and studied in the literature, we refer to ^{[7,8,9,10,11,12,13,14]} for population suppression models and ^[15,16,17] for population replacement models to cite a few. In this paper, we focus on a release strategy with supplementary releases of Wolbachia-infected males to speed up population replacement and lower the threshold infection frequency. This strategy has been proved in lab experiments ^[18] in that redundant release of infected males can increase the infection frequency by suppressing effective matings between uninfected mosquitoes.

Under the assumption that infected males are supplementarily released at a ratio $r$ to the total population size during each waiting period $T$ between two consecutive releases, two thresholds $r^*$ and $T^*$ are found, and the fate of population replacement is totally determined by the relation between $r$ with $r^*$, and $T$ with $T^*$. To be precise, we prove that when $0 < r < r^*$, or $r\ge r^*$ and $T > T^*$, an unstable $T$-periodic solution exists which serves as a threshold infection frequency that must be exceeded for the infection frequency to tend to increase. However, when we increase the release ratio to $r > r^*$ and shorten the waiting period to $T\leq T^*$, the unstable $T$-periodic solution disappears and population replacement is guaranteed since the threshold infection frequency is lowered to zero in such a case.

The rest of the paper is organized as follows. Based on ^[15] and followed the modeling idea firstly introduced in ^[19], we formulate a population replacement model in Section 2, which reads as a switching model consisting of two ordinary differential equations. Asymptotic dynamics of the switching model is translated into the qualitative property of the corresponding Poincar$\acute{e}$ map in Section 3 as preliminaries. Section 4 is devoted to proofs of our main results on the global dynamics driven by the switching model. Numerical examples and a brief discussion are provided in Section 5.

2.   Model formulation

We consider a formally hermaphroditic mosquito population where the ratio of infected males to infected females is the same as the ratio of uninfected males to uninfected females. By assuming homogeneous populations of mosquitoes, we let $x(t)$ and $y(t)$ denote the numbers of infected and uninfected mosquitoes at time $t$, respectively. We assume perfect maternal transmission and complete CI ^{[3,4,5,18,20]}, that is, all offspring produced from infected females are infected, and no egg laid by uninfected females mated with infected males will hatch. Let the birth rate for infected and uninfected individuals be $b_1$ and $b_2$, respectively. The number of infected offspring is $b_1x$ since it does not depend on the paternal infection status. In terms of the number of uninfected offspring from uninfected mothers, we must take CI into consideration. Under random mating behavior, the probability of CI occurrence is $\cfrac{x(t)}{x(t)+y(t)}$. With complete CI, the growth rate of uninfected individuals is decreased from $b_2$ to $b_2\Big(1-\cfrac{x(t)}{x(t)+y(t)}\Big) = \cfrac{b_2y(t)}{x(t)+y(t)}$. Furthermore, we assume that the death rate for both infected and uninfected mosquitoes is equal to $\delta$, irrelevant of their infection status. Taking all these considerations together, we have

It should be mentioned here that although Wolbachia infection may result in significant life-shortening effect on hosts ^[20], here we group all the fitness cost caused by Wolbachia infection to the parameter $b_1$ satisfying $b_1 < b_2$ throughout the paper. Under this assumption, by letting

to characterize the Wolbachia-infection frequency, we have from (2.1)

Model (2.2) admits three equilibria,

and generates bistable dynamics: if the initial infection frequency $p_0$ is larger than $\hat{p}(0)$, then $p(t; 0, p_0)\to 1$ as $t\to\infty$. Otherwise, $p(t; 0, p_0)\to 0$ as $t\to\infty$. Here, $p(t; 0, p_0)$ is solution to (2.2) satisfying $p(0) = p_0$.

The bistable dynamics driven by (2.2) shows that to guarantee the success of population replacement, manifested by $p(t)\to 1$ as $t\to\infty$, supplementary releases of Wolbachia-infected mosquitoes are required when $p_0 < \hat{p}(0)$ to make the reset initial infection frequency surpass $\hat{p}(0)$. To the end, besides releasing more infected females to increase the initial infection frequency, an alternative method is to release more infected males to promote population replacement by suppressing the effective matings between wild mosquitoes. In 2018, Yu in ^[19] introduced an innovative modeling idea which treated the released males as a given function rather than an independent variable. This treatment is biologically supported since the only mission of released males is to sterilize wild females through CI when they are sexually active. Once they lose their mating competitiveness, the released males will not make any contribution to population replacement.

Adopting this modeling idea, let $R(t)$ denote the number of sexually active males at time $t$. In such a case, the probability of CI occurrence increases from $\cfrac{x(t)}{x(t)+y(t)}$ to $\cfrac{x(t)+R(t)}{x(t)+y(t)+R(t)}$. Hence, model (2.1) becomes a planar non-autonomous system

As the implementation of Wolbachia release, the population size of wild mosquitoes decreases and hence the required number of infected males for effective population suppression also decreases ^[5]. Based on this observation, we introduce a release strategy with the number of sexually active males being kept as

In such a case, model (2.3) can be rewritten as

where

Compared (2.2) to (2.5), we see that with the release strategy implemented in (2.4), the threshold infection frequency decreases from $\hat{p}(0)$ to $\hat{p}(r)$. Furthermore, if we introduce

then a complete characterization of dynamics driven by (2.5) is stated as follows.

Theorem 2.1. On model (2.5),

(1) when $0 < r < r^*$, model (2.5) generates bistable dynamics, with the existence of an unstable equilibrium $\hat{p}(r)$ defined in (2.6), and both $p_0^* = 0$ and $p_1^* = 1$ are asymptotically stable.

(2) when $r\ge r^*$, $p_0^* = 0$ is unstable and $p_1^* = 1$ is globally asymptotically stable.

As a critical case, the release strategy satisfying (2.4) is technically hard to accomplish. In this paper, we focus on a more general release strategy satisfying

where $T$ is the waiting period between two consecutive releases, and in each release period, the number of sexually active males released is kept as $r(x(t)+y(t))$ for $t\in[iT, iT+q)$ with $0 < q < T$, which lose their mating competitiveness for $t\in[iT+q, (i+1)T)$. In such a case, model (2.3) switches between

and

with $i = 0, 1, 2, \cdots$. Or equivalently, the infection frequency is dictated to the following switching model

with $i = 0, 1, 2, \cdots.$

Model (2.8)-(2.9) generates much richer dynamics than model (2.5) whose dynamics has been completely described in Theorem 2.1. Besides $r^*$ defined in (2.7), a threshold $T^*$ of $T$ will be found. We shall prove that the equilibrium $p_1^* = 1$ of model (2.8)-(2.9) is globally asymptotically stable when $r > r^*$ and $T\leq T^*$, otherwise model (2.8)-(2.9) admits a unique nontrivial $T$-periodic solution, which is unstable. To prove these results, some preliminary works are offered in the next section.

3.   Preliminaries

It is obvious that $p_0^* = 0$ and $p_1^* = 1$ are two equilibria of the $T$-periodic model (2.8)-(2.9), which are also two trivial $T$-periodic solutions. For any $u\in(0, 1)$, we let $p(t): = p(t; 0, u)$ be the solution of (2.8)-(2.9) satisfying $p(0) = u$. Solution $p(t; 0, u)$ satisfies (2.8) for $t\in[0, q)$, and then follows (2.9) for $t\in[q, T)$ by defining $p(q) = p(q^-)$. Following this procedure, solution $p(t)$ of (2.8)-(2.9) is well-defined in each $T$-periodic interval $[kT, (k+1)T)$ with $k = 0, 1, 2, \cdots$, and hence being well-defined for all $t\ge 0$. Furthermore, $p(t; 0, u)$ is a continuous and piecewise differentiable function defined on $[0, +\infty)$, and is continuously differentiable in $u$.

To obtain the global dynamical characterization of (2.8)-(2.9), following the lines in ^{[12,13,14,16,17]}, we define

which are continuously differentiable in $u$. Furthermore, the existence and uniqueness of $T$-periodic solutions to (2.8)-(2.9) is equivalent to the existence and uniqueness of fixed points to the map $h(u)$. To be precise, $h(u) = u$ if and only if model (2.8)-(2.9) has a $T$-periodic solution initiated from $u$.

To characterize the asymptotic behavior of $p(t; 0, u)$, we define function sequences $\{\bar{h}_n\}$ and $\{h_n\}$ by

respectively, which satisfy

for $n = 1, 2, \cdots.$ Along the arguments in ^{[12,13,14,16,17]}, together with the uniqueness of solutions to model (2.8)-(2.9), we can get the monotonicity of function sequences $\{\bar{h}_n\}$ and $h_n$ defined in (3.2). The monotonicity is totally determined by the comparison between $h(u)$ and $u$, which is stated in the following lemma.

Lemma 3.1. On the monotonicity of $\{\bar{h}_n(u)\}$ and $\{h_n(u)\}$, the following results hold.

(1) If $h(u) > u$, then both $\{\bar{h}_n(u)\}$ and $\{h_n(u)\}$ are strictly increasing.

(2) If $h(u) = u$, then $p(t; 0, u)$ is a $T$-periodic solution to (2.8)-(2.9).

(3) If $h(u) < u$, then both $\{\bar{h}_n(u)\}$ and $\{h_n(u)\}$ are strictly decreasing.

To further explore the qualitative property of $\bar{h}(u)$ and $h(u)$ defined in (3.1), we solve (2.8)-(2.9) in $[0, T)$ initiated from $p(0) = u$ with $u\in(0, 1)$ in the following two cases.

Case 1: $r\neq r^*$. In this case, equation (2.8) can be rewritten as

where

Integrating (3.3) from $0$ to $q$ offers

which leads to

Similarly, equation (2.9) can be rewritten as

where

Integrating (3.6) from $q$ to $T$ reaches

and hence we arrive at

Noticing the fact that $\bar{h}(0) = 0$, $h(0) = 0$, from (3.5) and (3.8), we have

which leads to

Case 2: $r = r^*$. In this case, $\hat{p}(r) = 0$, and we rewrite (2.8) as

Integrating (3.10) from $0$ to $q$ offers

which leads to

It follows that

Since

we have two cases to consider when calculating $\bar{h}'(0)$.

$(1)$ If $\lim\limits_{u\to 0} \Big(\cfrac{1}{\bar{h}(u)}-\cfrac{1}{u}\Big)$ is finite, then (3.12) implies that $\bar{h}'(0) = 1$.

$(2)$ If $\lim\limits_{u\to 0} \Big(\cfrac{1}{\bar{h}(u)}-\cfrac{1}{u}\Big) = -\infty$, then $\bar{h}'(0) = 0$. However, revisiting (3.12) again leads to $\lim\limits_{u\to 0} \Big(\cfrac{1}{\bar{h}(u)}-\cfrac{1}{u}\Big) = +\infty$, a contradiction.

Combining the above two cases, we have $\bar{h}'(0) = 1$, and therefore,

By defining

we obtain our first result on the existence and uniqueness of the nontrivial $T$-periodic solutions to model (2.8)-(2.9) when the release ratio $r\in(0, r^*]$. To be precise, we have

Theorem 3.2. when $0 < r\leq r^*$ and $T > q$, model (2.8)-(2.9) has a unique $T$-periodic solution, which is unstable. Both $p_0^* = 0$ and $p_1^* = 1$ are asymptotically stable.

For the case of $r > r^*$, the global dynamics driven by (2.8)-(2.9) depends on the comparison between $T$ and $T^*$. Specifically, we get

Theorem 3.3. For $r > r^*$,

(1) if $T > T^*$, then model (2.8)-(2.9) has a unique $T$-periodic solution, which is unstable. Both $p_0^* = 0$ and $p_1^* = 1$ are asymptotically stable.

(2) If $T\leq T^*$, then $p_1^* = 1$ of (2.8)-(2.9) is globally asymptotically stable, and $p_0^* = 0$ is unstable.

The proofs of Theorems 3.2 and 3.3 are offered in the next section.

4.   Proofs of main results

4.1.   Proof of Theorem 3.2 for case $0 < r < r^*$

We treat the case $0 < r < r^*$ in this section, where we have $0 < \hat{p}(r) < \hat{p}(0)$, and from Theorem 2.1, we reach the following relations on $h(u)$ and $u$,

Hence, any nontrivial $T$-periodic solutions of model (2.8)-(2.9), if exist, must initiate from $(\hat{p}(r), \hat{p}(0))$. And the continuity of $h(u)$, together with (4.1) and (4.2), implies that there exists at least one $u^*\in (\hat{p}(r), \hat{p}(0))$ such that

i.e., model (2.8)-(2.9) has at least one nontrivial $T$-periodic solution initiated from $u^*$.

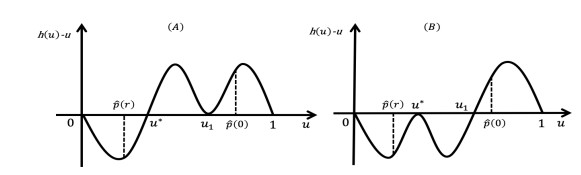
Assume by contradiction that besides $u^*$, there exists $u_1 > u^*$ such that $h(u_1) = u_1$. We start with the assumption that model (2.8)-(2.9) has exactly two nontrivial $T$-periodic solutions. Then one of the following two cases occurs.

See Figure 1 for illustration. To unload the notation burden, we define

Then from (3.4) we arrive at

and from (3.7) we get

respectively. Differentiating both sides of (4.4) yields

Direct computations offer

substituting it into (4.6), we have

By using (4.4), $\bar{h}'(u)$ can be achieved as

Similarly, differentiating both sides of (4.5) yields

Since

we have from (4.8),

By using (4.5) and (4.7), we achieve $h'(u)$ as

Therefore, for $u\in \Gamma: = \{u\in(\hat{p}(r), \hat{p}(0))|h(u) = u\}$, we have

where

Noticing that $Q(u) < 0$ for $u\in(\hat{p}(r), \hat{p}(0))$, and

we have that $Q(u)$ is strictly decreasing in $u\in(\hat{p}(r), \hat{p}(0))$ for $u\in \Gamma$.

Meanwhile, from (4.10), we also have the following relations:

For Case (A), (4.13) implies that at $u = u_1$,

However, from $\bar{h}(u_1) > u_1$ and $Q'(u) < 0$, we get $Q(\bar{h}(u_1)) < Q(u_1)$, a contradiction to (4.15). Similarly, for Case (B), we get

from $h'(u^*) = 1$. A contradiction to $Q(\bar{h}(u^*)) < Q(u^*)$ since $\bar{h}(u^*) > u^*$. It's easy to see that the monotonicity of $Q(u)$ can also exclude the possibility of existence of three or more $T$-periodic solutions to model (2.8)-(2.9).

The existence and uniqueness of $p(t; 0, u^*)$ determines the qualitative property of $h(u)$ as follows:

i.e., any solutions initiated near $u^*$ will be repelled away from $p(t; 0, u^*)$, and hence $p(t; 0, u^*)$ is unstable. Meanwhile, (4.16) guarantees the asymptotical stability of both $p_0^* = 0$ and $p_1^* = 1$. This completes the proof of Theorem 3.2 for $r\in (0, r^*)$.

To finish the proof of Theorem 3.2, we treat the critical case with $r = r^*$ in the next subsection.

4.2.   Proof of Theorem 3.2 for case $r=r^*$

When $r = r^*$, (3.13) implies $h'(0) < 1$ and there exists sufficiently small $\epsilon > 0$ such that

Together with the fact that $h(u) > u$ for $u\in [\hat{p}(0), 1)$, the existence of $u^*$ satisfying (4.3) has been proved. To obtain the uniqueness, let

Then (3.11) is

Differentiating both sides of (4.18), we arrive at

Since

from (4.19), we get

Together with the first equality of (4.9), we get

Hence, at $u\in\Gamma$, we have

where $R(u) = \cfrac{u}{u-\hat{p}(0)}$ with $R'(u) < 0$. The remaining part of proving the uniqueness of nontrivial $T$-periodic solutions to (2.8)-(2.9), as well as the stability analysis, is similar to the proof of Theorem 3.2 for case $r\in (0, r^*)$, and we omit here. This completes the proof for case $r = r^*$.

4.3.   Proof of Theorem 3.3 with $r > r^*$ and $T > T^*$

When $r > r^*$, we have $\hat{p}(r) < 0 < \hat{p}(0)$, and from Theorem 2.1,

Hence, if (2.8)-(2.9) has nontrivial periodic solutions, then it must initiate from $(0, \hat{p}(0))$.

When $T > T^*$, we have from (3.9) that $h'(0) < 1$. Combining (4.17) and (4.20), we see that there exists $u^*\in[\epsilon, \hat{p}(0))$ such that

proving the existence of at least one nontrivial $T$-periodic solution to (2.8)-(2.9). The rest proof is similar to the proof for case $r\in (0, r^*]$, and we omit here.

4.4.   Proof of Theorem 3.3 with $r > r^*$ and $T=T^*$

We shall prove the global asymptotical stability of $p_1^* = 1$. To the end, it suffices to prove

which excludes the existence of nontrivial $T$-periodic solutions of (2.8)-(2.9) and guarantees the instability of $p_0^* = 0$. As the unique stable equilibrium of (2.8)-(2.9), $p_1^* = 1$ is then globally asymptotically stable.

Regarding the critical case $T = T^*$, we have from (3.5) and (3.8),

Define

Then, from (4.22) we get $h(u) = u$ if and only if $H(u) = H(\bar{h}(u))$.

Taking the derivative of $H(u)$, we reach

Since $r > r^*$ implies $\hat{p}(r) < 0$, we have

Recalling the fact that $\bar{h}(u) > u$ for $u\in(0, \hat{p}(0))$ if $r > r^*$, we can always assume that $\bar{h}(u)\in(0, \hat{p}(0))$. Otherwise, $h(u) > \bar{h}(u)$ which yields $h(u) > u$ and (4.21) holds. When $\bar{h}(u) < \hat{p}(0)$, from (4.23), we have

Meanwhile, (4.22) implies that

Further define

Then

Combining the above three equalities, we have

If $h(u)\ge\hat{p}(0)$, then we have $h(u) > u$ and (4.21) holds. If $h(u) < \hat{p}(0)$, then we claim that $h(u) > u$ for all $u\in(0, \hat{p}(0))$. Otherwise, $h(u)\leq u$ and (4.26) lead to $P(h(u)) < P(u)$. However, from $P(u) > 0$ and (4.25), we have $P(h(u))\ge P(u)$ if $h(u)\leq u$. A contradiction. Hence, we arrive at (4.21) and the proof is complete.

4.5.   Proof of Theorem 3.3 with $r > r^*$ and $T < T^*$

If we further shorten $T$ from $T^*$ to $T < T^*$, then the equilibrium $p_1^* = 1$ is globally asymptotically stable. Although this result is obvious from a biological point of view since the global asymptotical stability has been guaranteed when $r > r^*$ and $T = T^*$, we provide the proof for mathematical completeness.

To prove it, we see from (3.9) that $h'(0) > 1$ when $T < T^*$, and (4.17) holds. Again, from (4.20), we only need to prove

If (4.27) does not hold, then we consider two cases below. See Figure 2 for illustration.

where $0 < u_1 < u_2 < \hat{p}(0)$.

Revisiting the proof of Theorem 3.2 for case $r\in (0, r^*)$, we can reach $Q(u)$ defined in (4.11) satisfying $Q(u) < 0$ for $u\in(0, \hat{p}(0))$, and $Q'(u) < 0$ still holds for $u\in(0, \hat{p}(0))$ when $r > r^*$. For Case (A), we have

which contradicts to $\bar{h}(u) > u$ for $u\in(0, \hat{p}(0))$. Similarly, for Case (B), if $\bar{h}(u_1)\ge\hat{p}(0)$, then (4.27) holds. If $\bar{h}(u_1) < \hat{p}(0)$, then

also contradicts to $\bar{h}(u_1) > u_1$. Hence, (4.27) holds, proving Theorem 3.3 with $r > r^*$ and $T < T^*$. The proofs of main results are completed.

5.   Discussion

Mosquitoes go through four complete metamorphic stages: egg, larva, pupa and adult. After a female mosquito sucks a blood meal, she lays eggs in water containers, including abandoned tyres, plastic cans, clay-earthenware pots, native pots, etc. To estimate $b_2$, we take the observation results in ^[21] which showed that Aedes albopictus, the sole vector of dengue in Guangzhou, has a seasonal dependent fecundity, and the number of eggs laid by each female ranges from 28.36 to 224.5. In the water, eggs hatch into larvae, which molt into pupae. Adult mosquitoes emerge from mature pupae. For Aedes albopictus, it was also observed in ^[21] that the survival probability for an egg to go through larva and pupa to become an adult ranges from $4/1000$ to $337/1000$. These findings lead us to estimate $b_2$ as

to get the maximal interval for $b_2$.

Besides CI intensity and the maternal inheritance rate, a key parameter in Wolbachia infection dynamics is mosquito fitness cost associated with infection, which are dependent on the specific Wolbachia strains. For example, in ^[3], the authors predicted from lab experiments an approximate 15% fecundity cost to be associated with wAlbB infection. However, in ^[20], it was observed that wMelPop infection almost halved the longevity of adult mosquitoes, which implies a substantial fitness cost associated with wMelPop. Here, we take a mild fitness cost as an example with $b_1 = 0.8b_2$. By letting

we have $r^* = 0.25$ and $\hat{p}(0) = 0.2$. Without supplementary release of Wolbachia-infected males, i.e., $r = 0$, $\hat{p}(0)$ serves as the threshold infection frequency as shown in Figure 3(A): to guarantee that wild mosquito populations would be replaced by Wolbachia-infected ones, the initial infection frequency should surpass $\hat{p}(0)$. With supplemental release of Wolbachia-infected males with $r = 0.2\in(0, r^*)$, we have $\hat{p}(r) = 0.04$. By solving (2.8)-(2.9) with initial value lying in $(\hat{p}(r), \hat{p}(0))$, we reach Figure 3(B) for dynamics of Wolbachia infection frequency. Our numerical trials show that the unique $T$-periodic solution initiates at $u^*\approx0.0422$. Being a threshold infection frequency, $u^*$ has been significantly decreased compared to the case $r = 0$, which confirms that supplementary releases of infected males do lower the threshold infection frequency.

If we take $r = 0.3 > r^*$, then we get $\hat{p}(r) = -0.04 < 0$ and $T^*\approx 3.4615$. When $T = 4 > T^*$, Figure 3(C) shows similar dynamics as shown in Figure 3(B), with the existence of a unique periodic solution initiated at about 0.002. In other words, when the release ratio $r$ is greater than the threshold $r^*$, there still exists a threshold on the infection frequency to surpass for successful population replacement when the release period $T$ is larger than $T^*$. However, when $r > r^*$, if we release more often with $T < T^*$, Figure 3(D) shows that population replacement is always guaranteed in that the infection frequency $p(t; 0, u)$ will go to 1 for any $u\in (0, 1)$.

As a research hotspot, Wolbachia spread dynamics in mosquito populations has attracted more and more attention. Motivated by lab observations that supplemental releases of infected males can speed up population replacement by suppressing compatible matings between uninfected individuals, we developed a switching ordinary differential equation model to study Wolbachia infection dynamics interfered by supplemental releases of infected males during each release period $T$. The release follows a proportional release with the release ratio being $r$. Under the assumptions of perfect maternal transmission and complete CI, we found two thresholds $r^*$ and $T^*$ defined in (3.14), which lead to a complete description of dynamics for the switching model as shown in Theorems 3.2 and 3.3.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11971127, 12071095).

Conflict of interest

The authors declare there is no conflicts of interest.