Stabilizing effect of elasticity on the motion of viscoelastic/elastic fluids

1.   Introduction

In recent years, there has been growing interest in the study of virus dynamics model with delays ^{[3,4,7,13,16,17,19,28,29]}. And the following ordinary differential equations are usually formulated a general virus infection dynamical model with constant delays ^[7]

where $u_{1}\left(t\right),$ $u_{2}\left(t\right), \ $ and $u_{3}\left(t\right)$ represent the population of target cells, infected cells, and free viruses, respectively the positive $b,$ $p,$ and $q$ are the respective death rates. The parameters $a,$ $r,$ and $k$ are the rates at which new target cells, infected cells, and free viruses are generated, respectively. The function $f\left(u_{1}\left(t\right), u_{3}\left(t\right) \right)$ represents the rate for the target cells to be infected by the mature viruses. $pg\left(u_{2}\left(t\right) \right)$ describes the death rate of the infected cells depending on the population of themselves. Once the virus contacts the target cell, such cell may survive the entire latent period $h_{1}.$ The delay $h_{2}$ represents the time necessary for the newly produced viruses to be infectious.

To be better understanding the dynamical behaviour of virus infection one introduces spatial coordinate $x\in \Omega$ and allows the unknowns to depend on it. The target cells, infected cells, and free viruses are assumed to follow the Fickian diffusion with the constant diffusion rate $d_{1}, d_{2},$ and $d_{3}.$ In earlier results where $d_{1} = d_{2} = 0\ $ and $d_{3} > 0$ (see e.g., for model without delay ^[20,21] and ^[4,13] with constant delay), were investigated by many researchers. For the case $d_{i} > 0,$ $i = 1, 2, 3,$ a very interesting phenomenon was discovered in paper ^[1]. Although this phenomenon was first discovered in the vaccinia virus, the researchers showed that the similar phenomenon was found in some other kinds of virus. Recently, there have been some interesting research developments on such virus infection dynamics models, see, e.g., for model without delay ^[9,22,24] and ^[14,23,25] with constant delay. On the other hand, it is clear that the constancy of the delay is an extra assumption which essentially simplifies the analysis. Whereas, the state-dependent delay is taken to be a bounded function of the total population (target cells, infected cells, and free viruses), which is more appropriate to describe the real-world processes in biological problem. Moreover, introducing such state-dependent delays in modeling real phenomena results frequently from an attempt to better account for the actual behavior of the population. Therefore, different from the existing results ^{[3,4,7,13,19,28,29]}, the diffusive virus dynamics model ^[17] with state-dependent delay is worthy of attention. And such topics have not been fully investigated, which remain a challenging issue.

Motivated by the above observations, we modify the model (1) to (2) that also extends the model in ^[17]. And we mainly consider the asymptotic stability of the system (2) from a dynamical systems point of view.

where $u_{1}\left(x, t\right),$ $u_{2}\left(x, t\right), \ $ and $u_{3}\left(x, t\right)$ defined as earlier, also represent the population of target cells, infected cells, and free viruses, at position $x$ at time $t$, respectively. $\Omega \ $ is a fixed, connected bounded domain in $\mathbb{R} ^{n}\ $ with smooth boundary $\ \partial \Omega.$ Denote $u = \left(u_{1}, u_{2}, u_{3}\right)$ and the history segment $u_{t}\left(x, \theta \right) \triangleq u\left(x, t+\theta \right),$ $\theta \in \left[ -h, 0\right],$ $h\triangleq \max \left\{ h_{1}, h_{2}\right\}.$ $\tau _{1}\left(u_{t}\right)$ and $\tau _{2}\left(u_{t}\right)$ where are taken to be some general functions of system populations with $0\leq \tau _{j}\left(u_{t}\right) \leq h_{j},$ $j = 1, 2$, represent the latent period that the cell survives once the virus contacts the target cell and the time that the newly produced viruses are infectious, respectively. $d_{i}, i = 1, 2, 3$ is the constant diffusion rate.

The rest of the paper is organized as follows. In section 2, we briefly recall some basic known results which will be used in the sequel. In section 3, we first present the positivity and boundedness results for the model (2). Next we mainly study the asymptotic stability of interior equilibria from a dynamical systems point of view. According to constructing a dynamical system on a nonlinear metric space, we apply [5,Theorem 4.1.4] and choose a novel Lyapunov functional to the model (2) and allow, but not require, diffusion terms in each state equation. In section 4, we generalize the method to such model with Logistic growth rate.

2.   Preliminary

In this section, we present some definitions, lemmas, and notations, which will be useful throughout this paper.

Denote the linear operator $-A^{0} = diag\left(d_{1}\triangle, \text{ }d_{2}\triangle, \text{ }d_{3}\triangle \right)$ in $C\left(\bar{\Omega}, \mathbb{R} ^{3}\right)$ with $D\left(A^{0}\right) \triangleq D\left(d_{1}\triangle \right) \times D\left(d_{2}\triangle \right) \times D\left(d_{3}\triangle \right).$ Let $D\left(d_{i}\triangle \right) \triangleq \left\{ y\in C^{2}\left(\bar{\Omega}, \mathbb{R} \right) :\frac{\partial y}{\partial \overrightarrow{n}}|_{\partial \Omega } = 0\right\}$ for $d_{i}\neq 0,$ $i = 1, 2, 3.$ Omit the space coordinate $x,$ we denote the unknown $u\left(t\right) = \left(u_{1}\left(t\right), u_{2}\left(t\right), u_{3}\left(t\right) \right) \in X\triangleq \left[ C\left(\bar{\Omega}, \mathbb{R} \right) \right] ^{3}\triangleq C\left(\bar{\Omega}, \mathbb{R} ^{3}\right).$ It is well-known that the closure $-A$ (in $X$) of the operator $-A^{0}$ generates a $C_{0}-$ semigroup $e^{-At}$ on $X$ which is analytic and nonexpansive [12,p.4-p.5]. Further, $-A$ is the infinitesimal generator of the analytic compact semigroup $e^{-At}$ on X (see [27,Theorem 1.2.2] for more details). We denote the space of continuous functions by $C\triangleq C\left(\left[ -h, 0\right], X\right)$ equipped with the sup-norm $\left\Vert \varphi \right\Vert _{C}\triangleq \sup\limits_{\theta \in \left[ -h, 0\right] }\left\Vert \varphi \left(\theta \right) \right\Vert _{X}.$

Now the system $\left(2\right)$ is rewritten in the following abstract form

where the nonlinear continuous mapping $F:C\rightarrow X$ is defined by

with $\phi \in \left(\phi _{1}, \phi _{2}, \phi _{3}\right) \in C.$

Set the initial value $\psi = \left(\psi _{1}, \psi _{2}, \psi _{3}\right) \in Lip\left(\left[ -h, 0\right], X\right)$ for the equation $\left(3\right),$ where

In our study we use the standard (c.f. ([15,Def. 2.3,p.106]) and ([15,Def. 2.1,p.105])).

Definition 2.1. A function $u\left(t\right) \in C\left([-h, t_{f}), \text{ }X\right)$ is a mild solution of initial value problem $\left(3\right) -\left(5\right)$ if $u_{0} = \phi \ $ and

Definition 2.2. A function $u\left(t\right) \in C\left([-h, t_{f}), \text{ }X\right) \cap C^{1}\left([0, t_{f}), \text{ }X\right)$ is a classical solution of initial value problem $\left(3\right) -\left(5\right)$ if $u\left(t\right) \in D\left(A\right)$ for $t\in \lbrack 0, t_{f})$ and $\left(3\right) -\left(5\right)$ are satisfied.

Next we present the existence and uniqueness of solution for the initial value problem $\left(3\right) -\left(5\right).$

Throughout the paper, we assume that functions $f:\mathbb{R} ^{2}\rightarrow \mathbb{R}$ and $g:\mathbb{R} \rightarrow \mathbb{R}$ satisfy the following conditions:

$\left(\mathbf{H1}\right)$ $f$ and $g$ are Lipschitz continuous.

$\left(\mathbf{H2}\right)$ $\left\vert f\left(u_{1}, u_{3}\right) \right\vert \leq \mu u_{1}\ $ for $u_{1},$ $u_{3}\geq 0,$ and $\left\vert g\left(u_{2}\right) \right\vert \leq \lambda u_{2}$ for $u_{2}\geq 0.$

We follow the streamline of the proof Lemma 1.2 in ^[10], (see also [8,Theorem 2]) established by [15,Theorem 3.1 and Corollary 3.3]. Moreover, the linear growth bounds of $f\ $ and $g$ imply the global continuation of the classical solution. Then we obtain the result as follows.

Lemma 2.3. Let the state-dependent delays $\tau _{j}:C\rightarrow \left[ 0, h_{j}\right],$ $\left(j = 1, 2\right)$ be locally Lipschitz. Suppose that $\left(\mathbf{H1}\right)$ and $\left(\mathbf{H2}\right)$ hold. Then initial value problem $\left(3\right) -\left(5\right)$ has a unique global classical solution for $t\geq 0.$

The following lemma provides a theoretical foundation for the stability of the equilibrium in a dynamical system.

Lemma 2.4. ([5,Theorem 4.1.4]) Let $\{S(t),$ $t\geq 0\}$ be a dynamical system on $Z.$ Set $0$ be an equilibrium point in $Z.$ Assume $V$ is a Lyapunov function on $Z$ satisfying $V\left(0\right) = 0,$ $V\left(y\right) \geq \alpha \left(\left\Vert y\right\Vert \right)$ for $y\in Z,$ $\left\Vert y\right\Vert = dist\left\{ y, 0\right\},$ where $\alpha \left(\cdot \right)$ is a continuous strictly increasing function, $\alpha \left(0\right) = 0$ and $\alpha \left(r\right) > 0$ for $r > 0.$ Then $0$ is stable. Suppose in addition that $V^{^{\prime }}\left(y\right) \leq -\beta \left(\left\Vert y\right\Vert \right),$ where $\beta \left(\cdot \right)$ is continuous, increasing and positive, with $\beta \left(0\right) = 0.$ Then $0$ is uniformly asymptotically stable.

In the sequel, we mainly discuss the asymptotic stability of interior equilibria of system $\left(2\right)$ on a metric space

endowed with

We know that $X_{f}$ is a complete metric space from ^[8,10].

The following proposition offers some properties of a function, which will play an important role in construction of Lyapunov functionals.

Proposition 2.5. A function $v:[0,$ $+\infty)\rightarrow \mathbb{R}$ is defined by $v\left(s\right) \triangleq s-1-\ln \left(s\right),$ which is of the following properties.

($i$) $v\left(s\right) \geq 0$ for all $s\in \lbrack 0,$ $+\infty).$

($ii$) $\dot{v}\left(s\right) = 1-\dfrac{1}{s},$ $\dot{v}\left(s\right) < 0$ for $s\in \left(0, \mathit{\text{ }} 1\right)$ and $\dot{v}\left(s\right) > 0$ for $s\in \left(1, \mathit{\text{ }} \infty \right).$

($iii$) $v\left(s\right) = 0$ if and only if $s = 1.$

($iv$) $\dfrac{\left(s-1\right) ^{2}}{2\left(1+\epsilon \right) }\leq v\left(s\right) \leq \dfrac{\left(s-1\right) ^{2}}{2\left(1-\epsilon \right) },$ $\forall$ $\epsilon \in \left(0, \mathit{\text{ }} 1\right)$ and $\forall$ $s\in \left(1-\epsilon, \mathit{\text{ }} 1+\epsilon \right).$ It is checked that

3.   Main result

3.1.   Positivity and boundedness

In the subsection, we prove the positivity and boundedness of solutions for system $\left(3\right).$

To get the results, we need further assumptions:

$\left(\mathbf{H3}\right)$ $g$ is increasing, $g\left(0\right) = 0$ and $g\left(u_{2}\right) \geq 0$ for $u_{2}\geq 0.$

$\left(\mathbf{H4}\right)$ $f\left(u_{1}, u_{3}\right) > 0$ for $u_{1},$ $u_{3} > 0$ and $f\left(u_{1}, 0\right) = f\left(0, u_{3}\right) = 0\ $ for $u_{1},$ $u_{3}\geq 0$.

Set $\mathbf{0 = }\left(0, 0, 0\right) ^{T}\ $ and $\mathbf{M = }\left(M_{1}, M_{2}, M_{3}\right) ^{T} = \left(\dfrac{a}{b}, \text{ }g^{-1}\left(\dfrac{r\mu a}{pb}\right), \text{ }\dfrac{rk\mu a}{qpb}\right) ^{T}.$ Denote

Lemma 3.1. Let $\tau _{j}$ in Lemma 2.3 be valid. Assume that $\left(\mathbf{H1}\right)$-$\left(\mathbf{H4}\right)$ are satisfied. Then $\left[ \mathbf{0}, \mathbf{M}\right] _{C}$ is invariant i.e., for each initial value $\phi = \left(\phi _{1}, \phi _{2}, \phi _{3}\right) \in \left[ \mathbf{0}, \mathbf{M}\right] _{C},$ the unique classical solution of initial value problem $\left(3\right) -\left(5\right)$ satisfies $u_{t}\in \left[ \mathbf{0}, \mathbf{M}\right] _{C}$ for all $t\geq 0.$

Proof. The existence and uniqueness of solution is proven as above Lemma 2.3. Let $K = \left[ \mathbf{0}, \mathbf{M}\right] _{X},$ $S\left(t, s\right) = e^{-A\left(t-s\right) },$ $B\left(t, \phi \right) = F\left(\phi \right).$ The proof of the invariance part follows the invariance result of ([12,Corollary 4] or [27,Corollary 8.1.3]) with the almost Lipschitz property of $F$ by the nomenclature of ^[11]. Next we check the estimates for the subtangential condition. For any $\phi \in \left[ \mathbf{0}, \mathbf{M}\right] _{C}$ and any $\varrho \geq 0$, we obtain

Note that $\left(\mathbf{H2}\right).$ Thus, for any $0\leq \rho \leq \min \left\{ \dfrac{1}{b+\mu }, \dfrac{1}{p\lambda }, \dfrac{1}{q}\right\},$ we have

and

Then we obtain $\phi \left(x, 0\right) +\rho F\left(\phi \right) \left(x\right) \in \left[ \mathbf{0}, \mathbf{M}\right] _{X}.$ This implies that

We complete the proof.

Remark 3.2 It should be pointed out that $K$ is a subset of $X.$ However, such fact is often ignored in some works ^[13,17,29], where $K$ had been chosen a subset of $C.$

3.2.   Stationary solution

Let us discuss stationary solutions of $\left(2\right)$. By such solutions we mean time independent $u^{\ast }$ which, in general, may depend on $x\in \overline{\Omega }.$ Since stationary solutions of $\left(2\right)$ do not depend on the type of delay (state-dependent or constant) we have

It is easy to see that the trivial stationary solution ($\dfrac{a}{b}$, $0,$ $0$) always exists if $f\left(u_{1}^{\ast }, 0\right) = 0$ and $g\left(0\right) = 0$. We are interested in nontrivial stationary solutions of $\left(2\right).$ Based on $\left(7\right),$ we have $u_{2}^{\ast } = g^{-1}\left(\frac{\left(a-bu_{1}^{\ast }\right) r}{p}\right)$ and $u_{3}^{\ast } = \frac{k\left(a-bu_{1}^{\ast }\right) r}{pq}.$ This gives the condition on the coordinate $u_{1}^{\ast }$ which should belong to $(0,$ $\dfrac{a}{b}].$ Denote

Incidentally, we assume that

Remark 3.3. ($i$) Since $\Omega$ is a connected set, a function $w\in C\left(\bar{\Omega}\right)$ may take either one or continuum values. The assumption $\left(\mathbf{H}_{f}\right)$ implies $u_{1}^{\ast }\left(x\right) = u_{1}^{\ast }$, then $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ is independent of $x.$ Moreover, if $\left(\mathbf{H4}\right)$ holds, then we know exactly one root of $E_{f}\left(s\right) = 0,$ such as the DeAngelis-Bendington functional response ^[2,6]

the saturated functional response ^[3,26]

the Crowley-Martin functional response ^[19,30]

And for more general class of $f,$ under additional conditions, one has exactly one root of $E_{f}\left(s\right) = 0.$

($ii$) It should be pointed out that in study of stability properties of stationary solutions for virus infection model one usually uses conditions on the so-called reproduction numbers. Then one can use such conditions to separate the case of a unique stationary solution. In this work, taking into account the state-dependence of the delay, the conditions on the reproduction numbers do not appear explicitly here, but could be seen as particular sufficient conditions for $\left(\mathbf{H}_{f}\right)$. As a consequence, such models admit of multiple equilibria. Then we believe this framework provides a way to model more complicated situations with rich dynamics.

($iii$) Based on $(\mathbf{H2})$ and $\left(\mathbf{H}_{f}\right)$, we have

And then we know that the interior equilibrium $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ belongs to the invariant set $\left[ \mathbf{0}, \mathbf{M}\right] _{C}$ by $\left(\mathbf{H}_{f}\right)$ and the monotone property of $g.$

3.3.   Stability of the interior equilibrium $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$

In this subsection, we discuss the stability of the interior equilibrium $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ from a dynamical systems point of view. Next we work out the stability of $\left(3\right) -\left(5\right)$ with smooth initial value belonging to $X_{f}$.

In the following, we assume that

$\left(\mathbf{H5}\right)$ $f$ is increasing for $u_{1},$ $u_{3} > 0$ and differentiable in a neighborhood of $\left(u_{1}^{\ast }, u_{3}^{\ast }\right),$

$\left(\mathbf{H6}\right)$ $\left(\dfrac{u_{3}}{u_{3}^{\ast }}-\dfrac{f\left(u_{1}, u_{3}\right) }{f\left(u_{1}, u_{3}^{\ast }\right) }\right) \left(\dfrac{f\left(u_{1}, u_{3}\right) }{f\left(u_{1}, u_{3}^{\ast }\right) }-1\right) > 0$ for $u_{1},$ $u_{3} > 0.$ The assumption $\left(\mathbf{H6}\right)$ implies that $\dfrac{f\left(u_{1}, u_{3}\right) }{f\left(u_{1}, u_{3}^{\ast }\right) }$ lies between $\dfrac{u_{3}}{u_{3}^{\ast }}$ and $1$ (c.f. with the non-strict property [13,p.74] and [17,p.8]). And it is easy to verify that the general class of nonlinear functional responses including (9), (10), and (11) is often appropriate for $\left(\mathbf{H6}\right).$

According to constructing a dynamical system on $X_{f}$, we prove the stability of the interior equilibrium of (2) by choosing a novel Lyapunov functional. Then we arrive at the following theorem.

Theorem 3.4. Let $\tau _{j},$ $\left(j = 1, 2\right)$ be locally Lipschitz on $C$ and be continuously differentiable in a neighbourhood of the equilibrium $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$. If $\left(\mathbf{H1}\right) -\left(\mathbf{H6}\right)$ and $\left(\mathbf{H}_{f}\right)$ hold, then the non-trivial steady-state solution $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ is asymptotically stable (in $X_{f}\cap \left[ \mathbf{0}, \mathit{\text{ }} \mathbf{M}\right] _{C}$).

Remark 3.5. For $u\in C^{1}\left([-h, s), X\right),$ we get

where $\left[ \left(D\tau _{j}\right) \left(\cdot \right) \right],$ $j = 1, 2,$ is the Fréchet derivative of $\tau _{j}$ at point $u_{t}.$ Hence, for a solution in $\varepsilon -$ neighborhood of the stationary solution $\psi ^{\ast },$ the estimate

guarantees

due to Lemma 3.1 and the boundedness of $\left\Vert \left(D\tau _{j}\right) \left(\psi \right) \right\Vert _{C\left(C, \text{ }\mathbb{R} \right) }$ as $\varepsilon \rightarrow 0$ (here $\left\Vert \psi -\psi ^{\ast }\right\Vert _{C} < \varepsilon$).

Proof. Based on $D\left(A\right) \subset D\left(A^{\frac{1}{2}}\right),$ we are sufficient to set $D\left(A^{-\frac{1}{2}}\right) = X$ in ^[18]. Thus, according to [18,p.831], we get that $\left(3\right) -\left(5\right)$ is described a dynamical system on $X_{f}.$ And then we use Lemma 2.4. Define a Lyapunov functional with state-dependent delays along a solution of $\left(2\right)$

where

According to Lemma 3.1, it follows that $u_{1},$ $u_{2}, \ $ and $u_{3}$ are bounded and nonnegative. And then Lyapunov functional is well-define. Next we shall show that $\dfrac{dV^{sd}\left(t\right) }{dt}$ is non-positive.

Let us consider

and start with the term $\frac{\partial }{\partial t}V^{sd\_x}\left(x, t\right).$

By computations, we have

where

From

we get

where

After a simple computation, (12) is equivalent to

By the definition of $v\left(s\right) = s-1-\ln \left(s\right),$ (13) is rewritten as

Then we obtain

Denote

Based on the Divergence Theorem and the Neumann boundary condition, we have

According to $\dfrac{df\left(u_{1}, u_{3}^{\ast }\right) }{du_{1}}\geq 0,$ we obtain $RD^{diff}\left(t\right) \leq 0.$

Thus we summarize what we have worked out as follows

According to (H5), one gets

Based on (H6) and the monotonicity of the function $v$, we have

Now we prove $\dfrac{d}{dt}V^{sd}\left(t\right) \leq 0$ in a small neighbourhood of the stationary solution with the equality only in case of $\left(u_{1}, u_{2}, u_{3}\right) = \left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right).$ In the particular case of constant delay, one has $d^{sd}\left(x, t\right) = 0$ which may lead to the global stability of $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right).$

In the following, we rewrite $\left(14\right)$ as

where

Let us consider the zero-set $\dfrac{dV^{sd}\left(t\right) }{dt}.$ We start with $\int_{\Omega }\left(1-\dfrac{f\left(u_{1}^{\ast }, u_{3}^{\ast }\right) }{f\left(u_{1}, u_{3}^{\ast }\right) }\right) \left(1-\dfrac{u_{1}}{u_{1}^{\ast }}\right) dx = 0$ due to $u_{1} = u_{1}^{\ast }.$ Note that $v\left(s\right) = 0$ if and only if $s = 1.$ For $Q^{sd}\left(x, t\right) = 0,$ we obtain $u_{2} = u_{2}^{\ast }\ $ and $u_{3} = u_{3}^{\ast }.$ Then one sees $f\left(u_{1}\left(x, t-\tau _{1}\left(u_{t}\right) \right), u_{3}\left(x, t-\tau _{1}\left(u_{t}\right) \right) \right) = f\left(u_{1}^{\ast }, u_{3}^{\ast }\right).$ Furthermore, $RD^{diff}\left(t\right) = 0$ implies that $u_{1},$ $u_{2}, \ $ and $u_{3}$ are independent of $x.$ The zero set $d^{sd}\left(x, t\right) = 0$ includes $g\left(u_{2}\left(x, t-\tau _{2}\left(u_{t}\right) \right) \right) = g\left(u_{2}^{\ast }\right),$ $f\left(u_{1}\left(x, t-\tau _{1}\left(u_{t}\right) \right), u_{3}\left(x, t-\tau _{1}\left(u_{t}\right) \right) \right) = f\left(u_{1}^{\ast }, u_{3}^{\ast }\right)$ or $\frac{d}{dt}\tau _{j}\left(u_{t}\right) = 0$ along a solution. Thus the zero-set consists of just the positive equilibrium $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ which is also a subset of $d^{sd}\left(x, t\right) = 0.$ We remind that $Q^{sd}\left(x, t\right) \geq 0$, while the sign of $d^{sd}\left(x, t\right)$ is undefined. We would show that there is a small neighbourhood of $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ such that $\left\vert d^{sd}\left(x, t\right) \right\vert < Q^{sd}\left(x, t\right).$ In order to prove such result, we need the statement (ⅳ) in Proposition 2.5.

The following discussions are in part analogous to [16,p.1559]. Based on Proposition 2.5 (ⅳ), let us first consider the following auxiliary functions $Q\left(y\right)$ and $D\left(y\right),$ defined on $\mathbb{R} ^{6},$ where we simplify $y = \left(y_{1}, y_{2}, y_{3}, y_{4}, y_{5}, y_{6}\right) \in \mathbb{R} ^{6}$ for $y_{1} = u_{1}\left(x, t\right),$ $y_{2} = u_{2}\left(x, t\right),$ $y_{3} = u_{3}\left(x, t\right),$ $y_{4} = u_{1}\left(x, t-\tau _{1}\right),$ $y_{5} = u_{2}\left(x, t-\tau _{2}\right),$ $y_{6} = u_{3}\left(x, t-\tau _{1}\right),$

and

According to Proposition 2.5 (ⅳ) and Remark 3.5, it is observed that $Q\left(y\right) \leq Q^{sd}\left(x, t\right)$ and $\left\vert d^{sd}\left(x, t\right) \right\vert \leq D\left(y\right)$. And it should be pointed out that $Q\left(y\right) = 0$ if and only if $y = \left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }, u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right).$ Now we change the coordinates in $\mathbb{R} ^{6}$ to the spherical ones

$r\geq 0,$ $\xi _{j}\in \left[ -\frac{\pi }{2}, \frac{\pi }{2}\right],$ $j = 1,$ $\ldots 4,$ $\xi _{5}\in \lbrack 0, 2\pi).$

One can check that $Q\left(y\right) = r^{2}\cdot \Phi \left(r, \xi _{1}, \ldots \xi _{5}\right),$ where $\Phi \left(r, \xi _{1}, \ldots \xi _{5}\right)$ is continuous and $\Phi \left(r, \xi _{1}, \ldots \xi _{5}\right) \neq 0$ for $r\neq 0.$ It is proved by way of contradiction. If $\Phi \left(r, \xi _{1}, \ldots \xi _{5}\right) = 0$ for $r\neq 0$, then it is easy to see that this contradicts Proposition 2.5 (ⅳ). Hence the classical extreme value theorem shows that the continuous function on a closed neighborhood of $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ has a minimum $\Phi _{\min }$ $> 0$. It follows that $Q\left(y\right) \geq r^{2}\cdot \Phi _{\min }.$

According to Proposition 2.5 (ⅳ), we have

Next we adopt the analogous procedure as in the discussion of $Q\left(y\right)$. Remind that Remark 3.5. Then we obtain that $D\left(y\right) \leq \beta _{\varepsilon }r^{2}$ where the constant $\beta _{\varepsilon } = \max \left\{ \alpha _{1}, \text{ }\alpha _{2}\right\} \rightarrow 0$ as $\varepsilon \rightarrow 0.$ Finally, we choose a small enough $\varepsilon$ such that $\beta _{\varepsilon } < \Phi _{\min }$ which proves $\dfrac{d}{dt}V^{sd}\left(t\right) < 0.$ We complete the proof.

We now apply the above results to consider the following example.

Example 3.6. Consider the system (2) with

where $w_{j},$ $j = 1, 2$ is locally Lipschitz on $X$. We know that $f$ and $g$ are continuously differentiable on $\mathbb{R} ^{2}$ and $\mathbb{R}$, respectively. Moreover, $f$ is increasing and nonnegative on $\mathbb{R} _{+}^{2}.$ And $g$ is increasing on $\mathbb{R} \mathbb{.}$ Then it is easy to see that $\left(\mathbf{H1}\right)$ and $\left(\mathbf{H3}\right)$-$\left(\mathbf{H5}\right)$ are satisfied. By choosing $\mu = \max \{k_{1},$ $b\}$ and $\lambda = k_{4}+1,$ we get that for $u_{i}\geq 0,$ $i = 1, 2, 3$

which implies that $\left(\mathbf{H2}\right)$ holds. If $0 < \dfrac{pq+ak_{3}kr}{bk_{3}kr+k_{1}kr-k_{2}pq}\leq \dfrac{a}{b},$ we know that the equation

has two roots $z = \dfrac{a}{b}$ and $z = \dfrac{pq+ak_{3}kr}{bk_{3}kr+k_{1}kr-k_{2}pq}.$ It follows that $\left(\mathbf{H}_{f}\right)$ is satisfied. Then we obtain the non-trivial steady-state solution

with $0 < \dfrac{pq+ak_{3}kr}{bk_{3}kr+k_{1}kr-k_{2}pq}\leq \dfrac{a}{b}$ and $ak_{1}kr-ak_{2}pq-bpq > 0.$ And we have

lies between $\dfrac{u_{3}}{u_{3}^{\ast }}$ and $1$ for $u_{1},$ $u_{3} > 0,$ which means that $\left(\mathbf{H6}\right)$ holds. For $\tau _{j},$ $j = 1, 2,$ we get

Thus, in the $\varepsilon -$ neighborhood of $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right),$ we have

where $L_{w_{j}},$ $j = 1, 2,$ is Lipschitz constant of $w_{j}.$

Based on the above analysis and Lemma 3.1, we have the invariant set

where

with $\mathbf{M = }\left(M_{1}, M_{2}, M_{3}\right) ^{T} = \left(\dfrac{a}{b}, \text{ }\dfrac{r\mu a}{k_{4}pb}, \text{ }\dfrac{rk\mu a}{qpb}\right) ^{T}$. It is now evident to see that $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ is asymptotically stable (in $X_{f}\cap \left[ \mathbf{0}, \text{ }\mathbf{M}\right] _{C}$) from Theorem 3.4.

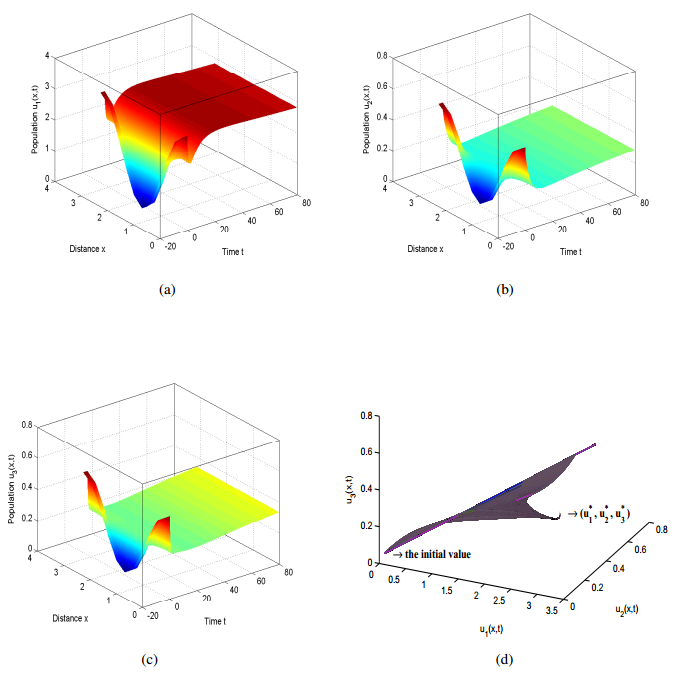
Next we perform numerical simulations of system (15) with the parameters $a = 0.8,$ $b = 0.2,$ $r = 0.1,$ $p = 0.1,$ $k = 0.3, \ q = 0.2, \ d_{1} = 0.2, \ d_{2} = 0.1, \ d_{3} = 0.7, \ k_{1} = 0.3, \ k_{2} = 0.01, \ k_{3} = 0.5,$ and$\ k_{4} = 0.8.$ By substituting the parameters, it follows that the non-trivial steady-state solution $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right) = \left(2.712, \text{ }0.322, \text{ }0.386\right)$ exists. According to choosing

we have that $\tau _{1}\left(\cdot \right)$ and $\tau _{2}\left(\cdot \right)$ are locally Lipschitz in $C$ and are continuously differentiable in a neighbourhood of the equilibrium $\left(u_{1}^{\ast }, \text{ }u_{2}^{\ast }, \text{ }u_{3}^{\ast }\right)$. Now one can check that $\left(\mathbf{H1}\right)$-$\left(\mathbf{H6}\right)$ and $\left(\mathbf{H}_{f}\right)$ are satisfied. Consequently, based on Theorem 3.4, we infer that $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right) = \left(2.712, \text{ }0.322, \text{ }0.386\right)$ is asymptotically stable (in $X_{f}\cap \left[ \mathbf{0}, \text{ }\mathbf{M}\right] _{C}$) which is illustrated in Figure 1, where

with

4.   Discussion

In this section, we generalize the above type of Lyapunov functional to such model with Logistic growth rate. Then the model is described as follows:

In the following, these results are completed by the method analogous to that used above.

Lemma 4.1. Let $\tau _{j}$ in Lemma 2.3 be valid. Suppose $\left(\mathbf{H1}\right)$ and $\left(\mathbf{H2}\right)$ hold. Then initial value problem has a unique global classical solution for $t\geq 0.$

Denote $\mathbf{\hat{M}}\triangleq \left(\frac{R}{b}, g^{-1}\left(\frac{r\mu R}{pb}\right), \frac{rk\mu R}{qpb}\right) ^{T}.$

Lemma 4.2. Let $\tau _{j}$ in Lemma 2.3 be valid. Assume that $\left(\mathbf{H1}\right)$-$\left(\mathbf{H4}\right)$ are satisfied. Then $\left[ \mathbf{0}, \mathit{\text{ }} \mathbf{\hat{M}}\right] _{C}$ is invariant i.e., for each initial value $\phi = \left(\phi _{1}, \phi _{2}, \phi _{3}\right) \in \left[ \mathbf{0}, \mathit{\text{ }} \mathbf{\hat{M}}\right] _{C},$ the unique classical solution of initial value problem satisfies $u_{t}\in \left[ \mathbf{0}, \mathit{\text{ }} \mathbf{\hat{M}}\right] _{C}$ for all $t\geq 0.$

Next we are interested in nontrivial stationary solutions of (16). Consider

Then we have $u_{2}^{\ast } = g^{-1}\left(\frac{ar}{p}u_{1}^{\ast }\left(1-\frac{bu_{1}^{\ast }}{R}\right) \right) \ $ and $u_{3}^{\ast } = \frac{kar}{pq}u_{1}^{\ast }\left(1-\frac{bu_{1}^{\ast }}{R}\right).$ Set

In the sequel the following assumption will be need.

We now obtain the following result.

Theorem 4.3. Let $\tau _{j},$ $(j = 1, 2)$ be locally Lipschitz on $C$ and be continuously differentiable in a neighbourhood of the equilibrium $\left(u_{1}^{\ast }, \mathit{\text{ }} u_{2}^{\ast }, \mathit{\text{ }} u_{3}^{\ast }\right)$. If $\left(\mathbf{H1}\right) -\left(\mathbf{H6}\right)$ and $\left(\mathbf{\bar{H}}_{f}\right)$ hold, then the non-trivial steady-state solution $\left(u_{1}^{\ast }, \mathit{\text{ }} u_{2}^{\ast }, \mathit{\text{ }} u_{3}^{\ast }\right)$ is asymptotically stable (in $X_{f}\cap \left[ \mathbf{0}, \mathbf{\hat{M}}\right] _{C}$).

In the proof we use the following Lyapunov functional with state-dependent delay along a solution of (16). Choose the Lyapunov functional

where

It is easy to verify that

where

The next works are similar to the proof of Theorem 3.4. We do not repeat here detailed calculations.

5.   Conclusion

In this paper, we study a virus dynamics model with diffusion, a general nonlinear functional response and state-dependent delays. Such delays $\tau _{1}\left(u_{t}\right)$ and $\tau _{2}\left(u_{t}\right)$ which are both related to the number of system populations, represent the latent period that the cell survives once the virus contacts the target cell and the time that the newly produced viruses are infectious, respectively. We mainly establish asymptotic stability of the interior equilibrium by applying a novel Lyapunov functional. Moreover, we generalize such type of Lyapunov functional to such model with Logistic growth rate. More specifically, target cells, infected cells, and free viruses do not extinct and ultimately survive at the equilibrium level $\left(u_{1}^{\ast }, u_{2}^{\ast }, u_{3}^{\ast }\right)$ if the following conditions are satisfied:

(Ⅰ) target cells and free viruses have strong intercellular infection, i.e., $\left\vert f\left(u_{1}, u_{3}\right) \right\vert \leq \mu u_{1}, \ \dfrac{f\left(u_{1}, u_{3}\right) }{f\left(u_{1}, u_{3}^{\ast }\right) }$ lies between $\dfrac{u_{3}}{u_{3}^{\ast }}$ and $1$ for $u_{1},$ $u_{3} > 0.$

(Ⅱ) the death rate of the infected cells is of a linear growth bound, i.e., $\left\vert g\left(u_{2}\right) \right\vert \leq \lambda u_{2}$ for $u_{2} > 0.$

(Ⅲ) the rate of change with respect to time of the state-dependent delays is limited, i.e., $\left\vert \frac{d}{dt}\tau _{j}\left(u_{t}\right) \right\vert \leq M_{\varepsilon }^{j}.$

Acknowledgments

We are extremely grateful to the critical comments and invaluable suggestions made by anonymous honorable reviewers. This research is supported by National Natural Science Foundation of China (No.11771109).

Conflict of interest

The authors declared that they have no conflicts of interest.