| Abbreviations: | |
| DOPC | dioleoylphosphatidylcholine |
| ECL | extracellular loop |
| GDP | Guanosinediphosphate |
| GPCR | G-protein coupled receptor |
| GTP | Guanosinetriphosphate |
| HCMV | Human cytomegalovirus |
| ICL | intracellular loop |
| MD | molecular dynamics |
| TM | transmembrane |
| RMS | root mean square |
1. Introduction
Communication is a basic task in everyday life and similarly to organisms interacting with their environment, cells have to communicate with each other. Cells use small molecules, peptides or even large proteins to address this task, but only tiny or hydrophobic molecules are able to cross the cell membrane directly. Cell entry is regulated for all other molecules through channels so that the molecules can cross the membrane and fulfill their intracellular tasks [1,2]. A different way to trigger cell responses is via receptors that interact with a molecule, transmit the signal over the membrane via structural changes and thus activate certain pathways inside the cell [3,4]. GPCRs are a protein family involved in many diseases, and many drugs available directly target GPCRs [5].
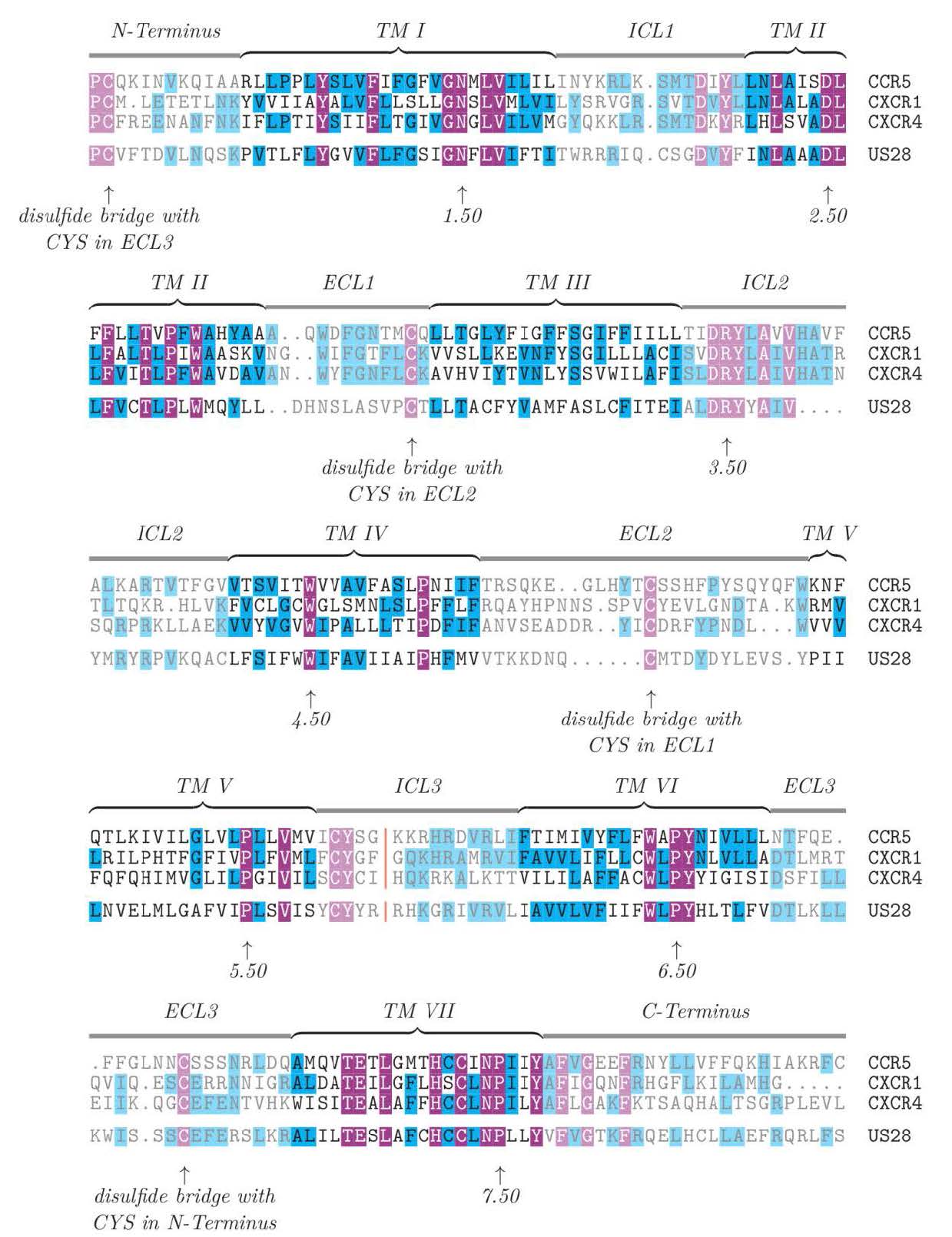
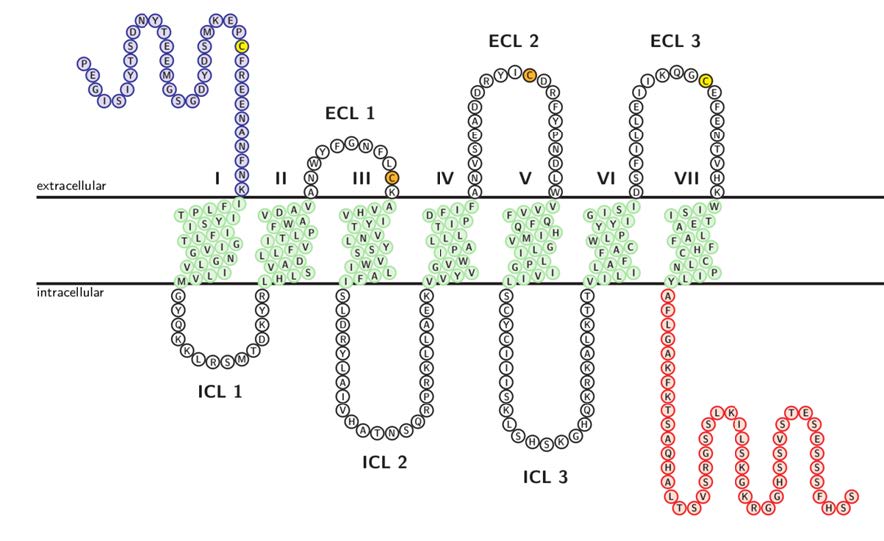
GPCRs span the cell membrane with their seven transmembrane (TM) helices and can interact with intracellular G-proteins. The ligand binding site of the receptor is located on the extracellular side of the membrane and can either consist of loops for protein ligands or protrude deeper into the receptor cavity for some organic ligands [4], whereas the G-protein binding site is on the intracellular side and involves the conserved DRY motif in TM III. Figure 1 gives an overview of the structural topology of the GPCR CXCR4; the length of loops and termini can vary in other receptors. Upon chemokine binding, chemokine receptors change their conformation in a way that activates the G-protein and leads to an exchange of GDP for GTP in the Gα-subunit. The G-protein subunits detach from the receptor, and then Gα dissociates from the other two G-protein subunits and triggers a signal inside the cell depending on the type of Gα. After inactivation of Gα through GTP hydrolysis, the subunit re-associates with the other two G-protein subunits and is ready for another activation signal [6,7].
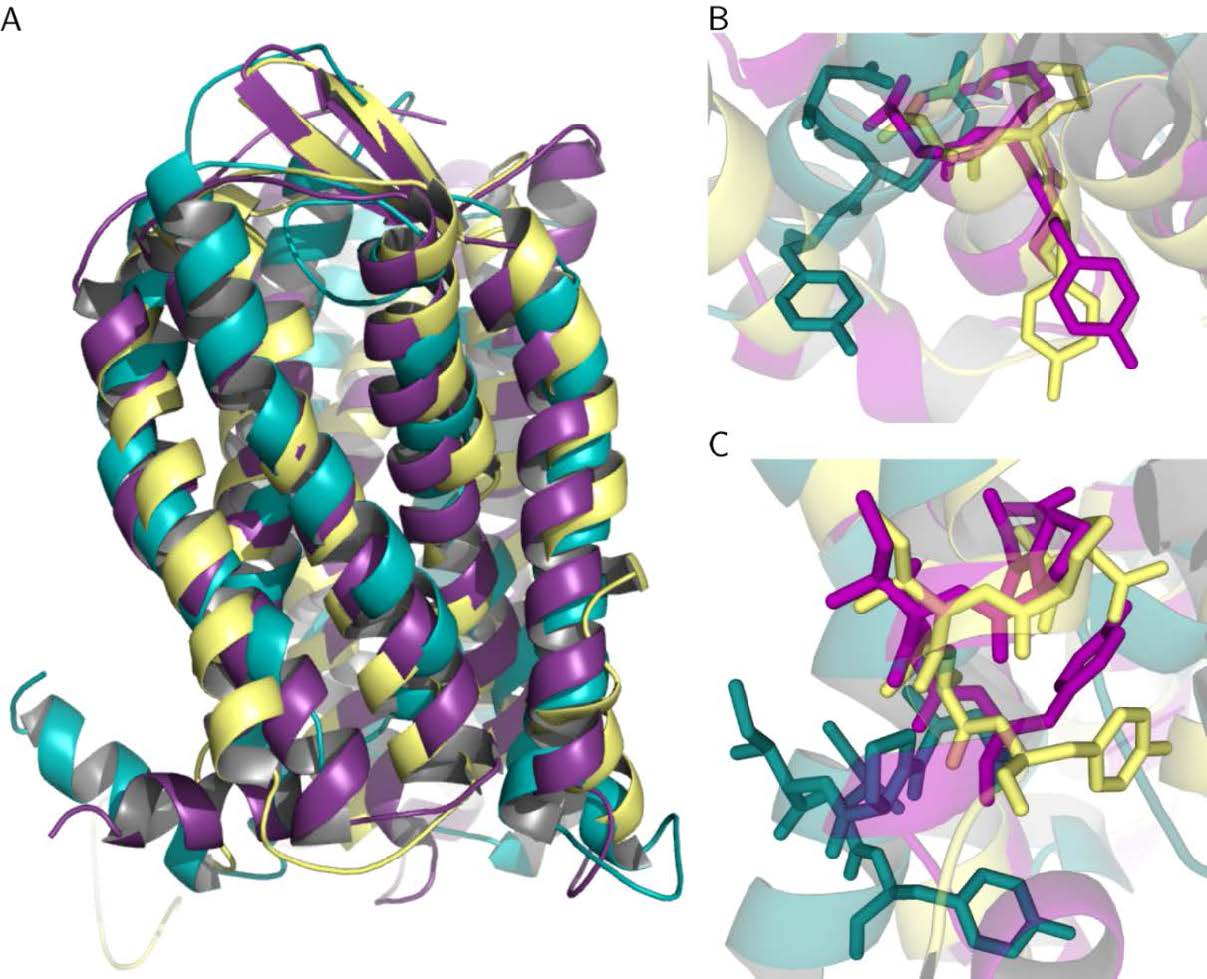
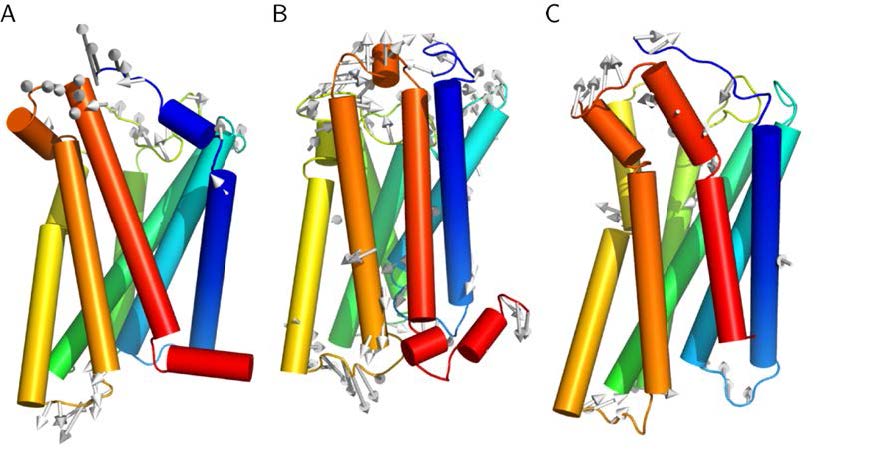
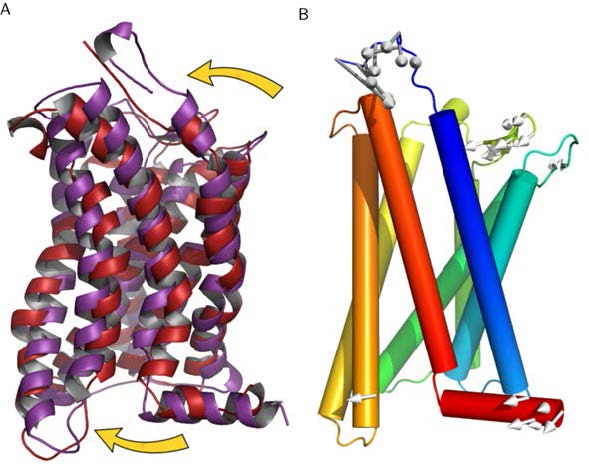
Up to 800 different GPCRs are encoded in the human genome and the receptors respond to a huge variety of ligands such as amines, nucleic acids, lipids, peptides, organic molecules, ions and photons [4]. The large GPCR family can be divided into six classes, of which class A is the largest and can further be divided into 19 sub-families [8]. GPCRs frequently show a low sequence identity of <30% and they also exhibit differences in their three-dimensional structure (Table 1). This observation even applies to those receptors that bind similar ligands. For example, the three chemokine receptors CXCR1, CXCR4 and CCR5 exhibit root mean square deviation (RMSD) values of 3.4 Å to 4.8 Å (Table 1) and differ in the conformation of the helices and loops (Figure 2).
Table 1. RMS deviation [Å] from a detailed pairwise DALI analysis to evaluate structural similarity. Bold numbers highlight the pairwise comparisons of chemokine receptors.
| receptor | N/OFQ opioid | CCR5 | μ-2 opioid | CXCR1 | δ opioid | κ opioid | CXCR4 |
| PDB | 4EA3 | 4MBS | 4DKL | 2LNL | 4EJ4 | 4DJH | 3ODU |
| CCR5 | 2.6 | | | | | | |
| μ-2 opioid | 1.4 | 2.4 | | | | | |
| CXCR1 | 4.6 | 4.8 | 4.5 | | | | |
| δ opioid | 1.9 | 3.6 | 1.7 | 5.3 | | | |
| κ opioid | 1.9 | 3.4 | 1.9 | 5.2 | 7.8 | | |
| CXCR4 | 2.7 | 3.4 | 2.2 | 4.6 | 6.3 | 8.6 | |
| β-2 adreno (PDB 2R4R) | 1.8 | 3.8 | 2.0 | 4.7 | 2.0 | 2.0 | 3.2 |
These structural deviations make a reliable structure prediction of novel chemokine receptors a challenging task. The aim of the present study was to predict the structure of the US28 receptor from human cytomegalovirus, which binds the chemokine CX3CL1 (fractalkine) [9]. For this purpose, we generated three independent models based on different template structures, refined the models by molecular dynamics simulations, and assessed the agreement of the models with typical structural features of the GPCR family. The most favorable model was finally validated against the recently determined crystal structure of US28, demonstrating that the strategy outlined above is indeed capable of distinguishing between good and poor GPCR models.
2. Materials and Methods
2.1. Structure preparation and homology modeling
The experimentally determined structures of CXCR1, CXCR4 and CCR5 were processed in the following way to serve as templates for homology modeling and for the MD simulations: From the crystal structure of CCR5 (PDB entry 4MBS [10]) the Rubredoxin was removed and the missing loop residues were added using Modeller9.10 [11]. From the crystal structure of CXCR4 (PDB entry 3ODU [12]) the T4 lysozyme was removed and the remaining gap was closed, and residue 125 was reverted to leucine using Modeller9.10. From the ensemble of NMR structures available for CXCR1 (PDB entry 2LNL [13]) Model 5 was used as the starting structure. The US28 crystal structure (PDB entry 4XT1 [14]) that was used in a control simulation was prepared in the following way: Both the nanobody and the chemokine chains were removed, and the gap between residues 95 and 101 was closed using Modeller9.10.
The sequences of the chemokine receptors were aligned using the respective raw HMM from the Pfam database [15] and the alignment tool Hmmer [16,17,18]. Then, the viral sequence was modeled independently onto each of the three chemokine receptor structures using Modeller9.10 [11] leading to three protein structures. Packing of the resulting structures was verified with Whatcheck [19] and protonation states were adjusted with Propka implemented in the PDB2PQR server [20]. Each modeled structure is henceforth named according to the template used, e.g. “onCXCR1”.
2.2. MD simulations
In all simulations with truncated protein sequences, an acetyl group was used to cap the N-terminal residue and an N-methyl amide capping group was added to the C-terminus to avoid non-physiologically charged termini. For the MD simulations all systems were neutralized by adding an appropriate amount of either sodium or chloride ions and solvated within a water box with periodic boundary conditions. The water model used was SPC/E [21] for the membrane simulations because it provides better representation of bulk water properties [22]. The amount of sodium and chloride ions that needed to be added to systems simulated at physiological salt concentration was calculated using the number of water molecules, the concentration of water, and the target salt concentration.
GPCRs are located in the cell membrane meaning they are surrounded by a lipid bilayer. To simulate the natural environment as best as possible, Böckmann and Siu developed a membrane model consisting of DOPC and water [22]. The already equilibrated membrane piece available for GROMACS was enlarged to fit the size of the receptor. A short simulation run of 1 ns was finally used to equilibrate the enlarged membrane and prepare it for the insertion of the protein. Afterwards, the minimized protein was correctly positioned using PyMOL [23] and embedded in the DOPC membrane using GROMACS [24,25,26,27,28]. First, all water molecules were removed from the protein and the protein was then solvated with DOPC molecules so that there were no overlapping molecules. Then, the system was neutralized, minimized with restraints on the protein and equilibrated for 20 ns. After each 100 ps-long equilibration run, water that diffused between the receptor and the membrane was removed using VMD [29]. The equilibrated systems were then subjected to a MD simulation of 100 ns length.
2.3. Program parameters for MD simulations
The AMBER 99SB force field [30,31] and default settings for non-bonded interactions were used for the protein and the water in the simulations. Long-range electrostatic interactions were calculated with the particle mesh Ewald approximation [32] using default parameters; bonds involving hydrogen atoms were held fixed using Lincs [33] and thus allowing a time step of 2 fs. Due to limitations in the commonly used AMBER force field ff99SB concerning organic molecules, the general AMBER force field GAFF [34] was used for the description of the DOPC molecules [22].
Energy minimization is crucial to remove regions with high potential energy that come from internal clashes or unfavorable side chain rotamers. The protein and/or membrane were held fixed at the beginning to relax the water molecules, and afterwards, the sidechains/membrane molecules were relaxed to enter a minimized state. Finally, the whole protein including the backbone underwent the minimization process. Thereafter, temperature coupling was turned on to gradually heat the system to the target temperature; this again has to be done in steps to give the system enough time to equilibrate. The final step was to turn on pressure coupling to keep the surrounding water at physiological density. To account for special properties of the lipid bilayer, a surface tension coupling was used where normal pressure coupling is used for the z-direction and the surface tension is coupled to the x/y-plane, i.e. the orientation of the bilayer. After minimization and gradual heating, the proteins were simulated in an isothermal and isobaric environment. Snapshots were collected every 5 ps; simulations and analyses were performed with GROMACS [24,25,26,27,28].
2.4. Programs for analyses and visualization
DSSP [35] was used for the calculation of secondary structure elements and DALI [36] for the superimposition of structures. PyMOL [23] was used for the addition of end groups on the protein chains and the calculation of modevectors. LIGPLOT [37,38] was used to analyze contacts between amino acids on an atomistic level. Visualization of trajectories was carried out with VMD [29]. Rendering images were performed with POV-Ray [39]. All simulations were performed on the computing clusters of the “Regionales Rechenzentrum Erlangen”.
3. Results and Discussion
3.1. Homology modeling of US28
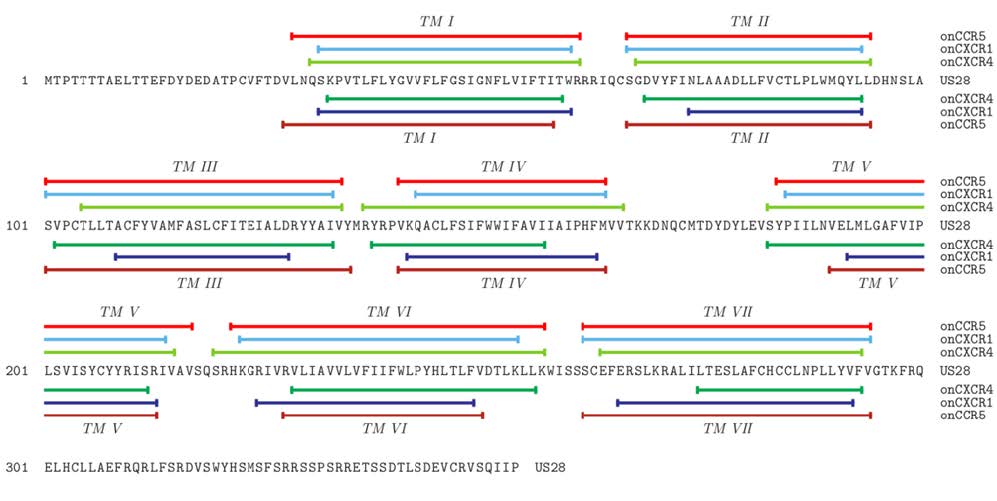
There are three chemokine receptors of known 3D structure (CCR5, CXCR1, and CXCR4) that can serve as a basis for homology modeling of the viral US28. The multiple sequence alignment (Figure 3) shows that the conserved residues are mainly located in the TM helices or form stabilizing disulfide bonds. The pairwise sequence identity between US28 and the chemokine receptors of known structure is rather similar (between 26 and 31%). Thus none of them can be readily selected as favorable template based on the degree of sequence identity alone.
A closer inspection of the three-dimensional structures reveals that the three chemokine receptors exhibit a remarkable divergence of structure, which also affects functionally important sites, like the DRY and NPxxY motifs shown in Figure 2. This structural divergence also becomes apparent from the structure-based sequence alignment shown in supplementary Figures S1-S3. Due to these structural differences, a combination of the structural information from all three chemokine receptors for the generationof one single model appears problematic and might result in structural inaccuracies.
We therefore preferred to generate three individual models and to compare their structural properties in order to identify the most accurate model. Such an approach has for example been used previously for the cannabinoid receptor (CB2) by Feng et al. [42]. For this protein, 10 models were generated based on different known GPCR structures and subsequently refined by MD simulations. To identify the most reliable model, the authors assessed the ability of the models to distinguish 20 active ligands from 980 randomly selected compounds. Subsequently, 170 known cannabinoid receptor compounds were used for further model validation [42].
Similar to the work of Feng et al., we also used molecular dynamics in explicit solvent and lipid environment for model refinement. However, since there is only a very limited number of US28 ligands known to date [43], we decided to use a different strategy for model validation. For that purpose, we used those structural properties that are conserved in class A GPCRs to identify the homology model that has the most GPCR-typical features.
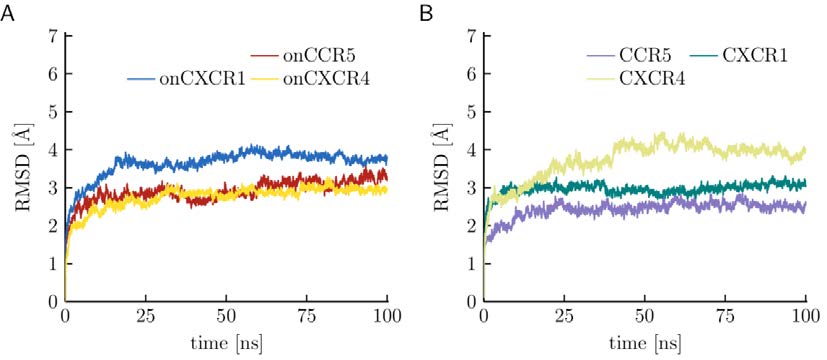
The three homology models for US28 were first subjected to 100 ns MD simulations for refining purposes, and RMS deviations and the number of residues in α-helical conformation were calculated as markers for structural stability.
The RMS deviation is lowest for the models based on CCR5 and CXCR4, whereas the model based on CXCR1 deviates up to 4 Å from the initial structure (Figure 4A). To address whether backbone deviations in the range of 2-4 Å may be indicative of modeling artifacts or poor sequence alignment, the chemokine receptors chosen as templates were also simulated using the same protocol as for the viral GPCR. The observed backbone RMS deviations of 2-4 Å (Figure 4B) are in the same range as those observed for the modeled structures.
Notably, the highest RMS deviation is observed for CXCR4, for which the ligand was removed prior to simulation. However, a previous study showed that the overall structure and dynamics of CXCR4 is not significantly affected by ligand removal [44]. Thus, the high RMSD value observed for CXCR4 might rather result from the fact that this receptor is stabilized by homodimer formation and also formed a homodimer in the crystal structure [12]. Additionally, no significant RMS differences could be observed between the ligand-free structure of CXCR1 and CCR5 where the ligand was removed before conducting MD simulations. Based on the considerations above, we conclude that backbone RMS deviation values of 2-4 Å reflect the intrinsic flexibility of this class of proteins, which has also been noted in previous studies [45,46]. Consequently, RMS deviations of the models of up to 4 Å cannot per se be taken as an indicator of modeling errors. Therefore, none of the models can be discarded based on the RMS deviation values alone.
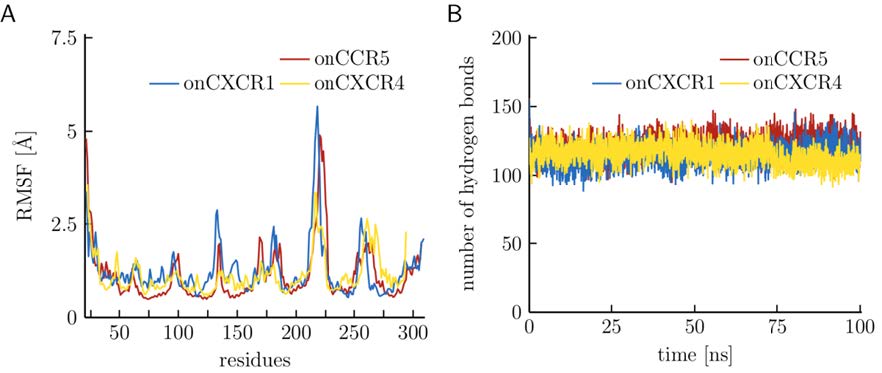
RMS fluctuations are plotted in Figure 5A and show that the largest motions can be observed in the loop regions. The three models have very similar overall dynamic behavior, which is in line with the almost identical number of hydrogen bonds (Figure 5B). A way of visualizing the flexibility in the loops is the use of modevectors in PyMOL, a plug-in that visualizes the direction and traveled distance of atoms from the initial to the final structure by arrows (Figure 6). The highest fluctuations are present in the N-terminus and the third intracellular loop, which are important regions for ligand binding and signal transduction, respectively [47,48]. The depiction of the modevectors also revealed some motions in the TM regions. To inspect these changes in more detail, the number of residues in α-helical conformation was counted.
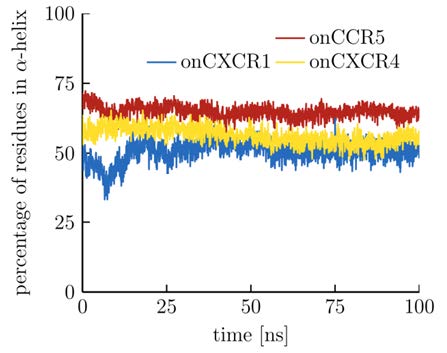
Figure 7 reveals that the percentage of residues in α-helical conformation in the three modeled viral GPCRs changes over simulation time. At the end of the simulation, 65% of residues in the model based on CCR5 were in the α-helical conformation, whereas 56% were in the helical conformation in the model based on CXCR4 and 51% in the model based on CXCR1. The time course for the model based on CXCR1 shows the largest changes in helix content over simulation time, indicative for some conformational rearrangements. To investigate this effect in more detail, the length of each helix was plotted directly after modeling and after MD simulation (Figure 8). The model based on CCR5 is the one where most of the residues remain in the helical conformation after the simulations, whereas part of the secondary structure is lost in the other two models. Interestingly, the very important TM III [49] is approximately one third shorter after simulation in the model based on CXCR1; thus, at least for TM III, the model based on CXCR1 exhibits a different conformation. Similar reduction in helix length can be observed for TM II in the model based on CXCR4; however, TM II is not as important for receptor stability as is TM III [50]. To gain information about the conformation of the helices and to investigate what changes occurred with TM III in the model based on CXCR1, kinks and bends in the helices were analyzed.
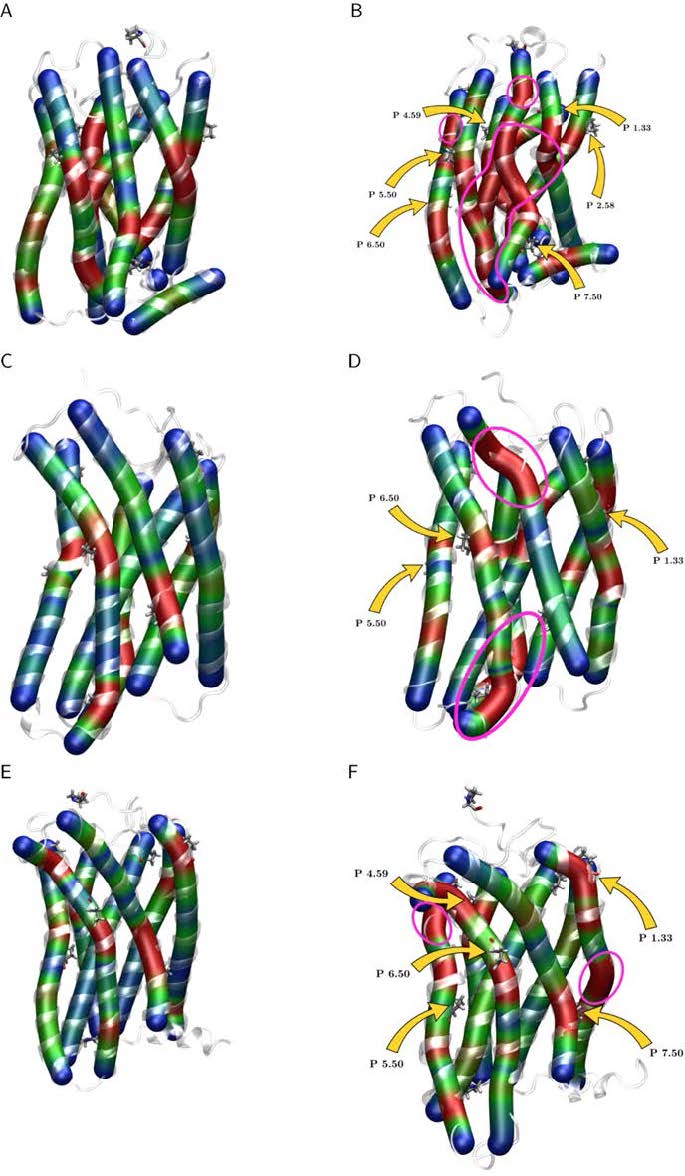
In GPCRs, proline residues in the helices are one important structural characteristic and can thus be used for structure evaluation because the TM helices should only have kinks and bends near those proline residues [51]. Bends, i.e. large angles in the TM helix, are colored in red in Figure 9 and are expected to exist only close to proline residues. However, many more such sites are present in the conformation modeled on CXCR1 and this indicates an unfavorable structure for the sequence of US28. The effect is even more pronounced after MD simulation (Figure 9B). Fewer bends in the helices are present in the model based on CXCR4 (Figure 9D) and the model based on CCR5 has almost ideal structural properties (Figure 9F). This type of analysis implies that the model based on CCR5 is most favorable. Interestingly, these differences are much less pronounced in the initial models (Figure 9, left panels), in which bends are only present near proline residues. After 100 ns simulation (Figure 9, right panels), however, the structures adapt to the intrinsic features of the US28 sequence, which is a better selection criterion of sequence-structure compatibility than sole calculation of RMS deviation values.
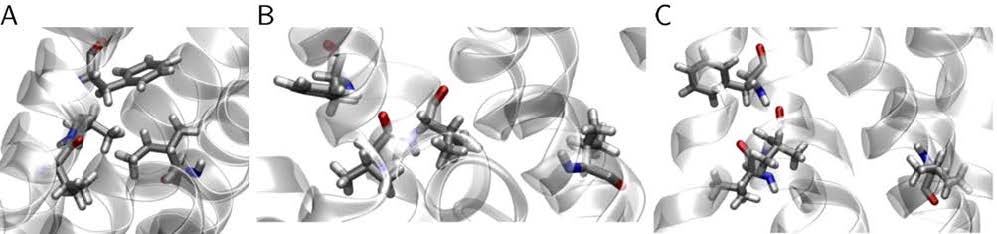
Additional structural features for selecting suitable templates include non-covalent contacts of TM III to almost all other TM helices, connecting the extracellular ligand binding site to the intracellular G-protein binding site and thus enabling signal transduction across the cell membrane. An important part of the activation mechanism is the so-called hydrophobic hindering mechanism that links TM III and TM VI via residues L3.43 (Ile in US28), F6.44, X6.40, and X6.41 (X = I/L/V/M) [50]. The three residues of TM VI should be tightly packed against L3.43 and upon activation the ring structure of phenylalanine rotates outwards to provide room for the rotating side chain of a nearby tryptophan. The amino acids in question are tightly packed in the model based on CCR5 and join TM III and TM VI together (Figure 10A). In contrast, the distances between the residues are too large to form hydrophobic interactions in the models based on CXCR1 and CXCR4. The side chains in Figure 10B and C are oriented in a way that is not in line with the described hydrophobic hindering mechanism [50]. Based on this, the structure modeled on CCR5 is the only homology model that exhibits the correct orientation of side chains in this part of the TM helices.
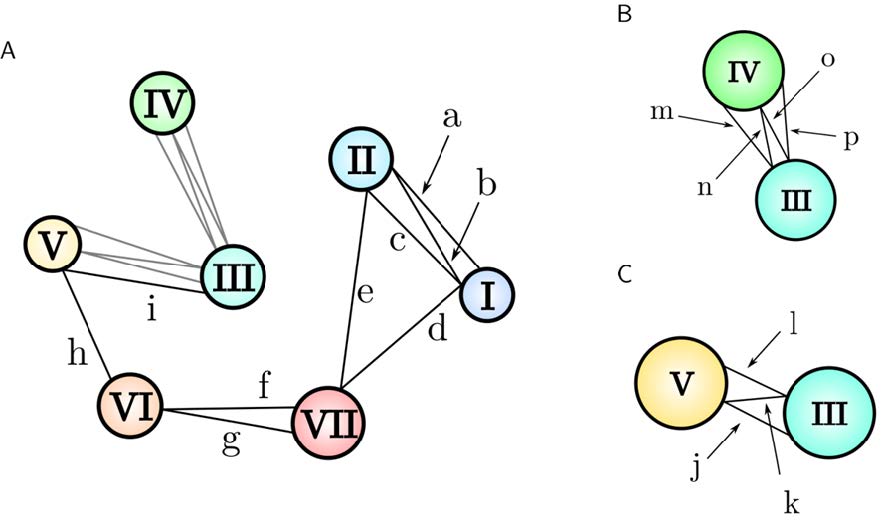
Highly conserved residues form a network of non-covalent contacts linking the TM helices and thereby stabilizing the GPCR fold [49]. Also, these contacts allow the transduction of a signal from the outside to the inside of the cell. Venkatakrishnan and coworkers reported 24 interhelical contacts from 36 topologically identical residues [49] that are partially depicted in Figure 11. Table 2 lists the distances of the 24 conserved contacts in the three homology models for the final structure of the MD simulation. The models based on CXCR1 and CXCR4 have only three and two conserved contacts, respectively, present in the final structure of the MD simulation, indicating that these conformations are rather unfavorable for the sequence of US28. Thirteen contacts are preserved in the final structure of the model based on CCR5, rendering it the model as the most favorable out of the three initial homology models by exhibiting most of the conserved non-covalent contacts. All in all, this analysis represents a useful selection criterion and favors the homology model based on CCR5.
Table 2. Closest distances between conserved non-covalent contacts in the homology models of US28. Location of the residues and formed networks can be found in Figure 11. Numbering is according to the Ballesteros-Weinstein numbering scheme [40]. All values are given in Angstrom.
| contact | onCCR5 | onCXCR1 | onCXCR4 | contact | onCCR5 | onCXCR1 | onCXCR4 |
| 1.53–2.47 (a) | – | – | – | 4.57–3.34 (m) | 3.82 | – | 3.46 |
| 2.47–1.50 (b) | – | 3.30 | – | 3.34–4.53 (n) | 3.82 | – | – |
| 1.50–2.50 (c) | 3.53 | 3.75 | – | 4.53–3.38 (o) | – | – | – |
| 1.50–7.46 (d) | 2.99 | – | – | 3.38–4.50 (p) | – | – | – |
| 2.50–7.46 (e) | 3.52 | – | – | 1.57–2.44 | 3.88 | – | – |
| 7.39–6.51 (f) | 3.64 | – | 3.73 | 2.42–3.46 | – | – | – |
| 6.51–7.38 (g) | 3.54 | – | – | 2.43–7.53 | 3.45 | – | – |
| 6.41–5.54 (h) | – | – | – | 3.36–6.48 | 3.86 | 3.62 | – |
| 5.54–3.44 (i) | – | – | – | 3.40–6.44 | – | – | – |
| 3.47–5.57 (j) | – | – | – | 1.46–7.47 | – | – | – |
| 5.57–3.51 (k) | – | – | – | 1.49–7.50 | 3.18 | – | – |
| 3.51–5.60 (l) | 3.11 | – | – | 6.47–7.45 | 3.88 | – | – |
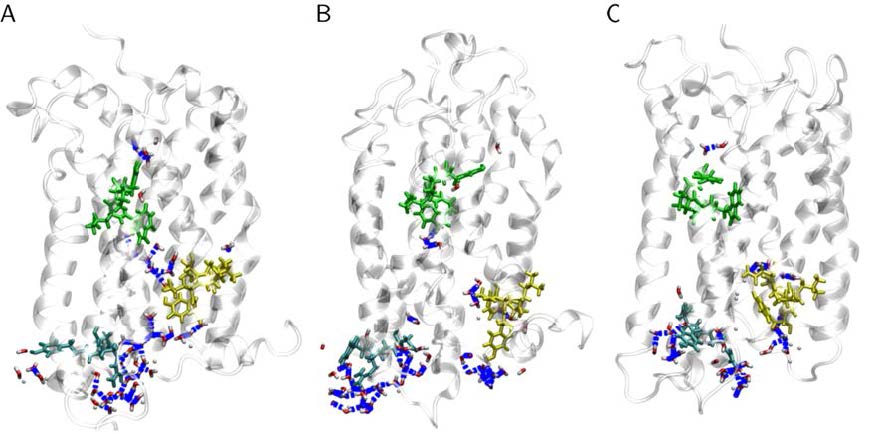
Analysis of known GPCRs structures revealed that further receptor stabilization is provided by a large water cluster that joins the ligand binding site to the G-protein binding site [52,53,54]. Figure 12A shows the connection between the amino acid motifs WLPY and NPLLY with intermediating water molecules in the model based on CCR5. Interestingly, this connection cannot be observed in the other two models, although small water clusters are also formed around the short sequence motifs (Figure 12B and C).
In summary, all analyses of structural properties from the MD simulations indicated that the model based on CCR5 constitutes a structural conformation favorable for the US28 sequence. Features especially related to conserved residues appear suitable for distinguishing between a properly folded protein, such as the model based on CCR5, and templates that force the US28 sequence into unfavorable conformations. For these reasons, the model based on CCR5 is considered the best fold of the viral GPCR US28. The fact that the US28 structure has been determined recently by experiment [14] gave us the opportunity to validate our modeling procedure. We would like to emphasize that information from the US28 crystal structure has not been used in any stage of our modeling approach, thus allowing the use of the crystal structure for an unbiased model validation.
3.2. Comparison of US28 models to the crystal structure
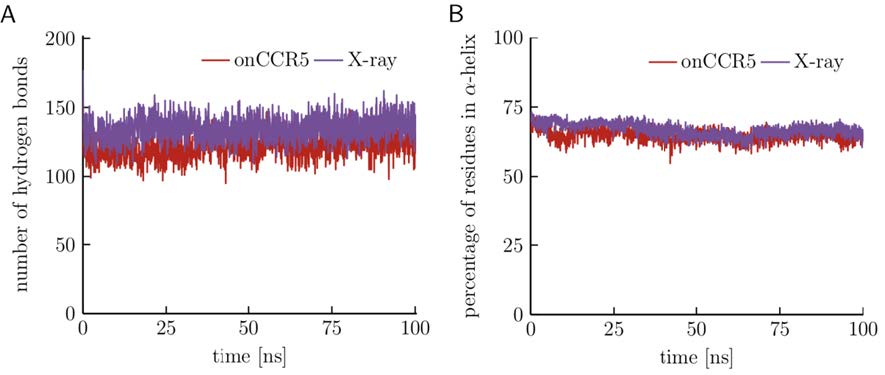
The crystal structure of the viral GPCR US28 contains an engineered nanobody within one loop to enhance stability [14]. In addition, the chemokine CX3CL1 (fractalkine) is bound as a ligand. In order to facilitate structure comparison to the unliganded US28 models, the fractalkine and nanobody were removed and the crystal structure was relaxed by 100 ns MD simulation. The number of hydrogen bonds and the percentage of residues in α-helical conformation are rather constant over simulation time and similar to the structural properties of the model based on CCR5 (Figure 13).
A structural overlay between the relaxed US28 crystal structure and the model based on CCR5 reveals an overall good agreement (Figure 14A). Differences are mainly observed for those loops in which the chemokine ligand and the nanobody were removed. The respective parts of the crystal structure also undergo the largest structural changes during the MD simulation as evidenced by a modevector analysis (Figure 14B).
A more quantitative structural comparison of the US28 models and the crystal structure was done by analyzing the portion of residues that are modeled at the correct spatial position. For this purpose, a structure superimposition was done using DALI [36] and the pairs of structurally equivalent amino acids were analyzed. The output of this analysis is exemplarily shown for the model based on CCR5 in Figure 15. The overall portion of correctly modeled residues (indicated by horizontal red lines in Figure 15) is 63.6%. Misalignment is mainly observed for the more flexible loop regions, whereas 80.8% of the residues within the TM helices were modeled correctly. In contrast, only 28.9% and 18.3% of the TM residues were modeled correctly in the models based on CXCR1 and CXCR4, respectively. This indicates that our modeling and selection procedure was able to identify the most accurate US28 model.
For a more detailed comparison of the three models, the percentage of correctly modeled residues for each TM helix is given separately in Table 3. The data show that all TM helices are more reliably modeled on the CCR5 template compared to the other templates.
Table 3. Percentage of residues in the TM regions modeled correctly as α-helices. Annotation of helical regions is taken from PDB entry 4XT1, the X-ray structure of US28.
| TM I | TM II | TM III | TM IV | TM V | TM VI | TM VII |
| onCCR5 | 94.1 | 100.0 | 96.7 | 91.3 | 28.1 | 66.7 | 96.4 |
| onCXCR1 | 44.1 | 50.0 | 3.3 | 95.7 | 12.5 | 6.1 | 7.1 |
| onCXCR4 | 14.7 | 21.4 | 6.7 | 65.2 | 6.3 | 9.1 | 17.9 |
These differences are most prominent for TM III (Table 3), which plays an important role in GPCR activation [49]. The higher accuracy of the TM III in the model based on CCR5 is also reflected in the structural parameters used for model evaluation: The hydrophobic hindering mechanism (Figure 10), the water cluster (Figure 12), and the conserved non-covalent contacts (Table 2) all point towards the higher quality of the “onCCR5” model in the vicinity of TM III.
TM V is the only helix that is poorly predicted in the model based on CCR5 (Table 3). Since TM V is functionally less important than TM III, its misalignment is not reflected by those structural parameters that are related to the activation process, such as the hydrophobic hindering mechanism (Figure 10) or the water cluster (Figure 12). However, the problems with the model for TM V become apparent from an inspection of the conserved non-covalent contacts (Table 2). None of the four contacts involving residues of TM V is formed in any of the models. Thus, the analysis of the conserved contacts might be used in the future to enhance the local accuracy of modeled GPCR structures.
4. Conclusion
In the present work, we showed that homology modeling and subsequent MD simulations are appropriate tools for generating and refining structures of a viral GPCR for which structural homologues are only available with low sequence identity. Exploiting conserved features of the protein family is extremely helpful for distinguishing between favorable and unfavorable three-dimensional conformations of a protein sequence. Based on the resulting structural agreement of our chosen protein model with the crystal structure, we suggest that this strategy to generate protein models may also be applicable to other GPCRs.
Acknowledgments
This work was supported by a grantfrom the Deutsche Forschungsgemeinschaft (SFB796, project A2) to HS. Furthermore, the authorswould like to thank Victoria Jackiw (LanguageCenter, Univ. Erlangen-Nürnberg) for readingthe manuscript.
Conflict of Interest
The authors declare no conflicts ofinterest in this paper









 DownLoad:
DownLoad: