1.
Introduction
Establishing a sustainable supply chain strategy to gain a competitive advantage is essential for any business enterprise because current technologies allow consumers, communities, public interest groups, and regulators to be well informed about all aspects of an organization's performance of sustainability [1]. There are several driving forces, such as environmental friendliness, social responsibility, and economic contribution, and integrative performance, which have been focused on [2]. Among those, environmental protection education, for instance, has encouraged consumers to pay more attention to the issue of the depletion of natural resources [3] and the destruction of environmental ecology [4]. Therefore, more and more business enterprises/ supply chains are nowadays focusing not only on business opportunities of cost and efficiency but also on sustainable management to the triple bottom line (TBL/3BL: people, planet, and profit) [5] to practice corporate social responsibility (CSR). For example, Walmart has adopted more efficient light bulbs to save energy consumption, Starbucks has incorporated fair trade coffee beans into its product line, and automakers Tesla, Toyota, and Nissan find shared value in low-emission vehicles [6]. Due to the recognized importance of the related issue of sustainability, a large number of research papers proposing and analyzing sustainable supply chain management have been generated. According to an evaluation of 882 papers by Koberg and Longoni [7] and an examination of 1079 papers of academic databases by Beske-Janssen et al. [8], they found a considerable number of existing studies on supply chain sustainability in the last two decades.
Furthermore, many scholars [1,3,7,8,9] claimed that the overall performance concerning sustainable supply chain management (SSCM) has been considered more significant than the individual performance of corporate sustainability management (CSM). It is usually described with a sustainable performance that each group has its own goals and agendas, and the goals and agendas of different groups may be contradictory and may reduce the overall sustainable supply chain performance among the supply chain members [10]. Therefore, the developed strategic objective must be aligned with the strategic objectives of both the whole sustainable supply chain and individual members [11]. Besides, most of the past studies on supply chain strategies emphasized either classification schemes or various coordination mechanisms. And the strategic implementation presented was too fragmented and scattered [12]. Few scholars have proposed some integrated strategies for sustainable supply chains. It seems necessary to create a strategic framework for sustainable supply chain parties involved, including to develop the whole sustainable supply chain objectives, classify various strategies and performance indicators for sustainable supply chain management [8]. For the aforementioned reasons, the paper is to develop a strategic framework for sustainable supply chain management. The purpose of the paper is to propose four specific perspectives, which are described as follows:
● to propose a process of sustainable supply chain management,
● to develop a strategic framework for sustainable supply chain management,
● to classify sustainable supply chain strategies and performance indicators under the proposed framework, and
● to validate the proposed strategic framework through a case study.
The rest of the paper is organized as follows: the second section describes the materials and methods; the third section presents the results of a strategic framework for sustainable supply chain management; the fourth section validates the strategic framework by case study; conclusions are finally drawn in section five.
2.
Materials and methods
As to the second section, the purpose is to illustrate material and methods for developing a strategic framework for sustainable supply chain, which is divided into three parts. Section 2.1. describes the material of literature review for stainable supply chain management. Section 2.2 explains a method of strategic classification applied to a proposed framework. Section 2.3 illustrates the GRA method of strategy prioritization.
2.1. Material of literature review
The objective of the paper is to develop a strategic framework for sustainable supply chain management. Literature reviews are comprehensive and valuable studies [8,9], which can be used to understand solutions to the needs in the past, as well as to help identify new solutions to the problems in the future [13], to help guide future research-orientation in emergent fields [5,14,15] or to help practices to continuously improve the sustainability of supply chain management [13].
To achieve the objective of the study, the paper examines journals that contain a number of strategic issues of the supply chain. 383 papers appear in publicly available electronic databases on Google Scholar or other electronic journal platforms, which include each link of DOI (Digital Object Identifier), URL (Uniform Resource Locator) or "[CorssRef]" used if the web address is too long, as shown in Appendix 1.
2.2. Method of strategy classification
The abductive reasoning process [16] approach has been utilized for developing a conceptual framework for sustainable supply chain management [5,17,18,19,20], which is used in the paper to classify various strategies into a strategic framework. Three types of reasoning process [16], including deductive, inductive, and abductive, are frequently used in social science research because they are important interpretations for cause-effect relationships while developing assumptions or theories [17], as well as helping academics guide managerial practice which explains an event, provides understanding, or suggests testable hypotheses [18]. According to the abduction theory [16], any conclusion can be explained in an expression. In addition, in this step, the analytic categories that allow classifying the reviewed literature of sustainability are identified [7]. It is typically understood as the process of searching for an explanation or classification [19] after a judged observation solely [20].
As suggested by the abduction reasoning process, the paper follows a two-step process combining deductive and inductive approaches for identifying analytic categories [7]. First, based on analytic categories of sustainable supply chain strategies, the strategic framework of the paper is deductively built by seven performance drivers in the classification. And then, with inductive observations focusing on the sustainable performance of supply chain indicators- time, cost, efficiency, and effectiveness, when the strategy performance of the observed literature has a significant influence on the improvement of time and cost, or enhancement of efficiency and effectiveness, the strategy will be classified into a strategic framework [21]. To classify strategies and performance indicators under the proposed framework, 383 papers were validated through an abductive reasoning process [16] and then classified in this strategic framework. The results of the classification of strategies and performance indicators are concisely described in Appendix 1 and Appendix 2, respectively.
2.3. Method of strategy prioritization
Most studies in economics and social sciences often lack prior information or objective data as references, and sometimes, the data collected are inadequate and discrete. Under this situation, grey system theory (GST) is considered a better method for researching the exploratory explanation [22]. Grey relational analysis (GRA) makes use of relatively simple mathematical procedures, a small amount of data, and works with great variability in factors, to arrive at salient relationships in a complex system [23]. With the GRA method, the relationships between the important factors can be identified, and the multiple factors can be explored objectively.
In addition, GRA has been used to deal with issues regarding performance indicators, such as time, cost, etc., to prioritize and validate selected sustainable supply chain strategies [24,25]. Besides, GRA is an important weight analysis method in which relative importance is weighted on a 7-point scale, as shown in Table 1 [22]. The obtained data are usually expressed as a specific range of a grey interval number where a_ and ¯a are the upper and lower limits of the information separately. The associated equations are described as follows:
Nomenclature [25,26,27]
● ⊗: the symbol of grey numbers.
● ⊗∈[a_, ¯a], a_ < ¯a an interval of values.
● xi(k)=D(matrix), where:
● i = 1, 2, 3, …, m, k = 1, 2, 3, … i, m, k ∈ I
● x0: Standard sequence.
● xi: Inspected sequence
● Δ0i=|| x0 (k) xi (k) ||: The difference between x0 and xi (norm).
ζ: Distinguishing coefficient, and ζ∈ [0, 1], normally, it takes 0.5
● Grey generating (larger is better): x∗i(k)=x(0)i(k)max∀i{x(0)i(k)}
● When calculating the grey relational coefficient, the mean of the grey relational coefficient is taken as the grey relational grade.
However, GRA has a common problem, which is the subjective judgment of the decision-makers. In order to improve this shortcoming, the application of GRA is expanded by applying entropy calculations to grey relational analysis [25], and their procedures are developed in the paper to deal with the evaluation of the related performance issues as follows [27]:
● Data: Performance/evaluation matrix: first, input data of entropy should be collected in the form of the matrix Rn×m, which means the performance of each evaluation criteria.
● where k is Boltzman's constant, which guarantees that 0 ≤ ej ≤ 1.
● Find Pij: This step means normalizing the matrix below.
● Entropy for all criteria: The entropy of all criteria is calculated according to Eq 7.
● The degree of diversification ¯ej of the information provided by the alternative performance/evaluation value of criteria j can be defined as
● Normalization for criteria: This makes the relative weights fall within the range of (0, 1) to satisfy the limitation of GRA, and the values obtained in this step should be normalized according to Eq 9
● Grade (degree) of grey relation (larger is better).
● Cardinal Grey Relational Grade: Nagai's globalization grey relational grade: The meaning of cardinal grey relational grade is taking x0 (k) as the reference sequence, and the others are inspected sequences. The globalization grey relational grade is shown below:
● where ¯Δoi is the mean of Δoi, and¯Δmax. and ¯Δmin are the maximum and minimum values of ¯Δoi respectively.
In order to achieve the study's objectives, the purpose of using the GRA approach to prioritize sustainable supply chain strategies is to validate whether the proposed strategic framework can be comprehended and whether strategic importance can be evaluated. Therefore, the process of prioritizing strategies is first to select the appropriate professionals in the supply chain industry, and then invite them to fill out a questionnaire. Also, the method of the weighted data of various strategies collected from the elite interview is used to validate the reliability and validity. And then, the weighted data of various strategies are prioritized using the GRA approach.
3.
Results
The third section first discusses the process of sustainable supply chain management in section 3.1, and then on this basis we develop a strategic framework for sustainable supply chain management in section 3.2. After that, a case study is further used to illustrate and validate the proposed strategic framework.
3.1. The process of sustainable supply chain management
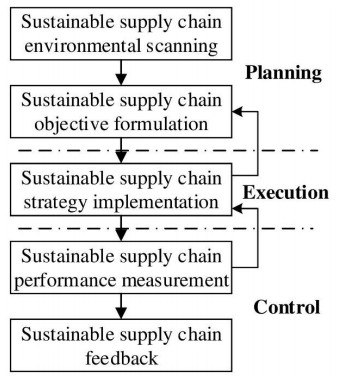
Referring to their OPDCA (observation-plan-do-check-adjust) approach of sustainable supply chain management, Schneider et al. [28] explained that the OPDCA framework could be viewed as a stepwise process that guides users to identify solutions from the strategic implementations to achieve objectives and, if necessary, repeating the cycle of the problem-solving effort to obtain better performances [29]. Besides, many studies also claim that a supply chain could be viewed as a virtual organization for management [10,11,30]. Therefore, the management theory of a business enterprise strategy can be applied to sustainable supply chain management. Past literature has shown that a system view of supply chain sustainability should be adopted [6], as well as that the strategic management should consist of planning, execution, and control phases [31,32,33,34].
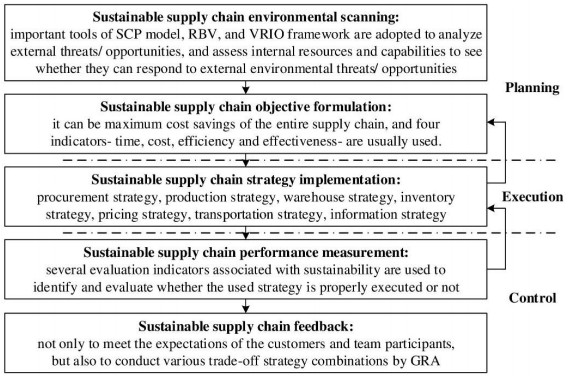
In the planning phase, it mainly involves two stages, sustainable supply chain environmental scanning and sustainable supply chain objective formulation as shown in Figure 1. In the sustainable supply chain environmental scanning stage, the main goal is to assess the environmental/social threats and economic opportunities of corporate organizations in the existing external industry, as well as to understand the strengths and weaknesses of corporate organizations in the existing internal resources and capabilities [35]. Once the sustainable supply chain environmental scanning is completed, and the key members of the supply chain understand internal strengths and weaknesses and external opportunities and threats, the next stage of sustainable supply chain objective setting can be planned [36].
According to the game theory [36], most supply chain transactions play out as "zero-sum" games, with the two parties vying with each other to push the outcome in their direction along the "win-lose" line. However, Taylor [36] claimed that supply chain transactions between the two parties are actually rarely zero-sum games. Therefore, he further suggested the trading partners in the supply chain should focus more on how to maximize supply chain performances rather than individual performances. If the objective is to maximize cost savings across the supply chain, the key members should first create strategic objectives for sustainable supply chain participants. And then they continue to coordinate with the members throughout the supply chain to align with the sustainable supply chain objectives, and also commit to sharing profit and risk with all the members. With a consensus among all sustainable supply chain members to their objectives, each member initiates its value-added activity to the product or service. The result must be that the added value of the entire sustainable supply chain will be enhanced.
A strategic framework suitable for various industries is proposed. Because of this, Taylor [36] proposed four general indicators- time, cost, efficiency, and effectiveness, which are directly referenced as strategic objectives for sustainable supply chain management. The main reason is that almost all performance indicators can be combined/integrated/classified into these four categories of time, cost, efficiency, and effectiveness, according to 27 papers for performance indicators as shown in Appendix 2. For example, Bai & Sarkis [37] proposed sustainable indicators for the supply chain in five domains: time, cost, quality, service, and innovation. Quality usually can be classified into efficiency and service also can be classified into effectiveness. In addition, innovation usually includes innovations of process or product. The innovative processes and innovative products are usually classified into efficiency and effectiveness, respectively.
Four general indicators are indispensable for the strategic framework assessment, and their importance for a sustainable supply chain is described as follows [36]:
● Time: It is one of the most frequently cited types and is used by people to develop objectives and evaluate performance because it is the simplest to measure, simply by adding or subtracting the length of time consumed.
● Cost: It has been thought one of the most important types to gain competitive advantages of the supply chain. However, there are various kinds of costs for each industry, making cost assessment more difficult and complicated when we try to mix or combine a wide variety of costs.
● Efficiency: Cost, although critical to supply chain performance, does not reflect the resource/capabilities utilization and efficiency, making it necessary to adopt various indicators for efficient management of sustainable supply chains.
● Effectiveness: Compared to effectiveness, efficiency is of little value unless it is paired with effectiveness. Efficiency focuses on how well we use resources, while effectiveness is the response to a program to achieve supply chain objectives.
In the execution phase, according to the definition of the sustainable supply chain performance drivers in the papers of [9], there are six main performance drivers of supply chain [38], including facilities, transportation, inventory, information, procurement, and pricing, which can support the execution of the sustainable supply chain. However, it is suggested by the researchers that the supply chain should possess seven drivers, including procurement, production, warehouse, inventory, pricing, transportation, and information, because "facility" usually includes transportation, production, warehouse, etc. In some related studies to supply chain management, "production" is usually discussed in a centralized and independent manner, and it directly affects the cost, efficiency, and surplus. In addition to the importance of "production", the study also focuses on "warehouse", which refers to sending and receiving the materials, storage, and the delivery of the goods to the end consumer. Warehouse management can effectively improve defects and enhance performance to reduce time and cost. It also helps maintain a proper inventory level and reduces the cost of suppliers. Therefore, the study specifically evaluates/points out that "production" and "warehouse" should be used instead of "facilities" in sustainable supply chain management. For the aforementioned reasons, the study of the classification method was proposed. The strategic framework proposed in the execution phase has seven significant performance drivers, which include procurement, production, warehouse, inventory, pricing, transportation, and information.
In the control phase, it mainly involves two stages: sustainable supply chain performance measurement and sustainable supply chain feedback. The main goal of performance measurements is to assess whether the used strategy is properly executed, or whether outcomes meet the objective. In practice, a business enterprise that wants to achieve optimal performance needs to repeatedly select one or several measurements from each category, to conduct performance assessment, and to check whether the sustainable supply chain goals are being met. In the feedback stage, the goal might need to be continuously adjusted in terms of objectives, strategies, or controls to meet the customer needs based on changes in internal resources/capabilities or external environmental conditions. Wal-Mart and Procter & Gamble are good examples of companies that have become leaders in their industries in an ever-changing industry environment. In order to continuously improve the overall competitiveness, and maximize profits to both individual companies and the entire supply chain organizations, they constantly make plans, analyze each market, select target markets and suppliers, coordinate resources, lower constraints, assess performance, share profit and risk, and get the maximum performances from all the upstream and downstream members of the supply chain in a feedback loop [10].
3.2. A strategic framework for sustainable supply chain management
In the sustainable supply chain environmental scanning phase, the goal is first to understand the strengths and weaknesses of the internal environment, as well as the opportunities and threats of the external environment before the strategic objective formulation of sustainable entire supply chain, which is illustrated in Figure 2. Structure-conduct-performance (S-C-P) is an important strategic tool of external analysis and its framework was originally designed to evaluate the competitiveness of industries to assist government regulators, and to describe the conditions under which perfect-competition dynamics would not develop in an industry in the 1930s [35]. And then it has become known as the SCP model which is used for environmental scanning to understand opportunities and threats from three specific types which include the industry structure, firm/ supply chain conduct and their performance. Besides, resource-based view (RBV) [39] and VRIO (value, rarity, imitability, and organization) framework [40] are also important internal analysis tools which are used to understand strengths and weaknesses in the environmental scanning stage, in order to examine the state of whether internal resources/ capabilities can respond to external environmental threats/ opportunities or not.
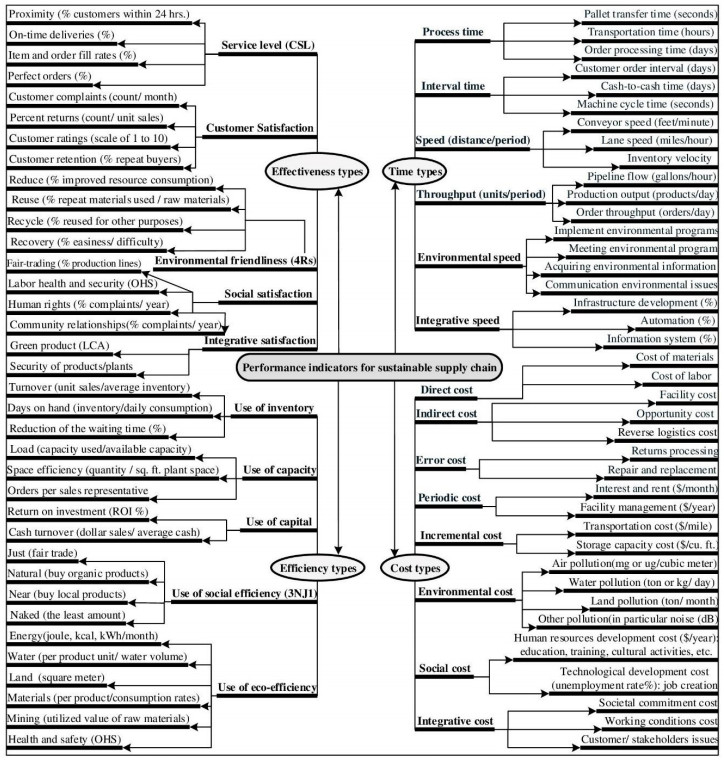
In the sustainable supply chain objective formulation phase, according to the conclusion in section 3.1, the objective formulation is based on four significant categories, including time, cost, efficiency and effectiveness as shown in Figure 3. In addition, each category is then broken down into several sub-categories. A total of 24 sub-categories is aimed at positioning itself in one/ several sub-categories of a given category for sustainable supply chain management. A total of 74 detailed indicators is integrated and classified using 27 papers which is described in details in Appendix 2.
When selecting indicators and strategies, multiple-criteria decision-making approaches are needed to achieve synergetic results [41]. Research approaches such as analytic hierarchy process (AHP), technique for order of preference by similarity to ideal solution (TOPSIS), strategy aligned fuzzy simple multi-attribute rating technique (SMART) grey systems theory (GST), rough set theory (RST) and fuzzy logic and mathematics are often recommended for their noticeable economic performance [41]. Furthermore, Grey relational analysis (GRA), a multiple-criteria decision-making-based grey system theory (GST) is highly recommended for developing a strategic objective of sustainable supply chain. Key members of the supply chain can choose one/several indicators suitable for their respective industries for the development of their own strategic objectives.
In the sustainable supply chain strategy implementation phase, according to the conclusion in section 3.1, the strategy implementation is based on seven significant categories, including procurement, production, warehouse, inventory, pricing, transportation, and information, which are described as follows:
● Procurement strategy: It has been played an important role in enhancing sustainable supply chain performance. For example, early supplier involvement (ESI) strategy is used to reduce development time of new product, while purchasing consortia strategy is used to reduce costs of procurement. In fact, the environmental performance must be enhanced if the key members of the supply chain require that suppliers should have certifications of the environmental management system (EMS) or ISO 14001. In terms of the average percentage of the procurement amount, Walmart spends around 75 % of its revenue in sourcing the products it sells to consumers. Therefore, the first consideration for managers is to make good use of procurement strategies to enhance sustainable supply chain performance.
● Production strategy: Production is a process of value creation that directly or indirectly meets human needs. The production process involves converting inputs (natural resources, various materials, human resources, and capital) into outputs (products or services). A production strategy is often described as a value-adding process. For production across a range of activities, decisions regarding location, capacity, flexibility, etc. have significant impacts on the supply chain performance. For example, a Just-in-time (JIT) strategy can generate a great reduction of lead time in procurement and a great reduction of cost in inventory and warehouse.
● Warehouse strategy: The warehouse should be viewed as a temporary place to store inventory and acted as a buffer in the demand chain. Its primary aim is to facilitate the flow of goods from suppliers to customers and to meet demand in a timely and cost-effective manner. Therefore, it seems essential to choose the proper strategy to conduct effective management for enhancing sustainable supply chain performance. For example, Walmart has successfully applied cross-docking in its retails industry to decrease the time consumed in the order period and transportation, thereby reducing the inventory simultaneously.
● Inventory strategy: Inventory also refers to any kind of resources maintained to meet the present and future needs of an organization. Inventory encompasses all raw materials, work in process, and finished goods, which is held to increase the level of product availability, to provide desirable service to customers and to achieve sales turnover target. For example, QR can quickly respond to both supply process and customer needs, and is used by Spanish apparel retailer Zara to shorten the lead times of its new products and replenishment. As a result, the company is very responsive but carries low levels of inventory.
● Pricing strategy: Pricing is crucial in affecting demand and supply, because it directly determines how much a firm will charge for goods or services, as well as indirectly influences buyers' behavior. Any charge in the pricing process directly affects revenues and also affects changes in other strategic drivers. Pricing strategy has always been an important part of the mission and vision for an enterprise organization. It is also a part of a company's long-term strategic planning for formulating its market value. For example, the cost driver strategy is used by Southwest Airlines to save costs by reducing service levels, including seat assignments and provision of food and beverages. Although the fares offered are cheaper compared to other airlines, it still makes profits.
● Transportation strategy: It is an activity that uses different means to move goods from one location to their destination. The objective of transportation is that goods must be moved fast, safely, and punctually. The process of transportation usually covers several members, such as manufacturers, distribution centers (DC), inventory handlers, customers, and vehicles. The appropriate choice of transportation/distribution allows a firm/supply chain to adjust the location of its warehouse and inventory to find the right balance between responsiveness and efficiency. Shared logistics services are used to maximize transportation efficiencies. Nabisco is a good example of a company that successfully uses the vehicles of its customers to perform transportation tasks to reduce the number of empties backhaul trips, to lower transportation costs and CO2 emissions.
● Information strategy: Information consists of data/analysis on procurement, production, warehousing, inventory, transportation, pricing, costs, prices, customers, etc. throughout the supply chain. It is potentially the biggest driver of performance in the supply chain because it directly affects other drivers. Good information data/analysis helps improve the utilization of sustainable supply chain assets. Many examples regard information as a key driver that is used to provide higher responsiveness while simultaneously improve efficiency, such as Electronic Point of Sale (POS), Electronic Data Interchange (EDI), Enterprise Resource Planning (ERP), etc. Most importantly, the supply chain managers need to make good use of information strategies to enhance sustainable supply chain performance.
In the sustainable supply chain performance measurement phase, it is essential to have several evaluation indicators of the non-economic outcomes associated with sustainability [42], to determine whether each strategy is being effectively executed [8]. In the paper, the balance among the four dimensions of environmental friendliness, social responsibility, economic contribution, and integrative performance is classified in practice in the four domains of time, cost, efficiency and effectiveness for general industry. A business enterprise that wants to achieve optimal performance needs to repeatedly select one or several measurements from each category, and conduct performance assessment to check whether the sustainable supply chain goals are being achieved [43]. After each implementation of the strategy, it is essential to collect, organize and analyze the causal relationship in the performance evaluation, and compare them with the set goals to see whether they are consistent with the executed performance. When strategies are not being executed well in sustainable supply chain performance, supply chain members should revisit and address these issues and solve the problems. Or when an objective goes wrong or is difficult to achieve during the execution phase, they even need to return to the planning phase to revise the objective, or even form a new one.
In the sustainable supply chain feedback phase, the aim is to continuously set new objectives and uses feedback to seek a higher performance of sustainable supply chain. If the verification shows that the new objective of the implemented new strategy is an improvement over the prior standard (baseline), then the new objective becomes the new benchmark for the ongoing adjustment. However, if the verification shows no improvement in the implemented strategy, the existing baseline will remain unchanged. In addition, there are some common approaches that are recommended for the development of a new objective for sustainable supply chain management. The new objective seems able to set up a percentage for improvement that can be higher than the current performance. Furthermore, the sustainable supply chain performance of a supply chain organization should be benchmarked against its competitors, general benchmark, or a top business enterprise of the industry, and then work up a percentage for performance improvement. Due to the ever-changing industry environment, supply chain organizations are often faced with changes in internal resources, external conditions, or customer needs, etc. Even top-tier business enterprises need to use other models to identify opportunities for improvement, and can repeatedly amend newly identified shortcomings, restart a new objective, re-adjust the strategy, develop relative measures and etc., to meet the performance expected for sustainable supply chain management over and over again.
4.
Case study
A case study is used to illustrate the previously established strategic framework for sustainable supply chain management. The purpose of prioritizing strategies is to validate whether the strategic framework can be comprehended and whether the strategic importance can be evaluated. The method of the weighted data of various strategies collected from the elite interview is used to evaluate the reliability and validity. Kevin Liao (廖文順), who was selected as the subject for the elite interviewee, works in the biotechnology & medicine R & D department of ANDLIFE Corporation [44] and in a supporting role at Huili Pharmacy, which is part of the medical industry.
For the past 20 years, Kevin Liao has been an information engineer since he graduated from college with a degree in electronic engineering. At present, he works at KIZONE Information Company [45], Taiwan, where he is in charge of special projects. Therefore, he knows well about the processes of procurement and manufacturing of the company. Besides, he also works for an affiliated enterprise of ANDLIFE, Huili Pharmacy, where he deals with procurement, distribution, and sales issues. Therefore, he seems to be the ideal candidate for the study. Besides, both Philip Tsou (鄒伯衡) and Jia-Ling Huang (黃嘉玲) were interviewed as triangulation in order for the researcher to obtain correct references for the analysis and interpretation of the case study. Philip Tsou is currently CEO of the Global Logistics & Commerce Council of Taiwan [46], where he is mainly in charge of planning, matching, training, consultation, cross-border e-Commerce, etc. In the meantime, Philip Tsou acts as the CEO of SOLE-The International Society of Logistics Taiwan (Taipei) Chapter [47] an important logistics education and research institution, whose goals are to enhance technology management, education, humanities and social sciences in logistics, and particularly promotion of international logistics certification. And Jia-Ling Huang is the retail store manager of Huilii Pharmacy, and she has graduated from a nursing school for more than 20 years.
In the environmental scanning phase, according to the industry structure analysis of SCP, although the medical industry is strictly regulated by medical-related laws and regulations, it is also highly regulated by the Taiwan government. For example, during the pandemic of COVID-19 in 2020, Taiwan successfully brought it under control and prevented community transmission from happening. One of the most important contributions might be the introduction of the face mask supply chain system by the Taiwan government. 92 mask production lines were set up completely within 40 days. And the production capacity of masks was increased from 1.88 to 20 million pieces per day. And then the information system for mask distribution introduced by the Taiwan government not only made the information open and timely to the general public but also integrated mask manufacturers and retailers, enabling the higher performance of mask purchase in related pharmacies in terms of economic, social, and integrative factors. The average price of a mask was about US$0.18 during the pandemic of COVID-19 in 2020. In fact, meanwhile, the price of masks had increased by more than 10 times in Europe, North American, or other countries but it did not happen in Taiwan. Kevin Liao mentioned that the drugstores cannot refuse to sell masks during the pandemic of COVID-19 in 2020, because it is a highly regulated industry by the government in Taiwan.
According to the conducted SCP analysis by firms, Taiwan is one of the countries in the world that provide quality national health insurance, making health care available to every citizen at a reasonable expense. And in Taiwan, there are many medical institutions, public and private hospitals, clinics, and pharmacies close to home. The market segmentation is mainly distinguished into chain store pharmacies (such as Watsons or Cosmetic) and community store pharmacies. Huili Pharmacy belongs to community store pharmacies. With a small number of diversified market trends, Huili Pharmacy cannot resemble the "one-stop shopping" strategy of chain pharmacies because of the lack of economic scale.
According to the performance of SCP analysis, due to the separation of medicine and pharmacy, Huili's strategy is to develop community services by having pharmacists dispense "refillable prescriptions for patients with chronic illnesses" and notify consumers to pick up their medications with LINE. Therefore, general orders for medical supplies or health foods can be done by using interactive LINE. General orders will arrive and consumers are notified in 3–5 days so that the service goal of "one-stop shopping" can be achieved. The cost advantage of Huili performance mainly comes from better resource allocations, such as less manpower, less inventory, and strategic purchasing alliances to enhance procurement economic scale, etc. In addition, due to the lack of economic scale in Taiwan's market environment, the strategy of ANDLIFE Corporation, which is an affiliated enterprise of Huili Pharmacy, is mainly focused on the authorized manufacturing and development of drugs, with North America and Europe as its primary markets.
Two in-depth interviews were conducted with Liao. He was asked to fill in a questionnaire in the first interview to collect preliminary data for the ranking. In addition, the weighted strategies were ranked in importance based on four performance indicators- time, cost, efficiency and effectiveness with the GRA method. The results of prioritizing strategies were thereafter obtained by using the Excel tool. The calculation method is explained in section 2.3. After the ranking, a second interview was conducted to obtain Liao's approval. The goal was to determine if the result of the importance ranking was consistent with supply chain industrial demands in Taiwan or it needed to be modified. The interviewee, Kevin Liao, agreed that the importance of the ranked strategies is closely in line with the current industrial situation.
In the objective formulation phase, the approach of grey relational analysis (GRA) is chosen as the mathematical core to analyze the related importance. The calculation methods are explained in Section 2.3, and Eqs 1 to 4 are used for the ranking, as shown in Tables 2 and 3. The ranking of the importance of GRA shows that cost > effectiveness > efficiency > time, as shown in Table 2. Kevin Liao agreed that the most important objective is cost reduction. The main reason may be that liberalization of import and export has been allowed to perform since Taiwan joined World Trade Organization (WTO) and the General Agreement on Tariffs and Trade (GATT). Since then, pharmacies in Taiwan have been growing rapidly. Nowadays, pharmacies have become a highly competitive industry, with over 6000 pharmacies throughout Taiwan.
In the strategy implementation phase, the importance ranking of GRA shows that procurement > information > production > pricing > inventory > warehouse > transportation, as shown in Table 3. Each strategy field is then broken down into seven sub-fields for sustainable supply chain management in the paper. The classification results of strategies are concisely described in Appendix 1. Eqs 1 to 11 of GRA are used for strategy ranking, which is described in Section 2.3. The GRA results of the strategy priority ranking can be obtained by using the Excel tool, as shown in Table 4, where the top-ranked strategies are recommended to be first used for sustainable supply chain management.
Because each employee in a company may specialize in his or her field without knowing other supply chain strategies, it seems important to involve people from different fields or departments in evaluating, integrating and selecting hybrid strategic options. For example, RFID is very important to KIZONE, but not to ANDLIFE, according to Kevin Liao, the elite interviewee. Since different strategies are of different importance to each supply chain organization, which needs to be levered appropriately and combined efficaciously through GRA approach, according to the individual needs of the supply chain organization.
In the phases of the performance measurement and feedback, each field is then broken down into several sub-categories for sustainable supply chain management. A total of 24 sub-categories, each not homogeneous, are suggested to allow compensations between sub-categories. The aim is to be able to position itself in one/several sub-fields of a given field. Also, a total of 74 detailed indicators can be used to measure performance as shown in Figure 3. Kevin Liao mentioned that the company needs to continuously develop plans to reduce constraints and improve cost performance. Currently at Huili Pharmacy, the demand for ordering goods is judged by humans rather than the use of electronic automatic procurement strategy to place orders. The application of RBV/VRIO is a good example, because Kevin Liao owns professional skills in information programming design, he is therefore expected by the company using information to execute resource allocation and connection, reduce inventory and procurement costs, enhance operational efficiency and strengthen community service, etc. in the future. Kevin Liao stated that his company has had a few new plans and goals to develop resources and capabilities not currently available to improve performance constantly in the highly competitive environment of the medical industry.
To sum up, in practice, for each sustainable supply chain in different fields it is suggested to evaluate the strategy importance first, and then select the best combination of strategies through the GRA approach to develop strategic objectives in the planning phase and achieve development objectives in the execution phase. Also, the performance measurement should be used to determine whether the objectives developed are consistent with those of the sustainable supply chain as a whole and of individual members in the control phase.
For example, if one of the objectives of a sustainable supply chain is to maximize cost savings throughout the supply chain, and meanwhile the key member commits to sharing profits and risks with other members, with all members agreeing on the objective, then each member will initiate its own value-added activity to the product or service. And the whole sustainable supply chain performance will then be improved. Performance evaluation is conducted to examine if the objective is reached. When there is an inconsistent objective, or a failure performance, for example, the members cannot achieve a preset objective, the key member of sustainable supply chain has to consider revising the objective, using the second best solution as the new objective, and even being able to consider selecting new members or lowering productivity constraints of the current members. Also, in terms of considering the selection of new sustainable supply chain members, suppliers or other objectives, it is highly recommended to evaluate the importance using the multiple-criteria decision-making-based GRA approach. GRA is well suited for ranking, as shown in Tables 2, 3 and 4. GRA makes use of relatively simple mathematical procedures, working with high variability in factors, to arrive at salient relationships in a complex system. With the GRA method, the relationships among the important factors can be identified, and the multiple factors can be explored objectively.
Due to the limitation of research time, this paper only illustrates the proposed strategic framework through a case study in the medical industry, and has not yet explored other industries or other objectives such as supplier selections. It is hence suggested that future research should focus on the issue of different rankings in different industries.
5.
Conclusion
A strategic framework is a cyclical approach with continuous improvement that develops into support for the triple bottom line of the three P's: people, planet, and profit. It consists of three phases of planning, execution, and control, including important classifications of existing strategies, performance indicators, and evaluation methods. Also, it can be used to improve sustainable supply chain performance of environmental friendliness, social responsibility, and economic contribution. Besides, the strategic framework is verified that the importance of strategies can be evaluated and the process of the framework can be comprehended. Thus, it seems to be able to create values for sustainable supply chain management in practice. At the same time, it makes up for the insufficiency of a comprehensive strategic framework for sustainable supply chain management in the past studies.
Acknowledgements
The authors deeply appreciate the reviewers providing valuable suggestions.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: