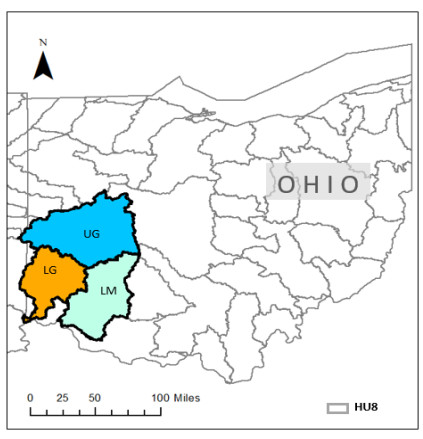
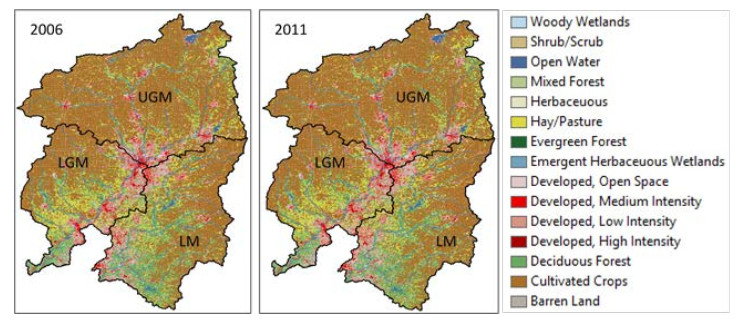
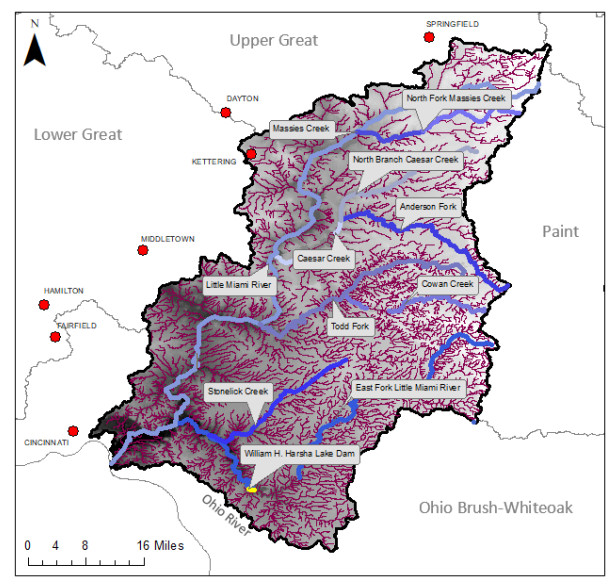
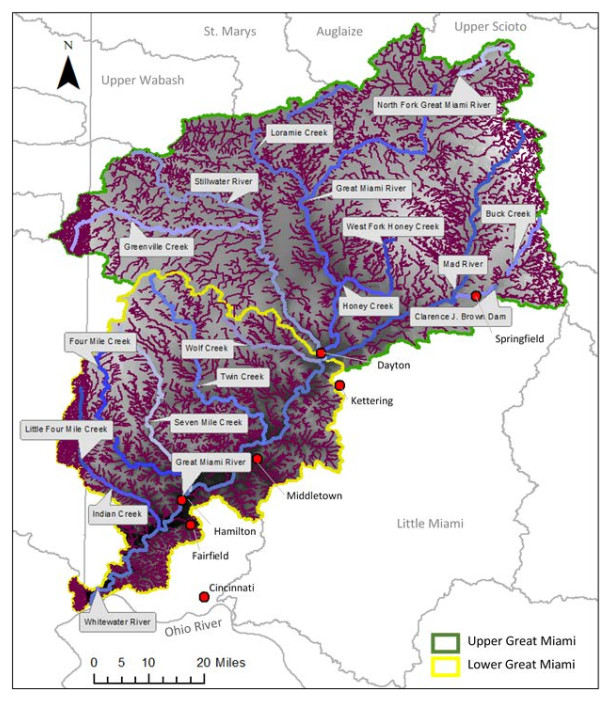
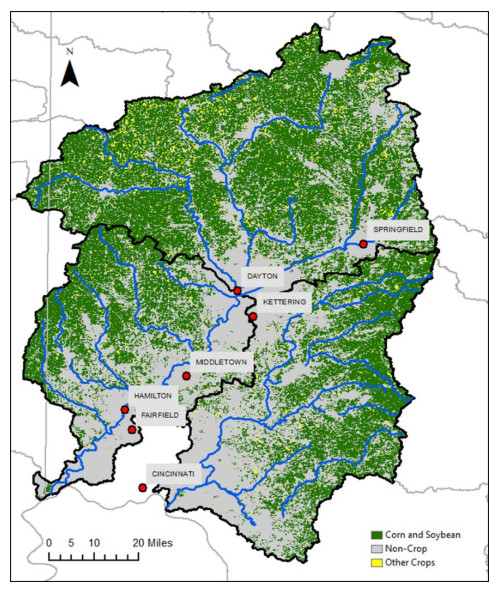
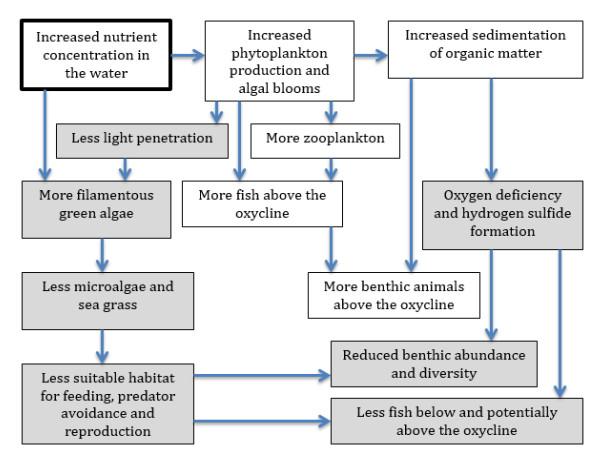
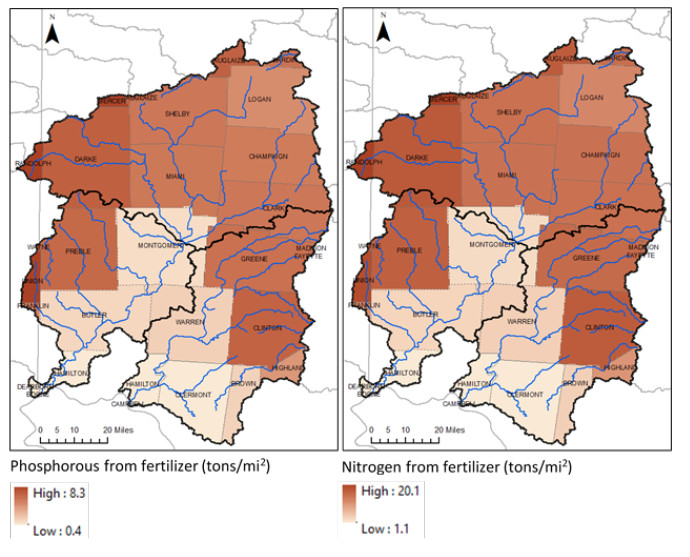
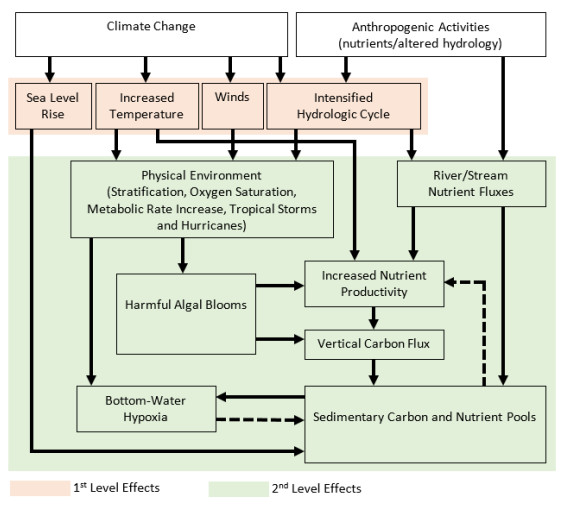
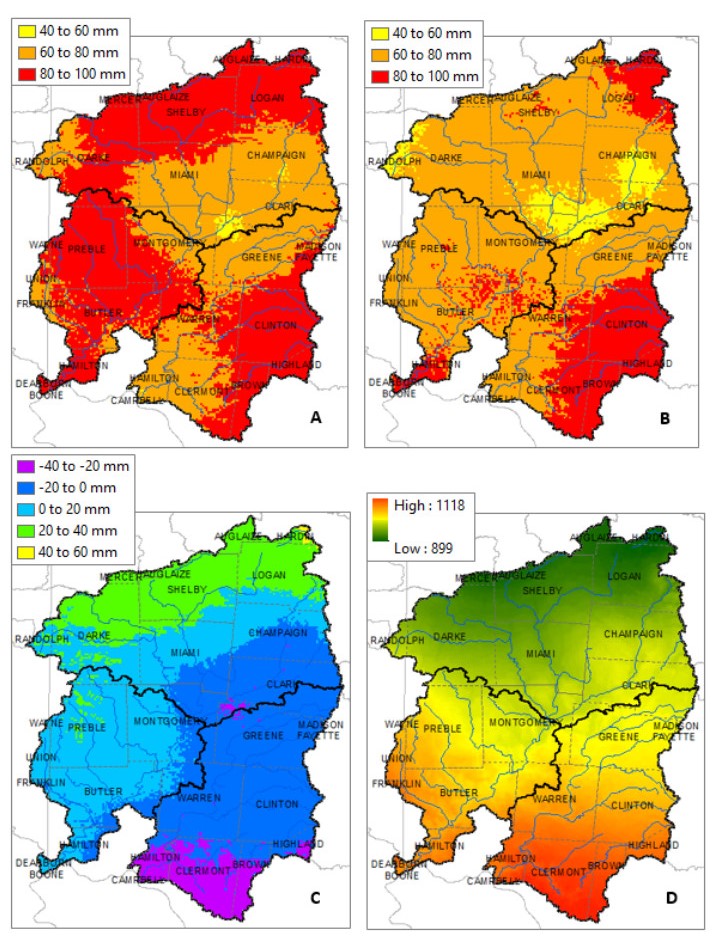
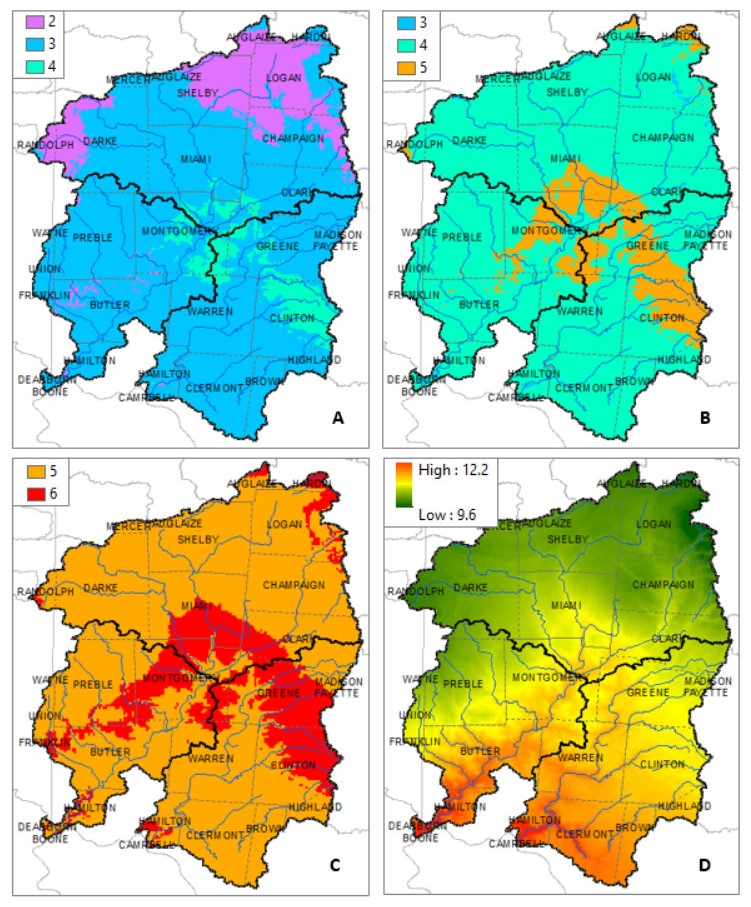
Implications of climate change on nutrient pollution: a look into the nitrogen and phosphorus loadings in the Great Miami and Little Miami watersheds in Ohio

1.   Introduction

Understanding human displacement is very important since it influences the population's dynamic. In light of the recent COVID-19 epidemic outbreak, human travel is critical to understand how a virus spreads at the scale of a city, a country, and the scale of the earth, see ^[1,2]. Human mobility is also essential to understand and quantify the changes in social behavior.

The spatial motion of populations is sometimes modeled using Brownian motion and diffusion equations at the population scale. For instance, reaction-diffusion equations are widely used to model the spatial invasion of populations both in ecology and epidemiology. We refer for instance to Cantrell and Cosner ^[3], Cantrell, Cosner and Ruan ^[4], Murray ^[5], Perthame ^[6], Roques ^[7] and the references therein. In particular, the spatial propagation for the solutions of reaction-diffusion equations has been observed and studied in the 30s by Fisher ^[8], and Kolmogorov, Petrovski, and Piskunov ^[9]. Diffusion is a good representation of the process of invasion or colonization for humans and animals. Nevertheless, once the population is established, the return to home process (i.e., diffusion combined with a return to home) seems to be more adapted to the daily life of humans.

This article aims at describing short-distance human mobility. We aim at considering the local human movement at the scale of the city with a special focus on how to model the returning home of humans. The return to home behavior is also very important in ecology, agriculture and fisheries. In agriculture, a return to home model for bees has been proposed and studied in ^[10,11].

Roughly speaking, we can classify the human movement into 1) short-distance movement: working, shopping, and other activities; 2) long-distance movement: intercity travels, plane, train, cars, etc. These considerations have been developed recently in ^{[12,13,14,15]}. A global description of the human movement has been proposed (by extending the idea of the Brownian motion) by considering the Lévy flight process. The long-distance movement can be covered by using patch models (see Cosner et al. ^[16] for more results about this).

In Section 2, we present the return to home model. Section 3 explores some properties of the return to home model. Section 4 presents a semi-explicit formula for the solutions of the return to home model. Section 5 studies the equilibrium distributions. Section 6 develops a functional framework to understand the mild solutions for the return to home model. Section 7 is devoted to an extension of the Fisher KPP model with return to home and colonization. By analogy to the Fisher KPP problem, we obtain a monotone semiflow. The last section is devoted to an epidemic model with return to home.

2.   Return to home model

In this section we describe a model for the movement of individuals within a city. To simplify the presentation, we consider a population moving in the whole plane $\mathbb{R}^2$. Our goal is to focus on the most important processes involved in the model. The presentation would be more complicated for a model in a bounded set taking into account boundary conditions.

Let $y \to u(t, y)$ be the distribution of population of individual staying at home at time $t$. This means that the quantity

represents the number of individuals staying at home in the sub-region $\omega \subset \mathbb{R}^2$ at time $t$.

Let $x \to v_y(t, x) = v(t, x, y)$ be the distribution of a population of individuals out of the house (called travelers) and originated from their home located at $y \in \mathbb{R}^2$. Here originated from $y \in \mathbb{R}^2$ means that their home is located (or possibly centered at y according to the spatial scale) at the position $y$. Then the quantity

is the number of individuals (originated from the home located at $y \in \mathbb{R}^2$) and traveling in the sub-region $\omega \subset \mathbb{R}^2$ at time $t$.

Model for individuals staying at home: The following equation describes the flux between individuals staying at home at the location $y \in \mathbb{R}^2$ and individuals out of the house

where $1/\alpha > 0$ is the average time spent by individuals out of the home, and $1/\beta > 0$ is the average time spent by individuals at home.

Model for travelers (people who are not staying at home): The following equation describes the flux between individuals staying at home at the location $y$ and the travelers

where $\bigtriangleup_x$ denotes the Laplace operator for the the variable $x = (x_1, x_2)\in \mathbb{R}^2$, that is

In Eq (2.2), $\varepsilon > 0$ is the diffusivity of the travelers. The map $x \to \rho(x-y)$ is a Gaussian distribution representing the location of a house centered at the position $y \in \mathbb{R}^2$. Here by a Gaussian distribution centered at $0$ we mean that the function $\rho$ is given by

for some $\sigma^2 > 0$, so that the covariance matrix is given by the diagonal matrix $\sigma^2 I_2$. Note also that for all $y\in \mathbb{R}^2$, the translated map $\rho(\cdot-y)$ satisfies

Initial condition: Systems (2.1) and (2.2) is complemented with some initial distributions

Remark 2.1. Here in the model we have neglected a possible convection term describing for instance the transport of individuals from their home to their workplace, shopping mall etc. Such a convection term describes the tendency of individuals to start moving from their home location $y$:

where $c_y (x)$ is the travel speed at location $x$. This speed may depend on the location of the house $y$ to distinguish the individual's origin in the city.

Remark 2.2. If we formally replace $u(t, y)$ by $\dfrac{\alpha}{\gamma}\int_{ \mathbb{R}^2}v(t, x, y)dx$ in the $v$-equation (see (2.2)) of the model, we obtain the following single non local equation

Indeed, replacing $u(t, y)$ by $\dfrac{\alpha}{\gamma}\int_{ \mathbb{R}^2}v(t, x, y)dx$ corresponds to slow-fast system idea. Under suitable assumptions on the parameters (i.e. $\alpha = \widehat{\alpha}/\varepsilon$ and $\gamma = \widehat{\gamma}/\varepsilon$ with $\varepsilon > 0$ small enough), we can formally assume that $u(t, y) = \dfrac{\alpha}{\gamma}\int_{ \mathbb{R}^2}v(t, x, y)dx$.

3.   Remarkable distributions

3.1.   Total distribution of population in space

The total distribution of population originated from a house located at $y \in \mathbb{R}^2$ is

By integrating the distribution with respect to $y$ (homes locations), we obtain the total distribution of population in space (including both individuals staying at home or travelers)

3.2.   The total distribution of individuals at home

The map $y \to h(t, y) = u(t, y)+\int_{\mathbb R^2}v(t, x, y)dx$ is the density of individuals per home at time $t$. That is to say that

is the total number of individuals (staying at home or traveling) with their home in the sub-region $\omega \subset \mathbb{R}^2$ at time $t$. Data representing this distribution is usually available. This is true for example in USA ^[17] where such a distribution is known per county (a home is identified to a county).

If we neglect the newborns and the deaths, and people moving house, we can assume that $h(t, y) = h_0(y)$ is independent of time. Let $y \to h_0(y)$ be the spatial distribution of individuals with their home located at the position $y$. This means that

denotes the number of people having their home in the region $\omega \subset \mathbb{R}^2$.

In that case, we obtain

or equivalently

4.   Explicit formula for the solutions

By using Eqs (2.1) and (2.2), we have

Therefore the solution (2.1) and (2.2) satisfies (3.1).

By replacing the formula (3.2) in the $u$-equation (2.1), we obtain

and we deduce an explicit form for the solutions

In order to derive an explicit formula for $v(t, x, y)$ we define the two-dimensional heat kernel $K:(0, \infty)\times \mathbb{R}^2\to \mathbb{R}$ be

and we will use the simplifying assumption (2.3).

Lemma 4.1. Assume that $\rho(x)$ is a Gaussian distribution (2.3). Then there exists $t_0 > 0$ such that

Moreover the convolution of $\rho$ with the kernel $K(t, .)$ satisfies

Proof. Note that (2.3) rewrites as

We deduce that

and the result follows by the semigroup property of the diffusion semigroup.

Define

and

where

We obtain

Next, by replacing the explicit formula (4.1) for $u(t, y)$ in the above formula, we obtain

with

and

By using the above formula for $v_2$, we obtain

and by using Lemma 4.1 and formula (4.2), we deduce that

By using the expression for $v_3$, we obtain

By using the change of variable $\widehat{\sigma} = t-\sigma$ we obtain

Therefore, combining Eqs (4.3)–(4.6), we obtain an explicit formula for $v(t, x, y)$.

5.   Equilibrium and their stability

The equilibrium distribution must satisfy the following coupled system of equations

and

The first Eq (5.1) provides

By using in (5.2) we obtain

and since $\overline{u}(y)$ is independent of $x$, we obtain

and

Define now

so that we get

Remark 5.1. We observe that

Therefore by using (3.1) we obtain

6.   Mild solutions for the non-homogeneous equation

6.1.   A change of variable of some interest

Recall that the return to home model reads as follows

In the above formulation of the return to home model $x$ denotes the position of travelers and their home located at $y$. So we use an Eulerian system of coordinate for $x$ that is independent of the home location $y$. Instead, we can consider the spatial location

which can be regarded as a Lagrangian system of coordinate for $z$ centered at the home location $y$. By using the change of variables

we obtain the following system of equations

In order to understand our choice of Banach spaces, one may observe that the term in (6.1), which is a typical term,

becomes in (6.2)

when rewritten with the variable $z = x-y$. In this system of coordinate, the two variables $z$ and $y$ are mostly uncoupled. This explain our choice of the Banach $Y_2$ below.

6.2.   Some Banach spaces

We consider ${{\rm{BUC}}}\left(\mathbb{R}^2\right)$ the space of bounded and uniformly continuous maps from $\mathbb{R}^2$ to $\mathbb{R}$, which is a Banach space endowed with the supremum norm

The space $Y_1$: We define

The space $Y_1$ becomes a Banach space when it is endowed with the norm

The space $Y_2$: We also define $Y_2$ to be the space of maps $(x, y)\to v(x, y)$ such that the function $w(x, y) = v(x+y, y)$ satisfies

That is also equivalent to say that $Y_2$ is the space of maps $(x, y)\to w(x-y, y)$ such that

Therefore $Y_2$ is a Banach space endowed with the norm

Note that the maps in $Y_2$ enjoy the following property.

Lemma 6.1. Let $v \in Y_2$ be given. Then the map

is bounded and uniformly continuous on $\mathbb{R}^2$.

Proof. By construction, the map

is bounded and uniformly continuous. But by using a change of variable we deduce that

Hence the map

is bounded and uniformly continuous.

6.3.   The semigroup of the heat equation in ${{\rm{BUC}}}(\mathbb{R}^2, Z)$

Let $(Z, \Vert. \Vert _Z)$ be a Banach space. Let us consider the semigroup generated by the heat equation on $Y = {{\rm{BUC}}}(\mathbb{R}^2, Z)$ given by

Here recall that the function $K$ is the two-dimensional heat kernel. Now we will prove the following lemma. We refer to ^[18] for more results on vector valued elliptic operators and related evolution problems.

Lemma 6.2. The semigroup $\{T(t)\}$ is strongly continuous in $Y = {{\rm{BUC}}} \left(\mathbb{R}^2, Z \right)$.

Proof. First observe that

To prove the strong continuity of $T(t)$ we fix $\varphi\in Y$. We have

Let $\varepsilon > 0$ be given. By using the fact that $x \to \varphi(x)$ is uniformly continuous, we deduce that there exists $\eta > 0$ such that

and we have

Hence

and since

the result follows.

6.4.   The semigroup of the heat equation in $L^1(\mathbb{R}^2, Z)$

We consider the heat semigroup on $Y = L^1(\mathbb{R}^2, Z)$ given by

We have the following lemma.

Lemma 6.3. The semigroup $\{T(t)\}$ is strongly continuous in $Y = L^1(\mathbb{R}^2, Z)$.

Proof. First observe that

To prove the strong continuity of $T(t)$ we fix $\varphi\in Y$. Next fix $\epsilon > 0$ and note that there exists $\phi\in C_c(\mathbb{R}^2; Z)$ (compactly supported) such that

Next one has for all $t > 0$

and

and the result follows by using similar argument than in the proof of Lemma 6.2.

Now assume that $v \in Y_2$. Then $v$ can be written as

for some

We obtain that

therefore

So by using the same arguments as in the proof of Lemma 6.3 combine with the above observations, we deduce the following lemma.

Lemma 6.4. The semigroup $\{T(t)\}$ is strongly continuous in $Y_2$.

6.5.   Existence of a linear semigroup

Let us consider a non-autonomous perturbation of the return to home model

with the initial distribution

We define the state space

which becomes a Banach space when it is endowed with the standard product norm $\|\cdot\|_X$ given by

Then the following lemma holds.

Lemma 6.5. The family of linear operators defined for $t\geq 0$ by

defines a strongly continuous semigroup of bounded linear operators on $(X, \Vert.\Vert_X)$.

6.6.   Bounded linear perturbation

We define the linear operators $B_1, B_2: {{\rm{BUC}}}\left(\mathbb{R}^2\right) \times Y_1 \cap Y_2 \to {{\rm{BUC}}}\left(\mathbb{R}^2\right) \times Y_1 \cap Y_2$ by

Note that $\phi\in {{\rm{BUC}}}\left(\mathbb{R}^2\right)$ due to Lemma 6.1. Next the following lemma holds true.

Lemma 6.6. The linear operators $B_1$ and $B_2$ are bounded on $(X, \|\cdot\|_X)$.

Proof. Let $u \in {{\rm{BUC}}}(\mathbb{R}^2)$ and $v \in Y_1 \cap Y_2$. As noticed above, from Lemma 6.1 and since $v \in Y_2$, we know that the map $y \to \alpha \int_{ \mathbb{R}^2}v(x, y)dx$ is bounded and uniformly continuous. Moreover, we have

while

and

The result follows.

Let us consider the return to home model

with the initial distribution

Let $A:D(A) \subset X \to X$ be the infinitesimal generator of the strongly continuous semigroup $\left\{T_A(t)\right\}_{t \geq 0}$. By considering $W = \left(\begin{array}{c} u\\ v \end{array} \right)$ and setting $B = B_1+B_2$, the problem (6.6) can be rewritten as the following abstract Cauchy problem

Applying usual bounded perturbation results for strongly continuous semigroup (see for instance ^[20] and the reference therein), we obtain the following result.

Theorem 6.7. The linear operator $A+B:D(A) \subset X \to X$ is the infinitesimal generator of a strongly continuous semigroup $\left\{T_{A+B}(t)\right\}_{t \geq 0}$ of bounded linear operator on $X$. Moreover $t \to W(t) = T_{A+B}(t)W_0$ is the unique continuous map satisfying

Furthermore, for each $t \geq 0$, the positive cone $X_+ = {{\rm{BUC}}}_+\left(\mathbb{R}^2\right) \times Y_{1+} \cap Y_{2+}$ (where the plus sign stands for the space of non-negative functions) is positive invariant by $T_{A+B}(t)$.

7.   Model with colonization and return to home

In this section we incorporate a colonization phenomenon in the return to home model. This new feature turns out to be important especially when dealing with animal dispersal behavior. The following model takes into account a colonization effect that corresponds to the fact that when it is time to return home for the travelers, a fraction $p$ (with $0 \leq p \leq 1$) returns back home like before, and a fraction $1-p$ colonizes the location they have reached at the end of their traveling period. This return to home model with colonization reads as the following system of equations

where $p \in [0, 1]$.

Remark 7.1. Recall that $1/\gamma$ is the average time spent at home while $1/\alpha$ stands for the average time spent to travel. If we assume that $p = 0$ (that is no individuals return to home after traveling), the process described above corresponds to rest during a period $1/\gamma$ after a period of travel $1/\alpha$. So the case where $p = 0$ is also realistic and this extends the standard diffusion process. The corresponding system could be called for short the "diffuse and rest model".

In the model the term $\alpha \, (1-p) \int_{ \mathbb{R}^2}v(t, y, y')dy'$ counts the fraction of individuals who colonize the location $y$ at the end of their travel. It is summed over all their previous home locations $y'\in \mathbb{R}^2$. Hence $1-p$ is the fraction of the travelers that will change their home location by the end of their travel period.

Lemma 7.2. Let $v \in Y_1$ be given. Then the map

is bounded and uniformly continuous on $\mathbb{R}^2$, and one has

In other words the linear map $v\to \int_{ \mathbb{R}^2}v(\cdot, y)dy$ is bounded from $Y_1$ into ${{\rm{BUC}}} \left(\mathbb{R}^2\right)$.

Proof. Recall that the space $Y_1$ is the set of maps $x \to v(x, .)$ which belongs to ${{\rm{BUC}}} \left(\mathbb{R}^2, L^1 \left(\mathbb{R}^2\right) \right)$. The linear form

is bounded linear on $L^1(\mathbb{R}^2)$. Therefore the map $x \to G(u(x, .))$ must be bounded and uniformly continuous on $\mathbb{R}^2$.

We define the linear bounded operator $C:X \to X$ by

By considering $W = \left(\begin{array}{c} u\\ v \end{array} \right)$ the problem (7.1) can be rewritten as the following abstract Cauchy problem in $X$

Theorem 7.3. Let $p\in [0, 1]$ be given. Then the linear operator $A+pB_1+B_2+(1-p)C:D(A) \subset X \to X$ is the infinitesimal generator of a strongly continuous semigroup $\left\{T_{A+pB_1+B_2+(1-p)C}(t)\right\}_{t \geq 0}$ of bounded linear operator on $X$. Moreover $t \to W(t) = T_{A+pB_1+B_2+(1-p)C}(t)W_0$ is the unique continuous map satisfying

Furthermore, for each $t \geq 0$, the positive cone $X_+ = {{\rm{BUC}}}_+\left(\mathbb{R}^2\right) \times \left(Y_{1+} \cap Y_{2+}\right)$ (where the plus sign stands for the space of non-negative functions) is positively invariant by $T_{A+pB_1+B_2+(1-p)C}(t)$.

Colonization and return to home model: If we add a vital dynamic on the individual staying at home in the model with colonization and return home, we have

where $p \in [0, 1]$.

To deal with the above system we consider the nonlinear map $F:X\to X$ given by

Together with the notation of the previous section and replacing $\alpha$ by $\alpha+\nu$ into (6.5), problem (7.2) rewrites as the following abstract Cauchy problem for $W = \left(\begin{array}{c} u\\ v \end{array} \right)\in X$:

and

Note that the function $f: \mathbb{R}\to \mathbb{R}$ given by $f(u) = (\beta-\mu)u-\kappa u^2$ satisfies: For each $M > 0$ there exists $\lambda(M)\in \mathbb{R}$ such that the function $u\to f(u)+\lambda(M)u$ is non-negative and increasing on $[0, M]$. Hence since $F$ is locally Lipschitz continuous on $X$ and the semigroup $\{T_{A+pB_1+B_2+(1-p)C}(t)\}$ is positive (with respect to the cone $X_+$) we obtain the following theorem.

The following theorem is a consequence of the results proved in Magal and Ruan ^[19,20]. The result on monotone semiflows are consequences of Hal Smith ^[21,22]. We also refer to Magal, Seydi, and Wang ^[23] for recent extensions.

Theorem 7.4. The Cauchy problem (7.3)–(7.4) generates a maximal semiflow $U: \mathbb{R}_+\times X_+ \to X_+$ on $X_+$. Moreover $U$ is monotone on $X_+$, that is

Remark 7.5. In the Lagrangian system of coordinate the above system becomes

8.   Application to an epidemic model with return to home

Epidemic model for people staying at home: The following equation describes the flux between individuals staying at home at the location $y \in \mathbb{R}^2$ and individuals out of the house

Epidemic model for travelers: The following equation describes the flux between individuals staying at home at the location $y$ and the travelers

In the above epidemic model we assume that the transmission occurs locally in space. At home (see (8.1)) the term $\kappa_1 s_1(t, y) i_1(t, y)$ means that susceptible individuals located at $y$ can only be infected by the infectious at home and located at the same position $y$. For travelers susceptible individuals originated from $y$ and located at $x$ at time $t$ can be infected by infected travelers located at $x$ at time $t$ whatever the location of their home position. In other words, for the travelers the incidence rate at time $t$ and spatial location $x$ reads as $\kappa_2 s_2(t, x, y) \int_{ \mathbb{R}^2} i_2(t, x, \widehat{y}) d\widehat{y}$.

Initial condition: The systems (8.1) and (8.2) is complemented with the initial distributions

and

As above, to handle this problem we consider the Banach space $\mathbb X: = X\times X$ endowed with the product norm. We define the linear operator $\mathbb A: D(\mathbb A)\subset \mathbb X\to \mathbb X$ by

and

We also define the bounded linear operator $\mathbb L:X\times X\to X\times X$ by

so that $\mathbb A+\mathbb L:D(\mathbb A):\mathbb X\to \mathbb X$ is the infinitesimal generator of a strongly continuous semigroup on $\mathbb X$, leaving the positive cone $\mathbb X_+ = X_+\times X_+$ positively invariant. For the contamination terms, we define the nonlinear map $\mathbb F:X\times X\to X\times X$ by

Next setting

systems (8.1)–(8.4) becomes

together with

Since $\mathbb F$ is locally Lipschitz continuous on $\mathbb X$, (8.5) generates a strongly continuous maximal semiflow on $\mathbb X$. Moreover for each $M > 0$ there exists $\lambda(M)$ such that for all $W\in \mathbb X_+$ with $\|W\|_{\mathbb X}\leq M$ one has

As a consequence, since $\mathbb A+\mathbb L$ generates a strongly continuous semigroup on $\mathbb X$ which is positive (with respect to the positive cone $\mathbb X_+$), the cone $\mathbb X_+$ is positively invariant with respect to this maximal semiflow. In other words, when the initial data are positive then the maximal solution is positive as well.

To see that the semiflow is globally defined, fix an initial data $W(0) = ((s_{10}, s_{20}), (i_{10}, i_{20}))^T\in \mathbb X_+$ and denote by $W = ((s_{1}, s_{1}), (i_{1}, i_{2}))^T\in \mathbb X_+$ the maximal solution with initial data $w(0)$ defined on $[0, \tau)$ with $\tau\in (0, \infty]$. Let us show that $\tau = \infty$ Adding the Eqs (8.1) and (8.2) integrated with respect to $x\in \mathbb{R}^2$ yields for any $t\geq 0$ and $y\in \mathbb{R}^2$:

Now from (8.2) and the positivity of the solution we obtain for $t\in [0, \tau)$, $(x, y)\in \mathbb{R}^2\times \mathbb{R}^2$ that

This proves that the map $t\to \|s_2(t, \cdot)\|_{Y_1}+\|s_2(t, \cdot)\|_{Y_2}$ is uniformly bounded on $[0, \tau)$. From these bounds, the equation for $i_2$ becomes sub-linear so that $t\to \|i_2(t, \cdot)\|_{Y_1\cap Y_2}$ has at most an exponential growth. This prevents from finite time blow-up and ensures that $\tau = \infty$ and the semiflow is globally defined on $\mathbb X_+$.

The following theorem is a consequence of the results proved in Magal and Ruan ^[19,20].

Theorem 8.1. The Cauchy problem (8.5)–(8.6) generates a continuous semiflow $U: \mathbb{R}_+ \times \mathbb X_+ \to \mathbb X_+$. More precisely, for each $W_0 \in \mathbb{X}_+$, the map $t \to W(t)W$ is the unique continuous map from $[0, \infty)$ into $\mathbb{X}$ satisfying

Acknowledgement

The authors are grateful to the anonymous referees for their helpful comments.

Conflict of interest

The authors declare there is no conflict of interest.