Mercury and its toxic effects on fish

1.   Introduction

The rapid proliferation of cloud computing, the Internet of Things, and online video applications has led to an exponential surge in network traffic. This causes network capacity to quickly reach its limits, making congestion control a critical issue in ensuring efficient network operation. Since the birth of the Internet, the congestion problem of network transmission has received widespread attention^[1,2,3,4,5]. For this reason, many methods to solve network congestion came into being. Traditional queue management policies adopt the "Drop-Tail" policy, which is easy to produce continuous full queue state, and even lead to data flow deadlock and global synchronization. Therefore, active queue management (AQM) has attracted the attention of many scholars^[6]. It can effectively mitigates congestion, diminishes packet loss rates, enhances network utilization, and averts network crashes. The initial AQM algorithm introduced is Random Early Detection (RED), which computes the likelihood of packet loss based on the average queue length^[7]. Although RED algorithm can effectively control the congestion in the network, the performance of RED algorithm can not adapt to the change of network load because it is sensitive to static parameters. In the following decades, many scholars have improved the RED algorithm^[8,9], but these improved RED algorithms have high requirements for parameter tuning and are easily affected by the environment^[10]. Due to the lack of systematic theory, the algorithm basically relies on intuition and inspiration, which leads to some problems in stability and robustness. To avoid this problem, Misra established a new TCP/AQM model based on fluid flow theory combined with stochastic differential equations, which laid the foundation for applying control theory to settle the corresponding congestion problem^[11]. Due to the complexity of the network, scholars focus on different issues. Ren introduced an AQM algorithm grounded in linear control principles^[12]. However, the AQM controller based on linear theory can not well compensate the nonlinearity of the network system, and is vulnerable to the disturbance of unresponsive flow and other factors, its robustness is poor, the stability of the algorithm is difficult to be guaranteed. ^[13] uses linear matrix inequality (LMI) to linearize the nonlinear model, and compensates the influence of uncertainty in the network through the designed sliding surface. These studies are based on linear systems, ignoring the nonlinear dynamic nature of TCP networks. Therefore, many scholars have proposed congestion control algorithms for nonlinear TCP networks. Liu applies the prescribed performance technology to the TCP/AQM congestion problem, and designs congestion control combined with $H_\infty$ control, which can estimate the unknown link capacity^[14]. Considering the dynamic nature of the session count during network transmission, Chen adapted the TCP/AQM model into a switching model. Subsequently, a network congestion controller was devised, integrating prescribed performance technology. This designed controller adeptly manages the frequent fluctuations in the number of sessions^[15]. Furthermore, certain studies also use intelligent control methods^[16], data segmentation methods^[17] and various other control methodologies to formulate network congestion controllers. The author develops an AQM algorithm using Neural Network (NN) approaches and fuzzy variable structure control respectively^[18,19]. The output weight of radial basis function NN was obtained by particle swarm optimization, and then AQM controller was implemented in ^[20].

The dynamic nonlinear system of TCP network has saturation characteristics, which may deteriorate the performance of the network system and inducing instability of the system. Therefore, accounting for the saturation characteristics of the control input becomes imperative when designing AQM algorithm^{[21,22,23,24]}. ^[21] considers the input constraint of the TCP network system, and replaces the non-differentiable saturation function with the smooth differentiable function, the designed AQM algorithm enables the system to obtain better asymptotic stability. ^[22] designs robust enhanced proportional derivatives affected by input saturation, and solves the controller design problem for linear systems with asymmetric constraints by the scaling small gain theorem. Considering the input saturation within the TCP/AQM system, Shen proposed a new AQM control combined with the prescribed performance control. Employing FLS, the approach effectively addresses error disturbances stemming from input saturation, thereby enhancing the overall control effectiveness of the system.^[23]. Similarly, dead zone may exist in the actual dynamic system^[25,26,27], although many scholars have noticed the input nonlinearity such as dead zone and saturation, have also proposed corresponding solutions, the existing researches on TCP network congestion control only consider the dynamic characteristics of a single characteristic. So the control problems of multi-type input nonlinearity, particularly those associated with uncertain nonlinearities, remain relatively scarce. In this paper, the effects of dead zone and saturation inputs concurrently on TCP network congestion control are considered at the same time, and the performance of the system is controlled effectively.

In the Internet, under the influence of the environment, there are always some uncertainties in practical TCP network, such as the uncertainty of network parameters and unresponsive User Datagram Protocol (UDP) flows. At present, the most effective solution is to learn the uncertain functions in the nonlinear systems with the neural networks or the fuzzy logical systems^{[28,29,30,31,32]}. Based on the approximate characteristics of FLS, Liu et al. introduced an adaptive fuzzy control scheme to improve the robustness and convergence of nonlinear stochastic switching systems^[33]. In the context of a nonlinear system characterized by uncertain function constraints, a fuzzy state observer is devised to estimate the unmeasurable state variables, so that the system state is no longer constrained by the function^[34]. Based on the above analysis, the application of FLS in TCP/AQM system can effectively alleviate the congestion problem. Mohammadi et al. proposed a PID controller for TCP/AQM systems with saturated input delay, which reduces packet loss and improves network utilization. In the design process of the controller, fuzzy algorithm is used to approximate the optimal PID control gain^[35]. In view of the time-varying number of sessions during network transmission, Chen modified the TCP/AQM model into a switching model and established a network congestion controller combined FLS with prescribed performance technology, the designed controller can cope with frequent changes in the number of sessions^[36]. The incorporation of FLS is undertaken to address unknown elements, accompanied by the formulation of a novel practical control law. The designed adaptive tracking controller ensures the actual boundary of all signals in the TCP/AQM network system ^[37].

At present, in the big data environment, the number of network nodes and data traffic are very large, especially UDP flow represented by audio and video occupy a large amount of bandwidth. Therefore, Controlling traffic for a single node proves challenging in mitigating network congestion. Recognizing this, in the development of a congestion control algorithm, a holistic approach that considers the entire network becomes imperative to effectively avert congestion issues within the expansive realm of big data. Based on this, this paper studies delves into an exploration of an adaptive fuzzy control for AQM network nonlinear systems, incorporating considerations for both saturated input and dead zones. The principal contributions of this study can be summarized in the following three key points.

(1) Considering the unknown response flow and the interplay among network nodes, this paper takes the TCP network as a whole and builds a multi-bottleneck TCP/AQM network model, which can more accurately describe the real network and improve the window utilization.

(2) In this paper, for the first time, the dead zone and saturation input nonlinear characteristics of the network model are considered at the same time, by confining the input within the permissible range, this approach renders the model in this study notably more comprehensive and inclusive.

(3) Combined with the backstepping technique, this paper designs the adaptive fuzzy control algorithm, which guarantees the steady-state and transient performance of the tracking error, allowing the queue length of nodes to effectively track the desired queue length.

The subsequent sections of this paper are structured as follows: Section 2 provides the TCP network model and outlines the preliminaries. Section 3 presents the primary result. To illustrate the effectiveness of the proposed method, Section 4 conducts simulation experiments. Finally, Section 5 summarizes the conclusion.

2.   Model and preliminaries

2.1.   TCP/AQM nonlinear switching model

Building upon Misra's fluid model in 2001, this paper considers the following multi-bottleneck TCP network

where $W_{s, i}(t)$ is the total congestion window size, $R_i(t)$ is the round-trip delay, $q_i(t)$ is the queue length in the router, $p_i(t)$ is the probability of packet loss, $N_i(t)$ and $C_i(t)$ is the number of TCP sessions and available link capacity, respectively. $\omega_i (t)$ is the external disturbance caused by unresponsive flows like UDP flows. $i$ is the $i$-th network node.

Remark 1. A multi-bottleneck TCP/AQM network is different from a single-bottleneck network in that it contains multiple bottleneck nodes. In the transmission process, the upstream node acts as the sender of the downstream node, and its link capacity is affected by the adjustment of the downstream node to the size of the sender window. Hence, in formulating the network model, this paper takes into account how downstream nodes affect the link capacity of upstream nodes. It is worth noting that the queue capacity of each bottleneck node is usually not the same, making its transmission model different.

Due to the complexity of multi-bottleneck networks, the queue length in single-bottleneck networks is no longer suitable. Therefore, in the congestion control design, this paper considers tracking the queue usage rate $q_{u, i}$. Assuming the known total number of queues that a single router can accommodate, denoted as $q_{max}$, and the queue usage rate of a single router as $q_{u, i} = \frac{q_i}{q_{max}}$, model (2.1) can be reformulated as follows:

Let $x_{1, i} = q_{u, i}$, $x_{2, i} = W_{s, i}(t)$, $N_i\in \mathbb{N}_+$, The network dynamics model (2.2) can be written as

where $f_i(x_{2, i}) = \frac{x_{2, i}}{R_i(t)q_{max, i}}$, $g_{\sigma (t), i} = \frac{N_{\sigma (t), i}(t)}{R_i(t)}$, $h_{\sigma (t), i}(x_{2, i}) = \frac{-x^2_{2, i}(t)}{2N_{\sigma (t), i}(t)R_i(t)}$, $u_i(t) = p_i(t)$, $\sigma(t):[0, \infty)\rightarrow \mathbb{N} = {1, \cdots, N_{max}}$ is switching signal.

Assumption 1. Suppose that the unknown disturbance $\omega_i(t)$ is bounded, and $0\leq\omega_i\leq\omega_{max}$.

2.2.   Model of dead-zone and saturation

$u_i(t)$ is a nonsymmetric dead-zone input nonlinearity which is defined as follows:

where the parameters $u_r > 0$ and $u_l < 0$ represent the breakpoints of control signal nonlinearity. $m_l > 0$ and $m_r > 0$ denote the right slope and the left slope of the dead zone.

Given that the control signal $u_i(t)$ for TCP/AQM represents the marking probability, with a value range of $[0, 1]$, the system input is constrained by nonlinear saturation as defined by

where $u_{max} > 0$ and $u_{min} > 0$ are unknown constants, respectively.

Let's assume $u_{max} > m_ru_r$ and $u_{min} > m_lu_l$. Defined $\wp(u)$ as follows:

Obviously, $\wp(u)\in R$ and $\eta\leq\wp(u)\leq1$, where $\eta > 0$ is an unknown constant.

Remark 2. Significantly, both the input dead zone and saturation characteristics of the network model are considered in this paper, which makes the application more extensive.

Thus, according to (2.4–2.6), $sat(D(u))$ can be characterized as

2.3.   Fuzzy logic system

Consider the $j$th IF-THEN rule of the following form:

$R_\ell$: IF $x_1$ is $F_1^\ell$ and $\dots$ and $x_n$ is $F_n^\ell$.

Then $y$ is $G^\ell$, $l = 1, 2, \dots, N$, where $x = \left [x_1, x_2, \ldots, x_n \right]^T \in R^n$, and $y\in R$ are input and output of the FLS, respectively. $F_i^\ell$ and $G^\ell$ are fuzzy sets in $R$. By using the singleton fuzzification, the product inference and the center-average defuzzification, the FLS can be given as

where $N$ is the number of IF-THEN rules, $\varpi _j$ is the point at which fuzzy membership function $\mu_{P^\ell}(\varpi _\ell) = 1$.

Let

where $\zeta(x) = \left [\zeta _1(x), \zeta _2(x), \ldots, \zeta _N(x) \right]^T$ Then the FLS can be described as

Lemma 1. ^[38] Let $f(x)$ be a continuous function defined on a compact set $\Omega$. Then, for $\forall \epsilon > 0$, there exists a FLS (2.8) such that

Lemma 2. (Young's inequality) For $\forall(x, y)\in R^2$, the following inequality holds:

where $\alpha > 0$, $p > 1$, $q > 1$, and $(p-1)(q-1) = 1$.

Lemma 3. For $1\leq i\leq n$, there is an unknown constant $b > 0$ that satisfies:

3.   Main results

This section introduces an adaptive fuzzy control scheme utilizing the backstepping method for system (2.3). The backstepping design scheme includes $n$ steps. First of all, the transfer error of network nodes is given as follows:

where $\alpha _{1, i}$ is the virtual control law and $y_{ref}$ is the tracking objective function.

Theorem 1. Under assumption 1, using virtual control law (3.2), adaptive law (3.3), (3.4) and control law (3.12), multi-bottleneck TCP/AQM system (2.2) exhibits the following characteristics:

(1) The queue length required for the output tracking of the system.

(2) All signals within the closed-loop system are semi-globally uniform and ultimately bounded.

(3) The tracking error of each bottleneck node converges to a small neighborhood near the origin.

Before designing the controller, it is necessary to establish the constants $\theta _{k, i} = \|\Phi _{k, i}^* \|^2, k = 1, 2, \cdots, n$, where $\hat{\theta}_{k, i}$ represents the estimation of $\theta _{k, i}$, with the estimation error denoted as $\tilde{\theta}_{k, i} = \theta _{k, i}-\hat{\theta}_{k, i}$.

Select the virtual control law and adaptive law as follows:

Step 1. Consider the following Lyapunov function:

Then, differentiating $V_{1, i}$ with respect to time results in

Let $\sum_{j = 1}^{N} a_{ij}+1 = d_i$, then (3.6) can be written as

The following nonlinear functions are approximated by FLS. According to Lemma 1, there are fuzzy logic functions $\Phi _{1, i}^T\xi _{1, i}(X)$ that satisfy

From young's inequality of Lemma 2

Therefore, (3.7) can be reformulated as

According to the (3.3), we have

It is noted that

Due to $z_{2, i} = x_{2, i}-\alpha_{1, i}\Rightarrow x_{2, i} = z_{2, i}+\alpha_{1, i}$. Substituting (3.2) into (3.8), the calculation of $V_{1, i}$ can be determined as:

Step 2. Consider the following Lyapunov function:

The computation of the derivative of $V_{2, i}$ is expressed as follows:

Define the following control laws:

where $u_i^\prime\geq 0$, $\theta_{2, i} = h_{\sigma (t), i}\eta_i m_i$ and $m_i = min\{m_{r, i}, m_{l, i}\}$.

We'll delve into the discussion of the following two cases:

Case 1:$z_{2, i} < 0$

Since $z_{2, i} < 0$, It follows from (3.12) that one has

Since $u_i > u_{r, i}$, from (2.4), one has

For the analysis of $sat(D(u_i))$, we have the following two cases:

$(1)$ $u_i\leq \frac{u_{max, i}}{m_{r, i}} +u_{r, i}$

From (2.7), it gives

According to Lemma 3 and combine (3.12) and (3.13), we have

This case is based on $z_{2, i} < 0$ discussion, one has $z_{2, i} = -|z_{2, i}|$. Then, (3.14) can be rewritten as

where $0 < \eta_i\leq\wp (D(u_i))\leq1$.

Substituting (3.15) into (3.11) yields

(2) $u_i > \frac{u_{max, i}}{m_{r, i}} +u_{r, i}$

From (2.7), it gives

According to Lemma 3 and combine (3.12), (3.17), we have

Since $0 < \eta_i < \wp (D(u_i))\le 1$, similar to (3.15), we have

Substituting (3.19) into (3.11) yields

Based on the above discussion of (1) and (2), in Case 1, when subjected to the control law defined in (3.12), (3.11) can be formulated as

Case 2:$z_{2, i}\geq0$

Since $z_{2, i}\geq0$, It follows from (3.12) that one has

Since $u_i\leq u_{r, i}$, from (2.4), one has

For the analysis of $sat(D(u_i))$, we have the following two cases:

$(1)$ $u_i\ge - \frac{u_{min, i}}{m_{l, i}} +u_{l, i}$

From (2.7), it gives

According to Lemma 3 and combine (3.12), (3.22), we have

This case is based on $z_{2, i} < 0$ discussion, one has $z_{2, i} = -|z_{2, i}|$. Then, (3.23) can be rewritten as

where $0 < \eta_i\leq\wp (D(u_i))\leq1$.

Substituting (3.24) into (3.11) yields

$(2)$ $u_i < -\frac{u_{min, i}}{m_{l, i}} +u_{l, i}$

From (2.7), it gives

According to Lemma 3 and combine (3.12), (3.26), we have

Since $0 < \eta_i < \wp (D(u_i))\le 1$, similar to (3.24), we have

Substituting (3.28) into (3.11) yields

Based on the above discussion of (1) and (2), in Case 2, when subjected to the control law defined in (3.12), (3.11) can be formulated as

Due to $\theta_{2, i} = h_{\sigma (t), i}\eta_i m_i$ and $m_i = min\{m_{r, i}, m_{l, i}\}$, the following inequalities are obtained:

Therefore, according to the discussions in Cases 1 and 2, from (3.20) and (3.29), we have

According to Lemma 1, we can approximate the unknown function $F_{2, i}(X)$ using fuzzy logic functions $\Phi _{2, i}^T\xi _{2, i}(X)$. Similarly, one easily obtains

Following a procedure akin to Step 1, we can derive the subsequent inequality:

It follows from the young's inequality that we have

Applying (3.32)–(3.34), we have

Now, $u_i^\prime$ in control law $u_i$ can be defined by

Substituting (3.9) and (3.36) into (3.35) yields

where $K_i = min\{1, -\tau_{1, i}, -\tau_{2, i}\}$, $\triangle_i = { \sum_{j = 1}^{2}}\left (\frac{1}{2}a_j^2+\frac{1}{2}\varepsilon_{j, i}^2 +\frac{\tau _{j, i}}{2r_j}\theta _{j, i}^2\right)$.

Consider the following Lyapunov function:

Substitute $V_{2, i}$, the derivative of (3.38) can be given by

where $K = { \sum_{i = 1}^{n}}K_i$, $\triangle = { \sum_{i = 1}^{n}}\triangle_i$.

Obviously, $V$ satisfies the following inequality

It is readily apparent from (3.40) that $V$ is bounded. The demonstration of Theorem 1 is now concluded.

4.   Simulation results

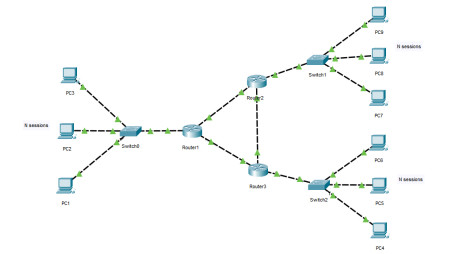
This chapter simulates the proposed AQM network congestion control algorithm and evaluates the efficiency and superiority of the controller. A multi-bottleneck network featuring three bottlenecks is examined, and its topology is illustrated in Figure 1. Matlab is used to simulate the presented method, the parameters of the TCP/AQM network system are set as follows:

The initial state of the system is $x_0 = [0.205, 1, 0.205, 1, 0.205, 1, 1, 1, 1, 1,$ $1, 1, 1]$, and the results of the simulations are depicted in Figures 2–8.

In Figure 2, the dynamic evolution of the queue length for each node is illustrated. Notably, as the target queue length is set at $180$, the queue length for each node converges to a stable state, demonstrating a rapid response and effective control. This underscores the robustness and superiority of the AQM scheme devised in this paper.

Figure 3 showcases the trajectory of the tracking error for each node. As depicted in the Figure 3, the tracking error remains stable, confined within the specified upper and lower bounds, and converges in close proximity to the origin. This observation underscores the superior transient performance of the controller devised in this paper.

In Figure 4, the packet loss probability is introduced, and it is obvious that the packet loss probability is always in $p\in[0, 1]$.

Figure 5 represents the variation of the adaptive law. After $1s$, the adaptive law tends to be stable and bounded, indicating that the controller formulated in this paper can make good use of the adaptive law for precise estimation of link capacity.

In order to verify the effectiveness of the proposed algorithm, the tracking error and queue length are compared respectively. The comparison results are shown in Figures 6–11. The comparison objects are the proposed algorithm, single bottleneck network (different topographs)^[31], EO-PID^[39], PSO-PID, and RED.

In Figures 6-8, obviously, the single-bottleneck network and the multi-bottleneck network in this paper are the most stable in the experimental results. The single-bottleneck network tends to be stable at $0.88s$, while the multi-bottleneck network in this paper tends to be stable at $1.56s$. However, it is worth noting that the queue length of the multi-bottleneck network in this paper is $2.5$ times that of the single bottleneck, so the multi-bottleneck network in this paper is more suitable for actual congestion control.

In Figures 6–8, the tracking error of the five algorithms tends to $0$ stably, but EO-PID and PSO-PID have obvious jitter, while the tracking error of RED is stable but larger than that of other algorithms. Compared with other algorithms, the tracking error of the multi-bottleneck network and the single-bottleneck network in this paper is the most stable and the smallest. Careful comparison shows that the multi-bottleneck network in this paper is superior to the single-bottleneck network. It shows that the multi-bottleneck AQM algorithm in this paper has good robustness.

5.   Conclusions

In this paper, a novel adaptive congestion control algorithm is developed specifically for multi-bottleneck TCP/AQM network system, considering both dead zone and saturated input interference for the first time. Combined with the approximation characteristics of the FLS and the backstepping technology, the algorithm regards the multi-bottleneck network as a cohesive entity. The adaptive fuzzy controller enhances the robustness of individual nodes within the multi-bottleneck network, and all the network nodes can track the required queue length according to different queue capacity. Finally, through simulation, the feasibility of the designed AQM network congestion control algorithm is verified.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This project is funded by the National Natural Science Foundation of China, No. 61932005.

Conflict of interest

The authors have declared no conflicts of interest.