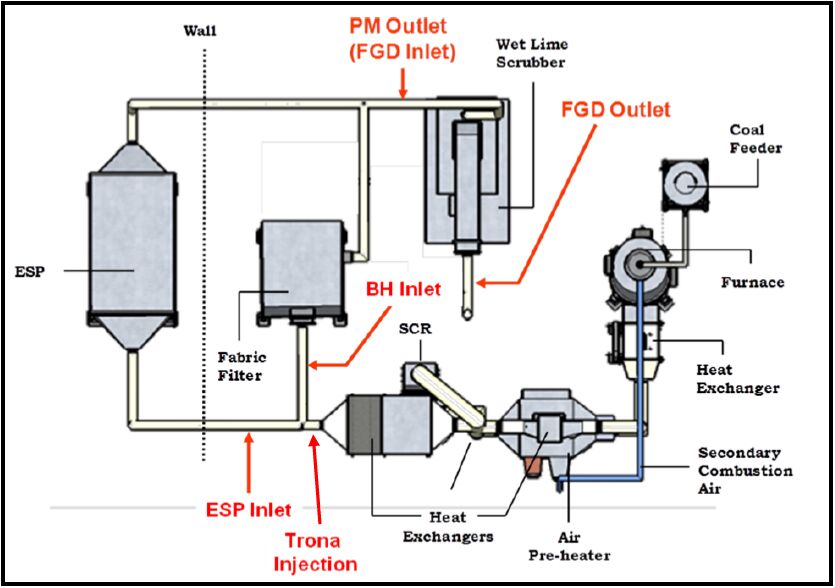
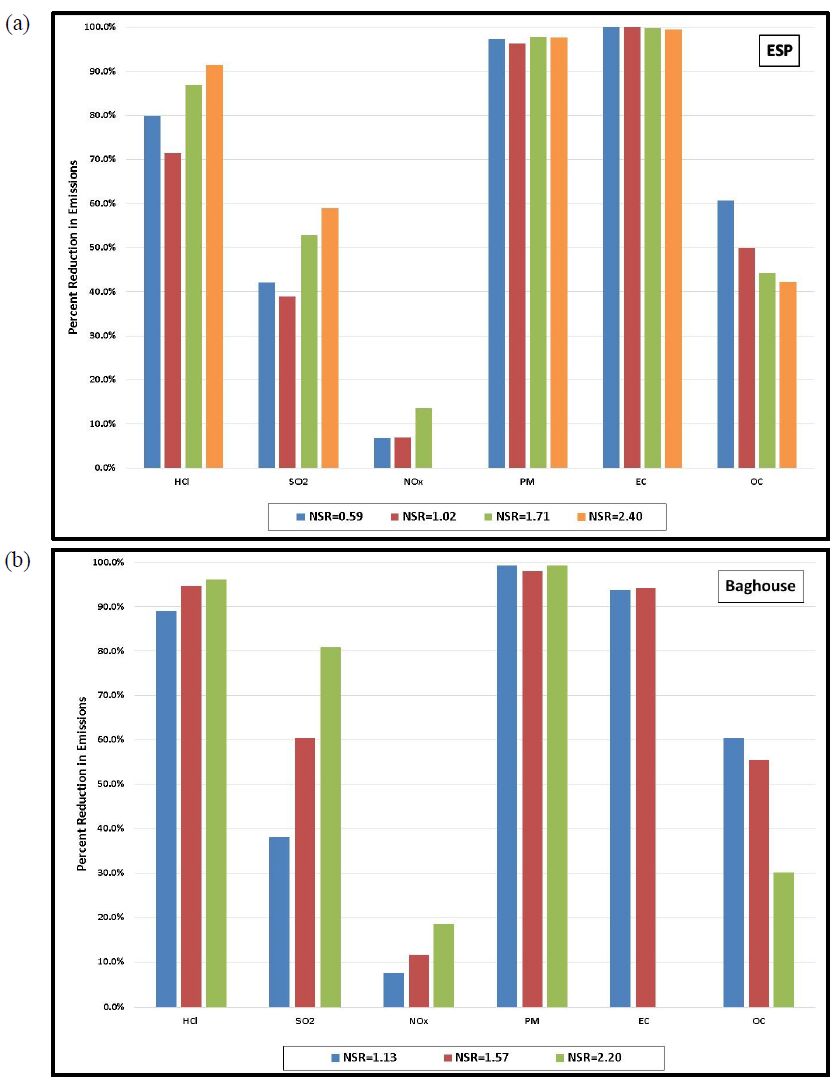
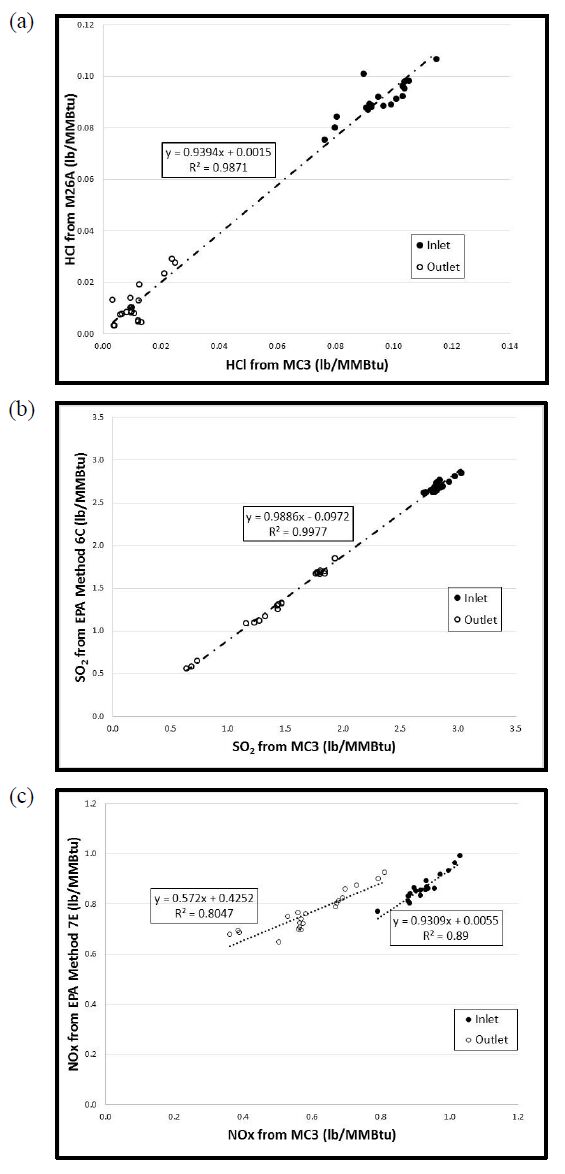
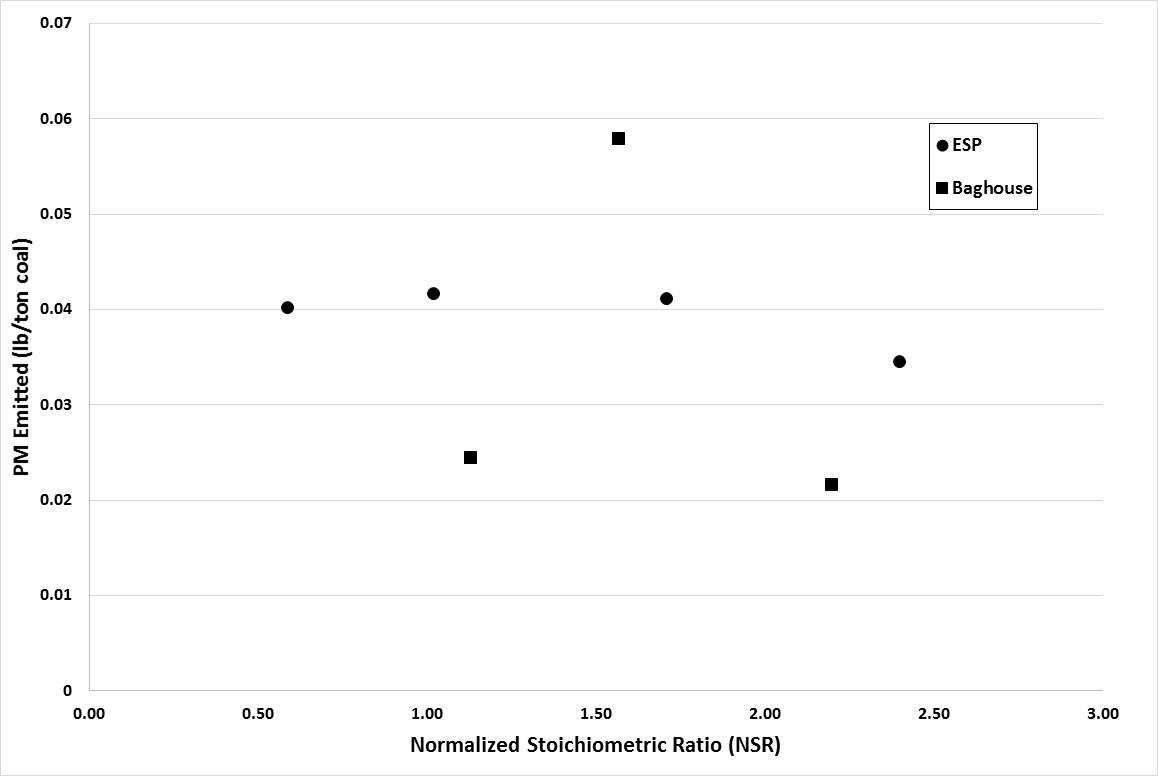
Gaseous and particulate emissions from the combustion of coal have been associated with adverse effects on human and environmental health, and have for that reason been subject to regulation by federal and state governments. Recent regulations by the United States Environmental Protection Agency have further restricted the emissions of acid gases from electricity generating facilities and other industrial facilities, and upcoming deadlines are forcing industry to consider both pre- and post-combustion controls to maintain compliance. As a result of these recent regulations, dry sorbent injection of trona to remove acid gas emissions (e.g. HCl, SO2, and NOx) from coal combustion, specifically 90% removal of HCl, was the focus of the current investigation. Along with the measurement of HCl, SO2, and NOx, measurements of particulate matter (PM), elemental (EC), and organic carbon (OC) were also accomplished on a pilot-scale coal-fired combustion facility.
Gaseous and particulate emissions from a coal-fired combustor burning bituminous coal and using dry sorbent injection were the focus of the current study. From this investigation it was shown that high levels of trona were needed to achieve the goal of 90% HCl removal, but with this increased level of trona injection the ESP and BH were still able to achieve greater than 95% fine PM control. In addition to emissions reported, measurement of acid gases by standard EPA methods were compared to those of an infrared multi-component gas analyzer. This comparison revealed good correlation for emissions of HCl and SO2, but poor correlation in the measurement of NOx emissions.
1.
Introduction
In the last few years, the uncertainties general consist in the nonlinear systems, the most important is that it is also widely applied in constraint. By taking adaptive control [1], the parametric uncertainty of nonlinear system is presented in [2]. In the actual systems, out of the realistic need as well as the difficulty of operations, the unknown continuous functions are approximated, which is based on fuzzy logic systems (FLSs) or neural networks (NNs) in [3,4,5,6,7]. On the basis of NNs or FLSs, adaptive control algorithm comes up for nonlinear single-input single-output (SISO) systems [8]. As same as for MIMO nonlinear systems [9] with unknown functions and discrete-time systems, the above method also applies. Besides, a multilayer NNs estimator was first developed in [10] to improve the compensation accuracy of model-based feedforward control terms. However, the aforementioned results do not refer to constraint.
As one of the most important factors restricting the system performance, constraints extensive exist in actual systems, such as robotic manipulator system, nonuniform gantry crane and so on. Constraint cannot be omitted, otherwise it may have an impact on the equipment and something unexpected, thus, constraint control has become a significant portion of nonlinear control. As we all know, the Barrier Lyapunov function (BLF) is the significant tool to dispose constrained problem. So far it widespread application in nonlinear systems with output constraint in [11] and full state constraints in [12,13], and its effectiveness is also verified. The NNs or FLSs is used to design adaptive controllers for nonlinear systems using neural networks with constant constraint in [5]. Nevertheless, none of the above methods mention time-varying constraints in [14]. In this article, the time-varying with full state constraints are further studied. Adaptive controllers are designed for time-varying output constraints and time-varying full-state constraints [15], respectively. However, the above backstepping recursion method ignore the feasibility conditions of virtual controllers, namely, the virtual controller is within the given constraint bounded. In [16], a new coordinate transformation is introduced to completely remove this limitation.
The constraints of the above research are all direct constraints on the states, whether full state constraints or other types of constraints. Subsequent some studies are not limited to state constraints. At present, the state transfer function is introduced for coordinate transformation in [17] indirect processing constraint such as constrain the error. Compared with the above-mentioned research methods, the advantage of this approach is not only independent of initial tracking condition, but also suitable for asymmetric time-varying constraints, which is studied in [15]. However, in any of these cases, the effect of dead-zone on constraint is omitted.
Mention nonlinear input, the most common are dead-zones, saturation, time-delay, and so on. An innovative approach is to propose a dead-zone compensation in motion control systems using adaptive fuzzy logic control. In this paper, the dead-zone nonlinear input is our focus. The existing dead-zones prevent us from getting the desired control results, and the problem caused by it is serious. For instance, if the robot servo system has nonlinear links such as friction and unknown dead zone, it not only reduces the efficiency of the control system, but also lead to the instability of the system. In recent years, the study of dead-zone has become the focus of control research. In [18], for discrete-time plants with unknown dead-zone, a new control structure with adaptive dead region inverse is put forward. To this purpose, some adaptive control method is proposed, such as neural network control and adaptive fuzzy sliding mode control. Adaptive tracking of asymmetric dead-zone input nonlinear systems with uncertain parameters is proposed. As is well-known, for dead-zone in multi-input multi-output nonlinear system, which has lower triangular structure and asymmetric structure, a new control method is proposed. To eliminate dead-zone effects, the dead-zones compensation control is implemented for precision instrument control.
In this paper, the adaptive neural network control method is proposed, it is the realization of the control target. The design of the controller is beneficial. After comprehension of above achievements, the control scheme has the following advantages.
1) Compared with previous adaptive neural network control methods, this article takes into account more complex case. The effects of delay constraints and dead-zones on system performance are considered, which is more practical in line with the needs of the actual system.
2) State transition function is introduced; the appropriate time node is selected to ensure that the states are in the constraint bounds. Namely, the initial state is out of bounds, and then in the bounds. There is no mention of delay constraints in [16], the problem of delay constraints is considered in this paper. It provides convenience for error tracking that not widely involved in the previous research for nonlinear adaptive control.
3) In this paper, based on the introduction of BLF, potential dead-zones in the system is resolved, which affects the stability of the system and increases steady state error. Manipulative know $ m$ and unknown $ d$, the difficult problem of controller design is solved.
2.
Problem formulation and preliminaries
Consider a class of nonlinear strict-feedback systems with dead-zones as following:
where $ x = {[{x_1}, \ldots, {x_n}]^T} \in R$ with $ {\bar x_i} = {[{x_1}, \ldots, {x_j}]^T}$ $ j = 1, \ldots, n$, $ {x_i} \in R, $ $ D\left({u\left(t \right)} \right) \in R$ and $ y \in R$ are the state variables, the input and the output of the systems, respectively, $ {g_i}\left({{{\bar x}_i}} \right)$ are unknown control coefficients and $ {f_i}\left({{{\bar x}_i}} \right)$ are unknown smooth functions. $ {x_i} \in \left({ - {{\underline k _{ci}}}\left(t \right), {{\bar k}_{ci}}\left(t \right)} \right)$, $ {x_i}$ is unconstrained when $ t \in \left[{0, T} \right]$. Nevertheless, when $ t \in [T, \infty)$, $ {x_i}$ are within the given bound. So as to ensure the validity of the constraint, the value of $ T$ is crucial. Let $ - {\underline k _{ci}}\left(t \right) < {x_i}\left(t \right) < {\bar k_{ci}}\left(t \right)$, where $ {\underline k _{ci}}\left(t \right)$ and $ {\bar k_{ci}}\left(t \right)$ are given.
Remark 1: There are many factors that affect system performance, but one of the most significant is constraint. In order to ensure that constraint is not violated in the control process, the work that needs attention in the adaptive control strategy is proposed in [19,20,21,22,23,24,25,26,27,28,29,30]. In this paper, to make sure constraints are not violated, the transfer function is introduced for coordinate transformation. Constraints appear some time later, the system stability is improved.
The delay constraint means that the constraint occurs over a period of time, which does not have to constrain the signal all the time. By designing the appropriate controller, the signal satisfies the constraint condition after a certain time.
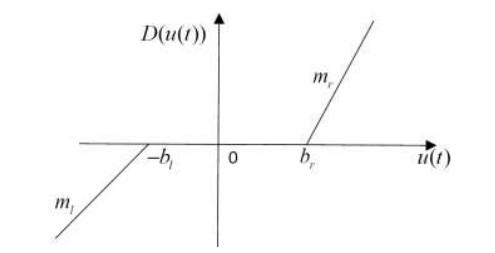
All of state variables in the system (2.1) are constrained in the compact set. $ D\left({u\left(t \right)} \right)$ is a dead-zone defined as:
where $ u\left(t \right)$ is the dead-zone input, $ {m_r}$ and $ {m_l}$ respectively stand for dead-zone right slope and left slope, $ {b_r}$ and $ {b_l}$ represent the right and left cut point of the input nonlinearity. The detailed structure diagram of dead zone is given in Figure 1.
The aforementioned model can be transformed into the following form:
where
and
Assumption 1. The function $ m\left(t \right)$ is known, $ b\left(t \right)$ is unknown and its up bound is $ \bar b\left(t \right)$, namely, $ \left| {b\left(t \right)} \right| \leqslant \bar b\left(t \right)$.
3.
Control objective
The task is to design an adaptive controller $ u$, such that the system output $ y$ tracks a desired trajectory $ {y_d}\left(t \right)$. All the signals in the closed-loop system are bounded, meanwhile the full state constraints are not violated. It holds that $ - {\underline y _{d}}\left(t \right) \leqslant {y_d}\left(t \right) \leqslant {\bar y_d}\left(t \right)$, where $ {\underline y _{d}}\left(t \right)$ and $ {\bar y_d}\left(t \right)$ are continuous positive functions, with $ {\underline k_{c1}}\left(t \right) \geqslant {\underline y _{d}}\left(t \right)$ and $ {\bar k_{c1}}\left(t \right) > {\bar y_d}\left(t \right)$.
In this paper, on account of radial basis function neural networks (RBFNNs) approximate ability, it is chosen to approximate unknown and continuous function.
Consider a continuous function $ h\left(z \right)$: $ {R^q} \to R$, the following form can be obtained:
where the input variable $ z \in {\Omega _z} \subset {R^q}$, desired weight matrix $ {\theta ^*} = {[{\theta _1}, {\theta _2}, \ldots {\theta _l}]^T} \in {R^l}$, $ l > 1$ is the NN node number. In addition, $ S\left(z \right) = {\left[{{s_1}\left(z \right), \ldots, {s_l}\left(z \right)} \right]^T}$, it is often expressed by Gaussian function, which has the following form:
where $ {\mu _i} = \left[{{\mu _{i1}}, {\mu _{i2}}, \ldots, {\mu _{iq}}} \right]$ is the center of NNs and $ {\eta _i}$ is the width of the Gaussian function.
According to the character of NNs, with regard to any continuous unknown function, it can be represented as
where $ \varepsilon \left(z \right)$ is alluded to as the least approximate error and $ \left| {\varepsilon \left(z \right)} \right| \leqslant \varepsilon $ with $ \varepsilon > 0$ for any $ z \in {\Omega _z}$. The weight matrix $ {\theta ^*}$ has the following representation
Assumption 2. The function $ {g_i}\left({{{\bar x}_i}} \right)$ is unknown, time-varying, and bounded away from zero, respectively. Its upper bound and lower bound are $ {\bar g_i}$ and $ {\underline g _i}$, They are also unknown continuous function, such that $ 0 < {\underline g _i} \leqslant \left| {{g_i}\left({{{\bar x}_i}} \right)} \right| \leqslant {\bar g_i}$, $ \forall {\bar x_i} \in \Omega \subset {R^n}$.
A new asymmetric Barrier Lyapunov function is introduced
where $ {F_1}\left(t \right)$ and $ {F_2}\left(t \right)$ are positive functions, $ \zeta \left(t \right)$ will be defined later. Note that $ V$ is valid in the interval $ - {F_1}\left(t \right) < \zeta \left(t \right) < {F_2}\left(t \right)$.
Then, the transfer function is introduced to better constrain the states. The function is defined as
where
The effect of (3.4) is to solve the problem of uncertain initial conditions. In the meantime, $ \tau (t)$ is a continuous and differentiable function.
Remark 2: The $ T$ is a time node. There exist two crucial features for $ \tau (t)$, $ \tau (0) = 0$ and $ \tau (t) = 1$ for $ t \geqslant T$. These two properties have important applications in the conversion of initial values, that is to transform a non-zero initial value into a zero initial value. In the end, their values will converge to a finite bounded.
4.
Adaptive neural controller design and stability analysis
In the following study, adaptive control method and backstepping recursive are used to design virtual controllers $ {\alpha _i}$, actual controller $ u$ and adaptive laws $ {\hat w_i}$. Adaptive control process has a total of $ n$ steps, the coordinate transformation is introduced as
In the step $ 1$, virtual controller $ {\alpha _1}$ and adaptive law $ {\hat w_1}$ are defined as follows:
where $ {k_1}$ is a positive constant, $ {\delta _1} > 0$ is a constant, $ {\lambda _1} > 0$ is a constant, $ {\hat w_1}$ stands for adaptive parameter. In addition, $ {\psi _1}$, $ {P_1}$, and $ {G_1}$ will be defined later.
In the step $ i\left({2 \leqslant i \leqslant n - 1} \right)$, virtual controller $ {\alpha _i}$ and adaptive law $ {\hat w_i}$ are defined as follows:
where $ {k_i}$ is a positive constant, $ {\delta _i} > 0$ is a constant, $ {\lambda _i} > 0$ is a constant, $ {\hat w_i}$ stands for adaptive parameter. In addition, $ {\psi _i}$, $ {P_i}$, and $ {G_i}$ will be defined later.
In the last step, actual controller $ u$ and adaptive law for $ {\hat w_n}$ are defined as follows:
where $ {k_n}$ is a positive constant, $ {\delta _n} > 0$ is a constant, $ {\lambda _n} > 0$ is a constant, $ {\hat w_n}$ stands for adaptive parameter. In addition, $ {\psi _n}$, $ {P_n}$, and $ {G_n}$ will be defined later.
Let us consider tracking error $ {z_1} = {x_1} - {y_d}$. From the first Eq (2.1), we get the derivation of $ {z_1}$
From (3.4), we obtain
Remark 3: We just think about $ 0 < t < T$, so let $ {\zeta _i}\left(t \right) = \tau \left(t \right){z_i}\left(t \right)$. States are constrained indirectly through constraints on transition functions, this will be discussed below.
From $ {z_i} = {x_i} - {\alpha _{i - 1}}\left({i = 1, ..., n} \right)$, then we get
where
with
From (3.4), we obtain the following dynamics
Substituting (2.3) into $ {z_n} = {x_n} - {\alpha _{n - 1}}$, one deduces that
where
with
then, we obtain the following dynamics
Please see the appendix for the specific derivation process
Theorem 1: Consider a class of nonlinear system (2.1) with a dead-zone (2.2) under Assumptions 1–2, virtual controllers are designed in (4.2) and (4.4), and the actual controller is designed in (4.6). Meanwhile the adaption laws are constructed in (4.3), (4.5) and (4.7). If the design parameters are chosen appropriately, it ensures that all signals in the closed-loop system are UUB and bounded. The system output $ y$ tracks a desired trajectory $ {y_d}\left(t \right)$.
Proof. It is obvious that $\tilde{w}_{j} \hat{w}_{j} = \tilde{w}_{j}\left(w_{j}-\tilde{w}_{j}\right) \leq-\frac{\tilde{w}_{j}^{2}}{2}+\frac{w_{j}^{2}}{2}$ we can derive that
Then, we get
Hence, we have the following inequality:
where $ \rho = \min \left. {\left\{ {{k_j}{\underline g _j}} \right., {\delta _j}} \right\} > 0$, $ c = \sum\limits_{j = 1}^n {\frac{{{\underline g _j}{\delta _j}}}{{2{\lambda _j}}}} w_j^2 + \sum\limits_{j = 1}^n {{\Xi _j}} $
Besides, from (4.16), we get
Hence, we obtain that $ {V_n}\left(t \right) \in {l_\infty }$, it implies that $ {\hat w_1} \in {l_\infty }$ and $ {V_{i0}}\left(t \right) \in {l_\infty }$. The upper of $ {\zeta _i}\left(t \right)$ is $ - {F_{i1}}\left(t \right)$ and lower is $ {F_{i2}}\left(t \right)$, so $ - {F_{i1}}\left(t \right) < {\zeta _i}\left(t \right) < {F_{i2}}\left(t \right)$. Based on the shifting function $ \tau \left(t \right)$, when $ t \in [0, T)$, $ \tau \left(t \right)$ is strictly increasing. And $ \tau \left(0 \right) = 0$, when and only when $ t = 0$, then, $ {\zeta _i}\left(0 \right) = \tau \left(0 \right){z_i}\left(0 \right) = 0$. We get $ - {F_{i1}}\left(0 \right) < {\zeta _i}\left(0 \right) < {F_{i2}}\left(0 \right)$. When $ 0 < t < T$, $ \tau \left(t \right)$ is not zero. From (4.8), $z_{i}(t) = \zeta_{i}(t) / \tau(t)$, $ {z_i}\left(t \right)$ is bounded because $ {\zeta _i}\left(t \right)$ is bounded. When $ t \geqslant T$, $ \tau \left(t \right) = 1$, then we can get $ {z_i}\left(t \right) = {\zeta _i}\left(t \right)$, so $ - {F_{i1}}\left(t \right) < {z_i}\left(t \right) < {F_{i2}}\left(t \right)$. In conclusion, $ {z_i}\left(t \right)$ is bounded anyway. According to the definition of $ {F_{11}}$ and $ {F_{12}}$, thus $ {F_{11}}$, $ {F_{12}}$, $ {\dot F_{11}}$ and $ {\dot F_{12}}$ are bounded. From $ {z_1} = {x_1} - {y_d}$, $ {z_1}$ is bounded and $ {x_1}$ is also bounded. Because $ {F_{11}}$, $ {F_{12}}$, $ {\dot F_{11}}$, $ {\dot F_{12}}$, $ {\hat w_1}$, $ {y_d}$, $ {\dot y_d}$, $ \tau $ and $ \dot \tau $ are bounded, it follows that virtual controller $ {\alpha _1}$ and adaptive law $ {\dot {\hat w}_1}$ are bounded. Then follow the definition of $ {F_{21}}$ and $ {F_{22}}$, thus $ {F_{21}}$, $ {F_{22}}$, $ {\dot F_{21}}$ and $ {\dot F_{22}}$ are bounded. From $ {z_2} = {x_2} - {\alpha _1}$, $ {z_2}$ is bounded and $ {x_2}$ is also bounded. In the similar way, $ {\alpha _2}$ and $ {\dot {\hat w}_2}$ can also be bounded. Continue this derivation, we can obtain that $ {x_i}\left({i = 3, \cdots, n} \right)$, $ {\alpha _i}\left({i = 3, \cdots, n - 1} \right)$, $ {\dot {\hat w}_i}\left({i = 3, \cdots, n} \right)$ and control input $ u$ are bounded. In a word, all signals in closed-loop systems are bounded. The proof is completed.
5.
Simulation example
In this paper, to prove the effectiveness of this method, the simulation experiment is given. Consider the following nonlinear systems
where $ y$ and $ u$ are the outputs and inputs of the system. Meanwhile, $ D\left({u\left(t \right)} \right)$ is the output of the dead zone, described as
and the states $ {x_1}$ and $ {x_2}$ are constrained by $ {\bar k_{c1}}\left(t \right) < {x_1}\left(t \right) < - {\underline k_{c1}}\left(t \right)$ and $ {\bar k_{c2}}\left(t \right) < {x_2}\left(t \right) < - {\underline k_{c2}}\left(t \right)$ with $ {\bar k_{c1}}\left(t \right) = 0.07 + 0.01\sin (2t)$, $ {\underline k_{c1}}\left(t \right) = {\rm{0}}{\rm{.11 + 0}}{\rm{.05sin(4}}t{\rm{)}}$, $ {\bar k_{c2}}\left(t \right) = {\rm{0}}{\rm{.3sin(3}}t{\rm{) + 0}}{\rm{.6}}$, $ {\underline k_{c2}}\left(t \right) = {\rm{0}}{\rm{.4sin(2}}t{\rm{) + 0}}{\rm{.72}}$. The ideal trajectory $ {y_d}$ is chosen as $ {{\rm{y}}_d}{\rm{ = 0}}{\rm{.05cos(6}}t{\rm{)}}$. The initial states are chosen as $ {x_1}\left(0 \right) = 0.16$, $ {x_2}\left(0 \right) = 0.001$, $ {\hat w_1}\left(0 \right) = 0.6$, $ {\hat w_2}(0) = 0.279$. The controllers and adaptive laws of simulation system are chosen as follow:
In the simulation, the first NN includes 10 nodes with the center $ {\mu _1}$ evenly spaced on $ \left[{- 1, 1} \right] \times \left[{- 1, 1} \right] \times \left[{- 1, 1} \right]$ with width $ {\eta _1} = 1$, the second NN includes 16 nodes with the center $ {\mu _2}$ evenly spaced on $ \left[{- 3, 3} \right] \times \left[{- 3, 3} \right] \times \left[{- 3, 3} \right] \times \left[{- 3, 3} \right] \times \left[{- 3, 3} \right]$ with width $ {\eta _2} = 1$. The parameters in the simulation system are given as $ m = 1kg$, $ g = 9.8m/{s^2}$, $ l = 1m$, $ M = 0.5kg.{m^2}$, $ B = 1N.m.s$. The control parameters are selected as $ {k_1} = 29$, $ {k_2} = 44$, $ {\lambda _1} = 0.01$, $ {\lambda _2} = 0.01$, $ {\delta _1} = 0.1$, $ {\delta _2} = 0.5$. Delay constraint time $ T = 1$, $ {x_1}$ and $ {x_2}$ are out of bounds, when $ t \in \left({0, 1} \right)$ and while $ T \geqslant 1$, $ {x_1}$ and $ {x_2}$ are expected completely within the bounds. The selection of the delay constraint time is based on the minimum tracking error and the best tracking performance. Besides, according to the desired trajectory, we obtain that $ {F_{11}} = {\rm{0}}{\rm{.01sin(2}}t{\rm{)}} - {\rm{1}}{\rm{.93}}$ and $ {F_{12}} = {\rm{0}}{\rm{.05sin(4}}t{\rm{)}} - 1.89$, $ {F_{21}}{\rm{ = 0}}{\rm{.222 + 0}}{\rm{.1sin(5}}t{\rm{)}}$ and $ {F_{22}}{\rm{ = 0}}{\rm{.25 + 0}}{\rm{.05sin(10}}t{\rm{)}}$.
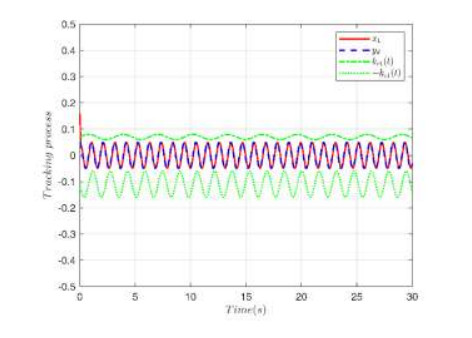
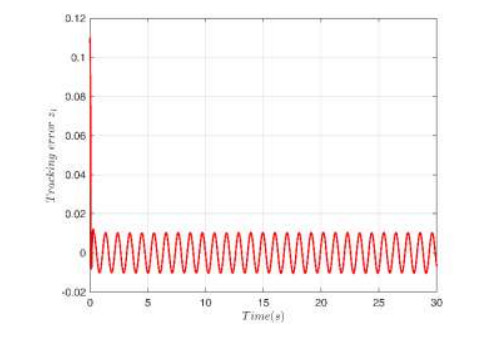
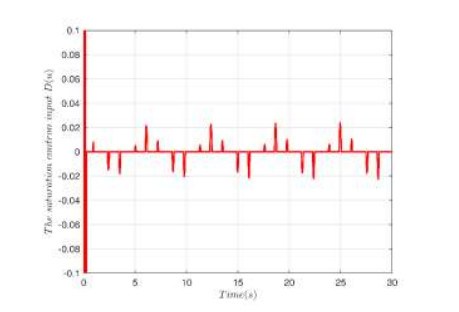
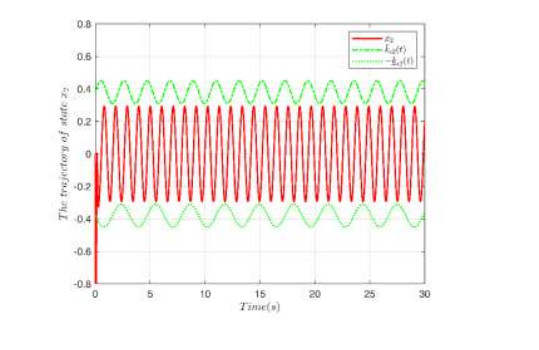
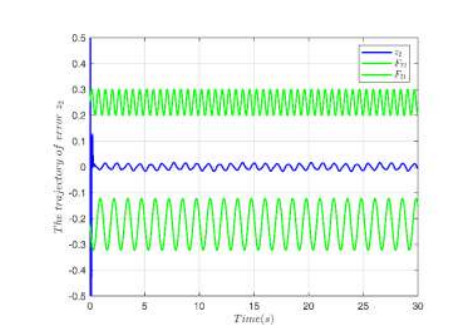
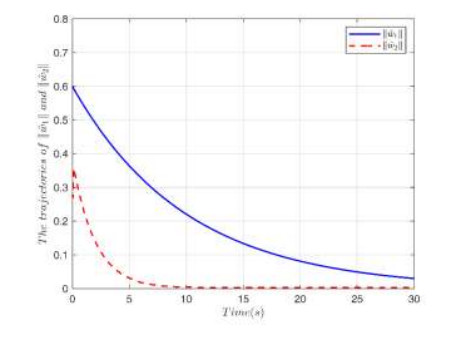
The simulation results are given in Figures 2–7. Figure 2 shows the trajectory $ {y_d}$, output $ y$ and constrained intervals with a good tracking performance. Figure 3 shows the trajectory of error $ {z_1}$. The trajectory of the dead-zone $ D\left(u \right)$ is given in Figure 4. The trajectory of state $ {x_2}$ is displayed in Figure 5. The trajectory of error $ {z_2}$ and adaptive laws are shown in Figure 6 and Figure 7, respectively. Simulation results prove that all signals are bounded.
6.
Conclusions
An adaptive neural network tracking control method is introduced for the strict feedback nonlinear systems with unknown dead-zones and full state constraints. The parameters of the dead-zones are unknown but bounded. Combining backsteping technique with neural network, it ensures that the state constraints are not violated. The feasibility of the control algorithm is proved. In the meantime, all signals in the closed-loop system are UUB. In this paper, delay constraint and BLF are combined. In other words, the constraint occurs after a period of time, it is not constrained from the beginning. Furthermore, the tracking error converges to a small area away from zero. In the end, simulation results verify the effectiveness of the design. We will further investigate the control performance by setting different delay times such as time-varying delay, which will enrich the applied range of the proposed control method. Besides, since the reliability is an interested topic and has been well discussed in [23,24,25,26,27], it will be taken into account in our future work.
7.
Appendix
$ Step$ $ 1$: In order to achieve the desired control objective, the following Barrier Lyapunov function is chosen
where $ {F_{11}}\left(t \right)$ and $ {F_{12}}\left(t \right)$ are time varying continuous functions. Its definition will be given later. For $ {\zeta _1}\left(t \right)$, its scope is $ {F_{11}}\left(t \right) < {\zeta _1}\left(t \right) < {F_{12}}\left(t \right)$. The time-varying functions $ {F_{11}}\left(t \right)$ and $ {F_{12}}\left(t \right)$ are chosen such that
where $ n$ is a positive constant.
Consider the Barrier Lyapunov function as
where $ {\lambda _1} > 0$ is a constant, $ {w_1} = {\max _{k \in K}}\left\{ {\left. {{{\left\| {\theta _{K1}^*} \right\|}^2}} \right\}} \right.$, $ {\tilde w_1} = {w_1} - {\hat w_1}$ stands for the estimation error, with $ {\hat w_1}$ being the estimation of $ {w_1}$. Based on (3.4), we get the time derivative of $ {V_1}$
where
and
In this way, the design of controller and adaptive law are simplified.
Combining the Assumption 2, on the basis of Young’s inequality, we get
Substituting (7.3), (7.4) and (7.5) into (7.2) leads to
Let
The unknown continuous function $ {h_1}({z_1})$ can be approximated by an RBF NN as
Substituting (7.7) and (7.8) into (7.6) and using Young’s inequality, one gets
Then, we obtain
with
From Assumption 2, we get
then
$ Step$ $ i$ $ \left({i = 2, ..., n - 1} \right)$: The following Barrier Lyapunov function is chosen as
Consider the BLF as
where $ {\lambda _i} > 0$ is a constant, $ {w_i} = {\max _{k \in K}}\left\{ {\left. {{{\left\| {\theta _{Ki}^*} \right\|}^2}} \right\}} \right.$, $ {\tilde w_i} = {w_i} - {\hat w_i}$ stands for the estimation error, with $ {\hat w_i}$ being the estimating of $ {w_i}$, Based on (3.4), we get the time derivative of $ {V_i}$
where
and
According to the Young’s inequality, it yields
The unknown continuous function $ {h_i}({z_i})$ can be approximated by an RBF NN as
Substituting (7.18) and (7.19) into (7.14) and using Young’s inequality, one gets
Then, we obtain
with
Let
Then, we get
$ Step$ $ n$: Because $ {\dot V_n}$ is similar to $ {\dot V_i}$, we can figure out the following formula
Since $ b$ is bounded, one obtains $ b/m \leqslant \bar b/m \triangleq \eta $ where $ \eta $ is a constant. Using Young’s inequality get the following formula:
According to the Young’s inequality, it causes
Denote
The unknown continuous function $ {h_n}({z_n})$ can be approximated by an RBF NN as
Substituting (7.28) and (7.29) into Error! Reference source not found., and using the Young’s inequality, it yields
Then, using the above inequalities we get
where
with
Then, we get
Conflict of interest
All authors declare no conflicts of interest.









 DownLoad:
DownLoad: