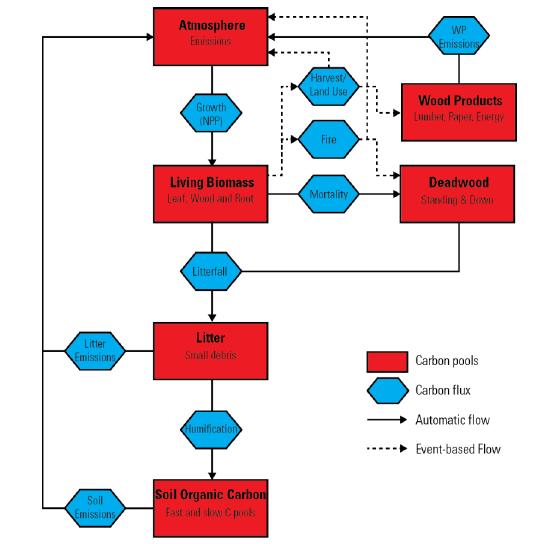
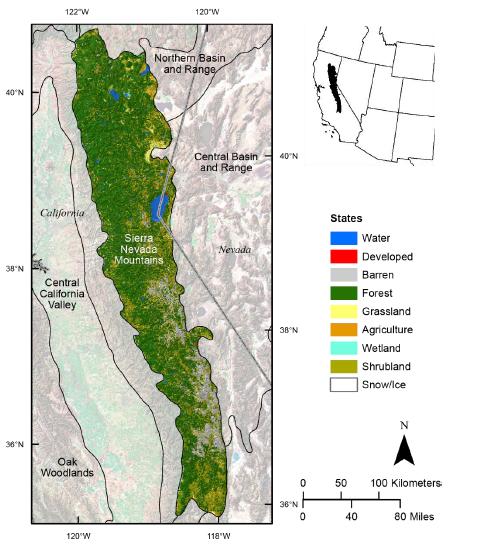
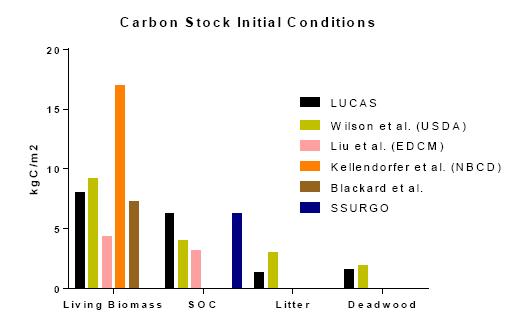
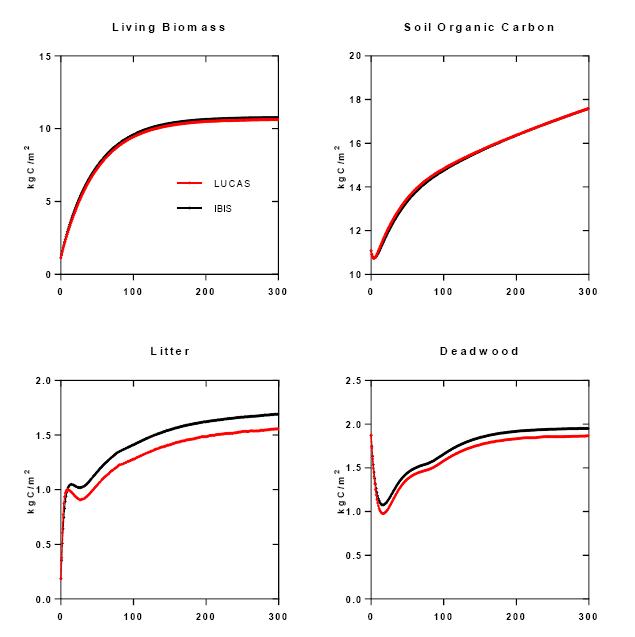
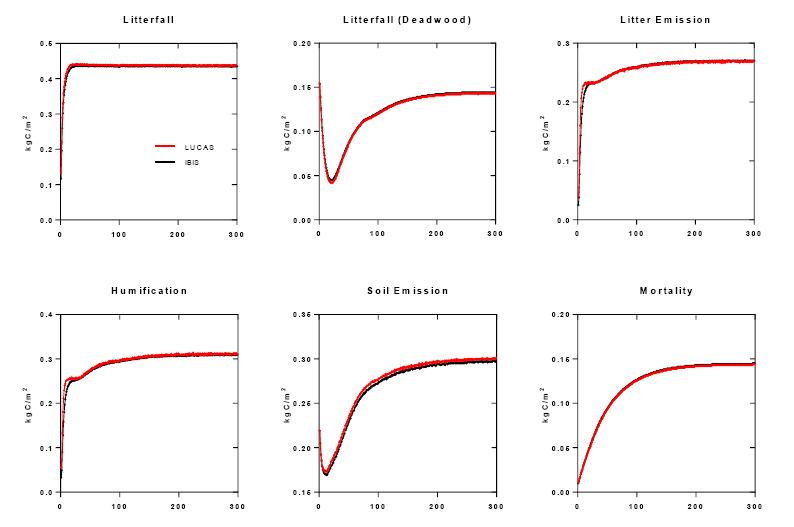
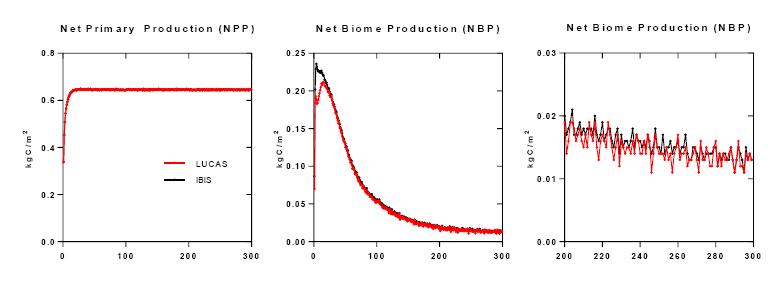
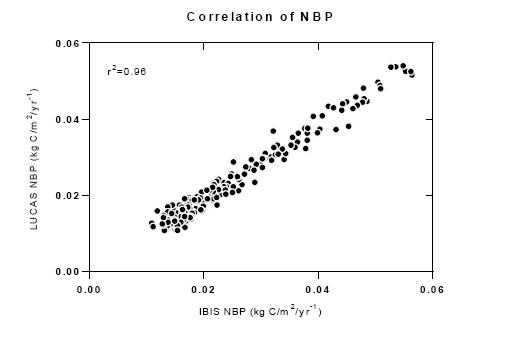
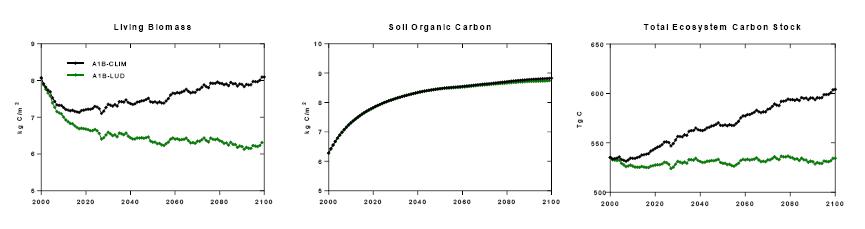
Increased land-use intensity (e.g. clearing of forests for cultivation, urbanization), often results in the loss of ecosystem carbon storage, while changes in productivity resulting from climate change may either help offset or exacerbate losses. However, there are large uncertainties in how land and climate systems will evolve and interact to shape future ecosystem carbon dynamics. To address this we developed the Land Use and Carbon Scenario Simulator (LUCAS) to track changes in land use, land cover, land management, and disturbance, and their impact on ecosystem carbon storage and flux within a scenario-based framework. We have combined a state-and-transition simulation model (STSM) of land change with a stock and flow model of carbon dynamics. Land-change projections downscaled from the Intergovernmental Panel on Climate Change’s (IPCC) Special Report on Emission Scenarios (SRES) were used to drive changes within the STSM, while the Integrated Biosphere Simulator (IBIS) ecosystem model was used to derive input parameters for the carbon stock and flow model. The model was applied to the Sierra Nevada Mountains ecoregion in California, USA, a region prone to large wildfires and a forestry sector projected to intensify over the next century. Three scenario simulations were conducted, including a calibration scenario, a climate-change scenario, and an integrated climate- and land-change scenario. Based on results from the calibration scenario, the LUCAS age-structured carbon accounting model was able to accurately reproduce results obtained from the process-based biogeochemical model. Under the climate-only scenario, the ecoregion was projected to be a reliable net sink of carbon, however, when land use and disturbance were introduced, the ecoregion switched to become a net source. This research demonstrates how an integrated approach to carbon accounting can be used to evaluate various drivers of ecosystem carbon change in a robust, yet transparent modeling environment.
1.
Introduction
In natural ecology, each species exhibits unique habits and complex biological relationships with other species. These interactions form a biological system, a key focus area in ecology. Among these, predator-prey dynamics are considered foundational to understanding biological systems. The basic predator-prey model was first proposed by Lotka and Volterra [1], laying the groundwork for subsequent studies. Numerous scholars have since expanded on this model [2,3,4,5], exploring interactions such as intra-species competition [6], cooperation [7], and stage structure [8,9,10,11,12,13]. Among them, Hu et al. [8], Meng and Qin [10], and Wu et al. [13] considered dynamical behaviors such as stability, boundedness, and bifurcation of predator-prey systems with stage structure in the absence of spatial diffusion. However, Xu and Liu [9], Xu et al. [11], and Mi et al. [12] investigated spatial dynamical behaviors such as global existence of predator-prey models with stage structure with spatial diffusion.
In the classical predator-prey model, it is assumed that all individuals of a species possess identical predation abilities. However, this assumption often fails to reflect real-world dynamics, as species exhibit variation due to historical and ecological differences. For instance, juvenile individuals often depend on their parents for survival as they lack independent predation skills. To address such realities, many researchers divide species into immature and mature stages when studying the dynamical behavior of stage-structured predator-prey models [14,15,16,17,18]. In 1990, Aiello and Freedman [14] introduced a delayed single-population model with stage structure, assuming that the average age of maturity was represented by a constant time delay. The model is expressed as follows:
where $ x_1(t) $ and $ x_2(t) $ are the densities of immature and mature population at time $ t $, respectively; $ a $ and $ \gamma $ are the birth rate and the death rate of the immature population, respectively; $ \beta $ is the intra-species competition rate of the mature population; $ \tau $ is the maturity time delay, and $ \alpha e^{-\gamma\tau}x_2(t-\tau) $ represents the quantity which the immature population born at time $ t-\tau $ can survive at time $ t $. Xu [15] and Song et al. [16] mainly studied the stability and Hopf bifurcation of a predator-prey model with stage structure and time delay. Li et al. [17] considered a stage-structured predator-prey model with Crowley-Martin functional response and analyzed the impaction of predator maturity delay and predator interference on the dynamics of the system. Certainly, Zhu et al. [18] developed a reaction-diffusion predator-prey model incorporating the Allee effect based on network and non-network environments, which represents a relatively novel research approach in the field. Based on model (1.1), many scholars have studied predator-prey models with stage structure by considering multiple populations [19,20,21].
Additionally, certain biological behaviors of predator and prey populations cannot be immediately captured in ecological models due to the presence of time delays. Compared with ordinary differential equations, delay differential equations can better reflect the complex dynamical behavior of the system. Due to the fact that the time delay makes the model more realistic and reliable, then the delayed predator-prey systems with stage structure have been studied [22,23,24,25,26]. For instance, Xu and Ma [22] investigated a predator-prey system incorporating stage structure for the predator and a time delay. Their study examined the existence of Hopf bifurcation and the global stability of the positive equilibrium. Similarly, Maiti and Dubey [27] introduced a delayed predator-prey system with a Crowley-Martin functional response and stage structure for the prey, which can be described as follows:
where $ y(t) $ is the density of the predator population at time $ t $; $ r $ is the conversion rate from immature prey to mature prey; $ d, d_1 $, and $ d_2 $ are the death rate of the immature prey, mature prey, and predator, respectively; $ \alpha $ and $ \gamma $ are the intra-specific competition rate of mature prey and predator, respectively; $ \beta $ and $ \beta_1 $ are the conversion rate from mature prey to predator and the intake rate of the predator, respectively. The term $ \frac{\beta x_2y}{(1+ax_2)(1+by)} $ is named the Crowley-Martin type functional response, which takes into account the interference between predators and preys. $ \tau $ is the time delay due to the gestation of the predator. The biological significance of other parameters remain consistent with system (1.1).
In biology, refuges provide shelter for prey that are vulnerable to predation or environmental pressures, reducing the risk of prey population extinction. For example, some small fish can avoid predation by hiding within coral reefs. Additionally, refuges can decrease direct interactions between predators and prey, potentially delaying or mitigating severe fluctuations in predator-prey systems, thereby maintaining the dynamic balance of biological systems. Thus, refuges play a important role in promoting the coexistence of predator and prey populations. Recently, many scholars have studied some predator-prey models including prey refuges [28,29,30,31,32]. For example, Fu and Wei [28] studied the effect of prey refuge on the stability of a predator-prey model with stage structure, they analyzed the global asymptotic stability of the positive equilibrium according to the comparison principle and the iterative principle. Song et al. [32] proposed a discrete one-predator two-prey system with Michaelis-Menten-type prey harvesting and prey refuge, and their findings demonstrated that both harvesting and refuge contribute to the stabilization of the system, with the stabilizing effect of harvesting outweighing that of refuge.
Actually, cooperation among populations plays a crucial role in population growth dynamics [7,33,34]. On one hand, it not only enhances the overall survival ability of the population, but also enables more efficient resource utilization. On the other hand, cooperation helps populations better adapt to environmental changes and natural disasters, while interspecies cooperation (such as mutualistic symbiosis) also has a key impact on the balance of ecosystems. Kundu and Maitra [33] analyzed the impact of prey cooperation on a delayed predator-prey system, concluding that cooperative interactions among prey positively influence the system and significantly enhance its stability. Similarly, Wu and Zhao [34] investigated a diffusion predator-prey model with predator cooperation, demonstrating that cooperation benefits the predator population. In 2023, Meng and Feng [7] proposed an intraguild predator-prey model with prey refuge and hunting cooperation, and they showed that prey refuge can change the stability of model and even have a stabilizing effect on this model. In addition, they found that hunting cooperation destabilizes the model in the absence of diffusion, but stabilizes it when diffusion is present.
In nature, humans exploit certain organisms to gain economic benefits, with the methods of capture directly influencing the outcomes. Recently, many scholars have studied different types of harvesting [35,36,37,38,39]. For instance, Meng and Li [37] analyzed a delayed prey-predator-scavenger system incorporating the fear effect and linear harvesting. They derived the optimal harvesting strategy for the delayed system using Pontryagin's maximum principle with delay. In 2023, Feng et al. [38] studied a single species model with seasonal Michaelis-Menten type harvesting. In particular, under the critical conditions on special harvest parameters, it was found that the T-periodic solution still exists as long as an arbitrary positive close season is formulated. Wu et al. [39] investigated an age-structured predator-prey system with Beddington-DeAngelis functional response and constant harvesting, and they obtained that the stability of system changes from a stable equilibrium to a stable limit cycle to an unstable limit cycle as the values of constant harvesting rate increase.
Considering the behavioral differences among species, we classify the prey population into immature and mature groups. However, studies that integrate time delay, cooperation, and harvesting within predator-prey models remain relatively scarce. This gap motivates our research. Thus, we consider the following facts and assumptions that are consistent with natural phenomena:
● To make the model more realistic, we assume that buffalos represent the prey population, and lions represent the predator population, forming a subsystem within the forest. Specifically, there is a cooperative relationship between immature and mature buffalos, while lions exclusively hunt the mature buffalos.
● Assume that the number of this immature prey populations is proportional to the number of existing immature prey populations; the number of mature prey populations is proportional to the number of existing mature prey populations. Similarly, the number of predator populations is directly proportional to the number of existing predator populations.
● Assume that immature and mature prey cooperate, providing mutual benefits. However, the benefit provided by mature prey to immature prey is significantly greater than the benefit provided by immature prey to mature prey.
● Assume that human harvesting of species for maximum economic benefit does not disrupt the balance of the ecosystem.
● Assume that the immature prey population transitions into the mature prey population at a constant rate, following a fixed time delay, denoted as $ \tau_1 $.
Motivated by the literature [27,33,37], we propose a stage structure predator-prey model with two time delays, prey refuge, cooperation, and linear harvesting as follows:
with the initial conditions
where $ x_1(t) $, $ x_2(t) $, and $ y(t) $ are the densities of immature prey, mature prey, and predator populations at time $ t $, respectively; $ a $ and $ b $ are the birth rate of immature prey and the conversion rate of immature prey into mature prey; $ r_1, r_2 $, and $ r_3 $ are the natural death rates of immature prey, mature prey, and predator, respectively; $ d $ is the intraspecific competition rate of mature prey; $ \sigma_1 $ and $ \sigma_2 $ are the cooperation coefficients of immature prey and mature prey $ (\sigma_1 > \sigma_2) $, respectively; $ \beta $ and $ c $ are the maximum capture rate and conversion rate of the predator, respectively; $ (1-m)x_2(m\in[0, 1)) $ is the number of prey that can be caught by predator; $ k $ is the half-saturation constant; $ \tau_1 $ is the maturity time delay and $ bx_1(t-\tau_1) $ represents the quantity which the immature prey born at time $ t-\tau_1 $ can survive at time $ t $; $ \tau_2 $ is the time delay since the gestation of the predator; $ \hbar $ is the harvesting effort, and $ q_1 $ and $ q_2 $ are the catch ability coefficient of the mature prey and predator. The biological interpretations of other parameters are same as in system (1.2), and all parameters are positive constants.
The highlights of this paper are as follows:
● A stage-structure predator-prey model is proposed, where the prey population is divided into two stages: immature prey and mature prey.
● The model incorporates two important time delays: the maturation time delay $ \tau_1 $ of the immature prey population and the gestation time delay $ \tau_2 $ of the predator population.
● Immature prey and mature prey cooperate to protect the immature prey from being predated. As a result, predators exclusively hunt the mature prey.
● A linear harvesting approach is applied to both the mature prey and the predator. By using an optimal harvesting strategy, the study determines the optimal harvesting effort.
● The analysis reveals that increases in the cooperation coefficient and the refuge coefficient have significant impacts on the stability of the system.
The organization of this paper is as follows. In Section 2, we discuss the positiveness and boundedness of system (1.3) without time delay. In addition, the existence and stability of the trivial equilibrium and the extinction equilibrium of the predator are given. In Section 3, the stability of the positive equilibrium and the existence of Hopf bifurcation of system with time delay are studied. In addition, the direction and the stability of Hopf bifurcation are shown based on the center manifold theorem and normal form theory. Based on Pontryagin's maximum principle, the optimal harvesting policy of the system is discussed in Section 4. To support our theoretical predictions, some numerical simulations are given in Section 5.
2.
The system (1.3) without time delay
In order to study some properties of system (1.3), we give system (1.3) without time delay as follows:
with the initial conditions
2.1. Positivity and boundedness of solutions
In natural ecology, the positiveness reflects the ability of populations to survive and sustain themselves over a long period, while boundedness ensures that population sizes remain within the limits imposed by available resources. These properties are crucial for the ecological viability and stability of populations. To effectively analyze the positiveness and boundedness of system (2.1), it is essential to carefully define the initial conditions of system (2.1), as they play a important role in determining the long-term dynamics of system. We can rewrite system (2.1) as the following matrix form:
where $ X = (x_1(t), x_2(t), y(t))^\mathbf{T}\in \mathbb{R}^3 $, and $ \mathcal{H}(X) $ are given by
Now, let $ \mathcal{H}:\mathbb{R}_+^{3}\rightarrow \mathbb{R}_+ $ satisfy the locally Lipschitz condition and $ [\mathcal{H}_i(X)]_{X\in \mathbb{R}_+^3}\geq0, i = 1, 2, 3 $. According to reference [40], the solution of (2.2) is positive, which means that all solutions of system (2.1) under positive initial conditions are positive. That is to say, each component of $ X $ remains in the interval $ [0, \mathcal{B}) $ for some $ \mathcal{B} > 0 $. If $ \mathcal{B} = \infty $, then $ \limsup\limits_{t\to \infty}(x_1(t)+x_2(t)+y(t)) = \infty $.
In the following lemma, we will prove that the solution of system (2.1) is bounded.
Lemma 2.1. All solutions of system (2.1) starting in $ \mathbb{R}_+^3 $ are confined to the region $ D^* = \Big\{(x_1(t) $, $ x_2(t), y(t))\in \mathbb{R}_+^3:V(t)\leq M^* = \frac{1}{4dr_0}(a-\frac{q_1\hbar}{2})^2\Big\} $ as $ t\rightarrow \infty $ for all positive initial values $ (x_1(\theta), x_2(\theta) $, $ y(\theta))\in \mathbb{R}_+^3 $, where $ V(t) = x_1(t)+x_2(t)+\frac{1}{c}y(t) $.
Proof. Let $ x_1(t), x_2(t) $, and $ y(t) $ be the solution of system (2.1) under the initial condition. In order to prove the boundedness of the solution of system (2.1), we construct a function $ V(t) $ as follows:
By differentiating (2.3) with respect to $ t $, we get
where $ r_0 = \text{min}\left\{r_1, r_2, r_3+q_2\hbar\right\} $. In addition, we need to discuss the sign of the $ q_1\hbar x_2\Big(1-\frac{\sigma_1+\sigma_2}{q_1\hbar}x_1\Big) $ term in separate cases:
1) If $ x_1\leq\frac{q_1\hbar}{2(\sigma_1+\sigma_2)} $, then we obtain that $ q_1\hbar x_2\Big(1-\frac{\sigma_1+\sigma_2}{q_1\hbar}x_1\Big)\geq\frac{q_1\hbar}{2}x_2 $ by using $ 1-\frac{\sigma_1+\sigma_2}{q_1\hbar}x_1\geq\frac{1}{2} $;
2) If $ x_1 > \frac{q_1\hbar}{2(\sigma_1+\sigma_2)} $, then we know that the above inequality holds if $ x_1 $ does not exceed this range in the long-term.
Thus, the above inequality becomes
According to the comparison principle, we have that $ \limsup\limits_{t\to \infty}V(t)\leq\frac{1}{4dr_0}\left(a-\frac{q_1\hbar}{2}\right)^2 = M^* $ and $ V(t)\leq M^*+\big(V_0-M^*\big)e^{-r_0t} $. Hence, there is at least a positive constant $ M > M^* $ and $ T > 0 $ such that $ V(t) < M^* $ when $ t > T $. Therefore, we can say that all trajectories of system (2.1) from any points in $ \mathbb{R}_+^3 $ are located on a fixed bounded area $ D^* $.
□
2.2. Existence and stability of equilibria
In this subsection, we will discuss the existence and the stability of equilibria $ E_0, \; \widetilde{E} $, and $ E^* $, respectively.
2.2.1. The trivial equilibrium
Theorem 2.1. The trivial equilibrium $ E_0 $ of system (2.1) is locally asymptotically stable if $ ab < (b+r_1)(r_2+q_1\hbar) $, but $ E_0 $ is unstable if $ ab > (b+r_1)(r_2+q_1\hbar) $.
Proof. The Jacobian matrix of system (2.1) is as follows:
where
Then, the Jacobian matrix at $ E_0 $ is
and the characteristic equation of system (2.1) at the trivial equilibrium $ E_{0} $ is
Thus, the first eigenvalue of Eq (2.5) is $ \lambda_1 = -(r_3+q_2\hbar) $, and the other two eigenvalues are determined by the following equation:
Then, we have $ \lambda_2+\lambda_3 = -(b+r_1+r_2+q_1\hbar) < 0 $ and $ \lambda_2\lambda_3 = (b+r_1)(r_2+q_1\hbar)-ab $. Thus, when $ ab < (b+r_1)(r_2+q_1\hbar) $, the trivial equilibrium $ E_0 $ is locally asymptotically stable, and the trivial equilibrium $ E_0 $ is unstable when $ ab > (b+r_1)(r_2+q_1\hbar) $.
□
2.2.2. The predator extinction equilibrium
For the predator extinction equilibrium $ \widetilde{E}(\tilde{x}_{1}, \tilde{x}_{2}, 0) $, we can obtain the following system:
By calculation from the first equation of (2.6), we get that $ \tilde{x}_2 = \frac{(b+r_1)\tilde{x}_1}{a+\sigma_1\tilde{x}_1} $. Furthermore, $ \tilde{x}_1 $ satisfies the following equation:
where $ A = b\sigma_1^2+\sigma_1\sigma_2(b+r_1), \; B = \sigma_1[2ab-(b+r_1)(r_2+q_1\hbar)]+a\sigma_2(b+r_1)-d(b+r_1)^2 $, and $ \digamma = a[ab-(b+r_1)(r_2+q_1\hbar)] $. Let $ \Delta_1 = B^2-4A\digamma $. Then, there is the following conclusion.
Lemma 2.2. The predator extinction equilibria $ \widetilde{E}(\tilde{x}_{1}, \tilde{x}_{2}, 0) $ of system (2.1) are as follows:
(i) If $ \Delta_1 = 0 $ and $ B < 0 $, that is, $ \sigma_1[2ab-(b+r_1)(r_2+q_1\hbar)] < d(b+r_1)^2-a\sigma_2(b+r_1) $, then system (2.1) has a unique extinction equilibrium given by $ \widetilde{E}_{1}\left(\tilde{x}_{11}, \frac{(b+r_1)\tilde{x}_{11}}{a+\sigma_1\tilde{x}_{11}}, 0\right) $, here $ \tilde{x}_{11} = -\frac{B}{2A} $;
(ii) If $ \Delta_1 > 0 $ and $ 0 < \digamma < \frac{B^2}{4A} $, then system (2.1) has two distinct extinction equilibria $ \widetilde{E}_{2}\left(\tilde{x}_{12}, \frac{(b+r_1)\tilde{x}_{12}}{a+\sigma_1\tilde{x}_{12}}, 0\right) $ and $ \widetilde{E}_{3}\left(\tilde{x}_{13}, \frac{(b+r_1)\tilde{x}_{13}}{a+\sigma_1\tilde{x}_{13}}, 0\right) $, here $ \tilde{x}_{12} = \frac{\sqrt{\Delta_1}-B}{2A} $ and $ \tilde{x}_{13} = \frac{-\sqrt{\Delta_1}-B}{2A} $;
(iii) If $ \Delta_1 > 0 $ and $ \digamma < 0 $, then system (2.1) has a extinction equilibrium $ \widetilde{E}_{2}\left(\tilde{x}_{12}, \frac{(b+r_1)\tilde{x}_{12}}{a+\sigma_1\tilde{x}_{12}}, 0\right) $, here $ \tilde{x}_{12} = \frac{\sqrt{\Delta_1}-B}{2A} $.
Now we prove the stability of the predator extinction equilibrium $ \widetilde{E}_1\left(\tilde{x}_{11}, \frac{(b+r_1)\tilde{x}_{11}}{a+\sigma_1\tilde{x}_{11}}, 0\right) $, at which point the local stability of other predator extinction equilibria can be proved by using similar methods.
Theorem 2.2. The predator extinction equilibrium $ \widetilde{E}_1 $ of system (2.1) is locally asymptotically stable if and only if the condition $ (\Upsilon_1) $ holds, but $ \widetilde{E}_1 $ is unstable if $ (\Upsilon_1) $ does not hold.
Proof. According to the matrix (2.4), we can know that the Jacobian matrix of the system at $ \widetilde{E}_1 $ is
where
Then, the characteristic equation of system (2.1) at the predator extinction equilibrium $ \widetilde{E}_1 $ is
where $ D = -(J_{11}+J_{22}+J_{33}), \; F = J_{11}J_{22}+J_{11}J_{33}+J_{22}J_{33}-J_{12}J_{21} $, and $ G = J_{12}J_{21}J_{33}-J_{11}J_{22}J_{33} $. According to the Hurwitz criterion, we find that all eigenvalues of Eq (2.7) have negative real parts if and only if
$ (\Upsilon_1) $: (i) $ \frac{2A(b+r_1)(2d-\sigma_1)-\sigma_2(2aA-\sigma_1B)}{2A(2aA-\sigma_1B)(b+r_1)}-\frac{c\beta(1-m)}{(2aA-\sigma_1B)-k(1-m)(b+r_1)B} < \frac{r_2+r_3+q_1\hbar+q_2\hbar}{B(b+r_1)}-\frac{1}{B} $;
(ii) $ a > \max\left\{\frac{2d(b+r_1)-\sigma_1(r_2+q_1\hbar)}{a\sigma_2(b+r_1)}, \frac{(b+r_1)(r_2+q_1\hbar)}{b}\right\} $ and $ \beta > \frac{(r_3+q_2\hbar)[2A+k(1-m)(b+r_1)B]}{c(1-m)B} $;
(iii) $ DF-G > 0 $
holds. Thus, the predator extinction equilibrium $ \widetilde{E}_1 $ is locally asymptotically stable, but is unstable if the condition $ (\Upsilon_1) $ does not hold. □
Remark 2.1. For $ (iii) $ of condition $ (\Upsilon_1) $, it should be noted that the explicit analytical expressions of the predator extinction equilibria $ \tilde{x}_{11} $ and $ \tilde{x}_{12} $ are not straightforward to derive due to the complexity of the system. As a result, the form $ (iii) $ of the condition $ (\Upsilon_1) $ is retained here without explicitly solving for $ \tilde{x}_{11} $ and $ \tilde{x}_{12} $. To address this limitation, computational techniques can be employed to verify the validity of this condition under specific parameter settings. These numerical explorations demonstrate that condition $ (iii) $ is indeed satisfied in certain cases, providing confidence in its applicability.
2.2.3. The positive equilibrium
Theorem 2.3. If the condition $ (\Upsilon_2) $ holds, then the positive equilibrium $ E^* $ of system (2.1) always exists. But, if one of the conditions does not hold, then the positive equilibrium $ E^* $ does not exist.
Proof. We assume that $ E^*(x_1^*, x_2^*, y^*) $ is a positive equilibrium of system (2.1). Then, $ x_1^*, x_2^* $, and $ y^* $ satisfy the following system:
By calculation from (2.8), we can obtain that
where
Thus, if the conditions
$ (\Upsilon_2) $: $ c\beta-k(r_3+q_2\hbar) > \frac{\sigma_1(r_3+q_2\hbar)}{(b+r_1)(1-m)} $, $ ab > (b+r_1)(r_2+q_1\hbar) $ and $ d > \frac{\sigma_1(r_2+q_1\hbar)+\sigma_2a}{(b+r_1)} $
hold, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ exists. □
Next, we will discuss the stability of the positive equilibrium $ E^* $ of system (1.3).
3.
Hopf bifurcation of system with time delay
3.1. The existence of Hopf bifurcation
From a biological perspective, analyzing the stability of the positive equilibrium of system (1.3) provides deeper insights into the dynamics of system. In this subsection, we discuss the local stability of the system at the positive equilibrium and the existence of Hopf bifurcation of system (1.3). For convenience, let $ \bar{x}_1(t) = x_1(t)-x_1^*, \; \bar{x}_2(t) = x_2(t)-x_2^* $, and $ \bar{y}(t) = y(t)-y^* $. We have the following linearized system:
where
Then, the characteristic equation of system (3.1) can be given by
where
In order to study the distribution of the root of Eq (3.2), we will discuss it in the following cases.
$ \textbf{Case 1}:\tau_1 = \tau_2 = 0 $
In this case, the Eq (3.2) is reduced to
where $ p_{12} = p_2+s_2+u_2, p_{11} = p_1+s_1+u_1+v_1 $ and $ p_{10} = p_0+s_0+u_0+v_0 $. Thus, we know that all roots of Eq (3.3) have negative real parts if the assumption
$ (\Upsilon_3): p_{12} > 0, \; p_{10} > 0 $ and $ p_{12}p_{11} > p_{10} $
holds. That is, system (1.3) is locally asymptotically stable at the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ if condition $ (\Upsilon_3) $ is satisfied.
Remark 3.1. With Remark 2.1, we can use the computer to determine that this condition can be established under certain circumstances for the condition $ (\Upsilon_3) $.
$ \textbf{Case 2}:\tau_1 > 0, \tau_2 = 0 $
Equation (3.2) is reduced to
where $ p_{22} = p_2+u_2, \; p_{21} = p_1+u_1, \; p_{20} = p_0+u_0, \; u_{22} = s_2, \; u_{21} = s_1+v_1 $, and $ u_{20} = s_0+v_0 $. Let $ i\omega_1(\omega_1 > 0) $ be a root of Eq (3.4). By separating the real and imaginary parts, it follows that
Adding squares of Eq (3.5), we can get
where $ e_{12} = p_{22}^2-2p_{21}-u_{22}^2, e_{11} = p_{21}^2+2(u_{20}u_{22}-p_{20}p_{22})-u_{21}^2, e_{10} = p_{20}^2-u_{20}^2 $. Let $ \omega_1^2 = n_1 $. Then, Equation (3.6) can be written as
Here, we denote $ f_1(n_1) = n_1^3+e_{12}n_1^2+e_{11}n_1+e_{10} $. Then, $ f_1(0) = e_{10}, \lim\limits_{n_1\to +\infty}f_1(n_1) = +\infty $, and $ f_1^{'}(n_1) = 3n_1^2+2e_{12}n_1+e_{11} $.
After discussion about the roots of Eq (3.7) by the method in [41], we have the following conditions:
$ (\Upsilon_4):e_{10}\geq0, \; \vartriangle = e_{12}^2-3e_{11}\leq 0 $,
$ (\Upsilon_5):e_{10}\geq0, \; \vartriangle = e_{12}^2-3e_{11} > 0 $, $ n_1^* = \frac{-e_{12}+\sqrt{\vartriangle}}{3} > 0 $ and $ f_1(n_1^*)\leq 0, $
$ (\Upsilon_6):e_{10} < 0 $.
Lemma 3.1. For the polynomial Eq (3.7), we have the following results. If $ (\Upsilon_4) $ holds, then Eq (3.7) has no positive root. If $ (\Upsilon_5) $ or $ (\Upsilon_6) $ holds, then Eq (3.7) has at least one positive root.
Without loss of generality, we assume that Eq (3.7) has three positive roots defined as $ n_{11}, n_{12} $, and $ n_{13} $. Then, Equation (3.6) has three positive roots $ \omega_{1k} = \sqrt{n_{1k}}, \; k = 1, 2, 3 $. According to (3.5), if $ n_{1k} > 0 $, then the corresponding critical value of time delay $ \tau_{1k}^{(j)} $ is
where
Therefore, $ \pm i\omega_{1k} $ is a pair of purely imaginary roots of Eq (3.4) with $ \tau_1 = \tau_{1k}^{(j)} $. And, let $ \tau_{10} = \mbox{min}_{k\in\{1, 2, 3\}}{\left\{\tau_{1k}^{(0)}\right\}}, \omega_{10} = \omega_{1k_0} $.
Lemma 3.2. Suppose that $ (\Upsilon_7):f_1^{'}(\omega_{10}^2)\neq0 $. Then, the following transversality condition $ \mathrm{sign}\left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_1}\Big|_{\lambda = i\omega_{10}}\right\}\neq0 $ holds.
Proof. Differentiating Eq (3.4) with respect to $ \tau_1 $, we obtain
From Eq (3.4), we have
and then, by substituting Eq (3.9) into Eq (3.8), we can get
Thus, we have
From Eq (3.10), we obtain that
It follows that $ \text{sign}\left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_1}\Big|_{\lambda = i\omega_{10}}\right\}\neq0 $, and the proof is complete.
□
By Lemmas 3.1 and 3.2 and the Hopf bifurcation theorem [42,43], we have the following results.
Theorem 3.1. For system (1.3) with $ \tau_1 > 0, \tau_2 = 0 $, the following results are true.
1) If $ (\Upsilon_4) $ holds, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is locally asymptotically stable for all $ \tau_1\geq0 $.
2) If $ (\Upsilon_5) $ or $ (\Upsilon_6) $ and $ (\Upsilon_7) $ hold, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is locally asymptotically stable for all $ \tau_1\in[0, \tau_{10}) $ and unstable for $ \tau_1 > \tau_{10} $. Furthermore, system (1.3) undergoes a Hopf bifurcation at the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ when $ \tau_1 = \tau_{10} $.
$ \textbf{Case 3}:\tau_1 = 0, \tau_2 > 0 $ Equation (3.2) is reduced to
where $ p_{32} = p_2+s_2, p_{31} = p_1+s_1, p_{30} = p_0+s_0, u_{32} = u_2, u_{31} = u_1+v_1 $, and $ u_{30} = u_0+v_0 $. Let $ i\omega_2(\omega_2 > 0) $ be a root of Eq (3.11). By separating real and imaginary parts, it follows that
Adding the sum of squares of Eq (3.12), we can get
where $ \; e_{22} = p_{32}^2-2p_{31}-u_{32}^2, \; e_{21} = p_{31}^2+2(u_{30}u_{32}-p_{30}p_{32})-u_{31}^2 $ and $ e_{20} = p_{30}^2-u_{30}^2. $ Let $ \omega_2^2 = n_2 $. Then, Equation (3.13) can be written as
Denote $ f_2(n_2) = n_2^3+e_{22}n_2^2+e_{21}n_2+e_{20} $. Then, $ f_2(0) = e_{20}, \lim\limits_{n_2\to +\infty}f_2(n_2) = +\infty $, and $ f_2^{'}(n_2) = 3n_2^2+2e_{22}n_2+e_{21}. $
After discussion about the roots of Eq (3.14) by the method in [41], we have the following assumptions:
$ (\Upsilon_{8}): e_{20}\geq0, \; \vartriangle = e_{22}^2-3e_{21}\leq 0, $
$ (\Upsilon_{9}): e_{20}\geq0, \; \vartriangle = e_{22}^2-3e_{21} > 0, \; n_2^* = \frac{-e_{22}+\sqrt{\vartriangle}}{3} > 0 $ and $ f_2(n_2^*)\leq 0, $
$ (\Upsilon_{10}): e_{20} < 0. $
Lemma 3.3. For the polynomial Eq (3.14), we have the following results. If $ (\Upsilon_{8}) $ holds, then Eq (3.14) has no positive root. If $ (\Upsilon_{9}) $ or $ (\Upsilon_{10}) $ holds, then Eq (3.14) has at least one positive root.
Generally, we assume that Eq (3.14) has positive roots. Without loss of generality, we assume that Eq (3.14) has three positive roots defined as $ n_{21}, n_{22} $, and $ n_{23} $. Then, Equation (3.13) has three positive roots $ \omega_{2k} = \sqrt{n_{2k}}, \; k = 1, 2, 3 $. According to (3.12), if $ n_{2k} > 0 $, the corresponding critical value of time delay $ \tau_{2k}^{(j)} $ is
where
Therefore, $ \pm i\omega_{2k} $ is a pair of purely imaginary roots of Eq (3.11) with $ \tau_2 = \tau_{2k}^{(j)} $. And, let $ \tau_{20} = \mathrm{min}_{k\in\{1, 2, 3\}}{\left\{\tau_{2k}^{(0)}\right\}}, \; \omega_{20} = \omega_{2k_0} $.
Lemma 3.4. Suppose that $ (\Upsilon_{11}):f_2^{'}(\omega_{20}^2)\neq0 $. Then, the following transversality condition $ \mathrm{sign}\left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_2}\Big|_{\lambda = i\omega_{20}}\right\}\neq0 $ holds.
Proof. Differentiating Eq (3.11) with respect to $ \tau_2 $, we have
Then, we have
It follows that $ \mathrm{sign}\left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_2}\Big|_{\lambda = i\omega_{20}}\right\}\neq0 $ if $ (\Upsilon_{11}) $ holds. The proof is complete.
□
By Lemmas 3.3 and 3.4 and the Hopf bifurcation theorem [42,43], we have the following results.
Theorem 3.2. For system (1.3) with $ \tau_1 = 0, \tau_2 > 0 $, the following results are true.
1) If $ (\Upsilon_{8}) $ holds, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is locally asymptotically stable for all $ \tau_2\geq0 $.
2) If $ (\Upsilon_{9}) $ or $ (\Upsilon_{10}) $ and $ (\Upsilon_{11}) $ hold, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is locally asymptotically stable for all $ \tau_2\in[0, \tau_{20}) $, but unstable for $ \tau_2 > \tau_{20} $. Furthermore, system (1.3) undergoes a Hopf bifurcation at the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ when $ \tau_2 = \tau_{20} $.
$ \textbf{Case 4}:\tau_1 = \tau_2 = \tau \neq0 $
Equation (3.2) is reduced to
where $ p_{42} = p_2, \; p_{41} = p_1, \; p_{40} = p_0, \; u_{42} = s_2+u_2, \; u_{41} = s_1+u_1, \; u_{40} = s_0+u_0, \; s_{41} = v_1 $, and $ s_{40} = v_0 $. Let $ i\omega(\omega > 0) $ be a root of Eq (3.15). By separating the real and imaginary parts, we can get
where
It follows that
where
From Eq (3.16), we can get
where
Let $ \omega^2 = n_3 $. Then, Equation (3.17) can be written as
Without loss of generality, we assume that it has six positive roots and define them as $ n_{3k}, k = 1, 2, \ldots, 6 $. Then, Equation (3.17) has six positive roots $ \omega_{k} = \sqrt{n_{3k}} $, $ k = 1, 2, \ldots, 6 $. According to (3.16), if $ n_{3k} > 0 $, the corresponding critical value of time delay $ \tau_{k}^{(j)} $ is
Therefore, $ \pm i\omega_{k} $ is a pair of purely imaginary roots of Eq (3.15) with $ \tau = \tau_{k}^{(j)} $. And, let $ \tau_{0} = \mathrm{min}_{k\in\{1, 2, \ldots, 6\}}\\{\left\{\tau_{k}^{(0)}\right\}} $, $ \omega_{0} = \omega_{k_0} $.
Lemma 3.5. Suppose that $ (\Upsilon_{12}):A_1C_1+B_1D_1\neq0 $. Then, the following transversality condition $ \frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau}\Big|_{\lambda = i\omega_0}\neq0 $ holds.
Proof. Differentiating Eq (3.15) with respect to $ \tau $, we obtain
where
Noting that $ \left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau}\right\}_{\lambda = i\omega_0} $ and $ \left\{\mathrm{Re}(\frac{\mathrm{d}\lambda}{\mathrm{d}\tau})^{-1}\right\}_{\lambda = i\omega_0} $ have the same sign, we get
If condition $ (\Upsilon_{12}) $ holds, then $ \frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau}\Big|_{\lambda = i\omega_0} \neq0 $. This completes the proof.
□
By applying Lemma 3.5 to Eq (3.15), we obtain the existence of Hopf bifurcation as stated in the following theorem.
Theorem 3.3. For system (1.3) with $ \tau_1 = \tau_2 = \tau\neq0 $, if $ (\Upsilon_{12}) $ holds, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is locally asymptotically stable for all $ \tau\in[0, \tau_0) $, but unstable for $ \tau > \tau_0 $. Furthermore, system (1.3) undergoes a Hopf bifurcation at the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ when $ \tau = \tau_0 $.
$ \textbf{Case 5}:\tau_1 > 0, \tau_2\in[0, \tau_{20}) $ and $ \tau_1\neq\tau_2. $
We consider Eq (3.2) with $ \tau_2 $ in its stable interval, and taking $ \tau_1 $ as bifurcation parameter. Let $ i\omega_{1*}(\omega_{1*} > 0) $ be the root of Eq (3.2). Then, we obtain
where
From Eq (3.18), we have
where
In order to reach some main conclusions, we give the following assumption.
$ (\Upsilon_{13}): $ Eq (3.19) has at least a finite positive root.
We denote the positive roots of Eq (3.19) by $ \omega_{1*}^{i}, (i = 1, 2, \ldots, 6 $). For every $ \omega_{1*}^i(i = 1, 2, \ldots, 6), $ the corresponding critical value of time delay $ \tau_{1i}^{(j)}, j = 1, 2, 3\ldots, $ is
Let $ \tau_{10}^{'} = min\left\{\tau_{1i}^{(0)}|i = 1, 2, \ldots; j = 0, 1, 2\ldots\right\} $ and $ \omega_{10}^{'} $ be the corresponding root of Eq (3.19) with $ \tau_{10}^{'} $.
Lemma 3.6. Suppose that $ (\Upsilon_{14}):A_2C_2+B_2D_2\neq0 $. Then, the transversality condition $ \frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_1}\Big|_{\lambda = i\omega_{10}^{'}}\neq0 $ holds.
Proof. Differentiating Eq (3.2) with respect to $ \tau_1 $, we can get
where
Noting that $ \left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_1}\right\}_{\lambda = i\omega_{10}^{'}} $ and $ \left\{\mathrm{Re}(\frac{\mathrm{d}\lambda}{\mathrm{d}\tau_1})^{-1}\right\}_{\lambda = i\omega_{10}^{'}} $ have the same sign, we have
If condition $ (\Upsilon_{14}) $ holds, then we obtain $ \text{sign}\left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_1}\Big|_{\lambda = i\omega_{10}^{'}} \right\} \neq0 $. This completes the proof.
□
Through the above analysis, we have the following theorem.
Theorem 3.4. For system (1.3) with $ \tau_1 > 0, \tau_2\in[0, \tau_{20}) $, and $ \tau_1\neq\tau_2 $, if $ (\Upsilon_{13}) $ and $ (\Upsilon_{14}) $ hold, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is locally asymptotically stable for all $ \tau_1\in[0, \tau_{10}^{'}) $, but unstable for $ \tau_1 > \tau_{10}^{'} $. Furthermore, system (1.3) undergoes a Hopf bifurcation at the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ when $ \tau_1 = \tau_{10}^{'} $.
$ \textbf{Case 6}:\tau_2 > 0, \tau_1\in[0, \tau_{10}) $, and $ \tau_1\neq\tau_2. $
We consider Eq (4.2) with $ \tau_1 $ in its stable interval, and taking $ \tau_2 $ is regarded as the bifurcation parameter. Let $ i\omega_{2*}(\omega_{2*} > 0) $ be the root of Eq (4.2). Then, we obtain
where
From Eq (3.20), we have
where
In order to obtain some main conclusions, we give the following assumption.
$ (\Upsilon_{15}): $ Eq (3.21) has at least a finite positive root.
We denote the positive roots of Eq (3.21) by $ \omega_{2*}^{i}, (i = 1, 2, \ldots, 6) $. For every $ \omega_{2*}^i(i = 1, 2, \ldots, 6), $ the corresponding critical value of time delay $ \tau_{2i}^{(j)}, j = 1, 2, 3\ldots, $ is
Let $ \tau_{20}^{'} = min\{\tau_{2i}^{(0)}|i = 1, 2, \ldots; j = 0, 1, 2\ldots\} $ and $ \omega_{20}^{'} $ be the corresponding root of Eq (3.21) with $ \tau_{20}^{'} $.
Lemma 3.7. Suppose that $ (\Upsilon_{16}):A_3C_3+B_3D_3\neq0 $. Then, the following transversality condition $ \frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_2}\Big|_{\lambda = i\omega_{20}^{'}}\neq0 $ holds.
Proof. Differentiating Eq (3.2) with respect to $ \tau_2 $, we can get
where
Noting that $ \left\{\frac{\mathrm{d}(\mathrm{Re}\lambda)}{\mathrm{d}\tau_2}\right\}_{\lambda = i\omega_{20}^{'}} $ and $ \left\{\mathrm{Re}\left(\frac{\mathrm{d}\lambda}{\mathrm{d}\tau_2}\right)^{-1}\right\}_{\lambda = i\omega_{20}^{'}} $ have the same sign, we get
If condition $ (\Upsilon_{16}) $ holds, then $ \frac{\mathrm{d}({\mathrm{Re}}\lambda)}{\mathrm{d}\tau_2}\Big|_{\lambda = i\omega_{20}^{'}} \neq0 $. This completes the proof. □
Through the above analysis, we have the following theorem.
Theorem 3.5. For system (1.3) with $ \tau_2 > 0, \tau_1\in[0, \tau_{10}) $ and $ \tau_1\neq\tau_2 $, if $ (\Upsilon_{15}) $ and $ (\Upsilon_{16}) $ hold, then the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ is asymptotically stable for all $ \tau_2\in[0, \tau_{20}^{'}) $, but unstable for $ \tau_2 > \tau_{20}^{'} $. Furthermore, system (1.3) undergoes a Hopf bifurcation at the positive equilibrium $ E^*(x_1^*, x_2^*, y^*) $ when $ \tau_2 = \tau_{20}^{'} $.
3.2. Direction and stability of Hopf bifurcation
In the previous subsection, we analyzed the various cases in which Hopf bifurcation occurs in system (1.3) at $ \tau_1 $ and $ \tau_2 $. In this subsection, we focus on determining the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions of system (1.3). To achieve this, we employ the normal form theory and center manifold theorem as outlined in [42]. For the analysis in this subsection, we assume that system (1.3) undergoes a Hopf bifurcation at $ \tau_1 = \tau_{10}^{'}, \tau_2\in[0, \tau_{20}) $.
Without loss of generality, it is assumed that $ \tau_{10}^{'} > \tau_2^{'} $. Let $ \tau_1 = \tau_{10}^{'}+\mu, \; \mu\in \mathbb{R}, \; t = s\tau_1, \; x_1(s\tau_1) = \hat{x}_1(s), \; x_2(s\tau_1) = \hat{x}_2(s) $, and $ y(s\tau_1) = \hat{y}(s). $ We denote $ \hat{x}_1(s) = x_1(s), \; \hat{x}_2(s) = x_2(s) $, and $ \hat{y}(s) = y(s) $. Then, system (2.1) can be written as a functional differential equation (FDE) in $ C = C([-1, 0], \mathbb{R}^3): $
where $ u(t) = (x_1(t), x_2(t), y(t))^\mathbf{T}\in C $, $ u_t(\theta) = u(t+\theta) = (x_1(t+\theta), x_2(t+\theta), y(t+\theta))^\mathbf{T}\in C $, and $ L_\mu:C\rightarrow \mathbb{R}^3 $, $ \mathcal{F}:\mathbb{R}\times C\rightarrow \mathbb{R}^3 $ are given by
and
where
with
By the Riesz representation theorem, there exists a $ 3\times3 $ matrix function $ \eta(\theta, \mu) $ for $ \theta\in[-1, 0) $ such that
In fact, we can choose
For $ \phi\in C^1([-1, 0], \mathbb{R}^3) $, we define
and
Then, system (3.22) can be rewritten as
For $ \varphi\in C^1([-1, 0], (\mathbb{R}^3)^*) $, where $ (\mathbb{R}^3)^* $ is the three-dimensional space of row vectors, we further define the adjoint operator $ A^* $ of $ A(0) $:
For $ \phi\in C^1([-1, 0], \mathbb{R}^3) $ and $ \varphi\in C^1([-1, 0], (\mathbb{R}^3)^*) $, we define the bilinear form
where $ \eta(\theta) = \eta(\theta, 0), A = A(0) $, and $ A^* $ are adjoint operators. By the discussion in Section 4, we know that $ \pm i\omega_{10}^{'}\tau_{10}^{'} $ are eigenvalues of $ A(0) $. Thus, they are also the eigenvalues of $ A^* $.
We suppose that $ \gamma(\theta) = (1, \gamma_2, \gamma_3)^\mathbf{T}e^{i\omega_{10}^{'}\tau_{10}^{'}\theta} $ is the eigenvector of $ A(0) $ corresponding to the eigenvalue $ i\omega_{10}^{'}\tau_{10}^{'} $, and $ \gamma^*(s) = D(1, \gamma_2^*, \gamma_3^*)e^{-i\omega_{10}^{'}\tau_{10}^{'}s} $ is the eigenvector of $ A^* $ corresponding to the eigenvalue $ -i\omega_{10}^{'}\tau_{10}^{'} $. By computation, we obtain
Then, from Eq (3.25), we get
Therefore, we choose
such that $ \langle \gamma^*(s), \gamma(\theta)\rangle = 1, \langle \gamma^*(s), \bar{\gamma}(\theta)\rangle = 0 $.
Next, let $ u_t $ be the solution of Eq (3.24) when $ \mu = 0 $. We define
On the center manifold $ C_0 $, we come to the conclusion that
where $ z $ and $ \bar{z} $ are local coordinates for $ C_0 $ in the direction of $ \gamma^* $ and $ \bar{\gamma}^* $.
Note that $ W $ is real if $ u_t $ is real, and we only consider the real solutions. From Eq (3.26), we get
For a solution $ u_t\in C_0 $ of Eqs (3.23)–(3.25) and $ \mu = 0 $, we have
Moreover, the above equation can be rewritten as follows:
where
It follows from Eqs (3.26) and (3.27) that
By Eqs (3.29) and (3.30), it derives that
Then, from Eq (3.29) and the above equation, we obtain the following relevant parameters, which help determine the direction and stability of Hopf bifurcation:
with
where $ E_1 = \left(E_1^{(1)}, E_1^{(2)}, E_1^{(3)}\right)^\mathbf{T}\in \mathbb{R}^3 $ and $ E_2 = \left(E_2^{(1)}, E_2^{(2)}, E_2^{(3)}\right)^\mathbf{T}\in \mathbb{R}^3 $ are also constant vectors and can be determined by the following equations, respectively:
where
and
Therefore, we can calculate $ g_{21} $ and the following values:
which determine the properties of bifurcating periodic solutions at $ \tau_1 = \tau_{10}^{'} $. From the discussion above, we have the following result.
Theorem 3.6. For system (1.3), the direction of Hopf bifurcation is determined by the sign of $ \mu_2 $: if $ \mu_2 > 0 (\mu_2 < 0) $, then the Hopf bifurcation is supercritical (subcritical). The stability of the bifurcating periodic solutions is determined by the sign of $ \beta_2 $: if $ \beta_2 < 0 (\beta_2 > 0) $, then the bifurcating periodic solutions are stable (unstable). The period of the bifurcating periodic solutions is determined by the sign of $ T_2 $: if $ T_2 > 0 (T_2 < 0) $, then the bifurcating periodic solutions increase (decrease).
4.
The optimal harvesting policy
The development and sustainable utilization of biological resources are common practices in fisheries, forestry, and wildlife management. Effective management of biological species, such as fisheries, is essential for maintaining ecological balance and ensuring long-term resource availability. With this in mind, we aim to analyze the optimal strategies that regulators can adopt to maximize the benefits of harvesting while preserving the ecosystem.
In particular, our study will focus on determining the optimal harvesting policy by employing the harvesting effort $ \hbar $ as a control tool. This involves balancing ecological considerations with economic gains to achieve a sustainable outcome. To better understand this dynamic, we will explore the relationship between the population densities of prey species $ (x_1, x_2) $, predator species $ (y) $ and the overall ecosystem response under optimal conditions. Our goal is to investigate the three-dimensional curve $ (x_1, x_2, y) $ that represents the behavior of the system at the optimal equilibrium level, achieved by applying the appropriate harvesting effort $ \hbar $. By analyzing this curve, we aim to identify the conditions that maximize net income from both prey and predator species, while ensuring the system remains ecologically and economically viable [35].
The net economic income to the society is
where $ c^{\prime} $ is the harvesting cost per unit effort, which in turn is given by $ c^{\prime} = c_1+c_2 $. Here, $ c_1 $ is the harvesting cost per unit effort corresponding to the adult prey species, and $ c_2 $ is the harvesting cost per unit effort corresponding to the predator species. $ p_1^{\prime} $ is the price per unit biomass of $ x_2 $, and $ p_2^{\prime} $ is the price per unit biomass of $ y $. $ p_1^{\prime} $, $ p_2^{\prime} $, and $ c^{\prime} $ are positive constants.
Our main problem is to optimize the objective function
subject to system (1.3) by using Pontryagin's maximum principle [44]. We construct the Hamiltonian function as
where $ \lambda_i = \lambda_i(t)(i = 1, 2, 3) $ are adjoint variables corresponding to the variables $ x_1, x_2 $, and $ y $, respectively. $ \hbar $ is the restricted control variable, $ 0\leq \hbar \leq \hbar_{max} $, where $ \hbar_{max} $ is the feasible upper limit of $ \hbar $ with the infrastructure support available for harvesting. The condition that the Hamiltonian function $ H $ must satisfy is given by
that is,
where $ F_1(x_2, y) = p_1^{\prime}q_1x_2+p_2^{\prime}q_2y-c^{\prime} $.
We suppose that $ \hbar $ is the optimal control, and $ x_1, \; x_2 $, and $ y $ are the response functions. By using the maximum principle, there are adjoint variables $ \lambda_1, \lambda_2 $, and $ \lambda_3 $ for $ t\geq0 $. Then, we have,
For positive optimal equilibrium solutions, $ \dot{x_2} = \dot{y} = 0 $ (in other words, $ x_2, y $ are not dependent on $ t $), and from the three equations of system (2.1), we have
From the above analysis, it is obvious that $ \hbar $ is also independent of $ t $. Furthermore, we get
From Eqs (4.1) and (4.5), we get
where
By Eqs (4.1) and (4.6), we can get
Now removing $ \hbar $ from Eqs (4.3) and (4.4), we obtain
which is the optimal trajectory of the steady state given by the optimal solutions $ x_2 = x_{2\delta}, y = y_\delta $. Then, we substitute $ \lambda_2 $ and $ \lambda_3 $ into Eq (4.5) and obtain the optimal equilibrium level of effort given by
By solving Eqs (4.7) and (4.8) when assigning a certain value to $ \delta $, we can obtain the optimal equilibrium level $ (x_{1\delta}, x_{2\delta}, y_{\delta}) $. The optimal harvesting effort at any time is determined by
where $ \hbar_{\text{min}} $ is the minimum harvesting effort. This study not only contributes to theoretical insights into ecological management, but also provides practical guidelines for policymakers to implement sustainable harvesting strategies that align with conservation and economic goals.
5.
Numerical simulations
To identify the parameters that significantly influence the output variables of system (2.1), we perform a global sensitivity analysis on selected parameters. Specifically, we calculate the partial rank correlation coefficients (PRCCs) for the parameters $ a, \beta, d, \sigma_1, \sigma_2 $, and $ m $ in system (2.1). Nonlinear and monotonic relationships are observed between the input parameters and the outputs of system (2.1), which is a key prerequisite for computing PRCCs. Then, a total of 1000 simulations of the model per Latin hypercube sampling (LHS) were carried out using the baseline values tabulated in Table 1.
According to the parameter values in Table 1, we analyze the influence of some parameters in the system on the correlation of mature prey. By sampling these parameters $ 1000 $ times and with a scatter plot with a fixed time point of $ 80 $, we obtain the sampling results in Figure 1 and the scatter plot in Figure 2. Monotonic increasing (decreasing) indicates a positive (negative) correlation of the parameter with the model output. It is known from Figure 1 that several selected parameters exhibit periodic correlation. From Figure 2, we can know that the parameters $ a, d $, and $ m $ show a positive correlation with the output of the system, the parameters $ \beta $ and $ \sigma_2 $ show a negative correlation with the output of the system, and the parameter $ \sigma_1 $ has no correlation with the output of the system.
5.1. Dynamics of system without time delay
In this part, we study how different dynamics occur by varying three parameters of system (2.1): the cooperation coefficients of immature prey and mature prey ($ \sigma_1 $ and $ \sigma_2 $), and the number of refuge for prey ($ m $). The values of all parameters in system (2.1) are sourced from Table 2. First, let $ \tau_1 = \tau_2 = 0 $, that is, we assume that condition $ (\Upsilon_3) $ is true. At the same time, we consider the cooperation of the prey population and provide a certain amount of refuge for the prey. We choose $ \sigma_1 = 0.1 $, $ \sigma_2 = 0.01 (\sigma_1 > \sigma_2) $, and $ m = 0.3 $ $ (m\in[0, 1)) $ by fixing the values of the other parameters as in Table 2 with initial conditions $ (1, 1, 1) $. By calculation and analysis, system (2.1) is locally asymptotically stable around the interior equilibrium point $ (0.8613, 0.1242, 0.2755) $ (see Figure 3).
Second, we select the number of refuge for prey ($ m $) as a parameter and keep the values of the other parameters in Table 2. According to the initial conditions, when $ m = 0.3 $ and $ m = 0 $, the stability of system (2.1) is given in Figure 4. Although the equilibrium of the system changes from $ (0.8613, 0.1242, 0.2755) $ to $ (0.6021, 0.0869, 0.2062) $, system (2.1) is locally asymptotically stable (see Figure 4). This shows that if the system has no refuges, then the number of various species will decrease. At the same time, the effect of the refuge parameter $ m $ on the steady-state level of prey and predator species is shown in Figure 5. We can see that the number of prey always increases. The predator population initially increases with the increase of $ m $, then begins to decrease when the value is bigger than $ m^* = 0.74 $, and disappears when $ m = 0.9 $. This means that the predator may by extinct due to lack of food resources. This indicates that if the refuge is lower than critical level, then it has a positive effect on the two species, but is harmful to the predator population once it exceeds its critical value. In biological terms, these results highlight the importance of prey refuges in maintaining the stability of predator-prey systems. A reasonable proportion of refuges help to sustain the dynamic balance of the ecosystem, while extreme conditions may lead to extinct populations or even instability of the system.
Next, we will consider the effect of the cooperative relationship between the prey. The mature prey protects the immature prey from being captured by predators, thus the benefits of mature prey to immature prey are bigger than the benefits of immature prey to mature prey. Here, let $ \sigma_1 = 0.1 $ and $ \sigma_2 = 0.01 $. By calculation, we can get that the interior equilibrium is $ (0.8570, 0.1242, 0.2620) $, and system (2.1) is locally asymptotically stable (see Figure 6). According to Figure 6, we can know that cooperation has a positive impact for all species. If there is a cooperative relationship between the prey, the number of immature prey will increase to a certain extent, but the number of mature prey will basically remain stable.
Finally, we choose $ \sigma_1 $ as a bifurcation parameter to discuss the stability of system (2.1). When $ \sigma_1 = 0.1 $, we know that system (2.1) is locally asymptotically stable (see Figure 7(a), (b)). As the value of $ \sigma_1 $ increases, it derives that system (2.1) undergoes Hopf bifurcation when $ \sigma_1 = 1 > 0.8 $ (see Figure 7(c), (d)). Thus, we can get that system (2.1) is stable when $ 0 < \sigma_1 < 0.8 $ and Hopf bifurcation occurs at the interior equilibrium when $ \sigma_1 = 0.8 $ (see Figure 8). We will discuss the stability of system (2.1) by taking $ \sigma_2 $ as a bifurcation parameter. When $ \sigma_2 = 0.01 $, we know that system (2.1) is locally asymptotically stable from Figure 9(a), (b). As the value of $ \sigma_2 $ increases, system (2.1) undergoes Hopf bifurcation around (1.2826, 0.2010, 0.0348) when $ \sigma_2 = 0.055 $ (see Figure 9(c), (d)). Therefore, the benefit of the cooperation between the immature prey and the mature prey becomes larger, then the number of mature prey increases, and so the number of other species also increases to a certain extent. By calculations, we can get that system (2.1) is stable when $ 0 < \sigma_2 < 0.055 $ and Hopf bifurcation occurs at the interior equilibrium when $ \sigma_2 = 0.055 $ (see Figure 10). These results indicate the importance of prey cooperation in maintaining the stability of predator-prey systems, and an appropriate level of cooperation help to sustain the dynamic balance of the ecosystem, while extreme conditions may lead to periodic fluctuations in population sizes or even instability of the system.
5.2. Dynamics of the system in the presence of time delay
In this subsection, we discuss the dynamical behavior of system (1.3) in the presence of time delay by fixing the values of the other parameters as in Table 2. According to Theorem 2.3, system (1.3) has a unique positive equilibrium $ E^*(0.8613, 0.1242, 0.2755) $.
When $ \tau_1 > 0 $ and $ \tau_2 = 0 $, we can get $ \omega_{10} = 0.4316 $, $ \tau_{10} = 2.2654 $ in Theorem 3.1. When $ \tau_1 = 2 < \tau_{10} = 2.2654 $, the positive equilibrium $ E^* $ is locally asymptotically stable (see Figure 11(a)). When $ \tau_1 = 3 > \tau_{10} = 2.2654 $, system (1.3) is unstable at the positive equilibrium $ E^* $, and system (1.3) undergoes Hopf bifurcation at $ \tau_{10} = 2.2654 $ (see Figure 11(b)).
When $ \tau_1 = 0, \tau_2 > 0 $, according to Theorem 3.2, we can get $ \omega_{20} = 0.2070 $, $ \tau_{20} = 0.8527 $. When $ \tau_2 = 0.5 < \tau_{20} = 0.8527 $, the positive equilibrium $ E^* $ is locally asymptotically stable (see Figure 12(a)). When $ \tau_2 = 1 > \tau_{20} = 0.8527 $, system (1.3) is unstable at the positive equilibrium $ E^* $, and system (1.3) undergoes Hopf bifurcation at $ \tau_{20} = 0.8527 $ (see Figure 12(b)). Taking $ \tau_2 $ as a bifurcation parameter, the bifurcation diagram obtained is shown in Figure 14(a).
When $ \tau_1 = \tau_2 = \tau $, we can get $ \omega_{0} = 0.0587 $, $ \tau_{0} = 1.0125 $ in Theorem 3.3. When $ \tau = 0.5 < \tau_{0} = 1.0125 $, the positive equilibrium $ E^* $ is locally asymptotically stable (see Figure 13(a)). When $ \tau = 3 > \tau_{0} = 1.0125 $, system (1.3) is unstable at the positive equilibrium $ E^* $, and system (1.3) undergoes Hopf bifurcation at $ \tau_{0} = 1.0125 $ (see Figure 13(b)). Taking $ \tau $ as a bifurcation parameter, the bifurcation diagram obtained is shown in Figure 14(b).
When $ \tau_1 > 0 $ and $ \tau_2 = 0.8\in[0, \tau_{20}) $, we can get $ \tau_{10}^{'} = 0.1 $ in Theorem 3.4. When $ \tau_1 = 0.01 < \tau_{10}^{'} = 0.1 $, then the positive equilibrium $ E^* $ is locally asymptotically stable (see Figure 15 (a), (b)). When $ \tau_1 = 2 > \tau_{10}^{'} = 0.1 $, we obtain that $ \mathcal{C}_1(0) = -0.4109+0.6987i, \mu_2 = 1.9830 > 0, \beta_2 = -0.8218 < 0, T_2 = -0.6724 < 0 $. From Theorem 3.6, the Hopf bifurcation is supercritical, system (1.3) has stable bifurcating periodic solutions, the period of the bifurcating periodic solutions is decreasing, and system (1.3) undergoes Hopf bifurcation at $ \tau_{10}^{'} = 0.1 $ (see Figure 15(c), (d)).
When $ \tau_2 > 0 $ and $ \tau_1 = 0.5\in[0, \tau_{10}) $, we can get $ \tau_{20}^{'} = 0.8 $ according to Theorem 3.5. When $ \tau_2 = 0.6 < \tau_{20}^{'} = 0.8 $, then the positive equilibrium $ E^* $ is locally asymptotically stable (see Figure 16(a), (b)). When $ \tau_2 = 2 > \tau_{20}^{'} = 0.8 $, the positive equilibrium $ E^* $ is unstable, and system (1.3) undergoes Hopf bifurcation at $ \tau_{20}^{'} = 0.8 $ (see Figure 16(c), (d)).
The above numerical simulation analysis shows that when the time delay is small, the system can maintain local asymptotic stability and the predator and prey populations can coexist under positive equilibrium. However, when the time delay exceeds the critical value (e.g., $ \tau_0 $), the system loses stability and undergoes a Hopf bifurcation, leading to periodic fluctuations in the populations. This result suggests that excessive time delay may disrupt the balance between populations, making the ecosystem more unstable.
Next, the Lyapunov exponents have been derived numerically from system (1.3) in absence of time delay for different species (see Figure 17(a)). All Lyapunov exponents are negative ($ L_1 = -0.2792, L_2 = -0.2037, L_3 = -3.1328 $), and thus system (1.3) is stable. We also show the maximum Lyapunov exponent [46] of system (1.3) for $ \tau_1 = 0, \tau_2 = 1 $ (see Figure 17(b)). In the figure, positive values of the maximum Lyapunov exponent indicates that system (1.3) is unstable. Therefore, it is consistent with $ Case $ $ 3 $ (Figure 12) in the theoretical results.
Finally, we consider the following parameter values: $ a = 6, \; k = 100, \; p_1 = 0.01, \; p_2 = 0.05, \; c = 0.1, \; \delta = 0.02 $, and the other parameters remain unchanged. Figure 18 shows the solution curve of the state variables. Figure 19(a)–(c) show the variation curves of the adjoint variables $ \lambda_1 $, $ \lambda_2 $, and $ \lambda_3 $, respectively. It is easy to see from Figure 19 that the adjoint variables $ \lambda_1 $, $ \lambda_2 $, and $ \lambda_3 $ tend ultimately to $ 0 $ with the increase of time. Dynamical responses of system (2.1) for different values of $ \hbar $ are given in Figure 20. From the calculations, we find that the optimal value of the harvesting effort $ \hbar $ is $ \hbar_\delta = 1.75 $. When the value of $ \hbar $ is less than $ \hbar_{\delta} $, the prey and predator populations coexist. However, if $ \hbar $ exceeds $ \hbar_{\delta} $, the optimal harvesting threshold is surpassed, causing the prey population to gradually decline and eventually go extinct. Consequently, the predator population also declines due to the increasing difficulty of capturing prey. Furthermore, the impact of the cooperation coefficients $ \sigma_1 $ and $ \sigma_2 $ (representing the cooperation between immature and mature prey) on the optimal harvesting effort is illustrated in Figure 21. The results indicate that the optimal harvesting effort decreases as $ \sigma_1 $ and $ \sigma_2 $ increase.
6.
Discussion and conclusions
In this article, we study a predator-prey model that incorporates stage-structure prey, prey refuge, and cooperative behavior. To enhance the realism of the system, we account for the effects of time delays associated with prey maturity and predator gestation. Additionally, the capture rate of the predator for the prey population is modeled using a Holling-II type functional response.
According to calculation, system (2.1) has a trivial equilibrium $ E_0 $, a predator extinction equilibrium $ \widetilde{E} $ and a unique positive equilibrium $ E^* $ when Lemma 2.2 and Theorem 2.3 are satisfied. In the absence of time delay, we found that the prey refuge $ m $ does not influence the stability of system (2.1) when $ m $ is relatively small from Figure 4. However, when $ m\geq0.9 $, the predator population eventually tends to zero, which is detrimental to the survival of the predator, leading to the instability of system (2.1) from Figure 5. Next, for the cooperation coefficients $ \sigma_1 $ and $ \sigma_2 $ of immature prey and mature prey, the research shows that the values of parameters $ \sigma_1 $ and $ \sigma_2 $ could change the stability of system (2.1). System (2.1) exhibits Hopf bifurcation when $ \sigma_1 = 0.8 $ and $ \sigma_2 = 0.055 $ (see Figures 7 and 9). In biological terms, these results highlight the importance of prey refuges and prey cooperation in maintaining the stability of predator-prey systems. A reasonable proportion of refuges and an appropriate level of cooperation help to sustain the dynamic balance of the ecosystem, while extreme conditions may lead to periodic fluctuations in population sizes or even instability of the system. This suggests that it is crucial to balance the protection of prey and the survival of predators to avoid ecological imbalances caused by excessive interventions in ecological conservation.
In the presence of time delay, we divided them into six cases to discuss the stability of the positive equilibrium and the existence of the Hopf bifurcation of system (1.3). For example, under the fourth case $ \tau_1 = \tau_2 = \tau $, the critical value of $ \tau $ is $ \tau_0 $, then system (1.3) is locally asymptotically stable when $ \tau < \tau_0 $, but is unstable when $ \tau > \tau_0 $. That is, the Hopf bifurcation occurs at $ \tau = \tau_0 $, which is demonstrated by Figure 13. Finally, we calculated the optimal value of harvesting effort $ \hbar $ is $ \hbar_\delta = 1.75 $ when $ \hbar < \hbar_\delta $, the prey and predator populations coexist, and the number of prey and predators gradually decrease when $ \hbar > \hbar_\delta $. In the long run, optimal control strategies are not only applicable to population harvesting, but can also be utilized for controlling epidemics in both homogeneous and heterogeneous networks [47]. In a biological sense, these results highlight the importance of studying the control of time delay in maintaining ecosystem stability, and provide a theoretical basis for understanding the impact of time delay on the dynamic behavior of ecosystems.
From an ecological perspective, this study holds greater realistic significance. Additionally, our research provides insights into the reasons behind the periodic dynamics observed in prey and predator populations in real life, effectively validating the reliability of the theoretical results. From the perspective of human economic interests, we examine the impact of harvesting on prey and predator populations, offering valuable reference points for sustainable harvesting practices. In the future, let $ u_1(t) $, $ u_2(t) $, and $ v(t) $ be the densities of immature prey, mature prey, and predator populations at time $ t $, respectively, then we can consider the exponential transformation between the prey and the nonlinear harvest into our model:
with the initial conditions
Additionally, due to the heterogeneity of spatial distribution, populations often migrate and diffuse within a certain spatial range. Therefore, future research can further incorporate stage-structure predator-prey models with spatial diffusion to more comprehensively describe the spatial behavioral characteristics and interaction mechanisms in population dynamics. Let $ u_1(t, x), \; u_2(t, x) $, and $ v(t, x) $ represent the population densities of immature prey, mature prey, and predator populations at location $ x\in\Omega $ and time $ t $, respectively. Here, $ \Omega\subset \mathbb{R}^n $ is a bounded, open, and connected domain with smooth boundary $ \partial\Omega $, then we have the following model:
with the initial conditions
where $ d_1, d_2 $, and $ d_3 $ are the diffusion rates for immature prey, mature prey, and predator populations, respectively.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
We are very grateful to the editor and five reviewers for taking your valuable time to provide constructive comments and useful suggestions for this manuscript, which help us to improve the quality of our manuscript. This work is supported by the National Natural Science Foundation of China (Grant No. 12161054 and 12161011), Funds for Innovative Fundamental Research Group Project of Gansu Province(Grant No. 24JRRA778), the Doctoral Foundation of Lanzhou University of Technology, and the HongLiu First-Class Disciplines Development Program of Lanzhou University of Technology.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: