Dynamic simulation and energy analysis of forced circulation solar thermal system in two various climate cities in Iraq

1.   Introduction

As computer technology and machinery manufacturing technology develops, people are expecting more and more from production automation. Since the last century, the manipulator system has gradually replaced human beings to complete the dangerous and repetitive work in various fields ^[1,2,3,4]. At the same time, the manipulator system can also significantly improve the production efficiency ^[5,6,7]. The flexible manipulator has better performance of high stability, high precision, high efficiency and low energy consumption than the traditional rigid manipulator ^[8,9,10,11]. Consequently, it is more adapted to the complex and changeable working environments in various fields. For example, for the sake of improving the automation level of agricultural production, the flexible manipulator system is adopted to pick fruit and vegetable crops in the field of agriculture, so as to further ensure the safety of agricultural products and improve the production efficiency in the process of processing and production. However, the flexible manipulator is characterized by its complex structure, low control accuracy, difficult control, etc. These defects may lead to vibration of the flexible manipulator system, which greatly affects the stability of the actual production. Thus, improving its stiffness and control accuracy, and suppressing the vibration of the flexible manipulator system have become the focus of current research.

By referring to the literature, we can know that the manipulator system with special flexible structure is a typical infinite dimensional distributed parameter system ^[12,13,14]. Most of the existing studies of the manipulators are based on the ordinary differential equation (ODE) dynamic models ^{[15,16,17,18]}. Nevertheless, these ODE models limit the system to a few key patterns, greatly affecting system performance ^[19]. For getting the accurate description of the flexible manipulator systems, the model cannot be constructed only through a single ODE; otherwise, there will be spillover instability ^[20]. Therefore, it is necessary to introduce partial differential equations (PDEs) in the flexible connection systems. At present, there are some research achievements on flexible systems described by PDEs. In ^[21], for the sake of the achievement of control goals, a boundary controller with input backlash is constructed based on the infinite-dimensional dynamic model. For the single flexible link manipulator system in ^[22], a sliding mode boundary controller is designed based on the adaptive radial basis function (RBF) neural network (NN) to drive the joint to the required position and quickly suppress the vibration on the beam. Then, an adaptive fault-tolerant control method is raised by using RBFNN and LaSalle's invariance principle to solve the failure problem of the actuator of the single-link flexible manipulator in ^[23].

Over the past two decades, systems modeled by PDEs have attracted more and more researchers because of their wide application in various fields, and numerous methods have been reported ^{[24,25,26,27,28]}. However, these results ^{[21,22,23,24,25,26,27,28]} all ignored the constraint problem. In fact, many real-world systems are limited by constraints in various ways ^[29]. It is possible that such constraints are due to physical restriction of systems, or caused by the requirements of safe operation ^[30]. Motivated by progress in constraints, lots of state constraint problems have been researched for ODE systems ^[31,32,33]. With the rise of the research on PDE systems, some scholars also put their attention to the problem of state constraints of PDE flexible mechanical systems. In ^[34], a class of flexible riser systems with backlash modeled by PDEs is considered. In order to solve its position and velocity constraints, logarithmic BLF is used. In ^[35], the state feedback control problem of moving vehicle-mounted manipulator modeled by PDE with output constraint is studied. Under the action of the designed control scheme, the position control and vibration suppression are effectively improved. For the uncertain PDE flexible manipulator system in ^[36], a NN fault-tolerant control scheme under state constraints is proposed. In the design process, the tangent BLF is utilized to handle the constraint problem, and get a good control.

In addition to the state constraint problem, in today's society, production resources are also tight. While meeting the quality of control, saving resources has become an important aspect that needs to be consider. In recent years, the event triggered control ^{[37,38,39,40]}, as an effective method that can not only achieve control objectives, but also save resources, has raised the broad interest of all researchers. The event triggered control is a control mechanism of sampling on demand. System resources can only be used when necessary, and can meet the expected control performance indicators. In ^[41], a collaborative design scheme consisted of switching event triggering mechanism and mode dependent adaptive control law is proposed which solves the mismatch problem and avoids the Zeno behavior. In ^[42], for nonlinear uncertain systems, besides the design methods on the basis of fixed threshold strategy and relative threshold strategy, a new switching threshold strategy is proposed. However, the above results are only applicable to the system modeled by ordinary differential methods. When these methods are directly applied to the control system modeled by partial differential methods, it may lead to the failure of control strategy, and even bring huge losses to practical engineering. In addition, in the actual production and life, many control systems need to be modeled by partial differential method to achieve better control effect. Among them, the flexible manipulator system modeled by partial differential method is widely used in ^[43,44,45]. Therefore, in order to make efficient use of resources, the event-triggered control of flexible manipulator systems modeled by PDEs under state constraints is a significant topic of study that has inspired our own research.

It can be seen from the above analysis that although researchers have put forward many research results for flexible manipulator system, there are still some limitations. Therefore, the event-triggered control of a PDE flexible manipulator with constraints will be taken as the research object in this paper, and the control goal of saving communication resources will be achieved by designing event-triggered controllers. On the premise of achieving the stable performance of the system, good vibration suppression effect of the flexible manipulator will be maintained. On account of the above discussion, the innovation of this article is given below: when dealing with the state constraint of PDE flexible manipulator system, an event trigger control strategy is introduced.

In this paper, an event-triggered control design problem is studied for flexible manipulator systems with full state constraints. Under frameworks of adaptive backstepping control design technique, an event-triggered control scheme is proposed for flexible manipulator systems. The main contribution of the paper is summarized as follows:

1) In this paper, the design problem of event-triggered control is studied for flexible manipulator system with full state constraints and an event-triggered control method is proposed. Different from the constraint control scheme in ^[31,32], the event-triggered control strategy proposed in this paper can save unnecessary control signal transmission and improve the system performance.

2) An event-triggered mechanism with relative threshold is designed, and the control signal update is event-driven under well-established event-triggered strategy. The proposed event-triggered control scheme effectively reduces the communication burden in the controller-to-the-actuator channel and still ensures the system stability, and it achieves the control objective.

The main contents of Sections 2 to 6 are as follows: Section 2 is the partial differential system model, and it gives the assumption and control objectives. The design procedure of the event trigger controllers based on Tan-BLF and backstepping technique is introduced in Section 3. Section 4 is the system stability analysis process. In Section 5, the effectiveness of the proposed method is further demonstrated with the help of a simulation example. Finally, the conclusion is given in Section 6.

Notations. To simplify and differentiate, notations ${\left( {\rm A} \right)_r} = {{\partial \left( {\rm A} \right)} \mathord{\left/ {\vphantom {{\partial \left( {\rm A} \right)} {\partial r}}} \right. } {\partial r}}$, $\left( {\dot {\rm A}} \right) = {{\partial \left( {\rm A} \right)} \mathord{\left/ {\vphantom {{\partial \left( {\rm A} \right)} {\partial \tau }}} \right. } {\partial \tau }}$ throughout this paper. In the same way, ${\left( {\rm A} \right)_{rr}}$ means ${{{{\partial ^2}\left( {\rm A} \right)} \mathord{\left/ {\vphantom {{{\partial ^2}\left( {\rm A} \right)} {\partial r}}} \right. } {\partial r}}^2}$, ${\left( {\rm A} \right)_{rrr}} = {{{{\partial ^3}\left( {\rm A} \right)} \mathord{\left/ {\vphantom {{{\partial ^3}\left( {\rm A} \right)} {\partial r}}} \right. } {\partial r}}^3}$ and ${\left( {\rm A} \right)_{rrrr}} = {{{{\partial ^4}\left( {\rm A} \right)} \mathord{\left/ {\vphantom {{{\partial ^4}\left( {\rm A} \right)} {\partial r}}} \right. } {\partial r}}^4}$, $\left( {\ddot {\rm A}} \right)$ ${{{ = {\partial ^2}\left( {\rm A} \right)} \mathord{\left/ {\vphantom {{ = {\partial ^2}\left( {\rm A} \right)} {\partial \tau }}} \right. } {\partial \tau }}^2}$. In addition, ${\left( {\rm A} \right)^T}$ stands for transposition of $\left( {\rm A} \right)$.

2.   System description and preliminaries

Based on the Hamiltonian principle ^[37], the dynamic model of the flexible manipulator system is solved as follows

where $ϵ\left({\rm A}\right)$ means the variation of $\left( {\rm A} \right)$. The expressions of kinetic energy ${E_k}$, potential energy ${E_p}$ and work $W$ produced in the operation of the system are respectively listed as

where ${I_h}$ stands for the hub inertia; $\varrho \left( \tau \right)$ represents the joint angle; $\ell$ and $Y$ are the mass per unit length and the arc length at $r$ of the flexible manipulator, respectively, where $Y\left( {r, \tau } \right) = r\varrho \left( \tau \right) + \zeta \left( {r, \tau } \right)$; the mass of the payload is $m$; the bending stiffness is denoted by $EI$; the manipulator length and the connecting rod vibration deflection at $r$ are expressed by $X$ and $\zeta (r, \tau )$; the torque input of the joint motor and the force input of the actuator are represented with $\Phi \left( \tau \right)$ and $O\left( \tau \right)$, respectively.

Combined with the Hamiltonian principle, through a series of derivations, the system PDE model can be written as follows:

Furthermore, $\varrho \left( \tau \right)$ and $\zeta \left( {X, \tau } \right)$ are the system outputs, and they meet $\varrho \left( \tau \right) < {k_{{d_1}}}$ and $\zeta \left( {X, \tau } \right) < {k_{{d_2}}}$ with ${k_{{d_1}}}$ and ${k_{{d_2}}}$ being constants. There are two constants ${k_{{c_1}}}$ and ${k_{{c_2}}}$ such that following formulas hold:

where ${z_1} = \varrho \left( \tau \right) - {\varrho _d}$, ${\varrho _d}$ is the ideal angle position, and ${\varrho _d}$ is a constant, and ${z_3} = \zeta \left( {X, \tau } \right) - {\zeta _d}\left( {X, \tau } \right)$, ${\zeta _d}\left( {X, \tau } \right)$ means the required vibration.

Assumption 1 ^[46]. Suppose that the parameters ${\zeta _{rr}}\left( {0, \tau } \right)$ and ${\zeta _{rrr}}\left( {X, \tau } \right)$ are attainable.

Control objective: The event-triggered controllers are designed to realize the following control objectives:

1) suppresses the vibration of the manipulator and stabilizes it in the desired position.

2) the joint angle $\varrho \left( \tau \right)$ and boundary vibration diversion $\zeta \left( {X, \tau } \right)$ are confined within the constraints.

3) the system signals are all bounded.

4) it can effectively avoid the occurrence of the Zeno behavior.

3.   Design of the event-triggered boundary control

The following Eqs (11) and (12) are the system boundary errors:

where $\mu \left( \tau \right) = - {k_1}{z_1}\left( \tau \right)$ and $\vartheta \left( \tau \right) = - {k_3}{z_3}\left( \tau \right)$ are virtual controls with ${\dot \varrho _d} = 0$ and ${\dot \zeta _d} = 0$, ${k_1} > 0$ and ${k_3} > 0$.

Taking the derivative of (11)–(14), and combining (5)–(8), one has

where $\rho = {m \mathord{\left/ {\vphantom {m {{I_h}}}} \right. } {{I_h}}}$.

Choose the following Lyapunov function:

Then, taking the derivative of ${V_1}\left( \tau \right)$ based on ${\dot z_1}\left( \tau \right)$, one gets

In order to eliminate the ${z_1}\left( \tau \right){z_2}\left( \tau \right)$ in (20), the Lyapunov function ${V_2}\left( \tau \right)$ is selected in the following form:

The derivative of ${V_2}\left( \tau \right)$ along time is

The boundary controller is designed as

where ${k_2} > 0$ is a constant. Substituting (23) into (22) yields

Construct the following Lyapunov function, ${V_3}\left( \tau \right)$, as

Then, from (17), the ${\dot V_3}\left( \tau \right)$ can be obtained as

Select ${V_4}\left( \tau \right)$ as

Then, the differential coefficient of ${V_4}\left( \tau \right)$ is

The desired boundary controller is designed as

where ${k_4} > 0$ is a constant.

From (29) and (28), one has

The event trigger mechanism is proposed so that the communication resources are commendably reduced.

Under the event-triggering mechanism, the boundary control strategy is designed as follows

where ${e_1}\left( \tau \right) = {\hbar _1}\left( \tau \right) - {\Phi _0}\left( \tau \right)$, ${e_2}\left( \tau \right) = {\hbar _2}\left( \tau \right) - {O_0}\left( \tau \right)$, ${\kappa _1}$, ${\kappa _2}$, $0 < {\delta _1} < 1$, $0 < {\delta _2} < 1$ are all positive design parameters. ${\tau _k}, k \in {\mathbb{Z}^ + }$, and ${\tau _s}, s \in {\mathbb{Z}^ + }$ are the moments when the event is triggered. The times will be respectively marked as ${\tau _{k + 1}}$ and ${\tau _{s + 1}}$ whenever (32) and (34) are triggered, and the control values ${\Phi _0}\left( {{\tau _{k + 1}}} \right)$ and ${O_0}\left( {{\tau _{s + 1}}} \right)$ will be applied to the system.

Design ${\hbar _1}\left( \tau \right)$ and ${\hbar _2}\left( \tau \right)$ as follows:

where

${a_i} > 0, i = 1, 2$, and ${\bar \kappa _i} > {{{\kappa _i}} \mathord{\left/ {\vphantom {{{\kappa _i}} {\left( {1 - {\delta _i}} \right)}}} \right. } {\left( {1 - {\delta _i}} \right)}}, i = 1, 2$.

According to (32) and (34), it holds that $\left| {{\hbar _1}\left( \tau \right) - {\Phi _0}\left( \tau \right)} \right| < {\delta _1}\left| {{\Phi _0}\left( \tau \right)} \right| + {\kappa _1}$ and $\left| {{\hbar _2}\left( \tau \right) - {O_0}\left( \tau \right)} \right| < {\delta _2}\left| {{O_0}\left( \tau \right)} \right| + {\kappa _2}$, for $\forall \tau \in \left[ {{\tau _k}, {\tau _{k + 1}}} \right)$ and $\forall \tau \in \left[ {{\tau _s}, {\tau _{s + 1}}} \right)$. Then, there are parameters ${\lambda _1}\left( \tau \right) \leqslant 1$ ${\lambda _2}\left( \tau \right) \leqslant 1$, ${\eta _1}\left( \tau \right) \leqslant 1$ and ${\eta _2}\left( \tau \right) \leqslant 1$, such that

Then, we get

Further, ${\dot V_2}\left( \tau \right)$ and ${\dot V_4}\left( \tau \right)$ can be rewritten as

Note that, for $\forall n \in R$ and ${a_i} > 0, i = 1, 2$, one has $- n\tanh \left( {{n \mathord{\left/ {\vphantom {n {{a_i}}}} \right. } {{a_i}}}} \right) \leqslant 0$. Then, based on (35), one has

In addition, due to ${\lambda _1}\left( \tau \right) \leqslant 1$ and ${\lambda _2}\left( \tau \right) \leqslant 1$, (41) and (42) hold

Thus, according to (35), one gets

Both adding and subtracting $\left| {{z_2}\left( \tau \right){{\bar \kappa }_1}} \right|$ and ${z_2}\left( \tau \right){\hbar _1}\left( \tau \right)$, one obtains

Consider the property of ${\rm{tanh}}(·)$ that

with $D \in R$ and $\gamma > 0$. Therefore, one has

Substituting (48) into (47), one has

Then, based on (44), this leads to

Further consider ${\bar \kappa _1} > {{{\kappa _1}} \mathord{\left/ {\vphantom {{{\kappa _1}} {\left( {1 - {\delta _1}} \right)}}} \right. } {\left( {1 - {\delta _1}} \right)}}$, this leads to

Then, ${\dot V_2}\left( \tau \right)$ is further expressed as

and ${\dot V_3}\left( \tau \right)$ can be rewritten as

In the same way, consider (40), and ${\dot V_4}\left( \tau \right)$ can be rewritten as

Note that when ${a_2} > 0$ for $\forall n \in R$, $- n\tanh \left( {{n \mathord{\left/ {\vphantom {n {{a_2}}}} \right. } {{a_2}}}} \right) \leqslant 0$ is always true. Thus, from (36), it can be sure that

Since $\left| {{\eta _i}} \right| \leqslant 1, {\kern 1pt} {\kern 1pt} i = 1, 2$, it can be seen that

Further, according to (36), one has

Then, both adding and subtracting $\left| {{z_4}\left( \tau \right){{\bar \kappa }_2}} \right|$ and ${z_4}\left( \tau \right){\hbar _2}\left( \tau \right)$ on the right side of (58), it holds that

Because of the property in (47), it is further known that

Substituting (60) into (54), one has

Then, based on (57), this leads to

Further consider ${\bar \kappa _2} > {{{\kappa _2}} \mathord{\left/ {\vphantom {{{\kappa _2}} {\left( {1 - {\delta _2}} \right)}}} \right. } {\left( {1 - {\delta _2}} \right)}}$, and one has

Then, ${\dot V_4}\left( \tau \right)$ is further expressed as

4.   Stability analysis

We can get the theorem result as below according to the above analysis process.

Theorem 1: Consider the flexible manipulator system as shown in (5)–(8), under Assumption 1, and design the event-triggered controllers in (35) and (36). Then the presented approach guarantees that 1) the vibration of the manipulator is effectively restrained and stabilized, 2) all the signals displaying in the closed-loop system are bounded, 3) the joint angle $\varrho \left( \tau \right)$ and the boundary vibration diversion $\zeta \left( {X, \tau } \right)$ fulfill the constraint conditions $\varrho \left( \tau \right) < {k_{{d_1}}}$ and $\zeta \left( {X, \tau } \right) < {k_{{d_2}}}$, respectively, and 4) the system can effectively avoid the occurrence of the Zeno behavior.

Proof:

The Barrier Lyapunov function is considered as

On the basis of the above analysis, one obtains

where $c = \min \left( {2{k_1}, {{2{k_2}} \mathord{\left/ {\vphantom {{2{k_2}} {{I_h}}}} \right. } {{I_h}}}, 2{k_3}, {{2{k_4}} \mathord{\left/ {\vphantom {{2{k_4}} m}} \right. } m}} \right)$, and $d = 0.557{a_1} + 0.557{a_2}$.

Multiplying ${e^{c\tau }}$ on both sides of (66), and integrating (66) over $\left[ {0, \tau } \right]$, one can obtained that

According to (66) and (67), the boundedness of errors ${z_i}, i = 1, 2, 3, 4$ is known. Meanwhile, since ${\varrho _d}$, $\mu$, ${\zeta _d}\left( {X, \tau } \right)$ and $\vartheta$ are bounded, according to (11)–(14), one gets that $\varrho \left( \tau \right)$, $\dot \varrho \left( \tau \right)$, $\zeta \left( {X, \tau } \right)$ and $\dot \zeta \left( {X, \tau } \right)$ are also bounded. Similarly, according to (35) and (36), the boundedness of ${\hbar _1}\left( \tau \right)$ and ${\hbar _2}\left( \tau \right)$ are obviously proved. Considering ${e_1} = \hbar \left( \tau \right) - {\nu _d}$ and ${e_3} = \rho \left( {X, \tau } \right) - {\rho _d}\left( {X, \tau } \right)$, we can get $\left| {\varrho \left( \tau \right)} \right| = \left| {{z_1} + {\varrho _d}} \right| \leqslant \left| {{z_1}} \right| + \left| {{\varrho _d}} \right|$ and $\left| {\zeta \left( {X, \tau } \right)} \right| = \left| {{z_3} + {\zeta _d}\left( {X, \tau } \right)} \right|$ $\leqslant \left| {{z_3}} \right| + \left| {{\zeta _d}\left( {X, \tau } \right)} \right|$. According to (9) and (10), it holds that $\left| {\varrho \left( \tau \right)} \right| \leqslant {k_{{c_1}}} + \left| {{\varrho _d}} \right| < {k_{{d_1}}}$ and $\left| {\zeta \left( {X, \tau } \right)} \right| \leqslant {k_{{c_2}}} + \left| {{\zeta _d}\left( {X, \tau } \right)} \right| < {k_{{d_2}}}$, which means that system states are within their constraint bounds.

Recall the definition of ${e_i}\left( \tau \right), i = 1, 2$, i.e., ${e_1}\left( \tau \right) = {\hbar _1}\left( \tau \right) - {\Phi _0}\left( \tau \right)$, ${e_2}\left( \tau \right) = {\hbar _2}\left( \tau \right) - {U_0}\left( \tau \right)$, where ${\Phi _0}\left( \tau \right) = {\hbar _1}\left( {{\tau _k}} \right)$ for $\forall \tau \in \left[ {{\tau _k}, {\tau _{k + 1}}} \right)$, and ${O_0}\left( \tau \right) = {\hbar _2}\left( {{s_k}} \right)$ for $\forall \tau \in \left[ {{\tau _s}, {\tau _{s + 1}}} \right)$. Then, one has

Here ${\dot \hbar _1}\left( {{\tau _k}} \right)$ and ${\dot \hbar _2}\left( {{\tau _s}} \right)$ can be regarded as constants at the time interval $\left[ {{\tau _k}, {\tau _{k + 1}}} \right)$ and $\left[ {{\tau _s}, {\tau _{s + 1}}} \right)$, which means that ${\dot \hbar _1}\left( {{\tau _k}} \right) = 0$ and ${\dot \hbar _2}\left( {{\tau _s}} \right) = 0$. Then, we have

According to the definition of ${\hbar _1}\left( \tau \right)$ and ${\hbar _2}\left( \tau \right)$ in (35) and (36), we know that ${\dot \hbar _1}\left( \tau \right)$ and ${\dot \hbar _2}\left( \tau \right)$ are the functions of ${z_i}, i = 1, 2, 3, 4$. From the result before, all the system signals are bounded, so ${\dot \hbar _1}\left( \tau \right)$ and ${\dot \hbar _2}\left( \tau \right)$ are bounded. Then, we assume that ${\dot \hbar _1}\left( \tau \right) \leqslant {\bar \hbar _1}$, ${\dot \hbar _2}\left( \tau \right) \leqslant {\bar \hbar _2}$ with ${\bar \hbar _1}$ and ${\bar \hbar _2}$ being constants. In addition, ${e_1}\left( {{\tau _k}} \right) = 0$, ${e_2}\left( {{\tau _s}} \right) = 0$ and ${\lim _{\tau \to {\tau _{k + 1}}}}{e_1}\left( {{\tau _{k + 1}}} \right) = {\delta _1}\left| {{\Phi _0}\left( \tau \right)} \right| + {\kappa _1}$, ${\lim _{\tau \to {\tau _{s + 1}}}}{e_2}\left( {{\tau _{s + 1}}} \right) = {\delta _2}\left| {{O_0}\left( \tau \right)} \right| + {\kappa _2}$. By integrating (68) and (69) on their both sides, one gets ${\tau _{k + 1}} - {\tau _k} \geqslant T = {{\left( {{\delta _1}\left| {{\Phi _0}\left( \tau \right)} \right| + {\kappa _1}} \right)} \mathord{\left/ {\vphantom {{\left( {{\delta _1}\left| {{\Phi _0}\left( \tau \right)} \right| + {\kappa _1}} \right)} {{{\bar \hbar }_1}}}} \right. } {{{\bar \hbar }_1}}}$ and ${\tau _{s + 1}} - {\tau _s} \geqslant T = {{\left( {{\delta _2}\left| {{O_0}\left( \tau \right)} \right| + {\kappa _2}} \right)} \mathord{\left/ {\vphantom {{\left( {{\delta _2}\left| {{O_0}\left( \tau \right)} \right| + {\kappa _2}} \right)} {{{\bar \hbar }_2}}}} \right. } {{{\bar \hbar }_2}}}$. Thus, the Zeno behavior can be avoided.

Theorem 1 is demonstrated integrally.

5.   Simulation

In order to verify the effectiveness of the control strategy designed in this paper, a system simulation based on (5)–(8) is considered. The system parameters are selected as follows: $EI = 10{\kern 1pt} {\kern 1pt} {\kern 1pt} N{m^2}$, $X = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m}}$, $\ell = 0.5{\kern 1pt} {\kern 1pt} {\kern 1pt} kg{m^{ - 1}}$, $m = 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} kg$, and ${I_h} = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} kg{m^2}$. The other related parameters are chosen as ${\varrho _d} = 0.03$, ${\zeta _d} = 0$, ${k_1} = 10$, ${k_2} = 10$, ${k_3} = 10$, ${k_4} = 10$, ${\kappa _1} = 1$, ${\kappa _2} = 1$, ${\delta _1} = 0.15$, ${\delta _2} = 0.15$, ${\bar \kappa _1} = 2$, ${\bar \kappa _2} = 2$, ${a_1} = 0.4$, ${a_2} = 0.4$. In order to further compare with other control methods, the proportional differential (PD) control ${\hbar _1}\left( \tau \right) = - 2.5{\zeta _{rr}}\left( {0, \tau } \right) - 1.5\varrho \left( \tau \right) - 1.5\dot \varrho \left( \tau \right)$, ${\hbar _2}\left( \tau \right) = - 2.5{\zeta _{rrr}}\left( {X, \tau } \right) - 1.5\zeta \left( {X, \tau } \right) - 1.5\dot \zeta \left( {X, \tau } \right)$ is proposed in this paper. The simulation results are given as Figures 1–9.

Figure 1.  Displacement $\zeta \left( {r, \tau } \right)$ of the system without control.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Displacement $\zeta \left( {r, \tau } \right)$ of the system with event trigger control.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Trajectories of $\zeta \left( {X, \tau } \right)$ under control (solid line) and without control (dotted line).

DownLoad: Full-Size Img PowerPoint

Figure 4.  Trajectories of $\varrho \left( \tau \right)$, ${\varrho _d}$, ${k_{{d_1}}}$ and $- {k_{{d_1}}}$.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Trajectories of $\zeta \left( {X, \tau } \right)$, c, ${k_{{d_2}}}$ and $- {k_{{d_2}}}$.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Trajectories of ${\hbar _1}\left( \tau \right)$ and ${\hbar _2}\left( \tau \right)$.

DownLoad: Full-Size Img PowerPoint

Figure 7.  The time intervals of the event-triggered manipulator.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Displacement $\zeta \left( {r, \tau } \right)$ of the system with PD control.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Trajectories of $\zeta \left( {X, \tau } \right)$, c, ${k_{{d_2}}}$ and $- {k_{{d_2}}}$ under PD control.

DownLoad: Full-Size Img PowerPoint

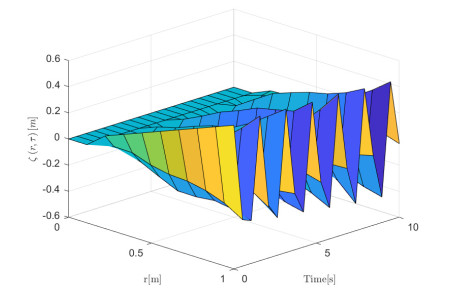
Figure 1 shows the system vibration deflection without any control. It is obvious that the manipulator moves freely with large amplitude. Figure 2 shows the system vibration deflection under the action of the event trigger controller. It can be seen from the figure that the amplitude of the manipulator becomes gentle within a short time, forming an obvious contrast with Figure 1. Figure 3 is the trajectory of boundary vibration deflection $\zeta \left( {X, \tau } \right)$ of the system with (curve) or without (dotted line) control. It can be seen that when the system does not apply any control, $\zeta \left( {X, \tau } \right)$ changes periodically, and the amplitude is changed greatly, which will damage the flexible manipulator system and reduce the working accuracy. In the case of control, the boundary vibration deflection $\zeta \left( {X, \tau } \right)$ gradually tends to be stable, which greatly reduces the system loss. Figures 4 and 5 respectively indicate the trajectories of state junction angle $\varrho \left( \tau \right)$ and state boundary deflection $\zeta \left( {X, \tau } \right)$. From the figures we can know, that $\varrho \left( \tau \right)$ and $\zeta \left( {X, \tau } \right)$ remain within the constraint boundaries. In the meantime, the tracking performances of $\varrho \left( \tau \right)$ and $\zeta \left( {X, \tau } \right)$ are good. It can be clearly seen that based on the adopted control solution; they are adjusted to the expected value. Figure 6 is the trajectories of event trigger controllers ${\hbar _1}\left( \tau \right)$ and ${\hbar _2}\left( \tau \right)$. Figure 7 is the time interval for triggering events, which indicates that the Zeno phenomenon is successfully avoided. The displacement and the boundary output changes under state constraints with PD control are shown in Figures 8 and 9. Compared with the simulation results in the previous case, it is obvious that the control strategy proposed in this paper is smoother and more effective than PD control. Obviously, they are bounded. From all the analysis so far, we conclude the following result. The control objectives of this paper can be realized under the action of the proposed control strategy.

6.   Conclusions

A vibration suppression control algorithm with event-triggered mechanism is proposed for manipulator system described by PDEs with state constraints. State constraints and event-triggered problems are considered simultaneously in the course controller design. Based on the BLF and relative threshold strategy, the method we developed reduces the cost of information transmission and guarantees that the system signals of the under consideration are all bounded. The elastic vibration of flexible manipulator is well suppressed, and the constrained states do not break the constraint bounds. In addition, the Zeno phenomenon is successfully avoided. Simulation results show the validity of the proposed algorithm. At a future date, the proposed scheme can be further studied and spread in other partial differential practical systems with DoS attacks like in ^[47].

Acknowledgments

The paper is supported by the National Key Research and Development Program of China (2018YFF0300605).

Conflict of interest

The authors declare that they have no conflict of interest.