India is a developing nation with 1.35 billion populations living in varied strata of living standards. Therefore, the energy demand is constantly increasing in an effort to accelerate industrial activities and boost the economy. The country mostly meets its electricity demand from fossil fuel. It has large generation capacity but in some remote and rural areas only 53% of the villages get electric supply for less than 12 hours a day. This is because of hilly and mountainous terrains especially in the north and north-eastern regions of the country and absence of utility grid owing to economic reasons. It is estimated that about 15% of country's population do not have access to electricity. With huge hydro potential in the country, especially in the Himalayan States, hydropower generation may be emphasized and pressed in to augment ever increasing energy demand. The emphasis should be on small hydropower (SHP) as construction of large hydropower involves huge capital cost and they are associated with various techno-economic and social issues. The article aims to provide important information for appropriate policy making in developing small hydropower in India.
1.
Introduction
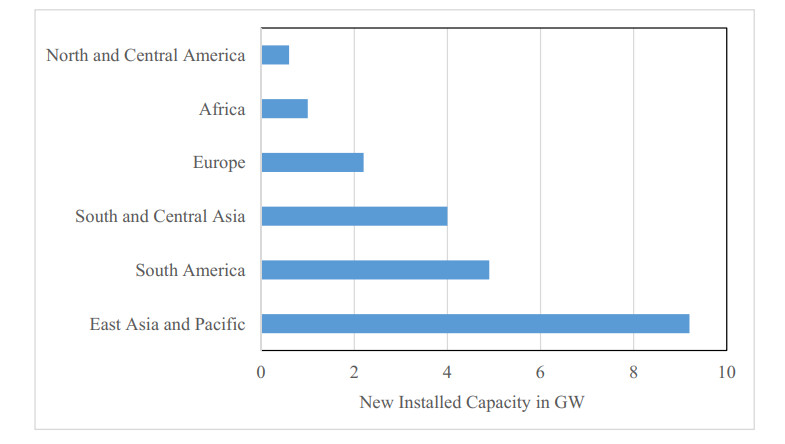
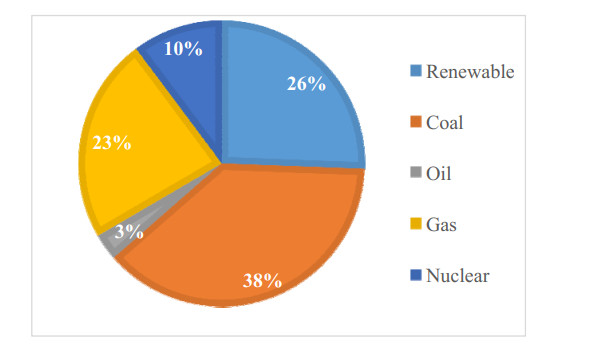
The economic development and societal progress is highly influenced by per capita energy consumption. In order to fulfil the energy requirements, more and more electricity generation is essential. Presently, 74.4% of the energy utilized in the world is obtained from fossil fuel based generating stations. But such generating stations are deterrent to cleanliness of environment. The worldwide energy generation from renewable energy sources stands at 26% as shown in Figure 3 [1]. The leading top 5 countries in hydropower generation are China, Brazil, United States, Canada and India which accounts for 53.4% of total installed capacity in the world. China has the highest hydropower installed capacity of 320 GW which stands at 27.2% of the total installed capacity followed by Brazil, United States, Canada and India at 8.04%, 7.9%, 6.2% and 3.86% respectively. Thus, many researchers are working on the prospects of harnessing biomass, hydro, solar and wind energy sources in order to produce clean energy and reduce the environmental damages. Hydropower is considered as leading renewable energy source and is gaining importance in the map of worldwide electricity generation [2,3,4]. Hydropower is “clean energy” as it comes naturally and is one of the most cost effective and sustainable energy. It can be replenished much faster than being consumed. According to report of International Hydropower Association, 26 PWh of electricity was generated in the year 2019 and Figure 4 shows the contribution of different source used for electricity generation. It shows that 16% of the total generation were from hydropower so, basically hydropower contribute the highest of approximate 62.10% of the total electricity produced by renewable energy source [1]. Contribution of Hydropower is very important in electricity generation for future and International Energy Association (IEA) stated that Hydropower will continue to become main energy source of renewable energy source in 2024 [5]. According to report of IEA 2019, the hydropower electricity generation attained nearly 4, 200 terawatt hours (TWh) and an approximate hydropower of 23.8 gigawatts (GW) capacity was put into operation bringing the world’s installed capacity to 1, 292 gigawatts (GW). The East Asia and Pacific region shows the fastest growth with 9.2 GW of hydropower installed capacity added to it. The total installed capacity and generation by region are represented through Table 1 and Figure 1 represent the new installed capacity by region.
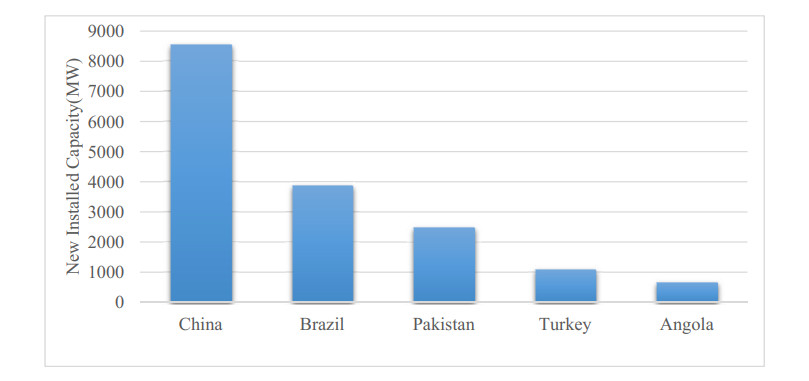
Many countries are also working to increase the hydropower capacity and in the year 2018 Forty eight countries added hydropower capacity among which China has the highest new installed capacity of 8, 540 MW. Figure 2 shows the top 5 countries with highest new installed capacity [1].
Hydropower emits the lowest greenhouse gas; it is predictable and has high efficiency. Because of its flexibility and reliability, such generating stations can be integrated with any other emerging energy systems and hence, hydropower is implemented on large and small scale power generation. Large hydropower, however, is associated with displacement of people, submergence of land in the catchment area, risk of dam malfunction, damage to ecosystem, etc. These issues are usually absent in small hydropower and it is found to be extremely beneficial in supplying electricity, especially to remote and rural areas where grid accessibility is constrained [6,7]. Utilizing hydropower for electricity generation in place of coal prevents release of 148 million tonnes of particulate, 62 million tonnes of sulphur dioxide and 8 million tonnes of nitrogen oxide every year. India has abundant water resources that can be harnessed for electricity generation. Thus, the prospects of hydropower in India need to be relooked with greater zeal and scientific temper. This paper aims to present the status of the water resources focusing mainly on present conditions, various schemes and obstacles of small hydropower development in India and around the world.
2.
Methodology
This article is based on studies and analyses of latest scientific literatures presented in journals and conferences, data obtained from various ministries of the government of India and books related to hydropower development. Extensive literature review is carried out and eventually large and small hydropower is segregated and a detail discussion is presented against short hydropower in India category. The article is divided in 5 section which cover status of SHP in India, review of recent article on SHP in India, policies and schemes of SHP development, challenges of SHP development, areas of research in SHP and conclusion.
3.
Small hydropower in India
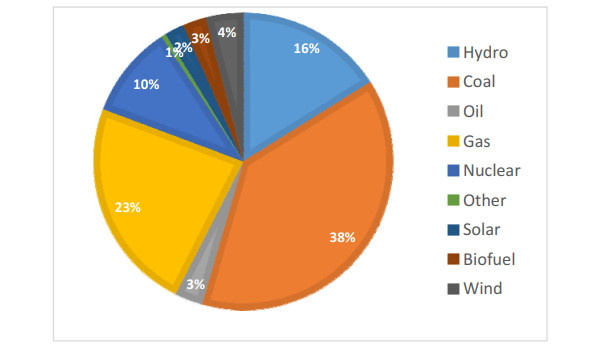
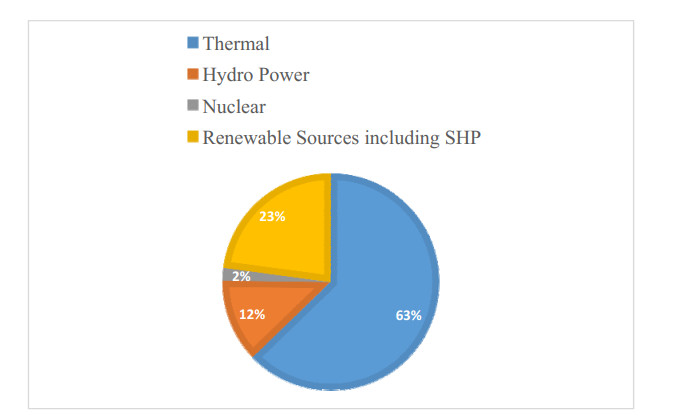
India is a country with 1.35 billion population and third largest electricity energy consumer in the world after China and US. According to Key World Energy Statics 2019, India is the third largest producer of electricity in the world with the generation of 1, 561 TWh. Although power generation has stretched more than 100 times since independence in 1947, the energy demand is ever increasing due to accelerating economic activities. In order to boost growth in primary sectors such as agriculture, industrial or manufacturing and service sectors abundant availability of electricity is inevitable. Electricity is one of the eight core industries of India and thus, it directly correlates electricity usage and economic development. By providing access to electricity, the country is putting all out efforts to reduce poverty. At present the total installed capacity of India is 370, 106 MW and the contributions of various sources of electricity are presented in Figure 5. It can be seen that fossil fuel such as coal, natural gas, and oil contributes 62.7% of electricity generation [8]. It is anticipated that energy demand will be more than double by 2030, while electricity demand will be almost triple [9]. But studies have shown that most of the fossil fuels will be exhausted by 22nd century. Therefore, shifting attention to generation of electricity from renewable energy sources needs to be emphasized. Government of India has targeted increase in renewable generation up to 175 GW by 2022 [10]. Presently India is 5th largest producer of hydro power energy in the world with an installed capacity of 45, 699 MW as on April 24, 2020 with more than 80% of the hydropower capacity being distributed among the Himalayan States. However, hydro power contributes only 12.4% of the total installed capacity in the country [9]. In India hydropower are commonly classified into small and large hydropower. The large hydropower is governed by Ministry of Power and small hydropower up to 25 MW is looked after by the Ministry of New and Renewable Energy [11]. The large hydropower is often opposed by societies, environmentalist and non-governmental organizations for fear of flooding, desertification, relocation issues, etc. Therefore, small hydropower can be envisaged as a better solution for electricity generation. Small hydropower is usually clean, sustainable and environmental friendly as most of the SHPs are canal based or run of river type which uses running water to drive the turbine. The weir or barrage is small and no water is stowed; it is free from problems such as relocation of local inhabitants or deforestation which are usually associated with large hydropower [12]. Because SHPs are sustainable, they are exempted from forest and land clearance and are free from public sitting/plenary inquiry in many countries including India [13,14]. SHPs are economically feasible and the gestation period is rather low [15]. SHPs are ideal for powering villages and far-flung or isolated areas. The accessibility of electricity in these areas will boost small scale industries and thereby improve the socio-economic status of the people [16,17]. SHP does not emit greenhouse gas; and lesser greenhouse gas means lesser carbon foot print thus, decreased CO2 release [18]. The capacity of SHP is different in different countries; for instance, in China, capacity up to 50 MW is considered as SHP while in USA the capacity is up to 100 MW [12]. The classification of SHP in India is shown in Table 2 and Table 3 shows the attainment of small hydropower along with other renewable source in grid connected renewable power in the country [19].
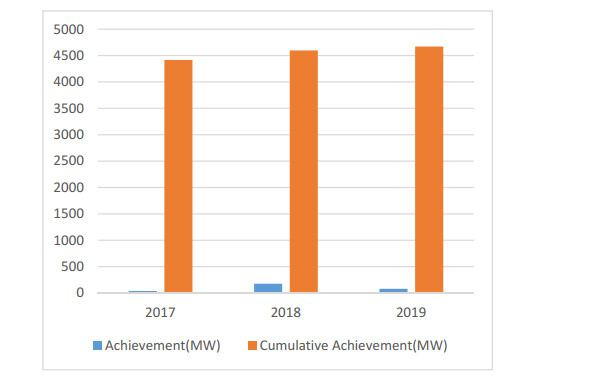
From 7, 133 odd sites situated in different parts of the country, the approximated potential of SHP in India is 21.13 GW out of which 1, 127 SHP plants contributes to 4, 671.55 MW installed capacity as recorded till December 31, 2019; another 109 SHP plants are in different phases of completion. SHPs are implemented by both public and private sectors or collaboration of both to enhance the contribution of SHP in the power market of India. The growth of SHP for the last three years is shown in Figure 6 [19,20,21]. Table 4 presents the potential and installed capacity of SHP in India.
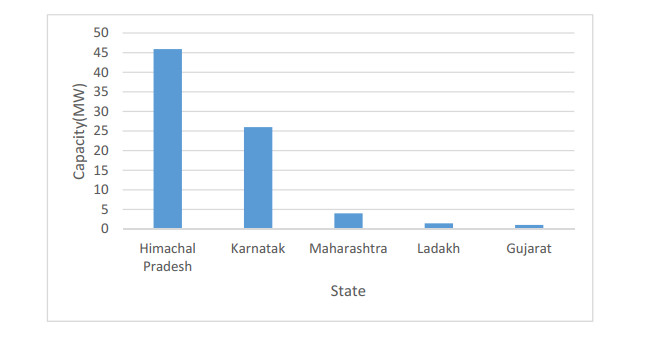
From the Table 4, it can be seen that the State of Karnataka has the highest installed capacity followed by Himachal Pradesh and Maharashtra. The north and north eastern region of India has high potential of SHP; the north eastern part of India is often called ‘Future Power House’ of India [22]. Table 5 details the tariff figures of SHP for the year 2019-20; it shows that the capital cost of the SHP plant is inversely proportional to plant size [23]. Government of India is promoting accelerated development of SHP and in the year 2019-20, 12 SHP projects were commissioned out of which 6 projects are in the State of Himachal Pradesh with generating capacity of 45.9 MW and is illustrated in Figure 7 [19].
4.
Review of recent articles of small hydropower in India
In this section, recent articles published between 2015 and 2020 are exhaustively reviewed and it is found that most of the studies discusses the environmental impact of SHP while few literatures details technological interventions. Table 6 summarizes the outcome of various studies carried out on SHP in India.
5.
Policies and schemes of SHP development
As per report of Mission Antyodaya about 53% of the villages in India receive electricity less than 12 hours a day [39]; it is also reported that about 15% population do not have access to electricity [40]. The economic development, therefore, is highly dispersed in the country. Currently, the GDP of the nation is about 4% only. In the backdrop of this kind of dismal economy, production of electricity utilizing renewable energy sources would be a welcome step. The advantages of harnessing renewable energy sources are manifold; these energy sources are inexhaustible, usually the gestation period is low, cost per unit energy is lower, etc. Thus, SHP presents a viable option as it is a clean source of energy and its peak power generation is in summer that coincides with the period when maximum power demand occur. As on date, many policies and schemes are in place to encourage the development of SHP projects in the country. The first SHP was installed before independence with a capacity of 130 kW in the hills of Darjeeling. Table 7 presents the chronology of SHP development along with the relevant policies and schemes in place in the country.
Table 8 shows recently commissioned SHPs in the country. Photographs of the power projects are also presented from Figure 8 to 10.
6.
Challenges of small hydro power development
Various stages of implementation of SHP are presented in Table 9. SHP generation necessitates enthusiastic participation of three main stakeholders namely, the developer, the government departments and the project affected people. Non-cooperation amongst the stakeholders in the procedure might cause delay in SHP development resulting in cost escalation and gestation period.
Planning and development of SHP endures many hurdles. The datasheet of head and discharge is fundamental to proper design of an SHP. The river flow changes with season thus, measurement of flow rate should be carried out throughout the year in order to obtain proper discharge data, a minimum of 5 years data should be collected; the absence of genuine data causes improper estimate of the power potential [12]. Sedimentation is another issue that is often faced in developing hydropower projects. Absence of geological and sedimentation data has resulted in wrong design and caused closure of many hydropower projects [58]. Problems are faced in acquiring land due to delay in obtaining permission from community or from department like forest and environment [58,59]. Shortage of manpower for planning and developing results in slow progress of SHP [58]. Lack of participation from local community [31], non-compliance of Renewable Purchase Obligation by States [47], lack of knowledge about SHP, isolated land and very small size SHP sometimes adversely affect the plant economy [12]. Thus, developing an SHP involves complex procedures and requires meticulous steps to decide the site, unit size and generating equipment [60]. Many SHPs are scrapped due to low consumption of electricity and limited funding from the government in terms of maintenance cost. Usually the life span of SHP is 35-50 years but some SHPs are closed down even before the end of the expected life due to faults in design and construction, obsolete equipment or non-availability of grid extension which causes huge waste of resources [61]. Along with regular maintenance, SHPs require check on the possibility of breakdown [62]. Often environmentalists pose delay in implementation of SHP as the normal procedure is not all allowed. This is due to the popular belief that the movement of personnel and equipment during construction invade wildlife habitats; also the operations of turbines or generators create noise which affects the local community. It is considered that the transmission lines may causes adverse effect to the local birds due to corona and magnetic effects around the conductors. It is also believed that the water passing through the machinery equipment may pollute or change the character of the river, increase the water temperature and affects the lives of aquatic flora and fauna [32,63,64]. Marginalization and unequal distribution of benefits of SHP is another factor that may slow down the development as the local community feel deceived and does not participate while the ecosystem and water bodies are disturbed [65]. Dissatisfaction on land compensation amongst the land donors also results in slow down of the entire process as it involves long process of dialogue between the stakeholders [66,67]. The lack of information between the developers and local community may impede the growth of SHP [68,69].
7.
Areas of research in small hydro power
There are many factors affecting successful implementation or operation of SHPs. Many of those problems are adequately addressed by the power developers however academics are still investigating all possible remedies to present the SHPs a better source of electricity generation. Table 10 illustrates some of the works carried out by researchers to make SHP more efficient, more economical and environment friendly.
8.
Conclusions
The article presented that there are many places in India where hydropower remains as untapped resource and extensive literature review is carried out and the feasibility and challenges of implementing small hydropower projects are detailed. Small hydropower emits less greenhouse gas and can be replenished over a period of time and hence, it can certainly play a major role in the future energy generation. However, it is found that many potential SHP sites remain as untapped resource in India. Also it is found that the opinion of public/local people is very important for successful implementation and operation of SHPs. Therefore, emphasis may be given to increased involvement of community as well as research/science for developing innovative technologies in order to balance hydropower and river conservation.
Conflict of interest
The authors declare no conflict of interest.
Author contributions
1. Ms. Oying Doso- Contribute to the idea and research, collected the information and wrote the paper;
2. Prof. Sarsing Gao- Supervised the work, devised the ideas and proof outline and review the paper.









 DownLoad:
DownLoad: