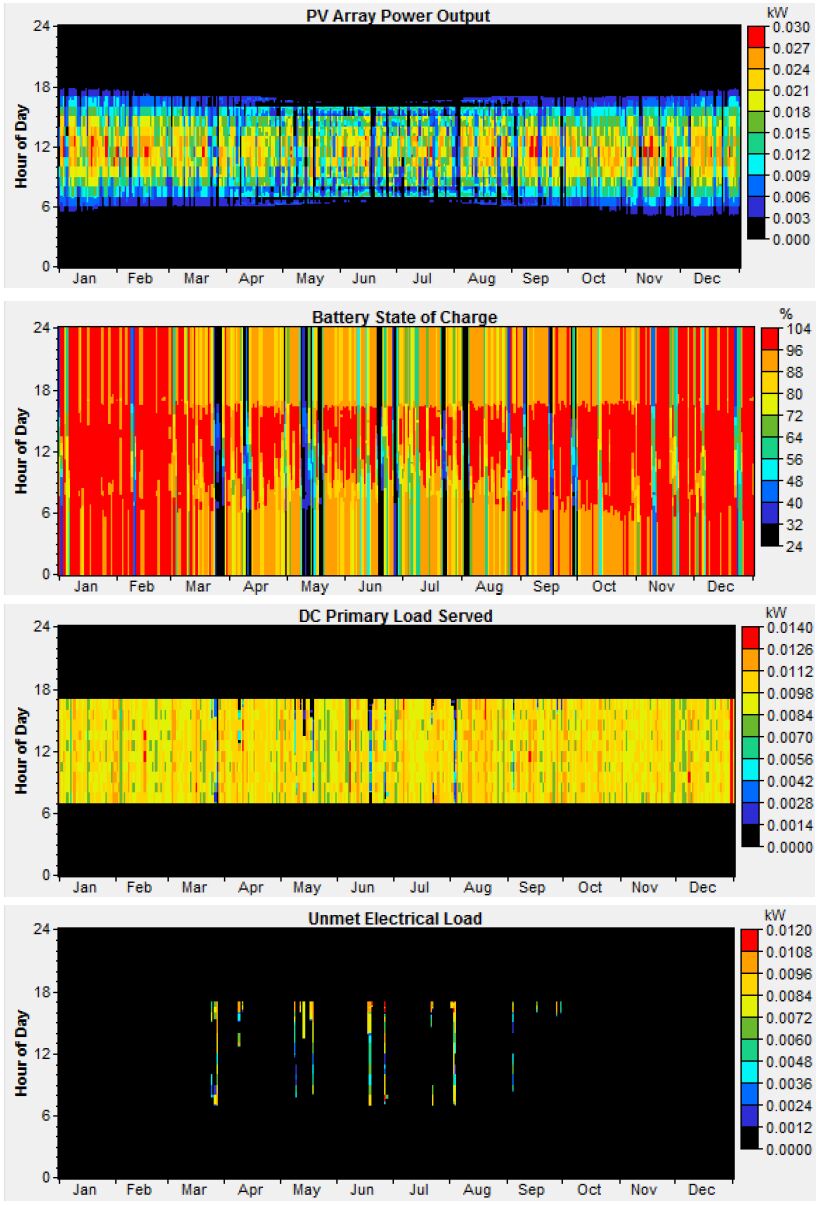
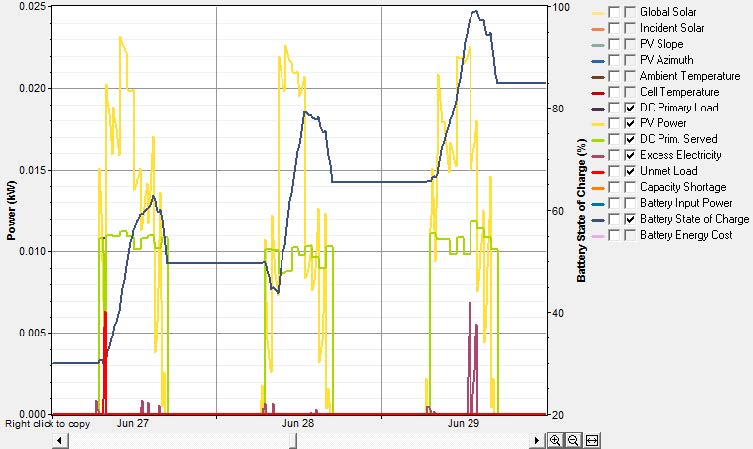
This research presents a technical simulation of theoretically portable desalination systems utilising low-energy and lightweight components that are either commercially available or currently in development. The commercially available components are small-scale flexible and portable photovoltaic (PV) modules, Li-ion battery-converter units, and high pressure low voltage brushless DC motor-powered micropumps. The theoretical and conventional small-scale desalination membranes are compared against each other: low-pressure reverse osmosis (RO), nanofilters, graphene, graphene oxide, and graphyne technology. The systems were designed with the identical PV-Li-ion specifications and simulation data to quantify the energy available to power the theoretical energy demand for desalinating a saline water at 30,000–40,000 ppm total dissolved solid (TDS) to reliably supply the minimum target of 3.5 L d−1 of freshwater for one theoretical year. The results demonstrate that modern portable commercially available PV-battery systems and new generations of energy-efficient membranes under development have the potential to enable users to sustainably procure daily drinking water needs from saline/contaminated water resources, with the system exhibiting a net reduction in weight than carrying water itself.
1.
Introduction
In 1929, relating to the study of value distribution theory for meromorphic functions, R. Nevanlinna [3] conjectured that the second main theorem for meromorphic functions is still valid if one replaces the fixed points by meromorphic functions of slow growth. This conjecture was solved by Osgood [4], Steinmetz [8], and Yamanoi [10] with truncation one. In 1991, Ru and Stoll [5] established the second main theorem for linearly nondegenerate holomorphic curves and moving hyperplanes in subgeneral position. We recall Ru and Stoll's result (for notations, see the following review of background materials).
Theorem 1.1 (Ru and Stoll [5]). Let $ f: \mathbb{C}\rightarrow \mathbb{P}^N (\mathbb{C}) $ be a holomorphic map, and let $ H_j, 1\leq j\leq q, $ be the moving hyperplanes in $ \mathbb{P}^N (\mathbb{C}) $ which are given by $ H_j = \{X = [X_0:\cdots:X_n] \ | \ a_{j0}X_0+\cdots+a_{jn}X_n = 0\}, $ where $ a_{j0}, \dots, a_{jn} $ are entire functions without common zeros. Let $ {\mathcal K}_{{\mathcal H}} $ be the smallest field that contains $ \mathbb{C} $ and all $ a_{j\mu}\over a_{j\nu} $ with $ a_{j\nu} \not\equiv 0. $ Suppose that $ {\mathcal H}: = \{H_1, ..., H_q\} $ is a family of slowly moving hyperplanes with respect to $ f $ located in $ m $-subgeneral position. Assume that $ f $ is linearly nondegenerate over $ {\mathcal K}_{{\mathcal H}} $. Then, for any $ \epsilon > 0 $,
where "$ \leq_{exc} $" means that the above inequality holds for all $ r $ outside a set with finite Lebesgue measure.
Before stating our main result, we recall some basic definitions for moving targets. Let $ f: \mathbb C \to \mathbb P^N (\mathbb C) $ be a holomorphic map. Denote by $ {\mathbf f} = (f_0, ..., f_N). $ $ {\mathbf f} $ is called a reduced representation of $ f $ if $ \mathbb{P}(f) = f $ and $ f_0, ..., f_N $ are entire functions without common zeros. Let $ \left\| {{\bf f}(z)} \right\| = \max \left\{ {\left| {f_0(z)} \right|, ..., \left| {f_N(z)} \right|} \right\} $. The characteristic function of $ f $ is defined by
We say a meromorphic function $ g $ on $ \mathbb C $ is of slow growth with respect to $ f $ if $ T_g(r) = o(T_f(r)) $. Let $ \mathcal K_f $ be the field of all meromorphic functions on $ \mathbb C $ of slow growth with respect to $ f, $ which is a subfield of meromorphic functions on $ \mathbb C $. For a positive integer $ d $, we set
and
A moving hypersurface $ D $ in $ \mathbb P^N(\mathbb C) $ of degree $ d $ is defined by a homogeneous polynomial $ Q = \sum\nolimits_{I \in {\mathcal I_d}} {{a_I}{{\bf x}^I}} $, where $ a_I, I \in \mathcal I_d $, are holomorphic functions on $ \mathbb C $ without common zeros, and $ {\bf x}^I = {x_0}^{i_0}\cdots{x_N}^{i_N} $. Note that $ D $ can be regarded as a holomorphic map $ a:\Bbb C \to {\Bbb P}^{{n_d} - 1}(\Bbb C) $ with a reduced representation $ ({..., {a_I}(z), ... })_{I \in \mathcal I_d} $. We call $ D $ a slowly moving hypersurface with respect to $ f $ if $ T_a(r) = o(T_f(r)) $. The proximity function of $ f $ with respect to the moving hypersurface $ D $ with defining homogeneous polynomial $ Q $ is defined by
where $ \lambda _{D(z)}({\bf f}(z)) = \log \frac{{{\left\| {{\bf f}(z)} \right\|}^d}\left\| {Q(z)} \right\|} {\left\| {Q({\bf f})(z)} \right\|} $ is the Weil function associated to $ D $ composites with $ f $ and $ \left\| {Q(z)} \right\| = \mathop {\max }\limits_{I \in \mathcal I_d} \left\{ {\left| {a_I(z)} \right|} \right\} $. If $ D $ is a slowly moving hypersurface with respect to $ f $ of degree $ d $, we have
by the first main theorem for moving targets.
Definition 1.2. Under the above notations, we say that $ f $ is linearly nondegenerate over $ \mathcal K_f $ if there is no nonzero linear form $ L \in \mathcal K_f \left[x_0, ..., x_N \right] $ such that $ L(f_0, ..., f_N) \equiv 0 $, and $ f $ is algebraically nondegenerate over $ \mathcal K_f $ if there is no nonzero homogeneous polynomial $ Q \in \mathcal K_f[x_0, ..., x_N] $ such that $ Q(f_0, ..., f_N) \equiv 0 $. If $ f $ is not algebraically nondegenerate over $ \mathcal K_f, $ we say that $ f $ is degenerate over $ \mathcal K_f. $
Remark 1.3. In this paper, we only consider those moving hypersurfaces $ D $ with defining function $ Q $ such that $ Q(f_0, ..., f_N) \not\equiv 0 $.
We say that the moving hypersurfaces $ D_1, \dots, D_q $ are in $ m $-subgeneral position if there exists $ z \in \mathbb C $ such that $ D_1(z), \dots, D_q(z) $ are in $ m $-subgeneral position (as fixed hypersurfaces), i.e., any $ m+1 $ of $ D_1(z), ..., D_q(z) $ do not meet at one point. Actually, if the condition is satisfied for one point $ z \in \mathbb C $, it is also satisfied for all $ z \in \mathbb C $ except for a discrete set.
In 2021, Heier and Levin generalized Schmidt's subspace theorem to closed subschemes in general position by using the concept of Seshadri constant, as shown in [1]. Recently, they extended this result to arbitrary closed subschemes without any assumption by using the notion of distributive constants and weights assigned to subvarieties [2]. As a corollary, they obtained a second main theorem for hypersurfaces in $ m $-subgeneral position in $ \Bbb P^n(\Bbb C) $, establishing an inequality with factor $ 3\over 2 $.
Main Theorem (Heier and Levin [2]). Let $ f : \Bbb C \rightarrow \Bbb P^N(\Bbb C) $ be a holomorphic map, and let $ D_1, \dots, D_q $ be hypersurfaces in $ \Bbb P^N(\Bbb C) $ of degree $ d_1, \dots, d_q, $ respectively. Assume that $ D_1, \dots, D_q $ are located in $ m $-subgeneral position. Then, for any $ \epsilon > 0 $,
Here "$ \leq_{exc} $" means that the above inequality holds for all $ r $ outside a set with finite Lebesgue measure.
A key point of their proof is the use of the last line segment of the Nochka diagram, where they proved that the slope of this line segment has a lower bound depending solely on $ m $ and $ N $.
In this paper, motivated by Heier and Levin's work, we consider the moving hypersurfaces in $ m $-subgeneral position and prove the following theorem.
Theorem 1.4 (Main Theorem). Let $ f: \Bbb C\rightarrow \Bbb P^N (\Bbb C) $ be a holomorphic map, and let $ D_1, \ldots, D_q $ be a family of slowly moving hypersurfaces with respect to $ f $ of degree $ d_1, \dots, d_q $, respectively. Assume that $ f $ is algebraically nondegenerate over $ \mathcal K_f $ and $ D_1, \dots, D_q $ are located in $ m $-subgeneral position. Then, for any $ \epsilon > 0 $,
Here "$ \leq_{exc} $" means that the above inequality holds for all $ r $ outside a set with finite Lebesgue measure.
Indeed, we prove a more general case when $ f $ is degenerate over $ \mathcal K_f $. To do so, we introduce the notion of "universal fields". Let $ k $ be a field. A universal field $ \Omega_k $ of $ k $ is a field extension of $ k $ that is algebraically closed and has infinite transcendence degree over $ k $. A useful fact of $ \Omega_k $ is that any field extension obtained by adjoining finitely many field elements to $ k $ can be isomorphically imbedded in $ \Omega_k, $ which fixes the base field $ k. $
In this paper, we take $ k = \mathcal K_f $ and fix a universal field $ \Omega $ over $ k = \mathcal K_f $. Let $ f = [f_0:f_1:\cdots:f_N] $ be a reduced representation of $ f $. We can regard each $ f_i $, $ 0 \leq i \leq N $, as an element in $ \Omega $. Hence $ f $ can be seen as a set of homogeneous coordinates of some point $ P $ in $ \mathbb P ^N(\Omega) $. Equip $ \mathbb P ^N(\Omega) $ with the natural Zariski topology.
Definition 1.5. Under the above assumptions, we define the closure of $ P $ in $ \mathbb P ^N(\Omega) $ over $ \mathcal K _f, $ denoted by $ V_f, $ by
Note that $ f $ is algebraically nondegenerate over $ \mathcal K_f, $ which is equivalent to $ V_f = \mathbb P ^N(\Omega) $. We also note that every moving hypersurface $ D $ with defining function $ Q\in \mathcal{K}_f[x_0, \dots, x_N] $ can be seen as a hypersurface determined by $ Q $ in $ \mathbb{P}^N(\Omega). $
Let $ V \subset {\Bbb P}^N(\Omega) $ be an algebraic subvariety defined by homogeneous polynomials $ h_1, \dots, h_s \in \mathcal{K}_f[x_0, \dots, x_N]. $ Let $ z $ be a point in $ \Bbb C $ such that all coefficients of $ h_1, \dots, h_s $ are holomorphic at $ z. $ We denote by $ V(z)\subset \Bbb P^N(\Bbb C) $ the algebraic subvariety of $ \Bbb P^N(\Bbb C) $ defined by $ h_1(z), \dots, h_s(z). $ Here if $ h_j = \sum_{I \in {\mathcal I_d}} {{a_I}{{\bf x}^I}}, $ we denote $ h_j(z) $ by $ h_j(z)(x_0, \dots, x_N) = \sum\nolimits_{I \in {\mathcal I_d}} {{a_I(z)}{{\bf x}^I}}\in \Bbb C[x_0, \dots, x_N]. $ We recall Lemma 3.3 in [11].
Lemma 1.6 (Lemma 3.3, [11]). $ \dim V(z) = \dim V $ and $ \deg V(z) = \deg V $ for all $ z\in \Bbb C $ except a discrete subset.
Definition 1.7. Let $ V $ be an algebraic subvariety of $ {\Bbb P}^N(\Omega) $. We say that $ V $ is defined over $ \mathcal{K}_f $ if $ V $ is an algebraic subvariety defined by some homogeneous polynomials in $ \mathcal{K}_f[x_0, \dots, x_N]. $
Let $ V \subset {\Bbb P}^N(\Omega) $ be an algebraic subvariety defined over $ \mathcal{K}_f $ and $ D_1, ..., D_q $ be $ q $ hypersurfaces in $ {\Bbb P}^N(\Omega) $ defined over $ \mathcal{K}_f $. We say that $ D_1, ..., D_q $ are in $ m $-subgeneral position on $ V $ if for any $ J \subset \{1, \cdots, q\} $ with $ {\#}J \leq m+1 $,
When $ m = n $, we say $ D_1, \cdots, D_q $ are in general position on $ V $. Note that $ \dim{ \cap _{j \in J}}{D_j}(z) \cap V(z) = \dim{ \cap _{j \in J}}{D_j} \cap V $ for all $ z \in \mathbb C $ excluding a discrete subset.
Remark 1.8. By Lemma 1.6, the definition of $ m $-subgeneral position above implies the definition of $ m $-subgeneral position below Remark 1.3.
We prove the following general result.
Theorem 1.9. Let $ f $ be a holomorphic map of $ {\Bbb C} $ into $ {\Bbb P}^N ({\Bbb C}) $. Let $ \mathcal D = \{D_1, \ldots, D_q\} $ be a family of slowly moving hypersurfaces in $ \mathbb P ^N(\mathbb C) $ with respect to $ f $ with $ \deg D_j = d_j (1\leq j \leq q $). Let $ V_f\subset {\Bbb P}^N(\Omega) $ be given as in (1.1). Assume that $ D_1, \dots, D_q $ are in $ m $-subgeneral position on $ V_f $ and $ \dim V_f = n $. Assume that the following Bezout property holds on $ V_f $ for intersections among the divisors: If $ I, J \subset \{1, ..., q\}, $ then
where for every subvariety $ Z $ of $ \mathbb{P}^N(\Omega), $ $ {\mbox{codim}}_{V_f}Z $ is given by $ {\mbox{codim}}_{V_f}Z: = {\mbox{dim}}V_f - {\mbox{dim}}V_f\cap Z. $ Then
Remark 1.10. Recall that we only consider those moving hypersurfaces $ D $ with defining function $ Q \in \mathcal K_f [x_0, ..., x_N] $ such that $ Q(f) \not\equiv 0 $. So we have $ V_f \not\subset D_j $ for every $ 1 \leq j \leq q $.
It is known that the Bezout property holds on projective spaces. Therefore, Theorem 1.4 is the special case of Theorem 1.9 when $ V_f = {\Bbb P}^N(\Omega) $. Therefore, the rest of the paper is devoted to proving Theorem 1.9.
2.
Distributive constants
In 2022, Quang [6] introduced the notion of distributive constant $ \Delta $ as follows:
Definition 2.1. Let $ f: \mathbb C \to \mathbb P^N (\mathbb C) $ be a holomorphic curve. Let $ D_1, \cdots, D_q $ be $ q $ hypersurfaces in $ {\Bbb P}^N(\Omega) $. Let $ V_f $ be given as in (1.1). We define the distributive constant for $ D_1, ..., D_q $ with respect to $ f $ by
We remark that Quang's original definition (see Definition 3.3 in [6]) is different from Definition 2.1. But by Lemma 3.3 in [11], we can see that Definition 2.1 is equivalent to Definition 3.3 in [6]. We rephrase the definition, according to Heier–Levin [2], as follows:
Definition 2.2. With the assumptions and notations in Definition 2.1, for a closed subset $ W $ of $ V_f $ (with respect to the Zariski topology on $ \Bbb P^N(\Omega) $), let
We define
We show that the above two definitions are equivalent. Suppose that $ \tilde{W} $ is a subvariety of $ V_f $ such that $ {\alpha(W)\over \mbox{codim}_{V_f} W} $ attains the maximum at $ W = \tilde{W}. $ Reordering if necessary, we assume that $ \tilde{W} \subset D_j $ for $ j = 1, \dots, \alpha(\tilde{W}). $ Let $ W' = \cap_{j = 1}^{\alpha(\tilde{W})}D_j. $ Then, clearly, $ \tilde{W} \subset W' $ and hence $ \mbox{codim}_{V_f} \tilde{W} \geq \mbox{codim}_{V_f} W'. $ On the other hand, $ \tilde{W} \nsubseteq D_j $ for all $ j > \alpha(\tilde{W}) $ implies that $ W' \nsubseteq D_j $ for all $ j > \alpha(\tilde{W}) $. So $ \alpha(\tilde{W}) = \alpha(W'). $ Thus we have
By our assumption for $ \tilde{W} $, we obtain
This means that, in Definition 2.2, we only need to consider those $ W $ that are the intersections of some $ D_i $'s, and our claim follows from this observation. In the following, when we deal with $ W $, we always assume that $ W $ is the intersection of some $ D_i $'s.
S. D. Quang obtained the following result.
Theorem 2.3 (S. D. Quang [6], Lei Shi, Qiming Yan, and Guangsheng Yu [7]). Let $ f $ be a holomorphic map of $ {\Bbb C} $ into $ {\Bbb P}^N ({\Bbb C}) $. Let $ \{D_j\}_{j = 1}^q $ be a family of slowly moving hypersurfaces in $ {\Bbb P}^N({\Bbb C}) $ with $ \deg D_j = d_j (1\leq j \leq q $). Let $ V_f \subset \mathbb P^N(\Omega) $ be given as in (1.1). Assume that $ \dim V_f = n $. Then, for any $ \epsilon > 0 $,
We derive the following corollary of Theorem 2.3.
Corollary 2.4. We adopt the assumptions in Theorem 2.3. Let $ W_0 $ be a closed subset of $ V_f\subset {\Bbb P}^N(\Omega) $. Then, for any $ \epsilon > 0, $ we have
Proof. Without loss of generality, we suppose that $ W_0 \subset \mbox{Supp} D_j $ for $ j = q-\alpha(W_0)+1, \dots, q $. Let $ q' = q-\alpha(W_0) $. Let
Note that $ \alpha'(W) = \alpha(W)-\alpha(W \cup W_0) $. Then by the first main theorem for moving targets and $ \alpha(W_0) = q-q' $,
Thus, Theorem 2.3 implies that
which is we desired. □
3.
Proof of Theorem 1.9
Proof of Theorem 1.9. We divide the proof into two cases. The first case is that for every algebraic subvariety $ W \subset V_f\subset {\Bbb P}^N(\Omega) $ with $ W\not = \emptyset $, we have $ \mbox{codim}_{V_f} W \ge {n+1\over 2m-n+1}\alpha(W) $. Then, by Definition 2.2, we have $ \Delta \leq {2m-n+1 \over n+1} $. So the result follows easily from Theorem 2.3.
Otherwise, we take a subvariety $ W_0 \subset V $ such that the quantity
is maximized at $ W = W_0 $. We assume that $ W_0 $ is an intersection $ D_I $ for some $ I \subset \{1, \cdots, q\} $. Let
Note that $ \sigma $ is the slope of the straight line passing through $ (2m-n+1, n+1) $ and $ (\alpha(W_0), \mbox{codim}_{V_f}W_0) $.
Take arbitrary $ \emptyset \subsetneq W \subsetneq V_f $. By Corollary 2.4, it suffices to show that
Assume that $ W = D_J $ for some nonempty $ J \subset \{1, ..., q\} $ (the case $ \alpha(W) = 0, J = \emptyset $, follows from $ m $-subgeneral position). From the claim on page 19 of Heier–Levin [2] (apply the same argument in [2]), we have
Hence
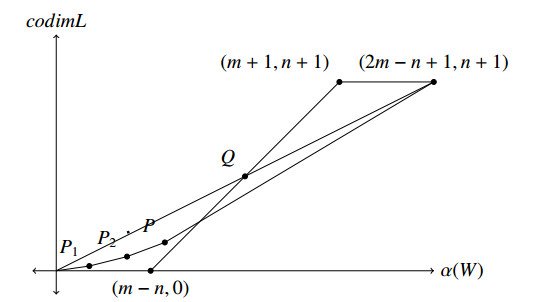
Finally, consider Vojta's Nochka-weight-diagram [9] (see Figure 1).
We note that from our assumption that $ \mathrm {codim}_{V_f} W_0 < {n+1 \over 2m-n+1} \alpha (W_0) $, $ P = (\alpha(W_0), \mbox{codim}_{V_f} W_0) $ lies below the line $ y = {n+1\over 2m-n+1} x $. From the $ m $-subgeneral position, it also lies to the left of the line $ y = x+n-m $. Therefore, $ P $ must lie below and to the left of the intersection point $ Q = \left({2m-n+1\over 2}, {n+1\over 2}\right) $ of the above two straight lines. Thus, we have
Since $ \sigma > {n+1\over 2m-n+1} $ (see Figure 1), by using (3.2), we obtain
Combing above with (3.1), we obtain
The theorem thus follows from Corollary 2.4. □
4.
Conclusions
It is a longstanding problem in Nevanlinna theory: we expect the second main theorem, under the setting of hypersurfaces in $ {\mathbb P}^N(\mathbb C) $ located in $ m $-subgeneral position, has the upper bound of $ (2m-N+1+\epsilon)T_f(r). $ This problem can also be considered in the context of moving hypersurfaces in $ m $-subgeneral position. Heier and Levin used an estimate on the slope of the last line segment of the Nochka diagram, along with the concept of distributive constants, to obtain a good coefficient $ {3\over 2}(2m-N+1+\epsilon) $ in the case of fixed hypersurfaces. In this paper, building upon the work of Heier and Levin and utilizing the concept of universal fields, we establish a general inequality with the same coefficient $ {3\over 2}(2m-N+1+\epsilon) $ in the case of moving hypersurfaces. From these theorems, it is seen that a more precise estimation of the slopes of the latter line segments in the Nochaka diagram could lead to a more precise upper bound.
Author contributions
Qili Cai: Conceptualization, formal analysis, investigation, visualization, writing – original draft, writing – review and editing; Chinjui Yang: Conceptualization, formal analysis, methodology, validation, writing – original draft, writing – review and editing. All authors have read and approved the final version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: