Utilization of commodity plastic wastes in flexible pavement: A review

1.   Introduction

Aging is a major global trend of the 21st century. With the aging population worldwide, retirement plans play an important role in maintaining and improving the quality of life of elders. Pension funds act as one of the most important institutions in financial markets since they provide financial security after retirement. Generally speaking, there are mainly two kinds of pension funds all over the world: The defined benefit (DB) scheme and the defined contribution (DC) scheme. In a DC plan, only contributions are determined and the retirement benefits are determined by the contribution and the performance of the fund's investment portfolios during the accumulation phase. In a DB plan, the benefits at retirement are initially fixed and the contributions are calculated according to the predetermined benefits. As the longevity and investment risks of the DC plan are shifted from the sponsor to the contributors, traditional DB pension plans are gradually losing their dominance in the occupational pension systems and there has been an ongoing shift from DB to DC pensions in recent years. It is therefore crucial to find the optimal asset allocations for the DC pension fund manager during the accumulation phase so that the members can receive sufficient funds after retirement. There already exists a lot of research works on the optimal investment problem for the DC pension plans (see ^{[1,2,3,4,5,6,7,8,9,10,11]}).

In the existing literature on the optimal investment strategies for DC pension plans, a widely adopted optimization objective is the expected utility maximization of the terminal wealth. Zhang et al. ^[12] investigated the optimal allocation of a DC pension plan by maximizing the expected utility of terminal wealth under inflation risk. Boulier et al. ^[13] derived the optimal allocations to maximize the coefficient of relative risk aversion (CRRA) utility of terminal value over a guarantee under a stochastic interest rate. Sun et al. ^[14] considered a robust portfolio choice problem for a DC pension plan in a stochastic income and stochastic interest rate framework by maximizing the expected utility of terminal wealth. In practice, an appropriate investment must take some regulatory constraints into account. Value-at-Risk (VaR) quantifies the worst expected loss given a preset confidence level and is widely applied in pensions and other financial institutions. See, for example, Guan and Liang ^[15] found the optimal allocation of a DC pension plan under a smooth concave utility criterion with a VaR constraint. Dong and Zheng ^[16] investigated the optimal allocation of a DC pension plan under the control and VaR constraints.

However, it has been shown in ^[17] that in difficult financial situations, a pure VaR constraint leads to a heavier loss than that without a VaR constraint under a concave utility. This is due to the fact that VaR-based risk management (VaR-RM) only focuses on the probability but not the magnitude of a loss when it occurs. The portfolio insurance (PI) constraint can well protect the members' benefits by keeping the optimal terminal wealth always above the minimum guarantee, but it may lead to over-cautious investment strategy and a relatively low expected terminal wealth ^[18,19]. Chen et al. ^[20] incorporated a VaR constraint with a higher protection level and a PI constraint with a lower protection level together to overcome the drawbacks of a pure VaR or PI constraint. Average Value-at-Risk (AVaR), which measures the risk by averaging all VaRs above a confidence level, has also attracted a lot of attention (see ^[21,22,23] and references therein). Comparing with a VaR constraint, the AVAR-constrained optimization problem is much more complex. Expected shortfall (ES, also known as limited loss) constraint in ^[17] has become an alternative of VaR since it can penalize both a high probability of a loss and a high expected loss, given there is a loss. Given a regulatory threshold, the shortfall occurs if the terminal wealth is below the threshold and the expected shortfall is the expectation of the losses. Basak and Shapiro ^[17] found that in difficult financial situations, the loss under an ES constraint is lower than that without risk constraint in a concave utility framework.

By some numerical analysis, we find that comparing with a VaR constraint, a better protection for bad economic states under an ES constraint than a VaR constraint is at a cost of lowering the optimal terminal wealth in intermediate-economic-states region. Therefore, an ES constraint results in a much higher volatility than a VaR constraint. So, extending ^[17], we shall investigate a utility maximization problem of a DC pension plan under a VaR-type regulation with a higher protection level and, at the same time, under an ES constraint with a lower protection level. The joint VaR-ES constraint on terminal wealth can well protect the investors' benefits in difficult financial situations, while at the same time lead to a less volatility of the optimal terminal wealth. Furthermore, a regulation with a joint VaR-ES constraint is so flexible that it can nest a pure VaR, ES or PI constraint.

In handling the utility maximization problems with or without risk constraints in a complete market, an efficient approach is the martingale method ^[24,25]. Extending ^[17], we use a martingale method to derive the optimal wealth process under a joint VaR-ES constraint. Comparing with ^[17] and ^[19], it is highly challenging and technically demanding to solve a utility maximization problem under a joint VaR-ES constraint since we need to choose two multipliers to reflect the bindingness of two risk constraints.

The paper is organized as follows. In section two, we formulate the investment problem for a DC pension fund. In section three, we use the concavification technique and the Lagrange dual method to derive the optimal terminal wealth under the joint VaR-ES constraint. In section four, we carry out some numerical analysis and investigate the impact of two risk constraints on the distribution of the optimal terminal wealth. Section five concludes the paper. The appendix contains some technical proofs.

2.   The investment problem for a DC pension fund

Consider a continuous-time model with a finite time horizon $\mathcal{T} = [0, T]$. Let $\left(\Omega, \mathcal{F}, \mathbb{F}, \mathbb{P}\right)$ be a complete filtered probability space with filtration $\mathbb{F}: = \left\{\mathcal{F}_{t} \mid t \in \mathcal{T}\right\}$ and $\mathcal{F}_{t}$ is the information available before time $t$ in the market. Assume that all random variables and stochastic processes in this paper are well-defined in this probability space. The pension fund starts at time zero and the retirement time is $T$.

As DC pension funds have a long investment cycle, inflation risk should be incorporated into the optimization model. To capture the inflation risk, we introduce an inflation index $L(t)$ characterized by the following geometric Brownian motion:

where $i > 0$ is the expected rate of inflation, ${W_I}(t)$ is a standard Brownian motion and $\sigma_{I} > 0$ is the volatility of inflation index.

Assume that the financial market consists of three traded assets: Cash, a stock and an inflation-indexed zero-coupon bond, which is used to hedge the inflation risk.

The riskless money market account ${S_0}(t)$ evolves as

where $r$ is a constant riskless nominal interest rate in the market.

The inflation-linked indexed zero-coupon bond $\overline{I}(t)$ satisfies the following stochastic differential equation:

where ${\lambda _I}$ represents the market price of risk of ${W_I}(t)$.

The dynamics of the stock price ${S_1}(t)$ are as follows:

where ${\sigma _{SI}}$ and ${\sigma _{S}}$ are constants and drive the volatility of the stock, ${W_S}(t)$ is a standard Brownian motion and independent of ${W_I}(t)$ and ${\lambda _S}$ represents the market price of risk of ${W_S}(t)$.

Before retirement, the pension members put part of their salary in the DC pension plan. Suppose that the contribution rate is a fixed percentage $c$ $(0 \leq c \leq 1)$ of the salary. Following ^[24], we assume the salary of the pension plan members depends on the inflation risk and the stock market risk and satisfies the following equation:

where $\mu$ is the appreciation rate and ${\sigma _{YI}}$ and ${\sigma _{YS}}$ are constants driving the volatility of the contribution rate.

Since the market is complete, there exists a unique pricing kernel given by

As explained in ^[17,20], the quantity $H(T, \omega)$ is the Arrow-Debreu price per unit probability of a security, which pays out one at time $T$ if the scenario $\omega$ happens and zero otherwise. As this value is high in a recession and low in prosperous times, $H(T, \omega)$ can directly reflect the overall state of the economy.

From Eq (2.5), we have

and, therefore, $\log(\frac{H(T)}{H(t)})$ is normally distributed with a mean $M(t)$ and a variance $V ^2(t)$, where

In order to manage the risks from the financial market, the pension manager invests in the market continuously within the time horizon $[0, T]$. Denote the money invested in the cash, the inflation-linked indexed zero-coupon bond and the stock at time $t$ by ${\pi _0}(t), {\pi _{1}}(t)$ and ${\pi _2}(t)$, respectively. Denote $\pi_1\doteq \{\pi_1(t)|0\leq t\leq T\}$, $\pi_2\doteq \{\pi_2(t)|0\leq t\leq T\},$ then under the investment strategy $\pi\doteq(\pi_1, \pi_2)$, the wealth process ${X^\pi }(t)$ of the pension fund is as follows:

where ${x_0} \ge 0$ is the initial wealth of the pension fund and $X^{\pi}(t) = \pi_0(t)+\pi_1(t)+\pi_2(t)$.

Definition 2.1. A portfolio strategy $\pi = \left({\pi _{1}}, {\pi _2}\right)$ is an admissible strategy if it satisfies the following conditions:

(ⅰ) ${\pi _{1}}$ and ${\pi _2}$ are progressively measurable with respect to the filtration $\mathbb{F}$.

(ⅱ) $E[\int_0^T (\pi _{1}^2(t) + \pi _2^2(t)) dt] < + \infty$ a.s., and there exists a unique strong solution $X^{\pi}(t)$ to (2.8). The set of all admissible portfolio strategies is denoted by $\mathcal{A}$.

Consider a utility $U$, which is a strictly increasing, strictly concave, continuously differentiable, real-valued function defined on $[0, \infty),$ satisfying

and

Condition (2.9) ensures that the strictly decreasing function $U'$ has a strictly decreasing inverse $I:(0, \infty)\rightarrow (0, \infty);$ that is,

Let $L_1, L_2$ with $L_1 < L_2$ be two given levels. In order to provide a downside protection, the pension manager is to find the optimal investment strategy to maximize the expected utility of the wealth at time $T$ under simultaneous VaR and ES constraints:

where $0\leq \varepsilon_1 < \infty, 0\leq \varepsilon_2\leq 1$ are two given constants. The VaR constraint $\mathbb{P}(X^\pi (T)\geq L_2)\geq 1-\varepsilon_2$ requires that the probability of the terminal wealth above the level $L_2$ is no less than $1-\varepsilon_2$ and the ES constraint $E[H(T)(L_1- X^\pi (T))^+]\leq \varepsilon_1$ requires that the expected present value of the losses, given the regulatory level $L_1,$ is no more than $\varepsilon_1$.

When $\varepsilon_1 = \infty$ and $\varepsilon_2 = 1$, (2.11) covers an unconstrained optimization problem:

When $\varepsilon_1 = \infty$ and $0 < \varepsilon_2 < 1$, (2.11) becomes a VaR-constrained optimization problem with regulatory level $L_2$ as follows:

When $0 < \varepsilon_1 < \infty$ and $\varepsilon_2 = 1$, (2.11) becomes an ES-constrained optimization problem:

Due to the existence of contribution rate, the wealth process $X^{\pi}(t)$ is not self-financing. We introduce an auxiliary wealth process $\tilde X^\pi (t)$ to convert the process into an equivalent self-financing one. Denote the expected present value of the payment $cY(s)$ at time $s$ by

By simple calculation, we obtain the explicit form of $D(t, s)$ as follows:

Moreover, $D(t, s)$ satisfies the following stochastic differential equation:

Integrating $D(t, \cdot)$ from time $t$ to time $T$, we construct a new process $F(t)$:

$F(t)$ represents the expected value of the accumulated contribution rates from time $t$ to $T$ at time $t$. In particular, we have

Based on the differential form of $D(t, s)$, the dynamics of $F$ are as follows:

Next, we construct the auxiliary process $\tilde X^\pi (t)$ as follows:

Note that $F(T) = 0, \tilde X^\pi (T) = X^{\pi}(T)$. Let $\tilde x_0 = \tilde{X}^\pi(0) = X^{\pi}(0)+F(0).$ As such, the optimization problem over $X^{\pi}(t)$ is equivalent to the optimization problem over $\tilde X^\pi (t)$. By Ito's formula, we have

Since the market is complete and $\tilde X^\pi (T) = X^{\pi}(T)$, the optimization problem (2.11) can be expressed as

Basak and Shapiro ^[17] has solved the ES- or VaR-constrained optimization problem.

3.   Optimal trading under VaR-ES constraints

In this section, we shall derive the optimal investment strategy under a joint VaR-ES constraint. We first present the optimal terminal wealths without constraints and with a VaR and an ES constraint presented in ^[17].

Lemma 3.1. For the unconstrained optimization problem (2.12), the optimal terminal wealth denoted by $X^{\pi^*, y^{M}}(T)$ is given by

where the Lagrangian multiplier $y^M$ solves

To avoid triviality, we make the following assumption:

Assumption 3.2. The risk constraints in problem (2.11) are binding, i.e.,

Lemma 3.3. Assume $\tilde x_0 \geq L_2E[H(T)1_{\{H(T)\leq H^*\}}]$, where $H^*$ solves $\mathbb{P}(H(T) \ge {H^{\rm{*}}}) = {\varepsilon _2}$ for a given $0 < \varepsilon _2 < 1,$ then for the VaR-constrained optimization problem (2.13), the optimal terminal wealth denoted by $X^{\pi^*, y^{VaR}}(T)$ is as follows, with $y^{VaR} > 0$ satisfying $E[H(T)X^{\pi^*, y^{VaR}}(T)] = \tilde x_0:$

where $H_2 = \frac{U'(L_2)}{y^{VaR}}$. Furthermore, $y^{VaR} > y^{M}.$

Proof. See Proposition 1 in ^[17].□

Lemma 3.4. Assume $\tilde x_0 \geq L_1 e^{-rT}-\varepsilon _1$ for a given $0 < \varepsilon _1 < \infty,$ then for the ES-constrained optimization problem (2.14), the optimal terminal wealth $X^{\pi^*, y^{ES}, \lambda ^{ES}}(T)$ is as follows

where $\underline{H}_1 = \frac{U'(L_1)}{y^{ES}}$, $\overline{H}_1 = \frac{U'(L_1)}{y^{ES}-\lambda ^{ES}}$ and $y^{ES} > 0, \lambda ^{ES} > 0$ are determined by

Proof. See Proposition 4 in ^[17].□

Note that $y^{ES} > y^{M}, y^{VaR} > y^{M}.$ Therefore, based on Assumption 3.2, we have that

Using a Lagrange dual method, we consider an unconstrained optimization problem as follows:

where

for any $\lambda_1 > 0, \lambda_2 > 0.$

Theorem 3.5. Under Assumption 3.2, if there exists $\lambda_1^* > 0, \lambda_2^* > 0$ such that $X^{\pi^*, \lambda_1^*, \lambda_2^{*}}(T)$ solves problem (3.8) and satisfies

then $X^{\pi^*, \lambda_1^*, \lambda_2^{*}}(T)$ is the optimal solution to optimization problem (2.11).

Proof. Assume that $X^{\pi^*, \lambda_1^*, \lambda_2^{*}}(T)$ is the optimal solution to problem (3.8) with condition (3.10). As $X^{\pi^*, \lambda_1^*, \lambda_2^{*}}(T)$ is feasible for problem (2.17), we have

where $X^\pi (T)$ is an arbitrary feasible solution for problem (2.17). On the other hand, since $X^{\pi^*, \lambda_1^*, \lambda_2^{*}}(T)$ solves (3.8), we have

That is,

Since $X^{\pi^*, \lambda_1^*, \lambda_2^{*}}(T)$ satisfies (3.10) and $X^{\pi }(T)$ satisfies the joint VaR-ES constraint, we have

Hence,

which concludes the proof.

Proposition 3.6. Let $H^*$ solve $\mathbb{P}(H(T) \ge {H^{\rm{*}}}) = {\varepsilon _2}$ for $0 < \varepsilon_2 < 1.$ Assume $\tilde x_0 \geq \tilde x_0^{min}$, where $\tilde x_0^{min} = L_1e^{\frac{2M(0)+V^2(0)}{2}}-\varepsilon_1+E[H(T)(L_2-L_1)1_{\{H(T) < H^{\rm{*}}\}}]$. Under Assumption 3.2, for the joint VaR-ES constrained optimization problem (2.11), the optimal terminal wealth $X^{\pi^*, \varepsilon_1, \varepsilon_2}(T)$ is as follows with the multipliers $\lambda_1^*$ and $y^{*},$ satisfying:

Case Ⅰ. If $\frac{U'(L_2)}{y^{*}} < H^{*} < \frac{U'(L_1)}{y^{*}}$, then

Case Ⅱ. If $\frac{U'(L_1)}{y^{*}}\leq H^{*} < \frac{U'(L_1)}{y^{*}-\lambda_1^*}$, then

Case Ⅲ. If $H^{*}\geq \frac{U'(L_1)}{y^{*}-\lambda_1^*}$, then

Proof. We solve problem (3.8) by the Lagrange dual theory, then for each $y > 0, \lambda_1 > 0, \lambda_2 > 0$, consider the following optimization problem:

where

Problem (3.15) can be viewed as a static optimization problem. To solve problem (3.15), we consider a pointwise optimization problem

where

Define

which is the slope of the straight line linking points $(L_1, U(L_1))$ and $(L_2, U(L_2)+\lambda_2).$

Since $\tilde{U}_{\lambda_1, \lambda_2}$ is non-concave, Proposition A.1 solves problem (3.16) by employing the concavification method, then an optimal terminal wealth to (3.15) is

where $x^{*, \lambda_1, \lambda_2}(z)$ is defined in (A.2), (A.5) and (A.7). It remains to find the multipliers $y^*, \lambda_1^*, \lambda_2^*$ via the complementary slackness conditions

To prove the existence of the Lagrange multipliers, we shall choose $\lambda_1, \lambda_2$ as functions of $y$ by using VaR and ES constraints.

Case Ⅰ. If $H^{*} < \frac{U'(L_1)}{y}$, then $\tilde x^{*, \lambda_1, \lambda_2}(z)$ in (3.19) is given by (A.2); that is,

where $\tilde{L}\in(L_1, L_2)$ is the solution to (A.3). To meet the VaR constraint, we let $H^{*} = \frac{U'(\tilde{L})}{y}$ and define

Since $\frac{d}{{dx}}(U(x)-U(L_2)+U'(x)(L_2-x)) = U''(x)({L_2} - x) < 0$ for $L_1 < x < L_2,$ we have $\lambda_2 > U(L_2)-U(L_2)+U'(L_2)(L_2-L_2) = 0.$

We next show $\lambda_1$ can also been chosen as a function of $y$ by using the ES constraint. For a given $y > \; 0$, define

We can conclude that $V_1(\lambda_1)$ is a continuous and decreasing function in $\lambda_1$ and, thus, bijective. Note that when $\lambda_1$ tends to zero, the optimal terminal wealth tends to $X^{\pi^*, y^{VaR}}(T)$ given in (3.4). Assumption 3.2 yields $\mathop {\lim }\limits_{{\lambda_1} \to 0} {V_1}({\lambda_1}) = E[H(T)(L_1-X^{\pi^*, y^{VaR}}(T))^+] > \varepsilon_1$. When $\lambda_1$ tends to $y$, it holds that

which implies that $\mathop {\lim }\limits_{{\lambda_1} \to y} {V_1}({\lambda_1}) = 0 < \varepsilon_1$. By the intermediate value theorem, for a given $y,$ there exists a unique $\lambda_1\hat{ = }h_1(y)$ such that ${V_1}({\lambda_1}) = \varepsilon_1$.

Case Ⅱ. If $\frac{U'(L_1)}{y} \leq H^{*} < \frac{U'(L_1)}{y-\lambda_1}$, then $\tilde x^{*, \lambda_1, \lambda_2}(z)$ in (3.19) is given by (A.5); that is,

To ensure the VaR constraint holds, we let $H^{*} = \frac{k_{\lambda_2}}{y}$ and define

It is easy to check $\lambda_2 = (L_1-L_2)(\frac{U(L_1)-U(L_2)}{L_1-L_2}-k_{\lambda_2}) > 0.$

Similarly, when $\lambda_1$ tends to zero, it holds $\mathop {\lim }\limits_{{\lambda_1} \to 0} {V_1}({\lambda_1}) = E[H(T)(L_1-X^{\pi^*, y^{VaR}}(T))^+] > \varepsilon_1$. When $\lambda_1$ tends to $y$, the optimal terminal wealth tends to

which implies $\mathop {\lim }\limits_{{\lambda_1} \to y} {V_1}({\lambda_1}) = 0 < \varepsilon_1$. Thus, for a given $y,$ there exists a unique $\lambda_1\hat{ = }h_2(y)$ such that ${V_1}({\lambda_1}) = \; \varepsilon_1$.

Case Ⅲ. If $H^{*}\geq \frac{U'(L_1)}{y-\lambda_1}$, then $\tilde x^{*, \lambda_1, \lambda_2}(z)$ in (3.19) is given by (A.7); that is,

where $\hat{L}\in (0, L_1)$ is the solution to (A.8).

For a given $y > 0$, we have $\mathop {\lim }\limits_{{\lambda_1} \to 0} {V_1}({\lambda_1}) = E[H(T)(L_1-X^{\pi^*, y^{VaR}}(T))^+] > \varepsilon_1$ and

Hence, $\mathop {\lim }\limits_{{\lambda_1} \to y} {V_1}({\lambda_1}) = 0 < \varepsilon_1$. By the intermediate value theorem, for a given $y,$ there exists a unique $\lambda_1\hat{ = }h_3(y)$ such that ${V_1}({\lambda_1}) = \varepsilon_1$.

To meet the VaR constraint, we let $H^{*} = \frac{U'(\hat{L})}{y-\lambda_1}$ and define

Since $\frac{d}{{dx}}(U(x) - U({L_2}) - {\lambda _1}({L_1} - x) + (U'(x) + {\lambda _1})({L_2} - x)) = U''(x)({L_2} - x) < 0,$ for $0\leq x \leq L_1,$ it holds that $\lambda_2 > (L_1-L_2)(\frac{U(L_1)- U(L_2)}{L_1 - L_2} - (U'(L_1)+\lambda_1)) > 0.$

In total, $\lambda_1, \lambda_2$ can be chosen as functions of $y:$

Define

It remains to show there exists a unique root $y^*$ to the budget constraint ${V_2}(y) = \tilde{x}_0$. Some simple calculations yield that

It is easy to conclude

Furthermore, ${V_2}(y)$ is a continuous and decreasing function with respect to $y$. Again, by the intermediate value theorem, we have that when $\tilde x_0 \geq \tilde{x}_0^{\min}$, there exists a unique solution $y^{*}$ to the equation ${V_2}(y) = \tilde x_0$. Therefore, $y^*, \lambda_1^* = h(y^*), \lambda_2^* = g(y^*)$ are corresponding Lagrange multipliers and $X^{\pi^*, \lambda _1^*, \lambda_2^*}(T)$ given in (3.12)–(3.14) is the optimal solution to problem (2.11).

Since $\lambda_1, \lambda_2$ are related to $\varepsilon_1, \varepsilon_2$, we use the superscript $\varepsilon_1, \varepsilon_2$ in place of $\lambda_1, \lambda_2$ in $X^{\pi^*, \lambda _1^*, \lambda_2^*}(T)$; that is, the optimal terminal wealth is written as $X^{\pi^*, \varepsilon_1, \varepsilon_2}(T)$.

Proposition 3.7. Let $H^*$ solve $\mathbb{P}(H(T) \ge {H^{\rm{*}}}) = {\varepsilon _2}$ for $0 < \varepsilon_2 < 1.$ Assume $\tilde x_0 \geq \tilde x_0^{min}$, where $\tilde x_0^{min} = L_1e^{\frac{2M(0)+V^2(0)}{2}}-\varepsilon_1+E[H(T)(L_2-L_1)1_{\{H(T) < H^{\rm{*}}\}}]$. Under Assumption 3.2, for the joint VaR-ES constrained optimization problem (2.11), the optimal wealth process and the optimal strategy are given as follows, with the multipliers $\lambda_1^*$ and $y^{*}$ satisfying (3.11):

Case Ⅰ. If $\frac{U'(L_2)}{y^{*}} < H^{*} < \frac{U'(L_1)}{y^{*}}$, then

where $F(t)$ is given in (2.15),

with $d_{1}(x, H(t), t) = (\log(x/H(t))-M(t))/V(t)$, $d_{2}(x, H(t), t) = d_{1}(x, H(t), t)-V(t)$, $R(x, t) = V(t)x+M(t)$, $M(t)$ and $V(t)$ given in (2.7) and $\Phi$ and $\varphi$ being the standard normal cumulative distribution function and the standard normal density function, respectively.

The optimal money invested in the inflation-linked indexed zero-coupon bond and the stock at time $t$ is given by:

where

with $\bar\varphi_i(u, H(t), t) = -\varphi(d_{i}(u, H(t), t))/(v(t)H(t)),$ for $i = 1, 2$,

and

Case Ⅱ. If $\frac{U'(L_1)}{y^{*}}\leq H^{*} < \frac{U'(L_1)}{y^{*}-\lambda_1^*}$, then

The optimal money invested in the inflation-linked indexed zero-coupon bond and the stock at time $t$ is given by:

where

Case Ⅲ. If $H^{*}\geq \frac{U'(L_1)}{y^{*}-\lambda_1^*}$, then

The optimal money invested in the inflation-linked indexed zero-coupon bond and the stock at time $t$ is given by:

where

Proof. Since $H(t)\tilde X^{\pi^*, \varepsilon_1, \varepsilon_2}(t)$ is an $\mathcal{F}-$martingale, we have

Note that $\log(\frac{H(T)}{H(t)})$ is normally distributed with a mean $M(t)$ and a variance $V^2(t)$, where $M(t)$ and $V(t)$ are given in (2.7). Therefore, substituting Eqs (3.12)–(3.14) into Eq (3.25), we can obtain the expressions for $X^{\pi^*, \varepsilon_1, \varepsilon_2}(t)$ by some straightforward calculations. Note that $X^{\pi^*, \varepsilon_1, \varepsilon_2}(t)$ is a function of $(t, H(t))$. By Ito's formula, we have

where $G(t, H(t))$ is a function of $(t, H(t))$. Since we are only interested in the diffusion part, here we explicitly derive the diffusion parts of ${\mathrm{d}}X^{\pi^*, \varepsilon_1, \varepsilon_2}(t)$. By comparing the diffusion terms of ${\mathrm{d}}X^{\pi^*, \varepsilon_1, \varepsilon_2}(t)$ with (2.8), we can derive the optimal money invested in the inflation-linked zero-coupon bond and stock. □

4.   Numerical studies

In this section, we carry out some numerical calculations to investigate the impact of the joint VaR-ES constraint on the optimal terminal wealth.

Assume that

For all the computations, the values of certain parameters are held fixed except otherwise indicated: $T = 10, \gamma = 0.3, r = 0.01, \mu = 0.03, c = 0.1, y_0 = 5, \lambda_I = 0.01, \lambda_S = 0.23, \sigma _{YI} = \sigma _{YS} = 0, x_0 = 14.5, L_1 = 10, L_2 = 20, \varepsilon_1 = 0.7, \varepsilon_2 = 0.1.$

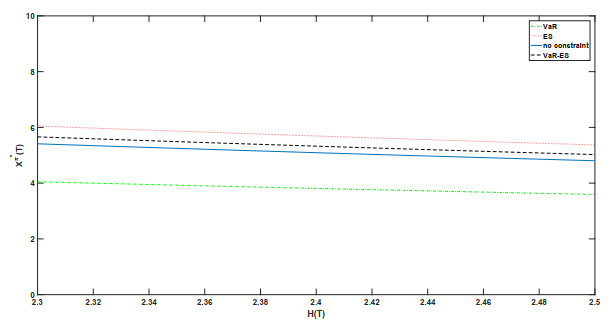
Figures 1 and 2 graph the optimal terminal value $X^{\pi^*}(T)$ versus $H(T)$ with different constraints. From Figure 1, we can observe that in the bad-economic-states region, the optimal terminal wealth corresponding to an ES constraint is higher than that without constraints, while the optimal terminal wealth corresponding to a VaR constraint is lower than that without constraints, which is consistent with the observations in ^[17]: An ES constraint can provide a better protection for bad economic states while a VaR constraint leads to heavier losses. It is noted that from Figure 1, a joint VaR-ES constraint can also improve the risk management of the bad economic states. Furthermore, we can find that from Figure 2, comparing with an ES constraint, more states are insured against and, therefore, the intermediate-economic-states region enlarges under a VaR-ES constraint, which implies a joint VaR-ES can not only provide a better protection for bad economic states, but also decrease the volatility of the optimal terminal wealth.

Table 1 lists means and standard deviations of the optimal terminal wealth and some probabilities for different constraints. We observe that the mean, the standard deviation of the optimal terminal wealth and the probability $\mathbb{P}(X^{\pi^{*}}(T)\ge 100)$ without constraints are much higher than those with constraints. This is because the manager shall take more conservative allocation strategies to attain the constraints at a cost of lowering the optimal terminal wealth in good economic states regions, resulting in lower means, less volatilities and smaller $\mathbb{P}(X^{\pi^{*}}(T)\ge 100)$. It can be seen from Table 1 that the probability $\mathbb{P}(X^{\pi^{*}}(T)\leq 3)$ corresponding to the case of no constraints is lower than that under a VaR constraint and is higher than that under an ES constraint or a joint VaR-ES constraint, consistent with the observations from Figure 1 that in the bad-economic-states region, an ES or a joint VaR-ES constraint can provide a better protection, while a VaR constraint leads to a lower optimal terminal wealth. Table 1 also numerically verifies the observations in Figures 1 and 2, where in contrast to a pure VaR or an ES constraint, a joint VaR-ES constraint can not only improve the risk management for the bad economic states but also decreases the volatility of the optimal terminal wealth.

Table 2 presents some probabilities, means and standard deviations of the optimal terminal wealth under a joint VaR-ES constraint for different $(\varepsilon_1, \varepsilon_2)$ with $(L_1, L_2) = (10, 20)$. From Table 2 we can see that for a fixed $\varepsilon_1,$ the mean, the standard deviation and the probability $\mathbb{P}(X^{\pi^{*}}(T)\geq 100)$ all increase in $\varepsilon_2$, while the probabilities $\mathbb{P}(X^{\pi^{*}}(T)\leq 3)$ and $\mathbb{P}(X^{\pi^{*}}(T) = L_2)$ decrease in $\varepsilon_2$. The reason is that in order to achieve a stricter VaR constraint with a smaller $\varepsilon_2$, the manager takes a more prudent strategy such that the optimal terminal wealth becomes less volatile, resulting in a lower expectation and a lower probability $\mathbb{P}(X^{\pi^{*}}(T)\geq 100)$. In addition, more bad economic states are insured against at a cost of lowering the optimal terminal wealth in bad-economic-states regions and, therefore, leads to a lower $\mathbb{P}(X^{\pi^{*}}(T)\leq 3).$ We can also observe that for a fixed $\varepsilon_2,$ the mean, the standard deviation and the probabilities $\mathbb{P}(X^{\pi^{*}}(T)\geq 100)$ and $\mathbb{P}(X^{\pi^{*}}(T)\leq 3)$ all increase in $\varepsilon_1$, while the probability $\mathbb{P}(X^{\pi^{*}}(T) = L_2)$ decreases in $\varepsilon_1$. This is due to the fact that with $\varepsilon_1$ decreasing, in order to achieve a stricter ES constraint, the manager becomes more conservative. Therefore, the optimal terminal wealth with a smaller $\varepsilon_1$ has a lower expectation, a less standard deviation and lower probabilities $\mathbb{P}(X^{\pi^{*}}(T)\geq 100)$ and $\mathbb{P}(X^{\pi^{*}}(T) = L_2)$. However, as an ES constraint can improve the risk management of the bad economic states, a smaller $\varepsilon_1$ brings a higher value of the optimal terminal wealth in the bad-economic-states region, leading to a lower probability $\mathbb{P}(X^{\pi^{*}}(T)\leq 3)$.

5.   Conclusions

In this paper, we investigated the optimal portfolio selection problem for a DC plan manager under a joint VaR-ES constraint. The constraint requires that the terminal wealth is no less than a constant protection level with a given probability, while at the same time requires that the expected present value of the losses given the regulatory level is no more than a predetermined constant. By using a concavification technique and a martingale method, we derived the semi-analytical formulas for the optimal wealth process and the optimal wealth invested in the risky assets. Numerical results illustrated that comparing with a pure VaR constraint, a regulation with a joint VaR-ES can provide a better protection for the bad economic states. Comparing with a pure ES, more bad economic states are insured under a joint VaR-ES constraint, resulting in a less volatility of the optimal terminal wealth.

A.   Appendix

Proposition A.1. For any $\lambda_1 > 0, \lambda_2 > 0,$ let $\tilde{U}_{\lambda_1, \lambda_2}$ and $k_{\lambda_2}$ be defined by (3.17) and (3.18), respectively, then for $y > 0,$ the concave envelope of $\tilde{U}_{\lambda_1, \lambda_2},$ denoted by $\tilde{U}_{\lambda_1, \lambda_2}^c,$ is as follows:

Case Ⅰ. If $k_{\lambda_2} < U'(L_1),$ then

and

where $\tilde{L}$ is the unique solution in the interval $(L_1, L_2)$ to the equation

Case Ⅱ. If $U'(L_1)\leq k_{\lambda_2} < U'(L_1)+\lambda_1,$ then

and

Case Ⅲ. If $k_{\lambda_2}\geq U'(L_1)+\lambda_1,$ then

and

where $\hat{L}$ is the unique solution in the interval $(0, L_1)$ to the equation

Proof. To find the concave envelope of $\tilde{U}$, we consider three cases: $k_{\lambda_2} < U'(L_1)$, $U'(L_1)\leq k_{\lambda_2} < U'(z_1)+\lambda_1$ and $k_{\lambda_2}\geq U'(z_1)+\lambda_1$, respectively.

Case Ⅰ. For $k_{\lambda_2} < U'(L_1),$ we let $\tilde{L}$ be the tangent point of the line starting at $(L_2, U(L_2)+\lambda_2)$ to the curve $U(x), L_1\leq x\leq L_2.$ It is easy to verify that there exists a unique solution to (A.3), then the concave envelope of $\tilde{U}_{\lambda_1, \lambda_2}$ over $[0, \infty)$ is given by (A.1).

It is easy to obtain the superdifferential of $\tilde{U}_{\lambda_1, \lambda_2}^{c}$ as follows:

We can derive the maximizer of $\{\tilde{U}_{\lambda_1, \lambda_2}^{c}(x)-xy\}$ by finding those points $x^{*, \lambda_1, \lambda_2}(y)\in [0, L_1]\cup [L_1, \tilde{L}]\cup [L_2, \infty)$ for which zero is in the super-differential of the function $\tilde{U}_{\lambda_1, \lambda_2}^{c}(x)-xy,$ which yields (A.2).

Case Ⅱ. For $U'(L_1)\leq k_{\lambda_2} < U'(L_1)+\lambda_1,$ we have that $\tilde{U}_{\lambda_1, \lambda_2}(x)\leq k_{\lambda_2}(x-L_1)+U(L_1)$ for $L_1\leq x < L_2$. Thus, the concave envelope of $\tilde{U}_{\lambda_1, \lambda_2}$ over $[0, \infty)$ is given by (A.4). Similar to derivation of (A.2), we can obtain the maximizer of $\{\tilde{U}_{\lambda_1, \lambda_2}^{c}(x)-xy\}$ is given by (A.5).

Case Ⅲ. For $k_{\lambda_2}\geq U'(L_1)+\lambda_1,$ we let $\hat{L}$ be the tangent point of the line starting at $(L_2, U(L_2)+\; \lambda_2)$ to the curve $\tilde{U}_{\lambda_1, \lambda_2}(x), x\leq L_1.$ It is easy to prove that Eq (A.8) has a unique solution in the interval $[0, L_1],$ then the concave envelope of $\tilde{U}_{\lambda_1, \lambda_2}$ over $[0, \infty)$ is given by (A.6). Using the same arguments as in deriving (A.2), we have that the maximizer of $\{\tilde{U}_{\lambda_1, \lambda_2}^{c}(x)-xy\}$ is given by (A.7).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the anonymous referees and the editor for their comments and suggestions.

The research of Yinghui Dong was supported by Humanities and Social Science Research Projects in Ministry of Education (20YJAZH025) and the NNSF of China (Grant Nos. 12071335, 12371474).

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.