1. Introduction
All types of bacteria studied so far (Gram-negative, Gram-positive, cell wall-less bacteria) and a number of archaea have revealed the presence of specialised secretion systems that are vital for their survival, pathogenicity and ability to adapt to changes in the environment [1]. These macromolecular machineries are responsible for the transport of DNA and effector molecules across the cell envelope. Secretion systems found in bacteria are currently classified into seven major classes [2,3,4,5,6,7]. The variety of substrates secreted by type IV secretion (T4S) systems and their nature (single proteins, protein complexes, DNA and nucleoprotein complexes) singles out these secretion systems from the others and make them the most functionally versatile class. Many T4S systems have been shown to inject (translocate) proteins into the cytosol of eukaryotic cells, where these proteins facilitate bacterial pathogenesis by specifically interfering with host cell function [2,3,4,5,6,7,8,9,10,11,12].
Depending on their function, T4S systems can be divided into three major groups. The first group includes T4S systems that transfer DNA unidirectionally from donor to recipient cell in a contact dependent way. Another group of T4S systems mediates the translocation of proteins, ranging from small protein effectors to large protein complexes. Pathogenic Gram-negative bacteria such as Helicobacter pylori, Brucella suis and Legionella pneumophila use the T4S system to inject virulence proteins into mammalian host cells [8,9,10] while Bordetella pertussis use the T4S systems to secrete pertussis toxin into the extracellular milieu [11]. As a result they cause different types of diseases e. g. respiratory diseases-like “whooping cough”, chronic gastric disorders or tumour growth in plants. The last and smallest group consists of T4S systems, which secrete or uptake DNA into or from the extracellular milieu, respectively. H. pylori and Neisseria gonorrhoeae are examples of bacteria with this type of T4S systems [12,13].
The first type of translocation related to DNA greatly contributes to the spread of antibiotic resistant genes among bacterial species and allows them to adapt to environmental changes. Members of this group are called conjugative type IV secretion systems. The phenomenon of conjugation in bacteria is an enormous public-health problem since this mechanism allows rapid dissemination of antibiotic-resistant genes and other virulence behaviour among pathogens. While the fact that DNA can move from one cell to another was established a long time ago [14,15], the mechanism of secretion is still poorly understood. However, structural information recently obtained allows better understanding of the type IV secretion systems architecture [16]. The revelation of the principles of action of these bacterial nanomachines has broad clinical importance not only due to delivery of bacterial toxins or effector proteins straight into targeted host cells, but for the direct involvement in the rapid horizontal spread of antibiotic resistance genes among the microbial population. In this review we describe the latest progress in structural studies of the T4S system using methods of electron microscopy.
2. Overall Organisation of the Type IV Secretion System
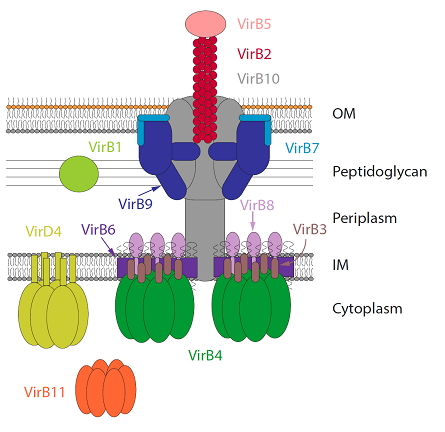
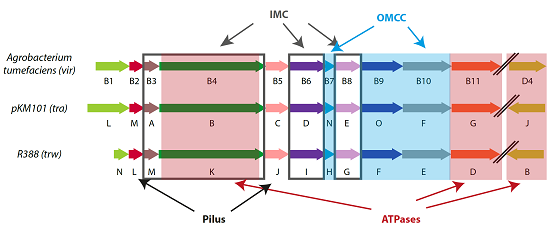
AllT4S systemsare evolutionarily related and share some structural features such as a specific channel spanning the cell envelope, through which the secreting process occurs in an ATP-dependent manner [17]. Numerous T4S systems are organized similarly to the VirB/D4 Agrobacterium tumefaciens system, which is composed of 12 proteins VirB1-VirB11 and VirD4 [18]. This nomenclature is used throughout this review. These proteins assemble into a complex with three distinct substructures: pilus, secretion channel and coupling protein (Figure 1). Other T4S systems which have evolved additional subunits and might be structurally organized in a different way than the VirB/D4 A. tumefaciens system e. g. L. pneumophila Dot/Icm and H. pylori cag system are not discussed in this review.
The pilus is an extracellular appendage, which connects the donor and recipient cell during the DNA transfer—conjugation [1]. Pilus is built up from two proteins, the major subunit VirB2 and the minor subunit VirB5. While multiple copies of VirB2 form a rod like structure, VirB5 can be found at the tip of the pili [19,20]. VirB2 is a small hydrophobic protein, which is proteolytically processed at its termini and polymerizes into a pilus [21]. Alternatively following proteolysis the N-termius and C-terminus of VirB2 is fused resulting in a cyclic peptide [22]. VirB5 is a periplasmic protein with an N terminally located signal peptide sequence. In order for VirB5 to form a complex with VirB2, VirB4 is required [23]. By studying various complexes of VirB4 and VirB5 it has been proposed that VirB4 enable assembly of VirB2 with VirB5 by stabilizing VirB8 and VirB10 complex [23]. Also VirB4 mediates VirB2 assembly into the pilus by extraction from the IM [24]. The structure of VirB5 has been solved by X-ray crystallography [25].
The secretion channel, which in Gram-negative bacteria spans both outer and inner membranes, is composed of an inner-membrane complex (IMC), attached to an outer-membrane core complex (OMCC) via a flexible stalk region (Figure 2). The OMCC is composed of 14 copies of 3 proteins VirB10, VirB9 and VirB7 [26]. It forms a channel, which is inserted in both inner and outer membrane, thereby spanning the whole bacterium envelope. Lipidation of VirB7 is required for anchoring of the OMCC in the outer membrane. The structural details of OMCC are discussed below.
The organisation of the stalk region is yet to be defined. However, it has been suggested that it consists of the N-terminal extensions of VirB10 that stretches out from OMCC towards the inner membrane. Pillus subunits are also likely comprise part of the stalk, or at least pass through the stalk during the pilus polymerization reaction. The IMC contains proteins VirB3, VirB4, VirB6 and VirB8, present in 12, 12, 24 and 12 copies respectively [27] (Figures 1 and 2). VirB3 protein, which is an inner -membrane protein with both N- and C- terminus facing the cytoplasm, is the smallest component of the IMC. For its stability VirB3 requires the presence of VirB4, VirB7, VirB8. VirB3 has been recently shown to form a complex with VirB4 [28]. Interestingly, several genome-sequencing studies have identified a fusion protein between VirB3 and VirB4. VirB6 is a polytopic inner membrane protein with a periplasmic N terminus, five transmembrane segments and a cytoplasmic C terminus [29]. It has been shown in immunofluorescence microscopy experiments that VirB6 localizes to cell poles. Additionally the co-localization of VirB6 with VirB3 and VirB9 has been documented [30]. The proposed function of VirB6 is to regulate T-pilus formation by interactions with VirB5. VirB6 protein also participates in the formation of a complex between VirB7 and VirB9 proteins. VirB8 is a bitopic protein with its N terminus localized in cytoplasm while the C terminus resides in the periplasm [31]. VirB8 interacts with VirB10 and VirB4 and positively regulates the stability of VirB1, VirB3, VirB4, VirB5, VirB6, VirB7 and VirB11 in the A. tumefaciens VirB/D4 system [32]. Structures of the periplasmic domain of VirB8 from Brucella suis and A. tumefaciens have been solved by X-ray crystallography [33,34]. VirB1 is responsible for the lysis of the peptidoglycan cell wall required for the type IV secretion complex insertion [28].
The IMC is powered by three hexameric ATPases on the cytosolic and IM sides: VirB4, VirB11 and VirD4 [35] (Figures 1 and 2). VirB4 is the most conserved T4S system component [36]. Typically it has two domains, the C-terminal domain being more conserved and responsible for ATPase activity while the N-terminal domain is presumably used for the interactions with the IMC of the T4S system. However, VirB4 has only recently been identified within the assembled complex [27]. Even though in some cases transmembrane regions were predicted within the N-terminal part of VirB4, the full-length protein was isolated from both membrane and cytoplasmic fractions. The oligomerization state of the protein remains unclear so far as it has been documented as monomeric, dimeric, trimeric, and hexameric complexes [36,37,38]. However, in a complex with other inner membrane components of the T4S system, VirB4 has been shown to form hexamers [27] (Figure 2). The crystal structure of the C-terminal domain of a homolog of VirB4 from a thermostable organism, Thermoanaerobacter pseudethanolicus, has been solved [36].
VirB11 is a soluble hexameric ATPase, which is divided into N- and C-terminal domains by a flexible linker [39]. As the closest structural homologues to VirB11 are AAA+ ATPases, which are involved in trafficking, it might be that VirB11 behaves like a chaperone, unfolding substrates and being involved in their translocation [40]. It has been suggested that VirB11 is regulating pilus biogenesis by interacting with VirB4 [35].
VirD4 is responsible for the recruitment of the substrate and is therefore often called a coupling protein. It is inserted into the inner membrane via two transmembrane helices [41,42]. VirD4 is known to interact in the cytosol with other ATPases VirB11 and VirB4 and with VirB10 in the IM. The crystal structure of the soluble part of VirD4 from R388 system reveals a hexameric structure [43].
3. Electron Microscopy and Hybrid Methods in Analysis of the T4S System Structural Organisation
Due to their intricacy multi-protein complexes are difficult candidates for structural studies, in particular when they are associated with membranes. In this case electron microscopy is the method of choice. This technique allows visualization of large complexes both within cells and in an isolated form under nearly native conditions [44]. The simplest way of examining the complexes in EM is negative staining (NS). The sample is spread on a support film and covered with a solution of NS (typically a salt of heavy atoms), which is more dense compared to the biological specimen itself [45]. This simple approach allows very quick examination of samples. However owing to the size of the stain grain, flattening effect due to drying at the time of sample preparation, and sometimes partial staining of the specimen, many structural details in images remain obscured. In order to obtain high-resolution structures of macromolecular assemblies, cryo EM techniques are used [46] where a sample is nearly instantly frozen in aqueous solution at liquid nitrogen temperatures. This allows observing biological complexes close to their native conditions. Here we report analysis of T4S systems using both NS and cryo methods (Figures 3 and 4).
4. Structure of the OMCC
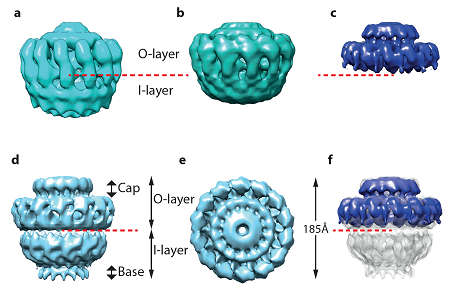
A first assembly of T4S systems that has been isolated and structurally characterized was the OMCC from pKM101 plasmid [26] (Figure 1). This large complex is composed of 14 copies of each proteins VirB7, VirB9 and VirB10 and has a molecular mass of ~1.1 MDa. The first NS EM reconstruction has revealed a ring like structure with 14-fold symmetry [26] (Figure 3a). Two layers can be clearly distinguished within this structure: the so-called O-layer consisting of a main body topped by a cap and the so-called I-layer below it. In order to identify the localization of the N-terminus of VirB10 within the structure, the full-length OMCC was subjected to mild proteolysis. As a result, a truncated version of the OMCC was obtained with 156 amino acids cleaved from the N-terminus of VirB10 using trypsin (Figure 3b). The only difference between the EM maps of the full OMCC and the truncated complex is the disappearance of part of the base in the latter one. This indicates that the N-terminal part of VirB10 is localized at the base of the OMCC.
The cryoEM structure of the full-length OMCC has been obtained at ~15 Å resolution and revealed more structural details [26] (Figure 3d-e). The structure clearly demonstrates a two-layer organisation: the upper layer, the 85Å high O-outer and the 85Å high I-inner layer, named referring to the position of the layers with respect to the outer and inner membranes. The overall dimensions of the complex are 185 Å both in width and length. Similarly to the negative stain structure of the OMCC, the O-layer includes a cap on top of a main body. The I-layer of the complex ends with a so-called base. Both the I-layer and O-layer have the I-chamber and the O-chamber (Figure 3f). The internal wall of the O-chamber forms a 20 Å wide opening within the cap area, which narrows down to 10 Å on the top of the O-layer. The inner parts of the O- and I-chambers have a diameter of ~60Å at widest points. The I-chamber narrows to 55 Å at its base [26] (Figure 3f). Further information about the localization of all the proteins within the OMCC has been obtained by digestion of the core complex with trypsin. This led to a formation of a ~500 kDa stable complex, where both VirB9 and VirB10 have been truncated at the N-terminus. The I-layer part of the OMCC was no longer present within the cryoEM reconstruction of the trypsin-digested complex (Figure 3c). Thus it has been concluded that the I-layer is exclusively composed of the N-terminal parts of VirB9 (VirB9NT) and VirB10 (VirB10NT). The position of the N-terminus of TraF/VirB10 has been localized within the base of the complex by antibody labelling [26].
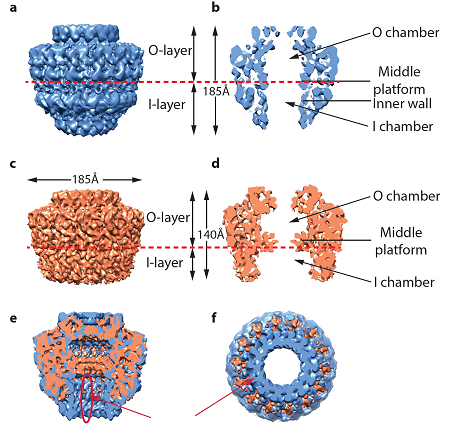
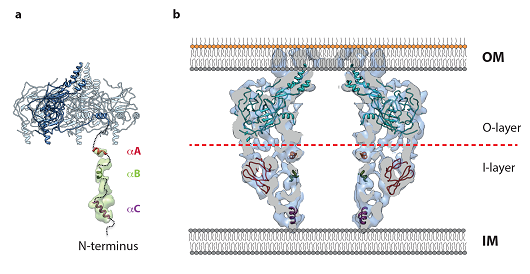
Later, an improved cryoEM map of the pKM101 full-length OMCC has been obtained at 12.4 Å resolution and revealed new features that were not identified previously [47] (Figure 1, Figure 4a, b). It has been found that the I-layer of the complex has a double-walled structure (Figure 4b). The inner wall diameter varies between 50 and 55 Å and is composed by 14 columns of density separated by 7 Å (Figure 4c, d). The columns are ~8Å in a diameter and 70Å in height. The tops of the columns are connected to the O-layer, while their lower parts form the base of the OMCC. More details were revealed in the cryo-EM reconstruction of an elastase-digested OMCC that was obtained at an 8 Å resolution [47] (Figure 4c, d). This complex lacked the first 160 residues of VirB10. Similarly to the trypsin-digested complex, part of the base structure is not present in the elastase-digested OMCC. Moreover, the structures of the I-layer differ between the full-length and elastase-digested OMCC (Figure 4d-e). In the elastase-digested complex, the opening to the cytoplasmic side is wider −65 Å and the inner wall of the I-layer is not present (Figure 4e, d). The composition of the O-layer within the elastase-digested complex has been defined by fitting of the X-ray structure of the ternary complex between VirB7 and the C terminal domains of VirB10 (VirB10CT) and VirB9 (VirB9CT) (Figure 5a, b) In addition, three helical peptides have been identified based on the sequence of VirB10NT as well as two regions rich in β-strands within the VirB9NT and successfully fitted within the EM map of the full length OMCC. Two of the peptides derived from VirB10NT have been fitted within the inner wall of the I-layer whereas the remaining peptide was found within the base. At the same time the VirB9NT model has been nicely fitted within the outer wall of the I-layer of the map (Figure 5) [47].
5. First Structural Insight into a Nearly Entire T4S Secretion Assembly
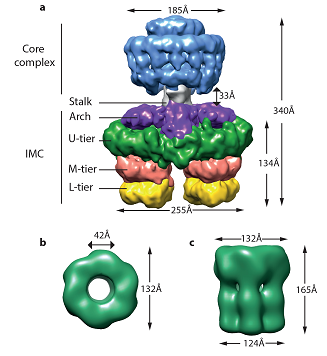
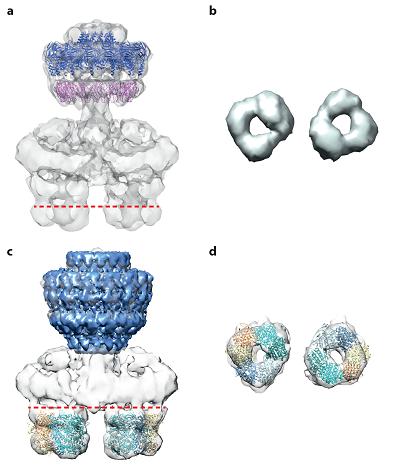
The latest EM reconstruction of the nearly whole T4S system from the R388 plasmid, lacking only the ATPases VirB11 and VirD4 and the major pilus subunit VirB2, shed light into the architecture of the T4S apparatus. The ~3 MDa complex, hereafter called T4SS3-10 is composed of 8 proteins. It has been expressed in E. coli and isolated from membranes using affinity purification and finally visualized by NS-EM [27]. The reconstruction shows three distinct structural parts of the complex: OMCC, IMC and the stalk region that holds them together. The complex is 340 Å in length and 255 Å at its widest point (Figure 6).
The structure of the OMCC within T4SS3-10 is consistent with the structure of the previously described OMCC of the pKM101 plasmid (Figure 1). Importantly the negative stain EM reconstruction of the R388 OMCC on its own is structurally similar to that of the pKM101 (Figures 7a and 7b). 14-fold symmetry of the OMCC has been clearly identified, as well as its separation into two layers (I and O). Interestingly the OMCC within the T4SS3-10 has an inner central stalk that was not observed previously.
The IMC is formed of three main parts (Figure 6): the arches, the trans-membrane platform, and two barrel-like structures. Each of the barrels is composed of three tiers called L-tier, M-tier and U-tier. Both L-tier and M-tier display 3 fold symmetry (Figures 6 and 7). The barrels are related by two-fold symmetry. Two T4S system components VirB4 and VirB6 have been localized within the barrel and the IMC platform, respectively, by gold labelling experiments [27]. The length of a monomer of VirB4, corresponds to the length of the two barrels of IMC [27]. Indeed the recently reported NS-EM reconstruction of the full-length VirB4 from the R388 plasmid shows high level of similarity with the two barrels present within the IMC [37]. Interestingly VirB4 in the absence of other T4S system components appears to be different in size, 165Å long, with a diameter between 132 Å and 124 Å [37], compared to 134 Å in height and ~105 Å in diameter in the T4SS3-10 complex (Figure 6).
6. Discussion and Future Directions
Significant progress has been made in understanding the architecture of the T4SS during the last decade [16,18]. The intensive structural studies have revealed a very distinct organisation of this secretion apparatus that spans both inner and outer-membranes and have localised different subunits within its structure. It has been shown that the OMCC is formed even in the absence of other T4SS components [26]. Moreover the T4S system formation is initiated by the assembly of the OMCC, which serves as a scaffold for the assembly of all the rest of the T4S components [48,49]. This complex might serve as a seed for the assembly of the other T4SS components. Detailed examination of the complete and truncated OMCCs indicates that VirB10 spans the entire cell envelope. This finding supports the hypothesis that ATP-driven conformational changes within N-terminus of VirB10 could serve as a gating mechanism in the T4SS channel [50,51]. Unfortunately, very little isknown about the connection between T4S channel components and ATPases and the composition of the IMC in general. The only available information has been derived from the recently obtained NS-EM reconstruction of the nearly complete T4SS from R388 [27] (Figure 7). However two ATPases, which are necessary for substrate recruitment and pilus biogenesis, VirD4 [52] and VirB11 [24], are not present within this structure. In order to understand the mechanism of substrate secretion, it is important to localize the missing ATPases with respect to the already assembled T4SS3-10 complex as well as observe if their presence impact the overall structure of the T4S system.
The only information about the pathway of the substrate during the transfer so far comes from the A. tumefaciens VirB/D4 system [53]. However the molecular details of this process are still unknown and further investigations are required to understand how the T4S system interacts with and transport substrates through the bacterial envelope. A role and function of the pilus also requires more structural and biochemical studies. These tasks represent a great challenge that can only be met by implementing novel biochemical and genetic approaches resulting in trapping T4S systems at different stages of substrate transfer. The revealed organisation of the T4S systems is very unusual: contrary to other secretion systems such as T6SS, or T3SS the T4S systems do not have a rigid organisation based on the rotational symmetry of their major components or helical organisation [54,55,56].
7. Conclusions
Advances in the structural biology achieved by methods of electron microscopy helped to resolve structures of huge biological macromolecular complexes that are amenable to other structural methods. The combination of EM structures and biochemical approaches made possible localisation of important protein components within the structures and therefore provide validated suggestions on the T4S system possible mechanism of action. Hopefully the use of recently developed direct electron detection system, as well as improvement of the statistical analysis software in combination with novel biochemical methods will allow to elucidate the high resolution structure of the missing stalk region as well as the IMC with the ATPases [57,58]. These structural studies will be crucial to gain a complete understanding of the mechanism of T4SSs.
Acknowledgments
This work was funded by grant 082227 from the Wellcome Trust to GW and K012401 from MRC to EVO and GW. The authors would also like to thank the Wellcome Trust for the EM equipment.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: