Expression and function of nicotinic acetylcholine receptors in stem cells

1.   Introduction

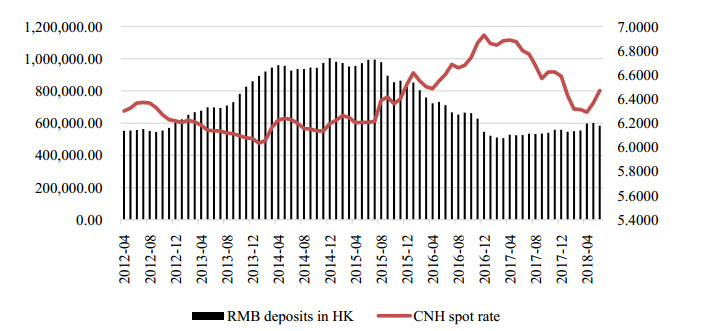
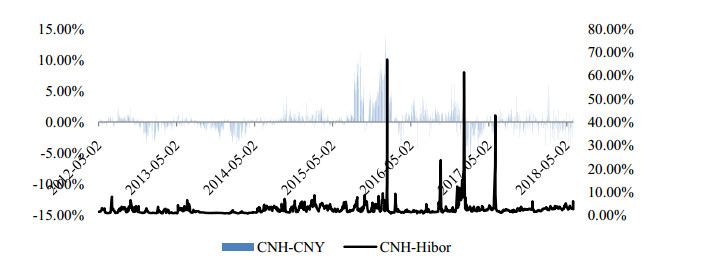
Renminbi (RMB) traded in onshore and offshore two separate markets, the RMB transacted in onshore market has the trading symbol CNY, while the RMB transacted in offshore market has the trading symbol CNH. There is a disparity in developments between CNY and CNH markets. The CNY market, with its comparatively long history and deep liquidity, the PBoC has a presence in the CNY market in order to maintain exchange rate stability (Fatum et al., 2013), while the CNH exchange rate floats freely and is determined by offshore market participants. For these reasons, CNH exchange rates frequently diverge from the CNY exchange rates, resulting in interactions between the onshore and offshore exchange rate markets. Hong Kong was established as the first offshore RMB center in 2009, and has developed the most liquid and premier offshore RMB financial center. Hong Kong Interbank Offered Rate (CNH-Hibor) is the official calculated industry interest rate benchmark, which provides a formal benchmark for market participants to reference when pricing RMB loan and interest rate contracts, with which market participants can manage the interest rate risk of their RMB businesses. On August 11, 2015, China announced the RMB central parity formation mechanism reform, the new mechanism made reference to the previous day close, which is considered as a historic move toward a market-determined exchange rate regime. Market calm in the offshore and onshore RMB business has been shifted, uncertainties in offshore RMB market sharply arise with various forms of shocks in exchange rate and interest rate. Figure 1 plots the co-movements of CNH-CNY spread and CNH-Hibor. Before August 11, 2015, the price of CNH-Hibor had not change over a long time, and the volatility of CNH-CNY spread was not high. After August 11, 2015, the volatility magnitude of CNH-CNY spread and price of CNH-Hibor became larger and changed frequently, while the “8.11” reform is expected to shrink the CNH-CNY pricing differential. It is important to investigate the reasons. Our main goal is to compare the connectedness of markets with a focus on the spillovers and apply the methodologies using daily return and daily return volatility data.

Figure 1.  The CNH-CNY difference and the CNH-Hibor.

DownLoad: Full-Size Img PowerPoint

The paper is organized as follows. Section 2 sets out the existing theoretical and empirical literature on the correlations between the onshore and offshore RMB markets. Section 3 describes the empirical methodologies utilized here. Section 4 presents the data set and sets out the main empirical results. Section 5 concludes.

2.   Literature review

The literature on the correlation of onshore RMB and offshore exchange rates has increased in the last few years. Before the PBoC and HKMA signed an amendment to the RMB Clearing Agreement in July 2010, the RMB non-deliverable forwards (NDF)¹ was the hedging instrument for entities in Asian countries after the 1997 Asian financial crisis. Therefore, earlier studies considered correlations between RMB NDF rates and the onshore spot rate CNY (Yang and Leatham, 2001; Fung et al., 2004; Peng et al., 2007; Li et al., 2019). After the establishment of CNH, the guidance effect from the NDF market to the CNY spot exchange rate has been weakened (Wu and Pei, 2012). The offshore spot rate has volatility spillover effects to the onshore spot rate (Wu and Chen, 2013). Granger causality, return spillovers and volatility spillovers between the NDF and CNY spot have experienced significant changes (Kou and Kong, 2014). Therefore, the development of CNH market has important implications for the pricing mechanism of CNY spot exchange rate. With the expansion of CNH market and the shrinking of NDF market, scholars began to focus on the correlations between CNY and CNH markets. Shen (2014) used a VECM-DCC-MVGARCH model to estimate the dynamic relationship between CNY and CNH exchange rate markets, the results show that the CNY and CNH are mean reversion, thus influence each other in the short run, while the CNH adjusts to a new equilibrium slower than that of CNY in the long run. Leung and Fu (2014) found onshore-to-offshore spillovers were larger than spillovers in the opposite direction in most cases. This probably reflects the fact that the CNH market, though rapidly growing, is small compared to the mainland market, and possibly more subject to onshore influences. Cheung and Rime (2014) found that the CNH exchange rate had an increasing impact on the CNY exchange rate, and shows significant predictive power for the RMB central parity rate. The CNH order flow also affects the CNY exchange rate and the RMB central parity rate. Owyong et al. (2015) examined the interactions between the RMB onshore and offshore markets affected by the widening of the onshore trading band, first in April 2012 and further in March 2014. Ties between the onshore and offshore markets were closest before the first band, widening and steadily loosened thereafter. The cointegration and lead-lag effects between offshore and onshore spot and forward markets show that there is a long-term equilibrium relationship between any pair of them. Funke et al. (2015) used GARCH models to explore the fundamental factors, related to RMB internationalization, driving the pricing differential between the onshore and offshore exchange rates. They found that differences in the liquidity of the two markets play an important role in explaining exchange rate gaps. Yan, Sun and Huang (2015) analyzed the linkage effects of CNH-Hibor and CNH, with daily trading data from January 1, 2012 to October 31, 2014, the results show there were significant bidirectional price spillover effects between CNH-Hibor and CNH. Xu et al. (2017) use the thermal optimal path method to explore the long-term and short-term interactions between the onshore CNY and offshore CNH exchange rates. They found that USD appreciation is associated with a lead-lag relationship running from offshore to onshore, while a contrarian RMB appreciation is associated with a lead-lag relationship running from onshore to offshore. Liang et al. (2019) using GARCH-type models, find robust evidence of the volatility clustering phenomenon and the leverage effect in the pricing differential between the onshore and offshore exchange rates, and the recent RMB currency market reforms all increased the volatility of the pricing differential between CNH and CNY. Chen, Du and Tan (2019) found the effect of EPU on the exchange rate volatility of China is significantly positive in China, the government can develop appropriate plans to reduce the exchange rate volatility according to the different periods of the exchange rate market.

¹ NDF is a forward transaction that there will be no need for a physical settlement of the principal. That is, for the RMB NDF in USD, at maturity, the difference between the contracted forward rate and the fixing spot rate is settled in USD. (Fung et al., 2004)

This paper contributes to three strands of literature. First，earlier studies focused on the interactions of CNH-to-CNY or CNH-to-CNH-Hibor, few considered the connectedness of the three markets. In this paper, we combine the correlations in CNH, CNY and CNH-Hibor markets, which is an innovative combination, and compare the results before and after the “8.11” reform. The study of market integration through the analysis of return and volatility spillover has important implications. Second, we analyze the price lead-lag relationship in the short term and the direction of information flow in three markets using VAR model and Granger causality test, this provides us with the means to show the pricing power of the RMB spot exchange rate between onshore and offshore markets. Third, there is the adoption of a multivariate GARCH framework for the empirical investigation of potential spillover effects in the three markets. Multivariate GARCH models are considered as one of the most useful tools for analyzing and forecasting the volatility of time series when volatility fluctuates over time. The study of volatility spillovers between markets is useful from a risk management perspective.

3.   Methodology

This study uses a VAR model to analyze the relationship among CNY, CNH, and CNH-Hibor price volatility. The benefit of using a VAR approach is that the model treats each of the series as endogenously determined within the system.

Under the three-variable model, we describe the VAR(1) model as:

where, ${\gamma }_{i}$ , ${\lambda }_{ij}$ are model parameters for i = 1, 2, 3 and j = 1, 2, 3. ${\mathrm{R}}_{1, \mathrm{t}}$ , ${\mathrm{R}}_{2, \mathrm{t}}$ and ${\mathrm{ }\mathrm{R}}_{3, \mathrm{t}\mathrm{ }}$ are the logarithmic returns of the CNH, CNY, CNH-Hibor return series respectively. The ${\mathrm{\varepsilon }}_{1, t}$ , ${\mathrm{\varepsilon }}_{2, t}$ and ${\mathrm{\varepsilon }}_{3, t}$ are residual terms for the equations respectively. Here, the parameter coefficients ( ${\mathrm{\lambda }}_{11},$ ${\mathrm{\lambda }}_{22}$ and ${\mathrm{ }\mathrm{\lambda }}_{33}$ ) measure their own mean return spillovers. However, the rest of the parameter coefficients measure the cross-mean spillover among pairs of CNH, CNY and CNH-Hibor. For example, ${\lambda }_{ij}$ measures the impact from j to i. The relationship between information flow provides an interesting perspective for interpreting the causation in variance between a pair of financial time series. The causation in variance between a pair of financial time series is termed spillover. Under this model specification, cross-market spillovers can be interpreted as the effect of a change in the residual terms of the mean equation on the conditional variances of the two markets. There are two methods to judge the return spillover effect, the first is verify whether the coefficient of the lag order term of VAR model is significantly different from zero, the second is to judge the return spillover effect with Granger causality. In this paper, we employ Granger causality to judge the return spillover effect

Volatility is the risk associated with unexpected movements in the CNH and CNY exchange rates, and CNH-Hibor interest rate. The existence of volatility spillover implies that one large shock increases volatility not only in its own market but also in other markets. In this paper we employ the MGARCH-BEKK approach and Wald test to estimate the volatility of spillovers in CNH, CNY and CNH-Hibor three markets. This model is one of the most widely used multivariate GARCH models, which was established by Engle and Kroner (1995), and the variance covariance matrix of the model depends on the cross product of the square of ${\varepsilon }_{t}$ and the hysteresis value of the market volatility ${H}_{t}$ . Under GARCH, shocks to the variance persist according to an autoregressive moving average (ARMA) model for the squared residuals of the process. The advantages of the MGARCH-BEKK model is to ensure the positive definite of ${H}_{t}$ , while allowing the conditional variance and covariance of different variables to interact with each other, as well as needing to estimate less parameters.

The residuals of the mean equation are assumed to follow a Student’s t-distribution with zero mean and a time-varying variance conditional on the past informational set ${\mathrm{ }\mathrm{\Omega }}_{t}$ :

The three-dimension MGARCH(1, 1)-BEKK condition volatility specification has the following form:

where ${\varepsilon }_{t }$ is the innovation vector and ${v}_{t}$ is the standardized residual matrix. We define ${H}_{t} = \left(\begin{array}{ccc}{h}_{11, t}& {h}_{12, t}& {h}_{13, t}\\ {h}_{21, t}& {h}_{22, t}& {h}_{23, t}\\ {h}_{31, t}& {h}_{32, t}& {h}_{33, t}\end{array}\right)$ as the residual’s conditional variance-covariance matrix with information known at time t-1 and before; further structure is added via a variance equation as follow:

Here $C = \left(\begin{array}{ccc}{c}_{11}& {c}_{12}& {c}_{13}\\ 0& {c}_{22}& {c}_{23}\\ 0& 0& {c}_{33}\end{array}\right)$ is a upper triangular constant matrix and its setting guarantees the positive definiteness of H_t. $A = \left(\begin{array}{ccc}{a}_{11}&{a}_{12}&{a}_{13}\\ {a}_{21}&{a}_{22}&{a}_{23}\\ {a}_{31}&{a}_{32}&{a}_{33}\end{array}\right)$ measures the ARCH effect, while $B = \left(\begin{array}{ccc}{b}_{11}&{b}_{12}&{b}_{13}\\ {b}_{21}&{b}_{22}&{b}_{23}\\ {b}_{31}&{b}_{32}&{b}_{33}\end{array}\right)$ measures the GARCH effect.

Note, ${ h}_{11, t }$ is the conditional variance of the CNH residual, ${h}_{22, t}$ is the conditional variance of the CNY residual, and ${h}_{33, t}$ is the conditional variance of the CNH-Hibor residual; while ${h}_{12, t}$ , ${h}_{13, t}\mathrm{a}\mathrm{n}\mathrm{d}{h}_{23, t}$ are their corresponding covariances. Therefore, it is possible to judge whether there are volatility spillovers between markets by examining the coefficient of ${a}_{ij}(i\ne j)$ and ${b}_{ij}\left(i\ne j\right)$ is significantly different from 0. For example, if ${ a}_{12}$ or ${b}_{12}$ is not significantly equal to 0, this indicates there are volatility spillovers from CNH to CNY, while the estimated ${a}_{21}$ and ${b}_{21}$ coefficients examine this effect in the opposite direction. We use Wald tests to examine several hypotheses about spillovers in means and variances, these are shown in Table 1.

Table 1.  Volatility spillovers among the three markets by joint tes.

	Hypothetical test1	Hypothetical test2
CNH and CNY	There is no volatility spillover from CNH to CNY ${H}_{0}$ : ${a}_{12}$ = ${b}_{12}$ =0 ${H}_{1}$ : ${a}_{12}\ne 0$ or ${b}_{12}\ne 0$	There is no volatility spillover from CNY to CNH ${\mathrm{H}}_{0}$ : ${a}_{21}$ = ${b}_{21}$ =0 ${\mathrm{H}}_{1}$ : ${a}_{21}\ne 0$ or ${\mathrm{b}}_{21}\ne 0$
CNH and CNH-Hibor	There is no volatility spillover from CNH to CNH-Hibor ${H}_{0}$ : ${a}_{13}$ = ${b}_{13}$ =0 ${H}_{1}$ : ${a}_{13}\ne 0$ or ${\mathrm{b}}_{13}\ne 0$	There is no volatility spillover from CNH-Hibor to CNH ${\mathrm{H}}_{0}$ : ${a}_{31}$ = ${b}_{31}$ =0 ${\mathrm{H}}_{1}$ : ${a}_{31}\ne 0$ or ${\mathrm{b}}_{31}\ne 0$
CNY and CNH-Hibor	There is no volatility spillover from CNY to CNH-Hibor ${H}_{0}$ : ${a}_{23}$ = ${b}_{23}$ =0 ${H}_{1}$ : ${a}_{23}\ne 0$ or ${\mathrm{b}}_{23}\ne 0$	There is no volatility spillover from CNH-Hibor to CNY ${\mathrm{H}}_{0}$ : ${a}_{32}$ = ${b}_{32}$ =0 ${\mathrm{H}}_{1}$ : ${a}_{32}\ne 0$ or ${\mathrm{b}}_{32}\ne 0$

---

 | Show Table

DownLoad: CSV

As we mentioned above, the ${\varepsilon }_{t}$ are assumed to follow a Student’s t-distribution with zero mean and time-varying conditional variance. Our estimations of the BEKK models are carried out by quasi-maximum likelihood (QML), where the conditional distribution of error term is assumed to follow a log-likelihood function of a sample of T observations and K = 3 as follows:

Lastly, we test whether the model is correctly specified. If so, the normalized residual ${\nu _t}$ should be a white noise process without autocorrelation and ARCH effects. Therefore, the Ljung-Box Q statistic can be used to test the randomness of standardized residuals and square of residuals in the econometric model, where the Ljung-Box Q statistic is as follows:

where $r(j$ ) is the autocorrelation coefficient of the residual lagged j times, and $T$ is the total number of samples, and $p$ is the lag order. The Q statistic meets the ${\chi }^{2}$ distribution with degrees of freedom (p-k) (k is the number of explanatory variables). If the Ljung-Box Q statistic of ${v}_{t}$ (and squares terms) are not significant, it is shown that there is no auto-correlation and ARCH effects in the standardized residual series, indicating that the model is reasonable.

4.   Data and empirical results

4.1.   Data set

Among different types of trading in the CNY market, the volume of spot contracts was nearly 17 times that of forward contracts by the end of 2017. USD is the main foreign currency in the China interbank foreign exchange market. For this reason, our data set comprise the daily nominal USD/RMB onshore spot exchange rate (CNY), offshore USD/RMB spot exchange rate (CNH), and offshore RMB overnight interbank interest rate (CNH-Hibor). The sample period starts from April 30, 2012 to June 1, 2018. The data set comprises 1424 observations, all data are collected from the “WIND” database². As the properties of China’s onshore and offshore foreign exchange markets are closely related to China’s foreign exchange reform revolution (McKinnon and Schnal, 2009; Li et al., 2018). The break date “8.11” has been estimated by Bai Perron test approach. we divide the full sample into two sub-periods: the first sub-period is before the “8.11” reform, which is from April 30, 2012 to August 10, 2015; the second sub-period is after the “8.11” reform, which is from August 11, 2015 to June 1, 2018. Because the trading day is not always the same between the Hong Kong and mainland China exchange markets, in order to maintain synchronization in the data set, we only collect the trading daily data when we have observations for both the onshore and offshore markets.

² WIND (http://www.wind.com.cn/en/).

To avoid drastic fluctuations of financial prices series, we transform the prices of CNY, CNH and CNH-Hibor into daily returns using logarithmic difference.³ Before applying VAR model, we checked the time-series data for stationarity. The ADF test results show that the daily returns of CNH, CNY and CNH-Hibor are I(0)⁴.

³ The return of a variable is computed by using R_{i, t} = ln(P_{i, t}/P_{i, t-1})×100, where P_t represents the exchange rate at time t and R_t represents the return of exchange rate at time t.

⁴ The ADF stationary test results are provided in appendix Table 1.

4.2.   Descriptive statistics

Table 2 provides the descriptive statistics of the three return series. Both the means and medians of CNH and CNY’s returns are negative before the “8.11” reform, while they are positive after the “8.11” reform. The standard deviations of CNH and CNY after the “8.11” reform are larger than those before the “8.11” reform, which means the volatility of CNH and CNY became larger after the “8.11” reform. The mean of CNH-Hibor’s return is positive before the “8.11” reform while became into negative after the “8.11” reform, which means the liquidity cost in the offshore market increased when introduced the “8.11” reform. All of the kurtosis of CNH, CNY and CNH-Hibor are greater than 3, and their skewness are not 0, so the three series are leptokurtic distributions. And the Jarque-Bara (JB) statistics confirm that all returns of variables do not follow Gaussian distribution but show fat-tailed distributions. Hence a conditional GARCH model appears appropriate for our data set.

Table 2.  Descriptive statistics.

	Variable	Mean	Median	Std. Dev.	Skewness	Kurtosis	JB	p-value
before the “8.11” reform	CNH	-0.002	-0.007	0.122	0.274	5.725	246.281	0.001
	CNY	-0.002	-0.002	0.103	0.489	10.286	1722.663	0.001
	CNH-Hibor	0.092	0	23.343	-0.169	6.382	368.062	0.001
after the “8.11” reform	CNH	0.005	0.008	0.316	0.667	16.610	5126.951	0.001
	CNY	0.005	0.003	0.224	0.550	12.847	2691.838	0.001
	CNH-Hibor	-0.024	0.227	32.147	-0.405	9.749	1266.617	0.001

---

 | Show Table

DownLoad: CSV

4.3.   Return spillover effect

We estimate the return spillover effects of pairs among CNH, CNY and CNH- Hibor with vector autoregressive (VAR) models. We compare the return spillover effects before and after the “8.11” reform, and then run Granger causality tests.

A critical element in the specification of VAR models is the determination of the lag length of the VAR. The popular lag selection criteria considered include Akaike’s information criterion (AIC) and Schwarz’s information criterion (SIC). Existing studies showed that AIC is not consistent and hence does not lead to the choice of the correct model, with high probability, in large samples (Shibata, 1976; Zhou, 2005). Schwarz (1978) developed a consistent criterion for models to overcome this lack of consistency, which is SIC. We use daily return series to examine the correlation estimates, based on 1424 days, therefore we choose SIC criteria to determine the lag length⁵, the test revealed that lag lengths was 1 in this study.

⁵ The SIC to select VAR lag length test results are provided in appendix Table 2.

Table 3 shows the coefficients of VAR model. Before the “8.11” reform, CNY had a greater impact in the RMB pricing. The significance level of ${\mathrm{\lambda }}_{12}$ and ${\mathrm{\lambda }}_{21}$ are at 1%, which imply that not only one period lag term of CNY can explain CNH but also one period lag term of CNH can also explain CNY. Meanwhile, the values of λ₁₂ and λ₂₁ are positive, implying that there is positive correlation between CNY and CNH, therefore they appreciate together. The coefficient of ${\mathrm{\lambda }}_{12}$ is larger than that of ${\mathrm{\lambda }}_{21}$ , implying that CNY had a greater price-guide impact on CNH before the “8.11” reform. The significance levels of ${\mathrm{\lambda }}_{31}$ and ${\mathrm{\lambda }}_{32}$ are at 10%, indicating that there are price-guide impacts from both CNH and CNY to CNH-Hibor. The coefficient of ${\mathrm{\lambda }}_{31}$ is negative while the coefficient of ${\mathrm{\lambda }}_{32}$ is positive, indicating that the appreciation of CNH would push CNH-Hibor up, and the appreciation of CNY would pull CNH-Hibor down. The significance level of λ₃₂ is at 1% while the significance level of λ₂₃ is above 10%, which means CNY has a unidirectional price-guide impact to CNH-Hibor.

Table 3.  the coefficients of VAR model.

	CNH ${\mathrm{R}}_{1}(i$ = 1)	CNY ${\mathrm{R}}_{2}$ ( $i$ = 2)	CNH-Hibor ${\mathrm{ }\mathrm{R}}_{3}$ ( $i$ = 3)
before the “8.11” reform
${\mathrm{\lambda }}_{i1}$	−0.104**	0.241***	−17.907**
${\mathrm{\lambda }}_{i2}$	0.277***	−0.148**	19.464*
${\mathrm{\lambda }}_{i3}$	−0.000	0.000	−0.028
${\mathrm{c}}_{i}$	−0.002	−0.002	0.100
after the “8.11” reform
${\mathrm{\lambda }}_{i1}$	0.012	0.376***	−19.105***
${\mathrm{\lambda }}_{i2}$	0.038	−0.221***	1.347
${\mathrm{\lambda }}_{i3}$	−0.000	0.001***	0.002
${\mathrm{c}}_{i}$	−0.000	0.001	0.014
Note: * significance at the 10% level, ** significance at the 5% level, *** significance at the 1% level.

---

 | Show Table

DownLoad: CSV

After the “8.11” reform, the RMB offshore market take a more active role in RMB pricing. Both the coefficients of λ₁₂ and λ₂₁ are positive, but only the significant level of λ₂₁ is at 1%, while λ₁₂ is not significant at any level, which means CNH has a unidirectional price-guide impact to CNY. The value of λ₃₁ is negative with 1% significance level, while λ₁₃ is not significant at any level, which means CNH has unidirectional price-guide impact to CNH-Hibor. The value of λ₂₃ is positive with 1% significance level, while λ₃₂ is not significant at any level, which means CNH-Hibor has unidirectional price-guide impact to CNY.

Table 4 shows the Granger causality tests before and after the “8.11” reform. Before the “8.11” reform, CNH and CNY have bidirectional return spillover relationships and the spillover effects from CNY to CNH are larger than spillovers in the opposite direction, which means the pricing power of the spot RMB exchange rate is in the onshore market. Both CNH and CNY have unidirectional return spillover relationships to CNH-Hibor, the information is transmitted from CNY or CNH market to CNH-Hibor market. After the “8.11” reform, there is only a unidirectional return spillover relationship from CNH to CNY, which means information is transmitted from the offshore to onshore market. Meanwhile, there is only a unidirectional return spillover relationship from CNH to CNH-Hibor, which means the information is also transmitted from CNH to CNH-Hibor. The direction of return spillover relationship between CNY and CNH-Hibor is opposite to that before the “8.11” reform.

Table 4.  Granger causality results for the two sub-periods.

	${\chi }^{2}$
null hypothesis	sub-period before the “8.11” reform	sub-period after the “8.11” reform
CNH $\nRightarrow$ CNY	43.191***	164.514***
CNY $\nRightarrow$ CNH	29.343***	0.345
CNH $\nRightarrow$ CNH-Hibor	4.469**	15.187***
CNH-Hibor $\nRightarrow$ CNH	0.451	0.176
CNY $\nRightarrow$ CNH-Hibor	3.815*
CNH-Hibor $\nRightarrow$ CNY	0.864
Note: * significance at the 10% level, ** significance at the 5% level, *** significance at the 1% level.

---

 | Show Table

DownLoad: CSV

We further depict the return spillover effects in Figure 2.

Figure 2.  Return spillover effects.

DownLoad: Full-Size Img PowerPoint

As shown in Figure 2, the return spillover effects among CNH, CNY and CNH-Hibor have been changed since the “8.11” reform. The crucial thing to understand the two-way of return spillover effects between CNH and CNY foreign exchange markets is that the arbitrage of currency speculators and RMB internalization. The arbitrage mechanism is that when the RMB’s exchange rate was expected to appreciate, the CNH will be much appreciated relative to the CNY. The premium of CNH means that RMB is more valuable in the offshore market, offering an opportunity for enterprises to earn extra benefit if settling imports in RMB. Therefore, the market has the incentive to pay RMB instead of USD for importing, thereby causing an outflow of RMB liquidity from onshore to offshore market (HKEX, 2017). Internalization of RMB has significantly boosted the use of RMB over the past few years, not only in cross-border businesses with mainland China, but also in offshore market activities.

As the trading volume in the offshore exchange market was smaller than that in onshore exchange market, then the price-guidance impact from CNY to CNH was bigger than that from CNH to CNY, and the pricing power of the RMB spot exchange rate was controlled by the CNY market. As for the relationships among CNH, CNY and CNH-Hibor, both CNH and CNY had return spillover effects to CNH-Hibor, and their spillovers are one-way.

The “8.11” reform changed the formalization mechanism of the daily central parity, the intention is to enable onshore foreign exchange market to effectively reflect market demand and supply in the long run. Since then, CNH rate shows more depreciation than CNY rate, leading to a reversal of the arbitrage mechanism and the flowing back of RMB capital to the onshore market, which strengthened the price-guide impact from CNH to CNY. There was only unidirectional return spillover effects from CNH to CNY, which means the offshore market has gradually obtained the pricing power for the RMB spot exchange rate.

When CNH depreciation exceeds that of CNY to a certain basis point, the PBoC intervened in the offshore market to narrow the gap. As a result, CNH borrowers needed to pay a higher interest rate in offshore markets and hence pushed up CNH-Hibor. Then overnight CNH-Hibor rates spiked dramatically higher, even up to 66.8%, and speculators found it very expensive to short the offshore RMB, uncertainties in offshore RMB market sharply arise with various forms of shocks in exchange rate and interest rate.

4.4.   Volatility spillover effect

In finance, volatility is defined as a measure of the variation in the price of an asset over time (Takaishi, 2018; Li and Zhong, 2019). Existence of volatility spillover implies that one large shock increases the volatilities not only in its own asset or market but also in other assets or markets as well. We employ a MGARCH-BEKK model to estimate the risk conduction effects of volatility in CNY, CNH and CNH-Hibor three markets.

We estimate whether there is a volatility spillover effect between variables by judging the significance level of the coefficients. In order to compare the difference of volatility spillover effects before and after the “8.11” reform furtherly, we undertake a joint significance test of the coefficients.

Table 5 reports the estimated coefficients from a BEKK-GARCH (1, 1) model. Before the “8.11” reform, the coefficient of b₁₂ is significant at 1% significance level, which means the volatility of CNH market has persistent shocks to CNY market. Meanwhile, the coefficients of ${a}_{21}$ and b₂₁ are not significant, which means the ARCH and GARCH effects of CNY has not impact CNH. Both ${a}_{13}$ and ${b}_{31}$ are significant, which means there are ARCH effect from CNH to CNH-Hibor and GARCH effect from CNH-Hibor to CNH. None of ${a}_{32}$ , ${a}_{23}, {b}_{32}$ and ${b}_{23}$ are significant at any level, which indicates there is no volatility spillover between CNY and CNH-Hibor market.

Table 5.  Coefficients of MGARCH-BEKK model.

	parameter	CNH(I = 1)	CNY(I = 2)	CNH-Hibor(I =3)
before the “8.11” reform	${a}_{1i}$	0.273***	−0.067	−11.721**
	${a}_{2i}$	−0.009	0.349***	12.900
	${a}_{3i}$	0.000	0.000	0.438***
	${b}_{1i}$	0.970***	0.058***	0.387
	${b}_{2i}$	−0.012	0.890***	3.740
	${b}_{3i}$	0.001***	0.000	−0.927***
	LB(Q)	17.45(0.13)	17.79(0.12)	18.75(0.1)
	LB(Q2)	18.47(0.1)	3.46(0.99)	4.32(0.98)
after the “8.11” reform	${a}_{1i}$	0.443***	0.258**	−22.830
	${a}_{2i}$	−0.415***	−0.067	−7.652
	${a}_{3i}$	−0.000	0.001**	0.500***
	${b}_{1i}$	0.472**	−0.366***	11.233
	${b}_{2i}$	0.496	1.020***	72.683***
	${b}_{3i}$	0.005***	0.001	−0.576***
	LB(Q)	7.45(0.59)	9.96(0.35)	11.34(0.25)
	LB(Q2)	3.49(0.94)	3.89(0.91)	2.30(0.98)
Note: * significance at the 10% level, ** significance at the 5% level, *** significance at the1% level. LB(Q) and LB(Q2) tests denote the p-values of Ljung-Box Q-statistics for level and squared residuals for 9 lags, P-values of estimated coefficients are reported in brackets, next to each parameter reported.

---

 | Show Table

DownLoad: CSV

After the “8.11” reform, the coefficients of ${a}_{12}$ and ${b}_{12}$ are significant, which shows there are ARCH and GARCH effects from CNH to CNY. With the development of CNH market, the volatility spillover effect from CNH market has increased. The coefficient ${b}_{31}$ is significant, which means there is GARCH effect from CNH-Hibor to CNH. Meanwhile, the coefficient of ${a}_{32}$ is significant, which means there is ARCH effect from CNH-Hibor to CNY.

We can see that CNH, CNY and CNH-Hibor all have ARCH or GARCH effects before and after the “8.11” reform, indicating there is volatility clustering among these three variables.

Based on the estimated results in tables 5 and 6, we compare the direction of the volatility spillover effects. Before the “8.11” reform, there was unidirectional volatility spillover effect from CNH to CNY, but after the “8.11” reform, there was bidirectional volatility spillover effect between CNH and CNY markets, which indicate the integration of the two markets has been greatly improved. More channels for cross-border portfolio investment flows and the development of the offshore RMB market in Hong Kong promoted the integration of onshore and offshore RMB markets. The CNH market has expanded at a very fast pace especially after the “8.11” reform, and its daily turnover had grown to USD 240 billion by March 2016.

Table 6.  Joint test of volatility.

	${\chi }^{2}$
null hypothesis	before the “8.11” reform	after the “8.11” reform
CNH $\nRightarrow$ CNY	9.548***	18.327***
CNY $\nRightarrow$ CNH	0.249	23.508***
CNH $\nRightarrow$ CNH-Hibor	4.817*	1.105
CNH-Hibor $\nRightarrow$ CNH	18.858***	15.465***
CNY $\nRightarrow$ CNH-Hibor	4.156	3.435
CNH-Hibor $\nRightarrow$ CNY	3.107	5.331*
Note: * significance at the 10% level, ** significance at the 5% level, *** significance at the 1% level.

---

 | Show Table

DownLoad: CSV

We further depict the volatility spillover effects in Figure 3.

Figure 3.  Volatility spillover effects.

DownLoad: Full-Size Img PowerPoint

After the “8.11” reform, the importance of CNH-Hibor market has been enhanced. There was bidirectional volatility spillover effects between CNH-Hibor and CNH before the “8.11” reform, while there was only unidirectional volatility spillover effect from CNH-Hibor to CNH after the “8.11” reform. There was no volatility spillover effect between CNY and CNH-Hibor before the “8.11” reform, while there was unidirectional volatility spillover effect from CNH-Hibor to CNY market after the “8.11” reform.

What do these differences in volatility spillover effects among CNH, CNY and CNH-Hibor tell us? Cross-border trade settlement has been the main channel to export RMB liquidity to the offshore market, which is easily susceptible to the fluctuation of RMB exchange rate and CNH-CNY pricing differential. The CNH exchange rate influences CNH-Hibor through its impact on the offshore RMB liquidity pool. When the CNH exchange rate falls, on the back of a strong USD, with worries about RMB devaluation, offshore investors converted their RMB deposits back into USD or HKD assets. These effects combined led to a drop of RMB deposits in Hong Kong market, as plotted in Figure 4. RMB deposits in Hong Kong market dropped from the peak of RMB1, 003.5 billion to RMB652.9 billion⁶, a decline of about 23% compared to the end of 2015. Rises in the CNH-Hibor suggest tightness in CNH liquidity, and that could mean shorting RMB became more expensive.

⁶ Source: HKMA, as of end-August 2016.

Figure 4.  RMB deposits in HK and CNH spot rate.

DownLoad: Full-Size Img PowerPoint

When the gap between CNY and CNH exchange rate becomes too large, the PBoC have to undertake both onshore spot intervention and an offshore funding squeeze in a swift unwind of long USD/CNH positions to narrow the exchange rate differential. The high overnight CNH-Hibor interest rates can easily exert an influence in the CNH market, against a small and declining pool of CNH liquidity. But pushing up CNH-Hibor and draining the offshore RMB pool is a double-edged sword. Sharp volatility in the short-term interest rate of offshore RMB market would most likely pressurize on the steady expansion of RMB offshore market.

The white-noise process was assessed by employing LB(Q) and LB(Q²) tests, according to the estimated values, and all models showed good statistical properties.

5.   Conclusions

This study using return and volatility spillovers to measure the connectedness in CNY, CNH and CNH-Hibor three markets, and compared the results of market connectedness under the impact of “8.11” exchange rate reform. This topic is meaningful not only to investors holding assets based on RMB but also to the China’s policy makers.

On the return spillover between the CNY exchange rate and CNH exchange rate, the empirical results support the notion that the RMB spot exchange rate pricing power has been passed from onshore to offshore market after the “8.11” reform, which has weakened the stability of RMB. Meanwhile, the two-way return spillover effect between CNH and CNY exchange rates has changed to one-way from CNH to CNY exchange rate，meanwhile the one-way return spillover effect from CNY to CNH-Hibor has been in the opposite direction. Therefore, the PBoC is busy fighting for pricing power on the RMB exchange rate. Up until now, the USD/CNY central parity is now based on “RMB closing price + its change against currency basket + countercyclical factor”, the RMB stopped depreciating further and remained quite stable. Under the current conditions, RMB faces the appreciation pressure, which is harmful to the interest of China. A weaker currency makes Chinese exports cheaper and more competitive in the international markets, and could potentially offset some of the impact from the US-China trade talk pressure. As mentioned above, RMB onshore exchange rate liberalization should be the key to easing China's economic downturn.

The “8.11” exchange reform has significantly increased the volatility in CNY, CNH and CNH-Hibor three markets, particularly in offshore markets. With the agammaavation of CNH-Hibor's volatility, CNH-Hibor played a leading role in onshore-offshore money and foreign exchange market interactions, which is critical for Chinese policymakers and contribute to the foreign exchange rate reform. Sharp volatility in offshore short-term RMB liquidity imposed hedging difficulties on international investors holding RMB assets. The sufficient offshore RMB liquidity is essential to ease the volatility of CNH-Hibor. The existing cross-border RMB liquidity provided to the offshore market is mainly accomplished under the current account and the mid- to long-term capital accounts, the short-term RMB liquidity is mainly provided under the scheme of currency swap agreements between monetary authorities and market financing. There isn't direct channel linking onshore and offshore markets for short-term liquidity flows. Policymakers should improve the liquidity provision mechanism and expand the range of CNH products available, which would help to eliminate the effect of offshore market interest rate volatility.

Acknowledgments

This work was supported by the National Social Science Fund of China under Grant [19BJY254].

Conflict of interest

All authors declare no conflicts of interest in this paper.