1. Introduction
Multilevel programming deals with decision-making situations in which decision makers are arranged within a hierarchical structure. Trilevel programming, the case of multilevel programming containing three planner, occurs in a variety of applications such as planning [6,7], security and accident management [1,18], supply chain management [14,17], economics, [10] and decentralized inventory [9]. In a trilevel decision-making process, the first-level planner (leader), in attempting to optimize his objective function, chooses values for the variables that he controls. Next, the second-level planner in attempting to optimize his objective function while considering the reactions of the third-level planner chooses values for the variables that he controls. Lastly, the third-level planner, with regard to the decisions made by the previous levels, optimizes his own objective function. A number of researchers have studied the linear trilevel programming (LTLP) problem, and have proposed some procedures to solve it. Some algorithms are proposed based on penalty method [16], Kuhn-Tucker transformation [2], multi-parametric approach [5], and enumerating extreme points of constraint region [19] to find the exact optimal solution to special classes of trilevel programming problem. In addition, because of the complexity of solving trilevel problems especially for large-scale problems, some other researches attempted to use fuzzy [13] and meta-heuristic approaches [8,15] to find good approximate solutions for these problems. For a good bibliography of the solution approaches to solve trilevel programming problems, the interested reader can refer to [11].
The present study investigates the trilevel Kth-best algorithm offered by Zhang et. al. [19] at a higher level of accuracy. First, some of the geometric properties of the feasible region of the LTLP problem have been stated and proven. It ought to be mentioned that despite the similarity of some presented theoretical results in this paper with Ref. [19], the techniques of the proof are different. Then, a modified version of the trilevel Kth-Best algorithm has been proposed regarding unboundedness of objective functions in both the second level and third level which is not considered in the proposed Kth-Best algorithm in reference [19]. Moreover, it is shown that the amount of computations in the solving process by the modified trilevel Kth-Best algorithm is less than of that of the solving process by the traditional trilevel Kth-Best algorithm. In addition, in case of finding the optimal solution of linear trilevel programming problems with conflicting objective functions, the modified Kth-Best algorithm is capable of giving more accurate solutions.
The organization of the paper is as follows. Basic definitions concerning LTLP problem that we shall investigate, are presented in Section 2. Some theoretical and geometric properties of the LTLP problem are studied in Section 3. Based on the facts stated in Section 3, a modified trilevel Kth-Best algorithm is proposed to solve the LTLP problem in Section 4. To show the superiority of the proposed algorithm over the traditional Kth-Best algorithm, some numerical examples are presented in Section 5. Ultimately, the paper is concluded with Section 6.
2. Basic definitions of linear trilevel programming problem
As it is mentioned before, we consider the linear trilevel programming problem which can be formulated as follows:
|
minx1∈X1f1(x1,x2,x3)=3∑j=1αT1jxjs.t3∑j=1A1jxj≤b1where x2,x3 solve:minx2∈X2f2(x1,x2,x3)=3∑j=1αT2jxjs.t3∑j=1A2jxj≤b2where x3 solves:minx3∈X3f3(x1,x2,x3)=3∑j=1αT3jxjs.t3∑j=1A3jxj≤b3
|
(2.1)
|
where xi∈Xi, Xi is an indiscrete subset of Rni+ for i=1,2,3 and αij,Aij,bi are vectors and matrices of conformal dimensions.
In this section, we state some definitions and notations about the LTLP problem.
● Constraint region:
S={(x1,x2,x3)∈X1×X2×X3:∑3j=1Aijxj≤bi, i=1,2,3}.
● Constraint region for middle and bottom level, for fixed ˉx1:
S2(ˉx1)={(x2,x3)∈X2×X3:∑3j=2Aijxj≤bi−Ai1ˉx1, i=2,3}.
● Feasible set for the level 3, for fixed (ˉx1,ˉx2) :
Ω3(ˉx1,ˉx2)={x3∈X3:A33x3≤b3−∑2j=1A3jˉxj}.
● Rational reaction set for level 3, for fixed (ˉx1,ˉx2) :
Ψ3(ˉx1,ˉx2)=argmin{f3(ˉx1,ˉx2,x3):x3∈Ω3(ˉx1,ˉx2)}.
● Feasible set for level 2, for fixed ˉx1:
Ω2(ˉx1)={(x2,x3)∈S2(ˉx1):x3∈Ψ3(ˉx1,x2)}.
● Rational reaction set for level 2, for fixed ˉx1:
Ψ2(ˉx1)=argmin{f2(ˉx1,x2,x3):(x2,x3)∈Ω2(ˉx1)}.
● Inducible region :
IR={(x1,x2,x3)∈S:(x2,x3)∈Ψ2(x1)}.
In the above definitions, the term argmin{f(x):x∈S} denotes the set of all minimizers of the function f over the set S. Now we can express the definition of the feasible solution and optimal solution to the LTLP problem as follows:
Definition 2.1. A point (x1,x2,x3) is said to be feasible solution to the LTLP problem (2.1) if (x1,x2,x3)∈IR.
Definition 2.2. A feasible point (x∗1,x∗2,x∗3) is said to be optimal solution to the LTLP problem (2.1) if f1(x∗1,x∗2,x∗3)≤f1(x1,x2,x3), for all (x1,x3,x3)∈IR.
In view of the above Definitions, determining the solution for the LTLP problem (2.1) is equal to solve the following problem:
|
min{f1(x1,x2,x3):(x1,x2,x3)∈IR}.
|
(2.2)
|
3. Theoretical properties
In this section, we will demonstrate some geometric properties of the problem (2.1). Let F1,...,Fr, denote the non-empty faces of S. We will denote by SXi and SXi×Xj the projection of S onto Xi and Xi×Xj respectively, for 1≤i,j≤3. We will also use the following assumptions to come up with the existence of an optimal solution.
Assumption 3.1. S is a non-empty and compact polyhedron.
Assumption 3.2. Ψ2(x1) and Ψ3(x1,x2), are non-empty and single-valued for all x1∈SX1 and (x1,x2)∈SX1×X2 respectively.
Assumption 3.3. Ψ2(.) is continuous on SX1.
Note that by Assumption 3.1, we can conclude that SXi, and SXi×Xj, for i,j∈{1,2,3}, and Fk for k∈{1,...,r} are also non-empty compact polyhedrons. The following example demonstrates that Assumption 3.3 is necessary for existence an optimal solution to the LTLP problem.
Example 3.1.
|
maxx1x1+10x2−2x3+x4s.t0≤x1≤1maxx2,x3x2+2x3s.tx2+x3≤x10≤x2,x3≤1x4=0maxx4x4s.tx4≤x3x4≤1−x3
|
In this example, we have
|
Ψ3(x1,x2,x3)={x3 if 0≤x3≤12,1−x3 if 12≤x3≤1.
|
Then,
Ω2(x1)={(x2,x3,x4):x2+x3≤x1,0≤x2≤1,0≤x3≤12,x4=x3=0}∪
{(x2,x3,x4):x2+x3≤x1,0≤x2≤1,12≤x3≤1,x4=1−x3=0},
and
|
Ψ2(x1)=argmax{x2+2x3:(x2,x3,x4)∈Ω2(x1)}
|
(3.1)
|
It is clear that if 0≤x1<1, the optimal solution of the problem (3.1) is (x1,0,0), and if x1=1, the optimal solution is (0,1,0). Therefore,
|
Ψ2(x1)={(x1,0,0) if0≤x1<1(0,1,0) ifx1=1
|
It is evident that Ψ2 is discontinuous at x1=1. Although, in this problem, the first level objective function has the supremum value equal to 11 when we approach the point (1,1,0,0), but the problem does not have an optimal solution.
Lemma 3.1. Let N={(ˉx1,x2,x3):(x2,x3)∈S2(ˉx1)} and (ˉx1,ˉx2,ˉx3)∈ri F∩IR where F is a non-empty face of S, then F∩N={(ˉx1,ˉx2,ˉx3)}. The term ri F denotes the relative interior of F.
Proof. It follows from (ˉx1,ˉx2,ˉx3)∈IR that (ˉx2,ˉx3)∈Ψ2(ˉx1). Moreover, Ψ2(ˉx1) is nonempty and single-valued. Therefore, (ˉx2,ˉx3) is the unique optimal solution of the following linear bilevel programming problem:
|
minx2≥03∑j=2αT2jxjs.t3∑j=2A2jxj≤b2−A21ˉx1where x3 solves:minx3≥03∑j=2αT3jxjs.t3∑j=2A3jxj≤b3−A31ˉx1
|
(3.2)
|
By Theorem 5.2.2 of [3] we conclude that (ˉx2,ˉx3) is an extreme point of S2(ˉx1). Now let (˜x2,˜x3) be another point of the S2(ˉx1) and (ˉx1,˜x2,˜x3) belongs to F∩N.
Since (ˉx1,ˉx2,ˉx3)∈ri F and (ˉx1,˜x2,˜x3)∈F, there exists a γ>1 such that
(ˉx1,ˆx2,ˆx3)=γ(ˉx1,ˉx2,ˉx3)+(1−γ)(ˉx1,˜x2,˜x3)∈F (Theorem 6.4 of [12]). If we set β=γ−1γ, then, 0<β<1 and (ˉx1,ˉx2,ˉx3) can be written as:
(ˉx1,ˉx2,ˉx3)=β(ˉx1,˜x2,˜x3)+(1−β)(ˉx1,ˆx2,ˆx3).
Thus, it can be concluded that (ˉx2,ˉx3)=β(˜x2,˜x3)+(1−β)(ˆx2,ˆx3). In addition, it can be clearly seen that (˜x2,˜x3) and (ˆx2,ˆx3) are belong to S2(ˉx1), which contradicts the fact that (ˉx2,ˉx3) is an extreme point of S2(ˉx1). This completes the proof.
Corollary 3.1. Let ˉN={(ˉx1,x2,x3):(ˉx1,x2,x3)∈S} and (ˉx1,ˉx2,ˉx3)∈ri F∩IR where F is a non-empty face of S . Then F∩ˉN={(ˉx1,ˉx2,ˉx3)}.
Proof. The statement is immediately derived from the fact that
ˉN⊂{(ˉx1,x2,x3):(x2,x3)∈S2(ˉx1)}
Theorem 3.1. Let IR∩ri F≠∅ where F is a non-empty face of S. Then, F⊂IR.
Proof. Let (ˆx1,ˆx2,ˆx3)∈IR∩ri F and let (ˉx1,ˉx2,ˉx3)∈F be arbitrary. Since (ˆx1,ˆx2,ˆx3)∈ri F, we can find a neighborhood ˆN around it such that
N=ˆN∩aff F⊂ri F, where aff F denotes the affine hull of face F. Since Ψ2 is a single-valued and continuous map over SX1, we can find a neighborhood W around ˆx such that:
{(x,Ψ2(x)): x∈W}⊂N⊂ri F.
Moreover, we can choose 0<γ1<1 such that
B={x1∈SX1:x1=γˉx1+(1−γ)ˆx1, 0≤γ≤γ1}⊂W. Then,
{(x1,Ψ2(x1)):x1∈B}⊂N⊂ri F.
Besides, for all β∈[0,1),
β(ˉx1,ˉx2,ˉx3)+(1−β)(ˆx1,ˆx2,ˆx3)∈ri F, (see Ref. [12], Theorem 6.1).
Consequently, from Corollary 3.1, it can be concluded that:
γ(ˉx2,ˉx3)+(1−γ)(ˆx2,ˆx3)=Ψ2(γˉx1+(1−γ)ˆx), for all 0≤γ≤γ1.
In addition, γ(ˉx1,ˉx2,ˉx3)+(1−γ)(ˆx1,ˆx2,ˆx3)∈ri F⊂S. Therefore,
γ(ˉx1,ˉx2,ˉx3)+(1−γ)(ˆx1,ˆx2,ˆx3)∈IR, for all 0≤γ≤γ1,
Eventually,
(˜x1,˜y1,˜z1)=γ1(ˉx1,ˉx2,ˉx3)+(1−γ1)(ˆx1,ˆx2,ˆx3)∈IR∩ri F.
If we repeat the process, we can construct from (˜x1,˜y1,˜z1) a new point called (˜x2,˜y2,˜z2)∈IR∩ri F which lies along the line segment among (ˉx1,ˉx2,ˉx3) and (˜x1,˜y1,˜z1).
Therefore, we approach point (ˉx1,ˉx2,ˉx3) along the line segment among (ˉx1,ˉx2,ˉx3) and (ˆx1,ˆx2,ˆx3), by the points which are belongs to IR and so by the continuity of Ψ2, it can be concluded that (ˉx1,ˉx2,ˉx3)∈IR and this completes the proof.
Corollary 3.2. The inducible region of the LTLP problem can be written as the union of some faces of S that are not necessarily connected.
Corollary 3.3. If IR≠∅, an optimal solution to the LTLP problem occurs at a vertex of IR and hence, at a vertex of S.
Proof. Notice that the problem (2.2) can be written equivalently as
|
min{f1(x1,x2,x3):(x1,x2,x3)∈conv IR}
|
(3.3)
|
where conv IR denotes the convex hull of IR. It is clear that there exists a solution to the problem (3.3) which is a vertex of conv IR [4]. Although, conv IR and IR are different sets their vertices are the same. Moreover, by Corollary 3.2, IR is formed from the union of some faces of S. Therefore, the vertices of IR (and conv IR) are also the vertices of S and this fact completes the proof.
Through the above results, it has been demonstrated that there exists at least a vertex of S which solves the problem (2.1). This fact allows us to develop enumerative algorithms which search amongst extreme points of the constraint region to solve the LTLP problem.
4. Modified trilevel Kth-Best algorithm
In this section, the modified trilevel Kth-Best algorithm is presented. In actual, the modified algorithm takes into account LTLP problems with unbounded middle and bottom level problems. These cases are not considered in the Kth-Best algorithm [19]. Also, it resolves some of drawbacks while finding an optimal solution for LTLP problems with opposing objectives. Moreover, in the next section, it is shown that in some LTLP problems, the proposed algorithm leads to reduction the amount of computations needed for finding an optimal solution.
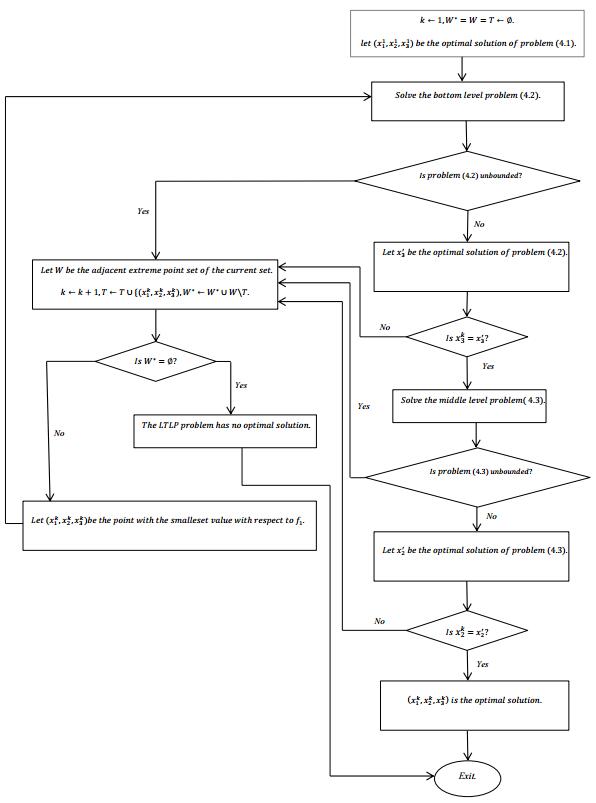
The process of the modified trilevel Kth-Best algorithm is as follows:
The Algorithm
Step 1. Initialization: Set k⟵1, W∗=T=W⟵∅. Go to Step 2
Step 2. Find the optimal solution of the optimization problem (4.1). Let it be (x[1]1,x[1]2,x[1]3) and go to Step 3.
|
min{f1(x1,x2,x3):(x1,x2,x3)∈S}
|
(4.1)
|
Step 3. Solve the following problem.
|
min{αT3 3x3:x3∈Ω3(x[k]1,x[k]2)}.
|
(4.2)
|
If the problem (4.2) is unbounded go to step 7, else let x′3 be the optimal solution and go to Step 4.
Step 4. If x[k]3=x′3, go to step 5 else go to step 7. [If x[k]3=x′3 then x[k]3∈Ψ3(x[k]1,x[k]2).]
Step 5. Solve the following problem.
|
min{αT2 2x2+αT2 3x3:(x2,x3)∈S2(x[k]1),x3=x[k]3}.
|
(4.3)
|
If problem (4.3) is unbounded go to step 7, else let x′2 be the optimal solution and go to step 6.
Step 6. If x[k]2=x′2, then (x[k]2,x[k]3)∈Ψ2(x[k]1) and (x[k]1,x[k]2,x[k]3) is the optimal solution, exit. Else go to Step 7.
Step 7. Set k⟵k+1 and T⟵T∪(x[k]1,x[k]2,x[k]3). Let W be the adjacent extreme points set of current extreme point i.e., (x[k]1,x[k]2,x[k]3). Set W∗⟵W∗∪W∖T. Go to Step 8
Step 8. If W∗=∅ there is no optimal solution, exit. Else let (x[k]1,x[k]2,x[k]3) be the point with the smallest value in W∗ with respect to f1, go to step 3.
Figure 1 illustrates the process of modified trilevel Kth-Best algorithm.
Remark 4.1. It is clear that if IR≠∅ and Assumption 3.3 is valid, the LTLP problem has an optimal solution. However, in spite of the fact that the constraint region S is bounded, the middle-level problem or the bottom level problem may be unbounded. In these cases, we have Ψ2(x1)=∅ for all x1∈SX1 or Ψ3(x1,x2)=∅ for all (x1,x2)∈SX1×X2. Hence, the inducible region will be empty set and consequently, the LTLP problem has no optimal solution. We have considered this case in the modified trilevel kth-Best algorithm. Indeed, when the optimality of the candidate vertex is examined, the unboundedness of the middle level or the bottom level problems are also inspected in step 3 and step 5. Eventually, if the middle-level or the bottom-level problem is unbounded, after the finite number of iterations (at most equal to the number of extreme points), the algorithm will terminate with the result that the trilevel programming problem has no optimal solution.
Proposition 4.1. Let the LTLP problem (2.1) has an optimal solution. Then the modified trilevel Kth-Best algorithm will terminate with an optimal solution of LTLP problem in a finite number of iterations.
Proof. Let (x[k]1,x[k]2,x[k]3) be the terminated point. The termination condition in Step 6 of the algorithm is equal to the fact that (x[k]1,x[k]2,x[k]3) belongs to the inducible region. Moreover, according to the algorithm procedure, we know that (x[k]1,x[k]2,x[k]3) is the optimal solution of the following problem:
min{f1(x1,x2,x3):(x1,x2,x3)∈S∖∪k−1i=1(x[i]1,x[i]2,x[i]3)}, (Theorem 2.3.4 of [3]). Therefore if termination occurs, this point has the smallest value between the points of IR with respect to f1.
It is worth mentioning that, by omitting the examined extreme points from W∗, the cycling is prevented. Moreover, since the extreme points of the constraint region are finite, the algorithm will terminate after a finite number of iterations.
5. Numerical examples
To illustrate the advantages of the modified trilevel Kth-Best algorithm, the following examples are solved according to the outline indicated in the previous section.
Example 5.1. Consider the following LTLP problem:
|
minx12x1+2x2+5x3x1≤8x2≤5 where x2,x3 solve:maxx26x1+x2−3x3x1+x2≤8x1+4x2≥87x1−2x2≥0 where x3 solves:minx32x1+x2−2x35x1+5x2+14x3≤40x1,x2,x3≥0
|
In this example, we have Ψ3(x1,x2)=114(40−5x1−5x2) for all 0≤x1,x2≤8, x1+x2≤8. Moreover,
|
Ψ2(x1)={(72x1,114(40−452x1)):815≤x1≤169}∪{(8−x1,0):169≤x1≤8}.
|
It is clear that for 107≤x1≤169, we have 72x1>5 and for 169≤x1<3, we have 8−x1>5. So, neither S nor IR include the following set:
{(x1,72x1,114(40−452x1):107<x1≤169}∪{(x1,8−x1,0):169≤x1<3}.
Actually,
IR={(x1,72x1,114(40−452x1):815≤x1≤107}∪{(x1,8−x1,0):3≤x1≤8}
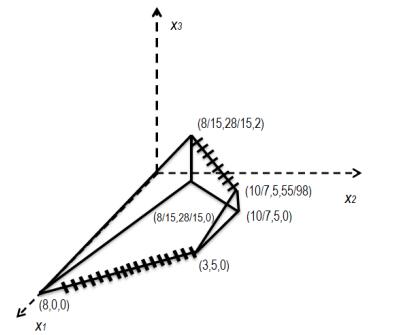
which is disconnected. This fact shows that despite the continuity of Ψ2, the inducible region is disconnected. The hatched lines at Figure 2 represent the inducible region.
By Corollary 3.3, an optimal solution of the above example occurs at the point (815,2815,2).
To solve the example by the modified trilevel Kth-Best algorithm, the process is as follows:
Iteration 1
1. (x[1]1,x[1]2,x[1]3)=(815,2815,0).
2. x′3=2≠x[1]3
3. T={(815,2815,0)}.
4. W∗={(8,0,0),(107,5,0),(815,2815,2)}.
Iteration 2
1. (x[2]1,x[2]2,x[2]3)=(107,5,0).
2. x′3=5598≠x[2]3
3. T={(815,2815,0),(107,5,0)}.
4. W∗={(8,0,0),(107,5,5598),(815,2815,2),(3,5,0)}.
Iteration 3
1. (x[3]1,x[3]2,x[3]3)=(815,2815,2).
2. x′3=2=x[3]3
3. x′2=2815=x[3]2
4. The point (x[3]1,x[3]2,x[3]3)=(815,2815,2) is the optimal solution.
As demonstrated in the solving process of this problem, although the number of iterations and the optimal solution found by the two algorithms are the same, the number of optimization problems needed to be solved in each iteration of the Kth-Best algorithm [19] are more than the number of optimization problems needed to be solved in the modified Kth-Best algorithm. Then the amount of computations in each iteration of the modified Kth-Best algorithm is less than that of the corresponding iteration in the Kth-Best algorithm..
The two following examples show some discrepancies in the Kth-Best algorithm [19] that cause an erroneous result.
Example 5.2.
|
minxf1(x,y,z)=−x−4z+2ywhere y, z soleve:s.tminyf2(x,y,z)=3y−2zwhere z solves:s.tminzf3(x,y,z)=2z−ys.tx+y+z≤20≤x,y,z≤1
|
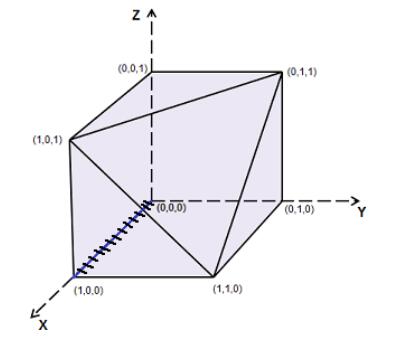
In this example, we have IR={(x,0,0):0≤x≤1}. The constraint region and inducible region are shown in Figure 3 by gray area and hatched line, respectively. It is easy to see that the constraint region is a compact set and lower levels reaction sets are single-valued. Therefore, all the assumptions of the trilevel Kth-Best algorithm [19] hold.
The Kth-Best algorithm process [19] for solving this problem is as follows:
Iteration 1 : (x[1],y[1],z[1])=(1,0,1), (y′[1],z′[1])=(0,1), z″[1]=0 and z[1]≠z″[1].
Therefore, (x[1],y[1],z[1])=(1,0,1) is not the optimal solution of the LTLP problem and we have to find the next best adjacent extreme point.
Iteration 2 : (x[2],y[2],z[2])=(0,0,1), (y′[2],z′[2])=(0,1), z″[2]=0. Since z″[2]≠z[2], then this point is not the optimal solution either. Following the algorithm, at iteration 7, we obtain:
Iteration 7 : (x[7],y[7],z[7])=(0,1,0). This is the last accessible extreme point which should be examined. At this iteration, we have (y′[7],z′[7])=(0,1) and since z′[7]≠z[7], this point is not the optimal solution either. Therefore, the trilevel Kth-Best algorithm [19] fails to find an optimal solution to this problem.
By solving the example via the modified trilevel Kth-Best algorithm, the process is as follows:
Iteration 1
1. (x[1],y[1],z[1])=(1,0,1).
2. z′=0≠z[1]
3. W∗={(0,0,1),(0,1,1),(1,0,0),(1,1,0)}.
Iteration 2
1. (x[2],y[2],z[2])=(0,0,1)
2. z′=0≠z[2]
3. W∗={(0,1,1),(1,0,0),(0,0,0),(1,1,0)}
Continuing this method, at iteration 4 we get:
(x[4],y[4],z[4])=(1,0,0), z′=0 and y′=0. Therefore, the point (1,0,0) is the optimal solution which is equal to the solution obtained by the multi-parametric approach [5].
Note that, in the trilevel Kth-Best algorithm [19], the bottom-level optimal solution which is found for some fixed values of upper and middle-level variables, is not considered as a constraint for the second level problem. This causes the Kth-best algorithm is not capable of finding an optimal solution for some LTLP problems. This fact is considered in step 5 of the modified trilevel Kth-Best algorithm by fixing the lower level variable which is found as the optimal solution of problem (4.2) and substituting it in the problem (4.3).
Example 5.3.
|
minx1x1−4x2+2x3−x1−x2≤−3−3x1+2x2−x3≥−10where x2,x3 solve:minx2x1+x2−x3−2x1+x2−2x3≤−12x1+x2+4x3≤14where x3 solves:minx3x1−2x2−2x32x1−x2−x3≤2x1,x2,x3≥0
|
(5.1)
|
The process of the modified trilevel Kth-Best algorithm to solve this problem is as follows:
Iteration 1
1. (x[1]1,x[1]2,x[1]3)=(3.75,6.5,0).
2. The bottom level problem corresponding to (x1,x2)=(3.75,6.5) is unbounded.
3. T={(3.75,6.5,0)}.
4. W={(4,6,0),(43,53,0),(0,4,2.5)}.
5. W∗=W.
Iteration 2
1. (x[2]1,x[2]2,x[2]3)=(4,6,0).
2. The bottom level problem corresponding to (x1,x2)=(4,6) is unbounded.
3. T={(3.75,6.5,0),(4,6,0)}.
4. W={(3.75,6.5,0),(53,43,0),(3113,813,2813)}.
5. W∗={(43,53,0),(0,4,2.5),(53,43,0),(3113,813,2813)}.
Iteration 3
1. (x[3]1,x[3]2,x[3]3)=(0,4,2.5).
2. The bottom level problem corresponding to (x1,x2)=(0,4) is unbounded.
3. T={(3.75,6.5,0),(4,6,0),(0,4,2.5)}.
4. W={(0,3,2.75),(0,3,2),(3.75,6.5,0)}
5. W∗={(43,53,0),(0,3,2),(53,43,0),(3113,813,2813),(0,3,2.75)}.
Iteration 4
1. (x[4]1,x[4]2,x[4]3)=(0,3,2).
2. The bottom level problem corresponding to (x1,x2)=(0,3) is unbounded.
3. T={(3.75,6.5,0),(4,6,0),(0,4,2.5),(0,3,2)}.
4. W={(0,4,2.5),(0,3,2.75)}.
5. W∗={(43,53,0),(53,43,0),(3113,813,2813),(0,3,2.75)}.
Iteration 5
1. (x[5]1,x[5]2,x[5]3)=(0,3,2.75).
2. The bottom level problem corresponding to (x1,x2)=(0,3) is unbounded.
3. T={(3.75,6.5,0),(4,6,0),(0,4,2.5),(0,3,2),(0,3,2.75)}.
4. W={(0,3,2),(0,4,2.5),(3113,813,2813)}.
5. W∗={(43,53,0),(53,43,0),(3113,813,2813)}.
Iteration 6
1. (x[6]1,x[6]2,x[6]3)=(43,53,0).
2. The bottom level problem corresponding to (x1,x2)=(43,53) is unbounded.
3. T={(3.75,6.5,0),(4,6,0),(0,4,2.5),(0,3,2),(0,3,2.75),(43,53,0)}.
4. W={(3.75,6.5,0),(53,43,0)(0,3,2)}.
5. W∗={(53,43,0),(3113,813,2813)}.
Iteration 7
1. (x[7]1,x[7]2,x[7]3)=(53,43,0).
2. The bottom level problem corresponding to (x1,x2)=(53,43) is unbounded.
. T={(3.75,6.5,0),(4,6,0),(0,4,2.5),(0,3,2),(0,3,2.75),(43,53,0),(53,43,0)}.
4. W={(4,6,0),(3113,813,2813),(43,53,0)}.
5. W∗={(3113,813,2813)}.
Iteration 8
1. (x[8]1,x[8]2,x[8]3)=(3113,813,2813).
2. The bottom level problem corresponding to (x1,x2)=(3113,813) is unbounded.
3. T={(3.75,6.5,0),(4,6,0),(0,4,2.5),(0,3,2),(0,3,2.75),(43,53,0),(53,43,0),(3113,813,2813)}.
4. W∗=∅.
5. There is no optimal solution.
In the above example, the constraint region is a bounded polyhedron. Let (x∗1,x∗2)∈SX1,X2 be chosen arbitrarily. To find the mapping Ψ3(x∗1,x∗2), the following parametric linear programming should be solved:
|
minx3x1−2x2−2x32x1−x2−x3≤2x1=x∗1 , x2=x∗2 , x3≥0
|
(5.2)
|
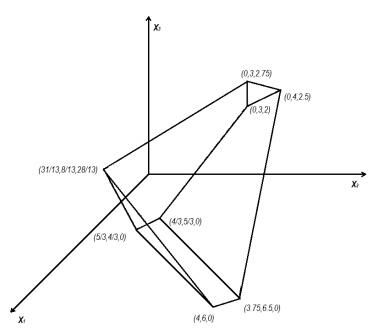
It is easy to see that the problem (5.2) is unbounded. Therefore, Ψ3(x∗1,x∗2)=∅ for all (x∗1,x∗2)∈SX1,X2. Consequently, IR is also empty and the problem (5.1) does not have any feasible solution and so any optimal solution. The constraint region is represented at Figure 4. Therefore, the modified trilevel Kth-Best algorithm concludes that the problem does not have an optimal solution, while the trilevel Kth-Best algorithm [19] has obtained the point (4,6,0) as the optimal solution ([19], section 5.1) which is incorrect.
6. Conclusion
In this study, the linear trilevel programming problem whereby each planner has his (her) own constraints, was considered. Some geometric properties of the inducible region were discussed. Under certain assumptions, it is proved that if the inducible region is non-empty, then it is composed of the union of some non-empty faces of the constraint region S and at least an optimal solution occurs at an extreme point of IR which is also an extreme point of S. Then, we proposed a modified trilevel Kth-Best algorithm to find an optimal solution. Finally, we presented some numerical examples to highlight some discrepancies between the modified trilevel Kth-Best algorithm and the trilevel Kth-Best algorithm.
Conflict of Interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: