CSR reporting in banks: does the composition of the board of directors matter?

1.   Introduction

Pest control aims to develop the science, and to design the practice of managing pests, plant diseases and other pest organisms that could have adverse impacts on agricultural production, natural environment, even for our lifestyle ^{[1,2,3,4,5,6]}. In particular, pest outbreaks decrease food production every year, from tomatoes and potatoes to corn. Such as, grape-nematodes can cause immense harvest losses of up to $50\%$ in several crops around the world ^[7], and the caterpillars of spodoptera frugiperda are able to damage more than $180$ species of plants due to they have a very wide host range, and can cause $15$–$73\%$ reduction in corn production ^[8]. For the above reasons, pest control has been a critical issue to be solved urgently in agriculture and ecology.

Integrated pest management (IPM) ^[9,10,11,12] is an ecosystem-based strategy that focuses on long-term prevention of pests through a comprehensive use of techniques such as biological control ^[13,14,15], habitat manipulation ^[16], modification of cultural practices ^[17,18], chemical control ^[19], and use of resistant varieties ^[20]. This is the most effective and environmentally sensitive approach to pest management which depends on the combination of common-sense practices, at the same time, in the process of pest control, both economical and environmental factors should be considered.

An important factor which influences the IPM strategy is the Threshold Policy Control (TPC) ^[21,22]. This includes two main concepts: The Economic Injury Level (EIL) ^[23] and the Economic Threshold (ET) ^[24,25]. When the pest density level is above EIL, control strategies have to be applied. The ET is the limit pest density that should not be reached. The two concepts have been developed and applied to guide the intervention strategies, to achieve the core goal of IPM, that is, to maintain the pest density below the EIL rather than seeking to eradicate them. Pest management models with threshold control strategies have been widely studied ^{[18,26,27,28,29,30]}, but in most studies, pest population growth is considered to be continuous. For certain species, however, there is no overlap between successive generations, so it is reasonable to consider a discrete model, in that the population has a short life expectancy. In this paper, we formulate a switching host-parasitoid ecosystem with Beverton-Holt growth and threshold control strategies, which consists of pesticide spraying and natural enemy releasing when the pest population reaches the ET. Some theoretical, numerical, biological analyses are given to investigate the effectiveness of the TPC for pest outbreaks.

The organization of the present paper is as follows: in the next section, we propose a switching host-parasitoid ecosystem induced by threshold control strategy. In section 3, by using qualitative analysis techniques related to discrete dynamical systems, we study the threshold conditions which guarantee the existence and stability of equilibria for the two subsystems. In sections 4 and 5, we provide some numerical simulations for the bifurcation and parameter sensitivity analysis respectively. The paper ends with some interesting biological conclusions, which complement the theoretical findings.

2.   Switching model formulation

The difference equation

is the well-known classic Beverton-Holt model ^[31], that describes the population intra-specific competition growth in a single species system. Here $H_t$ stands for the population density of generation $t$, $a$ is an inherent growth rate parameter (^[32] see for detail) and $b$ is a constant. Model (2.1) is also referred to as the discrete Pielou logistic model ^[33].

In order to describe the inter-specific interactions for two species, a classic discrete-generation host-parasitoid interaction model was developed by Nicholson and Bailey ^[34]. Tang ^[35] extended the Nicholson-Bailey model by including an intergenerational survival rate for the parasitoid

In model (2.2), $H_t$ and $P_t$ represent the density of hosts (pests) and parasitoids (natural enemies) at the $t$-th generation, respectively, $\alpha$ is the intrinsic growth rate for hosts in the absence of parasitoids, $\beta$ denotes the searching efficiency of parasitoids, $\gamma$ is the density-independent survival rate of the parasitoid, and $0 < \gamma < 1$. The terms $\exp(-\beta P_t)$ and $[1-\exp(-\beta P_t)]$ stand for the probability that a host individual succeeds and fails in escaping from parasitoids, respectively.

In ^[35], the authors investigated the existence and stability of the solutions for Host-parasitoid models with impulsive control at both fixed and unfixed times. Their results indicated that varying dosages and frequencies of insecticide applications, as well as the numbers of parasitoids released, are crucial in pest control. Here, we discuss the host-parasitoid model with Beverton-Holt growth and threshold control strategies.

Based on models (2.1) and (2.2), we establish the following host-parasitoid model with Beverton-Holt growth:

As mentioned in the introduction, the main purpose of IPM is to maintain the pest density below the EIL rather than seeking to eradicate them, by releasing natural enemies or spraying pesticide once the density of pests reaches the ET. This yields the following control model with threshold control strategies

where $k$ stands for the instantaneous killing rate for host population only, $r$ denotes the proportional release rate and $\tau$ is the release rate for parasitoid population, here, $0 < k < 1$, $0 < r < 1$ and $\tau > 0$.

As a consequence, combining models (2.3) and (2.4), we propose the following discrete switching host-parasitoid model induced by the threshold control strategies

where $ET$ is the control threshold, which depends on the crop output value and pest density.

Discrete switching model (2.5) is a dynamical system subject to a threshold policy: IPM control strategies are applied only when $H_t\geq ET$. Detailed explanation about the threshold policy can be found in ^[21,22].

3.   Mathematical analysis for two subsystems

In this section, we consider the dynamical behaviors of the two subsystems of model (2.5).

First, we define two regions as follows:

and the discrete switching model (2.5) in region $G_1$ (resp. $G_2$) as model $F_{G_1}$ (resp. $F_{G_2}$).

Furthermore, we investigate the dynamical behaviors of the two subsystems $F_{G_1}$ and $F_{G_2}$.

Theorem 3.1. If the following condition holds:

then subsystem $F_{G_1}$ contains a unique internal equilibrium $(H^*_{1}, P^*_{1})$ which is locally asymptotically stable provided that

and

Proof. We compute the internal equilibrium $(H^*_1, P^*_1)$ of subsystem $F_{G_1}$ by solving the following system of equations:

Through some simple computations, we deduce the following equation:

In order to analyse the above equation, we define two auxiliary functions:

It is easy to see that $f_1(0) = g_1(0) = 0$ and $\lim\limits_{x\rightarrow +\infty}g_1(x) = -b < 0$, and $f_1'(0) < g_1'(0)$ from inequality (3.1). These properties assure that there exists an $x^* > 0$ where $f_1$ and $g_1$ intersect. In addition, we find that there is a unique positive solution of $g_1'(x) = 0$:

which implies that Eq (3.5) has a unique positive solution $P_1^*$. Therefore, we have shown the existence and uniqueness of the internal equilibrium $(H^*_{1}, P^*_{1})$ of subsystem $F_{G_1}$.

Next, we investigate the local stability of $(H_1^*, P^*_1)$. We linearize subsystem $F_{G_1}$ around the positive equilibrium $(H_1^*, P^*_1)$ and construct the Jacobian matrix

The characteristic equation calculated at the internal equilibrium $(H_1^*, P^*_1)$ is given by

where $Trace(\mathcal{J}) = \frac{b}{b+H^*_1}+\frac{\beta H^*_1(b+H^*_1)}{a\exp\alpha}+\gamma$, $Det(\mathcal{J}) = \frac{b\gamma}{b+H^*_1}+\beta H^*_1-\frac{\beta {H^*_1}^2}{a\exp\alpha}$. We see that inequalities (3.2) and (3.3) deduce that $|Trace(\mathcal{J})| < 1+Det(\mathcal{J}) < 2$, and by Jury criteria ^[36], the local asymptotic stability of the internal equilibirum $(H_1^*, P^*_1)$ is obtained. This completes the proof.

We also obtain the existence and stability of the internal equilibrium of subsystem $F_{G_2}$.

Theorem 3.2. If $(1+r)\gamma < 1$, subsystem $F_{G_2}$ contains an internal equilibrium $(H^*_{2}, P^*_{2})$. It is also locally asymptotically stable if the following conditions are satisfied:

and

The proof of Theorem 3.2 is similar to Theorem 3.1 and we choose to omit it.

The above results suggest that parasitoids and hosts can co-exist under some conditions.

4.   Numerical bifurcation analysis

In order to explore the complexity of dynamical behaviors of model (2.5), we perform numerical simulations to show a variety of bifurcation phenomena including one-parameter and multi-parameter bifurcations. The definition and range of parameters are given in Table 1.

Table 1.  Parameters in model (2.5).

Parameters	Definitions	Units	Range	References
$\alpha$	Intrinsic growth rate of hosts	–	[1.5, 3.3]	[37,38]
$\beta$	Searching efficiency of parasitoids	–	[0.01, 3]	[37,38]
$\gamma$	Density-independent survival rate of parasitoids	Day$^{-1}$	[0.01, 0.5]	[39]
$a$	Inherent growth rate of hosts	Day$^{-1}$	[0.2, 1.5]	[40]
$b$	Half-saturation constant	Individual /m$^2$	[0.08, 6]	[40]
$k$	Instantaneous killing rate of hosts	–	[0.1, 0.9]	Assumed
$r$	Proportional release rate of parasitoids	–	[0.1, 0.7]	Assumed
$\tau$	Release rate for parasitoids	Individual/m$^2$	[0.04, 8]	Assumed
$ET$	Control threshold	Individual/m$^2$	[0.01, 4]	Assumed

---

 | Show Table

DownLoad: CSV

4.1.   Equilibrium set for switching system (2.5)

In this subsection, we focus on the set of equilibria for model (2.5) separately in the two different subsystems. First, we refer to the concept of real and virtual equilibria ^[37,41].

Definition 4.1. $E^*(H^*, P^*)$ is a real equilibrium of switching system (2.5) if $E^*$ is an equilibrium of subsystem $F_{G_1}$ (resp. $F_{G_2}$) and $H^* < ET$ (resp. $H^*\geq ET$). Similarly, $E^*$ is a virtual equilibrium if it is an equilibrium of subsystem $F_{G_1}$ (resp. $F_{G_2}$) and $H^*\geq ET$ (resp. $H^* < ET$). In the following, we denote by $E^1_{r}$ (resp. $E^2_r$) the real equilibrium of subsystem $F_{G_1}$ (resp. $F_{G_2}$) and by $E^1_{v}$ (resp. $E^2_v$) the virtual equilibrium of subsystem $F_{G_1}$ (resp. $F_{G_2}$) when they exist.

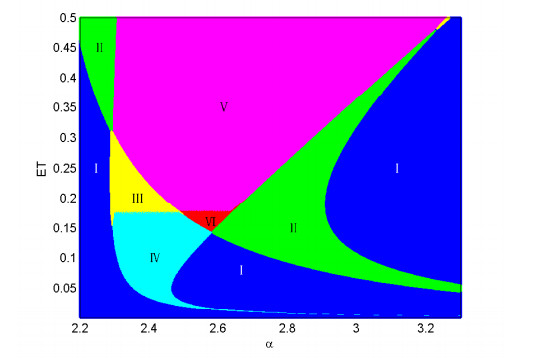
In Figure 1 we choose the intrinsic growth rate $\alpha$ of hosts and $ET$ as bifurcation parameters, and we can divide the parameter space into the following six regions according to the number and classification of equilibria:

Figure 1.  Bifurcation diagram obtained by varying $\alpha$ and $ET$ for the equilibria of model (2.5). The other parameters are $r = 0.54, a = 0.9, b = 6, \tau = 0.9, \gamma = 0.18, k = 0.3, \beta\in[0, 0.5]$.

DownLoad: Full-Size Img PowerPoint

Region Ⅰ (blue): No interior equilibria;

Region Ⅱ (green): Only $E_v^1$ exists;

Region Ⅲ (yellow): Only $E_v^2$ exists;

Region Ⅳ (cyan): Only $E_r^2$ exists;

Region Ⅴ (magenta): $E_v^1$ and $E_v^2$ coexist;

Region Ⅵ (red): $E_v^1$ and $E_r^2$ coexist.

For an optimal pest control, it is necessary to design an effective control to keep the density of pest population below the ET. This requires us to choose the appropriate parameters $\alpha$, $\beta$ and $ET$ such that the internal equilibria of both subsystems $F_{G_1}$ and $F_{G_2}$ become virtual. So the optimal control parameter regions are Ⅱ and Ⅴ in this case.

4.2.   Bifurcation analyses and chaos

In this subsection, we study how relevant control parameters, such as the killing rate $k$ of hosts and the constant releasing rate $\tau$ of parasitoids, affect the dynamics of model (2.5) using numerical simulations.

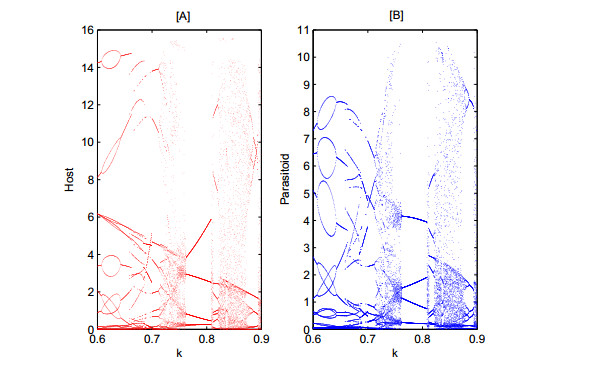
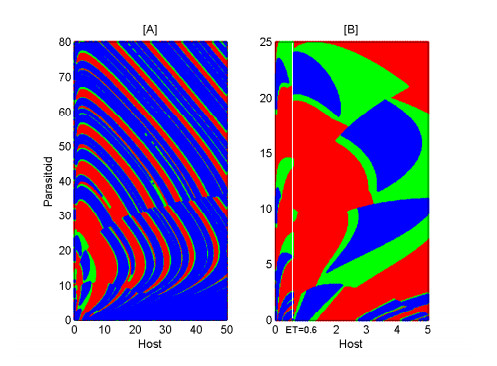
We first choose the killing rate $k$ of the host population as the bifurcation parameter and fix the other parameters as in Figure 2. It turns out that the choice of $k$ is critical to study some more complicated dynamics of system (2.5), especially for $k\in[0.6, 0.9]$. In particular, chaos appears as $k\in [0.715, 0.762], [0.808, 0.814], [0.825, 0.875]$ and $[0.895, 0.9]$. Furthermore, we can observe period-doubling and periodic-halving bifurcations as $k$ increases from 0.6 to 0.65.

Figure 2.  Bifurcation analyses with $k$ as bifurcation parameter. The other parameters are $\alpha = 3.3, \tau = 0.04, \beta = 1, \gamma = 0.08, a = 0.6, b = 0.08, r = 0.7, ET = 2.5$ and $(H_0, P_0) = (3, 2)$.

DownLoad: Full-Size Img PowerPoint

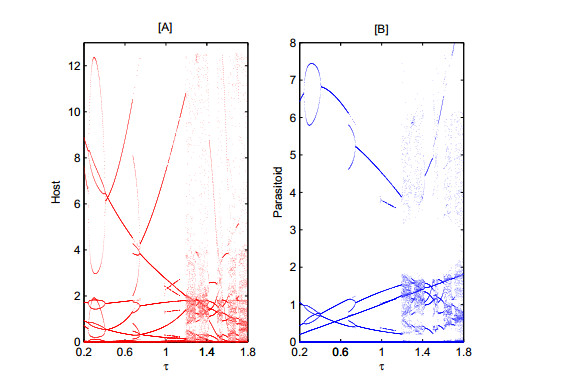
We then study the bifurcation diagram of model (2.5) with respect to the releasing rate $\tau$ of the parasitoid population. As $\tau$ increases from $0.2$ to $1.8$ in Figure 3, the switching host-parasitoid system experiences some complex and interesting phenomena such as periodic-doubling, periodic-adding, periodic-halving and periodic window bifurcations, chaos and so on. The dynamical behavior of model (2.5) is particularly sensitive to $\tau$, which makes it be a relevant pest control parameter.

Figure 3.  Bifurcation analyses with $\tau$ as bifurcation parameter. The other parameters are $\alpha = 3, \beta = 1.45, \gamma = 0.02, a = 1, b = 1.2, r = 0.48, ET = 2, k = 0.9$ and $(H_0, P_0) = (2, 3)$.

DownLoad: Full-Size Img PowerPoint

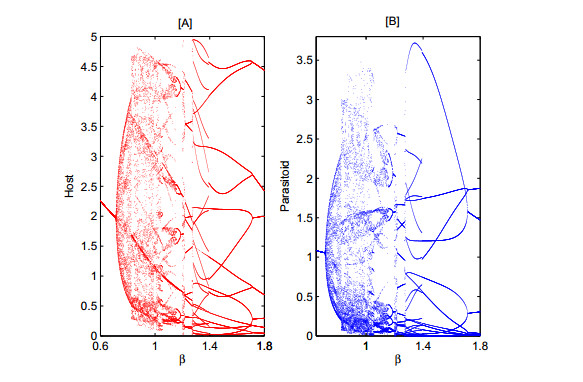
At last, we study the effect of the searching efficiency $\beta$ of the parasitoid population on the dynamics of switching model (2.5). It shows that several complex dynamical behaviours arise also in this case (Figure 4). Addressing these complexities is one of the main challenges for pest control, which requires us to focus on the interaction between host and parasitoid populations, and to design effective control strategies in accordance with IPM's goal.

Figure 4.  Bifurcation analyses with $\beta$ as bifurcation parameter. The other parameters are $\alpha = 1.5, \tau = 1.2, \gamma = 0.01, a = 1.5, b = 1.2, r = 0.1, ET = 4, k = 0.6$ and $(H_0, P_0) = (3, 5)$.

DownLoad: Full-Size Img PowerPoint

5.   Sensitivity analysis of the initial values

Interaction between hosts and parasitoids is a key to limit pest spread and to control the dynamics of both populations. Especially, the final state of model (2.5) is extremely sensitive to initial densities, hence this section we investigate how the initial values affect the switching frequencies, and analyse the cases of coexistence of multiple attractors in the proposed switching system.

5.1.   Switching frequency and control strategy

It is relevant to introduce the following definition of switching frequency ^[37,41].

Definition 5.1. If $(H_t-ET)(H_{t+1}-ET)\leq 0$ and $H_{t+1}\neq ET$ hold, then we say that switching system (2.5) experiences one time switch, where $t$ is a switch-point. An interval between two continuous switch-points is known as the switching frequency.

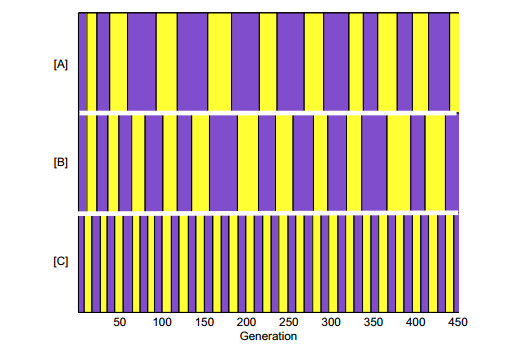
As shown in Figure 5, different initial values can lead to different stable or unstable states for the switching frequencies. That is, Figure 5A, B show unstable switching frequencies, while Figure 5C shows stable ones, and the frequency shown in Figure 5C is higher than the other two.

Figure 5.  Switching frequency of system (2.5) with $(H_0, P_0) = (3.0, 2.5)$, $(3.5, 2.2)$, $(4.0, 3.5)$ from [A] to [C]. Parameters are $a = 1.5, b = 0.2, \beta = 0.16, \tau = 0.9, \gamma = 0.6, k = 0.2, r = 0.2, \alpha = 1.7, ET = 0.8$.

DownLoad: Full-Size Img PowerPoint

We know that switching frequency plays an important role in pest control, since a high switching frequency requires strong control measures which include the use of resources, such as pesticides, labor force, equipments, and so on. However, in the real world, it could be difficult to have all available resources for economical or environmental reasons. Therefore it is necessary to keep everything into account in designing an optimal initial value for pest control.

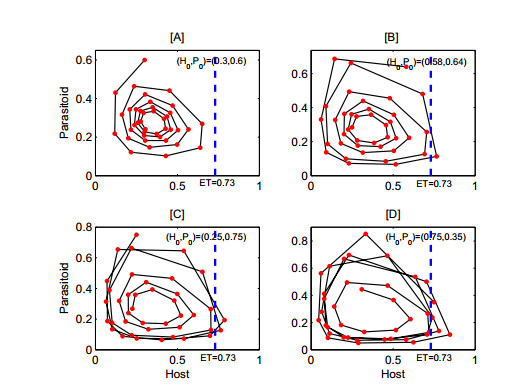
Next, we analyse the phase diagram of host-parasitoid densities for different initial values. For a given threshold $ET$, Figure 6 describes how the dynamics of model (2.5) changes as the initial values do with four different cases. In particular, Figure 6A shows a situation that does not require control strategies, while Figure 6B–D require respectively $1, 2$ and several applications of IPM strategies.

Figure 6.  The relationships between switching frequency and initial value. Parameters are $a = 0.2, b = 0.3, \beta = 3, \tau = 0.2, \gamma = 0.3, k = 0.1, r = 0.1, \alpha = 2$.

DownLoad: Full-Size Img PowerPoint

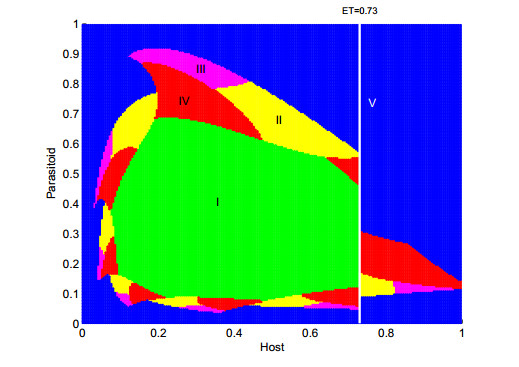
In addition, we discuss how the initial densities affect the pest outbreak frequency. In Figure 7, the initial values of host and parasitoid populations are divided into five regions denoted by Ⅰ (green), Ⅱ (yellow), Ⅲ (magenta), Ⅳ (red) and Ⅴ (blue), which depend on the number of outbreaks that model (2.5) has to face (respectively $0, 1, 2, 3$ and $4$ or more outbreaks). As expected, the choice of initial values in Region Ⅰ is the most favorable for pest control since it does not require any strategy, while initial values in Region Ⅴ can make pest control problematic, even can have a negative economical and environmental impact.

Figure 7.  Basin region for the initial densities of host and parasitoid populations, parameters are identical with those in Figure 6.

DownLoad: Full-Size Img PowerPoint

5.2.   Multiple attractors and their coexistence

We have already discussed multiple attractors and their coexistence in the previous section, so here we focus on how initial densities affect these.

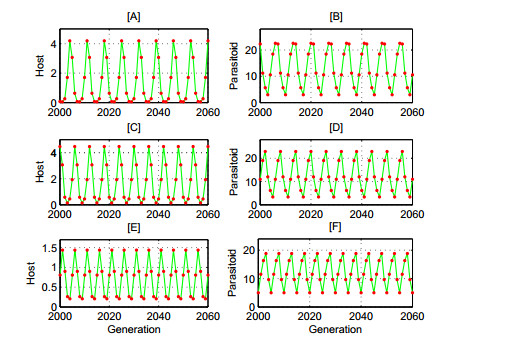
Figure 8 describes three host-outbreak periodic attractors with different amplitudes and periods for three choices of initial values. In particular, the period and amplitude of the host population of the third attractor is smaller, while the amplitude of the parasitoid population is similar in all attractors, but is slightly larger in the second case. In addition, the period is the largest in the first case which is seven generations.

Figure 8.  Three coexisting attractors of system (2.5) with $(H_0, P_0) = (1.5, 3.0)$, $(1.5, 3.5)$, $(1.5, 4.0)$ from top to bottom. Other parameters are $a = 1.5, b = 0.2, \beta = 0.16, \tau = 8, \gamma = 0.5, k = 0.2, r = 0.2, \alpha = 1.6, ET = 0.6$.

DownLoad: Full-Size Img PowerPoint

To further investigate the role of initial values in the dynamics of model (2.5), we study the basin of attraction of these three host-outbreak solutions in Figure 8. The parameter space of initial densities is divided into three regions (blue, green and red) shown in Figure 9, which correspond to the attractors from top to bottom of Figure 8. We see that choices of initial values in the red area may be ideal for pest control since this attractor has a smaller host amplitude than the other two. This study shows that it is necessary to understand the initial values of both hosts and parasitoids for a successful pest control.

Figure 9.  [A] Basin of attraction of the attractors shown in Figure 8; [B] The magnification of [A] around small host-parasitoid initial densities.

DownLoad: Full-Size Img PowerPoint

6.   Discussion

Pest control is an essential task of the agricultural and biological managements, which mainly involves chemical control through pesticide spraying and biological control through natural enemy releasing. In order to find the optimal time and dosage of these control methods, the threshold policy (TP) is introduced in the IPM strategies. Based on this, we propose a novel discrete switching ecosystem with threshold strategy, and do some mathematical, numerical and biological analyses to verify the effectiveness of the model in pest control.

The proposed switching model is highly sensitive to the choice of the threshold value $ET$, since it is the minimum pest density above which the chemical and biological control measures should be applied. The introduction of model (2.5) is consistent with the main purpose of IPM which is to maintain the pest density below the EIL instead of eradicating them completely.

We apply qualitative analysis techniques related to difference equations to study the existence and stability of equilibria for subsystems $F_{G_1}$ and $F_{G_2}$. The existence of a large number of possible equilibria for model (2.5) leads to the possibility of single and multiple-parameter bifurcations and chaos, then we show this complexity of dynamical behaviors of the switching ecosystem (2.5) through some numerical simulations.

Specially, the multi-parameter bifurcation diagram divides the space into regions by number of possible equilibria and their classification, while the single parameter bifurcation diagrams reveal the existence of periodic and chaotic solutions, period-doubling, periodic-halving, periodic window bifurcations, and so on. Both diagrams show how some key control parameters, such as the killing rate $k$ of $H_t$ and the constant releasing rate $\tau$ of $P_t$, affect the dynamics of model (2.5), therefore it is crucial to choose suitable control parameters for pest control.

In general, sensitivity analysis of initial value is a relevant tool to analyse the model numerically. In this paper, we focus on the initial state of host and parasitoid populations, and investigate how initial values affect the switching frequencies and the coexistence of multiple attractors of model (2.5) in Figures 5–9. Therefore, initial densities of host and parasitoid populations are essential for pest control, thus a complete understanding for the initial interaction of both populations would be a key for pest control.

In this paper, we only focus on the importance of threshold and IPM strategies in pest control. however there are several other factors including stochasticity in the environment, residual effects on hosts of pesticides and limited resources that can affect pest control in real life. Therefore it is of great theoretical and practical significance to introduce these factors into pest control model in future studies.

Acknowledgments

The authors would like to express their gratitude to Professor Jianhong Wu for his kind suggestions, and also to the referees for their helpful comments. This work was supported by the National Natural Science Foundation of China (Grant No. 11601268) and the Scientific Research Program Funded by Shaanxi Provincial Education Department(Grant No. 18JK0336).

Conflict of interest

All authors declare no conflicts of interest in this paper.