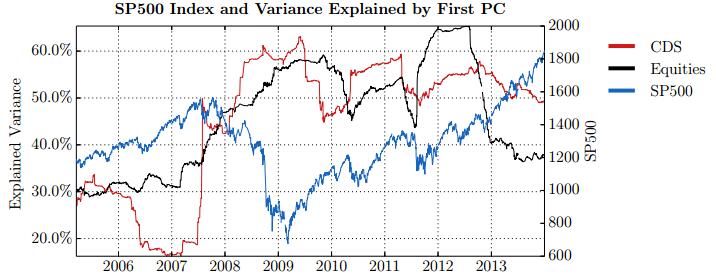
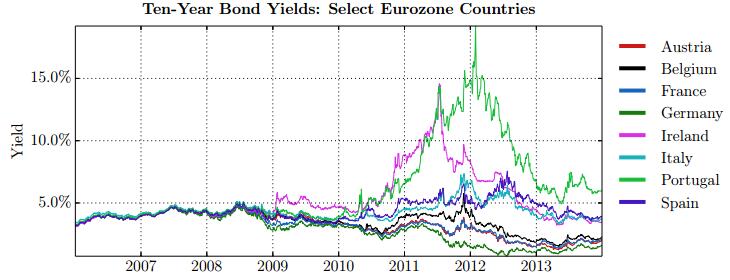
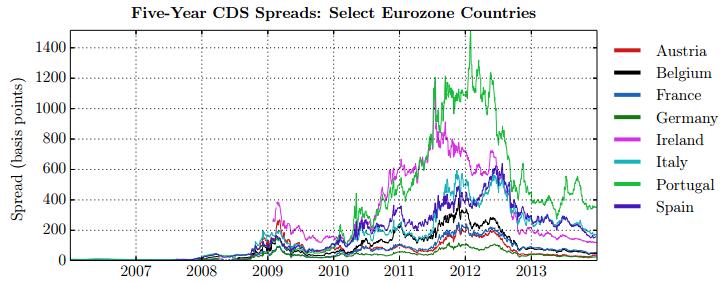
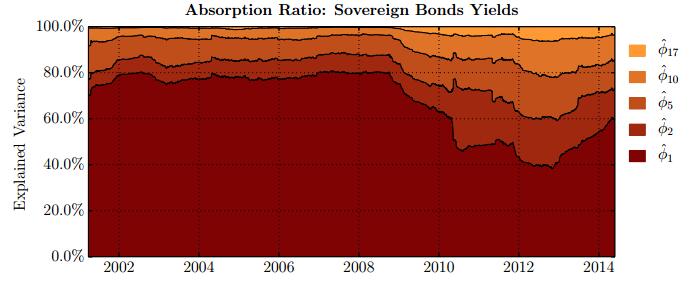
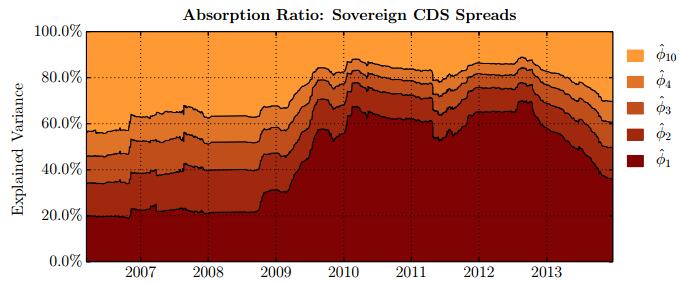
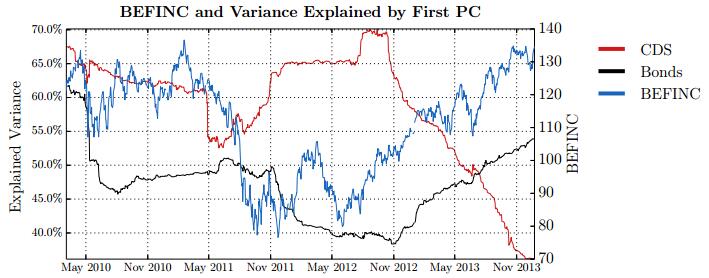
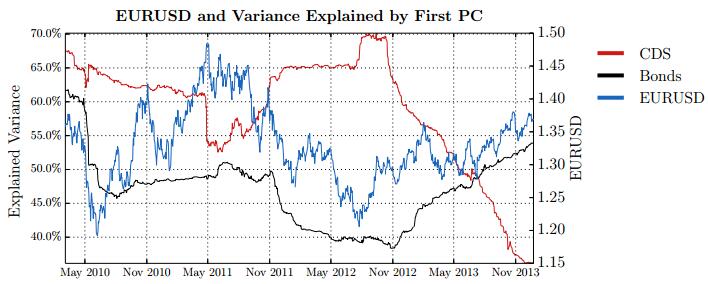
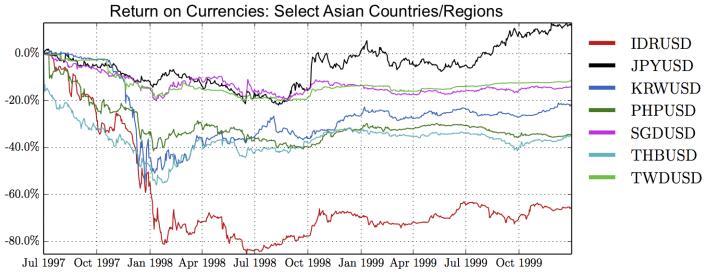
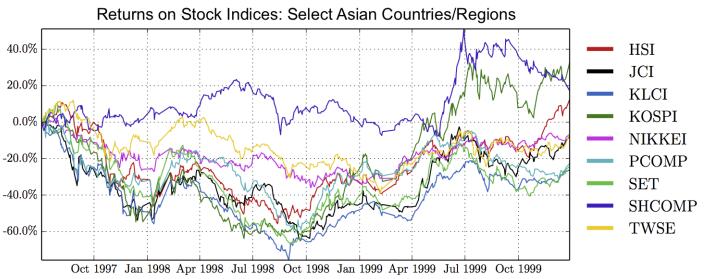
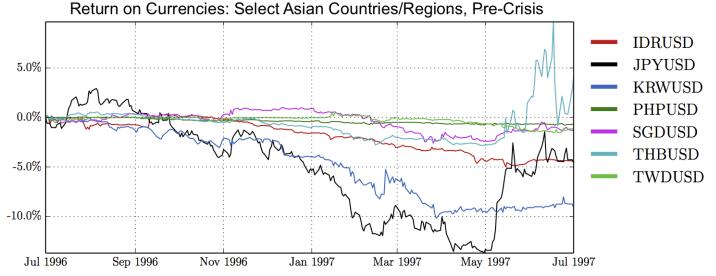
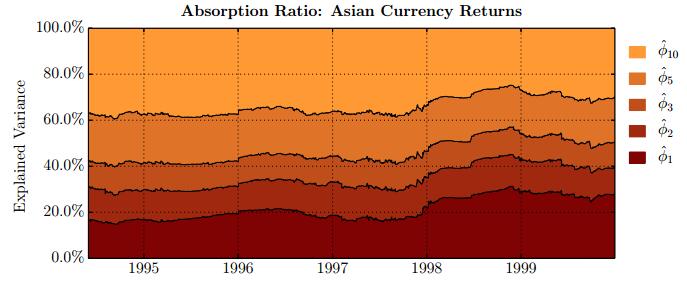
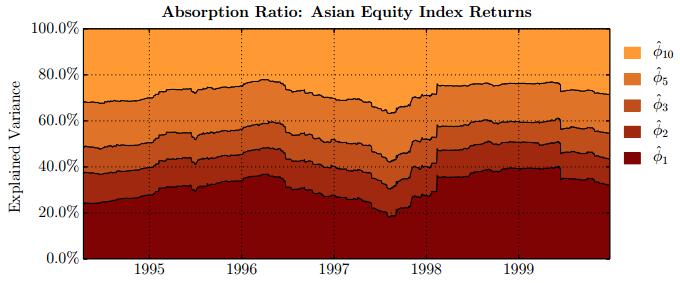
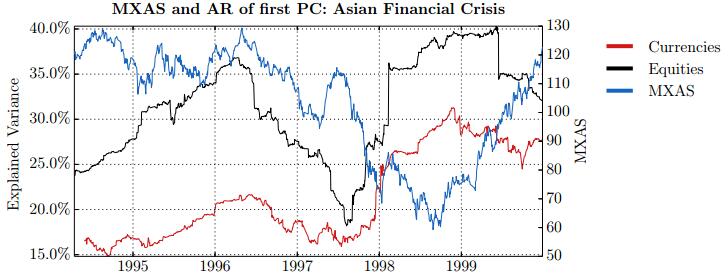
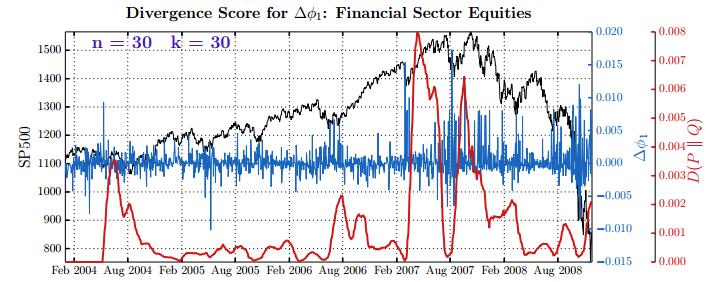
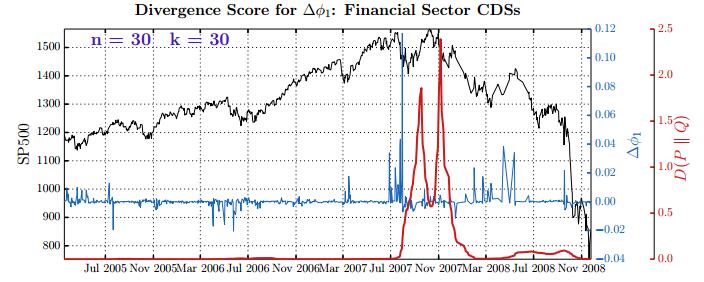
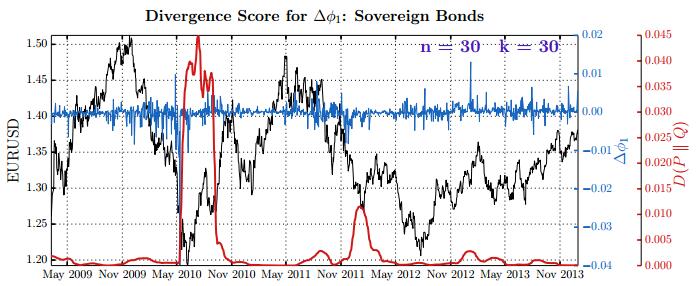
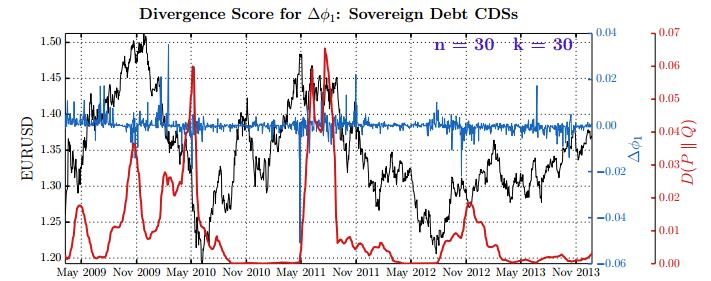
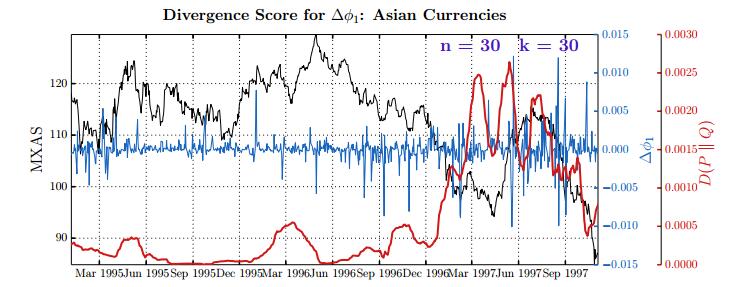
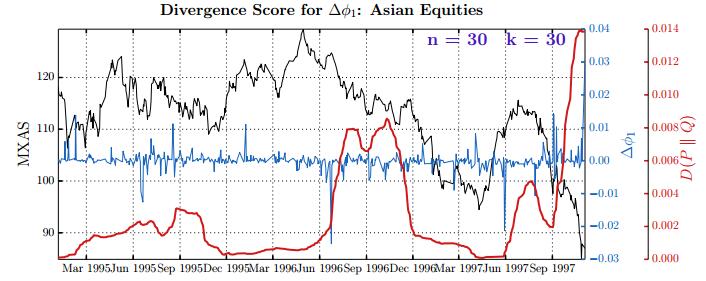
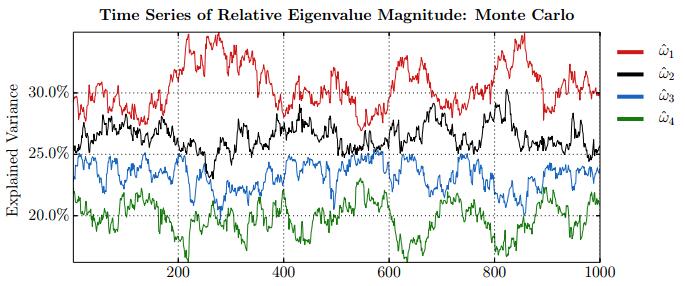
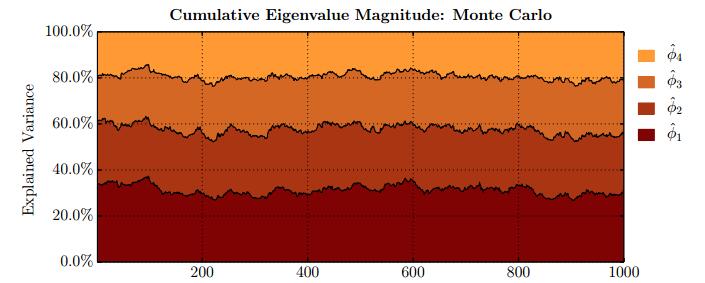
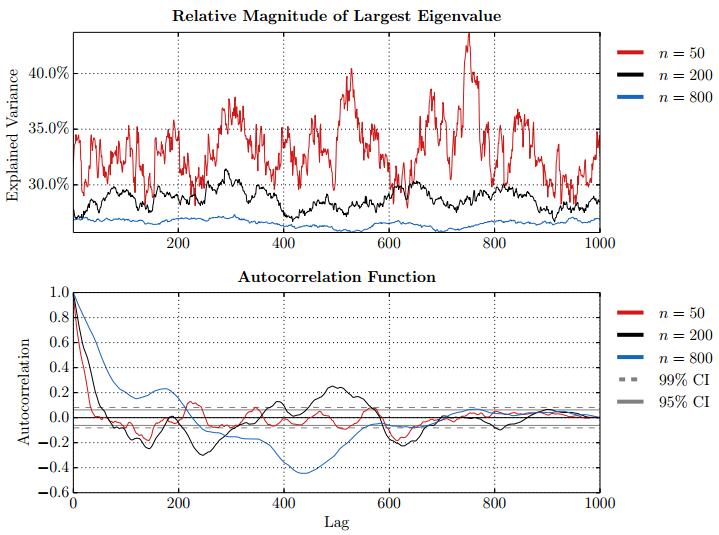
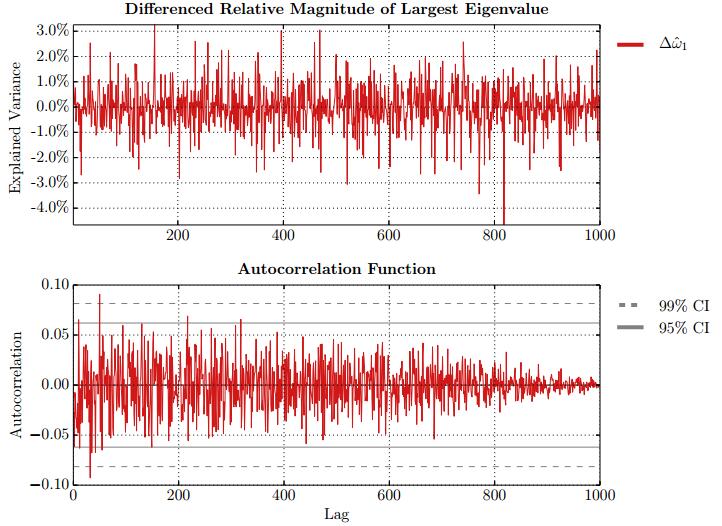
This paper studies association between changes in absorption ratio and aggregate market returns in three systemic crises across a broad class of assets. Time series of normalized eigenvalue estimates reveal that crises are characterized by a general breakdown of correlation structure. The structure of return correlations is nonlinear and nonstationary across di erent asset groups. So we introduce a nonparametric technique to monitor divergence in distributions underlying successive observations of normalized dominant eigenvalue of the returns. Periods of high divergence imply a change in the correlation structure of asset returns. They are found to either precede or coincide with systemic shocks. An additional parametric analysis is provided as an informal check on the results obtained in the paper.
1.
Introduction
In recent years, China has maintained a relatively stable development trend in its highway transportation, with significant improvements in its level of development. As of the end of 2022, the total length of highways in China has approached 5.2 million kilometers, and the mileage of the expressway network has reached 161,000 kilometers [1]. Given the swift advancement of highway construction in China, the country has now entered the phase of highway maintenance [2]. Therefore, it is crucial to timely detect and repair issues on the road surface. Road surface cracks are the most common type of pavement distress. If they can be detected promptly in their early stages and repaired, it not only effectively prevents them from evolving into more severe pavement issues but also extends the lifespan of expressways. Hence, a fast, convenient, and safe road surface crack detection method holds significant importance for road maintenance.
There are many problems in the traditional road crack detection algorithm. For instance, the road mileage is often too extensive, leading to high human resource costs. Human detection involves complex human factors and is not conducive to objectively evaluating road defect detection accuracy, which cannot be guaranteed. Additionally, the traditional manual road detection method is adverse to inspector safety. In recent years, with the rapid development of various new technologies, including computers, target detection, GPS (global position system), digital CCD (charge-coupled device), etc. [3,4,5], computer vision based on deep learning has gained wide acceptance and application in our daily lives. These issues can be addressed by adopting deep learning object detection algorithms. The YOLO (you only look once) series of algorithms is a neural network algorithm used for real-time object detection. Unlike traditional two-stage object detection methods, the YOLO series is a one-stage detector [6]. It directly predicts the position and category of targets through a single feed forward neural network without the need for candidate box generation and filtering steps, resulting in higher detection accuracy and faster inference speed. Currently, there is a substantial amount of research conducted both domestically and internationally on road surface crack detection and recognition using YOLO algorithms.
Researchers such as Park [7] have established a network model that combines segmentation and detection. During the segmentation process, only a part of the road surface is extracted, and road surface damage is detected based on that portion, which improves accuracy but reduces detection efficiency. X. Su [8] used MobileNetv2 as the backbone network for YOLOv4 and replaced conventional convolutions with depth-wise separable convolutions. Furthermore, the backbone and neck components of the original model also embedded coordinate attention processes and spatial attention mechanisms. These attention mechanisms significantly enhance the detection accuracy and speed for road surface cracks, but the model's final mean average precision (mAP) value is relatively low. M. Wang [9] proposed a method that replaces the GIoU (generalized intersection over union) loss function with EIoU (exponential intersection over union), resolving the issue of large GIoU errors while improving convergence speed and regression accuracy. However, the improved model's inference speed has decreased compared to the original model. A comprehensive analysis of the development from YOLOv1 to YOLOv8 is presented by J. R. Terven et al. [10]. The authors conclude that starting from YOLOv5 and moving onward, all official YOLO models have been fine-tuned to strike a balance between speed and accuracy, aiming to better adapt to specific applications and hardware requirements [11]. Classic YOLOv5 employs a simple convolutional neural network (CNN) architecture, while the latest YOLOv8 employs a more complex network structure comprising multiple residual units and branches [12]. Consequently, YOLOv5's detection accuracy is not on par with that of YOLOv8 when processing road crack images. Although YOLOv8 enhances the model's structure and training effectiveness, it sacrifices detection speed and has a larger parameter count. Therefore, YOLOv5 has been selected for improvement.
These aforementioned detection models each have their advantages and disadvantages, and cannot achieve a balance between detection accuracy and speed, limiting their practical application in engineering [8]. To achieve efficient and accurate road surface crack recognition, this paper introduces a road surface crack detection model that combines attention mechanisms. The main contributions of this paper can be summarized as follows:
1) Based on the Res2Net (a new multi-scale backbone architecture) network, an improved multi-scale Res2-C3 (a new multi-scale backbone architecture of C3) module is suggested to enhance the feature extraction performance.
2) The feature fusion network and backbone of YOLOv5 are combined with the GAM (global attention mechanism) attention mechanism to enhance the model's ability to perceive fracture information.
3) Integrating dynamic serpentine convolution into the feature fusion network, the improved network enhances the model's ability to address irregular shape and deformation problems, which is beneficial for improving the accuracy of road crack identification.
2.
Improvement of the YOLOv5s model
2.1. Model overall structure
YOLOv5s is a variant of the YOLOv5 series, which is an object detection deep learning algorithm. Compared to other versions of YOLOv5, YOLOv5s is a lightweight model that preserves strong detection performance while decreasing the model's size and computational complexity. The YOLOv5s algorithm network structure consists of the head, neck, and backbone. CSPDarknet53 (cross stage paritial network) serves as the backbone network for YOLOv5s and it effectively extracts image features. Using feature maps with multi-scale information created by combining feature maps from various levels, the neck network integrates these feature maps with the features produced by the backbone network to increase object detection accuracy [13]. The head network is responsible for the final detection steps, constructing a neural network that determines the bounding box positions and recognition types, forming the ultimate output vector 2. Figure 1 represents the improved YOLOv5s network structure.
2.2. Enhancing the multi-scale C3 structure
2.2.1. C3 module
As seen in Figure 2, the C3 module, which consists of two parallel branches, is the central component of the backbone network. After going through one of the branches' Conv modules, the input feature map is stacked with n bottleneck modules to extract high-level semantic information [14]. The output of the other branch, after passing through a Conv layer, is concatenated with the output of the first branch. Subsequently, feature fusion is performed through another Conv layer before the final output.
The C3 module of YOLOv5s mainly leverages the idea of extracting diversion using the CSPNet [15] and combines the concept of residual structures. It is designed with C3Block, and the bottleNeck module is the CSPNet main branch gradient module. The number of stacked modules is influenced by the parameter 'n', and the value of 'n' changes with the model's size. The bottleneck module is integrated multiple times within the C3 module, to capture higher-level semantic information from the image.
2.2.2. Res2-C3 module
Drawing inspiration from the design concepts of VGG (visual geometry group) [16], GoogleNet [17], and CSPNet [15], the C3 module processes input information through two branches. One branch stacks n bottleneck structures to extract high-level semantic features, while the other branch maintains the original image features through a shortcut connection of the Conv module. Finally, two parallel convolution branches are used to merge the image features, enhancing the feature information within the image. Therefore, the core of feature extraction lies in the design of the bottleneck structure.
In order to improve the model's capacity to extract feature information [18] and acquire richer feature information, deeper network architectures or a higher number of convolutional kernels are frequently used. A Res2-Bottleneck module is proposed by merging the bottleneck structure with the Res2Net module in order to improve the model's feature information extraction capability [19]. The primary idea is to decompose the feature maps from the 3 × 3 convolution layer in the original residual convolution, which receives feature maps from the 1 × 1 convolution layer of the input, into four parts [20]. The first part remains unchanged, the second part passes through a 3 × 3 convolution layer, the third part adds its features to those of the second part before passing through another 3 × 3 convolution layer, and the fourth part adds its features to those of the third part before passing through another 3 × 3 convolution layer. The parallel technique improves the model's capacity to extract characteristics across several scales. In the end, the feature maps from these four parts are concatenated to form feature maps with the same number of layers as the input layer, and are then sent to the output layer for 1 × 1 convolution to perform feature fusion. This structure is referred to as the enhanced multi-scale bottleneck (Res2-Bottleneck), as shown in Figure 3. The Res2-Bottleneck not only increases the multi-scale feature information, but also maximally preserves the original feature information through the residual structure, reducing the loss of shallow features. As a result, more information about pavement cracks may be stored, which is highly advantageous for raising the model's detection accuracy.
In the original C3 module, one branch performs feature extraction by stacking multiple bottleneck modules. To improve the feature extraction performance, the original bottleneck structure is replaced with the improved Res2-Bottleneck structure, resulting in the improved Res2-C3 module, as shown in Figure 4.
2.2.3. Multi-scale extraction module C3-RFEM
The C3 module is the heart of the YOLOv5 backbone network, and the bottleneck structure's design is essential to the C3 module. Building upon the bottleneck structure, the multi-scale extraction module C3-RFEM (receptive field enhancement module) is proposed based on the RFE (receptive field enhancement) module [21]. The main principle of the RFE module is to use four different scale expansion convolution branches to capture multi-scale information and different receptive ranges. These branches share weights, with the only difference being their receptive fields. This approach reduces model parameters and potential overfitting risks. Additionally, it allows for operations of different sizes, making full use of each feature's information. The RFE module can be divided into two parts: one is the multi-branch based on expansion convolution, and the other is the weighted layer, as shown in Figure 5. The multi-branch part uses different expansion convolutions with rates 1, 2, and 3; all these convolutions, however, employ a fixed 3 × 3 convolution kernel size. Residual connections are employed to prevent gradient explosion and vanishing during training. This structure can improve the model's detection accuracy and lessen feature loss during feature extraction.
Replacing the original bottleneck module with the RFE module results in C3RFEM, as illustrated in Figure 6. To ensure that the improved model exhibits better performance, comparative experiments are conducted between the C3RFEM module, which extracts multi-scale feature information based on the RFE module and the Res2-C3 module. This comparison aims to select a model with higher accuracy and faster speed.
2.3. Adaptive mechanism
The attention mechanism enables the model to selectively concentrate more on target information [22]. Separating the relevance of several channels and using it as a focus is the fundamental component of channel attention, thus weakening the role of uninterested channels. Hybrid attention combines channel attention with spatial attention, with these two parts being consecutive or parallel, forming an attention model for channel features and spatial features.
The SE (squeeze and excitation) [23] attention module is a channel attention module that enhances channel features in input feature maps. However, the SE attention mechanism neglects spatial information, failing to comprehensively extract the feature map information. CBAM (convolutional block attention module) [24] is a spatial attention mechanism that effectively overcomes the shortcomings of SE by utilizing channel information while considering spatial information. However, the CBAM attention mechanism loses cross-dimensional information by ignoring the relationship between channels and space. Recognizing the significance of interactions across dimensions, the GAM [25] attention mechanism is employed, which can lessen information dispersion and enhance global dimensions interaction features.
Though their approaches to channel attention and spatial attention are different, overall, the GAM and CBAM attention mechanisms are comparable. Figure 7 shows the full process, with Mc and Ms standing for channel attention maps and spatial attention maps, respectively.
Three-dimensional arrangements are used by the channel attention sub-module (CAM) to store information in three dimensions. Subsequently, a two-layer multilayer perceptron (MLP) is utilized to enhance the cross-dimensional interdependence across spatial channels. The channel attention sub-module is shown in Figure 8, where the input feature map undergoes dimension transformation, and the transformed feature map is processed through the MLP to restore its original dimensions, resulting in a Sigmoid output.
Two convolutional layers are employed for spatial information fusion in the spatial attention sub-module (SAM) in order to pay attention to spatial input [26]. For SAM, similar to the SE attention mechanism, it first reduces the quantity of channels before increasing them. A SAM is depicted in Figure 9, where channel reduction is achieved by a convolutional kernel with a size of 7, reducing computational load, followed by a convolution operation with a 7-sized kernel to boost the number of channels while preserving channel count consistency. Finally, a Sigmoid output is obtained.
2.4. Incorporate dynamic snake convolution
The receptive field of the traditional convolutional kernel is regular, but the shape of road cracks is irregular, causing some receptive fields not to be on the target. Additionally, the receptive field size of the convolutional kernel is fixed, but the size and extent of road cracks vary. If the target is too large, only local features can be extracted, and if the target is too small, interference from irrelevant information occurs. To address the limitation of traditional convolution in effectively adapting to geometric changes in objects, which makes it difficult to recognize objects undergoing rotation, symmetry, and scaling, dynamic snake convolution can be employed [27].
Inspired by deformable convolution [28], the model, in the process of learning features, obtains dynamic snake convolution by changing the shape of the convolutional kernel. Deformable convolution predicts offsets for sampling points, adaptively changes the sampling positions, and focuses on semantic feature points and geometric keypoints of the target. The sampling process of the convolutional kernel is illustrated in Figure 10. The input image first passes through the convolutional branch to calculate the offset. The output feature map has the same size as the input image, with dimensions of 2N. Then, based on the offset, the adaptive sampling points of the backbone network are obtained. Next, using bilinear interpolation, the feature values of the sampling points are obtained. However, the learning of the offset for sampling points is highly free, which may lead to positions far from the target. Moreover, each sampling point has the same weight for the output, and poor-quality sampling points can interfere with feature extraction. Dynamic snake convolution introduces continuity constraints into the design of the convolutional kernel. Each convolutional position is based on its previous position as a reference, freely choosing the oscillation direction and ensuring continuity of perception while allowing for free selection. This enables the convolutional kernel to fit structures and learn features freely on one hand, and on the other hand, it ensures that the convolutional kernel does not deviate too far from the target structure under constraint conditions. By adding dynamic snake convolution to the feature fusion network section of YOLOv5s, the improved network enhances the model's ability to handle irregular shapes and deformation problems. The adaptive changes in the receptive field size based on the target size are beneficial for improving the accuracy of road crack recognition.
3.
Experimental data
3.1. Dataset introduction
The data collection device for the experiment is a multipurpose road inspection vehicle. On the inspection vehicle, there are two cameras arranged in parallel for capturing road information. The images are processed in grayscale to reduce the original data volume and enhance image information. There are 3000 pictures in the dataset that were utilized for this experiment. Training, validation, and test sets of these photos are split into 8:1:1 ratios at random. A portion of the photos is used as the test set, a portion as the validation set, and a portion as the training set. The dataset's pictures used in the experiment are in JPG format with a size of 500 × 500 pixels.
3.2. Experimental environment
The experiments in this paper's software environment are built using PyTorch 1.8.0, a deep learning framework. It utilizes the GPU (graphics processing unit) of the NVIDIA GeForce RTX 3060 model for accelerated processing. The code is written in Python version 3.8, and it runs on the Windows 10 operating system. The hardware includes an Intel Xeon W-3225 processor, and the acceleration library is CUDA 10.0. There shall be 200 training batches in all [29], and the batch size is configured as 8. The weight file used is YOLOv5s.pt, with an initial learning rate of 0.001, a momentum of 0.9, a weight decay rate of 0.0005, and label smoothing set to 0.1.
4.
Experimental results and analysis
4.1. Evaluation metrics
The mAP, recall (R), frames per second (FPS), and computational complexity are frequently employed in deep learning to assess the efficacy of models. These are their formulas:
where: TP represents the number of true positive detections of positive samples; FP represents the number of false detections of negative samples; TN represents the number of false detections of positive samples; and FN represents the number of true negative detections of negative samples.
mAP, which is the average of average precision (AP), is a key metric for object detection algorithms [30]. In object detection models, a higher mAP indicates better detection results on a specific dataset. FPS, which gauges the model detection speed, is employed to evaluate the fracture detection speed; a higher FPS value indicates faster detection and better model performance. The computational complexity of a convolutional neural network model is represented by the number of floating-point operations, known as FLOPs. FLOPs are used as an indirect measure of the speed of neural network models. A smaller FLOPs value indicates lower model complexity and faster target recognition and is calculated as follows:
where: Cin represents the number of input channels; K represents the convolutional kernel size; HW represents the size of the output feature map; and Cout represents the number of output feature map channels [31].
4.2. Comparative experiments
To illustrate the appropriateness and efficacy of selecting the Res2-C3 module as a multi-scale extraction module, a horizontal comparison of the performance of Res2-C3 and C3RFEM as multi-scale feature extraction modules is presented. The outcomes of the comparative experiments are displayed in Table 1.
Table 1 illustrates how the Res2-C3 module model strikes a balance between speed and accuracy of detection. Regarding detection accuracy, compared to the original model and the model using the C3RFEM module, the model using the Res2-C3 module improved mAP by 5.9 and 2.4%, respectively. The model with the Res2-C3 module reduced the risk of overfitting because of a decrease in parameters, but it also exhibited a modest decrease in FPS when compared to the original model in terms of detecting speed. In comparison to the model using the C3RFEM module, the FPS increased by 11.852 frames/s, significantly improving the detection speed. Therefore, the Res2-C3 module was chosen as the multi-scale module for the final improved model.
4.3. Ablation experiments
To fully validate the effectiveness of the proposed improvements in this paper, ablation experiments were conducted on the road crack dataset. The label smoothing for all models was set to 0.1 to prevent model overfitting. Each improvement module was embedded into the YOLOv5s model one by one, and the same training parameters and environmental conditions were used in each experiment. Table 2 displays the outcomes of the experiment. In terms of detection accuracy, the model with the highest mAP is the YOLOv5s+Res2-C3+GAM+DSConv model, which improved mAP by 10.1% compared to the YOLOv5s model. When Res2-C3, GAM, and DSConv (dynamic snake convolution) act individually, the highest mAP value is achieved by the YOLOv5s+Res2-C3 model, with an mAP value of 89.7%, which is 5.9% higher than the YOLOv5s model. This indicates that by stacking numerous bottleneck modules, the Res2-C3 module improves the model's feature extraction capabilities and enhances the road fracture detection accuracy. When any two modules are combined, the model's detection accuracy is improved to varying degrees. This suggests the possibility of a synergistic effect between the modules where they complement and enhance each other's capabilities, contributing to improved accuracy and robustness.
In terms of the detection speed, FPS represents the model's speed in terms of detection speed, with higher FPS indicating faster detection. According to the experimental results, the fastest detection model is YOLOv5s, with the FPS value as 72.324. Compared to the original model, all improved models experienced a decrease in detection speed. Among these, the largest decrease in detection speed was observed in the YOLOv5s+Res2-C3+GAM+DSConv model with an FPS value of 49.97 FPS. This is mainly because obtaining more feature information leads to an increase in the model's parameter count. The model requires more computations and weight updates, which increases the time cost of training and reduces detection speed.
In terms of recall rate, the best-performing model is the YOLOv5s+Res2-C3+GAM+DSConv model, achieving a recall rate of 87.1%, which is a 10.5% improvement over the original model.
In summary, through the comparison of multiple indicators, the improved YOLOv5s+Res2-C3+GAM+DSConv model performs the best, with a 12.6% increase in AP for road crack detection and a 10.1% increase in mAP. Since the final improvement model adds three modules relative to the YOLOv5s network, the complexity of the model increases, and it is reasonable that the speed will decrease. The final improved model strikes a balance between mAP and FPS, maintaining high accuracy while achieving relatively fast speed.
4.4. Model Comparison
Tests were conducted on the YOLOv5s and the final improved model on the above-mentioned dataset, and their various parameters were compared with the newer YOLOv7 and YOLOv8 networks. Table 3 shows that, compared to other networks, the final improved model YOLOv5s+Res2-C3+GAM+DSConv has better parameters in terms of mAP and AP.
Compared to YOLOv7 and YOLOv8, YOLOv5 has the lowest accuracy, with mAP values for YOLOv7 and YOLOv8 models being 5.3 and 8.6% higher than YOLOv5, respectively. However, YOLOv8's FPS significantly decreases, leading to slower detection speed. Due to the larger model parameters and more complex network structures of YOLOv7 and YOLOv8, the detection speed becomes slower.
Compared to YOLOv7 and YOLOv8 models, the final improved model YOLOv5s+Res2-C3+GAM+DSConv has the highest detection accuracy, with mAP values 4.8 and 1.5% higher than the YOLOv7 and YOLOv8 models, respectively. In terms of detection speed, the YOLOv5s+Res2-C3+GAM+DSConv model has an FPS value only 0.509 FPS lower than YOLOv8. Although the YOLOv5s+Res2-C3+GAM+DSConv model exhibits a slight decrease in detection speed compared to YOLOv8, it achieves a 2.7% increase in detection accuracy over YOLOv8. Overall, the YOLOv5s+Res2-C3+GAM+DSConv model strikes a balance between detection accuracy and speed.
4.5. Analysis of detection results
The enhanced model's detection results are shown in Figure 11. The numbers represent confidence scores, indicating the model's confidence level in its predictions. High confidence scores indicate that the model is very confident in its predictions, while low confidence scores indicate that the model is less certain about the results [32]. From the detection results of road cracks in the images, it is evident that not only were small cracks successfully detected, but these cracks also exhibited relatively high confidence scores. This observation strongly validates the feasibility and effectiveness of the improved algorithm, demonstrating its outstanding performance in crack detection tasks and providing robust support for road maintenance and safety.
5.
Conclusions
In reaction to the shortcomings of conventional techniques for detecting road cracks, such as their poor speed and low accuracy, this paper proposes a method to improve the YOLOv5s model. The method involves using the proposed Res2-C3 module as the core of the backbone network to replace the original C3 module, enabling the extraction of more feature information from input images to reduce the omission of valuable information and increase detection accuracy. Furthermore, the GAM attention mechanism is added to both the YOLOv5s backbone network and the feature fusion network to increase the model's focus on crack information and reduce the false-negative rate for small cracks. Adding dynamic snake convolution to the feature fusion network enables the model's receptive field to adaptively change with the size of road cracks, which is advantageous for improving the accuracy of road crack detection. The paper also introduces label smoothing, setting the label smoothing value to 0.1, to enhance the model's generalization. This model achieves a balance between detection accuracy and speed while controlling the model's parameter size.
To enhance the model's accuracy and robustness, future research should consider collecting more samples of different types of road cracks and using data augmentation techniques to increase dataset diversity. Furthermore, considering real-time road crack detection and application on mobile devices would enhance the algorithm's practicality.
Use of AI tools declaration
The author declares they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported in part by the Shandong Provincial Department of Science and Technology Research Project on Key Technologies for the Development of All-Terrain Intelligent Orchard Platform. (2019GNC106032).
Conflict of interest
The author declares there is no conflict of interest.










 DownLoad:
DownLoad: